Machine Learning Recognition and Phase Velocity Estimation of Atmospheric Gravity Waves from OI 557.7 nm All-Sky Airglow Images
Abstract
1. Introduction
2. Methodology
2.1. Instrumentation
2.2. Data Preparation
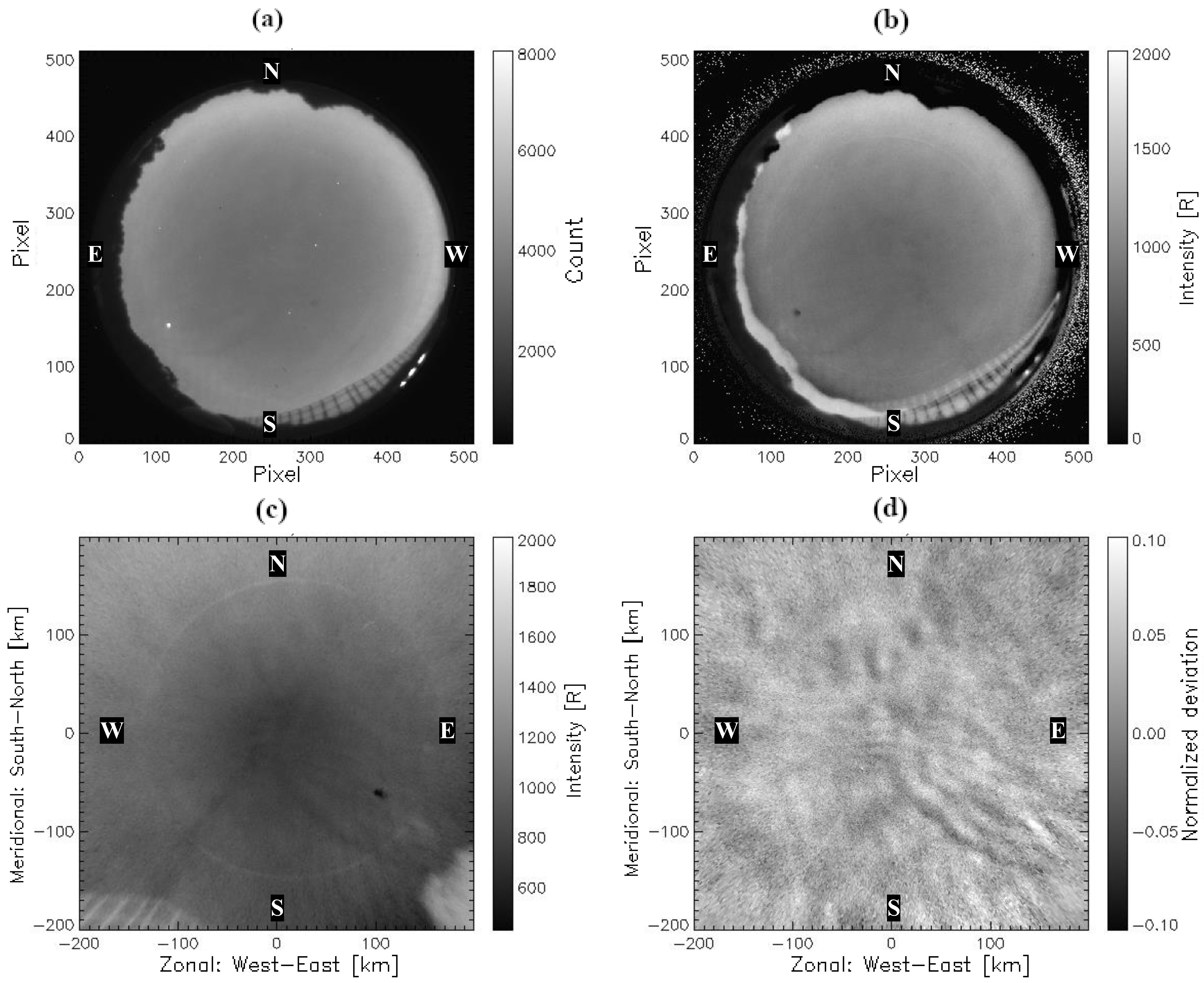
2.2.1. Image Extraction
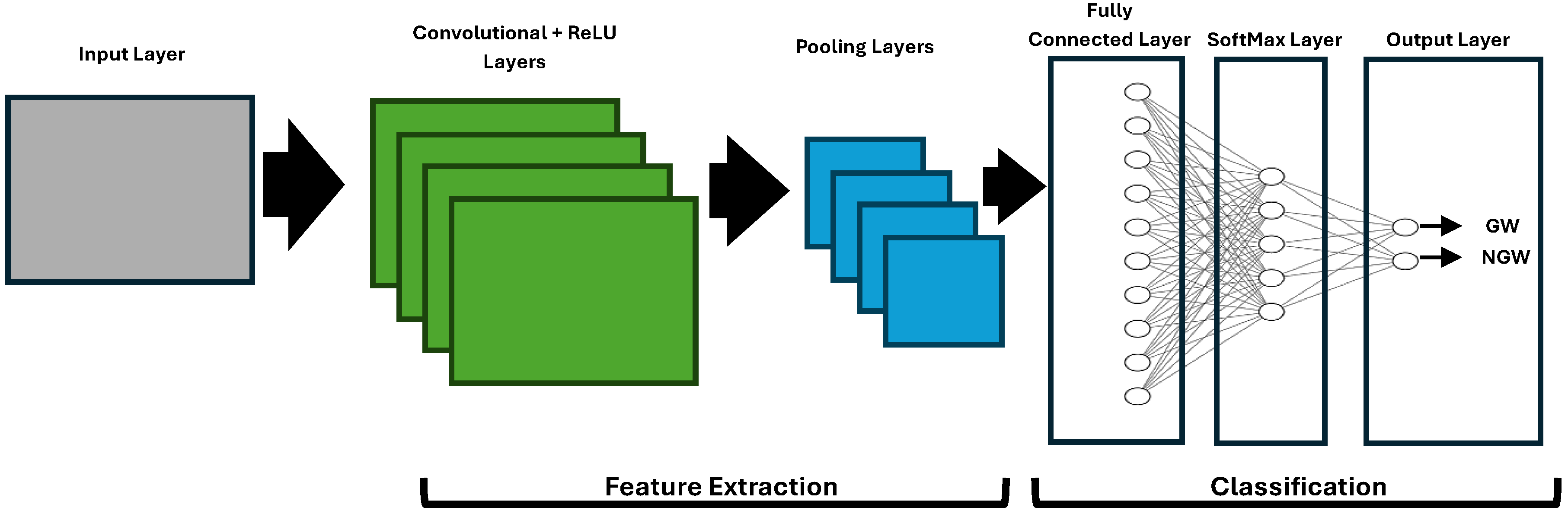
2.2.2. Image Classification
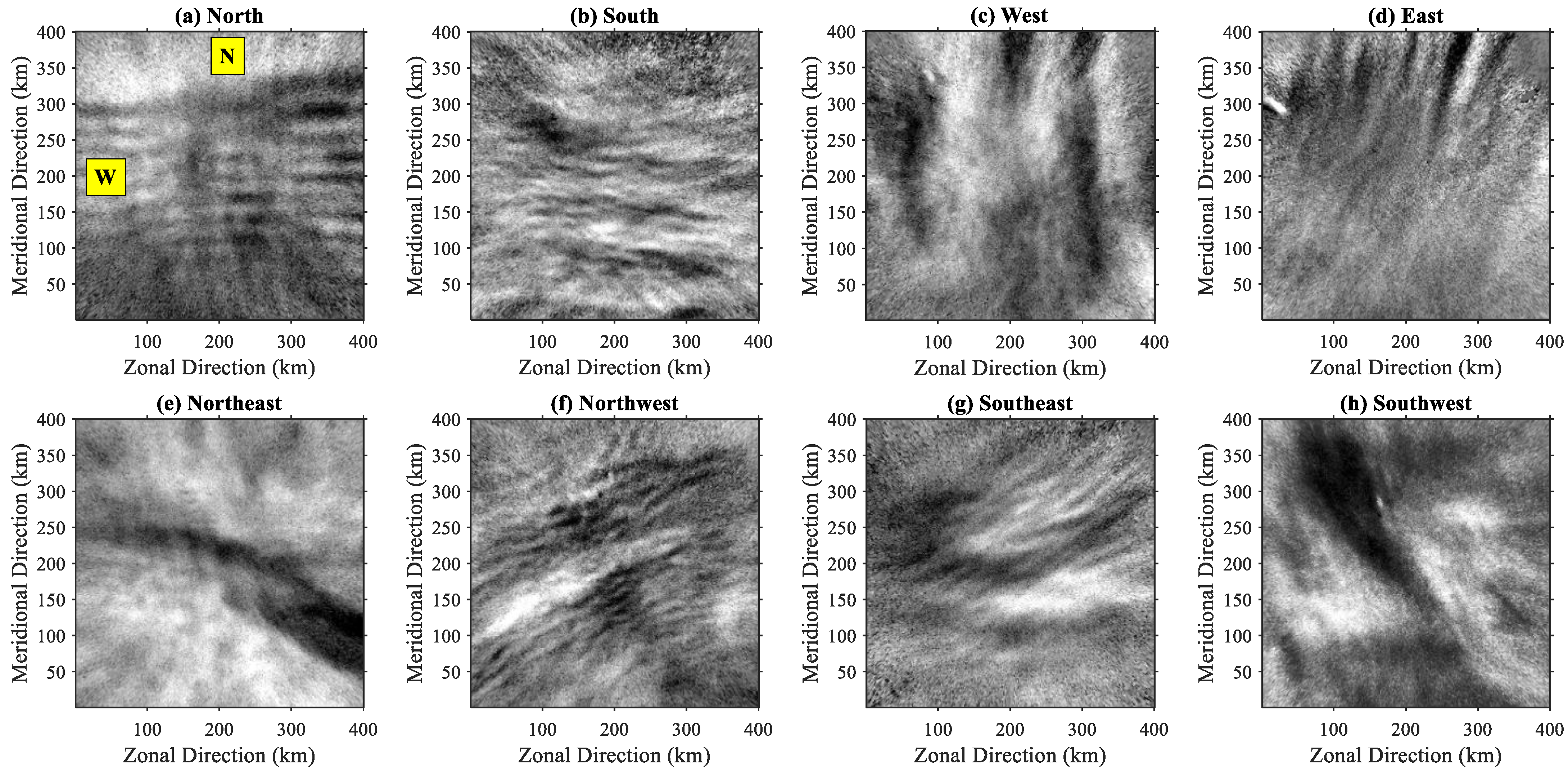
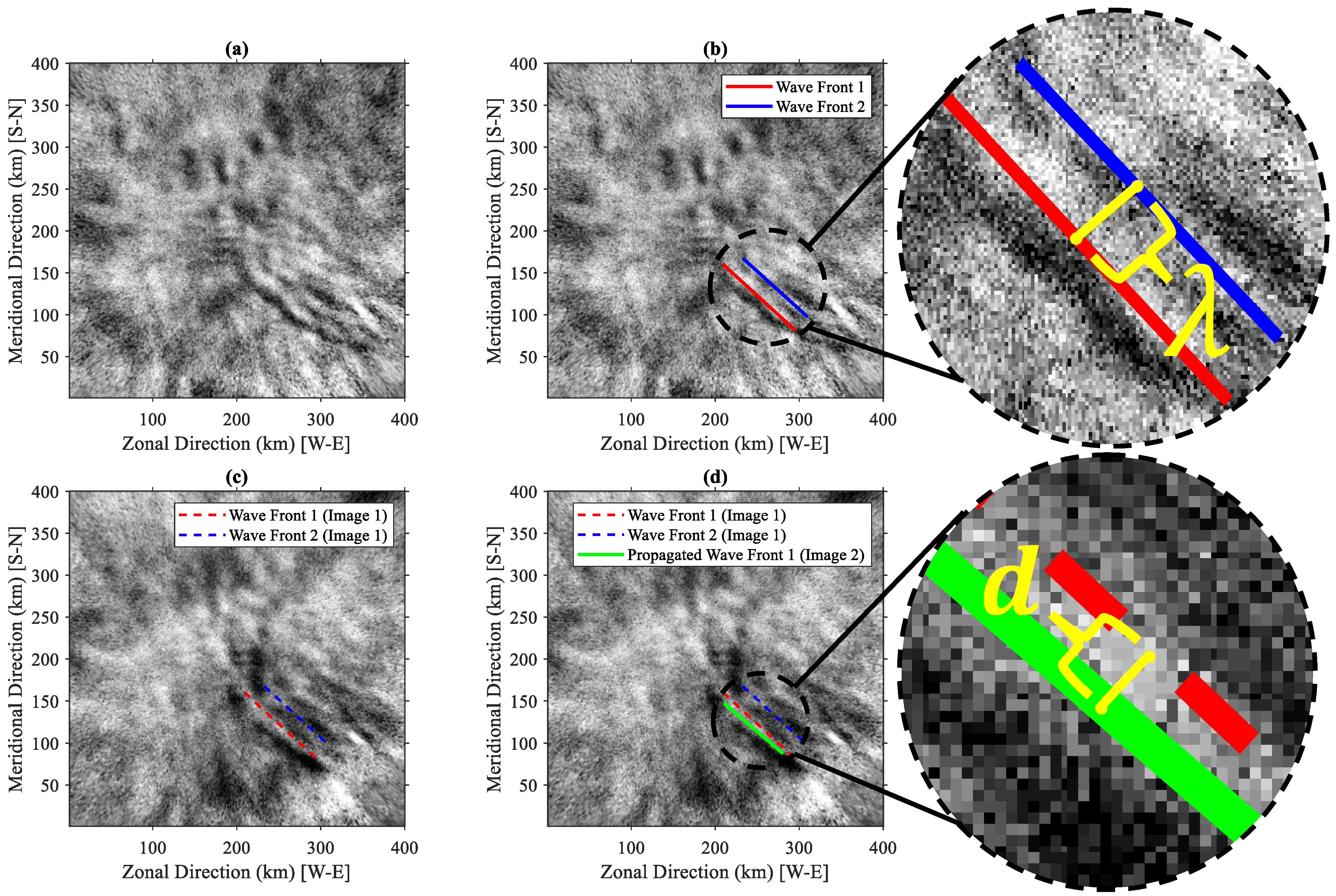
2.3. Atmospheric Gravity Wave Analysis
2.4. Cascade Forward Neural Network
2.5. Physics-Guided Database
3. Results and Discussion
3.1. Convolutional Neural Network Classification
3.2. Cascade Forward Neural Network Regression
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AGW | Atmospheric Gravity Waves |
| ASAI | All-Sky Airglow Imager |
| CFNN | Cascade Forward Neural Network |
| CCD | Charged Coupled Device |
| CNN | Convolutional Neural Network |
| DL | Deep Learning |
| DOY | Day of Year |
| FFNN | Feed-Forward Neural Network |
| HPSE | Horizontal Phase Speed Estimated |
| HPSO | Horizontal Phase Speed Observed |
| HWM | Horizontal Wind Model |
| LT | Local Time |
| ML | Machine Learning |
| MU Radar | Medium and Upper Atmosphere Radar |
| NN | Neural Network |
| OAI | Optical Airglow Imager |
| OMTI | Optical Mesosphere Thermosphere Imagers |
| UT | Universal Time |
References
- Hines, C.O. Internal Atmospheric Gravity Waves at Ionospheric Heights. Can. J. Phys. 1960, 38, 1441–1481. [Google Scholar] [CrossRef]
- Hecht, J.H.; Walterscheid, R.L.; Vincent, R.A. Airglow Observations of Dynamical (Wind Shear-induced) Instabilities over Adelaide, Australia, Associated with Atmospheric Gravity Waves. J. Geophys. Res. Atmos. 2001, 106, 28189–28197. [Google Scholar] [CrossRef]
- Taylor, M.J.; Ryan, E.H.; Tuan, T.F.; Edwards, R. Evidence of Preferential Directions for Gravity Wave Propagation Due to Wind Filtering in the Middle Atmosphere. J. Geophys. Res. Space Phys. 1993, 98, 6047–6057. [Google Scholar] [CrossRef]
- Lindzen, R.S. Turbulence and Stress Owing to Gravity Wave and Tidal Breakdown. J. Geophys. Res. Oceans 1981, 86, 9707–9714. [Google Scholar] [CrossRef]
- Fritts, D.C. Shear Excitation of Atmospheric Gravity Waves. J. Atmos. Sci. 1982, 39, 1936–1952. [Google Scholar] [CrossRef]
- Fritts, D.C. Gravity Wave Saturation in the Middle Atmosphere: A Review of Theory and Observations. Rev. Geophys. 1984, 22, 275–308. [Google Scholar] [CrossRef]
- Taylor, M.J. A review of advances in imaging techniques for measuring short period gravity waves in the mesosphere and lower thermosphere. Adv. Space Res. 1997, 19, 667–676. [Google Scholar] [CrossRef]
- Fritts, D.C.; Alexander, M.J. Gravity Wave Dynamics and Effects in the Middle Atmosphere. Rev. Geophys. 2003, 41, 1003. [Google Scholar] [CrossRef]
- Krichen, M. Convolutional Neural Networks: A Survey. Computers 2023, 12, 151. [Google Scholar] [CrossRef]
- Warsito, B.; Santoso, R.; Suparti; Yasin, H. Cascade Forward Neural Network for Time Series Prediction. J. Phys. Conf. Ser. 2018, 1025, 012097. [Google Scholar] [CrossRef]
- Ejiri, M.K.; Shiokawa, K.; Ogawa, T.; Igarashi, K.; Nakamura, T.; Tsuda, T. Statistical Study of Short-Period Gravity Waves on OH and OI Nightglow Images at Two Separated Sites. J. Geophys. Res. Atmos. 2003, 108, 4679. [Google Scholar] [CrossRef]
- Wrasse, C.M.; Nakamura, T.; Takahashi, H.; Medeiros, A.F.; Taylor, M.J.; Gobbi, D.; Denardini, C.M.; Fechine, J.; Buriti, R.A.; Salatun, A.; et al. Mesospheric Gravity Waves Observed near Equatorial and Low–Middle Latitude Stations: Wave Characteristics and Reverse Ray Tracing Results. Ann. Geophys. 2006, 24, 3229–3240. [Google Scholar] [CrossRef]
- Mukherjee, G.K. The Signature of Short-Period Gravity Waves Imaged in the OI and near Infrared OH Nightglow Emissions over Panhala. J. Atmos. Sol. Terr. Phys. 2003, 65, 1329–1335. [Google Scholar] [CrossRef]
- Kam, H.; Jee, G.; Kim, Y.; Ham, Y.; Song, I.-S. Statistical Analysis of Mesospheric Gravity Waves over King Sejong Station, Antarctica (62.2° S, 58.8° W). J. Atmos. Sol. Terr. Phys. 2017, 155, 86–94. [Google Scholar] [CrossRef]
- Huang, H.; Gu, S.; Qin, Y.; Li, G.; Yang, Z.; Wei, Y.; Gong, D.; Niu, S. Statistical Analysis of Gravity Waves in the Mesopause Region Based on OI 557.7 Nm Airglow Observation over Mohe, China. J. Geophys. Res. Space Phys. 2025, 130, e2025JA033917. [Google Scholar] [CrossRef]
- Hwang, J.-Y.; Lee, Y.-S.; Kim, Y.H.; Kam, H.; Song, S.-M.; Kwak, Y.-S.; Yang, T.-Y. Propagating Characteristics of Mesospheric Gravity Waves Observed by an OI 557.7 Nm Airglow All-Sky Camera at Mt. Bohyun (36.2° N, 128.9° E). Ann. Geophys. 2022, 40, 247–257. [Google Scholar] [CrossRef]
- Matsuoka, D.; Watanabe, S.; Sato, K.; Kawazoe, S.; Yu, W.; Easterbrook, S. Application of Deep Learning to Estimate Atmospheric Gravity Wave Parameters in Reanalysis Data Sets. Geophys. Res. Lett. 2020, 47, e2020GL089436. [Google Scholar] [CrossRef]
- Wu, Y.; Sheng, Z.; Zuo, X. Application of Deep Learning to Estimate Stratospheric Gravity Wave Potential Energy. Earth Planet. Phys. 2022, 6, 70–82. [Google Scholar] [CrossRef]
- Amiramjadi, M.; Plougonven, R.; Mohebalhojeh, A.R.; Mirzaei, M. Using Machine Learning to Estimate Nonorographic Gravity Wave Characteristics at Source Levels. J. Atmos. Sci. 2023, 80, 419–440. [Google Scholar] [CrossRef]
- Connelly, D.S.; Gerber, E.P. Regression Forest Approaches to Gravity Wave Parameterization for Climate Projection. J. Adv. Model. Earth Syst. 2024, 16, e2023MS004184. [Google Scholar] [CrossRef]
- Lai, C.; Xu, J.; Yue, J.; Yuan, W.; Liu, X.; Li, W.; Li, Q. Automatic Extraction of Gravity Waves from All-Sky Airglow Image Based on Machine Learning. Remote Sens 2019, 11, 1516. [Google Scholar] [CrossRef]
- Shiokawa, K.; Katoh, Y.; Satoh, M.; Ejiri, M.K.; Ogawa, T.; Nakamura, T.; Tsuda, T.; Wiens, R.H. Development of Optical Mesosphere Thermosphere Imagers (OMTI). Earth Planets Space 1999, 51, 887–896. [Google Scholar] [CrossRef]
- Nakamura, T.; Tsuda, T.; Tsutsumi, M.; Kita, K.; Uehara, T.; Kato, S.; Fukao, S. Meteor Wind Observations with the MU Radar. Radio. Sci. 1991, 26, 857–869. [Google Scholar] [CrossRef]
- Drob, D.P.; Emmert, J.T.; Meriwether, J.W.; Makela, J.J.; Doornbos, E.; Conde, M.; Hernandez, G.; Noto, J.; Zawdie, K.A.; McDonald, S.E.; et al. An Update to the Horizontal Wind Model (HWM): The Quiet Time Thermosphere. Earth Space Sci. 2015, 2, 301–319. [Google Scholar] [CrossRef]
- Nakamura, T.; Higashikawa, A.; Tsuda, T.; Matsushita, Y. Seasonal Variations of Gravity Wave Structures in OH Airglow with a CCD Imager at Shigaraki. Earth Planets Space 1999, 51, 897–906. [Google Scholar] [CrossRef]
- Kubota’, M.; Ishii’, M.; Shiokawa’, K.; Ejiri, M.K.; Ogawa, T. Height measurements of nightglow structures observed by all-sky imagers. Adv. Space Res. 1999, 24, 593–596. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y. Convolutional Networks for Images, Speech, and Time Series. Handb. Brain Theory Neural Netw. 1995, 3361, 1995. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Mittal, N. Automatic Contrast Enhancement of Low Contrast Images Using MATLAB. Int. J. Adv. Res. Comput. Sci. 2012, 3, 335–336. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, UK, 2016. [Google Scholar]
- Yamashita, R.; Nishio, M.; Do, R.K.G.; Togashi, K. Convolutional Neural Networks: An Overview and Application in Radiology. Insights Imaging 2018, 9, 611–629. [Google Scholar] [CrossRef] [PubMed]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Desai, C. Comparative Analysis of Optimizers in Deep Neural Networks. Int. J. Innov. Sci. Res. Technol. 2020, 5, 959–962. [Google Scholar]
- Navas-Olive, A.; Amaducci, R.; Jurado-Parras, M.-T.; Sebastian, E.R.; de la Prida, L.M. Deep Learning-Based Feature Extraction for Prediction and Interpretation of Sharp-Wave Ripples in the Rodent Hippocampus. Elife 2022, 11, e77772. [Google Scholar] [CrossRef] [PubMed]
- Yacoub, M.; Pacheco, E.E.; Abdelwahab, M.; De La Jara, C.; Mahrous, A. Automatic Detection and Classification of Spread-F in Ionograms Using Convolutional Neural Network. J. Atmos. Sol. Terr. Phys. 2025, 270, 106504. [Google Scholar] [CrossRef]
- Matsuda, T.S.; Nakamura, T.; Ejiri, M.K.; Tsutsumi, M.; Shiokawa, K. New Statistical Analysis of the Horizontal Phase Velocity Distribution of Gravity Waves Observed by Airglow Imaging. J. Geophys. Res. Atmos. 2014, 119, 9707–9718. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Hoboken, NJ, USA, 1994; ISBN 0023527617. [Google Scholar]
- Levenberg, K. A Method for the Solution of Certain Non-Linear Problems in Least Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Basterrech, S.; Mohammed, S.; Rubino, G.; Soliman, M. Levenberg—Marquardt Training Algorithms for Random Neural Networks. Comput. J. 2011, 54, 125–135. [Google Scholar] [CrossRef]
- Tiwari, S.; Naresh, R.; Jha, R. Comparative Study of Backpropagation Algorithms in Neural Network Based Identification of Power System. Int. J. Comput. Sci. Inf. Technol. 2013, 5, 93. [Google Scholar] [CrossRef]
- Minta, F.N.; Nozawa, S.; Kozarev, K.; Elsaid, A.; Mahrous, A. Forecasting the Transit Times of Earth-Directed Halo CMEs Using Artificial Neural Network: A Case Study Application with GCS Forward-Modeling Technique. J. Atmos. Sol. Terr. Phys. 2023, 247, 106080. [Google Scholar] [CrossRef]
- Otugo, V.; Okoh, D.; Okujagu, C.; Onwuneme, S.; Rabiu, B.; Uwamahoro, J.; Habarulema, J.B.; Tshisaphungo, M.; Ssessanga, N. Estimation of Ionospheric Critical Plasma Frequencies From GNSS-TEC Measurements Using Artificial Neural Networks. Space Weather. 2019, 17, 1329–1340. [Google Scholar] [CrossRef]
- Olden, J. An Accurate Comparison of Methods for Quantifying Variable Importance in Artificial Neural Networks Using Simulated Data. Ecol. Modell. 2004, 178, 389–397. [Google Scholar] [CrossRef]
- Olden, J.D.; Jackson, D.A. Illuminating the “Black Box”: A Randomization Approach for Understanding Variable Contributions in Artificial Neural Networks. Ecol. Modell. 2002, 154, 135–150. [Google Scholar] [CrossRef]
- Faroughi, S.A.; Pawar, N.; Fernandes, C.; Raissi, M.; Das, S.; Kalantari, N.K.; Mahjour, S.K. Physics-Guided, Physics-Informed, and Physics-Encoded Neural Networks in Scientific Computing. arXiv 2023, 3–13. [Google Scholar]
- Mohammadi, M.-R.; Hemmati-Sarapardeh, A.; Schaffie, M.; Husein, M.M.; Ranjbar, M. Application of Cascade Forward Neural Network and Group Method of Data Handling to Modeling Crude Oil Pyrolysis during Thermal Enhanced Oil Recovery. J. Pet. Sci. Eng. 2021, 205, 108836. [Google Scholar] [CrossRef]
- Terven, J.; Cordova-Esparza, D.-M.; Romero-González, J.-A.; Ramírez-Pedraza, A.; Chávez-Urbiola, E.A. A Comprehensive Survey of Loss Functions and Metrics in Deep Learning. Artif. Intell. Rev. 2025, 58, 195. [Google Scholar] [CrossRef]
- Takeo, D.; Shiokawa, K.; Fujinami, H.; Otsuka, Y.; Matsuda, T.S.; Ejiri, M.K.; Nakamura, T.; Yamamoto, M. Sixteen Year Variation of Horizontal Phase Velocity and Propagation Direction of Mesospheric and Thermospheric Waves in Airglow Images at Shigaraki, Japan. J. Geophys. Res. Space Phys. 2017, 122, 8770–8780. [Google Scholar] [CrossRef]
- Tsuchiya, S.; Shiokawa, K.; Fujinami, H.; Otsuka, Y.; Nakamura, T.; Yamamoto, M. Statistical Analysis of the Phase Velocity Distribution of Mesospheric and Ionospheric Waves Observed in Airglow Images over a 16-Year Period: Comparison Between Rikubetsu and Shigaraki, Japan. J. Geophys. Res. Space Phys. 2018, 123, 6930–6947. [Google Scholar] [CrossRef]
- Walterscheid, R.L.; Hecht, J.H.; Vincent, R.A.; Reid, I.M.; Woithe, J.; Hickey, M.P. Analysis and Interpretation of Airglow and Radar Observations of Quasi-Monochromatic Gravity Waves in the Upper Mesosphere and Lower Thermosphere over Adelaide, Australia (35° S, 138° E). J. Atmos. Sol. Terr. Phys. 1999, 61, 461–478. [Google Scholar] [CrossRef]
- Paulino, I.; Takahashi, H.; Medeiros, A.F.; Wrasse, C.M.; Buriti, R.A.; Sobral, J.H.A.; Gobbi, D. Mesospheric Gravity Waves and Ionospheric Plasma Bubbles Observed during the COPEX Campaign. J. Atmos. Sol. Terr. Phys. 2011, 73, 1575–1580. [Google Scholar] [CrossRef]

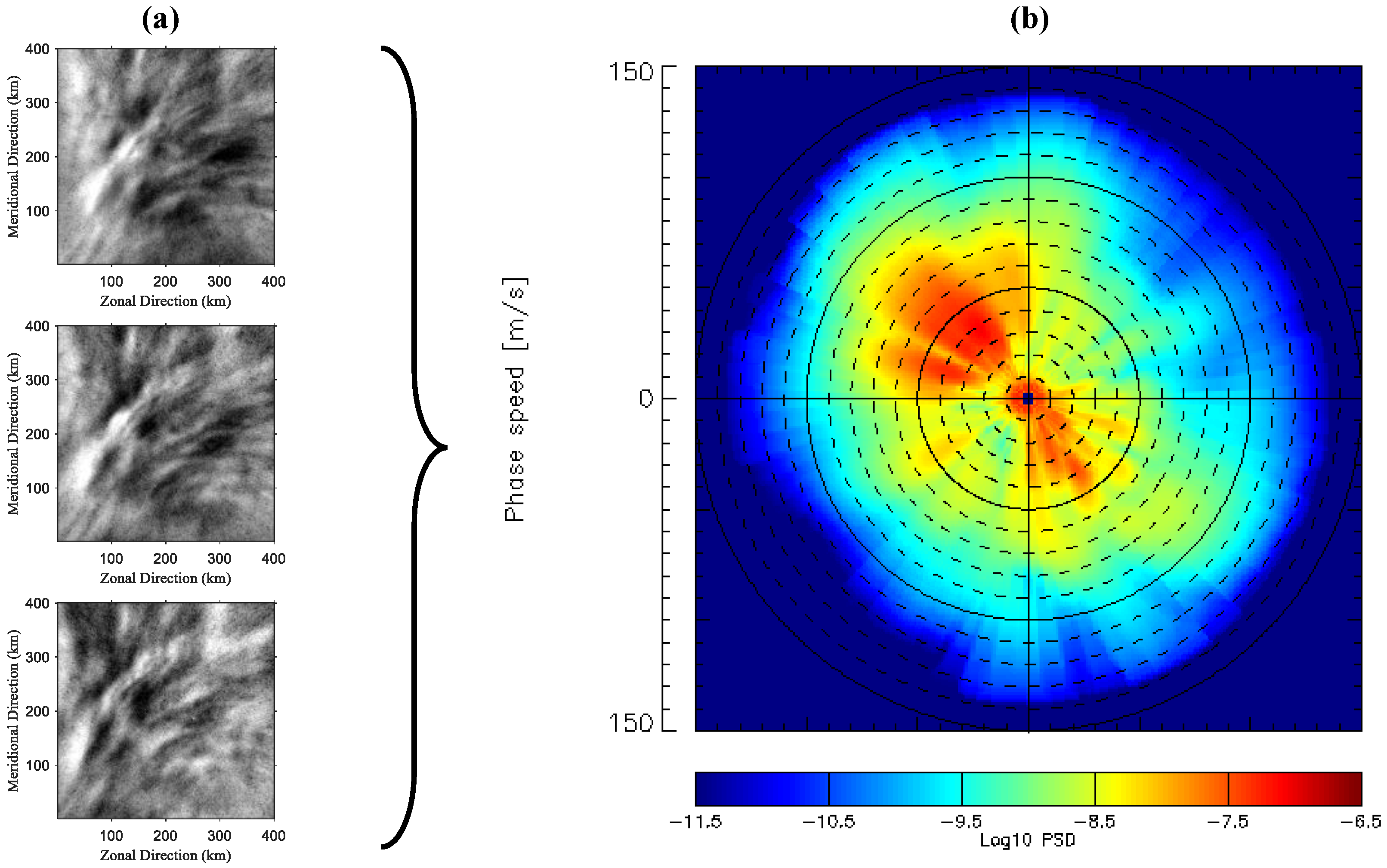
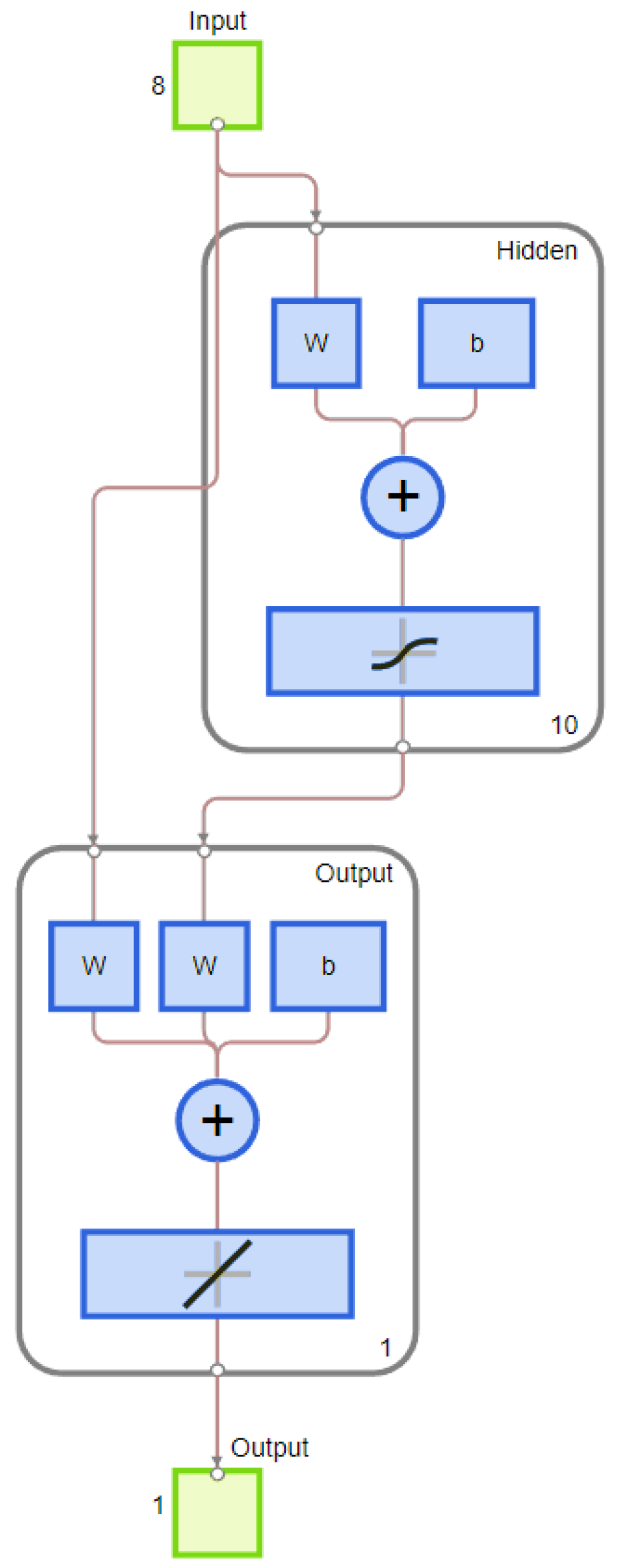



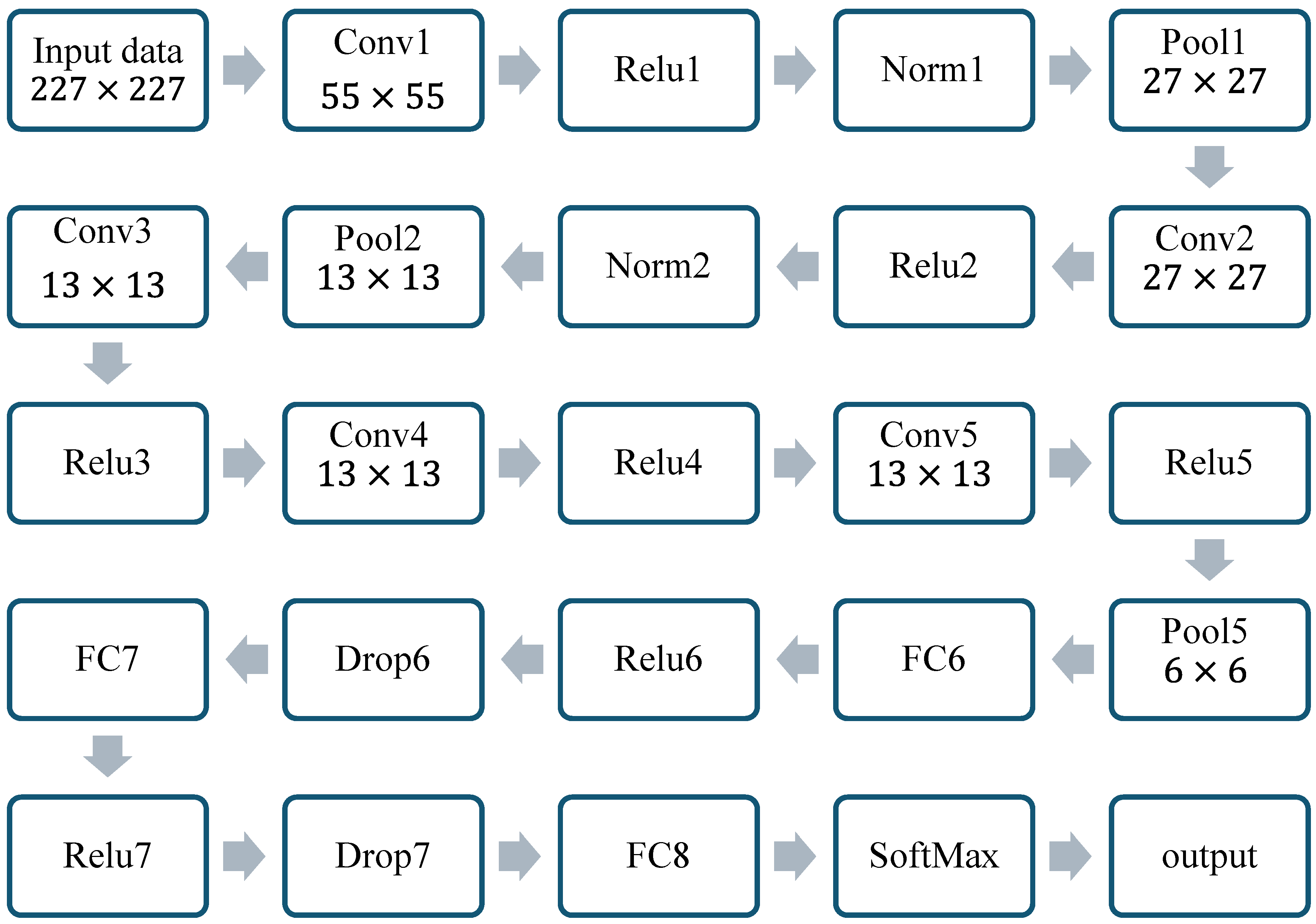
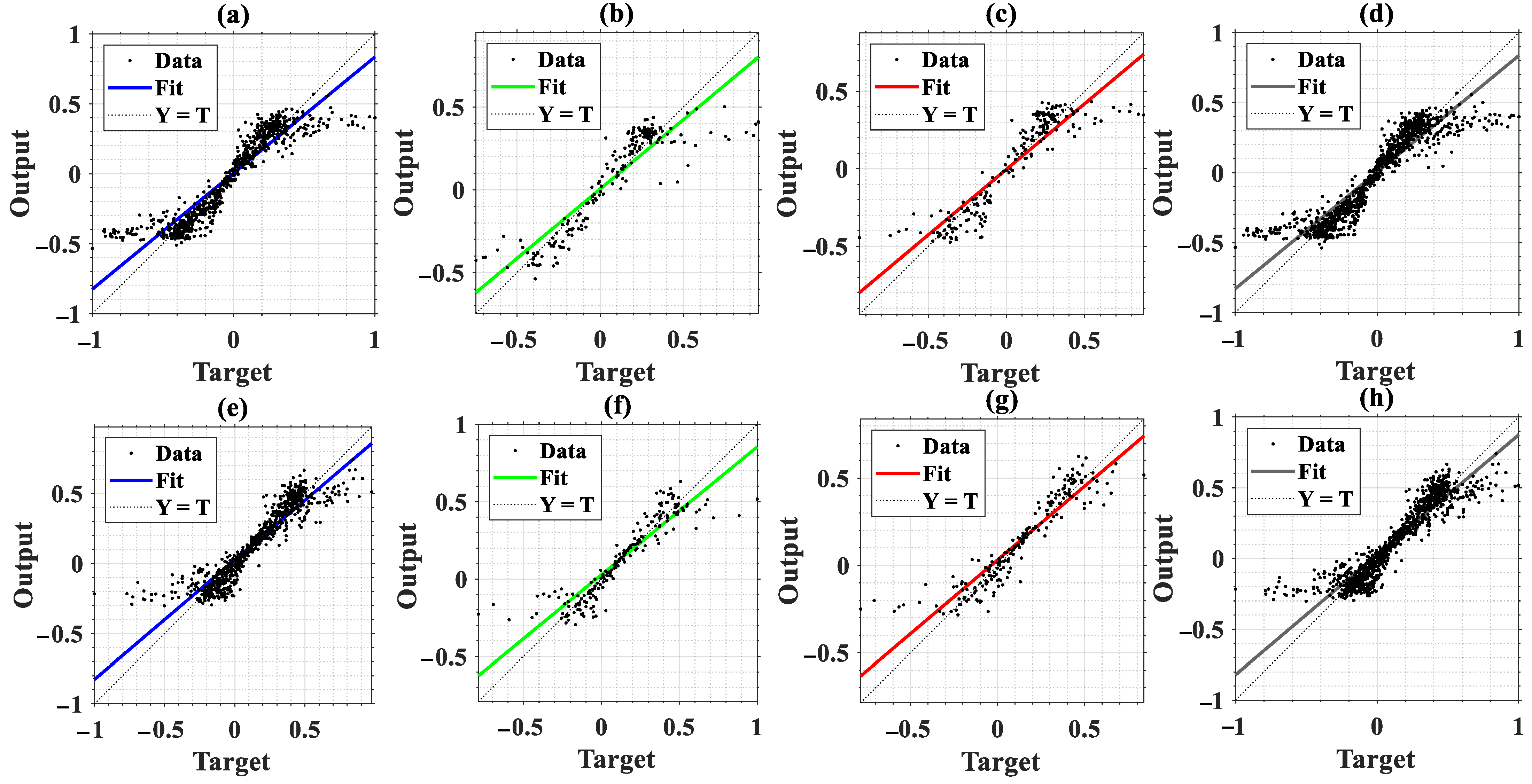
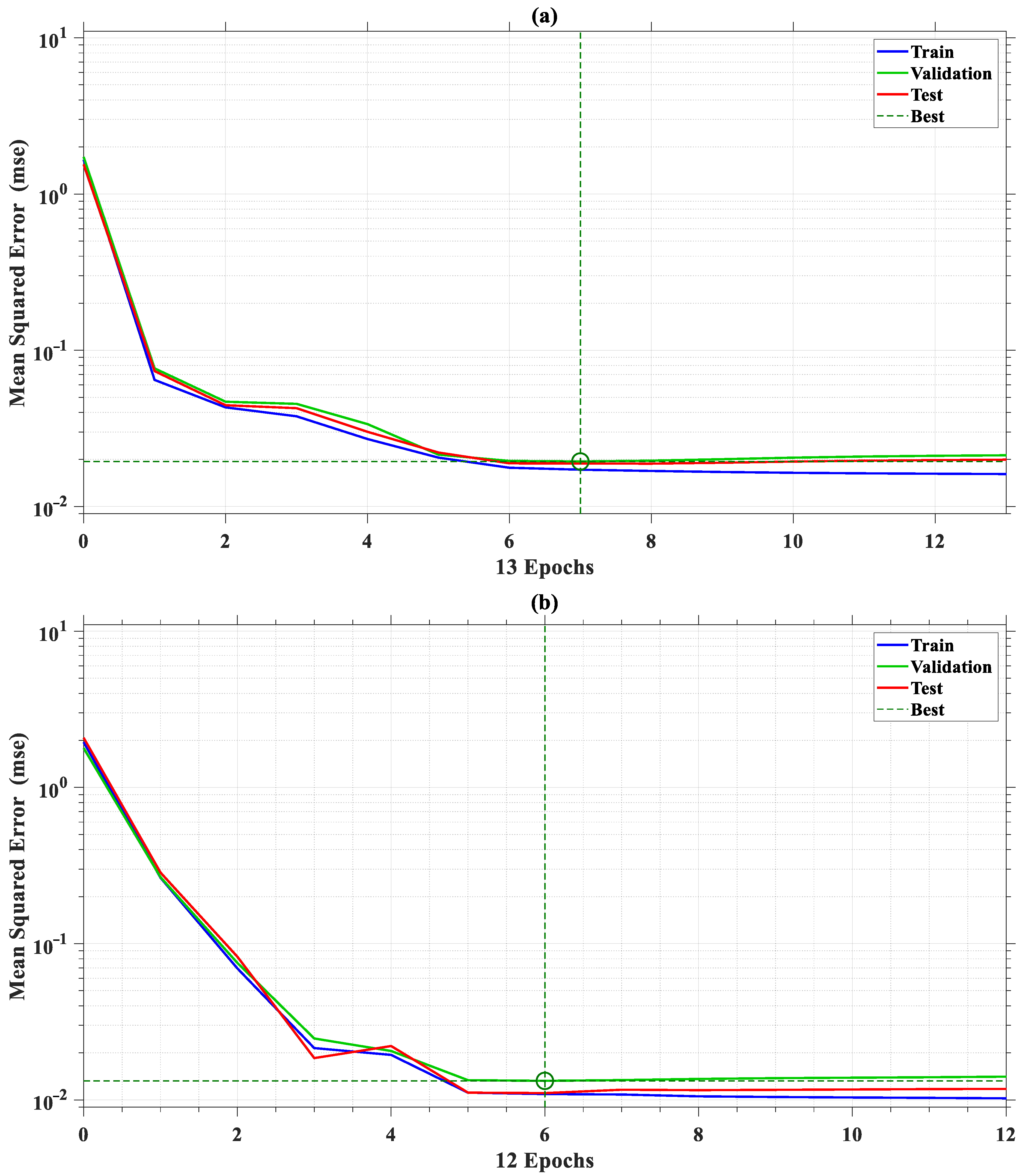
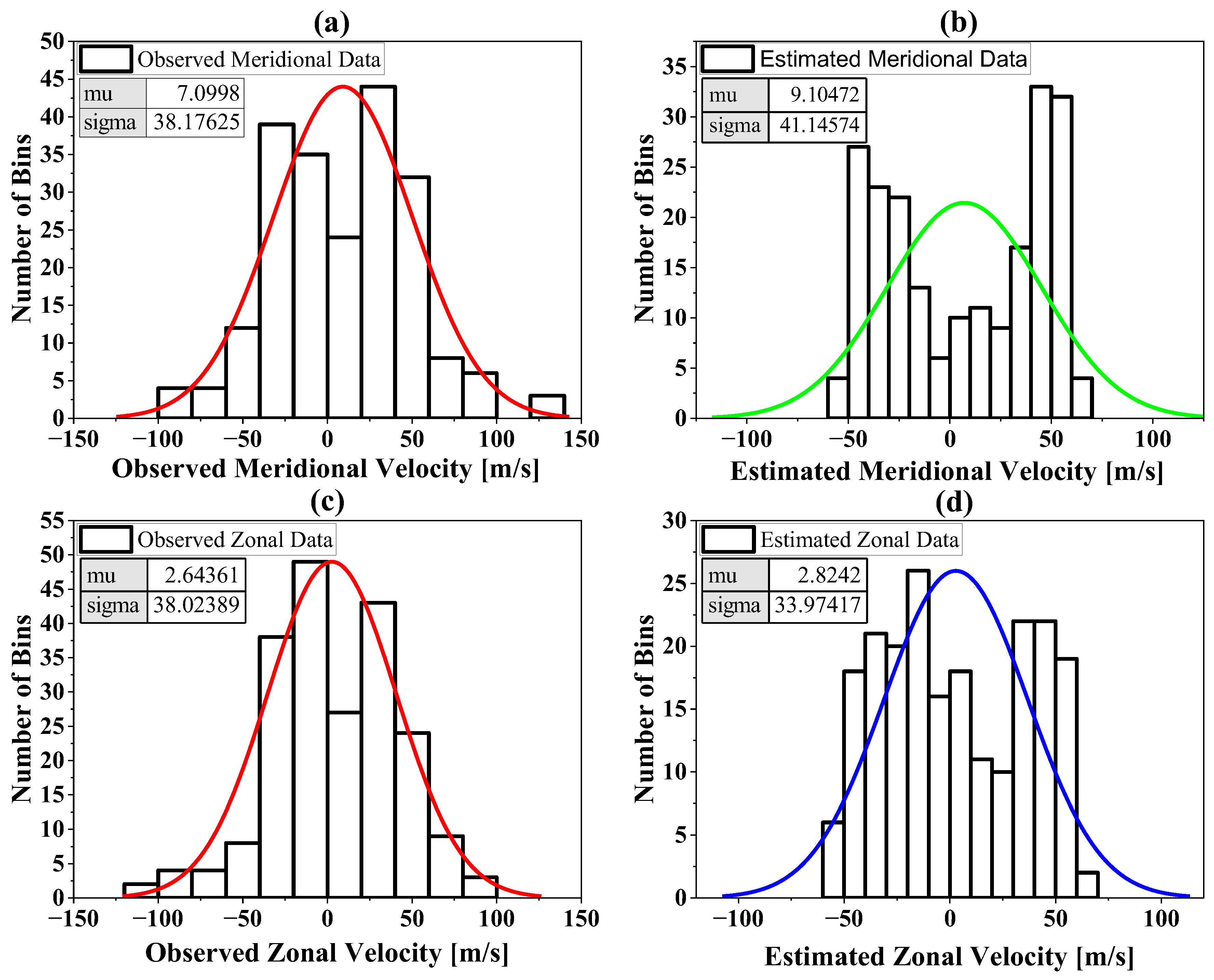
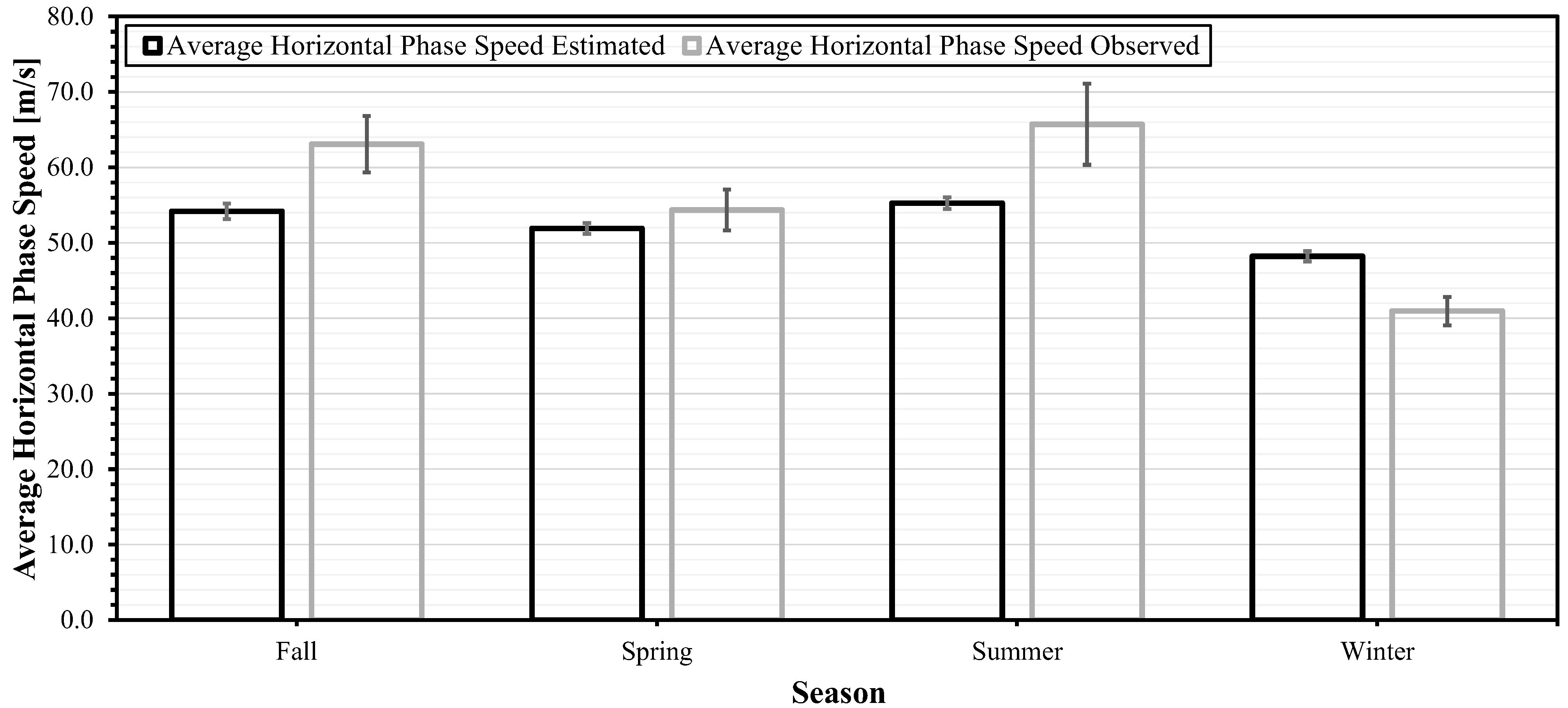

| Dataset Stage | Number of Images | Notes |
|---|---|---|
| Total deviated images | 13,201 | Initial dataset from OI-557.7 nm ASAI |
| Eliminated during quality control process using visual inspection criteria (movie of grayscale images) | 1194 | Contained very weak/unclear gravity wave patterns, removed to avoid bias during machine learning classification and estimation processes |
| Final dataset after quality control process | 12,007 | Used for classification and estimation processes |
| Hyperparameters | Best Performance | ||
|---|---|---|---|
| Network | AlexNet | GoogLeNet | ResNet-50 |
| Epochs | 15 | 15 | 15 |
| Batch Size | 64 | 64 | 64 |
| Input size (pixels) | 227 × 227 | 224 × 224 | 224 × 224 |
| Optimizer | SGDM | SGDM | SGDM |
| Activation Functions | ReLU, SoftMax | ReLU, SoftMax | ReLU, SoftMax |
| Learning Rate | 1 × 10−4 | 1 × 10−4 | 1 × 10−4 |
| Network | Time hh:mm:ss | Epoch | Training Accuracy | Validation Accuracy | Training Loss | Validation Loss |
|---|---|---|---|---|---|---|
| AlexNet | 00:07:05 | 16 | 100% | 99.26% | 0.0011 | 0.0206 |
| GoogLeNet | 00:22:47 | 16 | 100% | 98.80% | 0.0069 | 0.0359 |
| ResNet-50 | 03:27:55 | 16 | 100% | 98.61% | 0.0056 | 0.0467 |
| Network | N | Mean | Standard Deviation | Tukey Test |
|---|---|---|---|---|
| AlexNet | 46 | ~99.12% | ~0.216 | A |
| GoogLeNet | 46 | ~98.40% | ~0.501 | B |
| ResNet-50 | 46 | ~97.96% | ~0.813 | C |
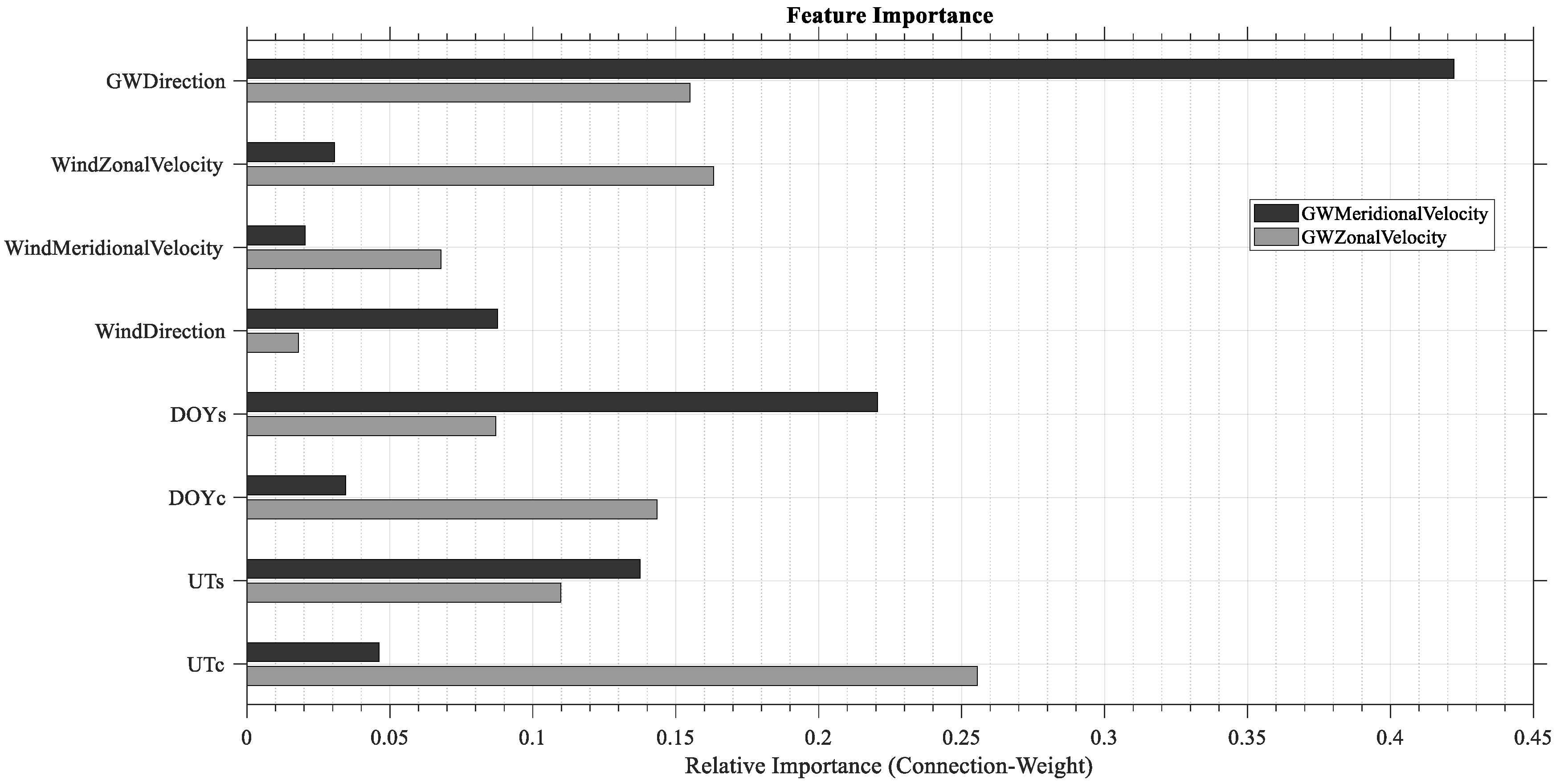
| Rank | AGW Meridional Velocity Component | Percentage (%) | AGW Zonal Velocity Component | Percentage (%) |
|---|---|---|---|---|
| 1 | Gravity Wave Direction | 42.22 | Cosine Component of Universal Time | 25.55 |
| 2 | Sine Component of Day of Year | 22.06 | Neutral Zonal Wind Velocity | 16.32 |
| 3 | Sine Component of Universal Time | 13.75 | Gravity Wave Direction | 15.51 |
| 4 | Neutral Wind Direction | 8.77 | Cosine Component of Day of Year | 14.34 |
| 5 | Cosine Component of Universal Time | 4.63 | Sine Component of Universal Time | 10.98 |
| 6 | Cosine Component of Day of Year | 3.46 | Sine Component of Day of Year | 8.71 |
| 7 | Neutral Zonal Wind Velocity | 3.07 | Neutral Meridional Wind Velocity | 6.79 |
| 8 | Neutral Meridional Wind Velocity | 2.04 | Neutral Wind Direction | 1.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmoud, R.; Abdelwahab, M.; Shiokawa, K.; Mahrous, A. Machine Learning Recognition and Phase Velocity Estimation of Atmospheric Gravity Waves from OI 557.7 nm All-Sky Airglow Images. AI 2025, 6, 262. https://doi.org/10.3390/ai6100262
Mahmoud R, Abdelwahab M, Shiokawa K, Mahrous A. Machine Learning Recognition and Phase Velocity Estimation of Atmospheric Gravity Waves from OI 557.7 nm All-Sky Airglow Images. AI. 2025; 6(10):262. https://doi.org/10.3390/ai6100262
Chicago/Turabian StyleMahmoud, Rady, Moataz Abdelwahab, Kazuo Shiokawa, and Ayman Mahrous. 2025. "Machine Learning Recognition and Phase Velocity Estimation of Atmospheric Gravity Waves from OI 557.7 nm All-Sky Airglow Images" AI 6, no. 10: 262. https://doi.org/10.3390/ai6100262
APA StyleMahmoud, R., Abdelwahab, M., Shiokawa, K., & Mahrous, A. (2025). Machine Learning Recognition and Phase Velocity Estimation of Atmospheric Gravity Waves from OI 557.7 nm All-Sky Airglow Images. AI, 6(10), 262. https://doi.org/10.3390/ai6100262







