Effective Hybrid Structure Health Monitoring through Parametric Study of GoogLeNet
Abstract
1. Introduction
2. Research Methodology
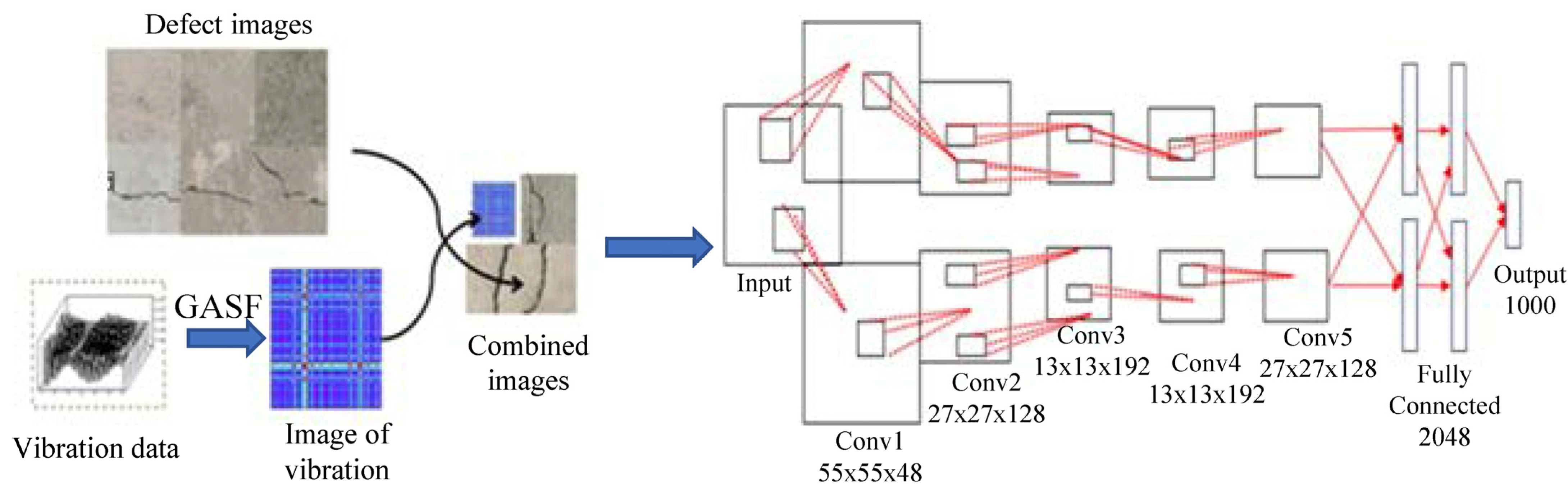
2.1. Deep Learning-Based Damage Detection Using the Fusion of Vibration Data and Defect Images
2.2. Transfer Learning Method Used
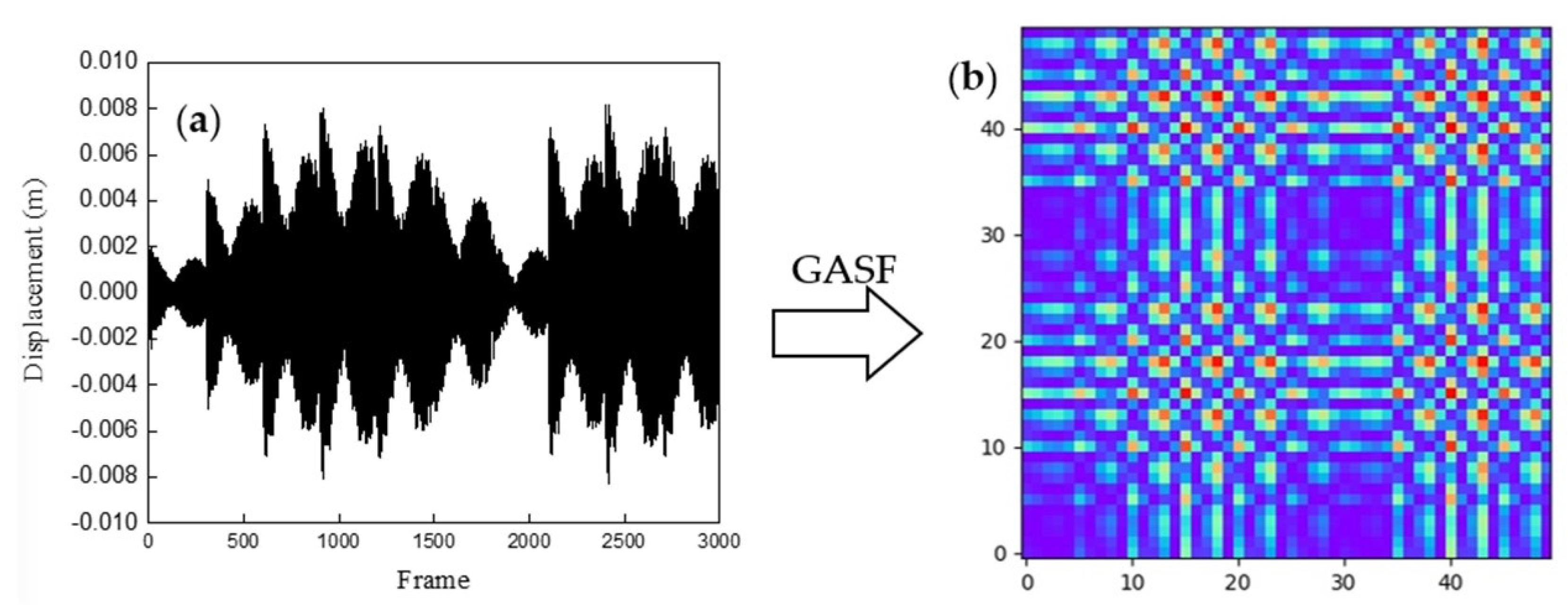
2.3. Gramian Angular Field (GAF)
3. Case Study and Validation
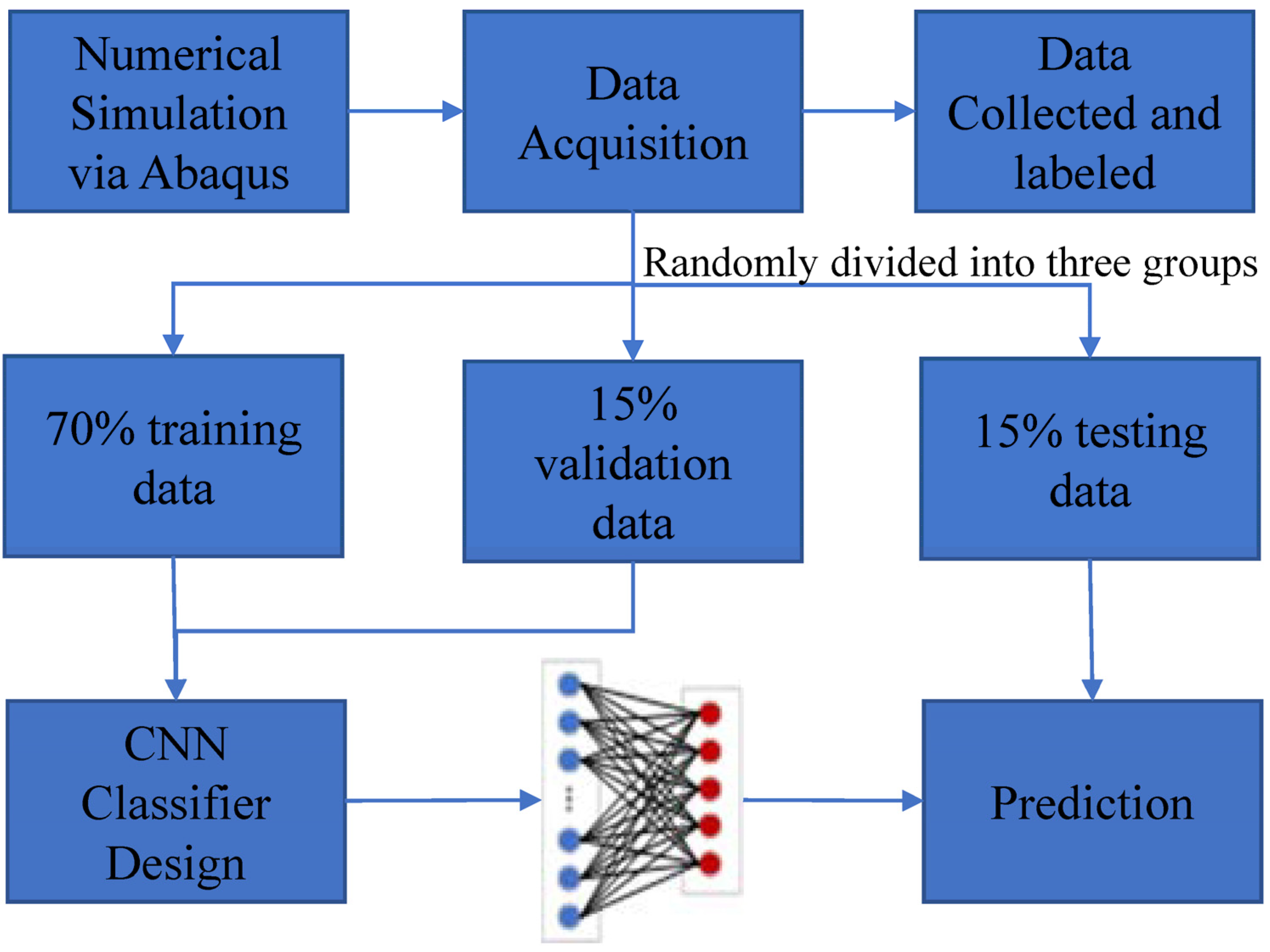
3.1. Data Collection through ABAQUS Modeling
3.2. Structural Evaluation Using a Novel Deep Learning-Based Method with Both Defect Image and Vibration Data
3.3. Gramian Angular Field
3.4. Paired Images
4. Results of the Proposed Method
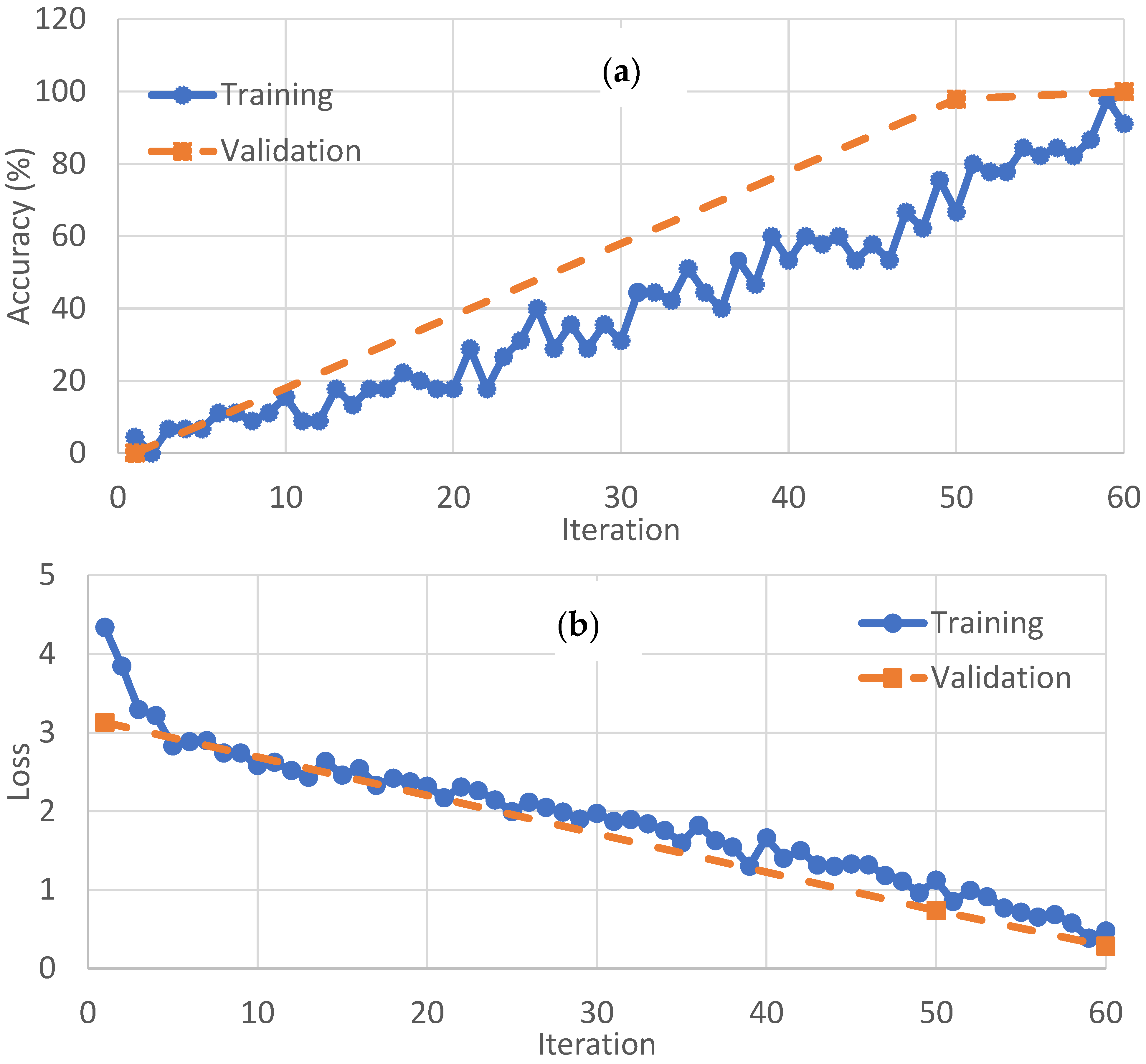
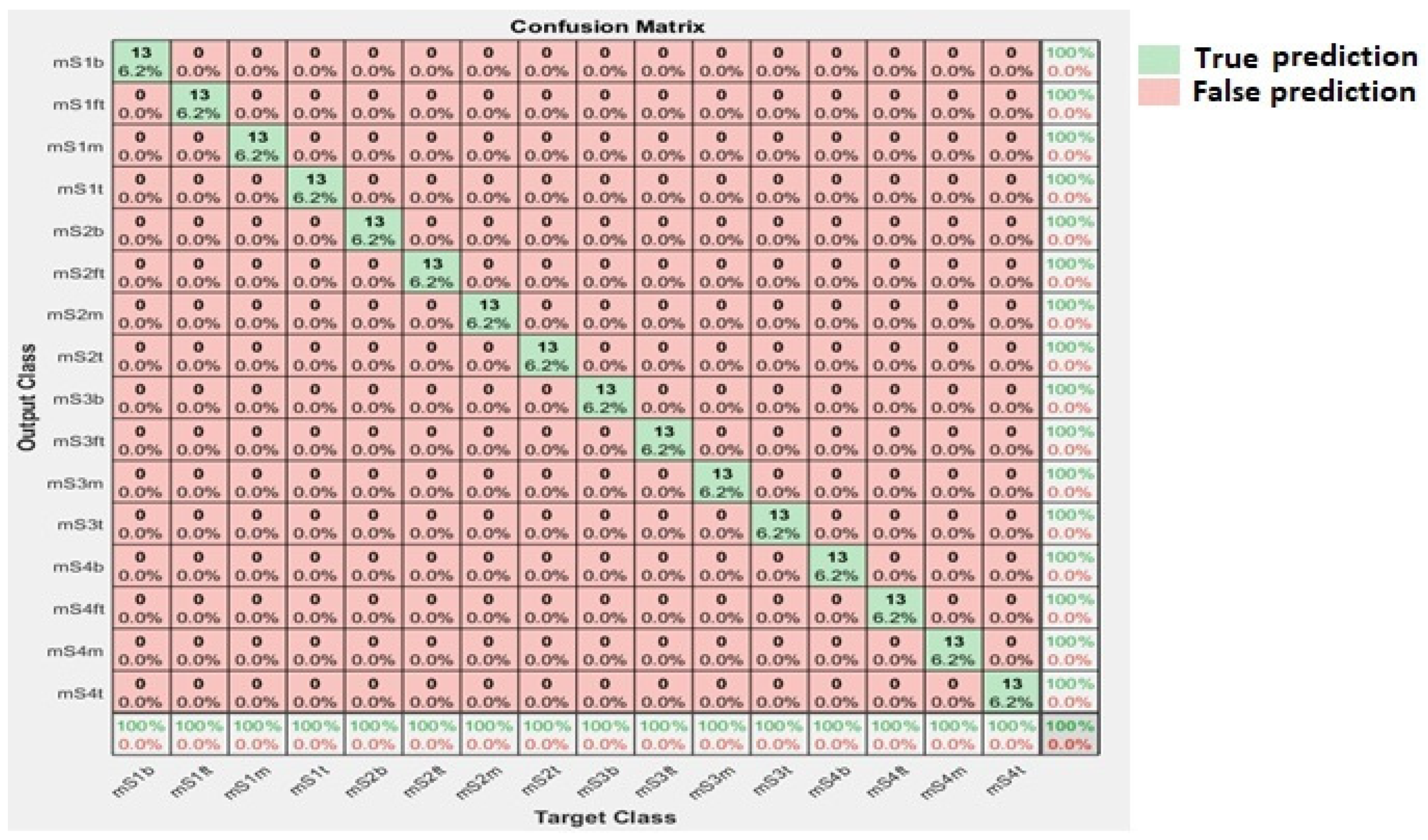
4.1. Results of Model Training, Validation, and Prediction
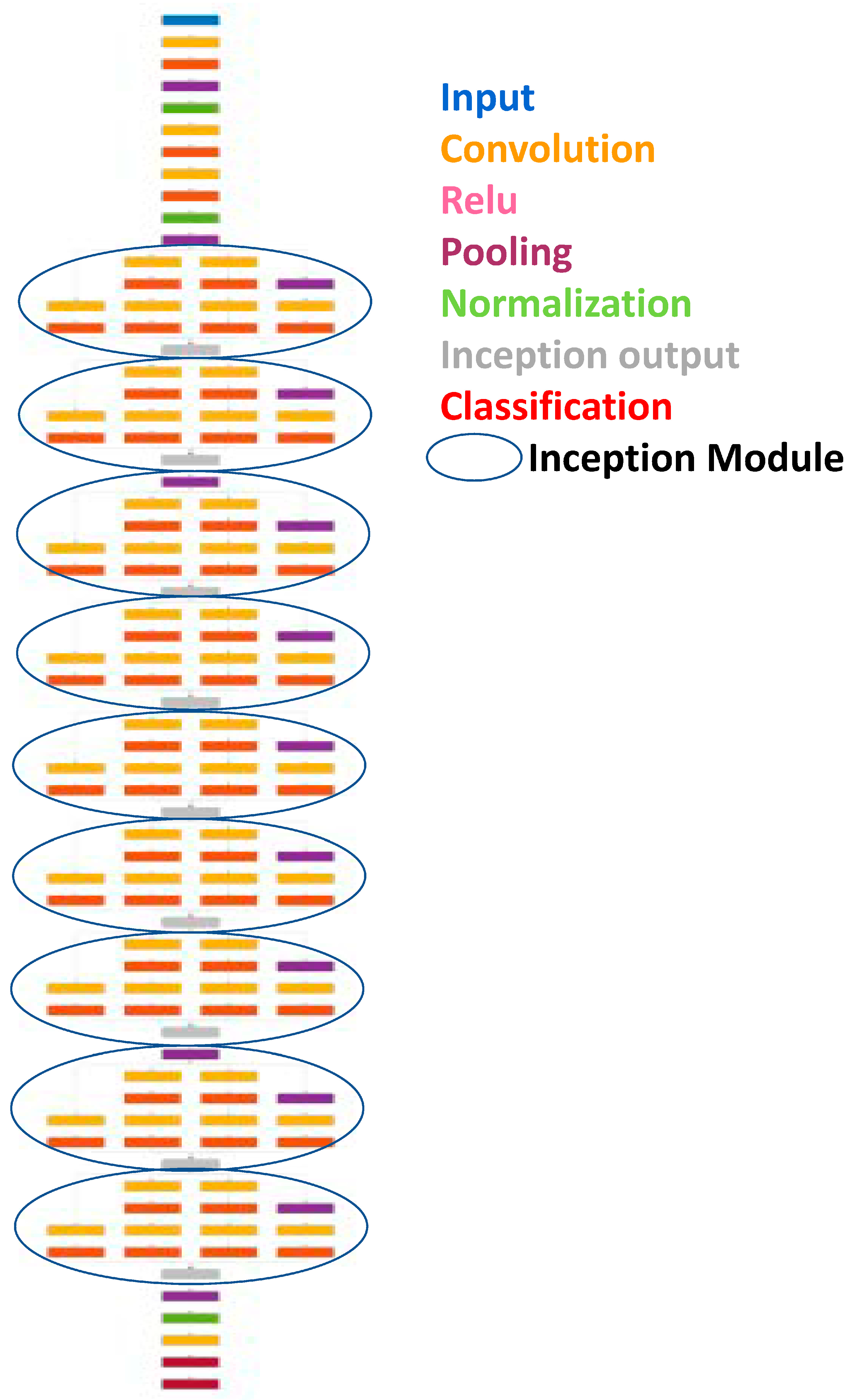
4.2. Effect of the Number of Inception Layers
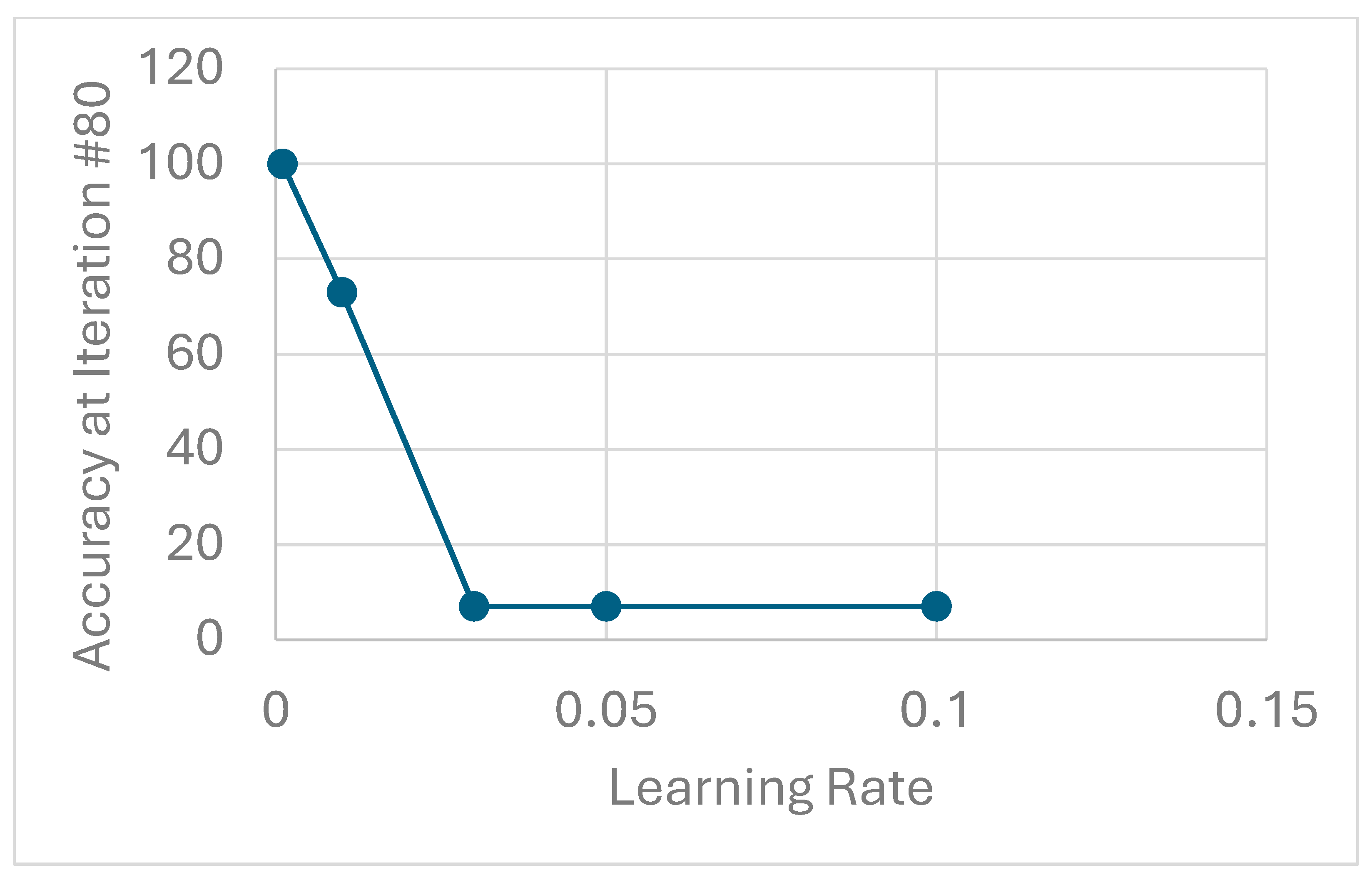
4.3. Effect of Learning Rate
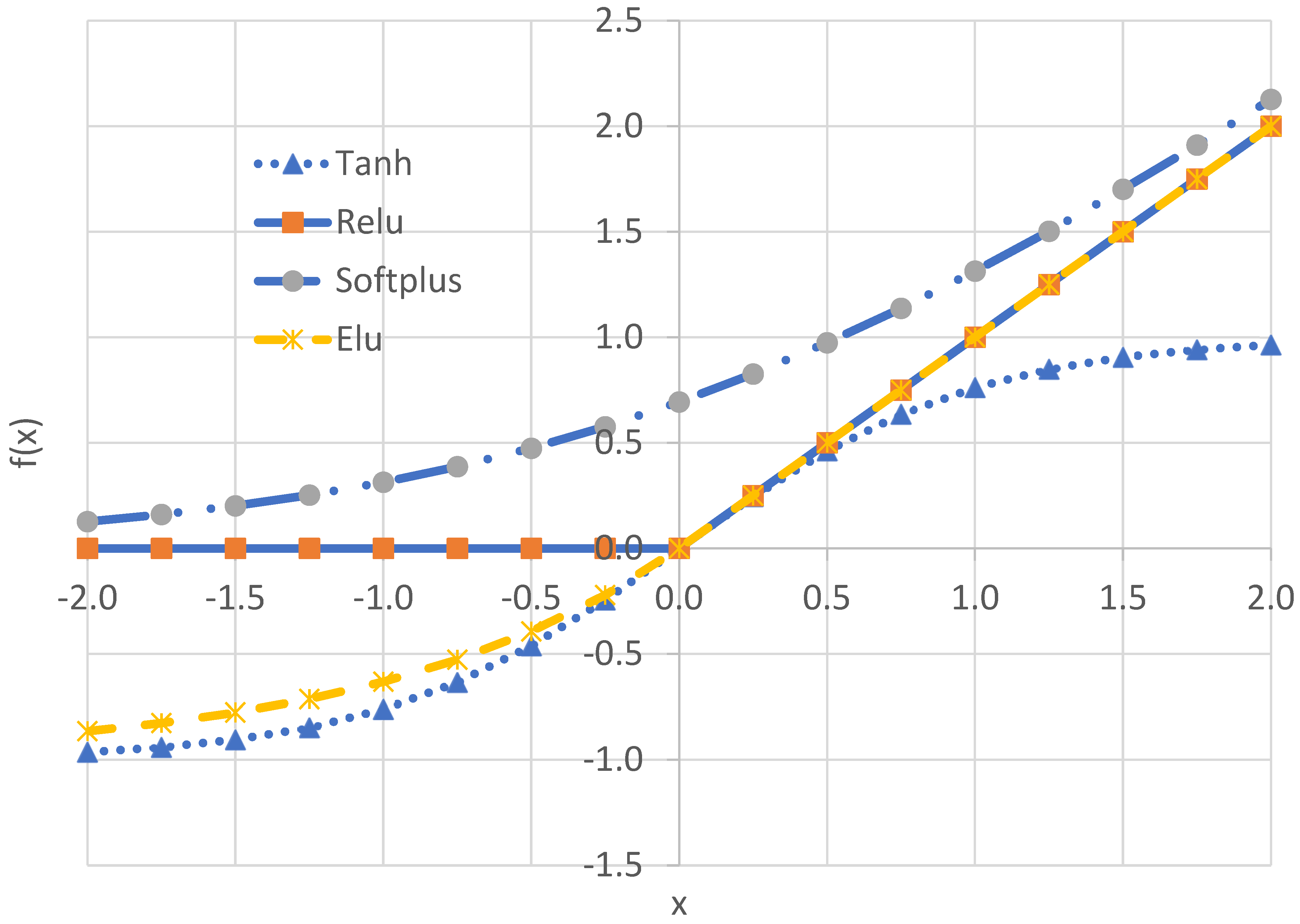
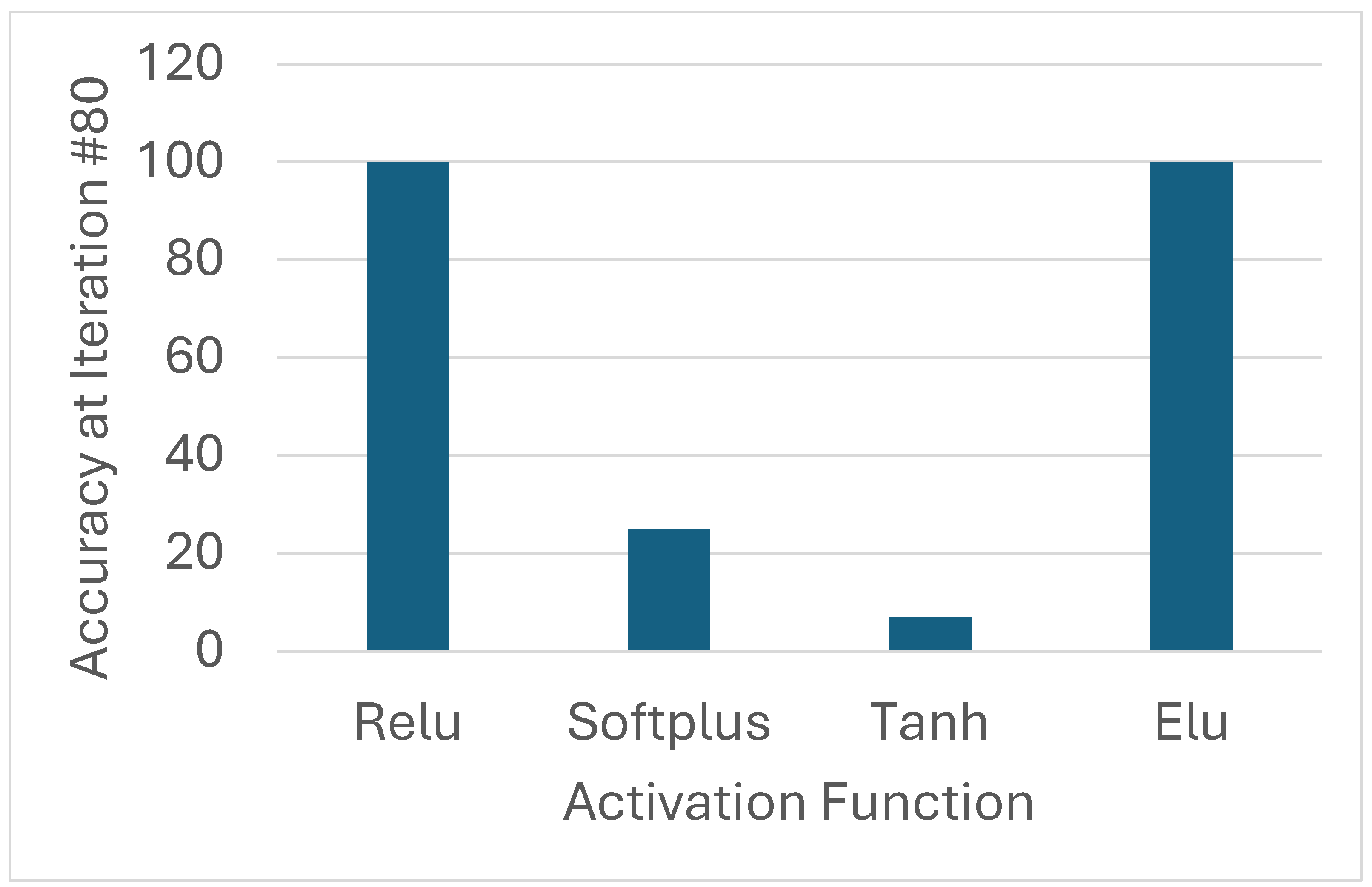
4.4. Effect of Activation Function
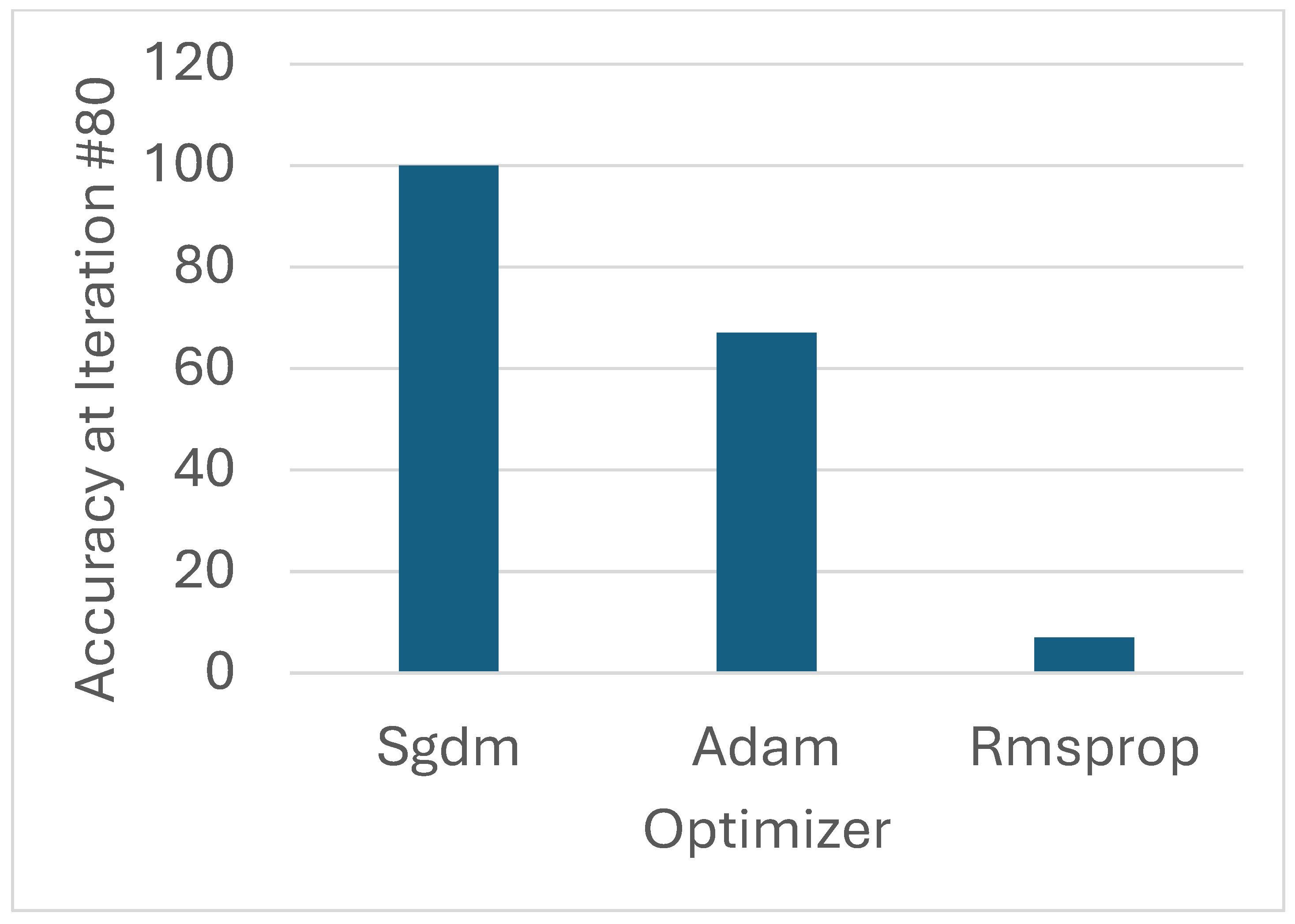
4.5. Effect of Different Optimizers
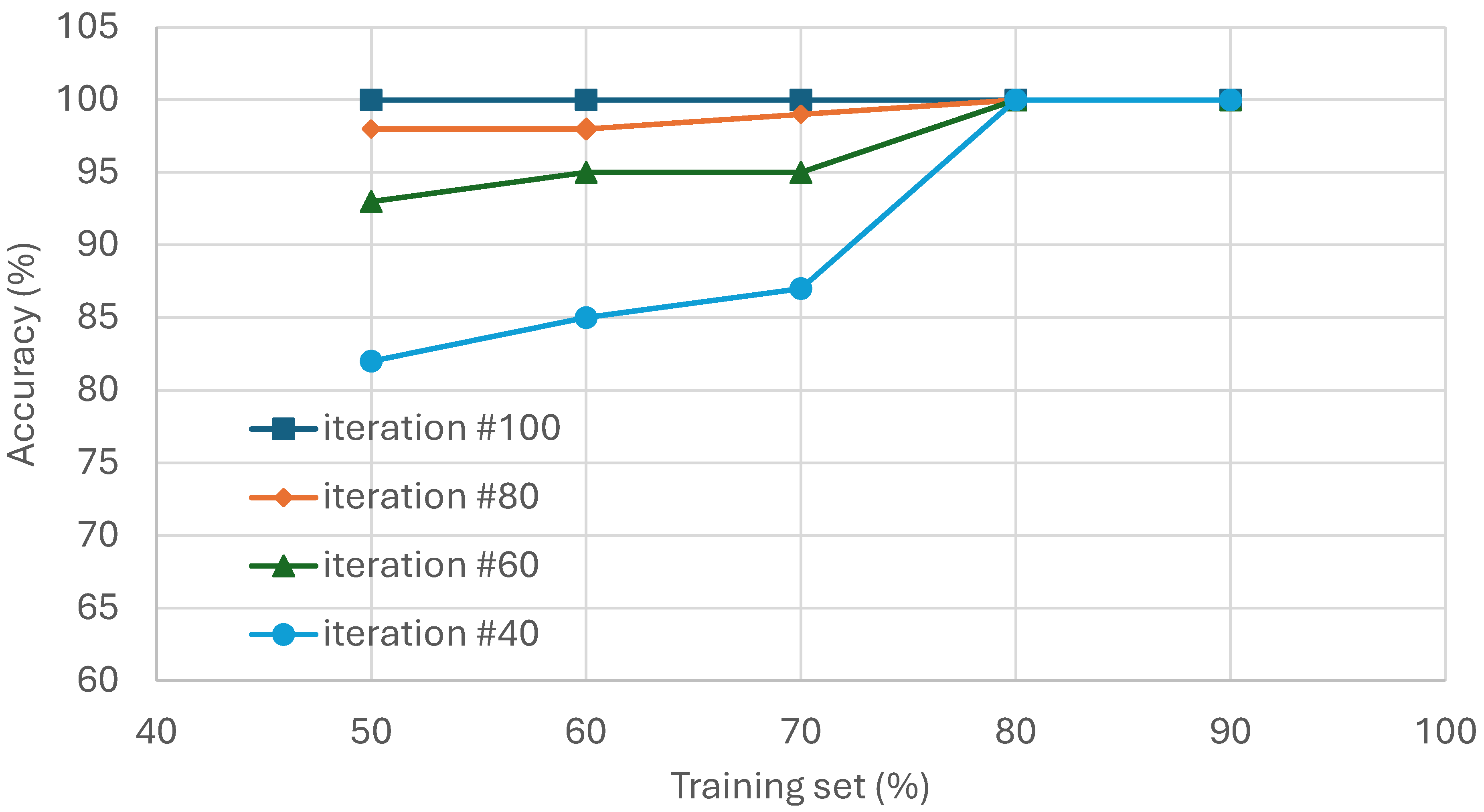
4.6. Effect of Training Data Set Sizes
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Almousa, M.; Olusegun, T.; Lim, Y.; Al-Zboon, K.; Khraisat, I.; Alshami, A.; Ammary, B. Chemical recovery of magnesium from the Dead Sea and its use in wastewater treatment. J. Water 2024, 14, 229–243. [Google Scholar] [CrossRef]
- Liu, Y.; Cho, S.; Spencer, B.F., Jr.; Fan, J. Automated assessment of cracks on concrete surfaces using adaptive digital image processing. Smart Struct. Syst. 2014, 14, 719–741. [Google Scholar] [CrossRef]
- Ebrahimkhanlou, A.; Farhidzadeh, A.; Salamone, S. Multifractal analysis of crack patterns in reinforced concrete shear walls. Struct. Health Monit. 2016, 15, 81–92. [Google Scholar] [CrossRef]
- Yang, X.; Li, H.; Yu, Y.; Luo, X.; Huang, T.; Yang, X. Automatic pixel-level crack detection and measurement using fully convolutional network. Comput.-Aided Civ. Infrastruct. Eng. 2018, 33, 1090–1109. [Google Scholar] [CrossRef]
- Rawat, W.; Wang, Z. Deep Convolutional Neural Networks for Image Classification: A Comprehensive Review. Neural Comput. 2017, 29, 2352–2449. [Google Scholar] [CrossRef]
- Chen, F.-C.; Jahanshahi, M.R. NB-CNN: Deep Learning-Based Crack Detection Using Convolutional Neural Network and Naïve Bayes Data Fusion. IEEE Trans. Ind. Electron. 2018, 65, 4392–4400. [Google Scholar] [CrossRef]
- Dorafshan, S.; Maguire, M.; Hoffer, N.V.; Coopmans, C. Fatigue Crack Detection Using Unmanned Aerial Systems in Under-Bridge Inspection; Idaho Transportation Department: Boise, ID, USA, 2017; Volume 2, pp. 1–120. [Google Scholar]
- Li, G.; Ma, B.; He, S.; Ren, X.; Liu, Q. Automatic Tunnel Crack Detection Based on U-Net and a Convolutional Neural Network with Alternately Updated Clique. Sensors 2020, 20, 717. [Google Scholar] [CrossRef]
- Soloviev, A.; Sobol, B.; Vasiliev, P. Identification of Defects in Pavement Images Using Deep Convolutional Neural Networks. Adv. Mater. 2019, 4, 615–626. [Google Scholar]
- Li, B.; Wang, K.C.P.; Zhang, A.; Yang, E.; Wang, G. Automatic classification of pavement crack using deep convolutional neural network. Int. J. Pavement Eng. 2020, 21, 457–463. [Google Scholar] [CrossRef]
- Tong, Z.; Gao, J.; Han, Z.; Wang, Z. Recognition of asphalt pavement crack length using deep convolutional neural networks. Road Mater. Pavement Des. 2018, 19, 1334–1349. [Google Scholar] [CrossRef]
- Fan, Z.; Li, C.; Chen, Y.; Mascio, P.D.; Chen, X.; Zhu, G.; Loprencipe, G. Ensemble of Deep Convolutional Neural Networks for Automatic Pavement Crack Detection and Measurement. Coatings 2020, 10, 152. [Google Scholar] [CrossRef]
- Adeli, H.; Jiang, X. Intelligent Infrastructure: Neural Networks, Wavelets, and Chaos Theory for Intelligent Transportation Systems and Smart Structures; CRC Press: Boca Raton, FL, USA, 2008; pp. 305–332. [Google Scholar]
- Al-Qudah, S.; Yang, M. Large Displacement Detection Using Improved Lucas–Kanade Optical Flow. Sensors 2023, 23, 3152. [Google Scholar] [CrossRef]
- Cawley, P.; Adams, R.D. The location of defects in structures from measurements of natural frequencies. J. Strain Anal. Eng. Des. 1979, 14, 49–57. [Google Scholar] [CrossRef]
- Pandey, A.; Biswas, M.; Samman, M. Damage detection from changes in curvature mode shapes. J. Sound Vib. 1991, 145, 321–332. [Google Scholar] [CrossRef]
- Chang, K.-C.; Kim, C.-W. Modal-parameter identification and vibration-based damage detection of a damaged steel truss bridge. Eng. Struct. 2016, 122, 156–173. [Google Scholar] [CrossRef]
- Reynders, E.; Wursten, G.; De Roeck, G. Output-Only Fault Detection in Structural Engineering Based on Kernel PCA. In Proceedings of the BIL2014 Workshop on Data-Driven Modeling Methods and Applications, Leuven, Belgium, 14–15 July 2014. [Google Scholar]
- Yan, A.M.; Kerschen, G.; De Boe, P.; Golinval, J.C. Structural damage diagnosis under varying environmental conditions. Part I: A linear analysis. Mech. Syst. Signal Process. 2005, 19, 847–864. [Google Scholar] [CrossRef]
- Lin, Y.Z.; Nie, Z.H.; Ma, H.W. Structural damage detection with automatic feature-extraction through deep learning. Comput. Civ. Infrastruct. Eng. 2017, 32, 1025–1046. [Google Scholar] [CrossRef]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Inman, D.J. Wireless and real-time structural damage detection: A novel decentralized method for wireless sensor networks. J. Sound Vib. 2018, 424, 158–172. [Google Scholar] [CrossRef]
- Abioye, S.O.; Oyedele, L.O.; Akanbi, L.; Ajayi, A.; Delgado, J.M.D.; Bilal, M.; Akinade, O.O.; Ahmed, A. Artificial intelligence in the construction industry: A review of present status, opportunities and future challenges. J. Build. Eng. 2021, 44, 103299. [Google Scholar] [CrossRef]
- Latif, K.; Sharafat, A.; Seo, J. Digital Twin-Driven Framework for TBM Performance Prediction, Visualization, and Monitoring through Machine Learning. Appl. Sci. 2023, 13, 11435. [Google Scholar] [CrossRef]
- Zheng, Z.; Wang, F.; Gong, G.; Yang, H.; Han, D. Intelligent technologies for construction machinery using data-driven methods. Autom. Constr. 2023, 147, 104711. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, L. Roles of artificial intelligence in construction engineering and management: A critical review and future trends. Autom. Constr. 2021, 122, 103517. [Google Scholar] [CrossRef]






| Type | Patch Size Stride | Output Size | Depth |
|---|---|---|---|
| Convolution | 7 × 7/2 | 112 × 112 × 64 | 1 |
| max pool | 3 × 3/2 | 56 × 56 × 64 | 0 |
| Convolution | 3 × 3/1 | 56 × 56 × 192 | 2 |
| max pool | 3 × 3/2 | 28 × 28 × 192 | 0 |
| inception (3a) | - | 28 × 28 × 256 | 2 |
| inception (3b) | - | 28 × 28 × 480 | 2 |
| max pool | 3 × 3/2 | 14 × 14 × 480 | 0 |
| inception (4a) | - | 14 × 14 × 512 | 2 |
| inception (4b) | - | 14 × 14 × 512 | 2 |
| inception (4c) | - | 14 × 14 × 512 | 2 |
| inception (4d) | - | 14 × 14 × 528 | 2 |
| inception (4e) | - | 14 × 14 × 832 | 2 |
| max pool | 3 × 3/2 | 7 × 7 × 832 | 0 |
| inception (5a) | - | 7 × 7 × 832 | 2 |
| inception (5b) | - | 7 × 7 × 1024 | 2 |
| avg pool | 7 × 7/1 | 1 × 1 × 1024 | 0 |
| Dropout (40%) | - | 1 × 1 × 1024 | 0 |
| Linear | - | 1 × 1 × 1000 | 1 |
| soft max | - | 1 × 1 × 1000 | 0 |
| case | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| span | - | S1 | S2 | S3 | S4 | S1 | S2 | S1 | S2 | S3 | S4 | S1 | S2 | S3 | S4 | S5 |
| face | - | f | f | f | f | t | t | f | f | f | f | f | f | f | f | f |
| element | - | T | T | T | T | m | m | m | m | m | m | r | r | r | r | m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Qudah, S.; Yang, M. Effective Hybrid Structure Health Monitoring through Parametric Study of GoogLeNet. AI 2024, 5, 1558-1574. https://doi.org/10.3390/ai5030075
Al-Qudah S, Yang M. Effective Hybrid Structure Health Monitoring through Parametric Study of GoogLeNet. AI. 2024; 5(3):1558-1574. https://doi.org/10.3390/ai5030075
Chicago/Turabian StyleAl-Qudah, Saleh, and Mijia Yang. 2024. "Effective Hybrid Structure Health Monitoring through Parametric Study of GoogLeNet" AI 5, no. 3: 1558-1574. https://doi.org/10.3390/ai5030075
APA StyleAl-Qudah, S., & Yang, M. (2024). Effective Hybrid Structure Health Monitoring through Parametric Study of GoogLeNet. AI, 5(3), 1558-1574. https://doi.org/10.3390/ai5030075






