Abstract
Multi-object tracking (MOT) aims at estimating locations and identities of objects in videos. Many modern multiple-object tracking systems follow the tracking-by-detection paradigm, consisting of a detector followed by a method for associating detections into tracks. Tracking by associating detections through motion-based similarity heuristics is the basic way. Motion models aim at utilizing motion information to estimate future locations, playing an important role in enhancing the performance of association. Recently, a large-scale dataset, DanceTrack, where objects have uniform appearance and diverse motion patterns, was proposed. With existing hand-crafted motion models, it is hard to achieve decent results on DanceTrack because of the lack of prior knowledge. In this work, we present a motion-based algorithm named TLtrack, which adopts a hybrid strategy to make motion estimates based on confidence scores. For high confidence score detections, TLtrack employs transformers to predict its locations. For low confidence score detections, a simple linear model that estimates locations through trajectory historical information is used. TLtrack can not only consider the historical information of the trajectory, but also analyze the latest movements. Our experimental results on the DanceTrack dataset show that our method achieves the best performance compared with other motion models.
1. Introduction
Multi-object tracking (MOT) has been a long-standing problem in computer vision, the aim being to predict the trajectories of objects in a video. It is one of the fundamental yet challenging tasks in computer vision [1] and forms the basis for important applications ranging from video surveillance [2,3] to autonomous driving [4,5].
Many modern multiple-object tracking systems follow the tracking-by-detection paradigm, consisting of a detector followed by a method for associating detections into tracks. The displacement of objects of interest provides important cues for object association. Many works have been inspired by tracking objects through motion estimation. SORT [6] uses the Kalman filter [7] as the motion model, which is a recursive Bayes filter that follows a typical predict–update cycle. The Kalman filter’s simplicity and effectiveness make it widely used in tracking algorithms [6,8,9]. But the Kalman filter as a hand-crafted motion model struggles to deal with diverse motion on DanceTrack [10]. OC-SORT [11] pointed out the limitations of SORT [6] from the use of the Kalman filter [7] and improved robustness against occlusion and nonlinear motion. CenterTrack [12] built on the CenterNet [13] detector to learn a 2D offset between two adjacent frames and associate them based on center distance. But CenterTrack [12] has bad association performance. Recently, MOTR [14], which extended DETR [15] and introduced track query to model the tracked instances in the entire video, has shown the potential of the transformer on data association. But MOTR [14] utilizes the same query to implement detection and tracking, resulting in poor detection performance.
DanceTrack [10] is a large-scale multi-object tracking dataset where objects have uniform appearance and diverse motion patterns. DanceTrack [10] focuses on situations where multiple objects are moving in a relatively large range, the occluded areas are dynamically changing, and they are even in crossover. Such cases are common in the real world, but naive motion models cannot handle them effectively. It can be concluded that the ability to analyze complex motion patterns is necessary for building a more comprehensive and intelligent tracker.
We aimed to develop a strong motion model capable of handling complex movements. Inspired by MOTR [14], we utilize transformers to analyze cross-frame motion patterns. Specifically, an object detector is used to generate detection results and track queries. A transformer architecture then takes the track queries and the image feature as input to predict the current location of the detections. In our method, we directly obtain the track queries from the detections of each frame. Consequently, the accuracy of motion prediction is highly influenced by the quality of the detections. While the detector is trained to locate object positions, its performance may fall short in certain scenes. In MOT tasks, occurrences like occlusion or blurring can result in less accurate detection bounding boxes than expected, as illustrated in Figure 1. This, in turn, renders the track queries less representative and leads to erroneous predictions. We point out that the confidence score can aid in addressing this issue. Thus, we have designed a hybrid strategy to make motion estimates based on the confidence score. For objects with a high confidence score, we adopt a transformer to predict their future locations. Conversely, for objects with a low detection score, we employ a simple linear model to estimate the position. Although the world does not move with constant velocity, many short-term movements, as in the case of two consecutive frames, can be approximated with linear models and by assuming a constant velocity. Additionally, a linear model predicts position through the historical velocity of the trajectory, reducing the impact of the current state. Generally, TLtrack designs a novel hybrid strategy to make motion estimates, not only by considering the historical information of trajectory but also by analyzing the latest movements of each object.
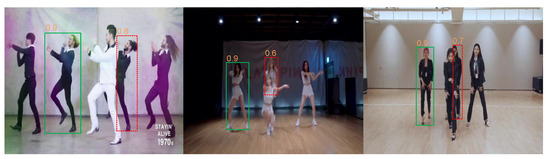
Figure 1.
Illustration of detections with different confidence scores, wherein the red box represents detections with a low score and the green box represents detections with a high score. As the detection confidence score decreases, the detection box cannot accurately represent the location of the object.
Towards pushing forwards the development of a motion-based MOT algorithm, we propose a novel motion model, named TLtrack. TLtrack adopts a novel hybrid strategy to make motion estimates, utilizing transformers to predict the locations of high confidence score detections and employing a linear model for low confidence score detections. Our experimental results on the DanceTrack dataset show that our method achieves the best performance compared with other motion models.
2. Related Work
2.1. Tracking by Detection
The tracking-by-detection paradigm consists of a detector followed by a method for associating detections into tracks. The performance of the object detector plays a pivotal role in tracking. As the field of object detection undergoes rapid development, an increasing number of methods are embracing more powerful detectors to enhance tracking performance. Notably, the two-stage detector Faster R-CNN [16] is employed by SORT [6], due to its exceptional detection accuracy. Additionally, many approaches have turned to the YOLO series detectors [17,18] for their commendable balance between accuracy and speed. Among the array of choices, CenterNet [13] has emerged as a preeminent selection, due to its simplicity and efficiency, garnering extensive adoption by numerous methods [19,20,21,22]. In a similar vein, Transformer-based detectors, such as DETR [15] and Deformable-DETR [23], have been incorporated by TransTrack [24] and Trackformer [25]. Introducing a different perspective, P3AFormer [26] employs pixel-wise techniques to achieve precise object predictions at the pixel level. In practice, these methods commonly leverage detection boxes from each input image directly for tracking purposes. Thus, judicious employment of these detection boxes becomes crucial for effective data association.
2.2. Motion Model
Motion model is widely used for data association to achieve robust ID assignment. Specifically, motion model utilizes the motion information of trajectories to predict the future position. Many methods [6,8,9] use Kalman filter [7] as the motion model, which is a recursive Bayes filter that follows a typical predict–update cycle. The Kalman filter is the predominant motion model for its simplicity and effectiveness. But the Kalman filter as a hand-crafted motion model fails to utilize non-linear or fast object motion. LSTM is adopted by Deft [27] as a motion model, which leads to decent association metrics. Optical flow [28] is adopted by Centertrack [12] as an alternative motion model. But Optical flow cannot achieve excellent performance. Recently, a transformer-based model has shown great performance in motion prediction. Transtrack [24] adopts two transformer decoders to achieve detection and motion estimation simultaneously in a single stage. MOTR [14] learns strong temporal motion and achieves advanced performance on the DanceTrack [10] dataset, which proves the potential of the transformer for diverse motion prediction.
2.3. Transformers in MOT
More recently, with the new focus on applying transformers [29] in vision tasks, many methods have made attempts to leverage the attention mechanism in tracking objects in videos. TransTrack [24] builds up a novel joint-detection-and-tracking paradigm by accomplishing object detection and object association in a single shot. Trackformer [25] extends DETR [15] by incorporating additional object queries sourced from existing tracks and propagates track IDs similarly to Tracktor [30]. MOTR [14] follows the structure of DETR [15] and continually propagates and updates track queries for association object identities. MO3TR [31] introduces a temporal attention module to update each track’s status over a temporal window, employing updated track features as queries in DETR [15]. GTR [32] designs a global tracking transformer that takes object features from all frames within a temporal window and groups objects into trajectories. In these works, the transformer architecture is carefully designed to suit the needs of tracking tasks. Our methods intend to utilize a transformer to build a strong motion model.
3. Methodology
In this section, we present the proposed tracking framework, as illustrated in Figure 2. The overall structure of the encoder and decoder can be seen in Figure 3.
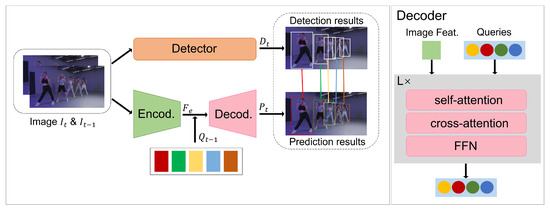
Figure 2.
Diagram of the proposed model: () The detector takes the current frame as input and generates the detection results. The features corresponding to detected objects are used as track queries for the next frame. The encoder takes two consecutive frames as input and outputs the enhanced image feature. The decoder takes the enhanced image feature and track queries as input. An MLP, which is omitted in this figure for simplicity, takes the output of the decoder to generate the final prediction results. Finally, Hungarian matching is used between the detections and predictions. () The detailed structure of the decoder consists of a self-attention layer, a cross-attention layer, and an FFN (Feed-Forward Neural Network) layer.
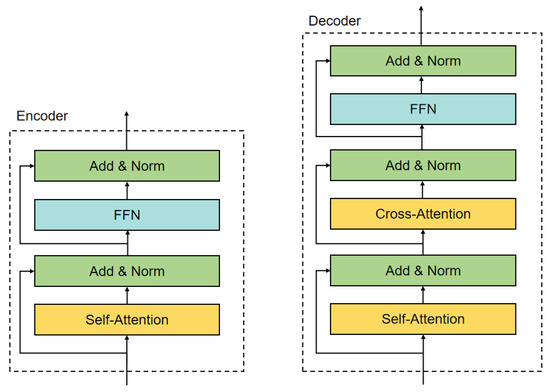
Figure 3.
The overall structure of the encoder and decoder.
3.1. Architecture
Following the tracking-by-detection paradigm, our model is built upon an object detector. An extra transformer architecture is employed to leverage motion cues. Given a frame , it is initially fed into the detector to generate the detection results (N represents the number of detected objects, 5 includes the bounding boxes and confidence score) and track queries , which are the features corresponding to each detected object. The backbone of the transformer takes two consecutive frames, and frame , as input and produces the stacked feature map . The transformer encoder consists of a self-attention block and a feed-forward block, taking as the query to generate the enhanced feature for the decoder. The transformer decoder, comprising a cross-attention block and a feed-forward block, utilizes the track queries and the enhanced feature as the query and key, respectively. An MLP is used after the decoder to obtain the prediction results (4 represents the bounding boxes). For each object detected in frame represented by the track query , the prediction results represent their predicted positions in frame t. The Hungarian algorithm is employed to achieve bipartite matching. The assignment is determined by a cost matrix that compares new detections with the tracks obtained in previous frames. We will discuss how to selectively use the prediction results to populate the cost matrix later.
3.2. Transformers and Linear Track
We have designed a hybrid strategy based on confidence scores to make motion estimates. Assuming to be the locations of the detections in frame , our goal is to predict their locations in frame t.
For high confidence score detections, we firstly turn their feature maps into track queries . Then, goes through a self-attention block, which can be expressed as
where is the dimension of the key vector and is the output of the self-attention block. is then fed into the cross-attention block, which can be expressed as
where is the output of the cross-attention block and represents the enhanced feature generated by the encoder. At the end, a feed-forward network and an MLP work on generating the final predictions:
where (4 represents the bounding boxes) are the predicted locations on frame t.
For low confidence score detections, we estimate their locations by a simple linear model. Assuming to be the location of one low confidence score detection on frame , its location on frame t can be represented by
where v is the mean velocity of this object between the last M frames. Further experiments will determine how many frames to compute the mean velocity it would be appropriate to choose. We set to be 1.
The whole hybrid strategy can be represented by
where represents location of the i-th detection in frame and represents its confidence score. represents the processing for high score detections that we discussed above and is the threshold for the confidence score. We set as 0.9 based on further experiments.
3.3. Training
Following the same settings as in TransTrack [24], we choose a static image as the train data; the adjacent frame is simulated by randomly scaling and translating the static image. Firstly, a trained detector generates detections and track queries from the original frame. Secondly, the track queries and the adjacent frame are fed into the transformer to obtain the prediction results. We apply a set prediction loss to supervise the prediction results. The set-based loss produces an optimal bipartite matching between the predictions and the ground truth objects. The matching cost is defined as
where is the focal loss, denotes the L1 loss, is the generalized IoU loss, and , , and are the corresponding weight coefficients. The training loss is the same as the matching cost except that it is only performed on matched pairs.
4. Experiments
4.1. Settings
Datasets. We evaluated our method on the multi-object tracking dataset DanceTrack [10] under the “private detection” protocol. DanceTrack [10] is a recently proposed dataset designed for human tracking, which focuses on promoting multi-object tracking studies with a stronger emphasis on association rather than mere detection. In this dataset, object localization is straightforward, but the object motion exhibits a highly non-linear behavior. Additionally, the objects share a close appearance, leading to significant occlusion and frequent crossovers. These aspects pose substantial challenges for both motion-based and appearance-matching-based tracking algorithms. As our main objective was to enhance tracking robustness in the presence of fast movements and non-linear object motion, we placed special emphasis on comparing TLtrack with previous methods, specifically on the DanceTrack [10] dataset, in the following experiments.
Metrics. We employed the CLEAR metrics [33], encompassing MOTA [34], FP, FN, and IDs, in addition to IDF1 and HOTA [35], to comprehensively assess various facets of tracking performance. MOTA is calculated based on FP, FN, and IDs, with a greater emphasis on detection performance due to the relatively larger presence of FP and FN. Conversely, IDF1 appraises the capability of preserving identities, with a stronger focus on association performance. Higher-order tracking accuracy (HOTA) explicitly balances the effect of performing accurate detection, association, and localization into a single unified metric for comparing trackers. HOTA decomposes into a family of sub-metrics that can evaluate each of the five basic error types separately, which enables clear analysis of tracking performance. The detection accuracy, DetA, is simply the percentage of aligning detections. The association accuracy, AssA, is simply the average alignment between matched trajectories, averaged over all detections.
Implementation details. TLtrack uses a default detection scores threshold of 0.6, unless specified otherwise. For the benchmark evaluation of DanceTrack [10], we solely adopted GIoU as the similarity metric. During the linear assignment step, a matching between the detection box and the tracklet box was rejected if the GIoU was smaller than −0.2. To address lost tracklets, we retained them for 30 frames in case they reappeared.
The detector utilized was YOLOX [17] with YOLOX-X as the backbone and a COCO-pretrained model as the initialized weights. With a trained detector, we trained the transformer for an input shape . The model was trained on 4 NVIDIA Titan xp GPUs with a batch size of 1. We used SGD as the optimizer with a weight decay of and a momentum of 0.9. The initial learning rate was for the transformer and for the backbone. All transformer weights were initialized with Xavier-init and the backbone model was pretrained on ImageNet with frozen batch-norm layers. We used data augmentation, including random horizontal, random crop, and scale augmentation. We trained the model for 20 epochs and the learning rate dropped by a factor of 10 at the 10th epoch. The total training time was approximately 7 days on the DanceTrack train set.
4.2. Benchmark Results
DanceTrack. In order to assess TLtrack’s performance under complex motion patterns, we present the results for the DanceTrack test set in Table 1. As evident from the results, TLtrack achieved advanced results when handling complex object motions. TLtrack achieved the highest HOTA, which meant achieving the best overall performance, but DetA was lower than CenterTrack and TransTrack. This was because the two algorithms were carefully designed for detection; at the same time, they did not have good association performance. The AssA of TLtrack was slightly lower than GTR, because this algorithm adopts a global association strategy. About IDF1, ByteTrack achieved the highest performance because lower confidence detections were recovered, but this strategy also affected the detection performance of the algorithm.

Table 1.
Results for DanceTrack test set. The methods in the bottom block use the same detections.
Comparison to other motion models. Our method, TLtrack, serves as a motion model aimed at dealing with complex motions. In this study, we compared TLtrack with other motion-based methods on the DanceTrack-test dataset: SORT [6], which applies a Kalman filter for motion prediction (the Kalman filter has been the predominant motion model for MOT); CenterTrack [12], which converts Centernet to an MOT architecture and predicts the center offset between two frames, utilizing the center offset to conduct greedy matching; and Transtrack [24], which consists of two transformer decoders, one for detection and another for predicting the position of each track. The results in Table 1 demonstrate that TLtrack outperforms all these methods, in terms of HOTA, IDF1, and AssA, showcasing its superior capabilities in handling complex motion patterns.
4.3. Ablation Studies
Component Ablation. To demonstrate the effectiveness of our hybrid strategy, we conducted experiments on the validation sets of Dancetrack [10]. We compared the performance of a linear model for all detections, a transformer for all detections, and our method. The results in Table 2 show that our hybrid strategy enables both models to reach their full potential on the DanceTrack dataset. When applying a transformer to predict the locations of all detections, the association performance is poor. When applying a transformer only to the high confidence score detections, the association performance is considerable. This phenomenon confirms our analysis that the accuracy of motion prediction is highly influenced by the quality of detections.

Table 2.
Ablation study on DanceTrack-val set.
Velocity in the linear model. In order to perform motion estimation using the linear model, the velocity of each track needs to be computed. In this section, we discuss how many last detections are appropriate to use to calculate the velocity. For the DanceTrack dataset, the motion is extreme. The results in Table 3 indicate that relying solely on the last four frames yields a reasonable estimation of future motion.

Table 3.
Influence of choice of M last detections to compute velocity on DanceTrack-val set.
TLtrack: . Based on the concept of enhancing the representativeness of track queries, we set to distinguish detections. The results in Table 4 show that 0.9 would be the appropriate threshold value. This phenomenon indicates that the confidence score plays a crucial role in handling challenging situations in MOT. For example, a decrease in the confidence score often signifies the occurrence of occlusion, which can easily lead to ID switches or target loss.

Table 4.
Ablation study on in the TLtrack on DanceTrack-val set.
Effect of input image size. Table 5 shows the effect of the input image size. As the input image size gradually increases, the HOTA performance reaches saturation when the short side of the input image is 800 pixels. Therefore, we set this as the default setting in TLtrack.

Table 5.
Ablation study on the input image size.
Effect of the frames of the video. Table 6 shows the effect of the frames of the video. We compared the model performance with the original video, sampling one frame every two frames, sampling one frame every three frames, and sampling one frame every four frames. As can be seen from the results, the performance of the model gradually decreased as the sampling frame rate increased.

Table 6.
The effect of the frames of the video.
5. Conclusions
This paper introduces TLtrack, a novel hybrid strategy to make motion estimates based on confidence scores. For detections with a high confidence score, TLtrack employs transformers to predict locations. Conversely, for detections with a low confidence score, it resorts to a straightforward linear model. In this way, not only the direction of the trajectory in the past can be considered, but also the latest movements can be analyzed. TLtrack’s strength lies in its simplicity, real-time processing capability, and effectiveness. An empirical evaluation on the Dancetrack dataset shows that our method achieves the best performance compared with other motion models.
Author Contributions
Conceptualization, Z.H.; methodology, Z.H.; software, K.Z.; validation, K.Z. and Z.H.; formal analysis, K.Z.; investigation, K.Z.; resources, D.Z.; data curation, D.Z.; writing—original draft preparation, Z.H.; writing—review and editing, K.Z.; visualization, Z.H.; supervision, D.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (No. 61572307).
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the institutional review board (IRB) of Shanghai University with a waiver of the requirement for informed consent.
Informed Consent Statement
Patient consent was waived because the the research used a public dataset that does not contain any identifiable information and there is no way to link the information back to identifiable information.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Luo, W.; Xing, J.; Milan, A.; Zhang, X.; Liu, W.; Kim, T.K. Multiple object tracking: A literature review. Artif. Intell. 2021, 293, 103448. [Google Scholar] [CrossRef]
- Zhu, J.; Lao, Y.; Zheng, Y.F. Object tracking in structured environments for video surveillance applications. IEEE Trans. Circuits Syst. Video Technol. 2009, 20, 223–235. [Google Scholar] [CrossRef]
- Xing, W.; Yang, Y.; Zhang, S.; Yu, Q.; Wang, L. NoisyOTNet: A robust real-time vehicle tracking model for traffic surveillance. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 2107–2119. [Google Scholar] [CrossRef]
- Lee, Y.G.; Tang, Z.; Hwang, J.N. Online-learning-based human tracking across non-overlapping cameras. IEEE Trans. Circuits Syst. Video Technol. 2017, 28, 2870–2883. [Google Scholar] [CrossRef]
- Zhang, K.; Li, Y.; Wang, J.; Cambria, E.; Li, X. Real-time video emotion recognition based on reinforcement learning and domain knowledge. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 1034–1047. [Google Scholar] [CrossRef]
- Bewley, A.; Ge, Z.; Ott, L.; Ramos, F.; Upcroft, B. Simple online and realtime tracking. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 3464–3468. [Google Scholar]
- Kalman, R.E. Contributions to the theory of optimal control. Bol. Soc. Mat. Mex. 1960, 5, 102–119. [Google Scholar]
- Zhang, Y.; Sun, P.; Jiang, Y.; Yu, D.; Weng, F.; Yuan, Z.; Luo, P.; Liu, W.; Wang, X. Bytetrack: Multi-object tracking by associating every detection box. In Proceedings of the Computer Vision–ECCV 2022: 17th European Conference, Tel Aviv, Israel, 23–27 October 2022; Proceedings, Part XXII. Springer: Berlin/Heidelberg, Germany, 2022; pp. 1–21. [Google Scholar]
- Wojke, N.; Bewley, A.; Paulus, D. Simple online and realtime tracking with a deep association metric. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3645–3649. [Google Scholar]
- Sun, P.; Cao, J.; Jiang, Y.; Yuan, Z.; Bai, S.; Kitani, K.; Luo, P. Dancetrack: Multi-object tracking in uniform appearance and diverse motion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 20993–21002. [Google Scholar]
- Cao, J.; Weng, X.; Khirodkar, R.; Pang, J.; Kitani, K. Observation-centric sort: Rethinking sort for robust multi-object tracking. arXiv 2022, arXiv:2203.14360. [Google Scholar]
- Zhou, X.; Koltun, V.; Krähenbühl, P. Tracking objects as points. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 474–490. [Google Scholar]
- Zhou, X.; Wang, D.; Krähenbühl, P. Objects as points. arXiv 2019, arXiv:1904.07850. [Google Scholar]
- Zeng, F.; Dong, B.; Zhang, Y.; Wang, T.; Zhang, X.; Wei, Y. Motr: End-to-end multiple-object tracking with transformer. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 659–675. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2020; pp. 213–229. [Google Scholar]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Ge, Z.; Liu, S.; Wang, F.; Li, Z.; Sun, J. Yolox: Exceeding yolo series in 2021. arXiv 2021, arXiv:2107.08430. [Google Scholar]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H.Y.M. Yolov4: Optimal speed and accuracy of object detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Tokmakov, P.; Li, J.; Burgard, W.; Gaidon, A. Learning to track with object permanence. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10860–10869. [Google Scholar]
- Wang, Q.; Zheng, Y.; Pan, P.; Xu, Y. Multiple object tracking with correlation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 3876–3886. [Google Scholar]
- Wang, Y.; Kitani, K.; Weng, X. Joint object detection and multi-object tracking with graph neural networks. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 13708–13715. [Google Scholar]
- Wu, J.; Cao, J.; Song, L.; Wang, Y.; Yang, M.; Yuan, J. Track to detect and segment: An online multi-object tracker. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 12352–12361. [Google Scholar]
- Zhu, X.; Su, W.; Lu, L.; Li, B.; Wang, X.; Dai, J. Deformable detr: Deformable transformers for end-to-end object detection. arXiv 2020, arXiv:2010.04159. [Google Scholar]
- Sun, P.; Cao, J.; Jiang, Y.; Zhang, R.; Xie, E.; Yuan, Z.; Wang, C.; Luo, P. Transtrack: Multiple object tracking with transformer. arXiv 2020, arXiv:2012.15460. [Google Scholar]
- Meinhardt, T.; Kirillov, A.; Leal-Taixe, L.; Feichtenhofer, C. Trackformer: Multi-object tracking with transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8844–8854. [Google Scholar]
- Zhao, Z.; Wu, Z.; Zhuang, Y.; Li, B.; Jia, J. Tracking objects as pixel-wise distributions. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27October 2022; pp. 76–94. [Google Scholar]
- Chaabane, M.; Zhang, P.; Beveridge, J.R.; O’Hara, S. Deft: Detection embeddings for tracking. arXiv 2021, arXiv:2102.02267. [Google Scholar]
- Ilg, E.; Mayer, N.; Saikia, T.; Keuper, M.; Dosovitskiy, A.; Brox, T. Flownet 2.0: Evolution of optical flow estimation with deep networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2462–2470. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Bergmann, P.; Meinhardt, T.; Leal-Taixe, L. Tracking without bells and whistles. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 941–951. [Google Scholar]
- Zhu, T.; Hiller, M.; Ehsanpour, M.; Ma, R.; Drummond, T.; Reid, I.; Rezatofighi, H. Looking beyond two frames: End-to-end multi-object tracking using spatial and temporal transformers. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 12783–12797. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Yin, T.; Koltun, V.; Krähenbühl, P. Global tracking transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8771–8780. [Google Scholar]
- Bernardin, K.; Stiefelhagen, R. Evaluating multiple object tracking performance: The clear mot metrics. EURASIP J. Image Video Process. 2008, 2008, 246309. [Google Scholar] [CrossRef]
- Milan, A.; Leal-Taixé, L.; Reid, I.; Roth, S.; Schindler, K. MOT16: A benchmark for multi-object tracking. arXiv 2016, arXiv:1603.00831. [Google Scholar]
- Luiten, J.; Osep, A.; Dendorfer, P.; Torr, P.; Geiger, A.; Leal-Taixé, L.; Leibe, B. Hota: A higher order metric for evaluating multi-object tracking. Int. J. Comput. Vis. 2021, 129, 548–578. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, C.; Wang, X.; Zeng, W.; Liu, W. Fairmot: On the fairness of detection and re-identification in multiple object tracking. Int. J. Comput. Vis. 2021, 129, 3069–3087. [Google Scholar] [CrossRef]
- Fischer, T.; Huang, T.E.; Pang, J.; Qiu, L.; Chen, H.; Darrell, T.; Yu, F. QDTrack: Quasi-dense similarity learning for appearance-only multiple object tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 15380–15393. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).