Generative Adversarial Networks for Synthetic Data Generation in Finance: Evaluating Statistical Similarities and Quality Assessment

Abstract

Generating synthetic data is a complex task that necessitates accurately replicating the statistical and mathematical properties of the original data elements. In sectors such as finance, utilizing and disseminating real data for research or model development can pose substantial privacy risks owing to the inclusion of sensitive information. Additionally, authentic data may be scarce, particularly in specialized domains where acquiring ample, varied, and high-quality data is difficult or costly. This scarcity or limited data availability can limit the training and testing of machine-learning models. In this paper, we address this challenge. In particular, our task is to synthesize a dataset with similar properties to an input dataset about the stock market. The input dataset is anonymized and consists of very few columns and rows, contains many inconsistencies, such as missing rows and duplicates, and its values are not normalized, scaled, or balanced. We explore the utilization of generative adversarial networks, a deep-learning technique, to generate synthetic data and evaluate its quality compared to the input stock dataset. Our innovation involves generating artificial datasets that mimic the statistical properties of the input elements without revealing complete information. For example, synthetic datasets can capture the distribution of stock prices, trading volumes, and market trends observed in the original dataset. The generated datasets cover a wider range of scenarios and variations, enabling researchers and practitioners to explore different market conditions and investment strategies. This diversity can enhance the robustness and generalization of machine-learning models. We evaluate our synthetic data in terms of the mean, similarities, and correlations.

1. Introduction

In today’s dynamic landscape, many organizations use deep-learning and machine-learning techniques to process and organize large amounts of data [1], especially in the medical [2], educational [3], and financial [4] fields. Companies allocate a significant portion of their budgets to unstructured data, aiming to transform it into actionable insights for decision-making. These efforts enable informed decision-making, empowering companies to strategize effectively, innovate, and maintain competitiveness in their respective industries.

Data scarcity poses a significant hurdle across diverse industries, affecting artificial intelligence (AI) projects [5,6]. For instance, in the financial domain, small or incomplete datasets can create challenges when predicting stock market indexes or evaluating investment strategies. When analyzing data from newly listed companies or startups, the lack of reliable data can significantly increase uncertainty and investment risk associated with these ventures [7,8,9,10].

Similarly, healthcare organizations within the medical sector face challenges due to small datasets, which hinder the development of predictive models for disease diagnosis and treatment outcomes. Stringent privacy regulations limit the sharing of patient-specific information, therefore impeding collaborative research and the creation of accurate predictive models needed for personalized medicine.

In such a context, the task we aim to tackle in this paper involves synthesizing a dataset resembling the input data with similar properties. The input dataset comes from the stock market and presents several constraints: a limited number of data instances and numerous inconsistencies, including missing values, duplicate rows, and unscaled values.

In the past, researchers have used statistical and mathematical techniques, like randomization-based methods or Bayesian network models [11,12], to generate synthetic or correlated data to meet their data requirements. With the advent of deep-learning technology, various methodologies have emerged to address this problem as well [13]. Despite these advancements, the existing methodologies have shown certain drawbacks and limitations, which will be discussed in depth in Section 2. With the introduction of generative modeling in AI, different neural network models like Variational Auto-Encoders (VAEs) [14] and Generative Adversarial Networks (GANs) [15] have been used to deal with such problems with great accuracy and performance [16,17].

For example, the work in [16] introduces the Differentiable Augmentation for Data-Efficient GAN Training, which aims to enhance the training efficiency of GANs by incorporating differentiable augmentation techniques. This involves applying data augmentation methods to both real and generated data during training, enabling the GAN model to produce more diverse and realistic data. The other study mentioned in [17] is about the generation of synthetic data with low-dimensional features for condition monitoring and utilizes GANs to create artificial data samples that closely mimic real-world conditions relevant to condition monitoring tasks. By generating synthetic data, this approach addresses challenges associated with limited or insufficient datasets, therefore enhancing the performance of machine-learning models in condition monitoring applications.

The primary motivation of this work lies in addressing the challenges of data scarcity, resolving inconsistencies, and producing more diverse datasets that are very cost-effective. We have implemented a GAN architecture with a carefully designed, customized parameter configuration optimized for data augmentation purposes.

The synthetically generated data offers enhanced model performance, enabling better generalization. Additionally, the flexibility of GANs allows us to adapt the data generation process to different domains, providing a valuable tool for various unsupervised learning tasks.

More in detail, the contributions we bring with our work are the following:

• Expansion of Dataset Size—Our methodology successfully expands the size of the original financial dataset, addressing the issue of limited data availability for training and producing diverse sizes of correlated samples.
• Enhanced Model Performance—Using synthetic data improves the performance of different models by providing more examples and diverse data, helping the models understand different scenarios and handle outliers and rare events more effectively.
• Cost-Effective Solution—Generating synthetic data proves to be a cost-effective alternative to the difficult and expensive processes involved in gathering, cleaning, and processing new datasets.
• Balanced Feature Distributions—Our method has the potential to address imbalances in non-continuous columns in the input dataset. By generating synthetic data, it effectively balances out these uneven feature distributions, enhancing its usefulness for machine-learning tasks.

The rest of this manuscript is structured as follows. In Section 2, we cover previous related work and methods proposed for data generation using various techniques, both with and without generative modeling. Section 3 details the task we aim to solve in this paper. Section 4 outlines the proposed GANs model’s architecture and discusses the optimizations we have performed to improve its efficiency. In Section 5, we show the performance evaluation we have carried out and show the statistical properties of the newly generated data and the original dataset. Finally, Section 6 ends the paper with a summary and future directions for where we are headed.

2. Related Work

This section explores various methodologies used in the economic and financial sectors to generate synthetic data, with the goal of addressing challenges such as data scarcity, limited data availability, and persistent issues related to unscaled and low-quality data. More in detail, Section 2.1 discusses synthetic data generation without relying on GANs. In contrast, Section 2.2 and Section 2.3 specifically address synthetic data generation utilizing VAEs and GANs, respectively.

2.1. Synthetic Data Generation without GANs

The study conducted by the authors in [18] is dedicated to overcoming the challenges posed by limited datasets through the application of synthetic data generation techniques. The primary focus lies in the implementation of Kernel Density Estimation (KDE) as the central method for approximating underlying probability distributions. KDE utilizes statistical estimation techniques, employing kernels like Gaussian or others, to estimate the probability density function of a provided dataset. While KDE is proficient in generating synthetic data, it does come with limitations. Its effectiveness depends heavily on assuming a specific dataset structure, which poses challenges when the actual distribution significantly deviates from this assumption or involves intricate patterns. Additionally, KDE encounters difficulties with high-dimensional or extremely sparse datasets, which impede its ability to accurately replicate the complexities inherent in such data scenarios.

Early attempts at generating synthetic financial data employed traditional statistical methods. In the study presented in [11], the authors introduced a technique based on bootstrapping to construct synthetic stock price time series data. They illustrated that this method effectively retained the statistical properties of the original data while preserving the temporal dependencies within the time series. However, this approach had limitations in capturing complex financial patterns and dependencies effectively. In the realm of data augmentation for stock price prediction tasks, alternative techniques such as time warping and random insertion have been explored [19,20].

Numerous investigations have delved into the creation of synthetic financial data through the application of mathematical models and Monte Carlo simulations, as discussed in [21]. Notably, researchers in [22] introduced a simulation methodology utilizing Stochastic Differential Equations (SDE). This approach aimed to generate synthetic stock price data by incorporating key elements such as drift and volatility to accurately preserve market characteristics.

Copula-based models, as demonstrated in [23], are adept at uncovering the dependencies between variables in a dataset without imposing rigid patterns. Their efficacy is particularly noteworthy in generating data with distinctive statistical characteristics, rendering them valuable in diverse fields such as weather and climate modeling [24]. However, their limitations become evident when confronted with complex relationships within datasets [25]. These challenges impact their overall performance and limit their applicability in handling highly complex relationships.

2.2. Synthetic Data Generation with VAEs

Introduced in 2014, VAEs [26] have gained renown for their proficiency in generating synthetic data. However, VAEs are often labeled as “black boxes” due to the intrinsic complexity in understanding their internal mechanisms [27]. Operating through complex and complicated mathematical processes, these models present a significant barrier to understanding how they discern patterns from input data and subsequently reconstruct new samples. In contrast to more transparent models, VAEs deliberately shroud their inner workings, posing a challenge in gaining insight into their underlying processes. This lack of transparency becomes particularly pronounced in fields such as finance [28], where the ability to comprehend the rationale behind decision-making is foremost. Despite this drawback, VAEs remain highly practical for synthesizing data and have demonstrated success in numerous applications [29].

In the domain of VAEs, data undergoes compression through an encoder and subsequent reconstruction via a decoder. Trained on real data, VAEs aim to generate new data with a semblance of similarity by identifying patterns acquired during training. Simply put, VAEs may prioritize a comprehensive understanding of broader trends in the data, potentially overlooking finer details. This tendency could potentially compromise the accuracy of synthetic data when compared to more realistic models, such as GANs [30]. In the context of finance, GANs emerge as a preferred alternative, excelling in the creation of synthetic data closely resembling the given input data. Utilizing GANs enables financial models to generate synthetic data that is more closely aligned with real-world data. This, in turn, enhances the precision of analyses and decisions [31].

The authors in [29] introduced the Oblivious Variational Auto-Encoder (OVAE), a model integrating differentiable oblivious decision trees (ODTs) into the VAE architecture. Despite its relative performance compared to previous GAN implementations, this model faces drawbacks. A key limitation is the complexity and interpretability of the generated latent space. The inclusion of ODTs, while beneficial for decision-making and synthesis, might lead to a less interpretable latent space compared to traditional VAEs.

Performance of OVAE might suffer when handling highly complex or diverse datasets [29]. Oblivious decision trees are known for their simplicity, which could restrict the model’s ability to capture complex patterns and relationships in the data. This limitation could lead to suboptimal reconstruction and synthesis of complex data distributions.

2.3. Synthetic Data Generation with GANs

The advent of GANs, pioneered by authors in [15], has revolutionized synthetic data generation, especially within the financial domain. Early applications utilizing Vanilla GANs [30] for the synthesis of financial time series data demonstrated their capacity to replicate data distributions, enabling the generation of authentic financial sequences [32]. In the realm of finance, GANs are valuable for generating synthetic data that accurately mirrors the statistical patterns and characteristics of authentic financial data [33]. This synthetic data serves various purposes, including training machine-learning models, conducting simulations for risk assessment, and augmenting limited datasets for analysis without compromising sensitive information. However, ensuring the quality and accuracy of generated financial data remains a significant challenge. GANs must strike a delicate balance between generating data that preserves the statistical properties of the original dataset and avoiding overfitting or introducing biases. Continuous advancements and refinements in GAN architectures and training methodologies strive to enhance the fidelity and reliability of synthetic financial data.

Specialized GAN variants like TimeGAN [34] have emerged to overcome the limitations faced by Vanilla GANs in generating financial time series data. They aim to enhance stability, quality, and fidelity by specifically addressing domain-specific complexities. In [35], authors proposed a conditional GAN approach, incorporating financial indicators as conditional inputs. This method notably improved the generation of multidimensional financial time series data and offered better control over the generated samples.

Wasserstein GANs (WGANs) were introduced in [36] and have been applied to financial data generation. The WGAN architecture improved training stability and mode collapse issues. WGANs encounter challenges in generating financial data due to the complex nature of financial datasets. While they improve stability, training demands careful adjustment to prevent instabilities. The high complexity and dimensionality of financial data pose challenges in ensuring both realistic and diverse outputs. Despite efforts to mitigate mode collapse, WGANs may still struggle to fully capture the complexity of financial data distributions.

GenerativeMTD is an approach introduced in [37] to tackle the problem of synthetic data generation for tabular datasets. Unlike conventional methods, GenerativeMTD utilizes pseudo-real data for model training, enhancing privacy protection. Employing a variational auto-encoder-based generative adversarial network architecture (VAE-GAN) ensures that synthetic data preserve statistical similarity with the real dataset while safeguarding data privacy through distance-based privacy metrics. However, the reliance on deep-learning techniques in GenerativeMTD introduces complexities, especially with small datasets. This complexity may impede model convergence and generalization, particularly in the presence of high dataset variability or noise.

Compared to existing methods, our proposed approach employs GANs, which excel in capturing complex data structures, modeling complicated patterns, and effectively representing high-dimensional spaces. Their capacity to generate synthetic data mirroring original datasets, while overcoming the limitations of traditional approaches, positions GANs as a more versatile and effective solution for synthetic data generation across various domains.

3. Description of the Task

Synthetic data generation is essential in many areas where data are scarce or limited, as is often the case in the economic and financial sectors. In this context, synthetic data generation helps to enhance decision-making by addressing issues like insufficient data or privacy concerns [33,38,39].

In our task focused on the financial domain, we specifically target continuous data derived from the stock market. This initiative was part of a global competition sponsored by BNP Paribas and Ecole Polytechnique Paris, drawing participation from various researchers worldwide. The primary objective of the competition was to synthesize diverse datasets from the provided input data. The input dataset for this task was anonymized and exclusively released for the competition.

The considered dataset (Dataset publicly available at: https://github.com/faisalramzan3725/Generative-Adversarial-Networks-GANs-for-Synthetic-Data-Generation-in-Finance-Evaluating-Statisti/tree/main accessed on 8 May 2024) provides some basic information about historical stock market trends, encompassing columns likely related to the opening price, closing price, highest price, and lowest price. These columns serve as input features that can be used for various prediction tasks in the stock market realm. For instance, these features could be employed to predict the next day’s closing price, analyze price trends (whether they will rise, fall, or remain steady), anticipate volatility in stock prices over a short period, or derive buy/sell signals based on technical indicators like moving averages or Moving Average Convergence Divergence (MACD). However, accurately predicting stock prices involves complexities influenced by multiple factors beyond historical data alone. Factors such as data quality, the choice of relevant features, the models used, and broader market conditions significantly impact the effectiveness of these predictions. Overcoming the limitations of data scarcity is a key goal, aiming to create a more diverse dataset that spans various scenarios. This pursuit goes beyond prediction tasks, focusing on enhancing data availability and diversity to better understand and adapt to the dynamic nature of the stock market.

The provided dataset is exclusively intended for this purpose, and our task consists of two stages. The first stage entails structuring the data, rectifying inconsistencies, and imposing constraints, which includes the removal of outliers. After preprocessing, we acquired a normalized dataset comprising 746 rows with four anonymized features. It is important to emphasize that the dataset is confidential, and we only use features relevant to the target, therefore excluding personal details and other sensitive information. Despite these limitations, the dataset plays a vital role in predicting stock market trends. However, its effectiveness in training models is hindered due to its size and feature constraints. Our primary objective is to overcome these limitations by improving the quality of the existing data and broadening its scope through data synthesis methods. Addressing the challenges posed by a dataset of this nature involves addressing three key problems:

• Limited Data Availability—The small size of the dataset in terms of rows poses constraints on our models, limiting their ability to learn effectively.
• Missing Data—Certain portions of the dataset lack information, creating challenges in understanding complete stock market trends. This might be due to privacy concerns or other data availability issues.
• Impact on Model Performance—Anomalies within the dataset significantly disrupt the accuracy and reliability of our models. Furthermore, the presence of missing or duplicated rows creates inconsistencies that negatively impact model performance.

The delineated constraints wield a substantial influence on the stock market prediction process, directly shaping decision-making systems. This impact holds particular significance for investors relying on precise predictions to refine their investment strategies. Acknowledging and proactively addressing these limitations becomes imperative. An essential strategy to overcome these challenges involves the careful creation of high-quality, diverse datasets. This approach empowers our models to learn more effectively, augmenting their capacity for generalization. Enhanced data quality, in turn, manifests in superior results, ultimately bolstering the reliability and efficacy of our predictive models. Such augmentation not only fortifies our internal processes but also extends its positive effects to the wider investor community. By furnishing more accurate market forecasts, we equip investors with the information necessary for well-informed decisions, therefore enriching their overall investment experience.

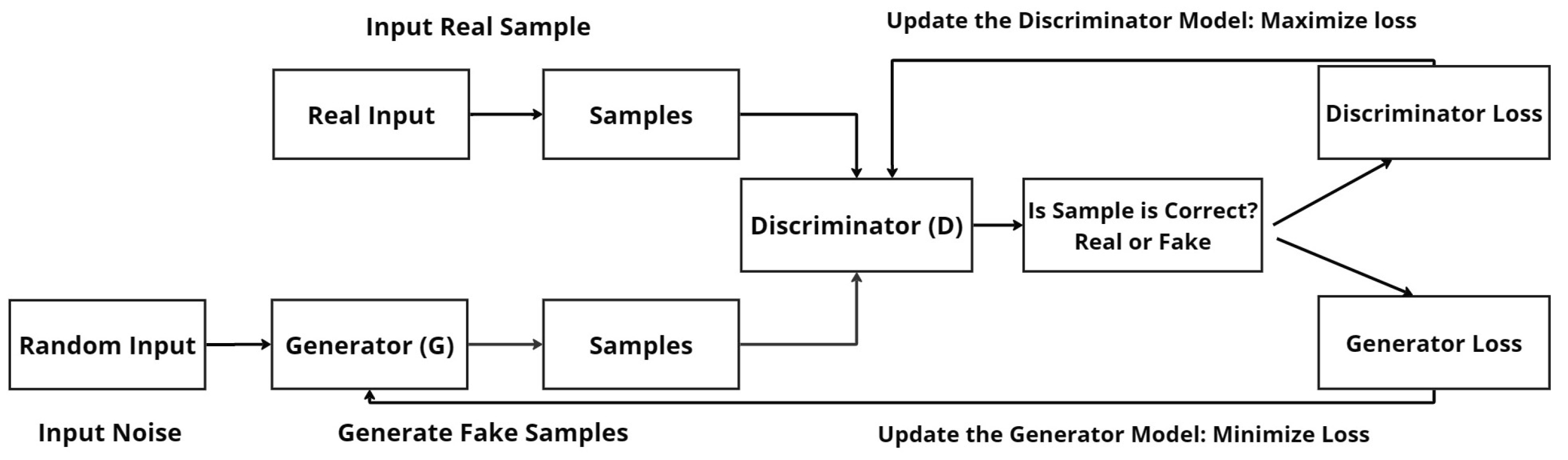
4. The Proposed Generative Adversarial Network

In this section, we detail the architecture of the developed GAN and discuss how we have optimized it for our synthetic data generation task. A traditional GAN consists of two main parts shown in Figure 1. In the generative network, the generator, G, takes random noise or latent input as its starting point from the latent space. This noisy input is typically generated from a random distribution, like a Gaussian distribution, and serves as the initial signal that the generator uses to create synthetic data. The generator then transforms this noise into data that ideally resembles the real data. The generator’s objective is to learn how to map random noise to data samples that closely resemble the real data, aiming to deceive the discriminator network within the framework. At the same time, the discriminator, D, identifies the difference between real and fake data points generated by G using noise from the latent space.

For a better understanding, consider the analogy of fake currency detection as an illustrative example clarifying the underlying concept of the GANs framework. Imagine the role of the police in distinguishing between authentic and fake currency, similar to the operation of a discriminator within this framework. Conversely, a criminal engaging in the illegal production of forged currency can be considered analogous to the function of a generator in GANs. In this scenario, the fake currency creator intensively endeavors to craft banknotes that closely resemble genuine ones to deceive the discerning abilities of the police. This dynamic mirrors the interplay between the discriminator and generator within the network as they collaborate to generate and classify samples as either authentic or counterfeit.

In a GAN, the generator network takes the random vectors or data points as input and, through its layers, transforms them into synthetic data samples resembling the real data distribution [40]. As the generator learns from successive iterations of training, it refines its ability to map points within this latent space to meaningful data points, ultimately creating more realistic samples by capturing the underlying patterns and structures of the real data. Generating noise for the latent space involves utilizing random number generators to create vectors of random data points following a specified distribution, allowing the generator to generate diverse synthetic data samples during the training phase [41].

The GAN model operates as a two-player game, where the discriminator (D) functions as a classifier distinguishing between real and synthetic points generated by the generator (G). The architecture of D is dependent on the designer’s choices, particularly in terms of the number of layers utilized. Its primary objective is to extract input features, with the output of these layers activated using the “rectified linear activation (ReLU)” function [42,43]. This activation function transforms the input features to the subsequent layer, operating solely on positive numbers; otherwise, it yields 0. In contrast, the “sigmoid" activation function [43] is responsible for activating the final output layer in D, aiding in its classification task of recognizing between real (1) and fake (0) samples.

The GAN model employs two distinct loss functions: one for the generator and another for the discriminator itself [15,40]. The functions play a critical role in assessing the model’s performance in a GAN. The disparity between real and synthetic data is measured by evaluating their likeness in terms of various factors, such as means, standard deviations, and common plot distributions. The loss functions in G and D play separate roles during different stages of the training process of the model. The primary GANs loss function, commonly termed “Vanilla” or minimax loss [44], assesses how closely the real and generated data align. It involves the minimization of the log-probability of the discriminator being correct (log(D(x))) for real data samples and the log-probability of the discriminator being incorrect (log(1 − D(G(z)))) for generated samples.

The evaluation of the minimax loss in GANs involves employing the cross-entropy loss function to assess the disparity between real and generated data distributions, particularly during discriminator optimization. It is important to note that while Jensen–Shannon (JS) [33,39] divergence measures the similarity between probability distributions, it is not directly integrated into the GAN’s loss function. Instead, JS divergence quantifies the difference between distributions and bears a relation to the Kullback–Leibler (KL) divergence [33,39]. However, directly computing JS divergence faces limitations, making it impractical for GAN training. In GANs, the training process focuses on minimizing the adversarial loss through a minimax game between the generator and discriminator.

While the generator aims to minimize this minimax loss, the discriminator seeks to maximize it. When D distinguishes between real and generated (fake) samples, it uses its loss function to penalize incorrect classifications. This means that if D wrongly identifies a real sample as fake or a fake sample as real, its loss function measures this error and guides the model to improve accuracy. As for the loss of D, the aim is to maximize the Log (1 − D(G(z))) expression, ensuring it does not directly affect Log D(x) [33,39,40], as shown in Equation (1):

$$G_{min}{D}_{max}V(D,G)=E_x\left[logD\left(x\right)\right]+E_z\left[log(1-D\left(G\left(z\right)\right))\right],$$

(1)

where:

• D(x) represents the output of the discriminator (D) when given a real instance (x) as input. It estimates the probability that the instance is real.
• $E_x$ is the expected value operator applied to all real instances. It represents the average value of the discriminator’s output given a real instance x as input.
• G(z) represents the output of the generator (G) when given a random input (noise or latent point) denoted as z. The generator uses this input to generate synthetic or fake samples.
• D(G(z)) represents the output of the discriminator when given the generated sample (G(z)) as input. It represents the discriminator’s classification or estimation of whether the generated sample is real or fake.
• $E_z$ is the expected value operator applied to all random inputs to the generator. It represents the average value of the discriminator’s output when given generated sample z as input.

The optimization process in Equation (1) drives the generator to create samples that increasingly resemble real data, reducing the discrepancy between the real and generated distributions.

Both G and D share similar neural network architectures. To improve the model’s performance, conventional backpropagation [45] is employed to optimize the network by minimizing the loss function. This process involves tracing back errors from the output layer to the input layer and adjusting the network weights in each layer accordingly. The goal is to reduce the difference between predicted and actual values, gradually enhancing the model’s ability to correctly classify samples. In this unsupervised learning task, classic gradient descent [39,40,45] is utilized within a limited number of iterations. Specifically, the “Adam” optimizer [33,40,45], an effective extension of gradient descent, dynamically updates the network parameters iteratively. Through this iterative process of updating network weights, the model becomes refined, improving its predictive capabilities with updated features and adjusted weights. Ultimately, this technique enables the network to learn from errors and make more accurate predictions.

In the initial stages of training, the generator (G) struggles to produce plausible synthetic samples, making it easy for the discriminator (D) to identify the fake ones. However, as training progresses, G improves its ability to generate synthetic samples, gradually deceiving D into misclassifying the samples. The objective of G is to reach a state where D can no longer reliably distinguish between real and synthetic data points.

From a data-driven perspective, GANs offer several advantages:

• Capturing Data Distribution: GANs learn the underlying data distribution directly from the input dataset without relying on explicit assumptions or predefined models. This enables the generation of synthetic data that closely resembles the real data distribution, capturing both global and local data patterns.
• Flexibility and Adaptability: GANs are highly flexible and adaptable, making them suitable for various data types and domains. They can support various data modalities, such as images, text, and numerical data, making them highly versatile for generating synthetic data across diverse domains.
• Non-linear Data Transformation: GANs can capture complex, non-linear relationships within the data, allowing for the generation of synthetic samples that exhibit intricate patterns and structures present in the real data. This is particularly beneficial for domains with intricate data dependencies, such as finance.
• Enhanced Privacy and Security: by generating synthetic data, GANs offer a means to share data for research or collaboration while preserving privacy and confidentiality. Synthetic data can be used in place of sensitive real data, reducing the risk of privacy breaches or data leaks.
• Continuous Improvement: GANs can be trained iteratively to enhance their performance and generate more realistic synthetic data over time. By fine-tuning the model architecture and training parameters, GANs can progressively improve their ability to generate data samples that align with the underlying data distribution.

The integration of GANs in synthetic data generation aligns with the data-driven approach by leveraging advanced machine-learning techniques to capture and replicate the complex data distributions present in real-world datasets. This approach provides the flexibility and scalability necessary for the privacy-preserving generation of synthetic data that closely represents the original dataset.

Model Setting and Parameters

Our primary goal is to synthesize continuous financial data, and for this purpose, we implemented the solution recently proposed in [46], which has previously addressed similar challenges in the domain of tabular data (Python code available from the authors at: https://github.com/Diyago/GAN-for-tabular-data, accessed on 8 May 2024). This TabularGAN, which we will use as a baseline, is specifically designed for uneven distributions. We tested our dataset using the suggested model, and we did not observe significant results capable of overcoming our specific challenges. This lack of impact can be attributed to the fact that our input dataset is highly specialized, and this opened up the possibility to implement various enhancements in the model, as will be detailed next, such that to align with our task requirements. In the rest of the paper, we will refer to this modified version of the GAN model as “FinGAN”. Indeed, the selection and tuning of a few hyperparameters, such as epochs, batch size, learning rate, and early stopping, play pivotal roles in GAN model training. Their different roles are explained in the following.

• Epochs: Determining the number of iterations the entire dataset passes through the network during training is critical. While a higher number of epochs can allow the model to learn more complex patterns, excessive epochs may lead to overfitting. In our FinGAN model, we carefully adjusted the epoch value, set to 500 in the baseline model, which proved insufficient for capturing complex network patterns. Excessively high epoch values risk memorizing training data instead of achieving effective generalization. Therefore, an optimal experimental setting was required, providing the value of 1000 epochs to be an optimal trade-off.
• Batch Size: The number of samples processed before updating the model’s parameters, known as batch size, plays a crucial role. Larger batch sizes, such as the baseline GAN model’s 500, might speed up training but come with increased memory demands. In FinGAN, we experimentally reduced the batch size to 128, aiming to enhance stability and potentially expedite convergence.
• Learning Rate: The learning rate, controlling the step size of parameter updates during training, is another important parameter. A higher learning rate can lead to faster convergence but may cause instability. In FinGAN, we experimentally opted for a lower learning rate of 0.0001, enhancing stability during convergence, in contrast to the baseline model’s use of 0.02. It is important to note that striking the right balance is key, as an excessively small learning rate may impede convergence speed.
• Early Stopping: Introducing early stopping as a mechanism for halting training when certain criteria are met is also important. This prevents overfitting by stopping training before the model starts fitting noise in the data, and it also helps conserve computational resources. FinGAN incorporates early stopping, whereas the baseline GAN model lacks this feature.

The methodology proposed in this paper is illustrated in the flowchart depicted in Figure 2. Each step of the methodology is described in detail below:

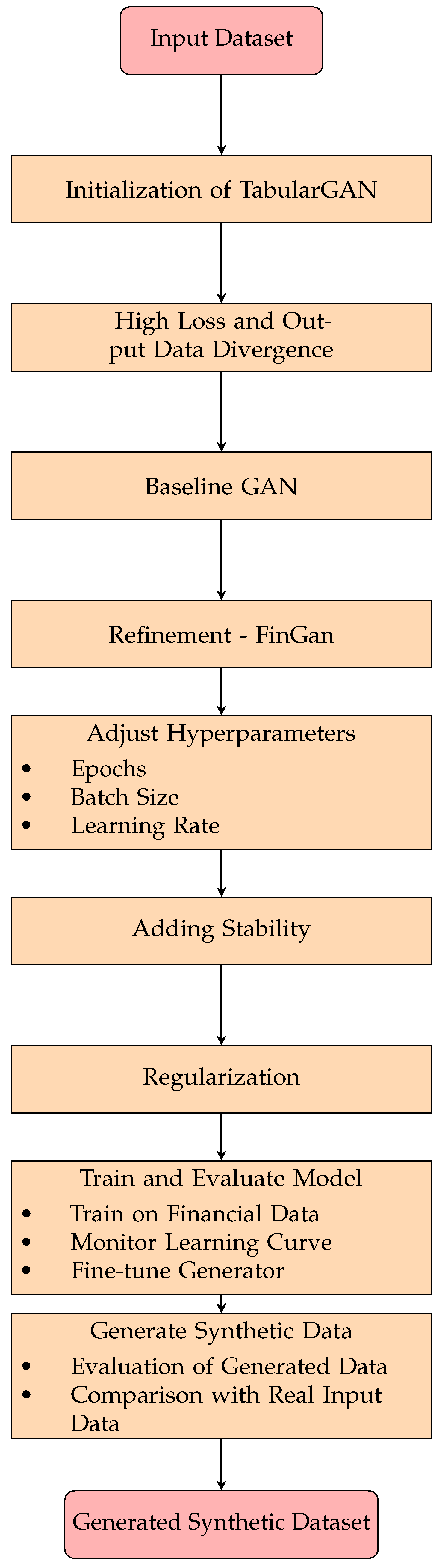
• Input Dataset: This represents the financial continuous dataset, which serves as the input data for the subsequent steps.
• Initialization of TabularGAN: Initially, we established the TabularGAN model as the starting point for our workflow.
• High Loss and Output Data Divergence: Throughout this process, we experienced high loss and divergence in the output data, particularly concerning the application of the TabularGAN model to our dataset.
• Baseline GAN: Then, we switched from the TabularGAN model to the baseline GAN model as an alternative approach.
• Refinement–FinGan: We refine the baseline GAN model to better suit financial data by modifying both the Generator (G) and Discriminator (D) architecture. This adaptation results in the creation of the FinGAN model.
• Adjust Hyperparameters: Fine-tuning of hyperparameters such as “Epochs”, “Batch Size”, and “Learning Rate” is performed to optimize the performance of the FinGAN model.
• Adding Stability: Additional features such as “Early Stopping” and “Batch Normalization” are incorporated into the FinGAN model to improve its stability and performance.
• Regularization: Techniques for controlling the latent space are applied, specifically using regularization to confine the range of generated data points.
• Train and Evaluate Model: The FinGAN model is trained on financial data, and its performance is evaluated. This involves monitoring the learning curve and fine-tuning the generator.
• Generated Synthetic Dataset: In the last phase of our workflow, we utilized the trained FinGAN model to generate the synthetic dataset that replicates the traits of the original financial data. This process entails employing the trained generator network to produce artificial data points that closely mirror the patterns and distributions found in the input real financial dataset.

In the final configuration of our model, we further included batch normalization relative to the baseline GAN model [46], which enhanced training stability by normalizing layer inputs and effectively addressing challenges such as vanishing or exploding gradients and promoting improved convergence. We calculated the loss by averaging real and generated data batches, guiding the model’s progress based on how accurately the generator replicated the real data. Early monitoring of the learning curve provides insights into the model’s behavior, enabling necessary adjustments to achieve the desired learning patterns. Batch normalization facilitated the integration of standardized inputs, leading to faster convergence and increased overall efficiency. Precise control over the generator’s output ensures realism in the generated data, allowing fine-tuning for a closer match to the real data distribution.

In the TabularGAN baseline, we identified high loss and a noticeable difference between the input data fed to the model and the output it generated. This discrepancy indicated that the generator component of TabularGAN was producing data points that were exceptionally high in value, causing a divergence from the intended distribution. To remedy this challenge, we delved into various techniques aimed at controlling the samples within the latent space of the GAN. We explored three primary methods: regularization [47], noise injection, and clamping [48].

Regularization methods played a vital role, specifically for the continuous nature of financial data. By applying regularization, we could confine the generated data points within desired ranges, better aligning them with the properties of the real financial data. Noise injection was another significant technique we adopted. It helped prevent the model from overfitting to specific data points by introducing controlled randomness into the latent space. Lastly, clamping sets limits or boundaries for the values in the latent space, ensuring that the generated data adheres to the characteristics of the continuous financial data.

In terms of computational complexity, GANs face challenges such as training instability, mode collapse, and finding the right balance between the Generator and Discriminator. To address these challenges, various solutions have been experimented with, including designing more stable network architectures, modifying learning objectives, regularizing objectives, and tuning hyperparameters. These efforts complement the enhancements made to our model, aiming to improve the overall effectiveness of GANs in generating synthetic financial continuous data. Overall, the computational complexity of GANs is a critical factor that influences their training stability, convergence, and the quality of generated samples. Researchers continue to explore innovative solutions to enhance the performance of GANs and address the challenges associated with their computational complexity, aligning with our focused training efforts tailored to specific goals.

5. Performance Evaluation

This section delineates the experiments conducted, commencing with Section 5.1, which provides an illustrative overview of the metrics utilized. Following this, a thorough analysis of the results is conducted in Section 5.2, where they are examined and scrutinized using standard statistical measures. Furthermore, we addressed study limitations in Section 5.3 and highlighted the advantages of utilizing synthetic datasets in Section 5.4.

5.1. Experimental Setup

When assessing the quality of synthetic continuous data, various established metrics serve as benchmarks to measure how closely the generated continuous data aligns with the input data. Our evaluation, guided by specific criteria mandating the use of predefined evaluation methods, relies on metrics such as the Kullback–Leibler Divergence (KL Divergence) [49], the Wasserstein Distance [50], the Energy Distance [51], and the Maximum Mean Discrepancy (MMD) [52]. These metrics provide quantitative measures for assessing the similarity between the generated continuous data and the actual data distributions, as depicted in

Table 1. Evaluation of Synthetic Financial Continuous Data.

Evaluation Method	Baseline GAN	FinGAN
KL Divergence	0.357	0.107
Wasserstein Distance	0.060	0.002
Energy Distance	0.220	0.017
MMD	0.196	0.0093

. Below, we describe each of them.

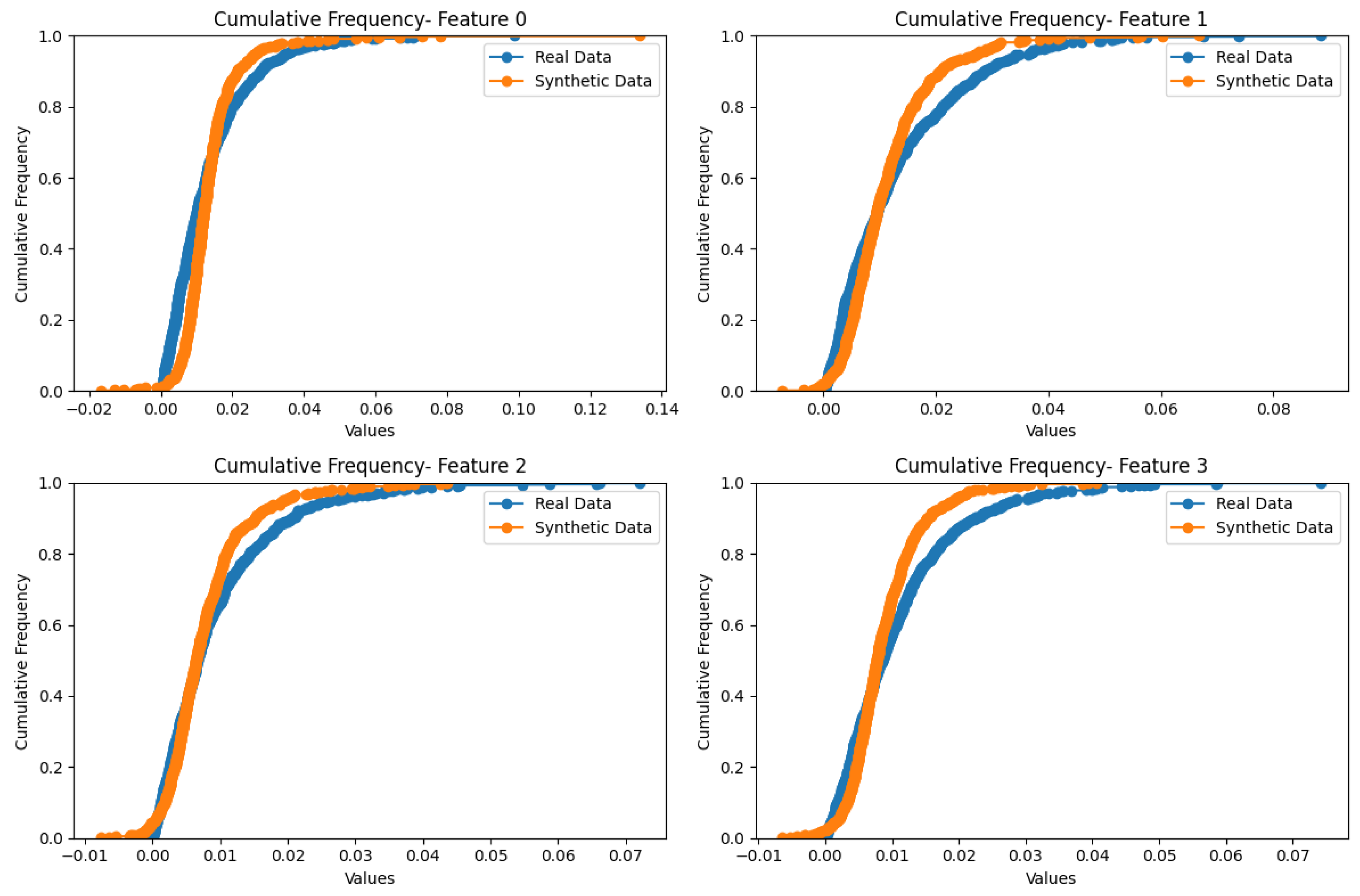
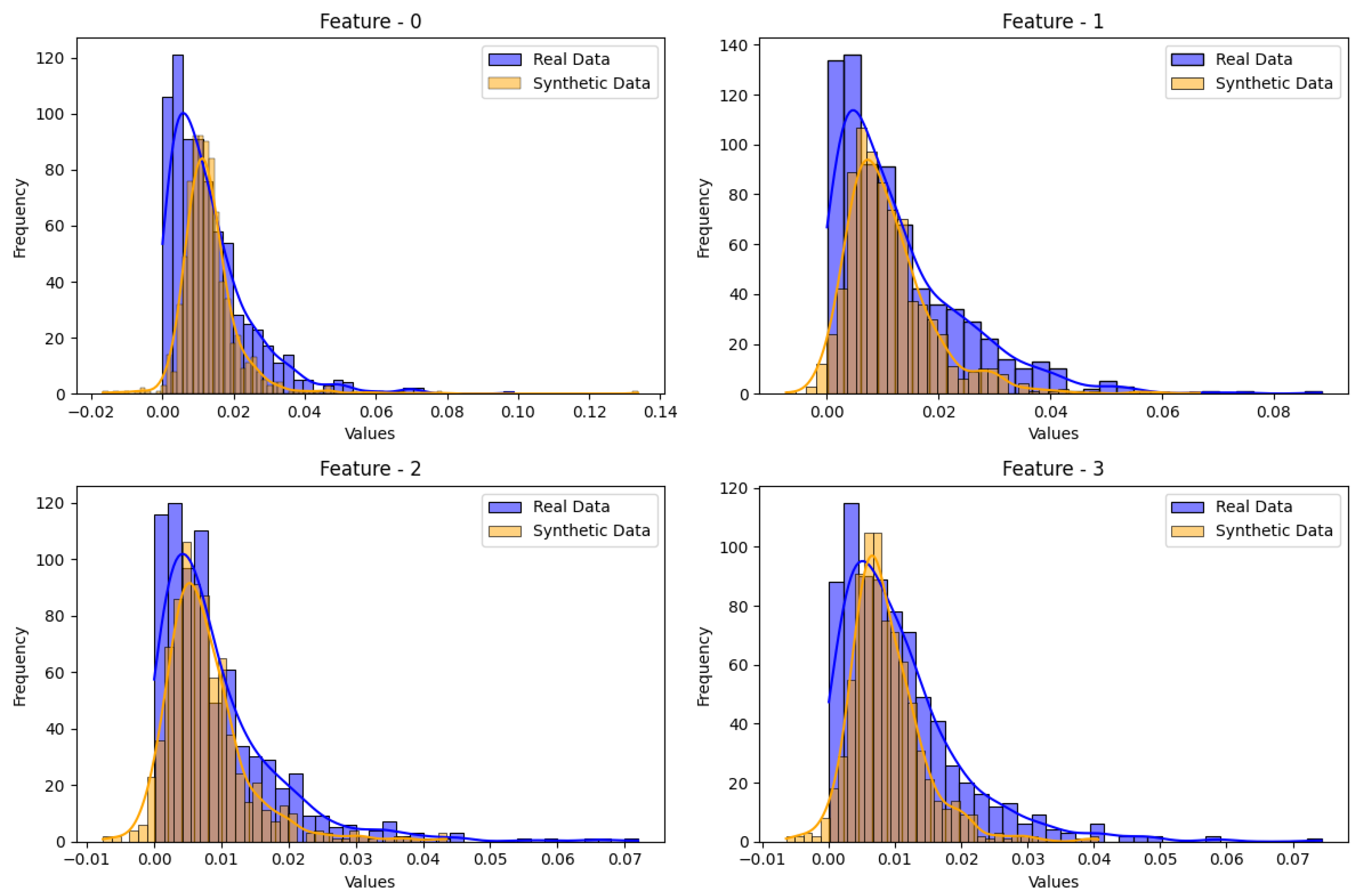
• The KL Divergence measures the difference between two probability distributions, ranging from 0 (perfect similarity) to positive infinity (complete dissimilarity). Values close to zero imply similar distributions, while higher values indicate greater dissimilarity, serving to differentiate between two continuous distributions [49].
• The Wasserstein Distance is a widely applied metric for continuous data, measuring the distance between two probability distributions in continuous spaces. It gauges the transformation needed to align one distribution with another, where smaller values signify higher similarity and larger values denote substantial dissimilarity [50].
• The Energy Distance, like the KL Divergence and the Wasserstein Distance, is another measure used to compare two probability distributions. It quantifies the difference between distributions in a continuous space, assessing how much they differ. Smaller values indicate greater similarity, while larger values suggest more significant dissimilarity between the two distributions [51].
• The Maximum Mean Discrepancy (MMD) is a statistical measure used to assess the dissimilarity between two datasets or probability distributions. It quantifies the difference between distributions by estimating the maximum difference in means between data samples drawn from each distribution. Smaller values of MMD indicate greater similarity, while larger values signify more substantial dissimilarities between the distributions [52].

We extensively evaluated and compared the performance and output quality of the two models on the input dataset against these metrics. Our objective consists of testing the capabilities of FinGAN in generating synthetic financial continuous data closely resembling real financial data in terms of distribution, features, and characteristics, ensuring effectiveness and relevance in financial applications.

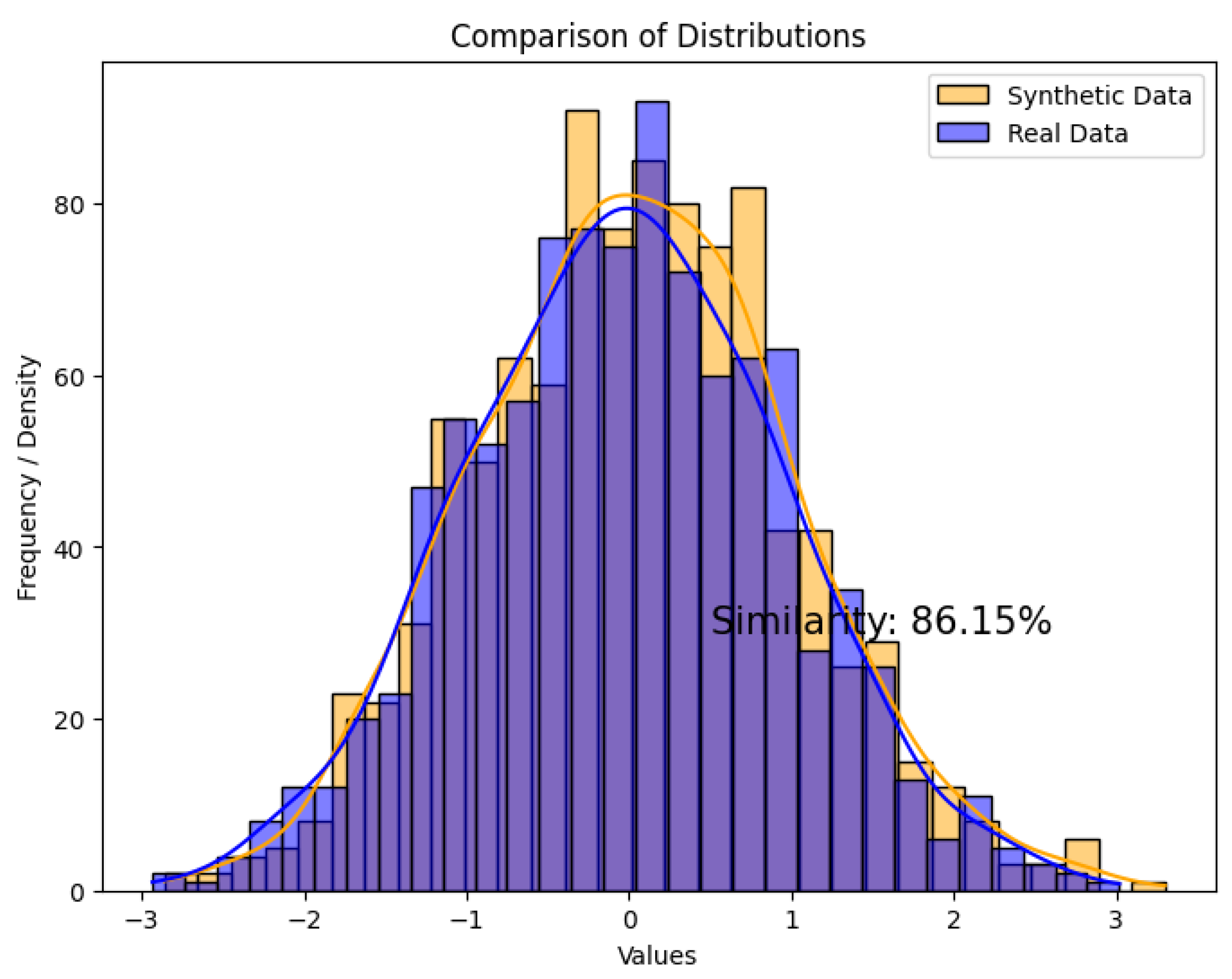
5.2. Analysis of the Results

In this section, we assess the outcomes derived from FinGAN and compare the results relative to the TabularGAN baseline [46]. Our focus is on evaluating the quality of the freshly generated synthetic continuous data compared to the real input data.

The evaluation results, reported in Table 1, show that FinGAN consistently outperforms the TabularGAN baseline across all evaluation metrics. To better comprehend the data, we have showcased statistical measures such as mean, standard deviation, minimum, maximum, and percentiles for both real (

Table 2. Mean, standard deviation, min, and max values from the original data.

#	0	1	2	3
count	746	746	746	746
mean	0.013144	0.012822	0.009366	0.010788
std	0.011914	0.011712	0.009283	0.009338
min	0.000012	0.000057	0.000014	0.000067
25%	0.004761	0.003878	0.003202	0.004226
50%	0.01003	0.009423	0.006641	0.008508
75%	0.017771	0.01781	0.012354	0.014221
max	0.098709	0.088502	0.072016	0.074291

) and synthetic data (

Table 3. Mean, standard deviation, min, and max values of newly synthetic generated data. The reader may observe that the generated data comprises 775 samples, in accordance with the specifications outlined in the original challenge.

#	0	1	2	3
count	775	775	775	775
mean	0.013919	0.009105	0.007335	0.013329
std	0.008142	0.004921	0.005163	0.005591
min	−0.00868	−0.01218	−0.00442	−0.00534
25%	0.0076	0.006267	0.004463	0.009149
50%	0.012524	0.008376	0.006556	0.012491
75%	0.018594	0.011219	0.009099	0.016423
max	0.051123	0.037024	0.078994	0.038933

). These tables highlight the datasets’ features and describe their statistical properties, emphasizing their similarities and close resemblance.

In order to provide a more robust comparison of the performance of the different algorithms, we used the Friedman Test [53,54] and its corresponding Nemenyi Post hoc Test [55,56] to evaluate the statistical significance of differences in ranks among FinGAN and TabularGAN. For more details on statistical tests used for algorithm comparison with multiple datasets, the reader is referred to Madjarov et al. [57] and Demśar [58].

Based on the Friedman Test, we find a significant difference between the evaluated ranks (at the 1% significance level). Since the null hypothesis of equivalence in algorithm rankings is rejected, we also perform a pairwise comparison using the Nemenyi post hoc test. This test considers the performance of two algorithms significantly different if the difference in average ranks is greater than a threshold critical difference, which, at a 1% significance level, corresponds to the critical value of $0.183$. We find that the calculated difference between the average ranks of the algorithms is $0.528$. The result proves that FinGAN statistically outperforms TabularGAN according to the Nemenyi test since the pairwise difference of its average rank with respect to the TabularGAN rank is larger compared to the critical value of $0.183$.

We have also calculated the Pearson correlation coefficients to assess the relationship between the values of corresponding features across the two datasets. They are illustrated in

Table 4. Pearson correlation coefficients for each of the four features across the real and synthetic datasets.

#	0	1	2	3
Pearson Correlation Coefficient	0.9415	0.9112	0.9968	0.9179
p-value	0.0015	0.004	1.05 × 10−6	0.0035

. Notably, each pair of the four corresponding features exhibits a strong positive correlation. The statistical relevance of these correlations is consistently established, as reflected in the p-values, all of which are below 0.005.

In addition, to visually illustrate this correlation, we also provide illustrations highlighting the characteristics of both datasets, examining each feature individually and giving an overview of the entire sample collection. In particular, the cumulative frequency distribution depicted in Figure 3 shows the distribution of values for each feature. This curve displays the cumulative sum of frequency distribution and offers insights into the overall pattern and shape of data distribution by comparing real data points (Blue) and synthetic data points (Orange).

Next, in Figure 4, we report the distribution per feature. The data distribution for real data is illustrated in blue, while the synthetic data distribution is represented in orange. As the reader might observe, there exist pronounced similarities and close correlations between them. Finally, Figure 5 indicates the distribution comparison and the similarity score between the entire continuous datasets.

Combining these qualitative visualizations with the quantitative metrics reported in Table 1, Table 2, Table 3 and Table 4 allows for an exhaustive evaluation of the resemblance between these distributions, demonstrating the promising performance of the FinGAN model for the considered task. From all the reported results, we can see that FinGAN is highly efficient in creating high-quality, continuous synthetic data closely mirroring the original distribution, thus offering solutions for data scarcity and availability issues in the financial domain.

5.3. Study Limitations

In our study, limitations arise from focusing solely on continuous financial datasets, which restricts the generalizability of our methodology. While effective within this context, our future research aims to broaden its applicability by incorporating diverse data types, including categorical variables like age and gender, into our algorithm. Presently, the FinGAN model is optimized for financial data characteristics. However, upcoming work will explore its use across various financial datasets to conduct additional experiments and tests.

Furthermore, we plan to integrate additional evaluation methods, such as TSTR (train on synthetic, test on real), or other downstream tasks, to further validate the effectiveness of our approach.

5.4. Benefits and Usage of Synthetic Datasets

To further stimulate the reader on the subject, in this section, we highlight the main benefits and usage deriving from our approach to the generation of synthetic datasets.

• Data Scarcity Mitigation: Newly generated synthetic datasets serve as a solution to overcome data scarcity issues often encountered in financial datasets. By generating additional synthetic data points, we augment the original dataset, enabling more robust analyses and model training.
• Inconsistency Resolution: This synthetic data generation also addresses inconsistencies present in the original data by ensuring that our synthetic dataset maintains coherence and consistency across various data attributes. This contributes to more reliable and accurate analyses and model development.
• Diversity Enhancement: Synthetic dataset incorporates diversity to compensate for situations where the original data might lack diversity or suffer from bias. This diversity is crucial for capturing a broader range of scenarios and ensuring the robustness of analytical models.
• Completeness Compensation: In scenarios where the original data are incomplete or restricted in access, a newly generated synthetic dataset provides a comprehensive and complete representation of the underlying data distribution. This completeness enhances the reliability and effectiveness of data-driven analyses and decision-making processes.

6. Conclusions and Future Work

This paper has presented FinGAN, an improved Generative Adversarial Network model designed for the creation of synthetic continuous data in the financial domain. This model adeptly captures complex patterns present in the original data by employing techniques such as adjusting layer count, neuron configurations, early stopping criteria, and fine-tuning hyperparameters, including learning rates and activation functions. The performance and output quality of FinGAN were evaluated and compared to a baseline GAN model. The results demonstrate that FinGAN is highly efficient in producing high-quality, continuous synthetic financial data that closely mirrors the original distribution. This makes it a promising solution for dealing with issues related to data scarcity and limited availability. Although we have focused on the financial domain, the described pipeline is completely generalizable and can be applied in principle to other problem domains with similar characteristics.

As far as the technical implementations are concerned, we have used Google Colab, a cloud-based Jupyter notebook platform, finding it suitable for our requirements. The code and dataset are publicly hosted on our GitHub page (https://github.com/faisalramzan3725/Generative-Adversarial-Networks-GANs-for-Synthetic-Data-Generation-in-Finance-Evaluating-Statisti/tree/main, accessed on 8 May 2024).

In future work, we aim to broaden the application of our methodology beyond the realm of continuous financial data. We aspire to integrate categorical and numerical data types, such as age and gender, into our algorithm to augment its versatility. Currently, the FinGAN model is tailored specifically for the financial domain and the characteristics of the dataset on which it operates. However, future endeavors will explore the utilization of FinGAN with diverse financial datasets to conduct additional experiments and tests. Additionally, we plan to incorporate additional evaluation methods such as TSTR (train on synthetic, test on real) or other downstream tasks to further validate the efficacy of our approach.