Improving Classification Performance in Credit Card Fraud Detection by Using New Data Augmentation
Abstract
1. Introduction
2. Related Work
2.1. Algorithm-Level Approaches
2.2. Data-Level Approaches
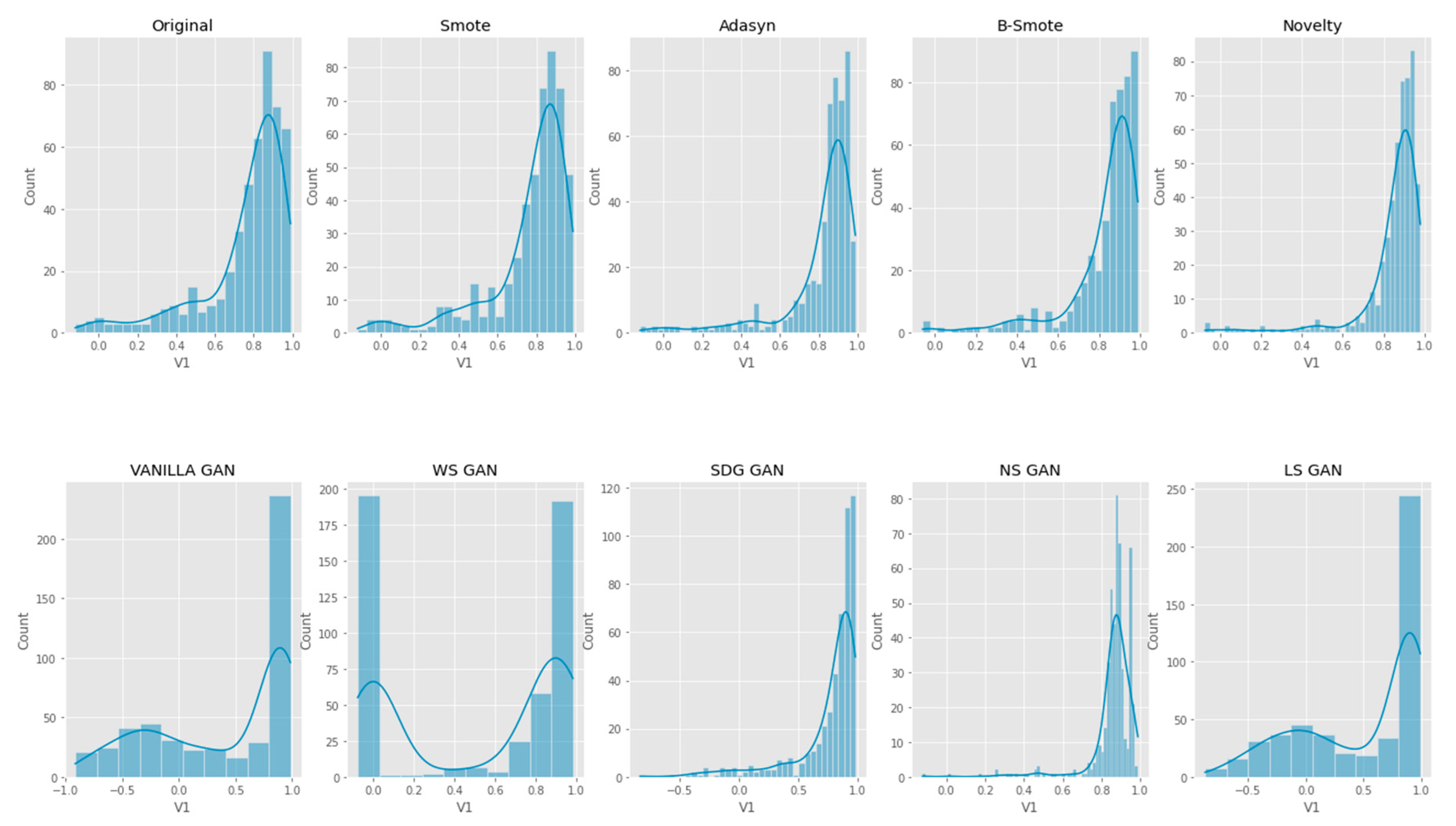
3. Data Augmentation Techniques
3.1. Sampling Based Techniques
3.1.1. SMOTE
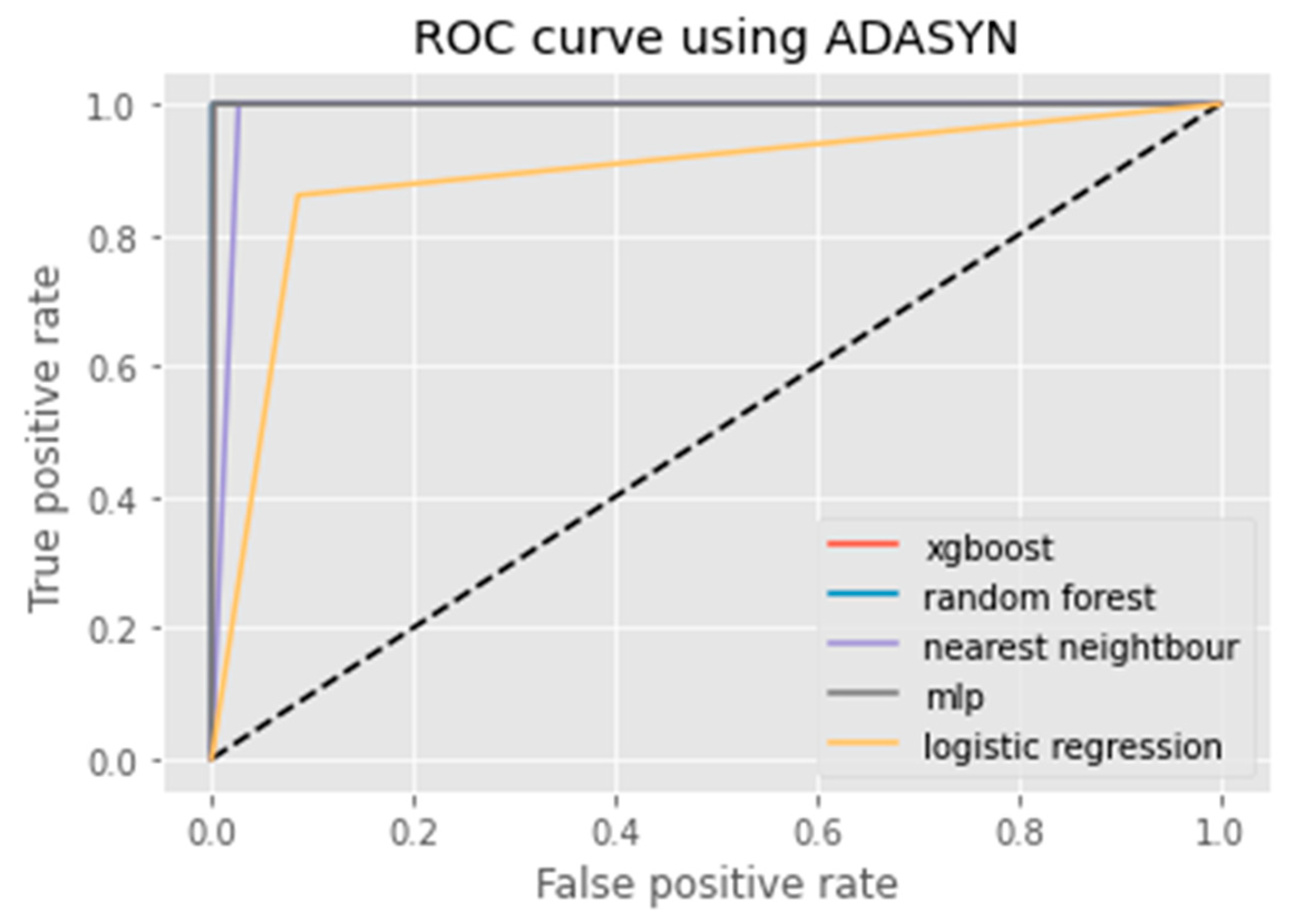
3.1.2. ADASYN
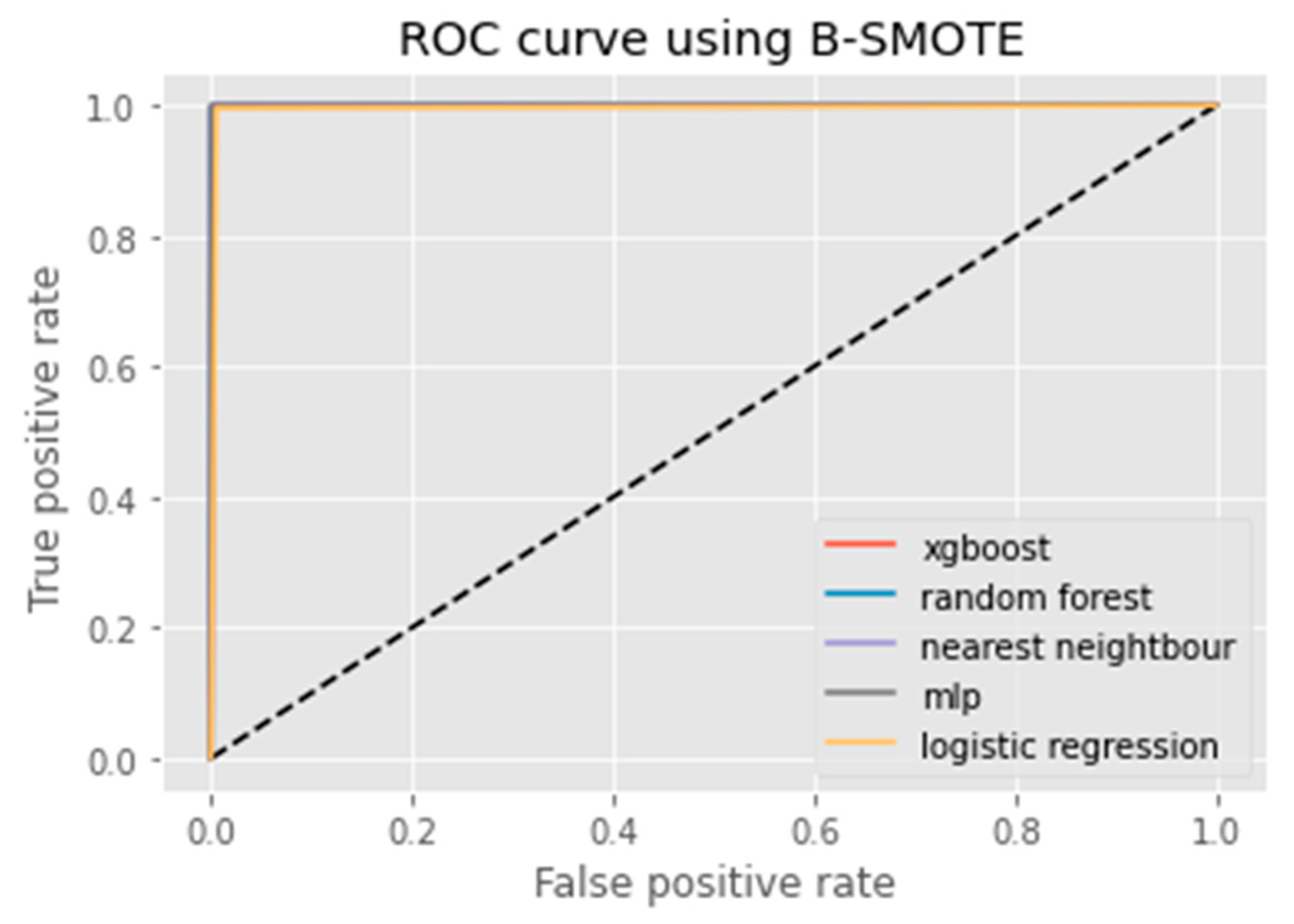
3.1.3. B-SMOTE
3.2. GAN-Based Techniques
3.2.1. cGAN
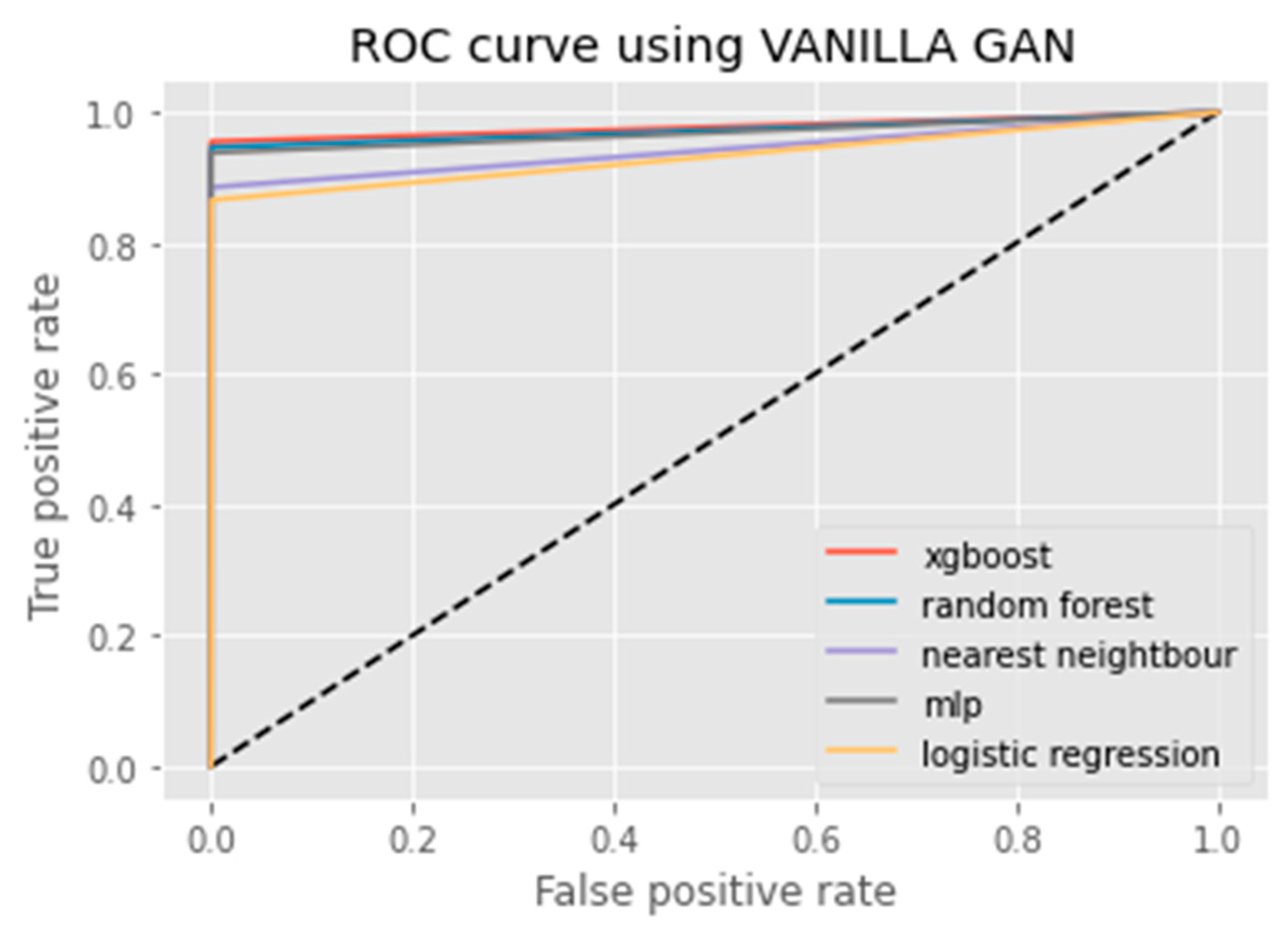
3.2.2. Vanilla GAN
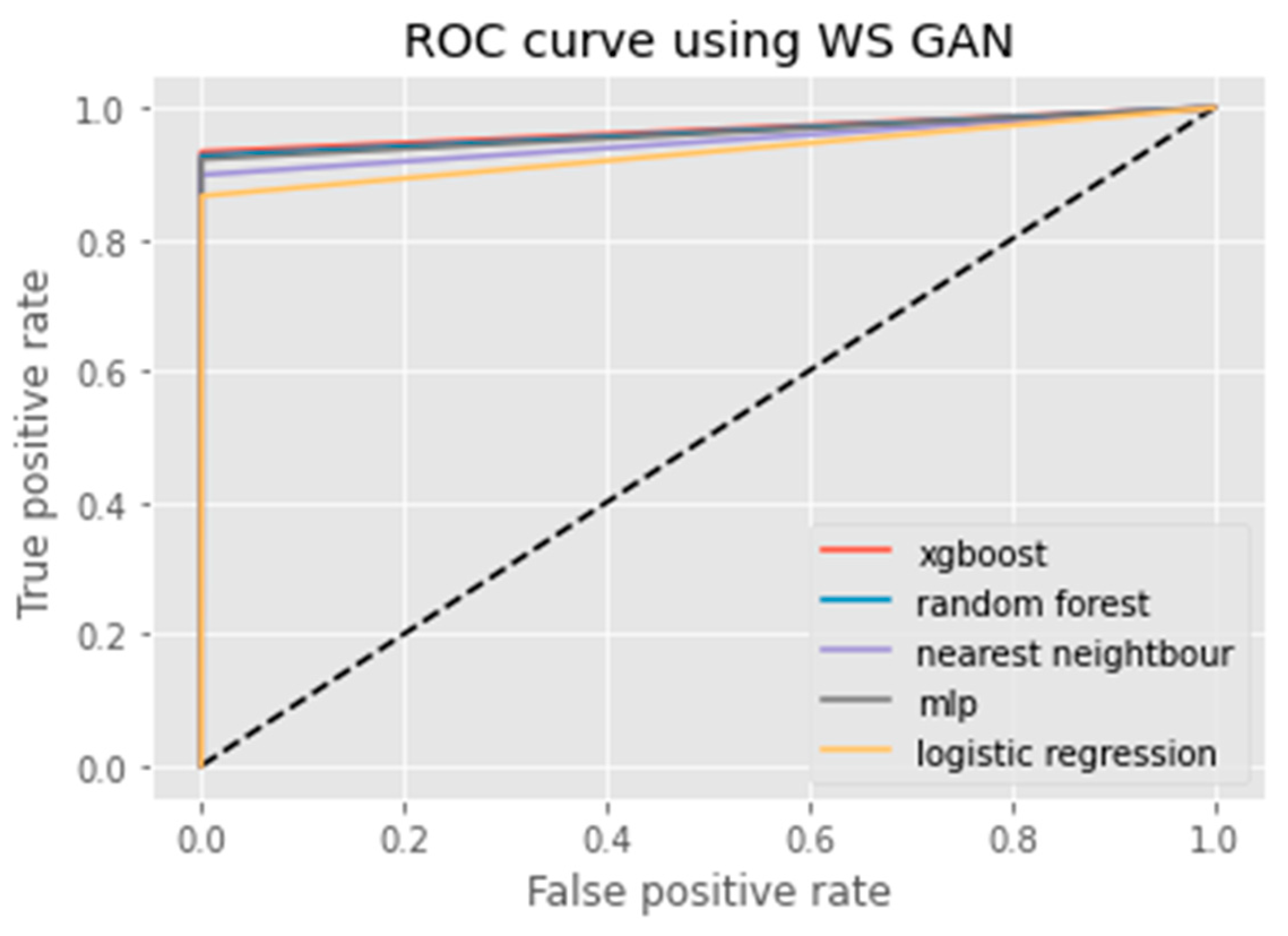
3.2.3. WS GAN
3.2.4. SDG GAN
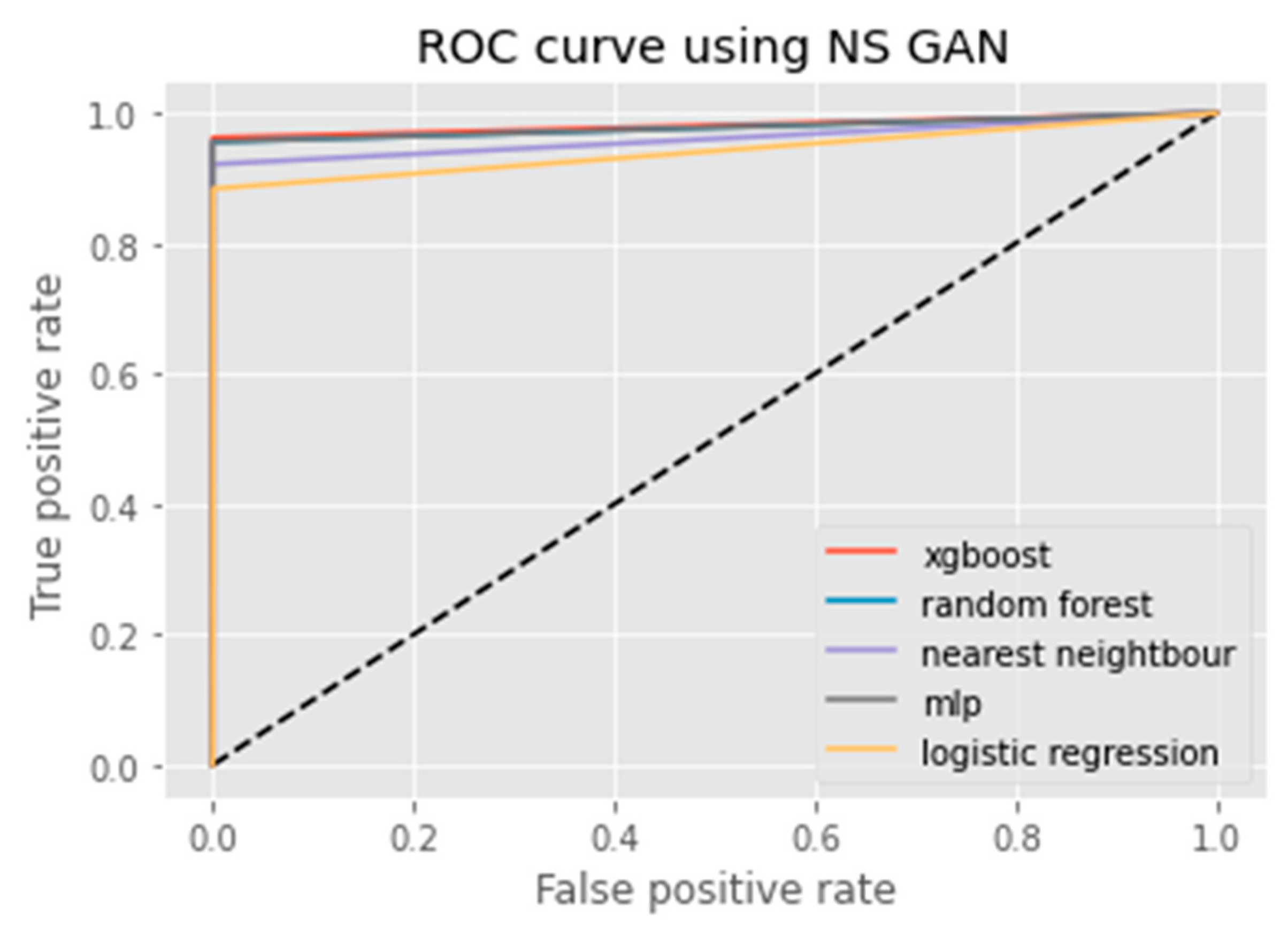
3.2.5. NS GAN
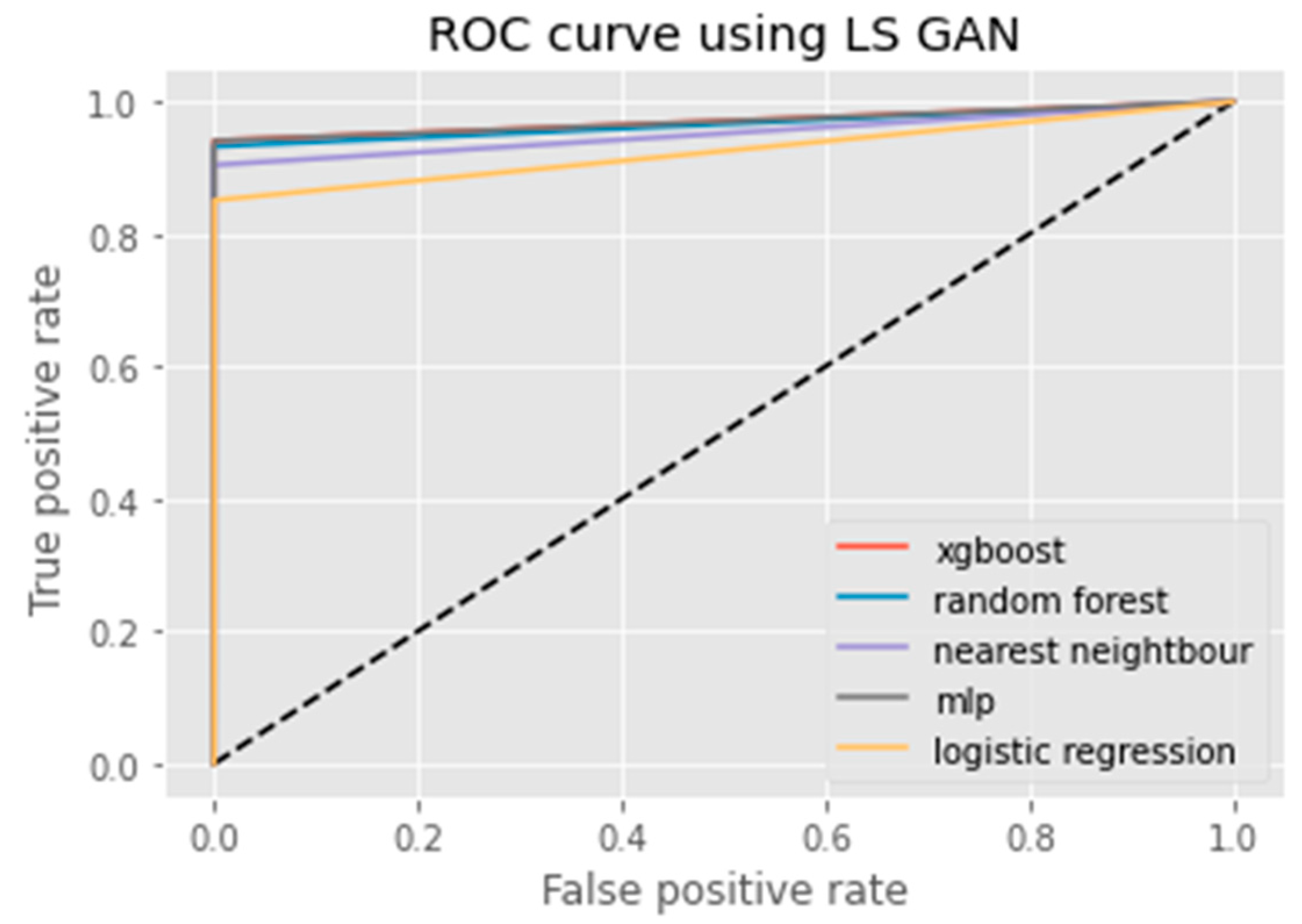
3.2.6. LS GAN
3.3. Classifiers
3.3.1. XG BOOST
3.3.2. Random Forest
3.3.3. K-Nearest Neighbor
3.3.4. MLP
3.3.5. Logistic Regression
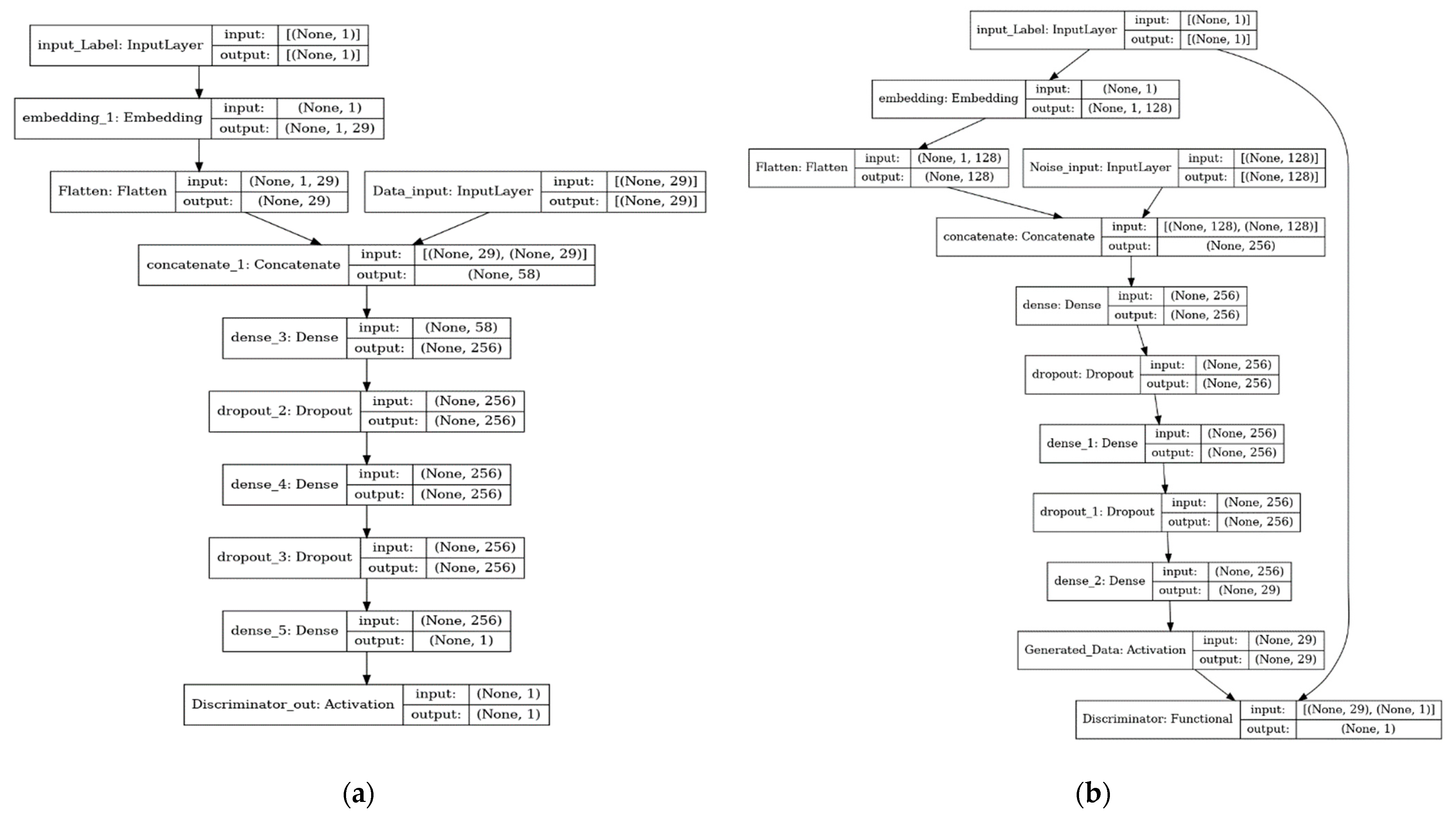
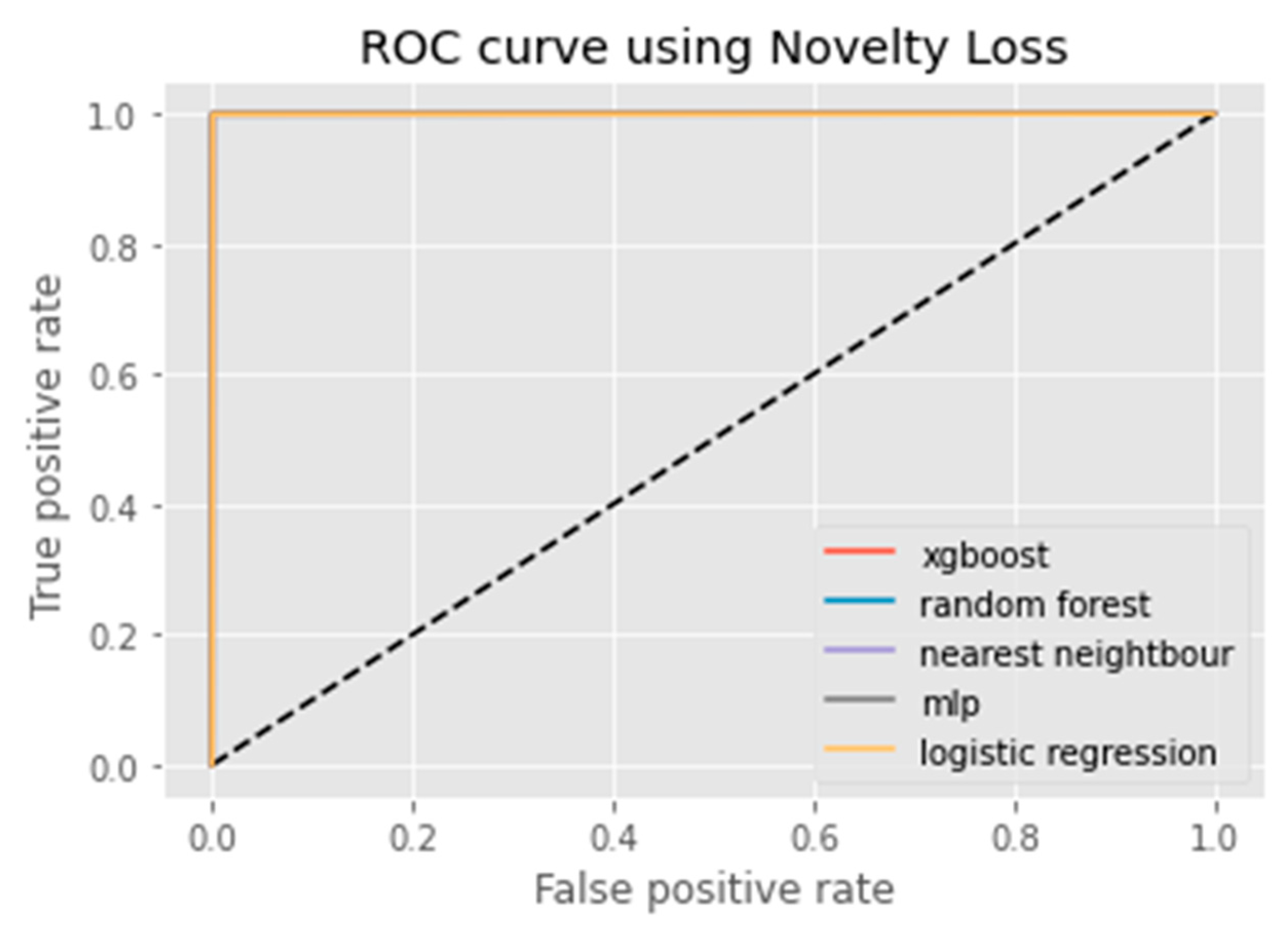
4. Proposed Data Augmentation Method: K-CGAN
4.1. Generator Loss
4.2. Discriminator Loss
5. Experiments
5.1. Dataset
5.2. Division of Dataset
5.3. Hyperparameters
K-CGAN
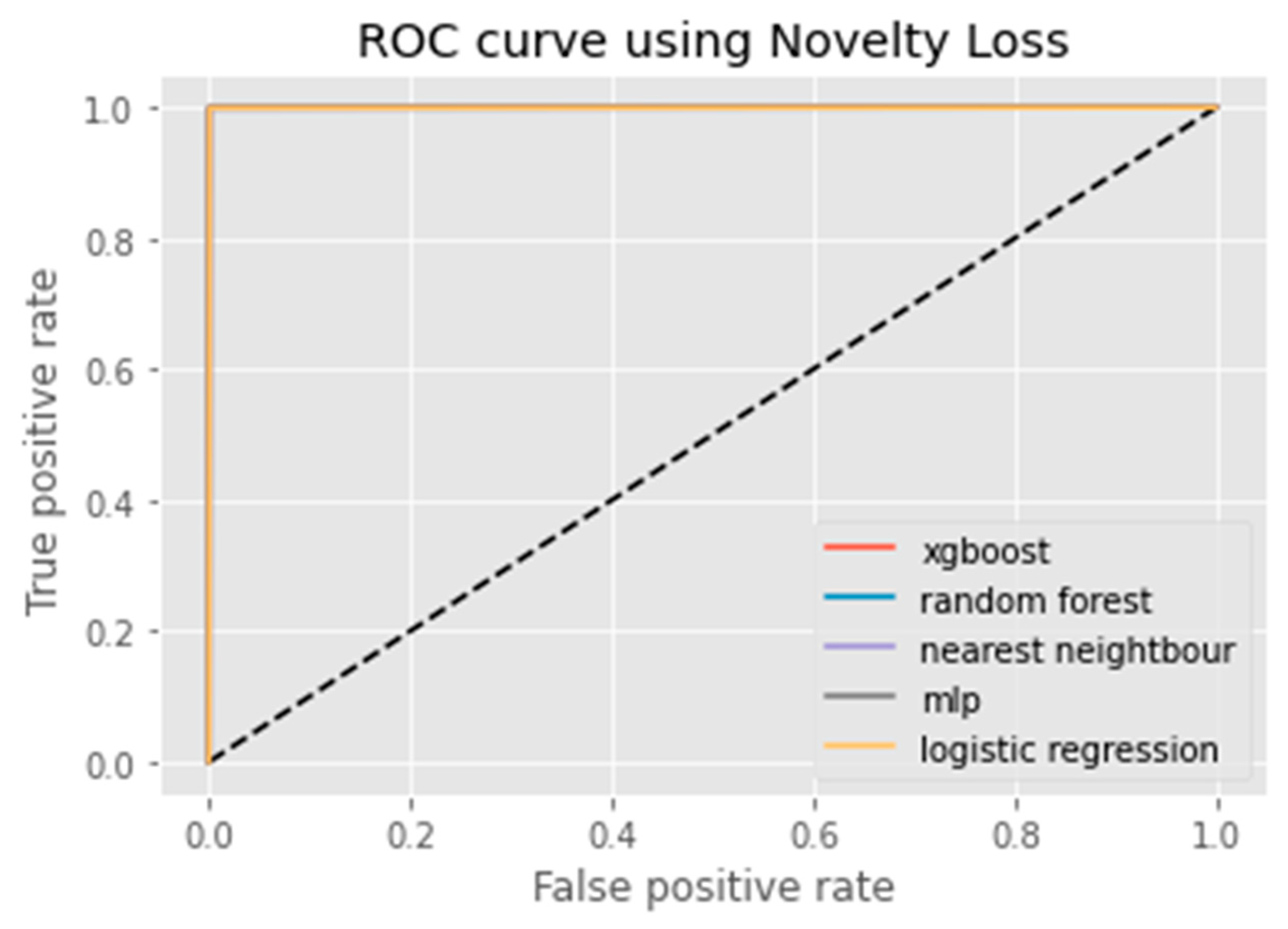
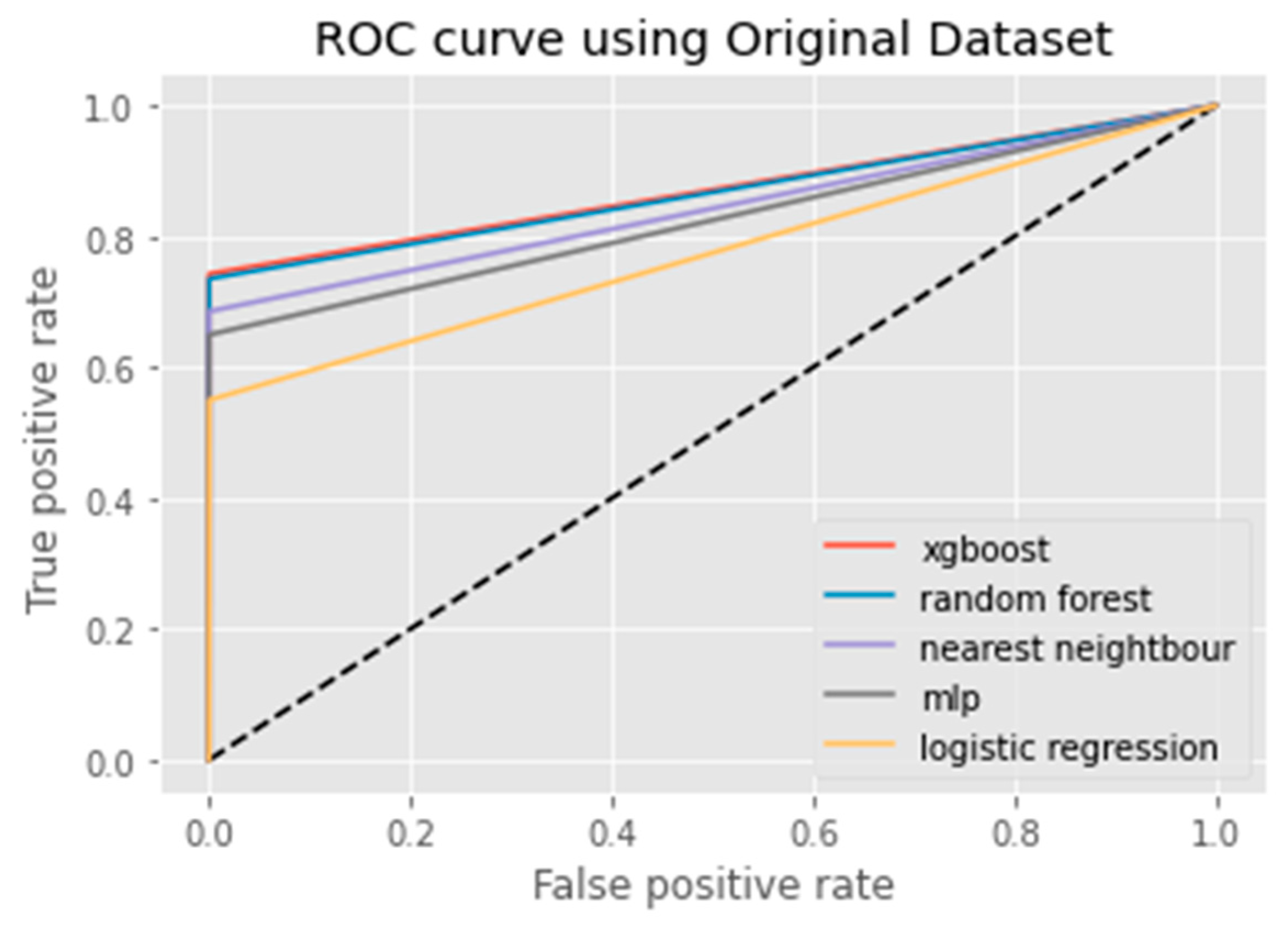
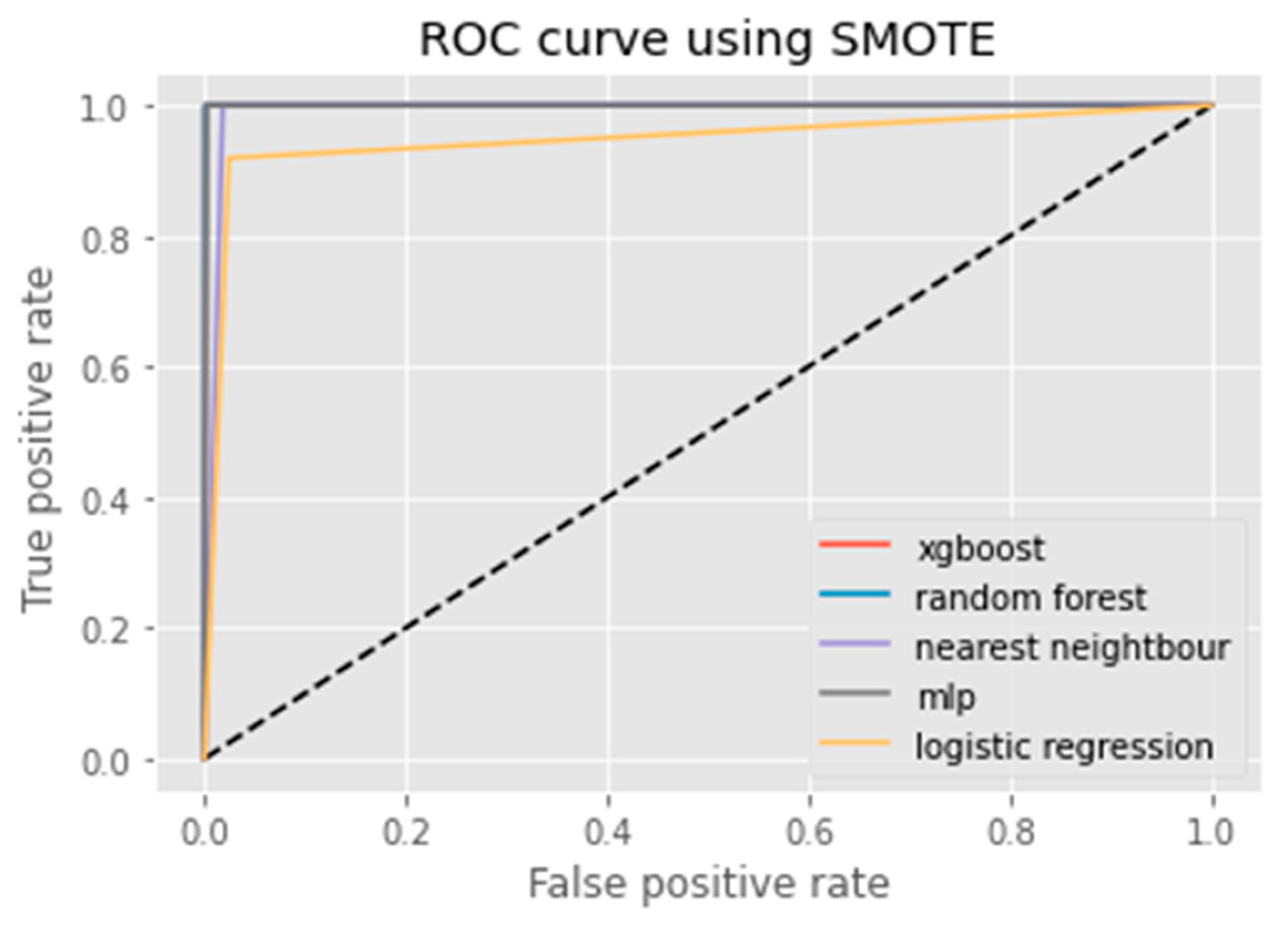
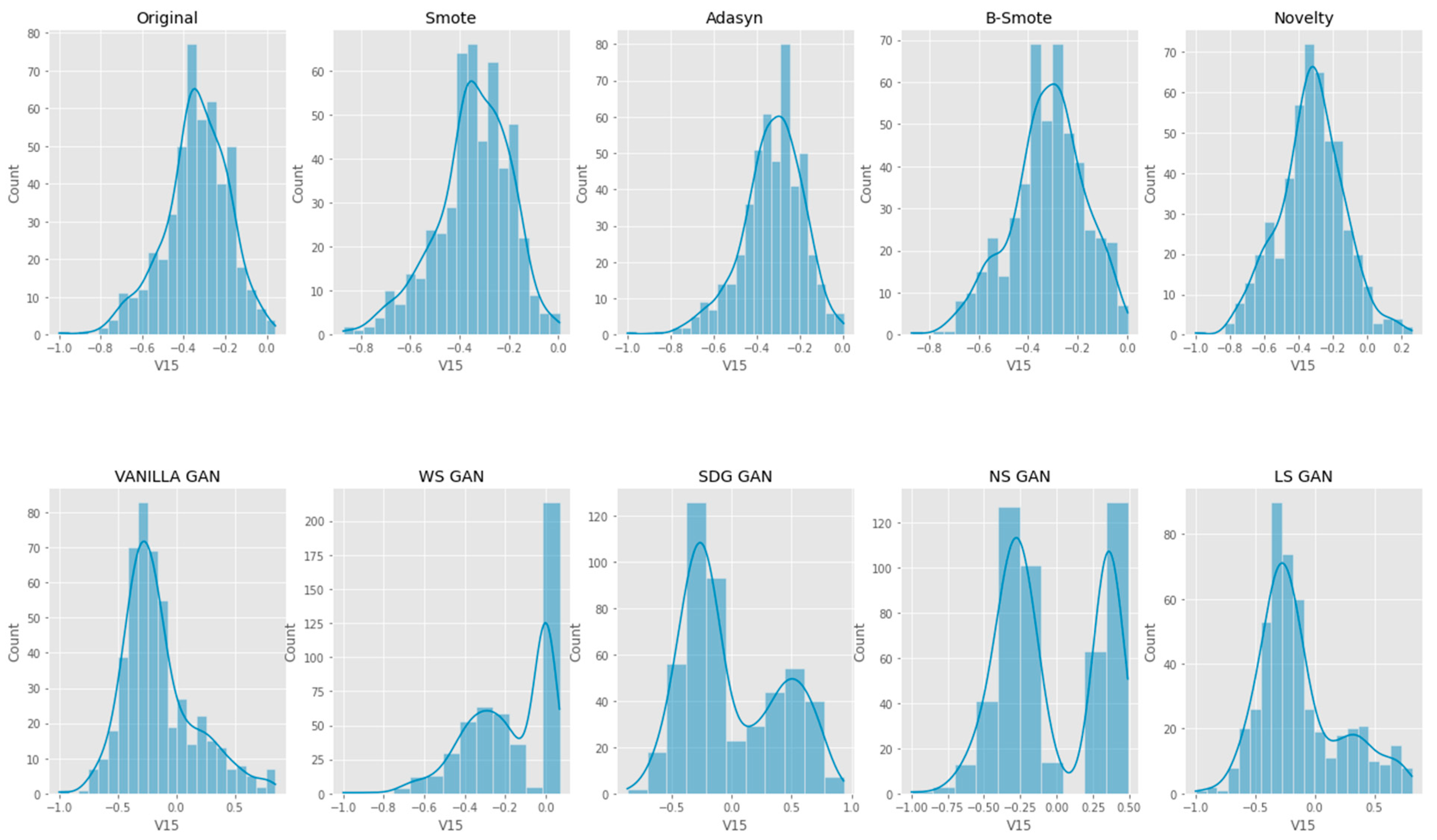
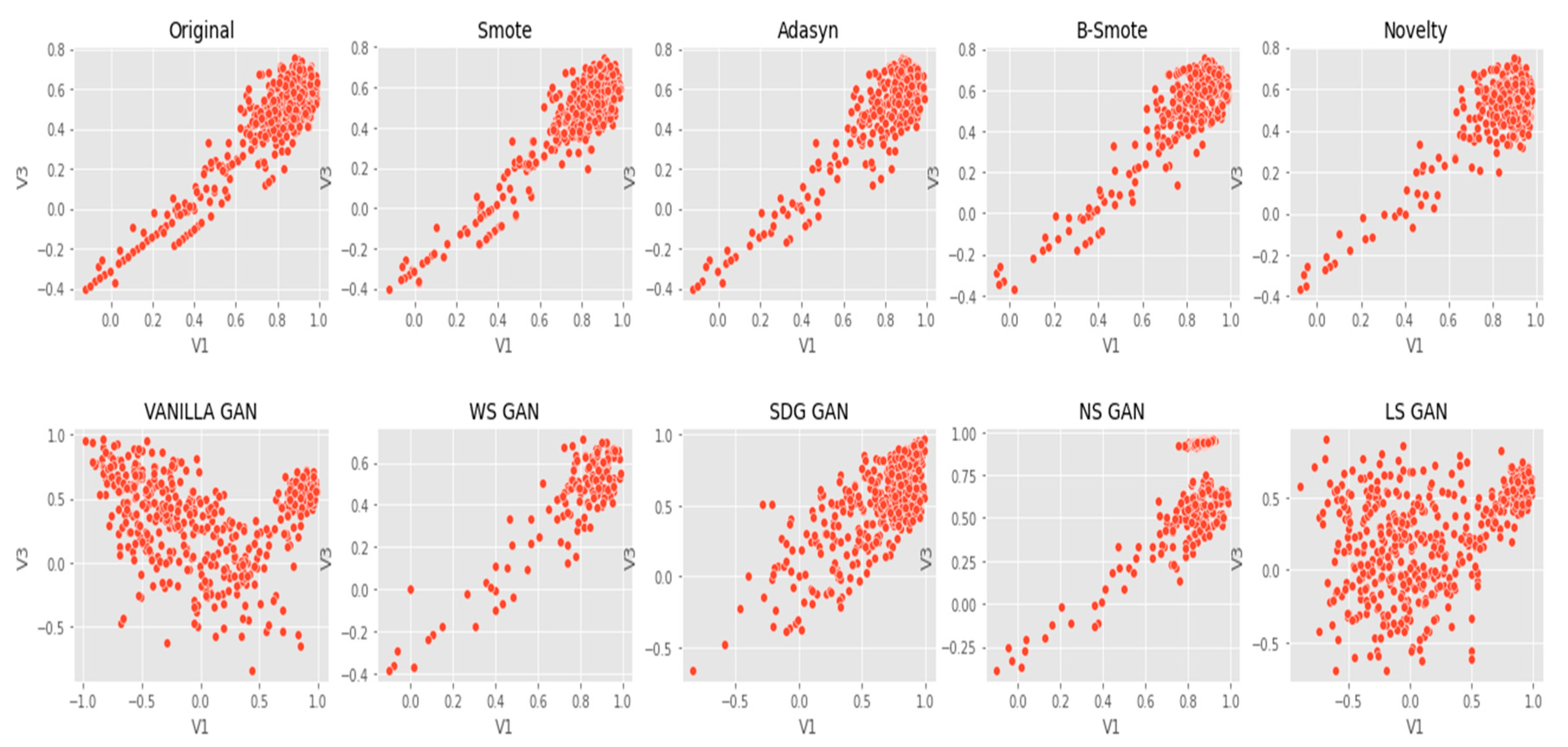
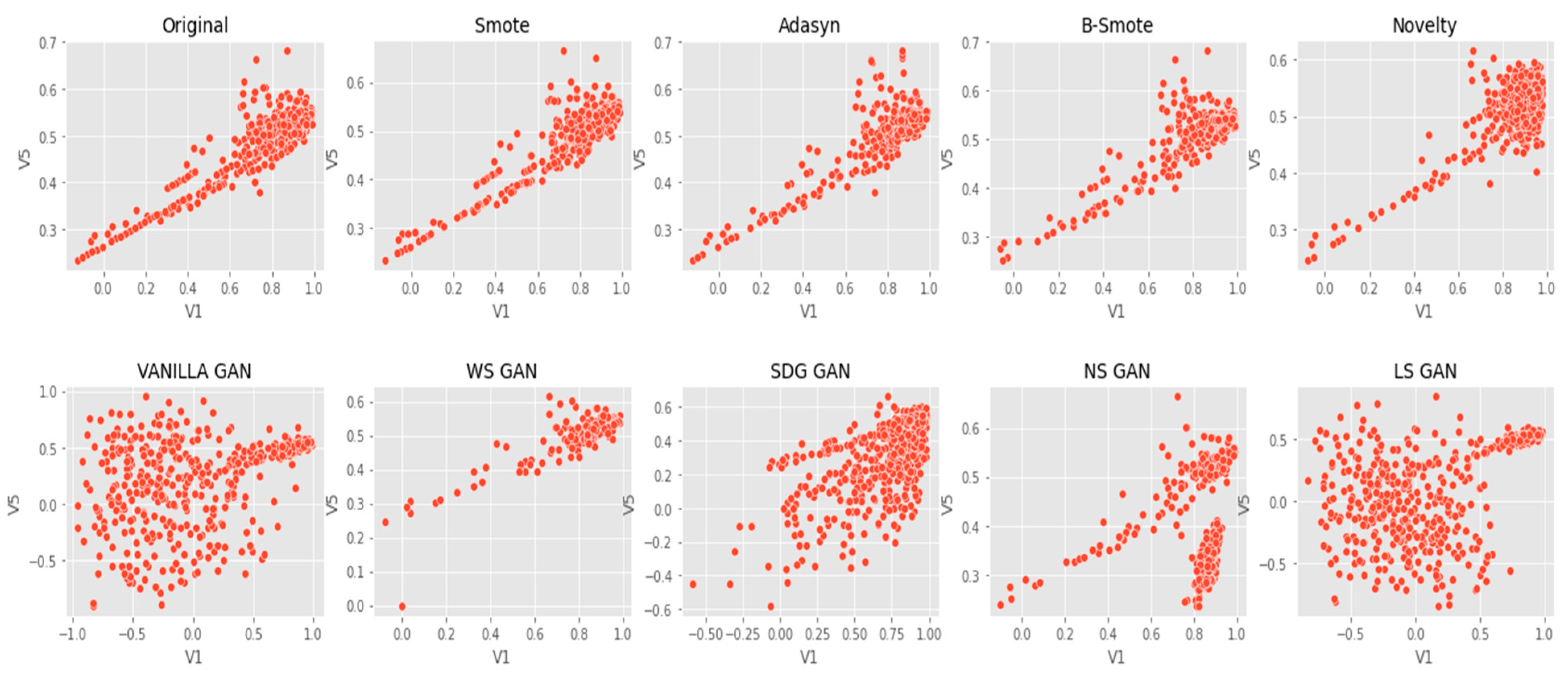
6. Results Analysis
Evaluation of Classification Models
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Asha, R.; Suresh, K. Credit card fraud detection using an artificial neural network. Glob. Transit. Proc. 2021, 2, 35–41. [Google Scholar]
- Garg, V.; Chaudhary, S.; Mishra, A. Analyzing Auto ML Model for Credit Card Fraud Detection. Int. J. Innov. Res. Comput. Sci. Technol. (IJIRCST) ISSN 2021, 9, 2347–5552. [Google Scholar]
- Alejo, R.; García, V.; Marqués, A.I.; Sánchez, J.S.; Antonio-Velázquez, J.A. Making accurate credit risk predictions with cost-sensitive mlp neural networks. In Management Intelligent Systems; Springer: Heidelberg, Germany, 2013; pp. 1–8. [Google Scholar]
- Sanober, S.; Alam, I.; Pande, S.; Arslan, F.; Rane, K.P.; Singh, B.K.; Khamparia, A.; Shabaz, M. An enhanced secure deep learning algorithm for fraud detection in wireless communication. Wirel. Commun. Mob. Comput. 2021, 2021, 6079582. [Google Scholar] [CrossRef]
- Xue, W.; Zhang, J. Dealing with imbalanced dataset: A re-sampling method based on the improved SMOTE algorithm. Commun. Stat. Simul. Comput. 2013, 45, 1160–1172. [Google Scholar] [CrossRef]
- Hajek, P.; Abedin, M.Z.; Sivarajah, U. Fraud Detection in Mobile Payment Systems using an XGBoost-based Framework. Inf. Syst. Front. 2022, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Jiang, C.; Song, J.; Liu, G.; Zheng, L.; Luan, W. Credit card fraud detection: A novel approach using aggregation strategy and feedback mechanism. IEEE Internet Things J. 2018, 5, 3637–3647. [Google Scholar] [CrossRef]
- Makki, S.; Assaghir, Z.; Taher, Y.; Haque, R.; Hacid, M.S.; Zeineddine, H. An experimental study with imbalanced classification approaches for credit card fraud detection. IEEE Access 2019, 7, 93010–93022. [Google Scholar] [CrossRef]
- Wang, T.; Zhao, Y. Credit Card Fraud Detection using Logistic Regression. In Proceedings of the 2022 International Conference on Big Data, Information and Computer Network (BDICN), Sanya, China, 20–22 January 2022; pp. 301–305. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Charitou, C.; Dragicevic, S.; Garcez, A.D.A. Synthetic Data Generation for Fraud Detection using GANs. arXiv 2021, arXiv:2109.12546. [Google Scholar]
- Chen, J.; Shen, Y.; Ali, R. Credit card fraud detection using sparse autoencoder and generative adversarial network. In Proceedings of the 2018 IEEE 9th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 1–3 November 2018; pp. 1054–1059. [Google Scholar]
- Ngwenduna, K.S.; Mbuvha, R. Alleviating class imbalance in actuarial applications using generative adversarial networks. Risks 2021, 9, 49. [Google Scholar] [CrossRef]
- Paasch, C.A. Credit Card Fraud Detection Using Artificial Neural Networks Tuned by Genetic Algorithms; Hong Kong University of Science and Technology: Hong Kong, China, 2008. [Google Scholar]
- Kumar, P.; Iqbal, F. Credit card fraud identification using machine learning approaches. In Proceedings of the 2019 1st International conference on innovations in information and communication technology (ICIICT), Chennai, India, 25–26 April 2019; pp. 1–4. [Google Scholar]
- Lamba, H. Credit Card Fraud Detection in Real-Time. Ph.D. Thesis, California State University San Marcos, San Marcos, CA, USA, 2020. [Google Scholar]
- Chen, X.W.; Wasikowski, M. Fast: A roc-based feature selection metric for small samples and imbalanced data classification problems. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 124–132. [Google Scholar]
- Prusti, D.; Rath, S.K. Web service based credit card fraud detection by applying machine learning techniques. In Proceedings of the TENCON 2019-2019 IEEE Region 10 Conference (TENCON), Kochi, India, 17–20 October 2019; pp. 492–497. [Google Scholar]
- Zheng, Y.J.; Zhou, X.H.; Sheng, W.G.; Xue, Y.; Chen, S.Y. Generative adversarial network-based telecom fraud detection at the receiving bank. Neural Netw. 2018, 102, 78–86. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Ranjan, R.K.; Tiwari, A. Credit card fraud detection under extreme imbalanced data: A comparative study of data-level algorithms. J. Exp. Theor. Artif. Intell. 2022, 34, 571–598. [Google Scholar] [CrossRef]
- Sadgali, I.; Nawal, S.A.E.L.; Benabbou, F. Fraud detection in credit card transaction using machine learning techniques. In Proceedings of the 2019 1st International Conference on Smart Systems and Data Science (ICSSD), Rabat, Morocco, 3–4 October 2019; pp. 1–4. [Google Scholar]
- Sethia, A.; Patel, R.; Raut, P. Data augmentation using generative models for credit card fraud detection. In Proceedings of the 2018 4th International Conference on Computing Communication and Automation (ICCCA), Greater Noida, India, 14–15 December 2018; pp. 1–6. [Google Scholar]
- Ullah, I.; Mahmoud, Q.H. Design and development of a deep learning-based model for anomaly detection in IoT networks. IEEE Access 2021, 9, 103906–103926. [Google Scholar] [CrossRef]
- Omar, B.; Rustam, F.; Mehmood, A.; Choi, G.S. Minimizing the overlapping degree to improve class-imbalanced learning under sparse feature selection: Application to fraud detection. IEEE Access 2021, 9, 28101–28110. [Google Scholar]
- Li, J.; Zhu, Q.; Wu, Q.; Fan, Z. A novel oversampling technique for class-imbalanced learning based on SMOTE and natural neighbours. Inf. Sci. 2021, 565, 438–455. [Google Scholar] [CrossRef]
- Grandini, M.; Bagli, E.; Visani, G. Metrics for multi-class classification: An overview. arXiv 2020, arXiv:2008.05756. [Google Scholar]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, 1–8 June 2008; pp. 1322–1328. [Google Scholar]
- Han, H.; Wang, W.Y.; Mao, B.H. August. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning. In International Conference on Intelligent Computing; Springer: Berlin/Heidelberg, Germany, 2005; pp. 878–887. [Google Scholar]
- Sohony, I.; Pratap, R.; Nambiar, U. Ensemble learning for credit card fraud detection. In Proceedings of the A.C.M. India Joint International Conference on Data Science and Management of Data, Goa, India, 11–13 January 2018; pp. 289–294. [Google Scholar]
- Taha, A.A.; Malebary, S.J. An intelligent approach to credit card fraud detection using an optimized light gradient boosting machine. IEEE Access 2020, 8, 25579–25587. [Google Scholar] [CrossRef]
- Kaggle.com. Available online: https://www.kaggle.com/mlg-ulb/creditcardfraud (accessed on 1 December 2022).




| Dataset | No. of Attributes | No. of Instances | No. of Fraud Instances | No. of Legal Instances |
|---|---|---|---|---|
| Kaggle | 30 | 31 | 492 | 284,315 |
| Time | V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 |
|---|---|---|---|---|---|---|---|---|
| 0 | −1.35981 | −0.07278 | 2.536347 | 1.378155 | −0.33832 | 0.462388 | 0.239599 | 0.098698 |
| 0 | 1.191857 | 0.266151 | 0.16648 | 0.448154 | 0.060018 | −0.08236 | −0.0788 | 0.085102 |
| 1 | −1.35835 | −1.34016 | 1.773209 | 0.37978 | −0.5032 | 1.800499 | 0.791461 | 0.247676 |
| 1 | −0.96627 | −0.18523 | 1.792993 | −0.86329 | −0.01031 | 1.247203 | 0.237609 | 0.377436 |
| 2 | −1.15823 | 0.877737 | 1.548718 | 0.403034 | −0.40719 | 0.095921 | 0.592941 | −0.27053 |
| 2 | −0.42597 | 0.960523 | 1.141109 | −0.16825 | 0.420987 | −0.02973 | 0.476201 | 0.260314 |
| 4 | 1.229658 | 0.141004 | 0.045371 | 1.202613 | 0.191881 | 0.272708 | −0.00516 | 0.081213 |
| 7 | −0.64427 | 1.417964 | 1.07438 | −0.4922 | 0.948934 | 0.428118 | 1.120631 | −3.80786 |
| 7 | −0.89429 | 0.286157 | −0.11319 | −0.27153 | 2.669599 | 3.721818 | 0.370145 | 0.851084 |
| V9 | V10 | V11 | V12 | V13 | V14 | V15 | V16 | V17 |
| 0.363787 | 0.090794 | −0.5516 | −0.6178 | −0.99139 | −0.31117 | 1.468177 | −0.4704 | 0.207971 |
| −0.25543 | −0.16697 | 1.612727 | 1.065235 | 0.489095 | −0.14377 | 0.635558 | 0.463917 | −0.1148 |
| −1.51465 | 0.207643 | 0.624501 | 0.066084 | 0.717293 | −0.16595 | 2.345865 | −2.89008 | 1.109969 |
| −1.38702 | −0.05495 | −0.22649 | 0.178228 | 0.507757 | −0.28792 | −0.63142 | −1.05965 | −0.68409 |
| 0.817739 | 0.753074 | −0.82284 | 0.538196 | 1.345852 | −1.11967 | 0.175121 | −0.45145 | −0.23703 |
| −0.56867 | −0.37141 | 1.341262 | 0.359894 | −0.35809 | −0.13713 | 0.517617 | 0.401726 | −0.05813 |
| 0.46496 | −0.09925 | −1.41691 | −0.15383 | −0.75106 | 0.167372 | 0.050144 | −0.44359 | 0.002821 |
| 0.615375 | 1.249376 | −0.61947 | 0.291474 | 1.757964 | −1.32387 | 0.686133 | −0.07613 | −1.22213 |
| −0.39205 | −0.41043 | −0.70512 | −0.11045 | −0.28625 | 0.074355 | −0.32878 | −0.21008 | −0.49977 |
| V18 | V19 | V20 | V21 | V22 | V23 | V24 | V25 | V26 |
| 0.025791 | 0.403993 | 0.251412 | −0.01831 | 0.277838 | −0.11047 | 0.066928 | 0.128539 | −0.18911 |
| −0.18336 | −0.14578 | −0.06908 | −0.22578 | −0.63867 | 0.101288 | −0.33985 | 0.16717 | 0.125895 |
| −0.12136 | −2.26186 | 0.52498 | 0.247998 | 0.771679 | 0.909412 | −0.68928 | −0.32764 | −0.1391 |
| 1.965775 | −1.23262 | −0.20804 | −0.1083 | 0.005274 | −0.19032 | −1.17558 | 0.647376 | −0.22193 |
| −0.03819 | 0.803487 | 0.408542 | −0.00943 | 0.798278 | −0.13746 | 0.141267 | −0.20601 | 0.502292 |
| 0.068653 | −0.03319 | 0.084968 | −0.20825 | −0.55982 | −0.0264 | −0.37143 | −0.23279 | 0.105915 |
| −0.61199 | −0.04558 | −0.21963 | −0.16772 | −0.27071 | −0.1541 | −0.78006 | 0.750137 | −0.25724 |
| −0.35822 | 0.324505 | −0.15674 | 1.943465 | −1.01545 | 0.057504 | −0.64971 | −0.41527 | −0.05163 |
| 0.118765 | 0.570328 | 0.052736 | −0.07343 | −0.26809 | −0.20423 | 1.011592 | 0.373205 | −0.38416 |
| V27 | V28 | Amount | ||||||
| 0.133558 | −0.02105 | 149.62 | ||||||
| −0.00898 | 0.014724 | 2.69 | ||||||
| −0.05535 | −0.05975 | 378.66 | ||||||
| 0.062723 | 0.061458 | 123.5 | ||||||
| 0.219422 | 0.215153 | 69.99 | ||||||
| 0.253844 | 0.08108 | 3.67 | ||||||
| 0.034507 | 0.005168 | 4.99 | ||||||
| −1.20692 | −1.08534 | 40.8 | ||||||
| 0.011747 | 0.142404 | 93.2 |
| Feature | VIF |
|---|---|
| Time | 1.104214 |
| V1 | 1.003973 |
| V2 | 1.000397 |
| V3 | 1.038927 |
| V4 | 1.002805 |
| V5 | 1.007125 |
| V6 | 1.000983 |
| V7 | 1.002670 |
| V8 | 1.001018 |
| V9 | 1.000367 |
| V10 | 1.001049 |
| V11 | 1.013779 |
| V12 | 1.003927 |
| V13 | 1.000932 |
| V14 | 1.002786 |
| V15 | 1.007373 |
| V16 | 1.000528 |
| V17 | 1.002051 |
| V18 | 1.002158 |
| V19 | 1.000196 |
| V20 | 1.000669 |
| V21 | 1.001252 |
| V22 | 1.004694 |
| V23 | 1.000729 |
| V24 | 1.000058 |
| V25 | 1.012106 |
| V26 | 1.000409 |
| V27 | 1.000941 |
| V28 | 1.000440 |
| Amount | 11.650240 |
| Parameter | Value |
|---|---|
| Learning Rate | 0.0001 |
| Hidden Layer Optimizer | Relu |
| Output Optimizer | Adam |
| Loss Function | Trained Discriminator Loss+ KL Divergence |
| Hidden Layers | 2, −128, 64 |
| Dropout | 0.1 |
| Random Noise Vector | 100 |
| Kernel Initializer | glorot_uniform |
| Kernel Regularizer | L2 method |
| Total Learning Parameters | 36,837 |
| Parameter | Value |
|---|---|
| Learning Rate | 0.0001 |
| Hidden Layer Optimizer | LeakyRelu |
| Output Optimizer | Adam |
| Loss Function | Binary Cross Entropy |
| Hidden Layers | 2, −20, 10 |
| Dropout | 0.1 |
| Kernel Regularizer | L2 method |
| Parameter | Value |
|---|---|
| Learning Rate | 0.0001 |
| Hidden Layer Optimizer | Relu |
| Output Optimizer | RMSprop |
| Loss Function | Trained Discriminator Loss |
| Hidden Layers | 64, 32 |
| Dropout | 0.5 |
| Random Noise Vector | 100 |
| Parameter | Value |
|---|---|
| Learning Rate | 0.0001 |
| Hidden Layer Optimizer | LeakyRelu |
| Output Optimizer | RMSprop |
| Loss Function | Binary Cross Entropy |
| Hidden Layers | 128, 64, 32 |
| Dropout | 0.1 |
| Precision Value for Balanced Dataset | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| K-CGAN | Original Dataset | SMOTE | ADASYN | B-SMOTE | Vanilla GAN | WS GAN | SDG GAN | NS GAN | LS GAN | |
| XG-Boost | 0.999762 | 0.924370 | 0.999467 | 0.999182 | 0.999816 | 0.997085 | 0.988636 | 0.986072 | 0.980831 | 0.982405 |
| Random Forest | 0.999776 | 0.931035 | 0.999762 | 0.999760 | 0.999958 | 0.994135 | 0.980170 | 0.986111 | 0.977564 | 0.982249 |
| Nearest Neighbor | 0.999608 | 0.864865 | 0.982366 | 0.973762 | 0.997603 | 0.960606 | 0.954416 | 0.966197 | 0.954545 | 0.961194 |
| MLP | 0.999692 | 0.881890 | 0.997690 | 0.997970 | 0.998082 | 0.982456 | 0.974504 | 0.957219 | 0.962145 | 0.959885 |
| Logistic Regression | 0.999566 | 0.890110 | 0.974443 | 0.909084 | 0.994725 | 0.965732 | 0.958457 | 0.970149 | 0.949495 | 0.968051 |
| Recall Value for Balanced Dataset | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| K-CGAN | Original Dataset | SMOTE | ADASYN | B-SMOTE | Vanilla GAN | WS GAN | SDG GAN | NS GAN | LS GAN | |
| XG-Boost | 0.999706 | 0.827068 | 1.000000 | 0.999986 | 0.999703 | 0.955307 | 0.932976 | 0.917098 | 0.962382 | 0.941011 |
| Random Forest | 0.999706 | 0.812030 | 1.000000 | 1.000000 | 0.999661 | 0.946927 | 0.927614 | 0.919689 | 0.956113 | 0.932584 |
| Nearest Neighbor | 0.999706 | 0.721804 | 0.999804 | 1.000000 | 0.999746 | 0.885475 | 0.898123 | 0.888601 | 0.921630 | 0.904494 |
| MLP | 0.999594 | 0.842105 | 1.000000 | 0.999929 | 0.999746 | 0.938547 | 0.922252 | 0.927461 | 0.956113 | 0.941011 |
| Logistic Regression | 0.999608 | 0.609023 | 0.919681 | 0.860942 | 0.996383 | 0.865922 | 0.865952 | 0.841969 | 0.884013 | 0.851124 |
| F1 Score Value for Balanced Dataset | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| K-CGAN | Original Dataset | SMOTE | ADASYN | B-SMOTE | Vanilla GAN | WS GAN | SDG GAN | NS GAN | LS GAN | |
| XG-Boost | 0.999734 | 0.873016 | 0.999733 | 0.999584 | 0.999760 | 0.975749 | 0.960000 | 0.950336 | 0.971519 | 0.961263 |
| Random Forest | 0.999741 | 0.867470 | 0.999881 | 0.999880 | 0.999809 | 0.969957 | 0.953168 | 0.951743 | 0.966720 | 0.956772 |
| Nearest Neighbor | 0.999657 | 0.786885 | 0.991008 | 0.986707 | 0.998673 | 0.921512 | 0.925414 | 0.925776 | 0.937799 | 0.931983 |
| MLP | 0.999643 | 0.861538 | 0.998844 | 0.998949 | 0.998913 | 0.960000 | 0.947658 | 0.942105 | 0.959119 | 0.950355 |
| Logistic Regression | 0.999587 | 0.723214 | 0.946270 | 0.884358 | 0.995553 | 0.913108 | 0.909859 | 0.901526 | 0.915584 | 0.905830 |
| Accuracy Value for Balanced Dataset | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| K-CGAN | Original Dataset | SMOTE | ADASYN | B-SMOTE | Vanilla GAN | WS GAN | SDG GAN | NS GAN | LS GAN | |
| XG-Boost | 0.999733 | 0.999551 | 0.999733 | 0.999585 | 0.999761 | 0.999762 | 0.999594 | 0.999482 | 0.999748 | 0.999622 |
| Random Forest | 0.999740 | 0.999537 | 0.999880 | 0.999880 | 0.999810 | 0.999706 | 0.999524 | 0.999496 | 0.999706 | 0.999580 |
| Nearest Neighbor | 0.999655 | 0.999270 | 0.990905 | 0.986578 | 0.998678 | 0.999244 | 0.999244 | 0.999230 | 0.999454 | 0.999342 |
| MLP | 0.999641 | 0.999494 | 0.998839 | 0.998952 | 0.998917 | 0.999608 | 0.999468 | 0.999384 | 0.999636 | 0.999510 |
| Logistic Regression | 0.999585 | 0.999129 | 0.947643 | 0.887842 | 0.995568 | 0.999174 | 0.999104 | 0.999006 | 0.999272 | 0.999118 |
| Algorithm | Precision | Recall | F1 Score | Accuracy |
|---|---|---|---|---|
| XG-Boost | 1.0 | 1.000000 | 1.000000 | 1.00000 |
| Random Forest | 1.0 | 0.982301 | 0.991071 | 0.99996 |
| Nearest Neighbor | 1.0 | 0.929204 | 0.963303 | 0.99984 |
| MLP | 1.0 | 1.000000 | 1.000000 | 1.00000 |
| Logistic Regression | 1.0 | 0.946903 | 0.972727 | 0.99988 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strelcenia, E.; Prakoonwit, S. Improving Classification Performance in Credit Card Fraud Detection by Using New Data Augmentation. AI 2023, 4, 172-198. https://doi.org/10.3390/ai4010008
Strelcenia E, Prakoonwit S. Improving Classification Performance in Credit Card Fraud Detection by Using New Data Augmentation. AI. 2023; 4(1):172-198. https://doi.org/10.3390/ai4010008
Chicago/Turabian StyleStrelcenia, Emilija, and Simant Prakoonwit. 2023. "Improving Classification Performance in Credit Card Fraud Detection by Using New Data Augmentation" AI 4, no. 1: 172-198. https://doi.org/10.3390/ai4010008
APA StyleStrelcenia, E., & Prakoonwit, S. (2023). Improving Classification Performance in Credit Card Fraud Detection by Using New Data Augmentation. AI, 4(1), 172-198. https://doi.org/10.3390/ai4010008






