Weight-Quantized SqueezeNet for Resource-Constrained Robot Vacuums for Indoor Obstacle Classification

Abstract

With the rapid development of artificial intelligence (AI) theory, particularly deep learning neural networks, robot vacuums equipped with AI power can automatically clean indoor floors by using intelligent programming and vacuuming services. To date, several deep AI models have been proposed to distinguish indoor objects between cleanable litter and noncleanable hazardous obstacles. Unfortunately, these existing deep AI models focus entirely on the accuracy enhancement of object classification, and little effort has been made to minimize the memory size and implementation cost of AI models. As a result, these existing deep AI models require far more memory space than a typical robot vacuum can provide. To address this shortcoming, this paper aims to study and find an efficient deep AI model that can achieve a good balance between classification accuracy and memory usage (i.e., implementation cost). In this work, we propose a weight-quantized SqueezeNet model for robot vacuums. This model can classify indoor cleanable litters from noncleanable hazardous obstacles based on the image or video captures from robot vacuums. Furthermore, we collect videos or pictures captured by built-in cameras of robot vacuums and use them to construct a diverse dataset. The dataset contains 20,000 images with a ground-view perspective of dining rooms, kitchens and living rooms for various houses under different lighting conditions. Experimental results show that the proposed deep AI model can achieve comparable object classification accuracy of around 93% while reducing memory usage by at least 22.5 times. More importantly, the memory footprint required by our AI model is only 0.8 MB, indicating that this model can run smoothly on resource-constrained robot vacuums, where low-end processors or microcontrollers are dedicated to running AI algorithms.

1. Introduction

Modern smart buildings are driven by emerging sensing, communication, the Internet of Things (IoT), and artificial intelligence (AI) technologies [1,2,3,4,5]. Among various smart building devices, robot vacuums can autonomously clean indoor floors by using intelligent programming and guided vacuuming services. Therefore, without manual intervention, ground waste is absorbed into a garbage storage bin through sweeping and vacuuming. In order to detect and bypass noncleanable obstacles, an ultrasonic distance sensor, an infrared sensor, a tactile sensor, or an integrated camera is generally installed at the front of robot vacuums. Unfortunately, because of severe drawbacks of ultrasonic, infrared, or tactile sensors [6], robot vacuums often become stuck under furniture, cabinets, and refrigerators; on door thresholds or thick carpets; and even trip over objects such as shoes, power cords, power strips, socks, ropes, remote controls, phone chargers, or kids’ toys. In addition, robot vacuums have been reported to run over dog or cat feces and ruin indoor floors by spreading feces throughout houses. Furthermore, robot vacuums may cause problems for pets, such as sucking food from pet food bowls. Consequently, it is concluded that modern robot vacuums are not intelligent enough to detect and recognize cleanable litters on indoor floors. In practice, before using robot vacuums, building users must inspect indoor floors and move noncleanable hazardous obstacles. Such pre-cleaning is inconvenient and a burden to robot vacuum users.

In order to make robot vacuums truly smart, researchers began to investigate artificial intelligence (AI) models, especially deep learning neural networks, to detect and identify indoor cleanable litters (e.g., dust, hair, and confetti) and noncleanable hazardous obstacles (e.g., socks, shoes, power cord, headphones, pet feces, dishcloths, and slippers). Deep AI models have great potential to support robot vacuums to avoid becoming stuck or trapped in noncleanable hazardous obstacles. AI brings a better user experience and attracts more customers to purchase AI robot vacuums. It is forecasted that AI and robotics will be closely integrated to perform many cleaning tasks for humans by 2025 [7]. Currently, the development of AI-powered robot vacuums is still in its infancy. In 2021, several robot vacuum companies began to collect thousands of real or fake dog feces for training deep AI models.

Essentially, a robot vacuum is a resource-constrained edge device, where low-end processors or microcontrollers are the computing device for running AI models [8]. Low-end processors or microcontrollers in robot vacuums have limited memory space, typically less than 1 MB. Unfortunately, these existing deep AI models in Table 1 focus entirely on the accuracy enhancement of object classification, and little effort has been made to significantly reduce the memory size below 1 MB. As a result, these existing deep AI models need far more memory space than a typical robot vacuum can provide. Hence, there is an urgent need to develop computationally efficient, small-memory deep AI models that can run smoothly on common low-end processors and microcontrollers [8]. Furthermore, researchers face another challenge, which is the lack of experimental datasets in complex indoor scenes from a ground-view perspective. Note that the appearance of indoor litters and obstacles is different from the ground-view perspective than the top-view perspective [9,10]. Therefore, the dataset unavailability problem is one of the focuses of this work.

In this work, we investigate and develop a new deep AI model, which can classify indoor cleanable litters from noncleanable hazardous obstacles with less trainable parameters and memory footprint. This work makes the following contributions. First, we collect videos or pictures captured by built-in cameras of robot vacuums and use them to construct a diverse dataset. The dataset contains 20,000 images with a ground-view perspective of dining rooms, kitchens, and living rooms for various houses under different lighting conditions. In this manner, data diversity in complex indoor scenes is guaranteed. This dataset comprises a sufficient number of image data with balanced classes. This experimental dataset meets the requirement of complex indoor scenes from a ground-view perspective. Second, we propose a weight-quantized SqueezeNet model to minimize the memory usage and computational complexity for deployment on resource-constrained robot vacuums. The techniques of post-training weight quantization and quantization-aware training are leveraged to significantly reduce the size of our deep AI model by 87% (from 6.1 MB to 0.8 MB). Experiments have been performed on the existing deep AI models in the literature (i.e., four-layer deep CNN, VGG-16, ResNet-34, 16-layer deep CNN, and MobileNet-V2) and the proposed weight-quantized SqueezeNet model. These AI models are fine-trained to achieve the highest accuracy with minimum loss. Then, classification accuracy and memory footprint are listed in a table for a comprehensive comparison. Experimental results show that when comparing with these existing deep AI models in the literature (i.e., four-layer deep CNN, VGG-16, ResNet-34, 16-layer deep CNN, and MobileNet-V2), the proposed AI model can achieve a comparable object classification accuracy of around 93% while reducing memory usage by at least 22.5 times. Furthermore, the memory footprint required by our proposed AI model is only 0.8 MB, indicating that our model can run smoothly on resource-constrained robot vacuums, where low-end processors or microcontrollers are dedicated to running AI models.

The rest of this paper is organized as follows. Section 2 introduces related work on several state-of-the-art deep AI models. Section 3 describes the proposed weight-quantized SqueezeNet and two techniques of weight quantization. Section 4 describes dataset generation and annotation and experimental environment setup. In order to highlight the benefits of our proposed AI model, Section 5 demonstrates extensive experimental results that are compared with the state-of-the-art works in the literature. Section 6 concludes the paper and discusses future work.

2. Related Work

In this subsection, we review several state-of-the-art deep AI models that have been recently employed in indoor object classification for robot vacuums. These AI models include CNN, VGG-16, ResNet, and MobileNet-V2, which will be elaborated as follows.

CNN: Convolutional Neural Network is a powerful deep learning model with excellent performance and a wide range of applications. The structure of a CNN can be divided into three types of layers: convolutional layers that extract features, max pooling layers that downsample features without corrupting recognition results, and fully connected layers that perform classification tasks. The pooling layer reduces the number of training parameters and ignore some information while keeping sampling unchanged. In CNNs, convolutional layers and pooling layers are usually repeated many times to form a deep network architecture with multiple hidden layers, commonly known as deep convolutional neural networks.

VGG-16: To build deeper convolutional neural networks, researchers proposed VGG models to avoid larger 5 × 5 or 7 × 7 convolutional kernels. The entire VGG network uses the same size of convolutional kernels (3 × 3) and maximum pooling (2 × 2). There are multiple variants of VGGNet, consisting of different numbers of layers in the network. The 16-layer model is called VGG-16. VGG-16 proves that increasing the network depth affects the final performance of VGG models to some extent. Unfortunately, VGG-16 contains more parameters and consumes more computing resources, resulting in more memory usage.

ResNet: During the back-propagation stage, traditional deep CNN models show the vanishing gradient problem, where the derivative value gradually becomes almost trivial. In response to this problem, the ResNet model refers to the VGG-19 network and adds the residual unit by using two types of shortcut connections (identity shortcut and projection shortcut). Therefore, ResNet solves the gradient degradation problem of deep neural networks by using residual learning, allowing researchers to train deeper networks. Unfortunately, ResNet models contain a large number of parameters and memory space; thus, they require a lot of training time.

MobileNet-V2: The main idea of MobileNet-V2 models is the depth-wise separable convolution, which is a factorized convolution including two smaller operations: depthwise convolution (i.e., different convolution kernels are used for each input channel) and pointwise convolution (i.e., 1 × 1 convolution kernel). The MobileNet-V2 model remarkably reduces the amount of computation and trainable parameters. Therefore, MobileNet-V2 is preferred for running on edge devices.

Table 1 summarizes existing deep AI models for object classification using computer vision techniques. In [11], a four-layer deep convolutional neural network (CNN) model was created to detect obstacles in complex scenes. Cross street pictures and sunny street pictures were used for training and testing, respectively. Testing accuracy of 80% was reported in [11]. Later, researchers conducted image-based obstacle classification with advanced deep learning in 2018. In [12], the VGG-16 model was employed, which contains 13 convolutional layers, 3 fully connected layers, a global averaging 2D pooling layer, and a dense layer of 1024 hidden nodes. Experiments were performed to train the VGG-16 model for binary object classification (obstacle or non-obstacle). The reported overall test accuracy is around 86%. Unfortunately, even though [11,12] achieved good classification accuracy, they require at least 1 GB of memory space, which is cost-prohibitive in resource-constrained robot vacuums. In [13], the AI model of ResNet-34 was chosen for garbage recognition on grass. Since ResNet is more memory efficient, it occupies 172 MB of memory space and the authors claimed 96% accuracy in practical testing. In [14], researchers proposed a 16-layer deep CNN model to classify food litters on tables into two categories (solid or liquid). To reduce the number of trainable parameters as well as the memory size, the authors excluded the use of fully connected layers. As a result, memory usage dropped to 128.5 MB while maintaining a high classification accuracy of 96%. Recently, the researchers in [15,16,17] proposed to adopt the MobileNet-V2 model [18,19] for indoor trash classification. The reported classification accuracy reached 93%, and the memory size is only 18.8 MB. To date, the MobileNet-V2 model consumes the least amount of memory and achieves comparable classification accuracy.

Table 1. Summary of existing deep AI models for classification of indoor litters by robot vacuums.

Existing Work	Year	AI Model for Object Classification	Weight Quantization	Reported Accuracy	Memory Usage
[11]	2013	4-layer Deep CNN	No	80%	2.1 GB
[12]	2018	VGG-16	No	86%	1.3 GB
[13]	2018	ResNet-34	No	96%	172 MB
[14]	2020	16-layer Deep CNN	No	96%	128.5 MB
[15,16,17]	2020	MobileNet-V2	No	93%	18.8 MB

Table 1. Summary of existing deep AI models for classification of indoor litters by robot vacuums.

Existing Work	Year	AI Model for Object Classification	Weight Quantization	Reported Accuracy	Memory Usage
[11]	2013	4-layer Deep CNN	No	80%	2.1 GB
[12]	2018	VGG-16	No	86%	1.3 GB
[13]	2018	ResNet-34	No	96%	172 MB
[14]	2020	16-layer Deep CNN	No	96%	128.5 MB
[15,16,17]	2020	MobileNet-V2	No	93%	18.8 MB

3. Proposed Weight-Quantized SqueezeNet

3.1. SqueezeNet Overview

SqueezeNet is a lightweight and efficient CNN model [20]. As SqueezeNet is mainly used in an embedded environment, it involves several methods of model compression. For example, many 3 × 3 convolution kernels in SqueezeNet are replaced by 1 × 1 convolution kernels. Using this approach, the number of parameters for one convolution operation is reduced by a factor of 9. In addition, the number of 3 × 3 convolution kernels is reduced and downsampling is delayed in the network layers of SqueezeNet. As a result, SqueezeNet reduces the number of trainable parameters and the computational effort of the entire work. Thus, it is potentially viable to deploy SqueezeNet in memory-limited hardware devices.

Table 2. Comparison of the number of parameters in these potential deep AI models.

Deep AI Model	Number of Parameters	Model Size	Comments
4-layer Deep CNN [11]	268,478,206	2.1 GB	SqueezeNet is a good candidate due to its smallest number of parameters
VGG-16 [12]	165,726,018	1.3 GB
ResNet-34 [13]	21,301,810	172 MB
16-layer Deep CNN [14]	16,055,077	128.5 MB
MobileNet-V2 [15,16,17]	2,260,546	18.8 MB
SqueezeNet	723,534	6.1 MB

summarizes the number of parameters in these potential deep AI models. Comparing with these existing state-of-the-art AI models in Section 2, we found that SqueezeNet has the smallest number of parameters; thus, it is a good choice for robot vacuum applications. Unfortunately, the model size of SqueezeNet (i.e., 6.1 MB) is still larger than the memory space available in typical robot vacuums. Therefore, model compression techniques will be used to further reduce the model size. Next, we will introduce two types of weight quantization techniques.

3.2. Weight Quantization Techniques

In order to ensure the high accuracy of deep learning models running on resource-constrained hardware platforms, researchers have started to study AI model compression. According to [21,22], the common model compression approaches include the following: network pruning [23], weight factorization [24], quantization [25], and weight sharing [26]. Based on some pruning criteria or thresholds, network pruning attempts to identify and remove unimportant neurons from a neural network. As a result, the number of neural connections is reduced, and the network becomes sparser. Efficient network pruning results in compact network architectures, fewer computing operations, and less memory space for parameter storage. Weight factorization is a mathematical technique for matrix compression, which is similar to the dimension reduction in vectors. The idea is to apply low-rank approximation to weights of a network layer, for which its weight matrix is factorized into a product of two smaller matrices. Only important weights of the decomposed matrices are stored. However, in deep neural networks, the time cost and workload of decomposing weight matrices are large overheads. The idea of weight quantization is to replace high-precision weights with low-precision weights without changing network architectures. Thus, approximate weights are used for a compressed representation. As perfect weight precision is scarified for low memory space, there is a trade-off between weight quantization and loss of accuracy. Weight sharing tends to reuse the same weights in certain locations of a neural network, rather than training a huge number of weight parameters. This technique saves massive computational costs by reducing the number of weights that must be trained.

In this paper, we investigate using the quantization technique for AI model compression [27]. Generally speaking, weight parameters in a format of 32-bit floating-point are used during model training and inference. However, in practical commercial applications, due to a large number of network layers and trainable parameters, inference and prediction require a large amount of computation, resulting in low inference efficiency. Weight quantization converts weight parameters in the format of 32-bit floating points to 8-bit integer points. In this manner, it reduces the overhead of memory and storage. At the same time, it may improve the efficiency of prediction. The challenge of weight quantization is how to make a trade-off between model compression and loss of accuracy. 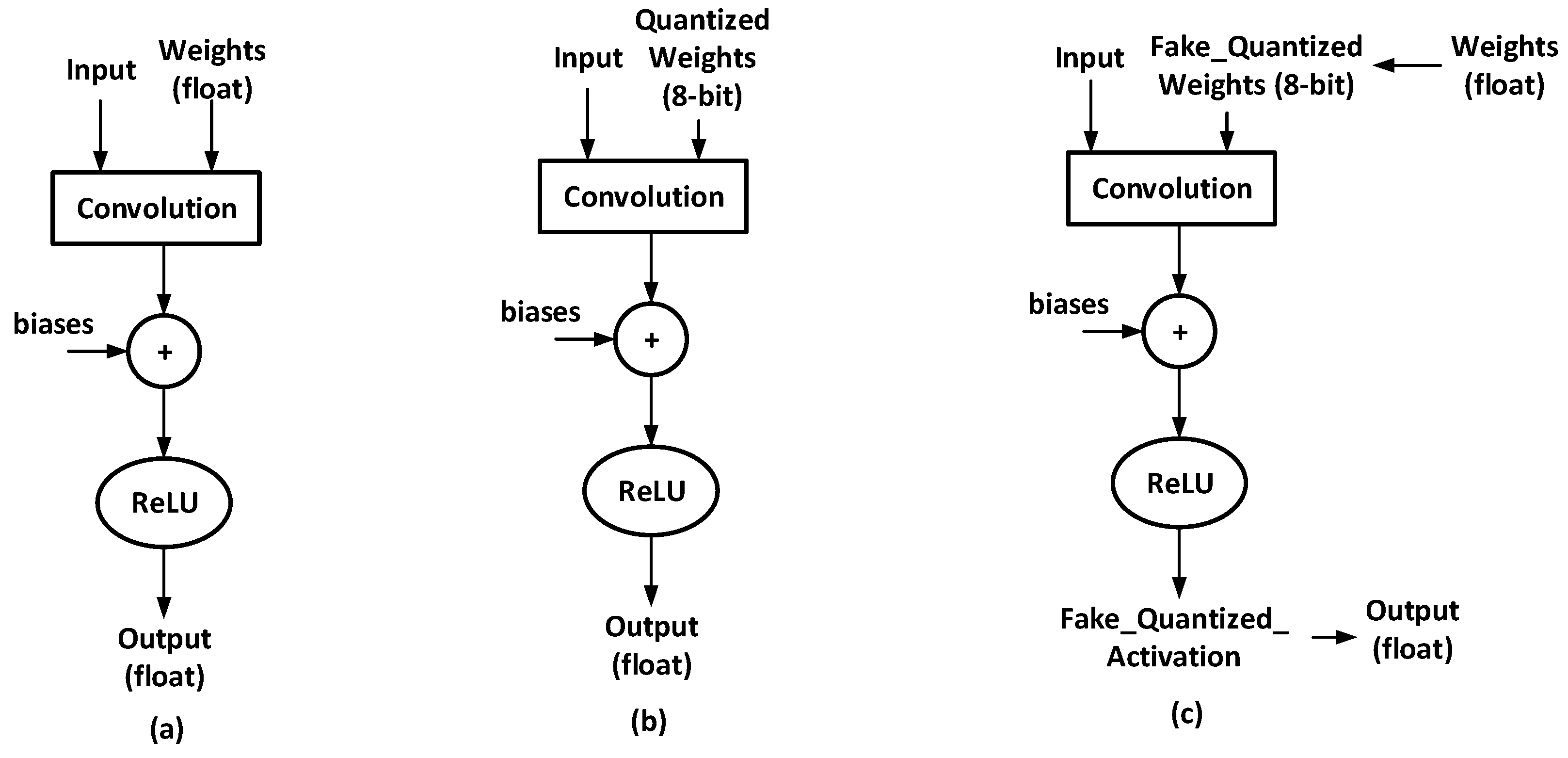Figure 1 illustrates the difference between convolutions without/with weight quantization, respectively. In this work, we implement both weight quantization techniques on the SqueezeNet model.

Post-training weight quantization [28,29]: Post-training refers to the quantization operation after the 32-bit floating-point model training has converged. Post-training weight quantization is a simple-to-use technique that quantization can be accomplished with a quantization tool such as TensorFlow Lite Converter [30]. As shown in Figure 1b, weight parameters in convolution operation are represented in the 8-bit fixed-point format, which is highly efficient during inference. The disadvantage of post-training weight quantization is that the performance of quantized models can sometimes drop significantly.

Quantization-aware weight training [31]: Quantization-aware training refers to the quantization of 32-bit floating-point models during training. Because quantization-aware weight training suffers less quantization loss, its accuracy drops less than post-training weight quantization. As shown in Figure 1c, fake quantization is applied to floating weights. Then, fake-quantized 8-bit weights are used in convolution operations. Once quantization-aware training is complete, floating-point models will be converted to 8-bit quantized models using the information stored during fake quantization.

In addition to reducing the amount of data that needs to be stored, model weight quantization also helps to significantly decrease inference time and required computational resources [32,33,34]. For example, it has been reported in [33] that inference time is shortened by 2.45 times for a quantized ResNet-50 model with 8-bit integer weights. Hardware cost reduction and energy-saving results have been presented in [34], from which we select the adder and multiplier results and plot them in Figure 2. It is clear that using 8-bit integer quantization to 32-bit floating-point weights results in one or two orders of magnitude area or energy savings. These features are attractive for AI model implementation in low-end processors or microcontrollers.

4. Experiments and Discussion

4.1. Datasets Generation and Annotation

We generate a dataset from videos or pictures captured by built-in cameras of robot vacuums. Each video file was first converted into a sequence of images. Then, each image frame was saved as a separate picture. These videos and pictures were taken from the dining rooms, kitchen rooms, and living rooms of different houses in various lighting conditions. In this manner, data diversity in complex indoor scenes is enhanced. As a good dataset should have balanced and uniform data distribution, our dataset is randomly divided into 70% for the training set, 15% for the validation set, and 15% for the testing set, as listed in

Table 3. Sample numbers and percentages of three subsets in our dataset.

Subset	Number of Samples	Percentage
Training Set	14,000	70%
Validation Set	3000	15%
Testing Set	3000	15%

. The training and validation sets were used for training, tuning, and the evaluation of AI models, while the testing set was used to estimate the final classification accuracy once the training process is completed. The total number of samples in our dataset is 20,000, which are labeled into two categories: cleanable and noncleanable. To increase dataset diversity and generalization, data augmentation techniques were used to reduce model overfitting [35,36].

In general, indoor objects larger than 2 cm are classified as noncleanable obstacles. Therefore, robot vacuums will avoid vacuuming any objects larger than 2 cm.

Table 4. Examples of indoor cleanable litters and noncleanable obstacles in our dataset.

Cleanable Litters	Noncleanable Obstacles
Rice	Power cords
Sunflower seed shell	Keychains
Soybean	Shoes
Red bean	Socks
Millet	Pet feces
Cat Litter	Kids’ toys
Cat food	Oil bottle
Dog food	Power strip

shows examples of indoor cleanable litters and noncleanable obstacles in our dataset. Cleanable litters in these captured images include rice, sunflower seed shell, soybean, red bean, millet, cat litter, dog litter, etc. Noncleanable obstacles in our dataset include power cords, keychains, shoes, socks, pet feces, kid’s toys, oil bottles, power strips, etc. Figure 3 and Figure 4 show the examples of images samples in our dataset. It is clear that the viewing angle of these built-in cameras is different from that of human beings.

4.2. Experimental Environment Setup

Python and TensorFlow were used in this work for experimental study. As a concise and practical programming language, Python has been loved by AI experts and programmers. TensorFlow is an open-source software platform for machine learning [37], running on a machine with eight Intel Core CPUs @2.60 GHz, four NVIDIA TITAN XP GPUs, and 12 GB video memory. This machine was built by NVIDIA in Santa Clara, CA, USA. Ubuntu 20.4, TensorFlow 2, and Python 3.7 were installed on this machine at Southern Illinois University Carbondale, Illinois, USA. Figure 5a shows AI training and evaluation processes without weight quantization. This training process is adopted in prior works [8,9,10,11,12,13,14]. In contrast, Figure 5b,c show AI model training and evaluation processes when weight quantization techniques were applied [38,39].

5. Experimental Results and Discussion

In this work, instead of implementing our model in a real vacuum cleaner, we use NVIDIA GPUs to train and test the performance of our proposed AI model. This is because although vacuum cleaners are used to collect images and videos for our dataset, we do not know the details of how to professionally disassemble vacuum cleaners and how to integrate the AI model we trained into the processors or microcontrollers of vacuum cleaners. In order to implement our model in vacuum cleaners for field experimental testing, technical support from vacuum cleaner manufacturers is required. Unfortunately, in this work, we have not received such technical support yet.

In our experiment, all weights of the AI models are trained by the SGD optimizer [40], which helps to minimize training loss by updating the weight parameters in back-propagation. The learning rate is configured as an exponential decay function, where the learning rate gradually decays from an initial value of the learning rate. The initial learning rate and the decay rate are set to 0.001 and 10⁻⁶, respectively. The epoch number is set to 200, which has been proved to be enough for the experiments to converge well. Due to the limitation of computational resources, we used a mini-batch size of 64 for SqueezeNet. The source codes and trained models can be downloaded from Google Drive. The link is as follows: https://drive.google.com/drive/folders/1N8QsH2HirWTLyiK3ltWFtNaU_d9SaSXW (accessed on 13 February 2022).

The main reference works [11,12,13,14,15,16,17] use their own datasets, most of which are not from a ground-view perspective, for model training and validation. Therefore, in this work, for a fair comparison, we conducted experiments on the same dataset we constructed to evaluate these AI models and our proposed model.

Table 5. Size and accuracy comparison of potential deep AI models without any weight quantization.

Deep AI Model	Model Size	Test Classification Accuracy	Comments
4-layer Deep CNN [11]	2.1 GB	90.2%	SqueezeNet achieves a comparable classification accuracy with the least amount of model size
VGG-16 [12]	1.3 GB	94.4%
ResNet-34 [13]	172 MB	93.1%
16-layer Deep CNN [14]	128.5 MB	93.7%
MobileNet-V2 [15,16,17]	18.8 MB	93.9%
SqueezeNet (this work)	6.1 MB	93.2%

lists information on the number of parameters, model size, and test classification accuracy of these deep AI models without any weight quantization techniques. We can see that the SqueezeNet model comprises a minimal number of parameters; hence, the smallest model size that is only 6.1 MB. Compared with these existing AI models [11,12,13,14,15,16,17], the SqueezeNet model can reduce the memory footprint by at least 87%, while achieving a comparable test classification accuracy of around 93%. As mentioned earlier, for cost reasons, robot vacuum manufacturers need to develop memory-efficient AI models for resource-constrained hardware devices such as low-end processors or microcontrollers. Despite the significant memory reduction, this memory footprint of 6.1 MB in the SqueezeNet model still exceeds what a typical microcontroller or low-end processor can provide.

Experiments were performed to check the AI model’s performance after using the post-training weight quantization technique.

Table 6. Size and accuracy comparison of potential deep AI models with post-training weight quantization.

Deep AI Model	Model Size	Size Reduction %	Test Classification Accuracy	Comments
4-layer Deep CNN [11]	268.5 MB	87%	90.5%	Post-training weight quantization reduces model size by ~87% with negligible loss in accuracy
VGG-16 [12]	165.9 MB	87%	94.1%
ResNet-34 [13]	21.8 MB	87%	93.1%
16-layer Deep CNN [14]	16.1 MB	87%	93.9%
MobileNet-V2 [15,16,17]	2.6 MB	86%	93.9%
SqueezeNet (this work)	0.8 MB	87%	93.2%

shows the model size, size reduction percentage, and test classification accuracy, respectively. We can see that the post-training weight quantization results in a size reduction of about 87%. Furthermore, the test accuracy of SqueezeNet is 93.2%, which is the same as that of the SqueezeNet model without weight quantization. These results indicate that, without any accuracy degradation, post-training weight quantization reduces the size of our deep AI model by 87% (from 6.1 MB to 0.8 MB). As the quantized SqueezeNet model is 0.8 MB in size, it has the great potential to run smoothly on resource-constrained robot vacuums.

Figure 6 plots four simulation curves of training loss, validation loss, training accuracy, and validation accuracy when post-training weight quantization was applied to our proposed SqueezeNet model. A good fit was observed because the training and validation loss curves decreased to a point and no longer started to increase. Training accuracy stabilizes at around 99%, while validation accuracy remains around 93%.

Experiments were also performed to check the AI model’s performance with the quantization-aware training technique.

Table 7. Size and accuracy comparison of potential deep AI models with quantization-aware training.

Deep AI Model	Model Size	Size Reduction %	Test Classification Accuracy	Comments
4-layer Deep CNN [11]	268.5 MB	87%	90.1%	Quantization-aware training weight reduces model size by ~87% with negligible loss in accuracy
VGG-16 [12]	165.9 MB	87%	94.7%
ResNet-34 [13]	21.8 MB	87%	93.4%
16-layer Deep CNN [14]	16.1 MB	87%	94.4%
MobileNet-V2 [15,16,17]	2.6 MB	86%	93.3%
SqueezeNet (this work)	0.8 MB	87%	92.9%

shows the model size, size reduction percentage, and test classification accuracy, respectively. Similar to Table 6, we can see that quantization-aware training results in an 87% reduction in size, and the quantized SqueezeNet model is 0.8 MB in size. The test accuracy of SqueezeNet is 92.9%, which is 0.3% lower than using the post-training weight quantization technique. Figure 7 plots four simulation curves of training loss, validation loss, training accuracy, and validation accuracy when quantization-aware training is applied to the SqueezeNet model.

Confusion matrix, also known as error matrix, is used to calculate the evaluation metrics of classifiers in machine learning. For the prediction result of a classifier, a confusion matrix is drawn as below. Each row of the table represents the predicted category, and each column represents the actual category.

Table 8. Confusion matrix comparison with existing AI models with post-training weight quantization on our dataset.

4-Layer Deep CNN [11]	Negative (Predicted)	Positive (Predicted)
Negative (actual)	TN = 0.82	FP = 0.18
Positive (actual)	FN = 0.06	TP = 0.94
VGG-16 [12]
Negative (actual)	TN = 0.92	FP = 0.08
Positive (actual)	FN = 0.04	TP = 0.96
ResNet-34 [13]
Negative (actual)	TN = 0.9	FP = 0.1
Positive (actual)	FN = 0.05	TP = 0.95
16-layer Deep CNN [14]
Negative (actual)	TN = 0.89	FP = 0.11
Positive (actual)	FN = 0.04	TP = 0.96
MobileNetV2 [15,16,17]
Negative (actual)	TN = 0.88	FP = 0.12
Positive (actual)	FN = 0.03	TP = 0.97
SqueezeNet (This work)
Negative (actual)	TN = 0.93	FP = 0.07
Positive (actual)	FN = 0.07	TP = 0.93

provides four types of values for true positive (TP), false positive (FP), false negative (FN), and true negative (TN). Since sensitivity refers to the proportion of model prediction as 1 and to all observations as 1, it is calculated as TP/(TP + FN). Since specificity refers to the proportion of model prediction as 0 and to all observations as 0, it is calculated as TN/(TN + FP). Table 7 shows that our SqueezeNet model achieves better performance in sensitivity and specificity.

To conduct a comprehensive comparison,

Table 9. Comparison of this work with existing AI Models when running experiments on our developed dataset.

Existing Work	Year	AI Model for Object Classification	Weight Quantization	Test Accuracy	Memory Usage
[11]	2013	4-layer Deep CNN	No	90.2%	2.1 GB
[12]	2018	VGG-16	No	94.4%	1.3 GB
[13]	2018	ResNet-34	No	93.1%	172 MB
[14]	2020	16-layer Deep CNN	No	93.7%	128.5 MB
[15,16,17]]	2020	MobileNet-V2	No	93.9%	18.8 MB
This work	2022	SqueezeNet	Post-training weight quantization	93.2%	0.8 MB

summarizes the performance metrics of the references [11,12,13,14,15,16,17] and this work. None of these previous works [11,12,13,14,15,16,17] used weight quantization for model size reduction. Regarding the proposed SqueezeNet model, because the weight quantization result in Table 5 is better than that in Table 6, we prefer to choose the post-training weight quantization technique. The values of test accuracy and memory usage are plotted in Figure 8 for visualization. Compared with the state-of-the-art references [15,16,17], this work reduces the memory footprint by at least 22.5 times with a test accuracy drop of 0.7%. These results demonstrate the advantages of this work. Compared to the state-of-the-art design with the highest classification accuracy, our proposed model achieves a memory reduction of approximately 1625 times with a slight 1.2% drop in accuracy. These results demonstrate the advantages of our proposed AI model.

6. Conclusions

In this work, we propose a weight-quantized SqueezeNet model for robot vacuums. This AI model can accurately classify indoor cleanable litters from noncleanable hazardous obstacles, based on the image or video captures from robot vacuums. We collect 20,000 ground-perspective images and use them to construct a diverse dataset. Both techniques of post-training weight quantization and quantization-aware training are implemented and evaluated. Experimental results show that the proposed deep AI model can achieve an object classification accuracy of around 93%, which is comparable to the accuracy of state-of-the-art works, while reducing the memory footprint at least 22.5 times. More importantly, the memory footprint required by our AI model is only 0.8 MB, indicating that this model can run smoothly on resource-constrained robot vacuums.

This work involves two limitations. First, in this work, we only use weight quantization to reduce memory footprint. It is highly attractive to combine multiple model compression techniques. For example, after weight quantization, weight sharing can be used to save only the unique values of quantized weights for each network layer. Network pruning may be applied first to reduce the number of neural connections, followed by weight quantization to further reduce memory size. In the future, we will explore the use of multiple model compression techniques on this research topic. Second, in this work, instead of implementing our model in a real vacuum cleaner, we used NVIDIA GPUs to train and test the performance of our proposed AI model. This is because although vacuum cleaners are used to collect images and videos for our dataset, we do not know the details of how to professionally disassemble vacuum cleaners and how to integrate the AI model we trained into the processors or microcontrollers of vacuum cleaners. In order to implement our model in vacuum cleaners for field experimental testing, technical support from vacuum cleaner manufacturers is required. Unfortunately, in this work, we have not received such technical support yet. In the future, we plan to contact several vacuum cleaner manufacturers to see if they are interested in supporting our model implementation and field testing.