MSG-GAN-SD: A Multi-Scale Gradients GAN for Statistical Downscaling of 2-Meter Temperature over the EURO-CORDEX Domain
Abstract
:1. Introduction
Related Work
2. Materials and Methods
2.1. Data
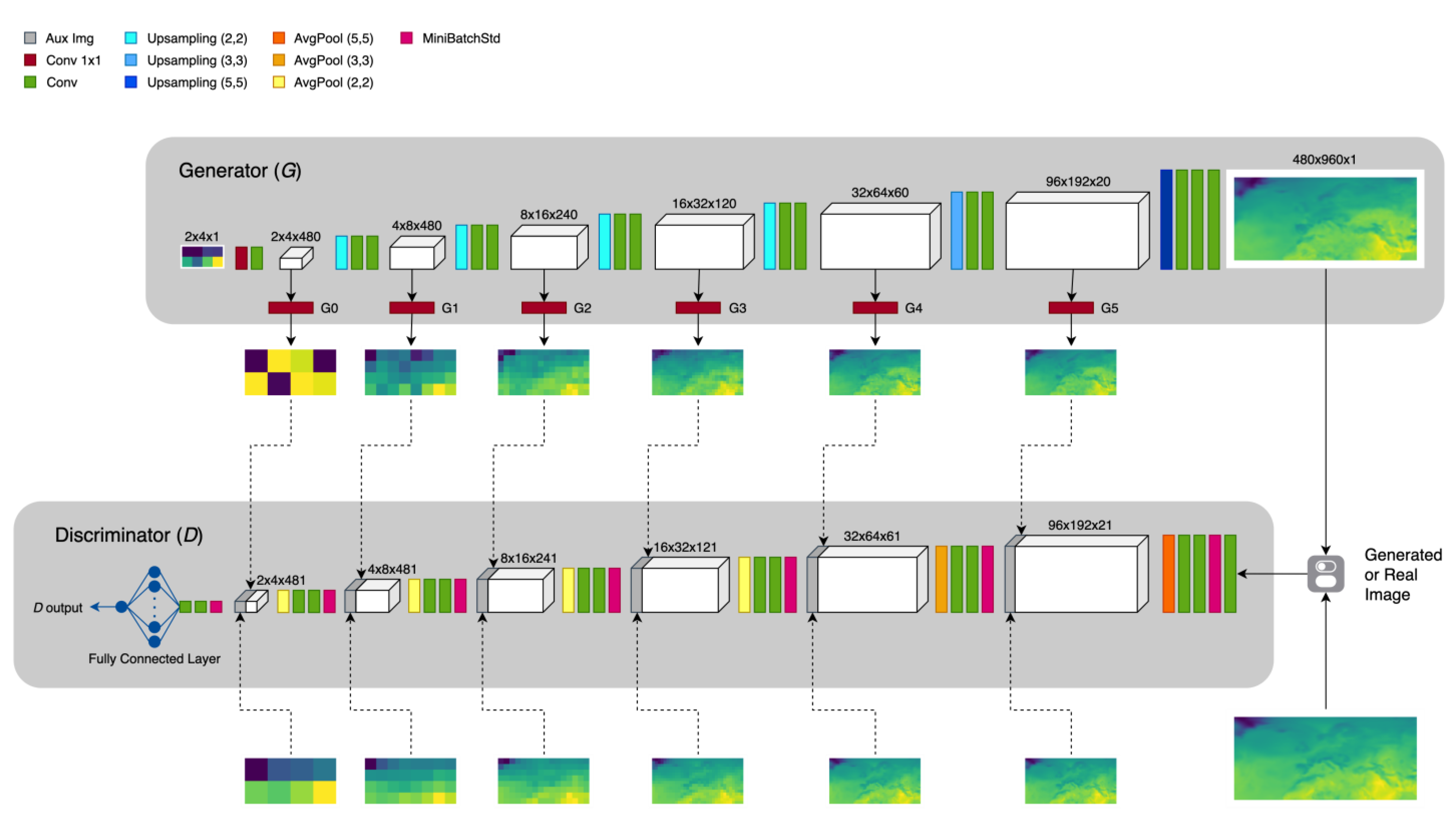
2.2. The Architecture: Multi-Scale Gradients GAN for Statistical Downscaling
2.3. Data Preprocessing
2.4. Experimental Setup
2.4.1. Training Set Arrangements
2.4.2. Training Configurations
2.4.3. The Validation Framework
- (1)
- Best Models Selection
- (2)
- Evaluation Procedure
- Mean Squared Error (MSE):
- Peak Signal-to-Noise Ratio (PSNR):
- Log Spectral Distance (LSD):
- Structural Similarity Index Measure (SSIM):
- Fréchet Inception Distance (FID):
- -
- and are real and generated T2M maps, respectively;
- -
- and refer to square windows of fixed size;
- -
- and are mean intensity and standard deviation of the window (similarly for );
- -
- is the covariance between and ;
- -
- and are non-negative constants used to stabilize the division with weak denominator;
- -
- represents the Fréchet distance between the Gaussian with mean ( obtained from the probability of generating model data and the Gaussian ( obtained from the probability of observing real-world data.
- -
- and represent vectors of T2M values for the same pixel location in the generated and real images, respectively. The dimension of these vectors is
- ○
- d = # daily samples x # days in a month (for the monthly arrangement)
- ○
- d = # daily samples x # days in a season (for the seasonal arrangement);
- -
- is the covariance between and ;
- -
- are the standard deviations of and , respectively;
- -
- are ranks of and , respectively;
- -
- are the standard deviations of and , respectively.
- (3)
- Final Test Procedure
3. Results and Discussion
3.1. Training Results
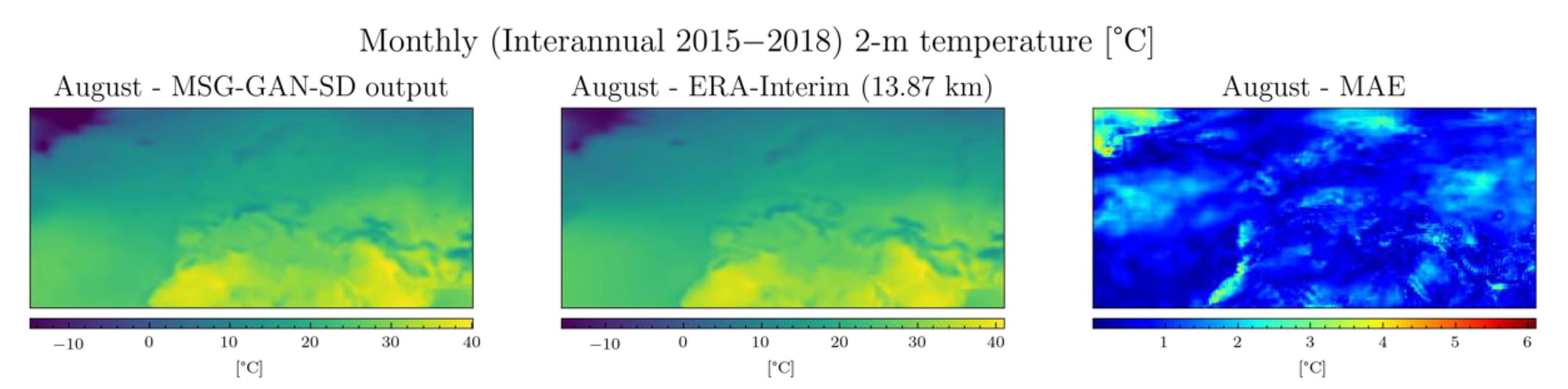
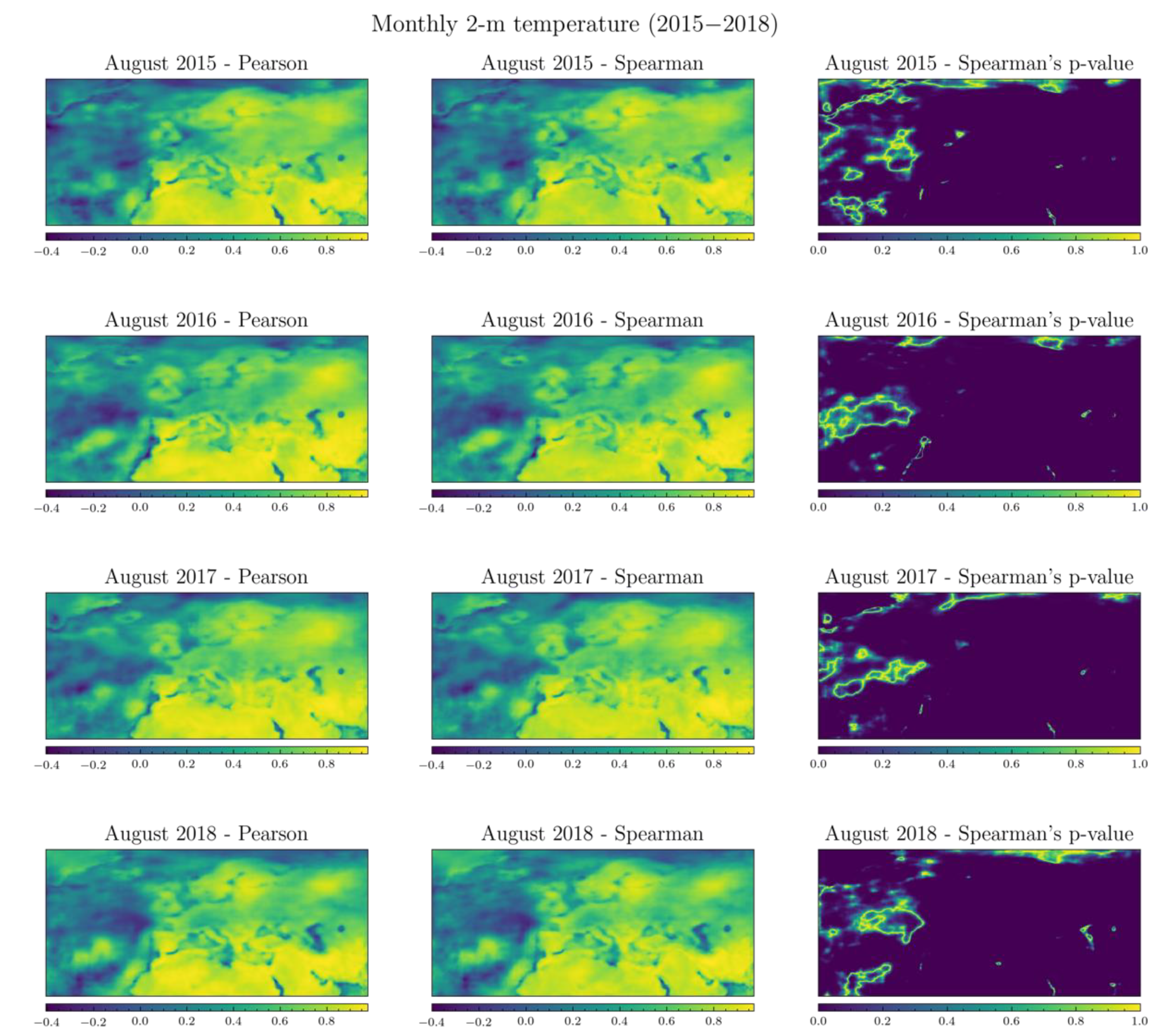
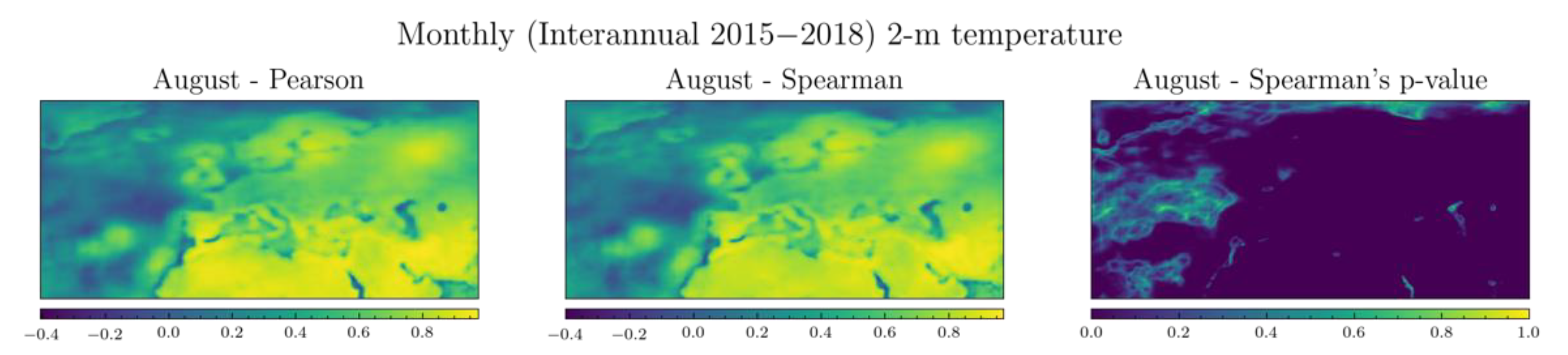
3.2. Evaluation Procedure
3.3. Test Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The MSG-GAN-SD Architecture
| Block | Layer | Activation | Output Shape |
|---|---|---|---|
| 0. | Input Conv 1 × 1 Conv 2 × 2 | – LReLU LReLU | 2 × 4 × 1 2 × 4 × 480 2 × 4 × 480 |
| Conv 1 × 1 | Tanh | 2 × 4 × 1 | |
| 1. | Input Upsampling (2, 2) Conv 3 × 3 Conv 3 × 3 | – – LReLU LReLU | 2 × 4 × 480 4 × 8 × 480 4 × 8 × 480 4 × 8 × 480 |
| Conv 1 × 1 | Tanh | 4 × 8 × 1 | |
| 2. | Input Upsampling (2, 2) Conv 3 × 3 Conv 3 × 3 | – – LReLU LReLU | 4 × 8 × 480 8 × 16 × 480 8 × 16 × 240 8 × 16 × 240 |
| Conv 1 × 1 | Tanh | 8 × 16 × 1 | |
| 3. | Input Upsampling (2, 2) Conv 3 × 3 Conv 3 × 3 | – – LReLU LReLU | 8 × 16 × 240 16 × 32 × 240 16 × 32 × 120 16 × 32 × 120 |
| Conv 1 × 1 | Tanh | 16 × 32 × 1 | |
| 4. | Input Upsampling (2, 2) Conv 3 × 3 Conv 3 × 3 | – – LReLU LReLU | 16 × 32 × 120 32 × 64 × 120 32 × 64 × 60 32 × 64 × 60 |
| Conv 1 × 1 | Tanh | 32 × 64 × 1 | |
| 5. | Input Upsampling (3, 3) Conv 3 × 3 Conv 3 × 3 | – – LReLU LReLU | 32 × 64 × 60 96 × 192 × 60 96 × 192 × 20 96 × 192 × 20 |
| Conv 1 × 1 | Tanh | 96 × 192 × 1 | |
| 6. | Input Upsampling (5, 5) Conv 3 × 3 Conv 3 × 3 Conv 3 × 3 | – – LReLU LReLU Tanh | 96 × 192 × 20 480 × 960 × 20 480 × 960 × 4 480 × 960 × 4 480 × 960 × 1 |
| Block | Layer | Activation | Output Shape |
|---|---|---|---|
| 0. | Input Conv 3 × 3 MiniBatchStd Conv 3 × 3 Conv 3 × 3 AvgPool (5, 5) | – LReLU – LReLU LReLU – | 480 × 960 × 1 480 × 960 × 4 480 × 960 × 5 480 × 960 × 4 480 × 960 × 20 96 × 192 × 20 |
| Auxiliary Image | – | 96 × 192 × 1 | |
| 1. | Input Concat MiniBatchStd Conv 3 × 3 Conv 3 × 3 AvgPool (3, 3) | – – – LReLU LReLU – | 96 × 192 × 20 96 × 192 × 21 96 × 192 × 22 96 × 192 × 20 96 × 192 × 60 32 × 64 × 60 |
| Auxiliary Image | – | 32 × 64 × 1 | |
| 2. | Input Concat MiniBatchStd Conv 3 × 3 Conv 3 × 3 AvgPool (2, 2) | – – – LReLU LReLU – | 32 × 64 × 60 32 × 64 × 61 32 × 64 × 62 32 × 64 × 60 32 × 64 × 120 16 × 32 × 120 |
| Auxiliary Image | – | 16 × 32 × 1 | |
| 3. | Input Concat MiniBatchStd Conv 3 × 3 Conv 3 × 3 AvgPool (2, 2) | – – – LReLU LReLU – | 16 × 32 × 120 16 × 32 × 121 16 × 32 × 122 16 × 32 × 120 16 × 32 × 240 8 × 16 × 240 |
| Auxiliary Image | – | 8 × 16 × 1 | |
| 4. | Input Concat MiniBatchStd Conv 3 × 3 Conv 3 × 3 AvgPool (2, 2) | – – – LReLU LReLU – | 8 × 16 × 240 8 × 16 × 241 8 × 16 × 242 8 × 16 × 240 8 × 16 × 480 4 × 8 × 480 |
| Auxiliary Image | – | 4 × 8 × 1 | |
| 5. | Input Concat MiniBatchStd Conv 3 × 3 Conv 3 × 3 AvgPool (2, 2) | – – – LReLU LReLU – | 4 × 8 × 480 4 × 8 × 481 4 × 8 × 482 4 × 8 × 480 4 × 8 × 480 2 × 4 × 480 |
| Auxiliary Image | – | 2 × 4 × 1 | |
| 6. | Input Concat MiniBatchStd Conv 2 × 2 Conv 2 × 4 Fully Connected | – – – LReLU LReLU Linear | 2 × 4 × 480 2 × 4 × 481 2 × 4 × 482 2 × 4 × 480 1 × 1 × 480 1 × 1 × 1 |
Appendix B. Best Model Selection and Evaluation Results
| Training Set Arrangements | Monthly | Seasonal | ||
|---|---|---|---|---|
| Months | # D updates | Epoch | # D updates | Epoch |
| January | 2 | 950 | 1 | 850 |
| February | 1 | 500 | 1 | 850 |
| March | 1 | 850 | 1 | 1000 |
| April | 2 | 600 | 1 | 1000 |
| May | 3 | 750 | 3 | 350 |
| June | 2 | 850 | 1 | 800 |
| July | 1 | 800 | 1 | 800 |
| August | 1 | 850 | 1 | 800 |
| September | 2 | 750 | 3 | 750 |
| October | 1 | 950 | 3 | 750 |
| November | 3 | 600 | 3 | 750 |
| December | 1 | 950 | 1 | 850 |
| Monthly-Based Training | MSE (↓) | PSNR (↑) | SSIM (↑) | FID (↓) | LSD (↓) | Accuracy (↑) | Perceptivity (↑) | |
|---|---|---|---|---|---|---|---|---|
| January | 0.012 | 17.478 | 0.811 | 0.099 | 8.294 | 1173.585 | 1.213 | 1423.007 |
| February | 0.010 | 18.052 | 0.834 | 0.062 | 8.086 | 1526.165 | 1.981 | 3023.297 |
| March | 0.009 | 18.562 | 0.842 | 0.051 | 8.918 | 1746.389 | 2.208 | 3856.081 |
| April | 0.009 | 18.507 | 0.839 | 0.047 | 9.761 | 1697.090 | 2.180 | 3699.364 |
| May | 0.010 | 18.137 | 0.799 | 0.066 | 9.505 | 1455.684 | 1.585 | 2307.581 |
| June | 0.006 | 20.284 | 0.831 | 0.067 | 9.192 | 2844.603 | 1.631 | 4639.858 |
| July | 0.006 | 20.009 | 0.812 | 0.064 | 9.245 | 2548.737 | 1.697 | 4325.116 |
| August | 0.005 | 20.692 | 0.836 | 0.045 | 7.960 | 3502.819 | 2.822 | 9885.056 |
| September | 0.007 | 19.840 | 0.894 | 0.063 | 7.767 | 2580.708 | 2.053 | 5298.983 |
| October | 0.007 | 20.040 | 0.905 | 0.046 | 8.378 | 2602.556 | 2.573 | 6697.147 |
| November | 0.009 | 19.367 | 0.877 | 0.091 | 7.893 | 1940.007 | 1.396 | 2708.218 |
| December | 0.010 | 18.699 | 0.853 | 0.082 | 8.416 | 1545.117 | 1.457 | 2251.966 |
| Season-Based Training | MSE (↓) | PSNR (↑) | SSIM (↑) | FID (↓) | LSD (↓) | Accuracy (↑) | Perceptivity (↑) | (↑) |
| January | 0.011 | 17.584 | 0.817 | 0.079 | 8.760 | 1324.248 | 1.438 | 1904.269 |
| February | 0.009 | 18.414 | 0.843 | 0.061 | 8.388 | 1645.494 | 1.968 | 3239.104 |
| March | 0.008 | 17.586 | 0.797 | 0.041 | 9.871 | 1651.174 | 2.478 | 4091.508 |
| April | 0.007 | 18.837 | 0.873 | 0.042 | 10.120 | 2233.076 | 2.351 | 5249.693 |
| May | 0.007 | 20.051 | 0.924 | 0.053 | 9.689 | 2739.662 | 1.949 | 5340.450 |
| June | 0.005 | 20.450 | 0.829 | 0.046 | 9.170 | 3110.453 | 2.382 | 7407.763 |
| July | 0.005 | 21.084 | 0.873 | 0.037 | 8.699 | 3733.963 | 3.109 | 11,607.422 |
| August | 0.004 | 21.395 | 0.877 | 0.039 | 7.316 | 4217.381 | 3.540 | 14,929.312 |
| September | 0.005 | 21.618 | 0.958 | 0.048 | 7.047 | 3970.463 | 2.966 | 11,777.042 |
| October | 0.005 | 20.731 | 0.908 | 0.043 | 7.538 | 3748.529 | 3.085 | 11,565.111 |
| November | 0.007 | 18.326 | 0.825 | 0.066 | 7.740 | 2138.194 | 1.954 | 4178.579 |
| December | 0.009 | 18.677 | 0.852 | 0.072 | 8.973 | 1794.051 | 1.542 | 2767.413 |
References
- Vandal, T.; Kodra, E.; Ganguly, S.; Michaelis, A.; Nemani, R.; Ganguly, A. DeepSD: Generating High Resolution Climate Change Projections through Single Image Super-Resolution. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017. [Google Scholar] [CrossRef]
- Vandal, T.; Kodra, E.; Ganguly, S.; Michaelis, A.; Nemani, R.; Ganguly, A. Generating High Resolution Climate Change Projections through Single Image Super-Resolution: An Abridged Version. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018. [Google Scholar] [CrossRef] [Green Version]
- Baño-Medina, J.; Gutiérrez, J.; Herrera, S. Deep Neural Networks for Statistical Downscaling of Climate Change Projections. In Proceedings of the XVIII Conferencia de la Asociación Española para la Inteligencia Artificial (CAEPIA 2018), Granada, España, 23–26 October 2018; pp. 1419–1424. [Google Scholar]
- Baño-Medina, J.; Manzanas, R.; Gutiérrez, J. Configuration and intercomparison of deep learning neural models for statistical downscaling. Geosci. Model Dev. 2020, 13, 2109–2124. [Google Scholar] [CrossRef]
- Rodrigues, E.; Oliveira, I.; Cunha, R.; Netto, M. DeepDownscale: A Deep Learning Strategy for High-Resolution Weather Forecast. In Proceedings of the 2018 IEEE 14th International Conference on e-Science (e-Science), Amsterdam, The Netherlands, 29 October–1 November 2018. [Google Scholar] [CrossRef] [Green Version]
- Wood, A.; Leung, L.; Sridhar, V.; Lettenmaier, D.P. Hydrologic implications of dynamical and statistical approaches to downscaling climate model outputs. Clim. Chang. 2004, 62, 189–216. [Google Scholar] [CrossRef]
- Fowler, H.J.; Blenkinsop, S.; Tebaldi, C. Linking climate change modelling to impacts studies: Recent advances in downscaling techniques for hydrological modelling. Int. J. Climatol. 2007, 27, 1547–1578. [Google Scholar] [CrossRef]
- Maraun, D.; Widmann, M. Statistical Downscaling and Bias Correction for Climate Research; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Yang, W.; Zhang, X.; Tian, Y.; Wang, W.; Xue, J.; Liao, Q. Deep Learning for Single Image Super-Resolution: A Brief Review. IEEE Trans. Multimed. 2019, 21, 3106–3121. [Google Scholar] [CrossRef] [Green Version]
- Leinonen, J.; Nerini, D.; Berne, A. Stochastic Super-Resolution for Downscaling Time-Evolving Atmospheric Fields with a Generative Adversarial Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7211–7223. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Hoi, S. Deep Learning for Image Super-resolution: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3365–3387. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vandal, T.; Kodra, E.; Ganguly, A. Intercomparison of machine learning methods for statistical downscaling: The case of daily and extreme precipitation. Theor. Appl. Climatol. 2019, 137, 557–570. [Google Scholar] [CrossRef] [Green Version]
- Pan, B.; Hsu, K.; AghaKouchak, A.; Sorooshian, S. Improving precipitation estimation using convolutional neural network. Water Resour. Res. 2019, 55, 2301–2321. [Google Scholar] [CrossRef] [Green Version]
- Sachindra, D.; Ahmed, K.; Rashid, M.; Shahid, S.; Perera, B. Statistical downscaling of precipitation using machine learning techniques. Atmos. Res. 2018, 212, 240–258. [Google Scholar] [CrossRef]
- Karnewar, A.; Wang, O. MSG-GAN: Multi-Scale Gradients for Generative Adversarial Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 7796–7805. [Google Scholar] [CrossRef]
- ERA-Interim. ECMWF. 2020. Available online: https://apps.ecmwf.int/datasets/data/interim-full-daily/levtype=sfc/ (accessed on 14 November 2021).
- Wilby, R.; Charles, S.; Zorita, E.; Timbal, B.; Whetton, P.; Mearns, L. Guidelines for Use of Climate Scenarios Developed from Statistical Downscaling Methods. Supporting Material to the IPCC; 2004; pp. 3–21. Available online: https://www.narccap.ucar.edu/ (accessed on 14 November 2021).
- Gao, L.; Schulz, K.; Bernhardt, M. Statistical Downscaling of ERA-Interim Forecast Precipitation Data in Complex Terrain Using LASSO Algorithm. Adv. Meteorol. 2014, 2014, 472741. [Google Scholar] [CrossRef] [Green Version]
- Coulibaly, P. Downscaling daily extreme temperatures with genetic programming. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Sachindra, D.; Kanae, S. Machine learning for downscaling: The use of parallel multiple populations in genetic programming. Stoch. Environ. Res. Risk Assess. 2019, 33, 1497–1533. [Google Scholar] [CrossRef] [Green Version]
- Bartkowiak, P.; Castelli, M.; Notarnicola, C. Downscaling Land Surface Temperature from MODIS Dataset with Random Forest Approach over Alpine Vegetated Areas. Remote Sens. 2019, 11, 1319. [Google Scholar] [CrossRef] [Green Version]
- Anh, Q.T.; Taniguchi, K. Coupling dynamical and statistical downscaling for high-resolution rainfall forecasting: Case study of the Red River Delta, Vietnam. Prog. Earth Planet. Sci. 2018, 5. [Google Scholar] [CrossRef]
- Salimi, A.; Samakosh, J.M.; Sharifi, E.; Hassanvand, M.; Noori, A.; von Rautenkranz, H. Optimized Artificial Neural Networks-Based Methods for Statistical Downscaling of Gridded Precipitation Data. Water 2019, 11, 1653. [Google Scholar] [CrossRef] [Green Version]
- Min, X.; Ma, Z.; Xu, J.; He, K.; Wang, Z.; Huang, Q.; Li, J. Spatially Downscaling IMERG at Daily Scale Using Machine Learning Approaches Over Zhejiang, Soualthoughtheastern China. Front. Earth Sci. 2020, 8. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Misra, S.; Sarkar, S.; Mitra, P. Statistical downscaling of precipitation using long short-term memory recurrent neural networks. Theor. Appl. Climatol. 2017, 134, 1179–1196. [Google Scholar] [CrossRef]
- Anh, D.T.; Van, S.; Dang, T.; Hoang, L. Downscaling rainfall using deep learning long short-term memory and feedforward neural network. Int. J. Climatol. 2019, 39, 4170–4188. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.; He, K.; Tang, X. Learning a Deep Convolutional Network for Image Super-Resolution. Lect. Notes Comput. Sci. 2014, 8692, 184–199. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef] [Green Version]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual losses for real-time style transfer and super-resolution. In Computer Vision—ECCV 2016, Proceedings of the 14th European Conference, Proceedings, Part II, Amsterdam, The Netherlands, 11–14 October 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer: Cham, Switzerland, 2016; pp. 694–711. [Google Scholar] [CrossRef]
- Kim, H.; Choi, M.; Lim, B.; Lee, K. Task-Aware Image Downscaling. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Park, D.; Kim, J.; Chun, S.Y. Down-Scaling with Learned Kernels in Multi-Scale Deep Neural Networks for Non-Uniform Single Image Deblurring. arXiv 2019, arXiv:1903.10157. [Google Scholar]
- Miao, Q.; Pan, B.; Wang, H.; Hsu, K.; Sorooshian, S. Improving Monsoon Precipitation Prediction Using Combined Convolutional and Long Short Term Memory Neural Network. Water 2019, 11, 977. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Lan, Y. Statistical downscaling of daily temperature and precipitation over China using deep learning neural models: Localization and comparison with other methods. Int. J. Climatol. 2020. [Google Scholar] [CrossRef]
- Huang, X. Deep-Learning Based Climate Downscaling Using the Super-Resolution Method: A Case Study over the Western US. Geosci. Model Dev. Discuss. 2020, preprint. [Google Scholar] [CrossRef]
- Kern, M.; Höhlein, K.; Hewson, T.; Westermann, R. Towards Operational Downscaling of Low Resolution Wind Fields Using Neural Networks. In Proceedings of the 22nd EGU General Assembly, EGU2020-5447. Online, 4–8 May 2020. [Google Scholar] [CrossRef]
- Shi, X. Enabling Smart Dynamical Downscaling of Extreme Precipitation Events with Machine Learning. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Sekiyama, T. Statistical Downscaling of Temperature Distributions from the Synoptic Scale to the Mesoscale Using Deep Convolutional Neural Networks. arXiv 2020, arXiv:2007.1083. [Google Scholar]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Loy, C.C. ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks. Lect. Notes Comput. Sci. 2019, 11133. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.; Albert, A.; White, B. Downscaling numerical weather models with gans. In Proceedings of the 9th International Conference on Climate Informatics 2019, Paris, France, 2–4 October 2019; pp. 275–278. [Google Scholar]
- Groenke, B.; Madaus, L.; Monteleoni, C. ClimAlign: Unsupervised statistical downscaling of climate variables via normalizing flows. In Proceedings of the 10th International Conference on Climate Informatics, Oxford, UK, 22–25 September 2020. [Google Scholar]
- Mendes, D.; Marengo, J. Temporal downscaling: A comparison between artificial neural network and autocorrelation techniques over the Amazon Basin in present and future climate change scenarios. Theor. Appl. Climatol. 2009, 100, 413–421. [Google Scholar] [CrossRef]
- Mouatadid, S.; Easterbrook, S.; Erler, A.R. A Machine Learning Approach to Non-uniform Spatial Downscaling of Climate Variables. In Proceedings of the 2017 IEEE International Conference on Data Mining Workshops (ICDMW), New Orleans, LA, USA, 18–21 November 2017; pp. 332–341. [Google Scholar] [CrossRef]
- Chang, Y.; Acierto, R.; Itaya, T.; Akiyuki, K.; Tung, C. A Deep Learning Approach to Downscaling Precipitation and Temperature over Myanmar. EGU Gen. Assem. Conf. Abstr. 2018, 4120. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y.; Jing, W.; Yue, X. Comparison of Different Machine Learning Approaches for Monthly Satellite-Based Soil Moisture Downscaling over Northeast China. Remote Sens. 2018, 10, 31. [Google Scholar] [CrossRef] [Green Version]
- Sharifi, E.; Saghafian, B.; Steinacker, R. Downscaling Satellite Precipitation Estimates with Multiple Linear Regression, Artificial Neural Networks, and Spline Interpolation Techniques. J. Geophys. Res. Atmos. 2019, 124, 789–805. [Google Scholar] [CrossRef] [Green Version]
- Höhlein, K.; Kern, M.; Hewson, T.; Westermann, R. A comparative study of convolutional neural network models for wind field downscaling. Meteorol. Appl. 2020, 27. [Google Scholar] [CrossRef]
- Xu, R.; Chen, N.; Chen, Y.; Chen, Z. Downscaling and Projection of Multi-CMIP5 Precipitation Using Machine Learning Methods in the Upper Han River Basin. Adv. Meteorol. 2020, 2020, 1–17. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Huang, W.; Zhou, P. Performance of statistical and machine learning ensembles for daily temperature downscaling. Theor. Appl. Climatol. 2020, 140, 571–588. [Google Scholar] [CrossRef]
- Sachindra, D.; Huang, F.; Barton, A.; Perera, B. Least square support vector and multi-linear regression for statistically downscaling general circulation model outputs to catchment streamflows. Int. J. Climatol. 2013, 33, 1087–1106. [Google Scholar] [CrossRef] [Green Version]
- Goly, A.; Teegavarapu, R.; Mondal, A. Development and Evaluation of Statistical Downscaling Models for Monthly Precipitation. Earth Interact. 2014, 18, 1–28. [Google Scholar] [CrossRef]
- Duhan, D.; Pandey, A. Statistical downscaling of temperature using three techniques in the Tons River basin in Central India. Theor. Appl. Climatol. 2014, 121, 605–622. [Google Scholar] [CrossRef]
- EURO-CORDEX. Available online: https://euro-cordex.net/index.php.en (accessed on 14 November 2021).
- NetCDF. Available online: https://www.unidata.ucar.edu/software/netcdf/ (accessed on 14 November 2021).
- ERA-Interim. Available online: https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim (accessed on 14 November 2021).
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 105–114. [Google Scholar] [CrossRef] [Green Version]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. arXiv 2014, arXiv:1406.2661. [Google Scholar] [CrossRef]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A. Improved Training of Wasserstein GANs. Adv. Neural Inf. Process. Syst. 2017, 30, 5767–5777. [Google Scholar]
- Karras, T.; Aila, T.; Laine, S.; Lehtinen, J. Progressive Growing of GANs for Improved Quality, Stability and Variation. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, CA, Canada, 30 April–3 May 2018. [Google Scholar]
- Denton, E.; Chintala, S.; Szlam, A.; Fergus, R. Deep generative image models using a Laplacian pyramid of adversarial networks. In Proceedings of the 28th International Conference on Neural Information Processing Systems (NIPS’15), Montréal, QC, Canada, 7–12 December 2015; Volume 1, pp. 1486–1494. [Google Scholar]
- Dinh, L.; Krueger, D.; Bengio, Y. NICE: Non-linear Independent Components Estimation. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Cineca. Available online: https://www.cineca.it (accessed on 14 November 2021).
- Marconi 100. Available online: https://www.hpc.cineca.it/hardware/marconi100 (accessed on 14 November 2021).
- Keras. Available online: https://keras.io (accessed on 14 November 2021).
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI ’16), Savannah, GA, USA, 2–4 November 2016. [Google Scholar]
- Distributed Training with TensorFlow. Available online: https://www.tensorflow.org/guide/distributed_training (accessed on 14 November 2021).
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein GAN. arXiv 2017, arXiv:1701.07875. [Google Scholar]
- Dauphin, Y.; de Vries, H.; Chung, J.; Bengio, Y. RMSProp and Equilibrated Adaptive Learning Rates for Non-Convex Optimization. arXiv 2015, arXiv:1502.04390v1. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium. Adv. Neural Inf. Process. Syst. 2017, 30, 6626–6637. [Google Scholar]
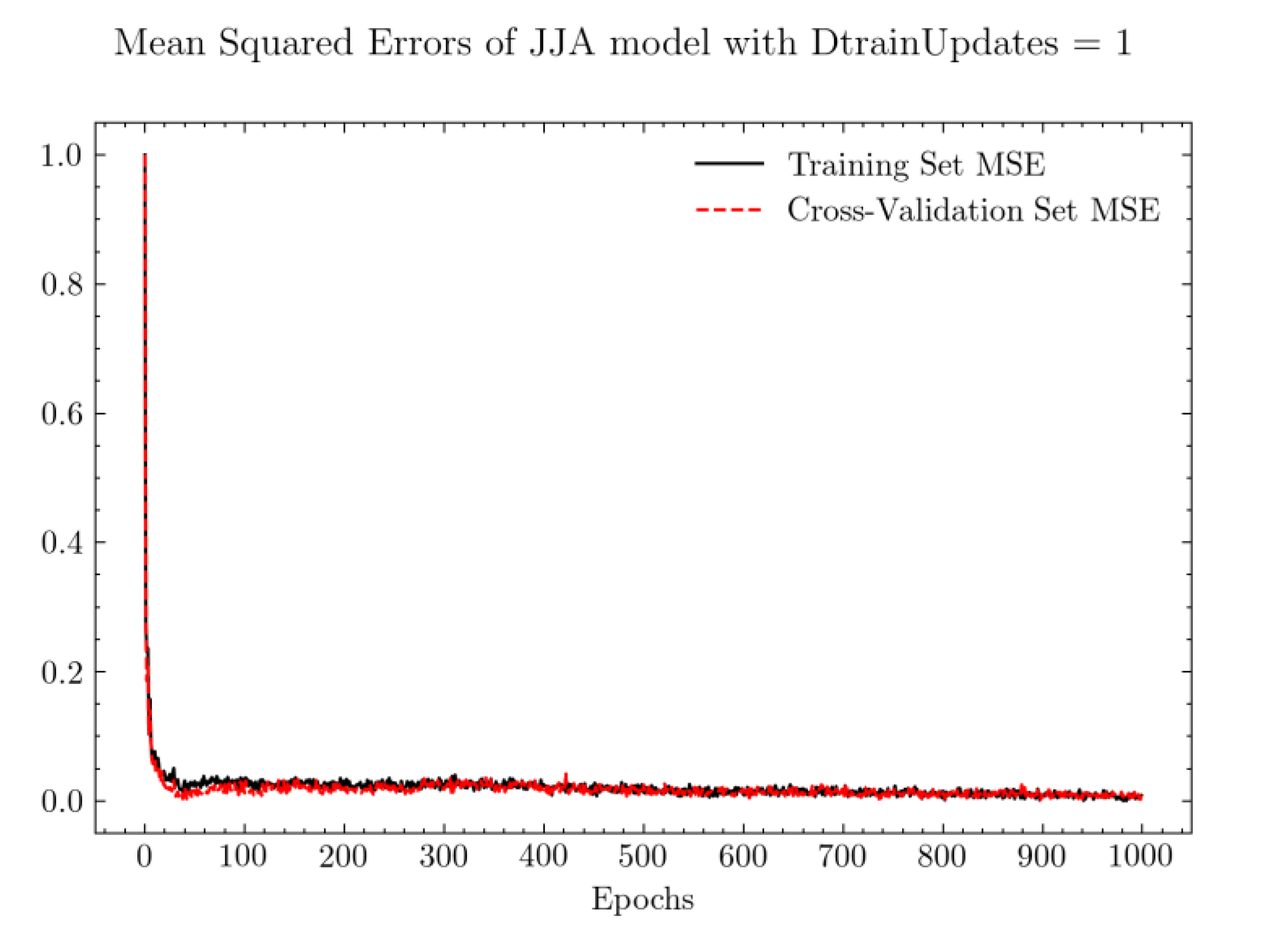
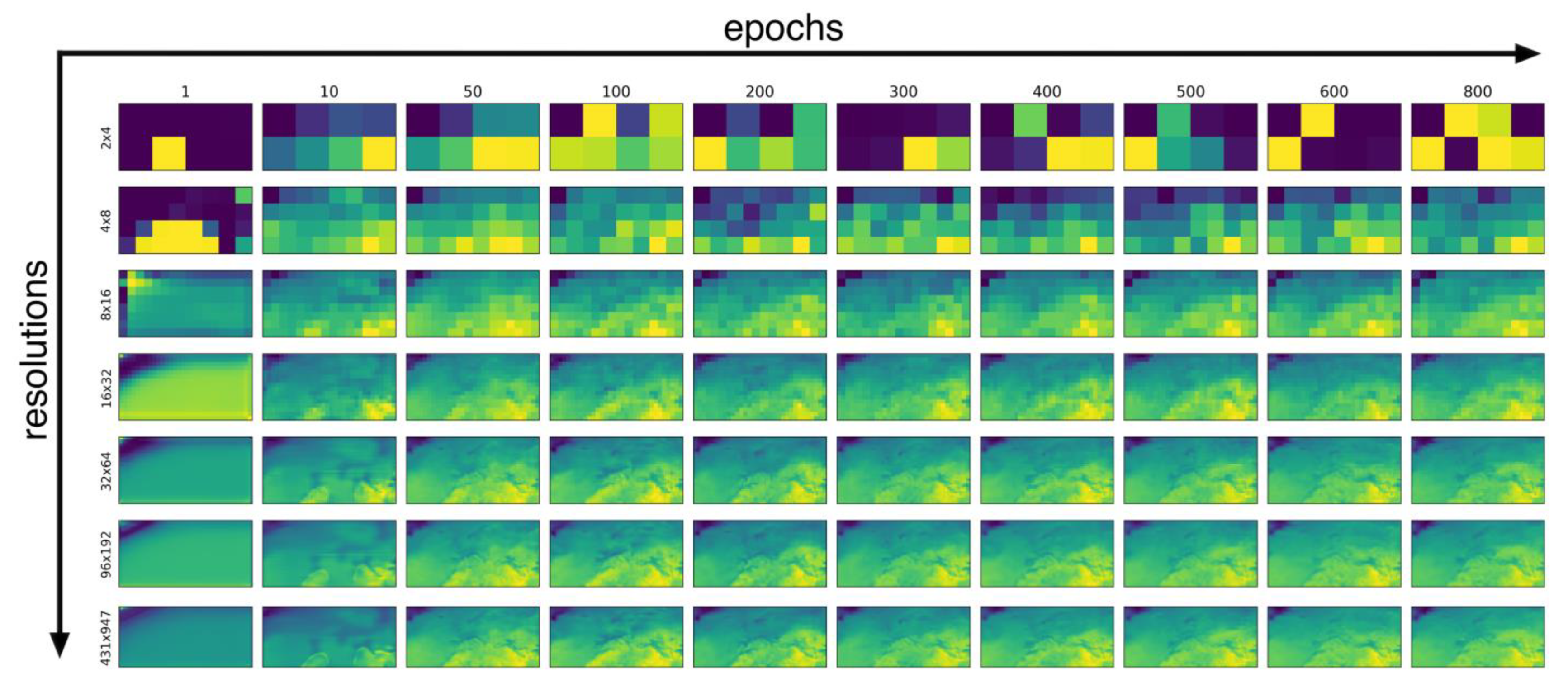
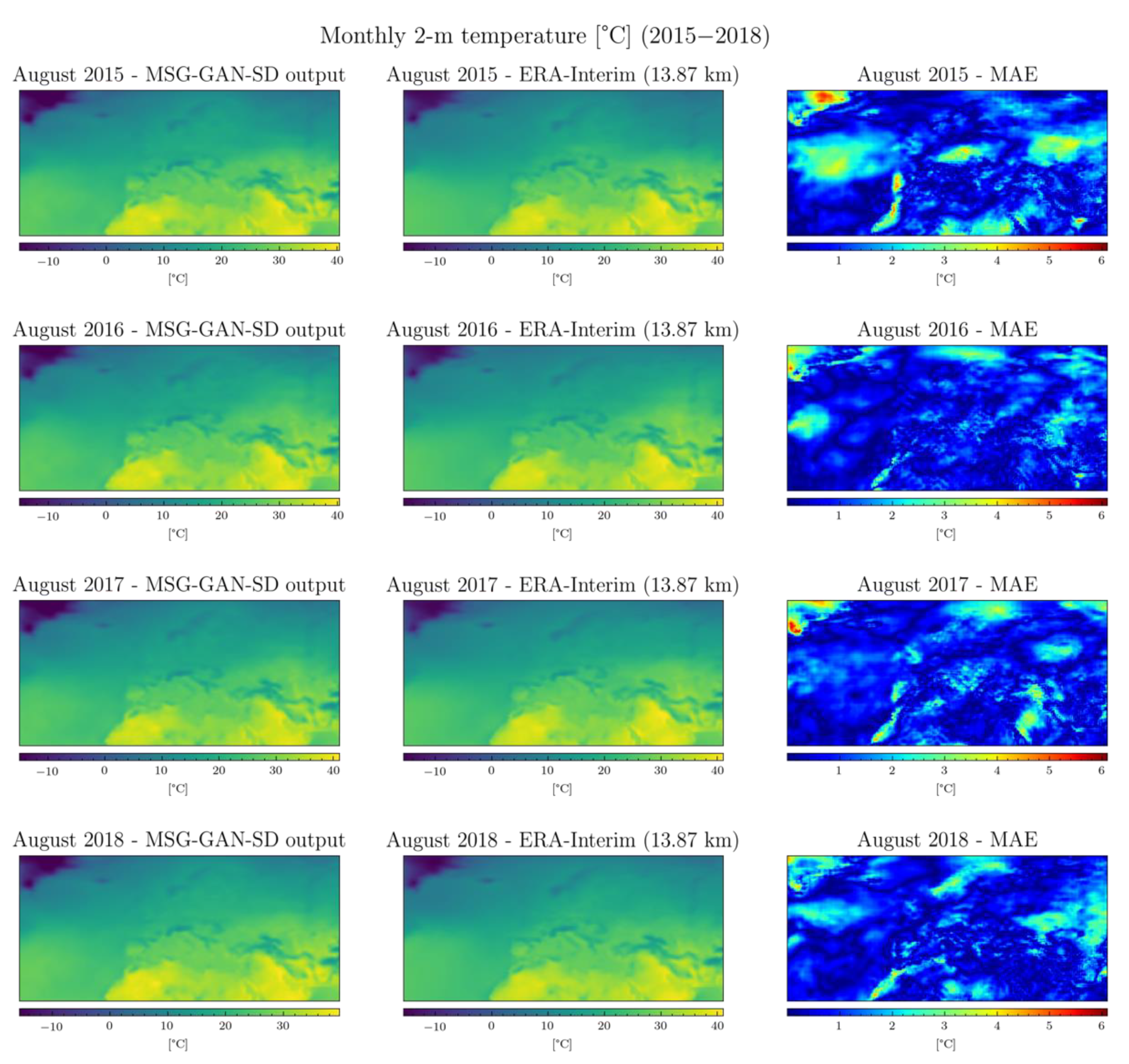
| Training Set Arrangements | Month-Based | Season-Based |
|---|---|---|
| DtrainUpdates = 1 | ~1 day | ~2 days |
| DtrainUpdates = 2 | ~1 day | ~3 days |
| DtrainUpdates = 3 | ~2 days | ~4 days |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Accarino, G.; Chiarelli, M.; Immorlano, F.; Aloisi, V.; Gatto, A.; Aloisio, G. MSG-GAN-SD: A Multi-Scale Gradients GAN for Statistical Downscaling of 2-Meter Temperature over the EURO-CORDEX Domain. AI 2021, 2, 600-620. https://doi.org/10.3390/ai2040036
Accarino G, Chiarelli M, Immorlano F, Aloisi V, Gatto A, Aloisio G. MSG-GAN-SD: A Multi-Scale Gradients GAN for Statistical Downscaling of 2-Meter Temperature over the EURO-CORDEX Domain. AI. 2021; 2(4):600-620. https://doi.org/10.3390/ai2040036
Chicago/Turabian StyleAccarino, Gabriele, Marco Chiarelli, Francesco Immorlano, Valeria Aloisi, Andrea Gatto, and Giovanni Aloisio. 2021. "MSG-GAN-SD: A Multi-Scale Gradients GAN for Statistical Downscaling of 2-Meter Temperature over the EURO-CORDEX Domain" AI 2, no. 4: 600-620. https://doi.org/10.3390/ai2040036
APA StyleAccarino, G., Chiarelli, M., Immorlano, F., Aloisi, V., Gatto, A., & Aloisio, G. (2021). MSG-GAN-SD: A Multi-Scale Gradients GAN for Statistical Downscaling of 2-Meter Temperature over the EURO-CORDEX Domain. AI, 2(4), 600-620. https://doi.org/10.3390/ai2040036






