The Research on Enhancing the Super-Resolving Effect of Noisy Images through Structural Information and Denoising Preprocessing
Abstract
1. Introduction
2. Related Works
3. Method
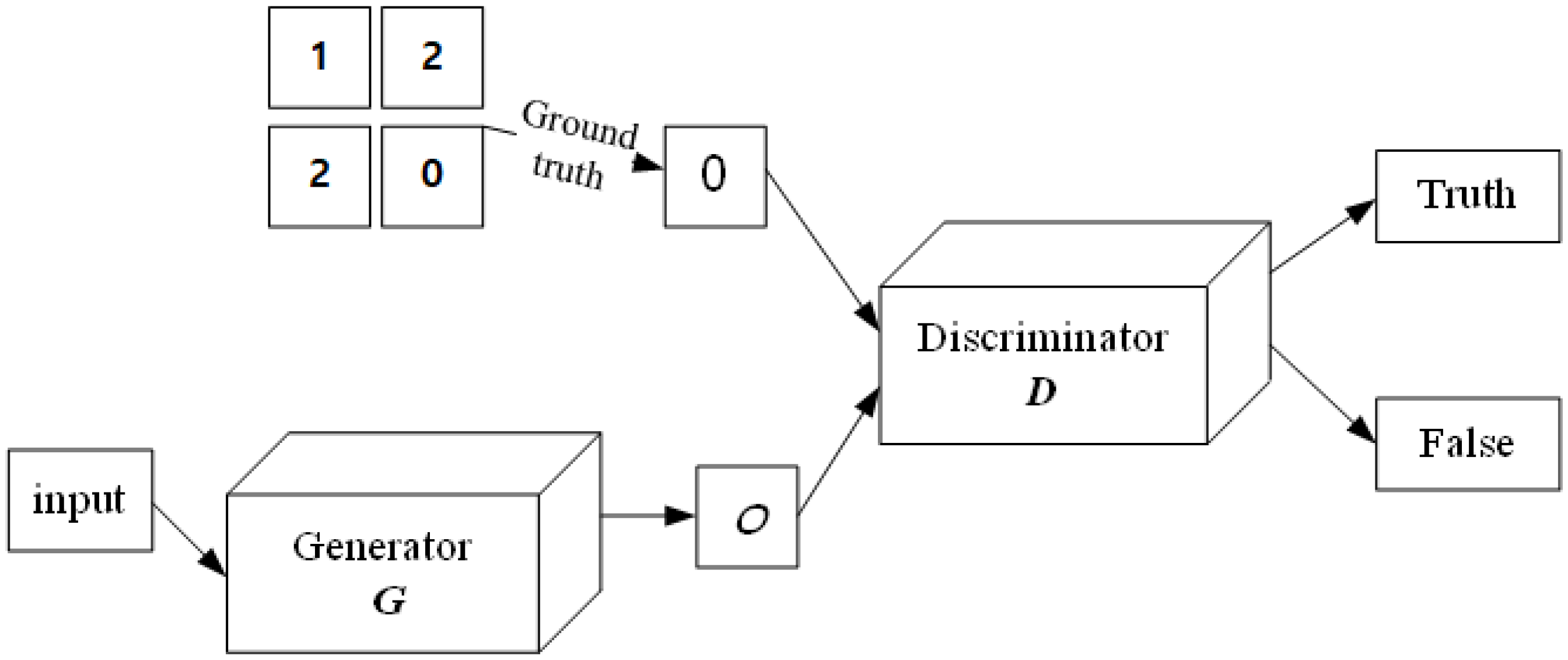
3.1. GAN
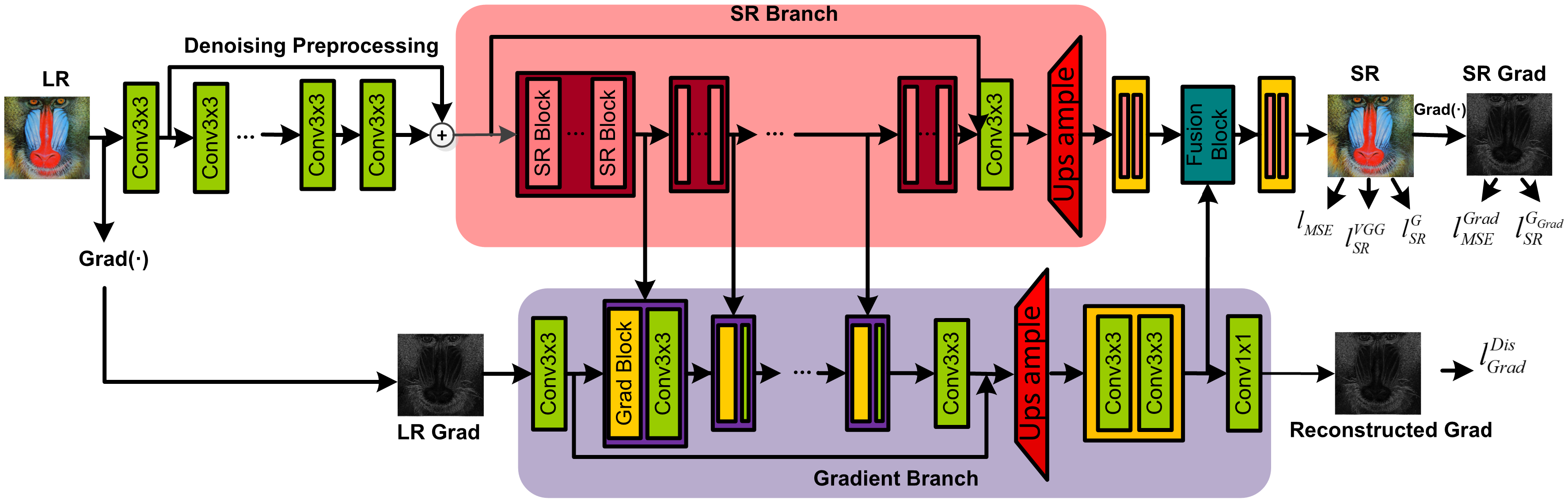
3.2. Details in Architecture
3.2.1. Denoising Preprocessing
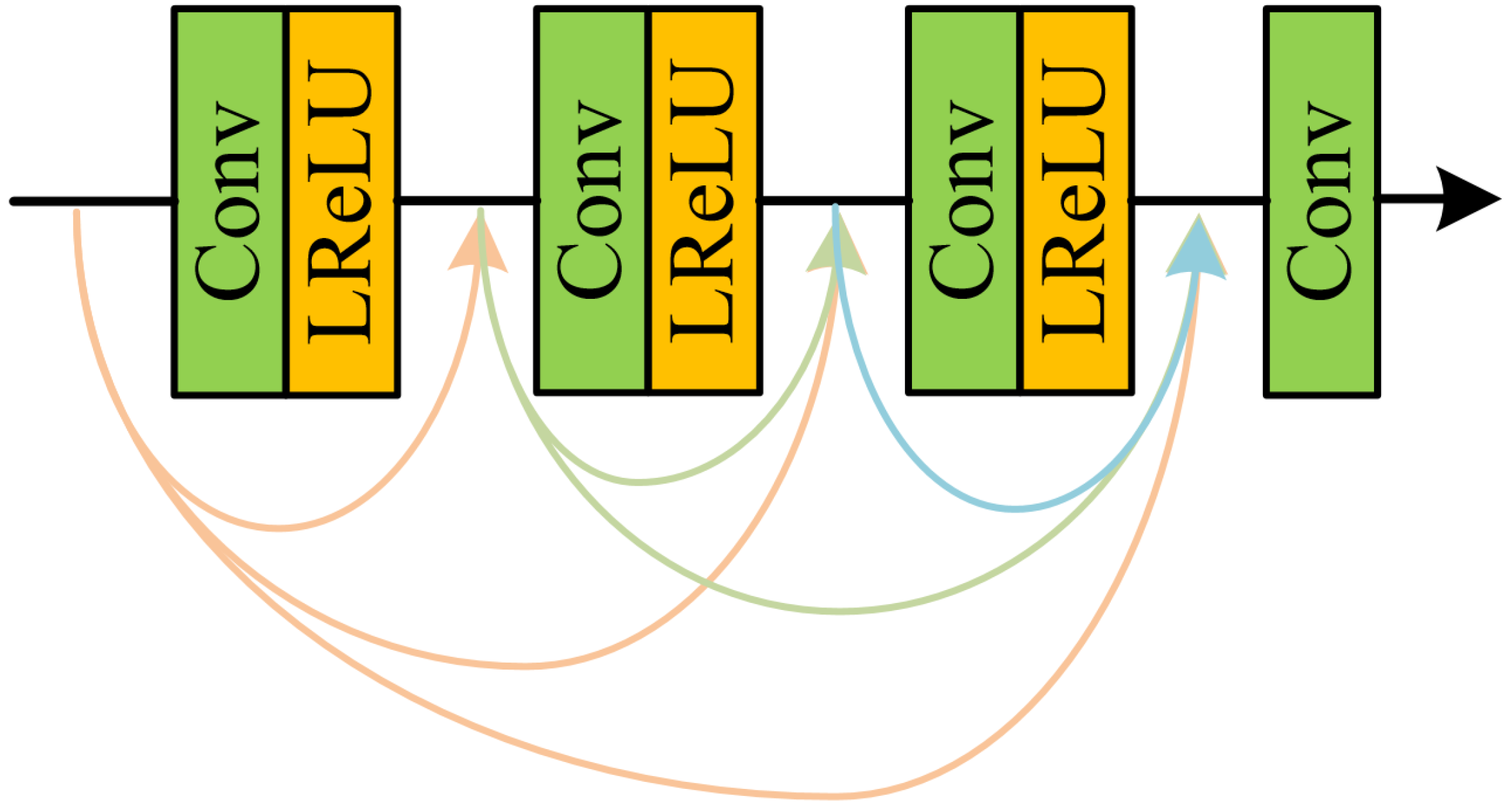
3.2.2. Gradient Branch
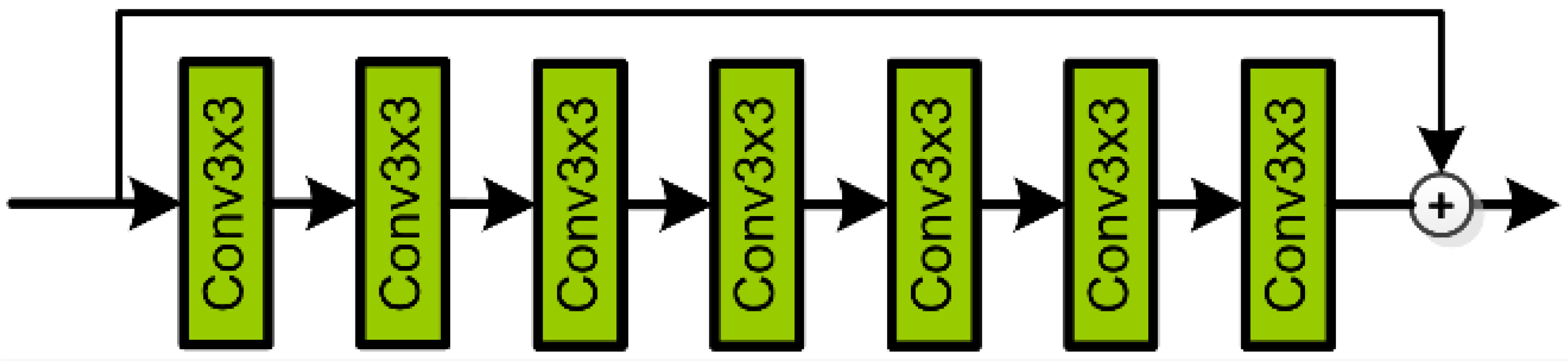
3.2.3. SR Branch
3.3. Loss Function
4. Experimental Settings
5. Result Analysis
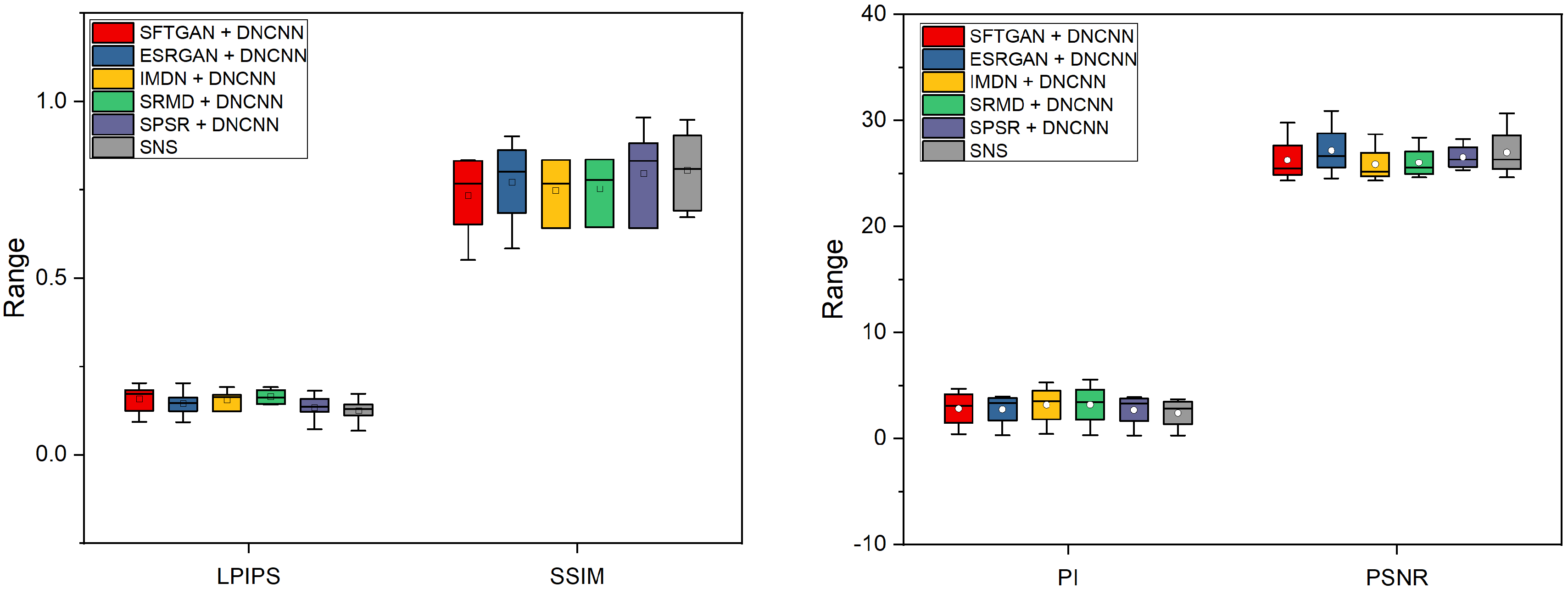
5.1. Quantitative Comparison
5.2. Qualitative Comparison
5.3. Denoising Preprocessing
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Advances in Neural Information Processing Systems 27; Neural Information Processing Systems Foundation, Inc.: San Diego, CA, USA, 2014. [Google Scholar]
- Zhang, K.; Zuo, W.M.; Chen, Y.J.; Meng, D.Y.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2007, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Rao, Y.; Cheng, Y.; Chen, C.; Lu, J.; Zhou, J. Structure-Preserving Super Resolution with Gradient Guidance. arXiv, 2020; arXiv:2003.13081. [Google Scholar]
- Hwang, H.; Haddad, R.A. Adaptive median filters: New algorithms and results. IEEE Trans. Image Process. 1995, 4, 499–502. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.X.; Li, F. A New Adaptive Weighted Mean Filter for Removing Salt-and-Pepper Noise. IEEE Signal Process. Lett. 2014, 21, 1280–1283. [Google Scholar] [CrossRef]
- Liu, L.; Chen, C.P.; Zhou, Y.; You, X. A new weighted mean filter with a two-phase detector for removing impulse noise. Inf. Sci. 2015, 315, 1–16. [Google Scholar] [CrossRef]
- Kandemir, C.; Kalyoncu, C.; Toygar, Ö. A weighted mean filter with spatial-bias elimination for impulse noise removal. Dig. Signal Process. 2015, 46, 164–174. [Google Scholar] [CrossRef]
- Zhou, Z. Cognition and Removal of Impulse Noise With Uncertainty. IEEE Trans. Image Process. 2012, 21, 3157–3167. [Google Scholar] [CrossRef]
- Li, Z.; Tang, K.; Cheng, Y.; Chen, X.; Zhou, C. Modified Adaptive Gaussian Filter for Removal of Salt and Pepper Noise. KSII Trans. Internet Inf. Syst. 2015, 9, 2928–2947. [Google Scholar] [CrossRef]
- Nasri, M.; Saryazdi, S.; Nezamabadi-pour, H. A Fast Adaptive Salt and Pepper Noise Reduction Method in Images. Circ. Syst. Signal Pr. 2013, 32, 1839–1857. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Li, N.; Chambers, J. A robust Gaussian approximate filter for nonlinear systems with heavy tailed measurement noises. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 4209–4213. [Google Scholar]
- Jain, V.; Seung, H.S. Natural image denoising with convolutional networks. In Proceedings of the 21st International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 3–6 December 2007; pp. 769–776. [Google Scholar]
- Burger, H.C.; Schuler, C.J.; Harmeling, S. Image denoising: Can plain neural networks compete with BM3D? In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2392–2399. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Lehtinen, J.; Munkberg, J.; Hasselgren, J.; Laine, S.; Karras, T.; Aittala, M.; Aila, T. Noise2Noise: Learning Image Restoration without Clean Data. arXiv, 2018; arXiv:1803.04189. [Google Scholar]
- Chen, J.W.; Chen, J.W.; Chao, H.Y.; Yang, M. Image Blind Denoising With Generative Adversarial Network Based Noise Modeling. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3155–3164. [Google Scholar] [CrossRef]
- Chowdhuri, D.; Sendhil, K.K.S.; Babu, M.R.; Reddy, C.P.J.I.J.o.C.S.; Technologies, I. Very Low Resolution Face Recognition in Parallel Environment. Int. J. Comput. Sci. Inf. Technol. 2012, 3, 4408–4410. [Google Scholar]
- Yang, Q.; Yang, R.; Davis, J.; Nister, D. Spatial-Depth Super Resolution for Range Images. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Nasrollahi, K.; Moeslund, T.B. Super-resolution: A comprehensive survey. Mach. Vis. Appl. 2014, 25, 1423–1468. [Google Scholar] [CrossRef]
- Ni, K.S.; Nguyen, T.Q. An Adaptable k-Nearest Neighbors Algorithm for MMSE Image Interpolation. IEEE Trans. Image Process. 2009, 18, 1976–1987. [Google Scholar] [CrossRef] [PubMed]
- Gribbon, K.T.; Bailey, D.G. A novel approach to real-time bilinear interpolation. In Proceedings of the DELTA 2004 Second IEEE International Workshop on Electronic Design, Test and Applications, Perth, Australia, 28–30 January 2004; pp. 126–131. [Google Scholar]
- Fritsch, F.; Carlson, R. Monotone Piecewise Cubic Interpolation. SIAM J. Numer. Anal. 1980, 17, 238–246. [Google Scholar] [CrossRef]
- Flowerdew, R.; Green, M.; Kehris, E. Using areal interpolation methods in geographic information systems. Pap. Reg. Sci. 1991, 70, 303–315. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; Tang, X.O. Accelerating the Super-Resolution Convolutional Neural Network. In Proceedings of the Computer Vision—ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; pp. 391–407. [Google Scholar] [CrossRef]
- Shi, W.Z.; Caballero, J.; Huszar, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z.H. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the 2016 Ieee Conference on Computer Vision and Pattern Recognition (Cvpr) 2016, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (Cvpr) 2016, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Deeply-Recursive Convolutional Network for Image Super-Resolution. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (Cvpr) 2016, Las Vegas, NV, USA, 27–30 June 2016; pp. 1637–1645. [Google Scholar] [CrossRef]
- Tai, Y.; Yang, J.; Liu, X.M. Image Super-Resolution via Deep Recursive Residual Network. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition (Cvpr 2017), Honolulu, HI, USA, 21–26 July 2017; pp. 2790–2798. [Google Scholar] [CrossRef]
- Tong, T.; Li, G.; Liu, X.J.; Gao, Q.Q. Image Super-Resolution Using Dense Skip Connections. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 4809–4817. [Google Scholar] [CrossRef]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Change Loy, C.; Qiao, Y.; Tang, X. ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks. arXiv, 2018; arXiv:1809.00219. [Google Scholar]
- Hu, X.; Mu, H.; Zhang, X.; Wang, Z.; Tan, T.; Sun, J. Meta-SR: A Magnification-Arbitrary Network for Super-Resolution. arXiv, 2019; arXiv:1903.00875. [Google Scholar]
- Wang, W.; Guo, R.; Tian, Y.; Yang, W. CFSNet: Toward a Controllable Feature Space for Image Restoration. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 4139–4148. [Google Scholar]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the Eighth IEEE International Conference on Computer Vision, Vancouver, BC, Canada, 7–14 July 2001; pp. 416–423. [Google Scholar] [CrossRef]
- Singh, A.; Porikli, F.; Ahuja, N. Super-resolving Noisy Images. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2846–2853. [Google Scholar]
- Laghrib, A.; Ezzaki, M.; El Rhabi, M.; Hakim, A.; Monasse, P.; Raghay, S. Simultaneous deconvolution and denoising using a second order variational approach applied to image super resolution. Comput. Vis. Image Underst. 2018, 168, 50–63. [Google Scholar] [CrossRef]
- Hu, J.; Wu, X.; Zhou, J.L. Noise robust single image super-resolution using a multiscale image pyramid. Signal Process 2018, 148, 157–171. [Google Scholar] [CrossRef]
- Chen, L.; Dan, W.; Cao, L.J.; Wang, C.; Li, J. Joint Denoising and Super-Resolution via Generative Adversarial Training. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 2753–2758. [Google Scholar]
- Anoosheh, A.; Sattler, T.; Timofte, R.; Pollefeys, M.; Van Gool, L. Night-to-Day Image Translation for Retrieval-based Localization. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 5958–5964. [Google Scholar]
- Luan, F.J.; Paris, S.; Shechtman, E.; Bala, K. Deep Photo Style Transfer. In Proceedings of the 30th Ieee Conference on Computer Vision and Pattern Recognition (Cvpr 2017), Honolulu, HI, USA, 21–26 July 2017; pp. 6997–7005. [Google Scholar] [CrossRef]
- Fattal, R. Image upsampling via imposed edge statistics. ACM Trans. Graph. 2007, 26. [Google Scholar] [CrossRef]
- Yan, Q.; Xu, Y.; Yang, X.K.; Nguyen, T.Q. Single Image Superresolution Based on Gradient Profile Sharpness. IEEE Trans. Image Process. 2015, 24. [Google Scholar] [CrossRef]
- Sun, J.; Sun, J.; Xu, Z.B.; Shum, H.Y. Gradient Profile Prior and Its Applications in Image Super-Resolution and Enhancement. IEEE Trans. Image Process. 2011, 20, 1529–1542. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zheng, C.W.; Zheng, Q.; Yuan, H.L. Removing Monte Carlo noise using a Sobel operator and a guided image filter. Vis. Comput. 2018, 34, 589–601. [Google Scholar] [CrossRef]
- Yang, W.H.; Feng, J.S.; Yang, J.C.; Zhao, F.; Liu, J.Y.; Guo, Z.M.; Yan, S.C. Deep Edge Guided Recurrent Residual Learning for Image Super-Resolution. IEEE Trans. Image Process. 2017, 26, 5895–5907. [Google Scholar] [CrossRef]
- Bevilacqua, M.; Roumy, A.; Guillemot, C.; Morel, M.L.A. Low-Complexity Single-Image Super-Resolution based on Nonnegative Neighbor Embedding. In Proceedings of the British Machine Vision Conference, Surrey, UK, 3–7 September 2012. [Google Scholar] [CrossRef]
- Hui, Z.; Gao, X.B.; Yang, Y.C.; Wang, X.M. Lightweight Image Super-Resolution with Information Multi-distillation Network. In Proceedings of the 27th Acm International Conference on Multimedia (Mm’19), Nice, France, 21–25 October 2019; pp. 2024–2032. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Zhang, L. Learning a Single Convolutional Super-Resolution Network for Multiple Degradations. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3262–3271. [Google Scholar] [CrossRef]
- Zeyde, R.; Elad, M.; Protter, M. On Single Image Scale-Up Using Sparse-Representations. In Proceedings of the 7th international conference on Curves and Surfaces, Avignon, France, 24–30 June 2010; pp. 711–730. [Google Scholar]
- Huang, J.B.; Singh, A.; Ahuja, N. Single Image Super-resolution from Transformed Self-Exemplars. In Proceedings of the 2015 Ieee Conference on Computer Vision and Pattern Recognition (Cvpr), Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar] [CrossRef]
- Blau, Y.; Mechrez, R.; Timofte, R.; Michaeli, T.; Zelnik-Manor, L. The 2018 PIRM Challenge on Perceptual Image Super-resolution. arXiv, 2018; arXiv:1809.07517. [Google Scholar]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The Unreasonable Effectiveness of Deep Features as a Perceptual Metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 586–595. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Wang, X.T.; Yu, K.; Dong, C.; Loy, C.C. Recovering Realistic Texture in Image Super-resolution by Deep Spatial Feature Transform. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 606–615. [Google Scholar] [CrossRef]




| Dataset | Metric |
DNCNN +SFTGAN ( = 15/ = 25/ = 50) |
DNCNN +ESRGAN ( = 15/ = 25/ = 50) |
DNCNN +IMDN ( = 15/ = 25/ = 50) |
DNCNN +SRMD ( = 15/ = 25/ = 50) |
DNCNN +SPSR ( = 15/ = 25/ = 50) |
SNS ( = 15/ = 25/ = 50) |
|---|---|---|---|---|---|---|---|
| Set5 | PI | 5.032/4.712/3.673 | 4.435/3.968/3.667 | 4.823/5.289/5.673 | 5.193/5.573/5.987 | 3.614/3.787/4.012 | 3.023/3.253/3.624 |
| LPIPS | 0.083/0.093/0.125 | 0.074/0.092/0.114 | 0.103/0.124/0.134 | 0.167/0.184/0.203 | 0.063/0.072/0.093 | 0.053/0.069/0.083 | |
| PSNR | 30.23/29.79/28.42 | 31.26/30.82/29.32 | 29.37/28.72/27.43 | 29.34/28.38/27.54 | 29.64/28.24/27.34 | 31.20/30.65/29.54 | |
| SSIM | 0.905/0.802/0.723 | 0.903/0.863/0.745 | 0.892/0.814/0.792 | 0.883/0.824/0.763 | 0.942/0.832/0.783 | 0.943/0.822/0.733 | |
| Set14 | PI | 0.343/0.424/0.534 | 0.301/0.325/0.432 | 0.378/0.432/0.543 | 0.295/0.334/0.423 | 0.274/0.303/0.438 | 0.246/0.294/0.405 |
| LPIPS | 0.132/0.172/0.234 | 0.122/0.137/0.234 | 0.142/0.169/0.234 | 0.132/0.157/0.167 | 0.123/0.138/0.142 | 0.124/0.132/0.141 | |
| PSNR | 26.76/25.52/24.43 | 27.34/26.58/25.23 | 26.85/25.24/24.34 | 26.63/25.83/24.58 | 27.74/26.75/25.34 | 27.47/26.17/25.74 | |
| SSIM | 0.834/0.734/0.674 | 0.837/0.802/0.739 | 0.802/0.723/0.702 | 0.823/0.735/0.683 | 0.892/0.832/0.734 | 0.903/0.793/0.763 | |
| BSDS100 | PI | 2.432/2.532/3.234 | 2.345/3.059/3.853 | 2.348/3.234/3.723 | 2.345/3.233/3.834 | 2.453/2.972/3.642 | 2.239/2.429/3.032 |
| LPIPS | 0.123/0.174/0.263 | 0.132/0.157/0.234 | 0.152/0.162/0.281 | 0.143/0.168/0.302 | 0.122/0.158/0.217 | 0.117/0.143/0.202 | |
| PSNR | 26.45/25.41/24.54 | 27.53/26.72/25.45 | 26.45/25.13/24.45 | 26.34/25.31/24.34 | 27.34/25.93/25.34 | 27.83/26.52/25.54 | |
| SSIM | 0.724/0.652/0.542 | 0.762/0.684/0.613 | 0.762/0.642/0.543 | 0.764/0.644/0.582 | 0.749/0.641/0.558 | 0.772/0.672/0.603 | |
| Urban100 | PI | 3.622/3.642/3.852 | 3.558/3.682/3.726 | 3.578/ 3.782/3.801 | 3.602/3.697/3.727 | 3.501/3.678/3.769 | 3.243/3.527/3.724 |
| LPIPS | 0.117/0.125/0.131 | 0.118/0.124/0.138 | 0.114/0.123/0.135 | 0.138/0.143/0.151 | 0.119/0.122/0.128 | 0.103/0.112/0.126 | |
| PSNR | 24.57/24.34/24.12 | 24.69/24.55/24.40 | 24.49/24.35/24.21 | 24.71/24.64/24.50 | 25.41/25.32/25.08 | 25.89/24.65/24.03 | |
| SSIM | 0.874/0.834/0.818 | 0.928/0.901/0.866 | 0.857/0.834/0.822 | 0.855/0.836/0.820 | 0.991/0.954/0.904 | 0.923/0.948/0.893 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, M.; Han, S.; Chen, G.; Zhang, X. The Research on Enhancing the Super-Resolving Effect of Noisy Images through Structural Information and Denoising Preprocessing. AI 2020, 1, 329-341. https://doi.org/10.3390/ai1030022
Chang M, Han S, Chen G, Zhang X. The Research on Enhancing the Super-Resolving Effect of Noisy Images through Structural Information and Denoising Preprocessing. AI. 2020; 1(3):329-341. https://doi.org/10.3390/ai1030022
Chicago/Turabian StyleChang, Min, Shuai Han, Guo Chen, and Xuedian Zhang. 2020. "The Research on Enhancing the Super-Resolving Effect of Noisy Images through Structural Information and Denoising Preprocessing" AI 1, no. 3: 329-341. https://doi.org/10.3390/ai1030022
APA StyleChang, M., Han, S., Chen, G., & Zhang, X. (2020). The Research on Enhancing the Super-Resolving Effect of Noisy Images through Structural Information and Denoising Preprocessing. AI, 1(3), 329-341. https://doi.org/10.3390/ai1030022




