Enhanced Hyperbox Classifier Model for Nanomaterial Discovery

Abstract

Machine learning tools can be applied to peptide-mediated biomineralization, which is an emerging biomimetic technique of creating functional nanomaterials. In particular, they can be used for the discovery of biomineralization peptides, which currently relies on combinatorial enumeration approaches. In this work, an enhanced hyperbox classifier is developed which can predict if a given peptide sequence has a strong or weak binding affinity towards a gold surface. A mixed-integer linear program is formulated to generate the rule-based classification model. The classifier is optimized to account for false positives and false negatives, and clearly articulates how the classification decision is made. This feature makes the decision-making process transparent, and the results easy to interpret for decision support. The method developed can help accelerate the discovery of more biomineralization peptide sequences, which may expand the utility of peptide-mediated biomineralization as a means for nanomaterial synthesis.

1. Introduction

Peptide-mediated biomineralization is a promising bio-inspired technique for creating inorganic nanomaterials that possess functional properties [1]. This biomimetic technique has produced nanomaterials for a wide array of applications, such as highly efficient catalysts [2], plasmonic materials with tailorable optical properties [3], and bimetallic nanoparticles for electrooxidation [4], among others. These interesting materials were produced due to the ability of the biomineralization peptide to regulate the size, shape, and morphology of the nanomaterial. This level of control is achieved due to the binding affinity of the biomineralization peptide towards a particular material surface, which leads to the selective binding of the biomineralization peptide at specific faces of the growing nanomaterial [5,6]. The binding affinity of the peptide is known to be affected by peptide properties such as the oligomerization state [7], conformation [8], and sequence [9].

In order to broaden the utility of peptide-mediated biomineralization as an effective platform for nanomaterial synthesis, a method for the quick identification of biomineralization peptide sequences should be developed. Currently, the discovery of biomineralization peptides has mainly depended on the tedious laboratory assays which are combinatorial in nature. Since acquisition of experimental data is costly, typically only small data sets are available in this domain [10]. Thus, the use of modern computational tools such as artificial intelligence (AI), data mining, and machine learning (ML) for this purpose presents significant potential to address this problem since these tools have been used for the discovery of novel materials [11,12,13] and their properties [14,15,16]. Data from both experimental results and computations from theoretical simulations can be used to train ML models [17,18]. ML may therefore accelerate the discovery of novel biomineralization peptide sequences, which will lower the costs of producing nanomaterials through biomineralization. Mainstream ML tools used for Big Data are not optimized for dealing with small data sets [19]. Interactive ML techniques that combine expert knowledge with information from these small data sets are more appropriate for such applications [20].

Past works on classifying biomineralization peptide binding affinity class have reported the creation of models that classify biomineralization peptide sequences into strong and weak binders. These models used the Needleman–Wunsch algorithm [21], graph theory [22], and support vector machines (SVMs) [23] for the classification task. While these classification algorithms demonstrate satisfactory predictive ability, the impact of the variables on the classification task is not clearly interpretable. This characteristic limits the practicality of the classification model, and renders the interpretation of the results by material scientists difficult. Thus, a rule-based algorithm is more appropriate for this kind of application. A rule-based algorithm clearly articulates the classification process through a set of rules extracted from the dataset, leading to transparent and unambiguous decision-making. Predictive models that rely on the generation of rules, such as rough sets and decision trees, can provide effective decision support for material scientists via case-based reasoning [24].

In this work, we develop a rule-based classification model built using the hyperbox algorithm for predicting biomineralization peptide binding class. The rest of this article is organized as follows. Section 2 describes the methodology itself. Section 3 applies the classifier model to this nanomaterial discovery problem. Section 4 gives conclusions and discusses prospects for future work.

2. Methodology

The hyperbox model developed here is an extension of the work of Xu and Papageorgiou [25]. The original approach they developed used a mixed integer linear programming (MILP) model to generate non-overlapping hyperboxes to enclose clusters of data; additional hyperboxes can be determined iteratively to improve classification performance. Further algorithmic improvements were reported by Maskooki [26] and Yang et al. [27]. The presence of user-defined parameters makes the training of hyperbox models highly interactive. Expert inputs can be integrated into the procedure to augment small data sets with mechanistic domain knowledge. The resulting optimized hyperboxes constitute a rule-based model that can be used as a classification model. One of the key advantages of this technique is that the hyperboxes can be readily interpreted as IF–THEN rules, which can be used effectively and intuitively to support decisions [27].

The main features of the model extension developed here are as follows:

• The model is a binary classifier such that a pre-defined number of hyperboxes are meant to enclose samples which positively belong to the group and to exclude samples which do not. The initial default assumption is that of negative classification, but the activation of at least one rule results in a positive classification. This approach eliminates the need for negative classification rules. The number of hyperboxes is user-defined and the training is done interactively with expert knowledge inputs to augment small data sets that are typical in this domain [19,20]. This consideration makes it possible to identify alternative rule sets which may make more sense to the expert or may improve the performance of the model. However, a balance should be made between generalizability and over-fitting.
• A user-defined margin is utilized as the minimum distance needed to separate the negative samples from the boundaries of the resulting hyperboxes. Thus, each hyperbox actually consists of concentric inner and outer hyperboxes separated by the said margin. This feature serves the same purpose as the gap between parallel hyperplanes in SVMs.
• The model accounts for Type I (number of false positives) and Type II (number of false negatives) errors such that a user may select which type of error should be minimized while indicating an upper limit for the other. This feature was introduced in an extension of the hyperbox model by Yang et al. [27].
• The model is meant to define the dimensions of the hyperboxes to adequately classify the training data. Reduction of attributes can result in more parsimonious ML models and is thus regarded as an important feature during training [28]. These dimensions may extend to infinity, rendering some attributes to be insignificant for classification. This feature is achieved by enabling the model to remove the lower bound and/or upper bound of each hyperbox along each dimension, as needed.

The overall objective of the model is to minimize Type I errors, α, while ensuring that Type II errors, β, are kept below a defined threshold ε. Type I (α) and Type II (β) errors are then defined where j represents a sample in the training set S^T.

$$Min\alpha$$

(1)

$$\beta \le \epsilon$$

(2)

$$\alpha >\frac{{{\displaystyle \sum }}_j^{}(c_j-C_j^{*})}{N^T},\forall j\in {\mathrm{S}}^{\mathrm{T}}$$

(3)

$$\beta >\frac{{{\displaystyle \sum }}_j^{}(C_j^{*}-c_j)}{P^T},\forall j\in {\mathrm{S}}^{\mathrm{T}}$$

(4)

Each sample j in the training data has performance level in attribute i with the value of $X_{ji}.$ The lower ($x_{ik}^L$) and upper ($x_{ik}^U$) limits along dimension i for hyperbox k are determined to enclose as many positive samples as possible. The dimensions of the outer hyperbox and the dimensions of the inner hyperbox are separated by the user-defined marginΔ.

$$X_{ji}>x_{ik}^L-\Delta -M\left(1-b_{jk}\right),\forall i,j$$

(5)

$$X_{ji}<x_{ik}^U+\Delta +M\left(1-b_{jk}\right),\forall i,j$$

(6)

$$X_{ji}>x_{ik}^L-M\left(1-b_{jk}\right),\forall i,j$$

(7)

$$X_{ji}<x_{ik}^U+M\left(1-b_{jk}\right),\forall i,j$$

(8)

The possibility of semi-infinite (i.e., having no lower limit or no upper limit) or infinite dimensions (i.e., having no lower and upper limits) for the hyperbox are also considered. In the latter case, the absence of lower and upper limits allows the hyperbox to be projected to a lower dimensional space, and removes the corresponding attribute from the associated decision rule.

$$\begin{gathered} Z_{ik}^L-M\left(1-b_{ik}^L\right)\le x_{ik}^L\le Z_{ik}^L+M{b}_{ik}^L,\forall i,k \\ If{b}_{ik}^L=1,Z_{ik}^L\le x_{ik}^L\le Z_{ik}^L+M,\forall i,k \\ If{b}_{ik}^L=0,Z_{ik}^L-M\le x_{ik}^L\le Z_{ik}^L,\forall i,k \end{gathered}$$

(9)

$$\begin{gathered} Z_{ik}^U-M{b}_{ik}^U\le x_{ik}^U\le Z_{ik}^U+M\left(1-b_{ik}^U\right),\forall i,k \\ \mathrm{If}{b}_{ik}^U=1,Z_{ik}^U-M\le x_{ik}^U\le Z_{ik}^U,\forall i,k \\ \mathrm{If}{b}_{ik}^U=0,Z_{ik}^U\le x_{ik}^U\le Z_{ik}^U+M,\forall i,k \end{gathered}$$

(10)

For instances in which sample j lies outside the boundaries of the hyperbox, sample $X_{ji}$ may lie below the lower limit of hyperbox k in dimension i by more than the user-defined margin, $\mathsf{\Delta }$ (11) or $X_{ji}$ may lie above the upper limit of hyperbox k in dimension i by more than the user-defined margin, $\mathsf{\Delta }$ (12). If the sample satisfies any of the two conditions, then this indicates that the sample is outside the hyperbox and $q_{ijk}^L$ or $q_{ijk}^U$ will be equal to 1. Consequently, in such instances, the sample should be considered a negative sample and $b_{jk}=0$.

$$X_{ji}\le x_{ik}^L-\Delta +M(1-q_{ijk}^L),\forall i,j$$

(11)

$$X_{ji}\ge x_{ik}^U+\Delta -M(1-q_{ijk}^U),\forall i,j$$

(12)

$${{\displaystyle \sum }}_i^{}{q}_{ijk}^L+q_{ijk}^U\le M\left(1-b_{jk}\right),\forall j,k$$

(13)

$${{\displaystyle \sum }}_i^{}{q}_{ijk}^L+q_{ijk}^U\ge \left(1-b_{jk}\right),\forall j,k$$

(14)

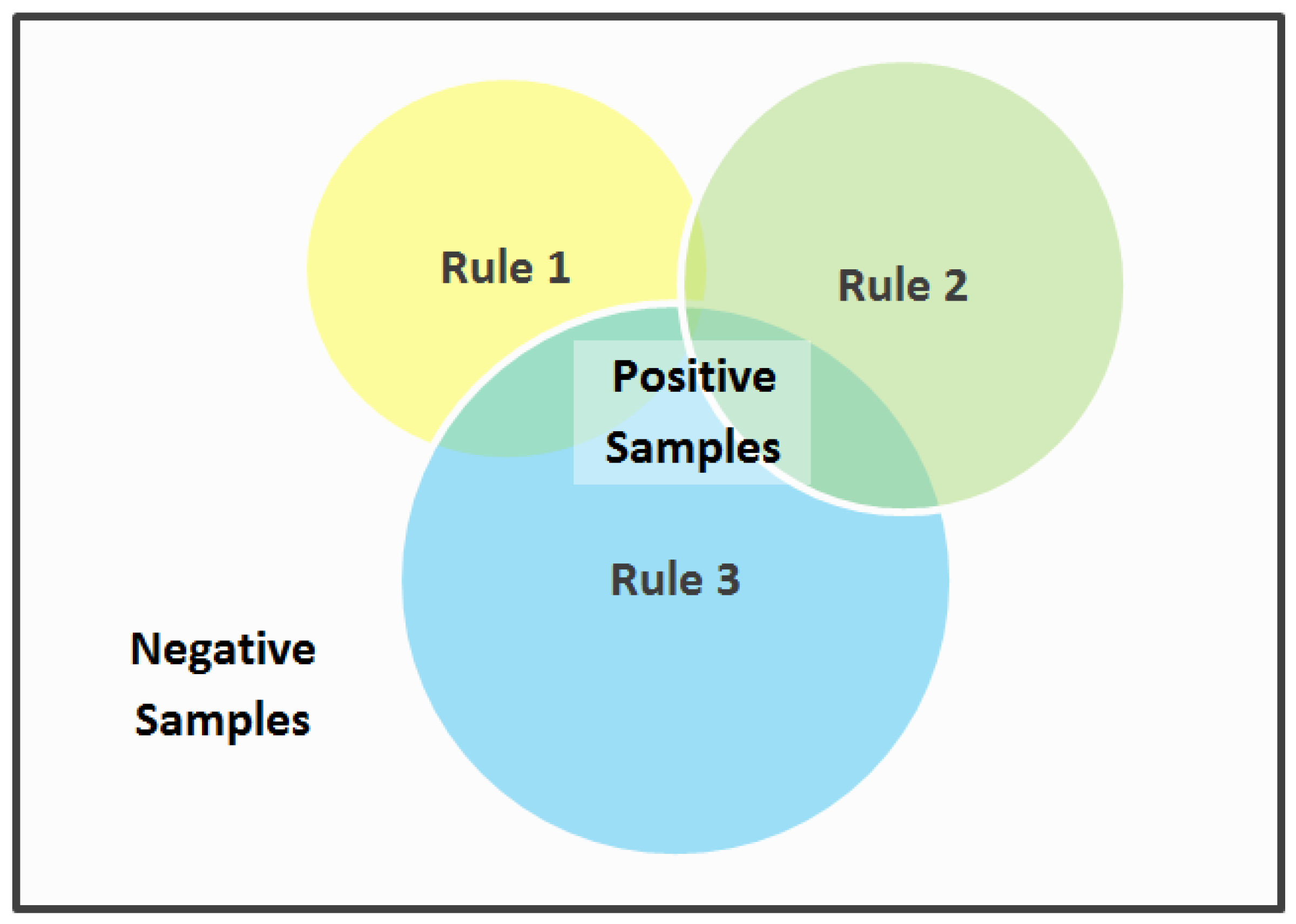
In instances in which there are multiple hyperboxes, a sample is said to be a positive sample, $c_j=1$, if it is enclosed by at least one hyperbox. Thus, each hyperbox corresponds to one rule, and the resulting classifier consists of a set of disjunctive rules. The relationship among a set of such rules can be represented by a Venn diagram as shown in Figure 1. Samples that do not activate any of the rules (i.e., are not enclosed by any of the hyperboxes) are classified as negative by default.

$${{\displaystyle \sum }}_k^{}{b}_{jk}\le M{c}_j^{},\forall j$$

(15)

$${{\displaystyle \sum }}_k^{}{b}_{jk}\ge c_j^{},\forall j$$

(16)

Finally, the binary variables are as follows:

$$b_{jk},b_{ik}^U,b_{ik}^L,q_{ijk}^U,q_{ijk}^L,c_j\in \{0,1\},\forall i,j,k$$

(17)

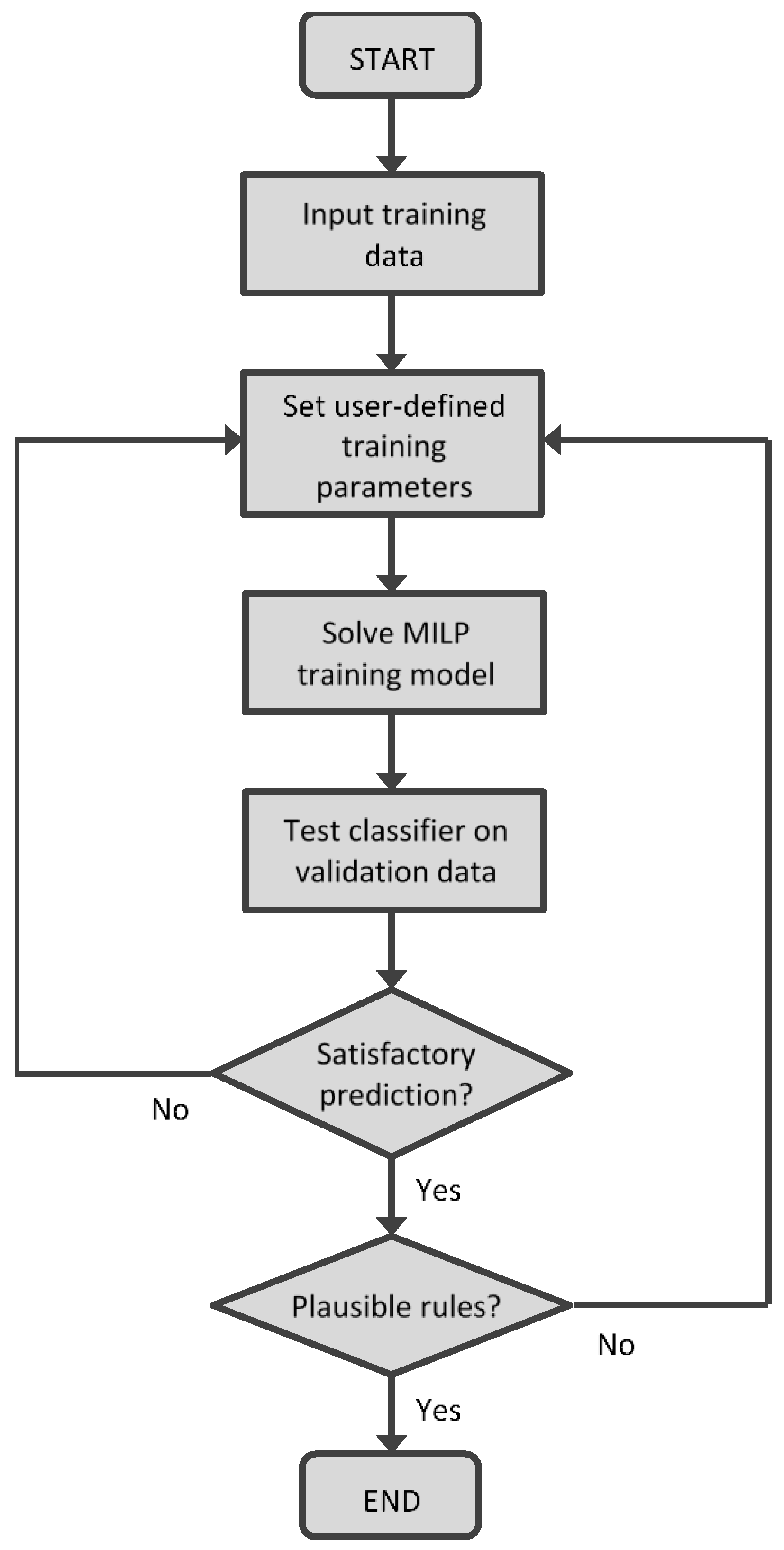
This MILP model can be solved to global optimality using the branch-and-bound algorithm, which is available as a standard feature in many commercial optimization software packages. Alternative solutions (rule sets) can be determined for any given MILP using standard integer-cut features in such software; additional solutions can also be found by adjusting the model parameters. Figure 2 shows the interactive training procedure for the hyperbox classifier.

The case study utilizes data from the work of Janairo [23], which looks into the classification of the biomineralization peptide binding affinity using SVM. There are 31 cases, each representing a biomineralization peptide sequence. These biomineralization peptide sequences are characterized by 10 parameters, called the Kidera factors, and the peptides are classified into two categories of either weak or strong binding affinity. Kidera factors are descriptors related to the structure and physico-chemical properties of proteins derived from rigorous statistical analyses [29]. The 10 Kidera factors are K1: helix/bend preference, K2: side-chain size, K3: extended structure preference, K4: hydrophobicity, K5: double-bend preference, K6: partial specific volume, K7: flat extended preference, K8: occurrence in alpha region, K9: pK-C, K10: surrounding hydrophobicity. The datapoints were randomized and further divided into two sets with 20 datapoints used for training and the remaining 11 used for validation. The data was initially normalized to transform $X_{ji}$ to $X_{ji}^{*}$, where $x_{ji}^{MIN}$ is the lowest value in dimension i among all samples j while $x_{ji}^{MAX}$ is the largest value observed in dimension i among all samples j. The raw data for all 31 datapoints are included in Table S1 of the supplementary material.

$$X_{ji}^{*}=\frac{X_{ji}^{}-x_{ji}^{MIN}}{x_{ji}^{MAX}-x_{ji}^{MIN}}$$

(18)

The training was done by solving (1) subject to constraints defined in (2) to (17) with a Δ = 0.05, Z^L_ik = −50.00 and Z^U_ik = 50.00. The model was implemented in LINGO 18.0 and solved using a laptop with an Intel^® Core^TM i7-6500U 2.5 GHz CPU with 8.0 GB RAM.

3. Case Study

Using just one hyperbox, with $\epsilon <0$ and a constraint that at least one attribute can be removed, the optimal solution was obtained in 0.20 s. The optimal solution was able to correctly classify all training data such that $\alpha =\beta =0$. The resulting dimensions for the 10 attributes considered are shown in

Table 1. Dimensions of Hyperbox Decision Model 1.

Attribute	${\mathit{x}}_{\mathit{i}1}^{\mathit{L}}$	${\mathit{x}}_{\mathit{i}1}^{\mathit{U}}$
K1	−50.00	50.00
K2	−50.00	50.00
K3	−0.9186	50.00
K4	−50.00	50.00
K5	−50.00	50.00
K6	−50.00	0.4148
K7	−0.7155	50.00
K8	−50.00	50.00
K9	−50.00	0.3411
K10	−0.5159	0.7397

Shaded entries indicate that limit has not been activated in corresponding attribute.

where shaded entries indicate that there is no limit for the lower or upper bound for the corresponding attribute. Table 1 can be translated into IF–THEN rules as follows. Only five attributes remained relevant—K3, K6, K7, K9, and K10—with K3, K6, K7, and K9 having one-sided limits and K10 being the only attribute bound by an upper and a lower limit.

• Rule 1: IF $\left(-0.9186\le K3\right)$. and IF $\left(K6\le 0.4148\right)$ and IF $\left(-0.7155\le K7\right)$ and IF $\left(K9\le 0.3411\right)$ IF $\left(-0.5159\le K10\le 0.7397\right)$ THEN binding is Strong.

Using this rule to classify the validation data resulted in all weak binding samples (total of eight out of 11) being correctly classified and all strong binding samples (total of three out of three) also correctly classified. The confusion matrix for this optimal rule is summarized in

Table 2. Confusion matrix of Hyperbox Decision Model 1.

N = 11	Predicted Positive	Predicted Negative
Actual Positive	3	0
Actual Negative	0	8
$\alpha =0.0$
$\beta =0.0$

. The previous SVM classifier also found that K3, K6, K7, and K9 as significant descriptors for the prediction of the biomineralization peptide binding affinity class [23]. However, the SVM classifier arrived at this model after 12 optimization steps, as opposed to the quick and straightforward manner of the present hyperbox model. Moreover, using the same set of descriptors, the hyperbox model outperforms the prediction accuracy of the SVM classifier, which was 92%.

It is also possible to identify alternative sets of rules from degenerate solutions or near-optimal solutions. An example is given in

Table 3. Dimensions of Hyperbox Decision Model 2.

Attribute	${\mathit{x}}_{\mathit{i}1}^{\mathit{L}}$	${\mathit{x}}_{\mathit{i}1}^{\mathit{U}}$
K1	−50.00	50.00
K2	−0.6154	50.00
K3	−50.00	50.00
K4	−50.00	50.00
K5	−50.00	1.1882
K6	−50.00	0.4163
K7	−0.6020	50.00
K8	−50.00	0.3285
K9	−50.00	1.3469
K10	−50.00	0.8883

Shaded entries indicate that limit has not been activated in corresponding attribute.

, which corresponds to the 10th solution for the problem considered. The rule generated is relatively more complex than Rule 1 because seven attributes (i.e., K2, K5, K6, K7, K8, K9, and K10) are needed to predict peptide binding affinity.

• Rule 2: IF $\left(-0.6154\le K2\right)$ and IF $\left(K5\le 1.1882\right)$ and IF $\left(K6\le 0.4163\right)$ and IF $\left(-0.6020\le K7\right)$ and IF $\left(K8\le 0.3285\right)$ and IF $\left(K9\le 1.3469\right)$ and IF $\left(K10\le 0.8883\right)$ THEN binding is Strong.

This rule was able to classify the training data correctly with $\alpha$ and $\beta$ still equal to 0. Similarly, it was effective in classifying all 11 samples in the validation data as summarized in

Table 4. Confusion matrix of Hyperbox Decision Model 2.

N = 11	Predicted Positive	Predicted Negative
Actual Positive	3	0
Actual Negative	0	8
$\alpha =0.0$
$\beta =0.0$

.

The model is then extended to consider five hyperboxes with $\epsilon =0.30$. The consideration of additional hyperboxes enables the possibility of identifying alternative rule sets which can be used to classify data and potentially improve the performance of the model. Five hyperboxes, for example, translates to having five different rule sets to classify objects. Additional constraints to limit attribute overlaps between the boxes have been added as indicated in (19) to (21).

$${\displaystyle \sum }_{k=1}^H{b}_{i,k}^L\le n_A$$

(19)

$${\displaystyle \sum }_{k=1}^H{b}_{i,k}^U\le n_A$$

(20)

$${\displaystyle \sum }_{k=1}^H\left(b_{i,k}^L+b_{i,k}^U\right)\le 2n_A$$

(21)

Optimizing with $n_A=3$ results in the boundaries summarized in

Table 5. Dimensions of Hyperbox Decision Model 3.

	Hyperbox 1		Hyperbox 2		Hyperbox 3		Hyperbox 4		Hyperbox 5
Attribute	${\mathit{x}}_{\mathit{i}1}^{\mathit{L}}$	${\mathit{x}}_{\mathit{i}1}^{\mathit{U}}$	${\mathit{x}}_{\mathit{i}2}^{\mathit{L}}$	${\mathit{x}}_{\mathit{i}2}^{\mathit{U}}$	${\mathit{x}}_{\mathit{i}3}^{\mathit{L}}$	${\mathit{x}}_{\mathit{i}3}^{\mathit{U}}$	${\mathit{x}}_{\mathit{i}4}^{\mathit{L}}$	${\mathit{x}}_{\mathit{i}4}^{\mathit{U}}$	${\mathit{x}}_{\mathit{i}5}^{\mathit{L}}$	${\mathit{x}}_{\mathit{i}5}^{\mathit{U}}$
K1	0.1400	50.00	−50.00	50.00	−50.00	50.00	−0.0043	50.00	−0.6343	50.00
K2	−0.6033	50.00	−50.00	50.00	−0.6033	50.00	−0.5721	50.00	−50.00	50.00
K3	−0.3300	50.00	−50.00	50.00	0.2083	50.00	−50.00	50.00	−0.5358	50.00
K4	−0.1750	50.00	−50.00	50.00	−50.00	50.00	0.3443	50.00	−0.4650	50.00
K5	−50.00	50.00	−50.00	50.00	−50.00	50.00	−50.00	50.00	−50.00	50.00
K6	−50.00	50.00	−50.00	50.00	−50.00	0.0636	0.0636	50.00	−50.00	50.00
K7	−50.00	50.00	0.5275	50.00	−50.00	50.00	−0.015	−0.015	−0.2775	50.00
K8	−0.9633	50.00	0.2092	0.2092	−50.00	50.00	−0.3142	50.00	−50.00	0.2092
K9	−50.00	0.2267	−50.00	50.00	−50.00	0.2683	−50.00	50.00	−50.00	50.00
K10	−50.00	0.3475	−50.00	50.00	−50.00	50.00	−50.00	50.00	−0.2421	50.00

Shaded entries indicate that limit has not been activated in corresponding attribute.

. The optimal solution was obtained in 5 s computational time and was able to classify seven out of nine positive samples and 11 out of 11 negative samples from the training data. The rules are disjunctive, and can be summarized as follows:

• Rule 3a: IF $\left(0.1400\le K1\right)$ and IF $\left(-0.6033\le K2\right)$ and IF $\left(-0.3300\le K3\right)$and IF $\left(-0.1750\le K4\right)$ and IF $\left(-0.9633\le K8\right)$ and IF $\left(K9\le 0.2267\right)$ IF $\left(K10\le 0.3475\right)$ THEN binding is Strong.
• or
• Rule 3b: IF $\left(0.5275\le K7\right)$ and IF $\left(0.2092\le K8\le 0.2092\right)$ THEN binding is Strong.
• or
• Rule 3c: IF $\left(-0.6033\le K2\right)$ and IF $\left(0.2083\le K3\right)$ and IF $\left(K6\le 0.0636\right)$and IF $\left(K9\le 0.2683\right)$ THEN binding is Strong.
• or
• Rule 3d: IF $\left(-0.0043\le K1\right)$ and IF $\left(-0.5721\le K2\right)$ and IF $\left(0.3443\le K4\right)$and IF $\left(0.0636\le K6\right)$ and IF $\left(K7=-0.015\right)$ and IF $\left(-0.3142\le K8\right)$ THEN binding is Strong.
• or
• Rule 3e: IF $\left(-0.6343\le K1\right)$ and IF $\left(-0.5358\le K3\right)$ and IF $\left(-0.4650\le K4\right)$and IF $\left(-0.2775\le K7\right)$ and IF $\left(K8\le 0.2092\right)$ and IF $\left(-0.2421\le K10\right)$.

If a sample meets at least one of these rules, then the sample can be considered to have Strong binding. The rules were then used to evaluate the validation data; its performance is summarized in

Table 6. Confusion matrix of Hyperbox Decision Model 3.

N = 11	Predicted Positive	Predicted Negative
Actual Positive	3	0
Actual Negative	2	6
$\alpha =0.25$
$\beta =0.0$

.

Again, an alternative set of rules (fifth near-optimal solution) is explored and the results are as shown in

Table 7. Dimensions of Hyperbox Decision Model 4.

Attribute	Hyperbox 1		Hyperbox 2		Hyperbox 3		Hyperbox 4		Hyperbox 5
	${\mathit{x}}_{\mathit{i}1}^{\mathit{L}}$	${\mathit{x}}_{\mathit{i}1}^{\mathit{U}}$	${\mathit{x}}_{\mathit{i}2}^{\mathit{L}}$	${\mathit{x}}_{\mathit{i}2}^{\mathit{U}}$	${\mathit{x}}_{\mathit{i}3}^{\mathit{L}}$	${\mathit{x}}_{\mathit{i}3}^{\mathit{U}}$	${\mathit{x}}_{\mathit{i}4}^{\mathit{L}}$	${\mathit{x}}_{\mathit{i}4}^{\mathit{U}}$	${\mathit{x}}_{\mathit{i}5}^{\mathit{L}}$	${\mathit{x}}_{\mathit{i}5}^{\mathit{U}}$
K1	0.7705	50.00	−50.00	0.2158	−50.00	0.0494	1.1655	50.00	−50.00	50.00
K2	−0.6154	50.00	−50.00	50.00	−50.00	50.00	−50.00	50.00	−0.4561	50.00
K3	−0.9186	50.00	−50.00	50.00	−50.00	0.4671	−50.00	50.00	−50.00	50.00
K4	−50.00	50.00	−0.3655	0.2448	0.3443	50.00	−50.00	50.00	0.1083	50.00
K5	−50.00	1.1882	−50.00	0.7986	−50.00	50.00	−50.00	50.00	−50.00	50.00
K6	−0.3512	0.0834	−50.00	50.00	−50.00	50.00	−50.00	50.00	−50.00	50.00
K7	−50.00	50.00	−1.744	50.00	−50.00	50.00	−50.00	50.00	−50.00	50.00
K8	−50.00	50.00	−50.00	50.00	−50.00	50.00	−50.00	−0.2287	−50.00	−0.4592
K9	−50.00	50.00	−50.00	0.2408	−50.00	50.00	0.3412	50.00	−50.00	50.00
K10	−50.00	50.00	−50.00	50.00	−0.5197	0.5854	−50.00	50.00	−50.00	0.3633

Shaded entries indicate that limit has not been activated in corresponding attribute.

. These can be translated into the following:

• Rule 4a: IF $\left(0.7705\le K1\right)$ and IF $\left(-0.6154\le K2\right)$ and IF $\left(-0.9186\le K3\right)$and IF $\left(K5\le 1.1882\right)$ and IF $\left(-0.3512\le K6\le 0.0834\right)$ THEN binding is Strong.
• or
• Rule 4b: IF $\left(K1\le 0.2158\right)$ and IF $\left(-0.3655\le K4\le 0.2448\right)$ and IF $\left(K5\le 0.7986\right)$and IF $\left(K9\le 0.2408\right)$ THEN binding is Strong.
• or
• Rule 4c: IF $\left(K1\le 0.0494\right)$ and IF $\left(K3\le 0.4671\right)$ and IF $\left(0.3443\le K4\right)$and IF $\left(-0.5197\le K10\le 0.5854\right)$ THEN binding is Strong.
• or
• Rule 4d: IF $\left(1.1655\le K1\right)$ and IF $\left(K8\le 0.2287\right)$ and IF $\left(0.3412\le K9\right)$THEN binding is Strong.
• or
• Rule 4e: IF $\left(-0.4561\le K2\right)$ and IF $\left(0.1083\le K4\right)$ and IF $\left(K8\le -0.4592\right)$and IF $\left(K10\le 0.3633\right)$ THEN binding is Strong.

This alternative solution was able to classify eight out of nine positive samples and 11 out of 11 negative samples, resulting in $\alpha =0$ and $\beta =0.1111$ for the training data set. The rules were then used for the validation data set and the confusion matrix is shown in

Table 8. Confusion matrix of Hyperbox Decision Model 4.

N = 11	Predicted Positive	Predicted Negative
Actual Positive	3	0
Actual Negative	0	8
$\alpha =0.0$
$\beta =0.0$

.

The performance of the algorithm was further tested by performing the procedure five more times using a different sampling of training and validation data each time. The k-fold validation was completed in 1 min and 38 s. The performance of the rules for training and validation data is summarized in

Table 9. Confusion matrix of k-fold validation.

Training			Validation
Fold 2	Predicted	Predicted		Predicted	Predicted
N = 20	Positive	Negative	N = 11	Positive	Negative
Actual Positive	6	2	Actual Positive	4	0
Actual Negative	10	2	Actual Negative	0	7
Fold 3	Predicted	Predicted		Predicted	Predicted
N = 20	Positive	Negative	N = 11	Positive	Negative
Actual Positive	7	0	Actual Positive	5	0
Actual Negative	0	13	Actual Negative	0	6
Fold 4	Predicted	Predicted		Predicted	Predicted
N = 20	Positive	Negative	N = 11	Positive	Negative
Actual Positive	8	0	Actual Positive	4	0
Actual Negative	0	12	Actual Negative	2	5
Fold 5	Predicted	Predicted		Predicted	Predicted
N = 20	Positive	Negative	N = 11	Positive	Negative
Actual Positive	6	0	Actual Positive	6	0
Actual Negative	0	14	Actual Negative	1	4
Fold 6	Predicted	Predicted		Predicted	Predicted
N = 20	Positive	Negative	N = 11	Positive	Negative
Actual Positive	5	2	Actual Positive	5	0
Actual Negative	0	13	Actual Negative	0	6

.

The variables that the enhanced hyperbox algorithm automatically determined to be significant in making the biomineralization peptide binding class prediction were K3 (extended structure preference), K6 (partial specific volume), K7 (flat extended preference), K9 (pK-C), and K10 (surrounding hydrophobicity). The inclusion of these variables in the algorithm affirms and reinforces the findings of past studies which systematically analyzed the factors that governed peptide binding to surfaces. The inclusion of the variables that relate to the peptide conformation (K3 and K7) and protonation state (K9) are consistent with the findings of Hughes et al., wherein they concluded that peptide conformation is a major feature that influences the size, shape, and stability of peptide-capped materials [30]. In addition, the incorporation of peptide variables related to water interaction, such as K6 and K10, likewise supports the results of the atomistic simulations of Verde et al., wherein they reported how peptide solvation influences structural flexibility and surface adsorption [31]. Thus, the presented enhanced hyperbox model has formalized these associations into a concise classifier, with a clearly articulated set of rules. Aside from transparency on how the decision was reached through rule generation, another major advantage of the enhanced hyperbox model is its accuracy, as shown in

Table 10. Performance comparison of the enhanced hyperbox model with commonly used machine learning algorithms.

Algorithm	Accuracy	Sensitivity	Specificity
SVM (as reported in [23])	85	90	67
Logistic Regression	55	100	29
k-Nearest Neighbor	82	100	71
Random Forest	82	100	71
Enhanced Hyperbox (this work)	100	100	100

. The present model outperforms common machine learning algorithms, which were simulated in R [32], in terms of accuracy, sensitivity, and specificity.

4. Conclusions

In this work, we developed a hyperbox-based ML technique that can accurately predict the binding affinity class of a biomineralization peptide based from the sequence. The rule-based model highlights a quick and straightforward model-building capability which does not compromise prediction accuracy. Interactive training via an MILP model allows the hyperbox technique to combine expert knowledge within formation drawn from small data sets that are typical in material science applications. The model also features a clear and transparent set of rules from which the predictions are based, making the classification tasks reproducible and the process interpretable. The presented model is a valuable addition to machine learning tools, which are becoming pivotal components in materials discovery and development. In particular, the presented model can accelerate the discovery of biomineralization peptides while minimizing trial-and-error, thereby reducing cost. The use of this ML technique for other problems in materials science and nanotechnology should thus be explored further. Future work can focus on expanding the model to automatically adjust the margin between the concentric boxes, establishing heuristics for defining the number of hyperboxes, and analyzing how variations in these parameters can potentially influence the performance of the model.