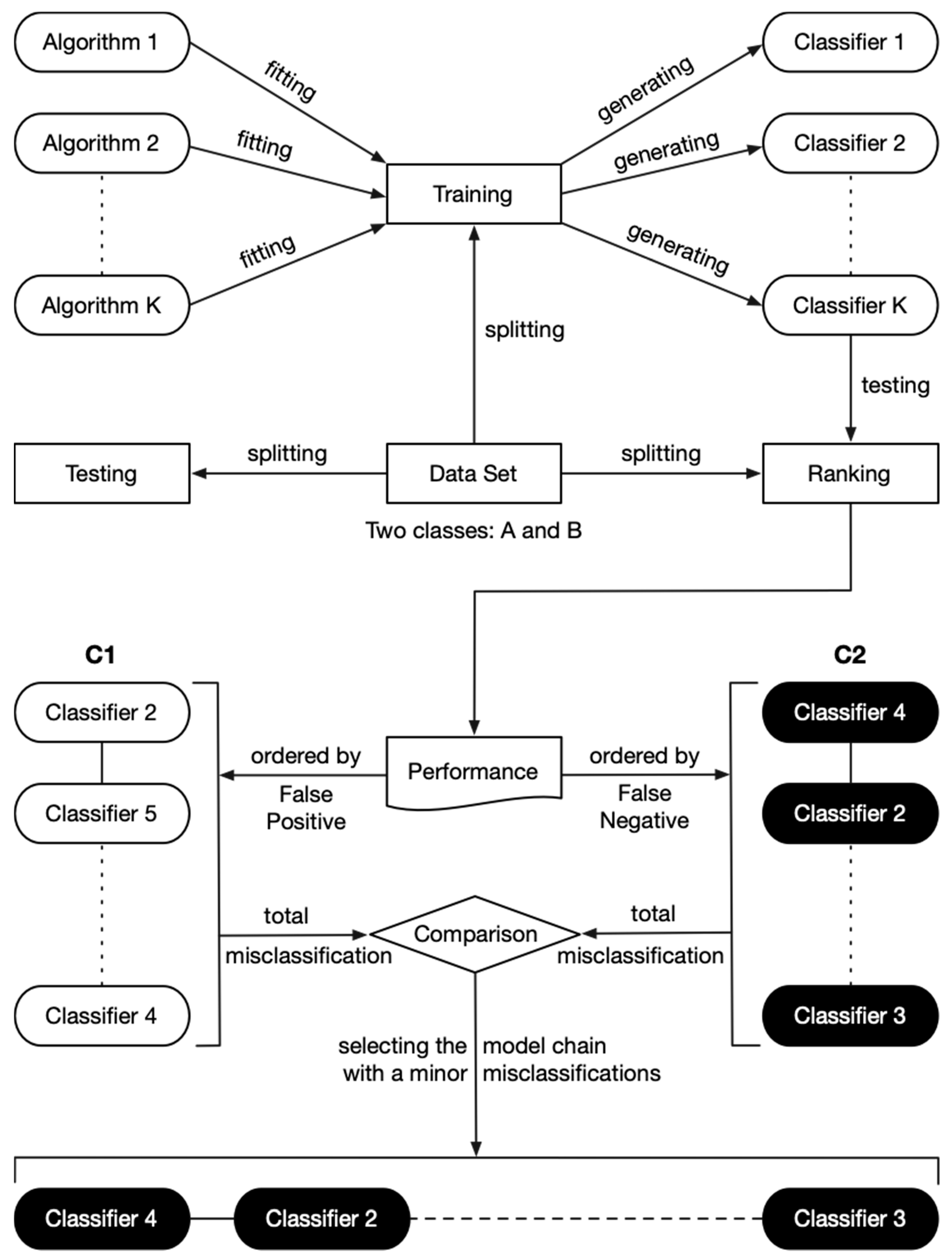
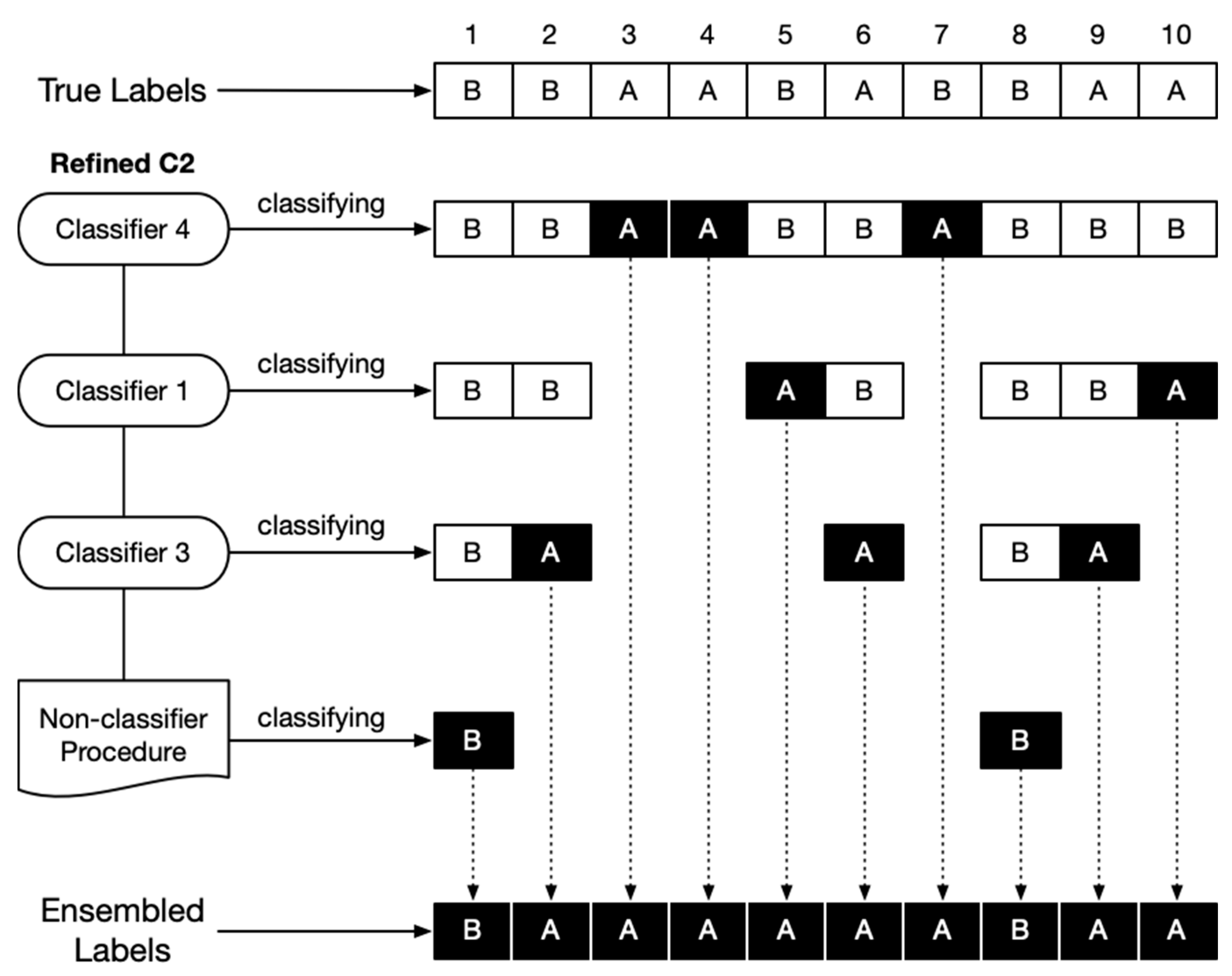
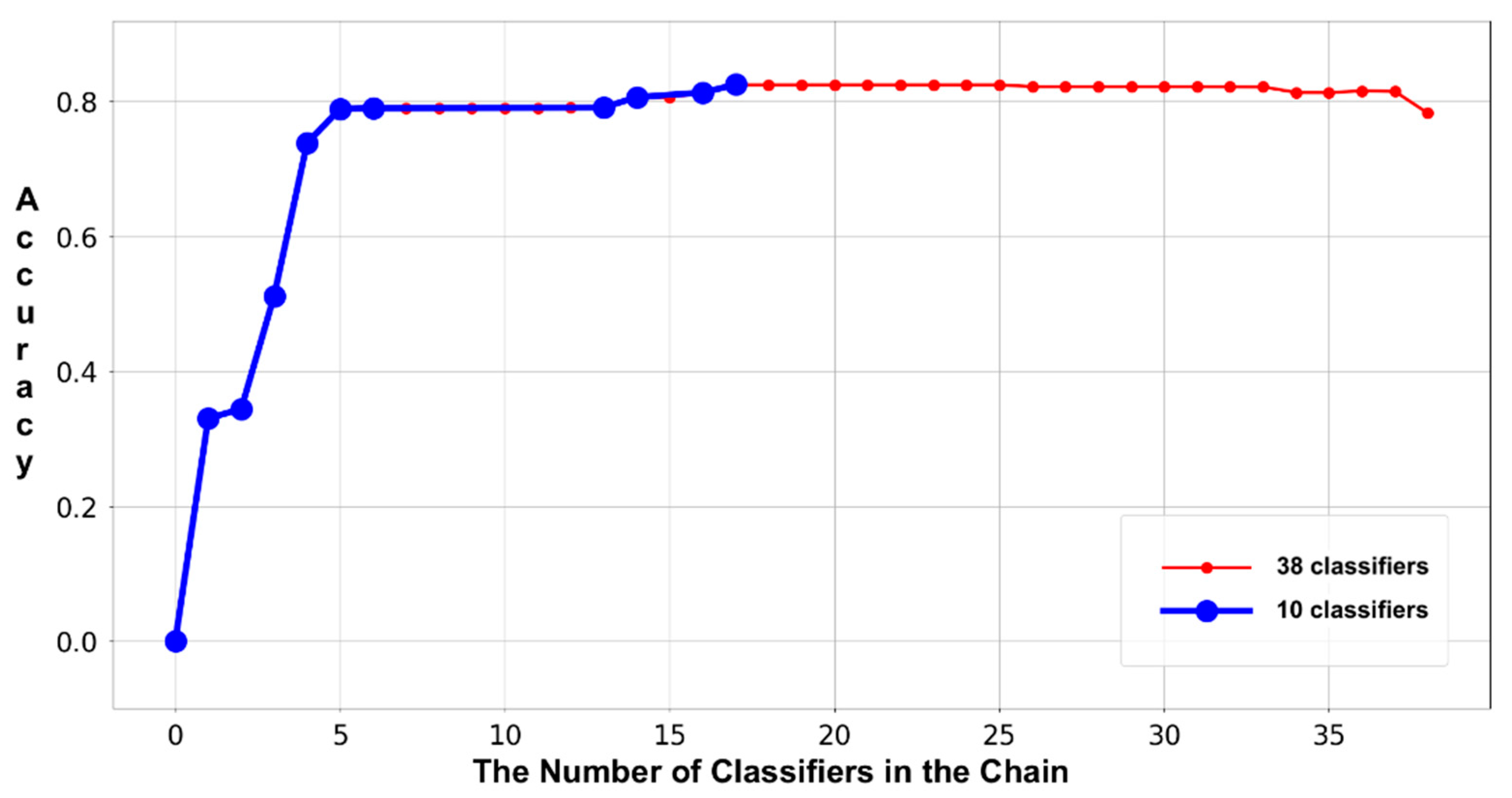
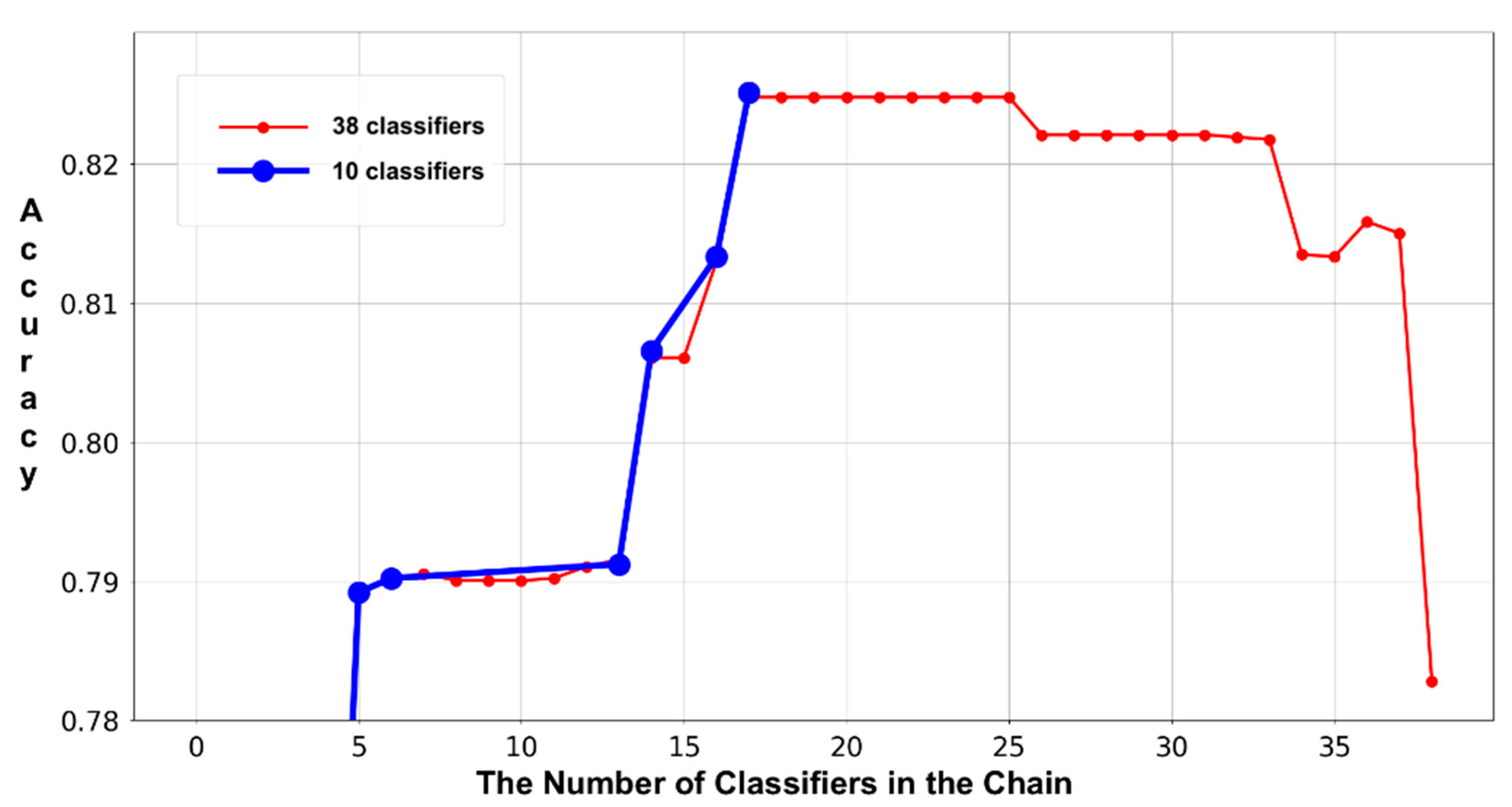
4.1. Objectives and Methodologies
Six experiments carried out in this study can be divided into three groups based on their objectives. The first three experiments focus on the Sieve and LC-series ensemble algorithms employing the same group of base classifiers to compare their accuracy and stability. The objective of the next two experiments is to demonstrate the effectiveness of the classifier chain refinement process in its accuracy and length variations between the original and refined classifier chains. Finally, the last experiment is performed to reveal that the GC has a significant structural advantage over the LC. It is important to note that the goal is not to achieve the highest accuracy possible, but to show a better “accuracy improvement” compared with the LC-series algorithms when using the same base classifiers. Therefore, base classifiers are trained using the default configurations setup by Scikit-learn [
22] and a dataset that has not been preprocessed to achieve consistency across these evaluations.
It is important to clarify that the stability (i.e., certainty of accuracy improvement) is a more important metric than the accuracy (i.e., the magnitude of accuracy improvement) in the evaluation of an ensemble classifier, because stability is the pre-requisite of the accuracy improvement. Therefore, only the accurate ensemble classifiers which have been validated in extensive experiments can truly reflect the performance of the existing practices. Accordingly, only 38 base classifiers and 20 LC-series ensemble classifiers trained by eight successful ensemble algorithms (i.e., Randomizable Filter [
23], Bagging [
24], AdaBoost [
25], Random Forest [
26], Random Sub-space [
27], Majority Vote [
28], Random Committee [
29], and Extra Trees [
30]) are involved in the first three experiments. Particularly, to maximize the accuracies of the compared ensemble classifiers (e.g., AdaBoost) which can only consensus upon the same type of base classifier; the most accurate base classifiers are employed as their base classifiers (refer to
Table A1,
Table A2,
Table A3 and
Table A4 in
Appendix A). With respect to the evaluation data, a well-known benchmark dataset NSL-KDD [
31], which includes two classes (i.e., Benign: B and Malicious: M) and two challenging test sets “test+” and “test-21” is employed to evaluate all the ensemble classifiers in terms of accuracy, precision, recall, F1-score and the Area Under the Receiver Operating Characteristic (AUROC). In addition, a dataset for Breast Cancer [
32] is also evaluated by employing the same approach, which is a representative of small data. Since the refined classifier chains result from the big data (i.e., NSL-KDD) are much longer on than the small data (i.e., Breast Cancer), we will mainly interpreter/demonstrate the principles of the Sieve based on the results achieved on the first two experiments. Consequently, we place the results of the third experiment in
Table A3,
Table A4,
Table A5 and
Table A6 in
Appendix A. The experiments will show the proposed algorithm can improve the performances on both the small and the big data.
4.2. Experiments 1, 2 and 3: Comparison of the Performances
We trained the 38 base classifiers on the dataset “KDDTrain+” (i.e., 125,937 samples).
Table 1 and
Table 2 show the performance of different ensemble techniques on the datasets, test-21 (i.e., 11,850 samples) and test+ (i.e., 22,544 samples), respectively. The rows above the third row from the bottom of the tables give the performance of the eight selected ensemble algorithms. More specifically, since five of the eight ensemble algorithms, denoted with asterisk, can produce multiple ensemble classifiers using varied base classifiers, we have to create multiple ensemble classifiers using these asterisk-marked algorithms to obtain a comprehensive result. Therefore, the performance of each of the algorithms with asterisk is averaged over the corresponding multiple ensemble base classifiers. For example, we built four AdaBoost ensemble classifiers by respectively employing four different base classifiers (i.e., algorithms), so in
Table 1 and
Table 2 the values under AdaBoost * are the average of the results from the four AdaBoost ensemble classifiers. As a result, the eight ensemble algorithms, with different ensemble classifiers and their corresponding performances are shown in
Table A1 and
Table A2 in
Appendix A. Then, the second and the third rows from the bottom of
Table 1 and
Table 2 are the averaged performance of the 38 base classifiers and the eight selected LC-series ensemble algorithms, respectively. Observe that the averaged accuracy of the 38 base classifiers is lower than the majority vote, this is due to the fact that the majority vote only ensembles the best four base classifiers for its performance. Finally, the last row in the same tables is the performance of the Sieve technique.
Overall, these two tables show that the Sieve significantly outperforms the 38 base classifiers and the eight LC-series ensemble algorithms. For example, the accuracy of the Sieve has been improved by 31.75% (i.e., 85.43% − 53.68%) and 16.34% (i.e., 90.29% − 73.95%) compared with the base classifiers and by 28.99% (i.e., 85.43% − 56.44%) and 14.40% (i.e., 90.29% − 75.89%) compared with the LC-series ensemble classifiers. Most importantly, the Sieve is able to resolve or at least largely mitigate the IC. For instance, due to the fact that the differences between the precision(M) and precision(B) of the base classifiers are 66.16% (i.e., 91.46% − 25.30%) and 29.71% (i.e., 93.25% − 63.54%), separately, it indicates that the base classifiers are seriously biased towards the class M in both experiments. However, the Sieve is able to reduce the corresponding differences to 33.97% (i.e., 92.55% − 58.58%) and 4.44% (i.e., 92.25% − 87.81%). By contrast, the LC-series ensemble classifiers still result in high differences of 61.68% (i.e., 87.61% − 25.93%) and 26.81% (i.e., 92.25% − 65.44%) on the same metrics. If the averaged reduction rates of the precision difference are used to evaluate the ability to calibrate the bias base classifiers (i.e., scale of 1), the Sieve and the LC-series ensemble classifiers are scored at 0.6686 (i.e., 66.86% = [(66.16% − 33.97%)/66.16% + (29.71% − 4.44%)/29.71%]/2) and 0.0827 (i.e., 8.27% = [(66.16% − 61.68%)/66.16% + (29.71% − 26.81%)/29.71%]/2), respectively. Accordingly, we can consider that the Sieve is 8.08 (i.e., 0.6686/0.0827) times stronger than the LC-series ensemble classifiers in terms of handling the IC problem.
On the other hand, since the data pattern of the test-21 and test+ are somewhat varied, it is inevitable that all the classifiers will generate different results based on these two test sets. However, when the same ensemble classifier performs very differently on the two test sets, it indicates that this classifier would be more vulnerable/sensitive to the pattern variations (i.e., unstable performance). According to the results of the experiments, the difference in accuracy when the LC-series ensemble classifiers were applied to these two test datasets can reach a value of 20% (i.e., 75.89% − 56.44%), whereas the same metric is only 4.86% (i.e., 90.29% − 85.43%) for the Sieve. This comparison indicates that the Sieve would be 4.12 (i.e., 20/4.86) times more stable on the unseen data/diversity patterns, which means that the Sieve has a much broader range of practical applications. In addition, since the difference in the accuracy of the base classifiers for the same two datasets is also about 20% (i.e., 73.95% − 53.68%), it indicates that the erratic accuracy achieved with the LC-series ensemble classifiers is actually derived from the base classifiers. Therefore, the Sieve is able to greatly mitigate the inherent instabilities that are associated with the base classifiers. The final assessment is that the Sieve’s advantage in accuracy and stability is attributed to the structural advantage of the GC.
Similar conclusions can also be found in the evaluation results of the Breast Cancer; please refer to
Table A3,
Table A4 and
Table A5 in
Appendix A for details. It is worth mentioning that the LC-series ensemble algorithms are not able to improve the accuracy of the base classifier when the number of training samples is limited (i.e., 210), whereas, the Sieve can still improve the accuracy even though the number of training samples is only 50% of the LC-series (i.e., 105).
4.3. Experiments 3 and 4: Verifying the Effectiveness of the Classifier Chain Refinement
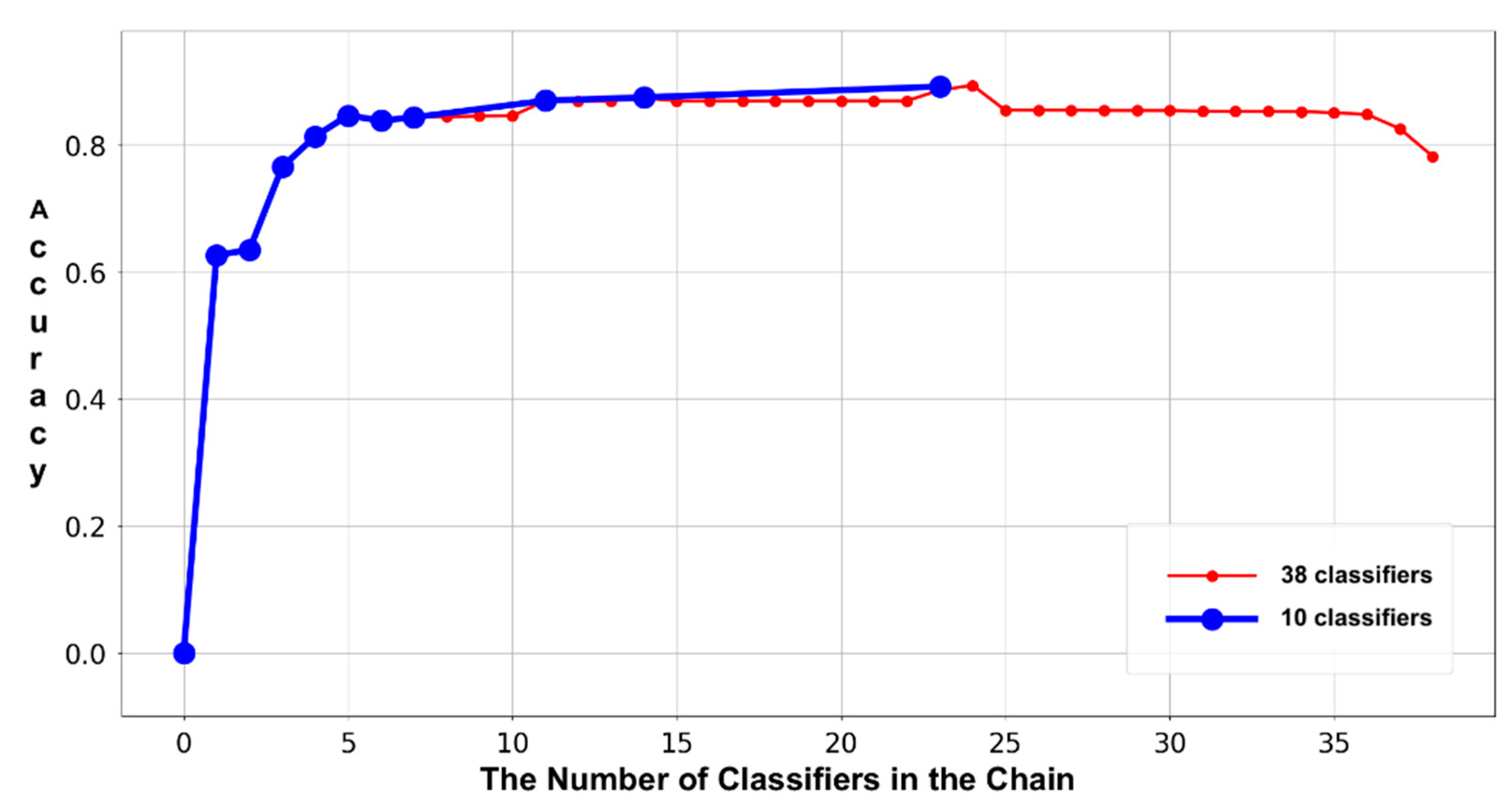
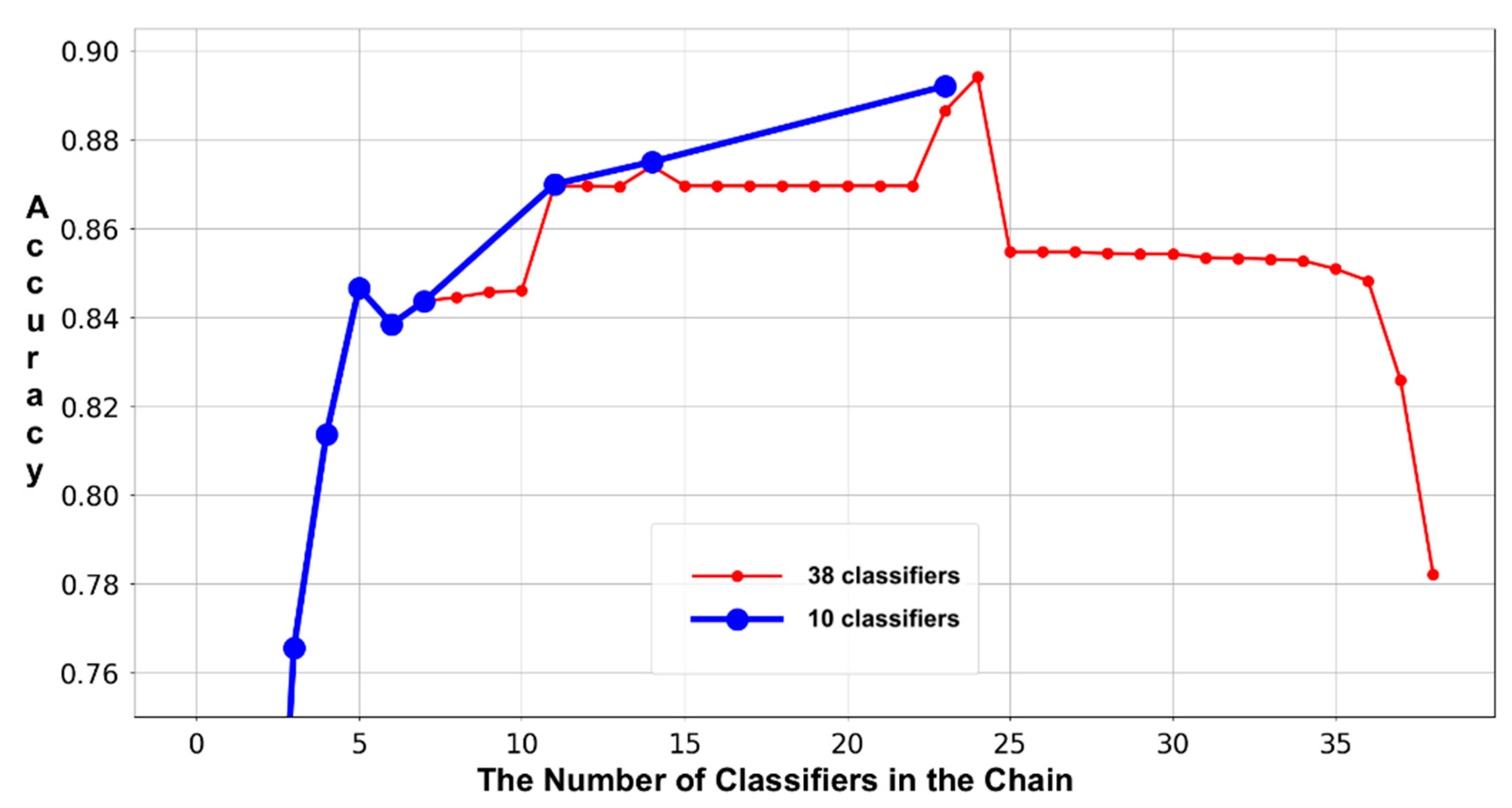
To verify the effectiveness of the refinement in the classifier chain, experiments 3 and 4 are performed to evaluate the variations in the accuracies and lengths of both the original and refined classifier chains on the two test sets. These two experiments record the accumulated accuracies of the invoked base classifier and form trajectories accordingly. As shown in the
Figure 5,
Figure 6,
Figure 7 and
Figure 8, the thin and thick lines are the trajectories that result from the original and refined classifier chains, separately. More specifically, each point represents the ratio between the number of correct-labeled samples and the number of all the samples in the dataset. Using the following example to demonstrate the method of calculating each accumulated accuracy point, assume there are 10 samples in the dataset; the first and last five samples belong to classes X and Y, respectively. Suppose also that the classifier chain that is biased towards class X includes two base classifiers: c1 and c2. If the c1 labels samples no.3–7 as class X, then all the rest of the samples are labeled as class Y. Then, the number of correct labels is six, which are samples no.3–5 (i.e., class X) and no.8–10 (i.e., class y). Therefore, the first accumulated accuracy point is 0.6 (i.e., 6/10). We have to emphasize that we are calculating every accuracy point by strictly executing the workflow of classifier chain employment. This means that we are simulating the workflow of employing a classifier chain with only one base classifier (i.e., c1) in the previous example. Since there are two base classifiers in the chain, adopting the same method, we need to clear all the labels that were not assigned by the c1 before calculating the second accumulated accuracy point, because the last base classifier c2 was not invoked. Accordingly, there are five samples (i.e., no.1, 2 and 8–10) passed to the c2. If the c2 labels samples no.1, 2, 10 as class X, then all the rest, samples no. 8 and 9, are labeled as class Y. Thus, the number of accumulated correct labels is 7: 3 labels (i.e., no.3–5, class X) result from the c1, 2 labels (i.e., no.1 and 2, class X) result from the c2 and the other two labels (i.e., no.8 and 9, the class Y) result from the last non-classifier procedure. Consequently, the second accumulated accuracy point is 0.7 (i.e., 7/10). In addition, we must distinguish the difference between calculating the accumulated accuracy and the accuracy that is used to eliminate the base classifiers. Referring to subsection “The Refinement of Classifier Chain,” a base classifier will be removed from the chain only when its accuracy is lower than 50%. In the previous example, the accuracy of the c2 for determining elimination is 0.67 instead of the accumulated accuracy 0.7, because it correctly labels the samples no.1, 2 and wrongly labels the sample no.10. In conclusion, the Sieve takes the accuracy that directly results from a base classifier into consideration when considering elimination and adopts the accumulated accuracy to verify the effectiveness of the classifier chain refinement. Referring to the figures, the accumulated accuracy might be increased, decreased or maintained, along with each new base classifier involved. Since the number of accumulated correct labels result from the newly involved base classifier, all the previous base classifiers and the last non-classifier procedure, it would be increased or decreased at some extents. There are also some points that maintain the accumulated accuracies, because the corresponding base classifiers do not label any new sample. The reason for this phenomenon is that all of their target samples have been labeled by the previous base classifiers, which means that their target samples are completely overlapping their predecessors. It is easy to understand that all the base classifiers that not improve the accumulated accuracies should be removed from the classifier chain and our classifier chain refinement successfully achieved this goal. The figures clearly indicate that the accuracy of each refined classifier chain (i.e., the last point on the thick lines) is roughly the same as that of the original classifier chain (i.e., the last point on the thin lines), which shows that the chain refinement procedure will not reduce the performance on accuracy.
In addition, the experiment data show that the low-ranked base classifiers are more vulnerable to being eliminated. This phenomenon is caused by two factors: the difference in accuracy and the overlap in terms of target samples between the high- and low-ranked base classifiers. For instance, there are 10 samples (i.e., including two classes, X and Y) and two base classifiers (i.e., c1 and c3, with the same accuracies of 60% in predicting the class X samples). In addition, let us make the following assumptions for the c1 and c3. If we invoke the c1 to label the 10 samples, it will label samples no.1–5 as the class X and the first three predictions (i.e., no.1–3) are correct. If we invoke the c3 to make predictions on the 10 samples, it will label samples no. 4–8 as the class X and the first three labels (i.e., no. 4–6) are correct. Under this assumption, if we form a classifier chain with the two base classifiers (i.e., the c1 in the first place) to label the 10 samples, the second-placed c3 will only label samples no.6–8 as the class X because samples no.1–5 have been labeled by the c1. Since the c3 (i.e., the low-ranked base classifier) can only make a correct prediction on sample no.6, its accuracy is only 33% and should be eliminated from the chain according to the chain refinement procedure. Furthermore, if there is another base classifier c2 between c1 and c3, and c2 has labeled sample no.6 as class X before invoking the c3, then the c3 will only label samples no.7, 8, hence reducing its accuracy to zero (i.e., more vulnerable to being eliminated). Although the exact assumed situation might rarely happen in practice, it is inevitable in reality, because any first-invoked base classifier would label (more or less) some samples that can be correctly labeled by its successors. Essentially, the magnitude of such affection (in terms of elimination) resulting from the high-ranked base classifiers toward a low-ranked base classifier is unpredictable, but the tendency is generally determined. Therefore, the aforementioned example is trying to explain a common phenomenon that a low-ranked base classifier is more vulnerable to being eliminated due to its low accuracy as well as the overlapping magnitude of the target samples between it and the predecessors. As a result, only the first several and a few middle base classifiers are retained in the classifier chain. The reduction rates in the two original classifier chains are 73.68% (i.e., (38 − 10)/38) in the first two experiments. Particularly, the reduction rate of the third experiment achieves 94.74% (i.e., 2/38; please refer to
Table A5 in
Appendix A). A possible reason for the difference in the reduction rates is that the small/big data would be more likely to be labeled/covered by a fewer/more base classifiers, so the length of the refined classifier chain would be proportion to the data size. However, this is only a trend instead of a definite conclusion because the reduction rate is determined by the base classifiers, and hence out of the control of the Sieve. As a result, the three experiments verify that the classifier chain refinement can effectively shorten the classifier chain without impacting the accuracy.
Moreover, the percentage of samples labeled by each base classifier/layer and the corresponding accuracy are shown in
Table 3, where the two columns “Labeling Percentage” are computed via dividing the number of labeled samples (i.e., by the current layer) by the total number of samples; the two columns “Accuracy” represent the accuracy achieved by the current layer. For example, assume the total number of samples is 10. If the first base classifier labels four of 10 samples and three of the four labeled samples are correct, the percentage and the accuracy of this base classifier are 40% (i.e., 4/10) and 75% (i.e., 3/4), respectively. As a result, we can observe that the percentages and accuracies are (roughly) becoming smaller as more base classifiers are invoked. However, this is also a trend instead of a definite conclusion because there are some data that violate this pattern. For instance, the two labeling percentages of the base classifier no.3 are higher than the base classifier no.2. The two accuracies of the base classifier no.8 are higher than the base classifier no.7. A similar pattern can also be found on the layer-based performances result from the Breast Cancer; please refer to
Table A6 in
Appendix A for details.
4.4. Revealing the Significant Structural Advantage on the Global Consensus
Essentially, there are only three differences between the Sieve and the LC-series ensemble algorithms. These are: (1) utilizing the capabilities of every base classifier fully (i.e., labeling both classes) or partially (i.e., only labeling one class); (2) employing the base classifiers with or without a certain order (i.e., invoking based on the ranking or not); (3) labeling each sample via a consensus approach (i.e., combining multiple base predictions) or not. Therefore, the performance on accuracy between these two algorithms must be linked to one or more of these three points. In order to identify the actual reason, multiple hybrid ensemble classifiers are created and each one of them is a mixture of the Sieve and the LC-series ensemble algorithms. With respect to the approach of making prediction, each hybrid classifier performs in the similar way to the Sieve, i.e., the base classifiers are orderly invoked based on the ranking, and each base classifier adds one more vote of a specific class (instead of direct labeling) to a sample, but only when it predicts the sample as that class. From the respective of labeling, each hybrid classifier performs in exactly the same way as a LC-series ensemble classifier that adopts the majority vote as the consensus approach. A sample will be labeled as a specific class if the votes of that class are more than a half of the number of the base classifiers, otherwise, it will be labeled as the other class. It should be noted that each hybrid classifier is actually a special Sieve with a LC procedure.
The created hybrid ensemble classifiers are evaluated on the datasets test-21 and test+. Referring to
Table 4 and
Table 5, the performance between the Sieve and the hybrid ensemble classifiers is considerably different. Particularly, the accuracy of each hybrid ensemble classifier is even worse than that of the corresponding traditional LC-series ensemble classifier, despite the fact that it can orderly invoke the base classifiers similar to the Sieve. Due to the fact that the only difference between the hybrid classifiers and the Sieve is the involvement of an LC procedure, it can be concluded that this LC is the only possible reason that would cause the reduction in accuracy. Therefore, the reason that the Sieve greatly outperforms the LC-series ensemble classifiers can be attributed to the structural advantage that comes with the GC.