Abstract
Deep learning architectures like Convolutional Neural Networks (CNNs) are quickly becoming the standard for detecting and counting objects in digital images. However, most of the experiments found in the literature train and test the neural networks using data from a single image source, making it difficult to infer how the trained models would perform under a more diverse context. The objective of this study was to assess the robustness of models trained using data from a varying number of sources. Nine different devices were used to acquire images of yellow sticky traps containing psyllids and a wide variety of other objects, with each model being trained and tested using different data combinations. The results from the experiments were used to draw several conclusions about how the training process should be conducted and how the robustness of the trained models is influenced by data quantity and variety.
1. Introduction
One of the most damaging problems in all agriculture is the citrus huanglongbing (HLB) [1], an incurable disease that is caused by the bacterium Liberibacter spp.) [2]. The main vector for this disease is the psyllid species , a two to three-millimeter light-brown insect that is most often found in citrus shoots. The constant monitoring of psyllid infestation is thus essential for timely preventive actions to avoid substantial economic losses.
Psyllids can be sampled in the field using a variety of methods [3], among which sticky traps are the most used for monitoring infestations due to their reliability [4]. However, accurate population estimates have to rely on a very time-consuming sorting and counting process. In addition, fatigue and well-known cognitive phenomena tend to decrease the accuracy of the visual assessment [5]. As a result, infestation estimates may become too inaccurate to properly support decisions. This is a problem that affects not only psyllids, but almost all methods of insect infestation estimation, which has given rise to many research efforts towards the automation of the process using imaging devices [6].
Depending on the type of infestation, the detection of insects directly on leaves [7,8,9,10,11,12], stems [13], and flowers [14] can be appropriate, but in most cases counting insects caught by traps is a better proxy for the real situation in a given region [15]. The literature has many examples of image-based insect monitoring that employ traps for sample collection [5,16,17,18,19,20,21,22]. In most cases, traps capture not only the specimens of interest, but also other invertebrate species, dust, and other types of debris. Detecting specific objects in images captured under this type of condition can be challenging. This is particularly true in the case of psyllids, as these tend to be among the smallest objects usually found in the traps. Pattern recognition in a busy environment is the type of task that can, in many cases, be suitably handled by machine learning algorithms. Thus, it is no surprise that this type of technique has been predominant in this context.
Traditional machine learning techniques such as multi-layered perceptron (MLP) neural networks [20], Support Vector Machines (SVM) [10,13,14,23], and K-means [21] have been applied to insect counting in sticky traps, with various degrees of success. However, an important limitation associated with those techniques is that they either require complex feature engineering to work properly, or are not capable of correctly modelling all the nuances and nonlinearities associated with pattern recognition with busy backgrounds. This may explain in part why deep learning techniques, and CNNs in particular, have gained so much popularity in the last few years for image recognition tasks.
The use of deep learning for insect recognition has mostly concentrated on the classification of samples into species and subspecies, with the insects of interest appearing prominently in the images captured either under natural [11,24] or controlled [25] conditions. Some investigations have also addressed pest detection amidst other disorders [26]. To the best of the authors’ knowledge, the only work found in the literature that uses deep learning for monitoring psyllids was proposed by Partel et al. [27], achieving precision and recall values of 80% and 95%, respectively. Another study with similar characteristics, but dedicated to moth detection in sticky traps, was carried out by Ding and Taylor [19]. In any case, a problem that is common to the vast majority of the investigations based on deep learning found in the literature is that training and tests are done with the datasets generated using the same camera or imaging device. As a result, the model will be trained using data that lack the variability that can be found in practice, reducing its reliability. This difference between the distribution of the data used to train the model and the data on which the model is to be applied in the real world is commonly called covariate shift [28], and is one of the main reasons for models to fail under real world conditions.
In order to investigate how severe is the covariate shift problem when CNNs are used to detect and count psyllids in yellow sticky traps, nine distinct datasets were built using different imaging devices. Extensive experiments were conducted in order to determine the impact that the lack of variability has on the ability of the trained model to handle image data acquired by different people using different devices. This study is a follow-up to a previous investigation about the influence of image quality on the detection of psyllids [29].
2. Material and Methods
2.1. Image Datasets
Psyllids were captured by means of yellow sticky traps (Isca Tecnologias, Ijuí, Brazil) placed in farms located in the State of São Paulo, Brazil. The traps were collected after two weeks in the field and encased in a transparent plastic overlay to prevent object displacement. Images were captured indoors under artificial illumination. Smartphones were hand held in a horizontal position at a distance of approximately 30 cm from the traps, such that the region of interest filled as much of the screen as possible. Seven different smartphones, handled by eight different people, were used to capture the images (Table 1). These devices were chosen due to their diversity of characteristics in terms of resolution, optical quality and capture settings, and also because they roughly represent the variety of devices that would be used in practice. Part of the traps was also imaged by a scanner located in a laboratory environment. The images associated with the Huawei Mate SE smartphone and to the scanner were captured in the context of a previous research [29], so the traps that were imaged were not the same as the ones used with the other devices. In the case of all other devices, the traps imaged were the same. Differences in the number of samples associated with each device are due to the fact that traps were imaged twice whenever deemed necessary, for example due to lack of focus or to unusual camera settings (which were always kept automatic) resulting in unexpected image attributes. Severely blurred or out-of-focus images were discarded and are not included in the numbers shown in Table 1.

Table 1.
Devices used to acquired images from sticky traps. The code column reveals the number used to identify each source from this point forward. The number of images for each class can be obtained simply by dividing the total numbers by two. The Motorola Moto Z2 Play smartphone was handled by two different people.
An experienced entomologist identified each psyllid and marked their positions on the transparent overlay using a felt tip marker. Each image contained between 1 and 30 psyllids. Next, the original images were cropped using a simple graphical interface which allowed the task to be performed with a single mouse click. The cropping process was divided into two parts. In the first part, small square regions containing each psyllid and immediate surroundings were selected. In order to guarantee that the entire insect bodies would fit inside the cropped regions, the size of the square side was defined as approximately 1.5 times the typical psyllid length. Because the imaging devices had different resolutions, the dimensions of the cropped regions ranged from 35 × 35 pixels to 97 × 97 pixels (Table 1). The second part of the cropping procedure was dedicated to building the non-psyllid dataset. In order to guarantee that classes were balanced, the number of cropped images generated for the non-psyllid dataset was exactly the same as for the psyllid class, and the dimensions of the cropped regions were also kept the same. The non-psyllid class was created to adequately represent the diversity of objects other than psyllids that can be found in the sticky traps. Approximately one third of this set contains bare background (with or without the reference lines), one third contains insects with characteristics similar to those of psyllids, one sixth contains insects (or parts of insects) with diverse visual features, and one sixth contains a diversity of debris, including dust, small leaves, etc. In total, 7594 cropped images were generated for each class. Some examples for the psyllid and non-psyllid classes are shown in Figure 1.
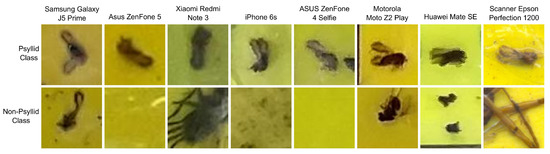
Figure 1.
Examples of cropped regions for each imaging device.
2.2. Experimental Setup
The CNN used in this work was Squeezenet [30]. This architecture is lightweight, thus being appropriate for use under relatively limited computational resources (e.g., mobile devices). This characteristic is important in the context of this work because the ultimate objective is, in the near future, to incorporate the model into a mobile application for psyllid counting. However, because the objective of this study was to investigate how this type of architecture deals with covariate shift, experiments were carried out using MatlabTM 9.4 (Mathworks, Natick, MA, USA) on a personal computer equipped with a 12-GB NvidiaTM Titan XP Graphics Processing Unit (GPU) (Santa Clara, CA, USA). The only aspect that would differ if the trained models were run on a mobile device would be the execution time, which was not the object of investigation in this study. The training parameters used in this work were: mini-batch size: 64; base learning rate, 0.001, reduced to 0.0001 after five epochs; L2 Regularization, 0.0001; number of epochs: 10; momentum, 0.9. The model was pretrained using the ImageNet dataset, which has more than 1 million images covering 1000 different classes; transfer learning was then applied, greatly speeding up convergence and reducing the number of images needed for training [31,32]. All cropped images were upsampled by bicubic interpolation to match the standard input size for the Squeezenet architecture (227 × 227 pixels). The training dataset was augmented using the following operations: 90 counter-clockwise rotation, 90 clockwise rotation, 180 rotation, horizontal and vertical flipping, random brightness increase, random brightness decrease, sharpness enhancement, contrast reduction, contrast enhancement, and addition of random Gaussian noise (0 mean, 0.001 variance). These operations were chosen to simulate most of the variations that can be found in practice for the specific problem tackled in this study. A 10-fold cross validation was adopted in all experiments in order to avoid biased results.
Three different experiments were carried out in order to test different aspects related to dataset diversity. In the first experiment, the number of images in the training dataset (840 images prior to augmentation) and test dataset (6754 images) were always kept the same, but the number of sources for the training dataset was varied from 1 to 9 (Table 2); all images from all sources were always present in the test dataset, with the exception of those used for training. All 511 possible combinations of data sources were tested, and considering that a 10-fold cross-validation was adopted, this meant that 5110 CNNs were trained for this experiment alone. The objective of this experiment was to investigate how the diversity of sources represented in the training dataset affects the ability of the model to correctly detect psyllids. The number of training samples was limited to the amount of images available when a single source was used, in order to ensure that only the source diversity factor influenced the results.

Table 2.
Training setup used in the first experiment. The values between parentheses in the second column are the number of samples after augmentation.
In the second experiment, both the number of sources and the number of images in the test set were varied. As more image sources were used, the number of samples in the training dataset was decreased (Table 3). The objective was to determine which of the two factors, diversity or number of samples, is more important for proper model training. Again, all images not used for training were included in the test dataset, and all 511 possible combinations of data sources were tested.

Table 3.
Training setup used in the second experiment. The values between parentheses in the second and third columns are the number of samples after augmentation.
The third experiment aimed at further investigating what would happen if the training set contained only samples from a single source. Each one of the nine devices was investigated separately, and results were tallied considering each other source individually. The objective was to determine if devices with certain characteristics were better (or worse) sources of training data, thus providing some cues on which aspects should be given priority when building the training dataset.
In addition to the three experiments above, all misclassification in all experiments were tallied together in order to determine which of the non-psyllid image types (insects with features similar to psyllids, insects with dissimilar features, bare background, or debris) caused more confusion with the psyllid class.
3. Results and Discussion
The results obtained in experiment 1 (Figure 2 and Table 4) clearly indicate that increasing the variability of the samples used for training the model, while keeping the number of images fixed, indeed improves the results, as error rates decreased by almost 40% (from 15.1% using a single source to 9.4% using all sources). The standard deviations were quite low, indicating that there was not much variation between repetitions and between different source combinations. However, when only a few sources were used, the inclusion of certain devices, especially the Xiaomi Redmi Note 3 and the iPhone 6s, led to slightly higher accuracies. On the other hand, the inclusion of the scanner images was not helpful in any case, confirming the conclusions reached in [29]. The explanation for this is that the scanner images, despite having a much higher quality in terms of resolution and illumination homogeneity, are too different from the smartphone images to cause a positive impact on the model training. Thus, with the number of sources fixed, there was not much difference when different devices were included in the training, except in the case of the scanner. This indicates that the quality variation of the samples acquired with different smartphones is important to better prepare the model to deal with the variability expected in practice. In addition, since each device covers part of that variability, their replacement does not cause a significant change in the accuracy (but the samples that are misclassified may be different).
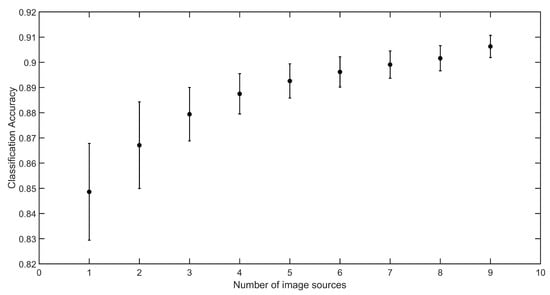
Figure 2.
Results obtained in the first experiment. The round markers represent the average accuracy obtained in each case, and vertical bars represent the respective standard deviations.

Table 4.
Results obtained in experiment 1, with increasing number of sources and fixed number of training samples. Sources are identified by the code numbers adopted in Table 1. The numbers between parentheses represent the average accuracies for those particular source combinations.
While the number of images used for training was above 300 (less than five sources included in the training set), the results obtained in experiment 2 were similar to those achieved in experiment 1 (Figure 3 and Table 5). As the number of images used for training fell below 300 and the number of sources increased, the accuracy plateaued, but did not fall significantly even when as few as 180 images (nine sources) were used. This indicates that data variability is more important than data quantity. Although it is evident that the more images are included, the higher the probability is that more variability is included, and a carefully selected training set may be effective even with a relatively low number of samples. This is very relevant considering that obtaining large amounts of labelled data is usually a challenge.
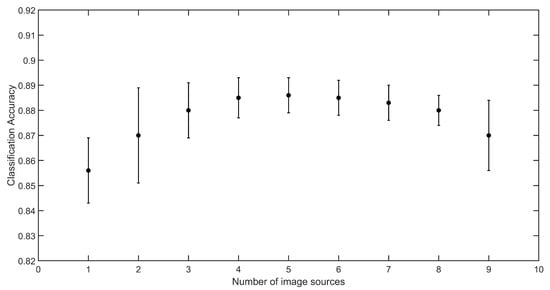
Figure 3.
Results obtained in the second experiment, with increasing number of sources and decreasing number of training samples. The round markers represent the average accuracy obtained in each case, and vertical bars represent the respective standard deviations.

Table 5.
Results obtained in experiment 2. Sources are identified by the code numbers adopted in Table 1. The numbers between parentheses represent the average accuracies for those particular source combinations.
The results obtained in experiment 3 (model training using a single source) were mostly consistent with those yielded by the previous two experiments (Table 6), but some relevant differences were observed as the source for the training samples was changed. The best training dataset was the first Motorola Moto Z2 Play, which resulted in an average accuracy of 0.876. A possible explanation for this is that this smartphone has an intermediate resolution and optical quality in comparison with the other devices, so the characteristics of its images tend to not be too dissimilar to those yielded by the other smartphones. In addition, the Motorola Moto Z2 Play was the only device operated by two people (thus generating two separate datasets), and very high accuracies (>0.92) were achieved when the model trained using the images captured by one person was used to classify the other set. Despite this, the accuracy associated with this smartphone would still be the highest if the second database was removed from the experiments. It is also worth noting that the two Motorola Moto Z2 Play models yielded relatively dissimilar results when used to classify images from other sources, with differences surpassing 5% when the trained models were applied to the Asus ZenFone 5 and Huawei Mate SE test sets. This is a clear indication that differences in the way people acquire images may have a sizeable impact on the characteristics of the dataset generated, even when the exact same imaging device is used.

Table 6.
Average accuracies obtained for for each device when the training set included samples from a single source. The first column shows the source used for training, and the first row shows the sources used for testing. The last column reveals the average accuracy for each training set, and the last row shows the accuracy obtained for each source averaged over all training sets.
As expected, accuracies dropped significantly when scanner images were used for training (0.708 in average), confirming the results obtained in the other experiments. However, models trained with smartphone images performed relatively well classifying scanner images (0.826). This unexpected asymmetry seems to indicate that, while CNN models trained with high quality images have problems dealing with samples of lower quality, the opposite is not necessarily true.
All models trained with smartphone images yielded classification accuracies above 0.89 when applied to the iPhone 6s dataset, a result that was considerably better than those obtained for the other test sets. A suitable explanation for this was only found upon a careful analysis of all images used in the experiments. Because all smartphone images were captured indoors with a relatively low light intensity, problems related to focus and motion blur were a relatively common occurrence. Images severely blurred or out-of-focus were not used, but those with mild distortions were included to better represent situations that can occur in practice. The iPhone 6s dataset was the least affected by distortions and, as observed in the case of the scanner images, high quality images tend to be suitably classified by models trained with more degraded images. It is not clear if this dataset was less distorted because of the operator dexterity, the effectiveness of the device’s post-processing, or both. Analyzing the image capture process and how to decrease distortions was beyond the scope of this work, but these may be interesting topics for future research.
The test dataset with the worst performance was the Huawei Mate SE (average accuracy of 0.786). This dataset was built for the previous research [29], so the traps that were imaged were not the same as the ones used with the other devices. One important characteristic of the traps imaged by the Huawei Mate SE is that most of them contained a very large amount of psyllids and other objects. As a result, images were very busy, and image crops containing psyllids usually also contained other objects. Since this kind of situation may happen in practice, the inclusion of such busy image was warranted, but it caused this dataset to be more difficult to be correctly classified. Interestingly, the results when this dataset was used for training were not nearly as poor (average accuracy of 0.847), which again indicates that including images with distortions or spurious elements actually helps to increase classification accuracies.
The vast majority of the false positive errors (non-psyllid images classified as psyllid) were due to the presence of insects with features similar to those of psyllids (Table 7). Because the features that distinguish different species of insects are often minor, it can be difficult for the model to properly learn those distinctive features if only a few representative samples are available for training. It is likely that one of the reasons for the steady model improvement as more data sources were included, even when the number of training samples was decreased, was that problematic cases were represented in a more diverse way in the training set. As a result, the model was better prepared to discriminate species under different circumstances.

Table 7.
Composition of the false positive errors (non-psyllid images classified as psyllid).
Finally, it is worth mentioning that testing CNNs with deeper and more complex architectures was beyond the objectives of this work, but experiments like this have been carried out previously under similar conditions [29]. In that study, the ResNet-101 architecture [33] yielded only slightly higher accuracies (between 1% and 4%) at the cost of a prediction time almost 10 times larger.
4. Conclusions
This article presented a study on the impact of using different data sources to train and validate CNN models, for the specific purpose of psyllid detection and counting using images of sticky traps. Relatively good results were achieved even when only samples from a single smartphone were used for training. This indicates that reasonably accurate estimates for the psyllid infestation may be possible even with models trained with limited datasets, as long as the characteristics of the training samples do not depart too much from those commonly found in practice. However, for more accurate estimates, or if a large number of devices with significantly different characteristics are expected to be employed in practice, the CNN model should be trained and tested using data that is as diverse as possible, otherwise results will not reflect reality and practical failure will become inevitable. This is not an easy task because data collection can be expensive and time consuming. Incremental evolution, in which the model is continuously improved as more data become available, may be a viable option, especially if a network of early adopters is already available.
Some factors that are relevant in the context of psyllid detection were only superficially investigated in this study and should receive more attention in the future, such as the influence of illumination, the consistency of the manual annotation of the reference material, the impact of unfocused and blurred images on training and testing, the importance of having multiple different people acquiring the images used to develop the models, and the consequences of having different psyllid densities in the traps, among others.
Author Contributions
Conceptualization, J.G.A.B. and G.B.C.; methodology, J.G.A.B. and G.B.C.; software, J.G.A.B.; validation, J.G.A.B. and G.B.C.; formal analysis, J.G.A.B.; investigation, J.G.A.B.; resources, J.G.A.B. and G.B.C.; data curation, J.G.A.B. and G.B.C.; writing–original draft preparation, J.G.A.B.; writing–review and editing, J.G.A.B. and G.B.C.; visualization, J.G.A.B.; supervision, J.G.A.B.; project administration, J.G.A.B.; funding acquisition, N/A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank Nvidia for donating the GPU used in the experiments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alvarez, S.; Rohrig, E.; Solís, D.; Thomas, M.H. Citrus Greening Disease (Huanglongbing) in Florida: Economic Impact, Management and the Potential for Biological Control. Agric. Res. 2016, 5, 109–118. [Google Scholar] [CrossRef]
- Hung, T.H.; Hung, S.C.; Chen, C.N.; Hsu, M.H.; Su, H.J. Detection by PCR of Candidatus Liberibacter asiaticus, the bacterium causing citrus huanglongbing in vector psyllids: Application to the study of vector-pathogen relationships. Plant Pathol. 2004, 53, 96–102. [Google Scholar] [CrossRef]
- Yen, A.L.; Madge, D.G.; Berry, N.A.; Yen, J.D.L. Evaluating the effectiveness of five sampling methods for detection of the tomato potato psyllid, Bactericera cockerelli (Sulc) (Hemiptera: Psylloidea: Triozidae). Aust. J. Entomol. 2013, 52, 168–174. [Google Scholar] [CrossRef]
- Monzo, C.; Arevalo, H.A.; Jones, M.M.; Vanaclocha, P.; Croxton, S.D.; Qureshi, J.A.; Stansly, P.A. Sampling Methods for Detection and Monitoring of the Asian Citrus Psyllid (Hemiptera: Psyllidae). Environ. Entomol. 2015, 44, 780–788. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Cheng, H.; Cheng, Q.; Zhou, H.; Li, M.; Fan, Y.; Shan, G.; Damerow, L.; Lammers, P.S.; Jones, S.B. A smart-vision algorithm for counting whiteflies and thrips on sticky traps using two-dimensional Fourier transform spectrum. Biosyst. Eng. 2017, 153, 82–88. [Google Scholar] [CrossRef]
- Martineau, M.; Conte, D.; Raveaux, R.; Arnault, I.; Munier, D.; Venturini, G. A survey on image-based insect classification. Pattern Recognit. 2017, 65, 273–284. [Google Scholar] [CrossRef]
- Boissard, P.; Martin, V.; Moisan, S. A cognitive vision approach to early pest detection in greenhouse crops. Comput. Electron. Agric. 2008, 62, 81–93. [Google Scholar] [CrossRef]
- Barbedo, J.G.A. Using digital image processing for counting whiteflies on soybean leaves. J. Asia-Pac. Entomol. 2014, 17, 685–694. [Google Scholar] [CrossRef]
- Li, Y.; Xia, C.; Lee, J. Detection of small-sized insect pest in greenhouses based on multifractal analysis. Opt. Int. J. Light Electron Opt. 2015, 126, 2138–2143. [Google Scholar] [CrossRef]
- Liu, T.; Chen, W.; Wu, W.; Sun, C.; Guo, W.; Zhu, X. Detection of aphids in wheat fields using a computer vision technique. Biosyst. Eng. 2016, 141, 82–93. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, Y.; Chen, Y.; Wu, Y.; Yue, Y. Pest identification via deep residual learning in complex background. Comput. Electron. Agric. 2017, 141, 351–356. [Google Scholar] [CrossRef]
- Deng, L.; Wang, Y.; Han, Z.; Yu, R. Research on insect pest image detection and recognition based on bio-inspired methods. Biosyst. Eng. 2018, 169, 139–148. [Google Scholar] [CrossRef]
- Yao, Q.; Xian, D.X.; Liu, Q.J.; Yang, B.J.; Diao, G.Q.; Tang, J. Automated Counting of Rice Planthoppers in Paddy Fields Based on Image Processing. J. Integr. Agric. 2014, 13, 1736–1745. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Khoshtaghaza, M.; Minaei, S.; Jamshidi, B. Vision-based pest detection based on SVM classification method. Comput. Electron. Agric. 2017, 137, 52–58. [Google Scholar] [CrossRef]
- Liu, H.; Lee, S.H.; Chahl, J.S. A review of recent sensing technologies to detect invertebrates on crops. Precis. Agric. 2017, 18, 635–666. [Google Scholar] [CrossRef]
- Cho, J.; Choi, J.; Qiao, M.; Ji, C.W.; Kim, H.Y.; Uhm, K.B.; Chon, T.S. Automatic identification of whiteflies, aphids and thrips in greenhouse based on image analysis. Int. J. Math. Comput. Simul. 2008, 1, 46–53. [Google Scholar]
- Solis-Sánchez, L.O.; Castañeda-Miranda, R.; García-Escalante, J.J.; Torres-Pacheco, I.; Guevara-González, R.G.; Castañeda-Miranda, C.L.; Alaniz-Lumbreras, P.D. Scale invariant feature approach for insect monitoring. Comput. Electron. Agric. 2011, 75, 92–99. [Google Scholar] [CrossRef]
- Xia, C.; Chon, T.S.; Ren, Z.; Lee, J.M. Automatic identification and counting of small size pests in greenhouse conditions with low computational cost. Ecol. Inform. 2015, 29, 139–146. [Google Scholar] [CrossRef]
- Ding, W.; Taylor, G. Automatic moth detection from trap images for pest management. Comput. Electron. Agric. 2016, 123, 17–28. [Google Scholar] [CrossRef]
- Espinoza, K.; Valera, D.L.; Torres, J.A.; López, A.; Molina-Aiz, F.D. Combination of image processing and artificial neural networks as a novel approach for the identification of Bemisia tabaci and Frankliniella occidentalis on sticky traps in greenhouse agriculture. Comput. Electron. Agric. 2016, 127, 495–505. [Google Scholar] [CrossRef]
- García, J.; Pope, C.; Altimiras, F. A Distributed K-Means Segmentation Algorithm Applied to Lobesia botrana Recognition. Complexity 2017, 2017, 5137317. [Google Scholar] [CrossRef]
- Goldshtein, E.; Cohen, Y.; Hetzroni, A.; Gazit, Y.; Timar, D.; Rosenfeld, L.; Grinshpon, Y.; Hoffman, A.; Mizrach, A. Development of an automatic monitoring trap for Mediterranean fruit fly (Ceratitis capitata) to optimize control applications frequency. Comput. Electron. Agric. 2017, 139, 115–125. [Google Scholar] [CrossRef]
- Qing, Y.; Jun, L.V.; Liu, Q.J.; Diao, G.Q.; Yang, B.J.; Chen, H.M.; Jian, T.A. An Insect Imaging System to Automate Rice Light-Trap Pest Identification. J. Integr. Agric. 2012, 11, 978–985. [Google Scholar] [CrossRef]
- Dawei, W.; Limiao, D.; Jiangong, N.; Jiyue, G.; Hongfei, Z.; Zhongzhi, H. Recognition Pest by Image-Based Transfer Learning. J. Sci. Food Agric. 2019, 99, 4524–4531. [Google Scholar] [CrossRef] [PubMed]
- Wen, C.; Wu, D.; Hu, H.; Pan, W. Pose estimation-dependent identification method for field moth images using deep learning architecture. Biosyst. Eng. 2015, 136, 117–128. [Google Scholar] [CrossRef]
- Fuentes, A.; Yoon, S.; Kim, S.C.; Park, D.S. A Robust Deep-Learning-Based Detector for Real-Time Tomato Plant Diseases and Pests Recognition. Sensors 2017, 17, 2022. [Google Scholar] [CrossRef]
- Partel, V.; Nunes, L.; Stansly, P.; Ampatzidis, Y. Automated vision-based system for monitoring Asian citrus psyllid in orchards utilizing artificial intelligence. Comput. Electron. Agric. 2019, 162, 328–336. [Google Scholar] [CrossRef]
- Sugiyama, M.; Nakajima, S.; Kashima, H.; Buenau, P.V.; Kawanabe, M. Direct Importance Estimation with Model Selection and Its Application to Covariate Shift Adaptation. In Advances in Neural Information Processing Systems 20; Platt, J.C., Koller, D., Singer, Y., Roweis, S.T., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2008; pp. 1433–1440. [Google Scholar]
- Barbedo, J.G.A.; Castro, G.B. The influence of image quality on the identification of Psyllids using CNNs. Biosyst. Eng. 2019, 182, 151–158. [Google Scholar] [CrossRef]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Bengio, Y. Deep Learning of Representations for Unsupervised and Transfer Learning. In Proceedings of the Workshop on Unsupervised and Transfer Learning, Edinburgh, UK, 26 June–1 July 2012; pp. 17–37. [Google Scholar]
- Huh, M.; Agrawal, P.; Efros, A.A. What makes ImageNet good for transfer learning? arXiv 2016, arXiv:1608.08614. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).