The Effect of ‘Roughness’ on Upwelling North of Cape Town in Austral Summer

Abstract

Cape Town, South Africa, experiences coastal upwelling during austral summer. In this study, the effects of kinematic and thermal ‘roughness’ on wind stress are analyzed using 5–25 km resolution multi-satellite and coupled reanalysis datasets in the period 2010–2024. Average conditions for austral summer (December–February) are calculated to identify east–west gradients in sensible heat flux, wave height, and equatorward winds and to assess their consequences for the drag coefficient, wind-driven Ekman transport, and entrainment over the shelf from 16.9 to 18.7° E, north of Cape Town (33.7° S). Statistical and numerical outcomes are compared for austral summer and during active coastal upwelling in January 2018 with chlorophyll concentrations > 3 mg/m³. A subtropical anticyclone generated shallow equatorward winds next to a wind shadow north of Cape Town. Sharp cross-shore gradients in momentum flux were amplified by shoreward reductions in sensible heat flux and wave height, which suppressed the drag coefficient 10-fold. The inclusion of kinematic and thermal roughness in wind stress calculations results in a higher average cyclonic curl (−2.4 × 10⁻⁶ N/m³), which translates into vertical entrainment > 3 m/day at 33.7° S, 18° E. The research links coastal upwelling leeward of a mountainous cape with cross-shore gradients in air–sea fluxes that support recirculation and phytoplankton blooms during austral summer.

1. Introduction

Cape Town, South Africa, is a focal point for coastal upwelling in austral summer via offshore transport by southeasterly winds channeled around a mountainous cape [1,2]. Sea surface temperatures (SSTs) below 15 °C are common within 30 km of the coast. Vertical uplift or entrainment into the mixed layer is sustained by Ekman pumping due to cyclonic shear of longshore winds and currents [2,3,4,5,6,7,8]. Frequent phytoplankton blooms (chlorophyll > 3 mg/m³) support a rich food web [9,10,11]. A unique feature beyond the shelf edge is the presence of warm water from the Agulhas Retroflection, accompanied by rough seas [12,13,14,15]. The coastal upwelling is pulsed by the eastward passage of mid-latitude troughs [16,17], which alter the position and intensity of the South Atlantic anticyclone [18,19]. Although the seasonal climate is unimodal, productivity crests in spring and autumn [20,21,22].

The transfer of momentum and heat across the air–sea interface is inefficient. Exchange coefficients of order 10⁻³ determined by extensive measurements [23,24,25] depend on turbulence and the change in wind and temperature with height, but their representation has circular dependencies [26]. Winds over the ocean naturally generate breaking waves that offer better traction for air–sea momentum transfer. In moderate airflow (<15 m/s), turbulence is damped by thermal stability when surface temperature (Ts) is less than air temperature (Ta) [27,28,29,30,31]. Sensible heat flux (Qh) combines kinematic and thermal effects as the covariance of vertical gust and temperature perturbation (w’T’); that is, it is typically parameterized in data-assimilation models as the product of air density, specific heat, wind speed, Ts–Ta, and a fixed heat exchange coefficient 10⁻³. In anticyclonic weather with shallow longshore airflow and coastal upwelling, the wave-induced roughness is segregated by upstream fetch. Fast offshore and slow inshore winds produce cross-shore gradients in sea state, amplified by offshore warming and inshore cooling to the north of Cape Town. The drag coefficient declines near the coast, and wind stress curl (vorticity) supersedes offshore transport as the main driver of uplift into the mixed layer. But this feature is under-represented by fixed drag coefficients, so it is necessary to account for feedback between kinematic and thermal roughness, particularly leeward of mountainous capes in the southern Benguela upwelling system, where cyclonic wind shear is reflected in clockwise current gyres.

In the following section, the data analysis is described and results are presented, with a focus on cross-shore gradients of the drag coefficient and downstream processes. Austral summer averages and periods of active coastal upwelling are studied. The research is novel in using a variety of high-resolution datasets to quantify cross-shore gradients in air–sea interactions.

2. Data Analysis

Coastal upwelling to the north of Cape Town was analyzed via daily 10 km resolution Hybrid Coordinate Ocean Model (Hycom3) [32] reanalysis of sea temperature, salinity, Qh, mixed layer depth (MLD), and currents. Monthly and daily chlorophyll and SST fields were derived from multi-satellite assimilation at 5 km resolution [33]. Meteorological fields were analyzed from the 25 km resolution European Community Reanalysis (ERA5) [34] and included monthly to hourly surface air pressure, air temperature, Qh, and surface wind fields. The 25 km ERA5 Qh is less sensitive to Ts–Ta than 10 km Hycom3, so its use was confined to long-term analysis. Wave data were extracted from W3 reanalysis [35] to determine cross-shore gradients of significant height.

The study area spans the Western Cape coast from 35.1 to 31° S, 16.9–19.4° E (Figure 1a). Austral summer (December–February) averages were calculated over the period 2010–2024 and focus on a section along 33.7° S, 16.9–18.7° E to the north of Cape Town. Temporal records were extracted at a ‘virtual buoy’ (33.7° S, 18.2° E, 100 m depth) 30 km offshore between Robben and Dassen Island. A 72-year time series was extracted for monthly ERA5 zonal wind and Qh (1950–2024) and analyzed for mean annual cycle (18-month low-pass filtered), inter-annual variability (via wavelet spectral analysis), and linear trend. Similarly, a monthly multi-satellite chlorophyll time series for 2012–2024 was analyzed in conjunction with ERA5 meridional wind to understand seasonality. For the case study of the period 10–22 January 2018 (which experienced pronounced wind stress curl), the vertical atmospheric structure was analyzed from airport radiosonde profiles (at 34.0° S, 18.6° E) of air temperature, dewpoint, and wind. Daily air temperature time series were obtained from a weather station (at 33.0° S, 18.2° E), and at the virtual buoy (at 33.7° S, 18.2° E), time series of daily chlorophyll, Qh, and wind were obtained. Spatial structure was studied for the period 17–19 January 2018 via Hycom3 SST, salinity, meridional (V) currents, ERA5 reanalysis wind, surface air pressure, multi-satellite chlorophyll, and Hysplit back-trajectories of low-level winds.

Our calculations focused on meridional wind stress Ʈ_y = C_d ρ_a V₁₀², with drag coefficient C_d = 2.8–0.6 10⁻³ due to roughness, air density ρ_a = 1.18 kg m⁻³, and 10 m meridional wind speed V₁₀² from ERA5. An important empirical derivation that quantifies how C_d varies with kinematic and thermal roughness (cf. [36]) is the sum of normalized values of ERA5 V wind, W3 wave height, and Hycom3 Qh to describe steep gradients in air–sea momentum transfer every 25 km along the 33.7° S section. Negative Qh over upwelling implies small vertical gusts and limited drag that decouples air–sea momentum transfer. Offshore Ekman transport in the wind-mixed layer (~30 m depth along 33.7° S) was calculated as Ʈ_y/f ρ_w, namely meridional wind stress divided by Coriolis and seawater density. The curl-induced uplift was derived from [15,22]: ∂/∂x(Ʈ_y/f ρ_w) − ∂/∂y(Ʈ_x/f ρ_w), namely the relative vorticity of wind stress components divided by f and ρ_w (0.083) with units ~10⁻⁷ N/m³. As the mean winds are from 180° north of Cape Town, the second term offers little contribution. The divergence of Ekman transport becomes the main driver of uplift and entrainment.

The calculation of December–February averages in the period 2010–2024 subsumed infrequent spells of poleward airflow and downwelling (~10% occurrence). Therefore, to focus on active upwelling in January 2018, the transport and entrainment calculations employed daily values of V wind, MLD, SST, Qh, and C_d. The cross-shelf circulation (0–200 m depth) during active upwelling was represented by Hycom3 with empirically formulated C_d. Inertial oscillations (with ~24 hr period at this latitude) were studied by calculating the mean diurnal cycle from ERA5 hourly wind velocity, Qh, and surface air pressure data for 2010–2024. Underpinning these methods were dense ship, buoy, and coastal observations, as well as multi-satellite measurements of sea height, surface temperature, and wind waves to the north of Cape Town, as identified by the World Meteorological Organization: https://space.oscar.wmo.int/gapanalyses?variable=112; https://space.oscar.wmo.int/gapanalyses?variable=134 (accessed on 17 November 2025).

3. Results

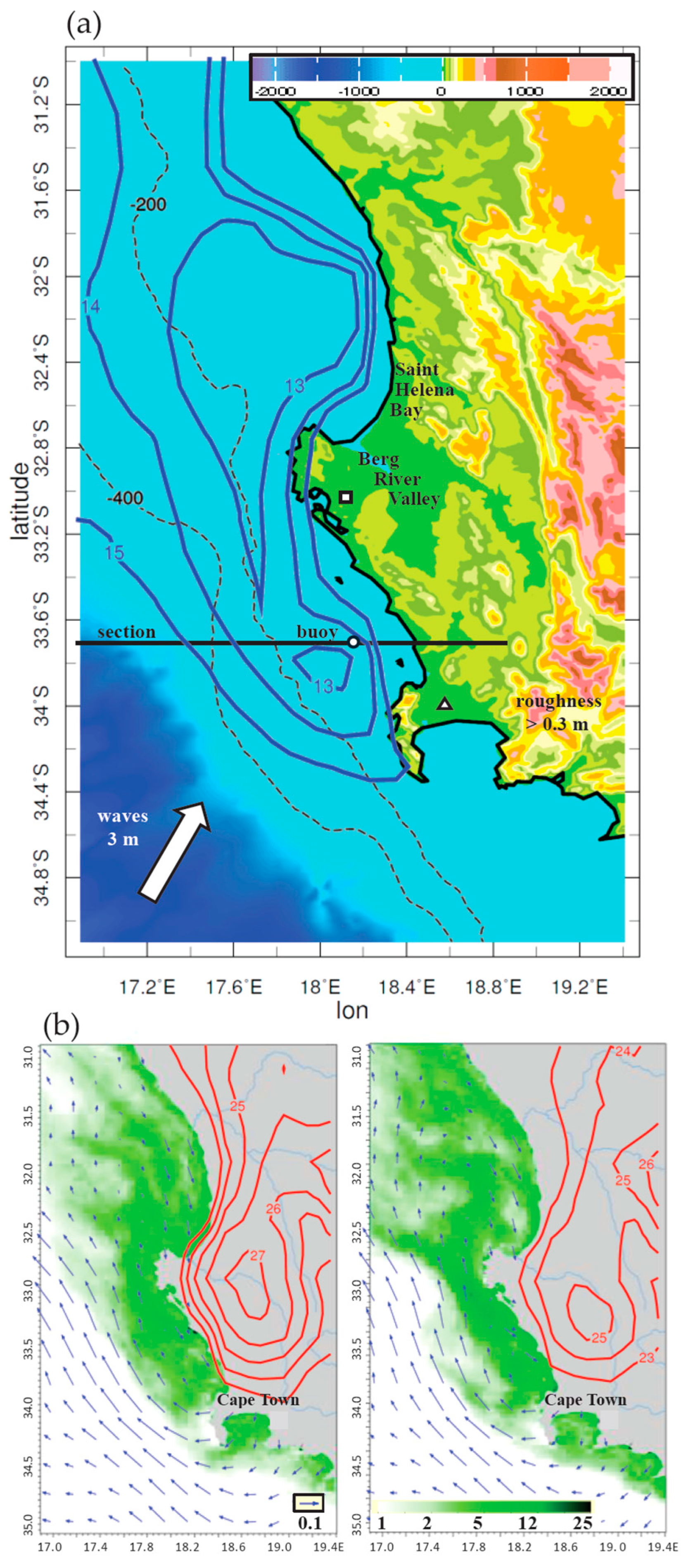
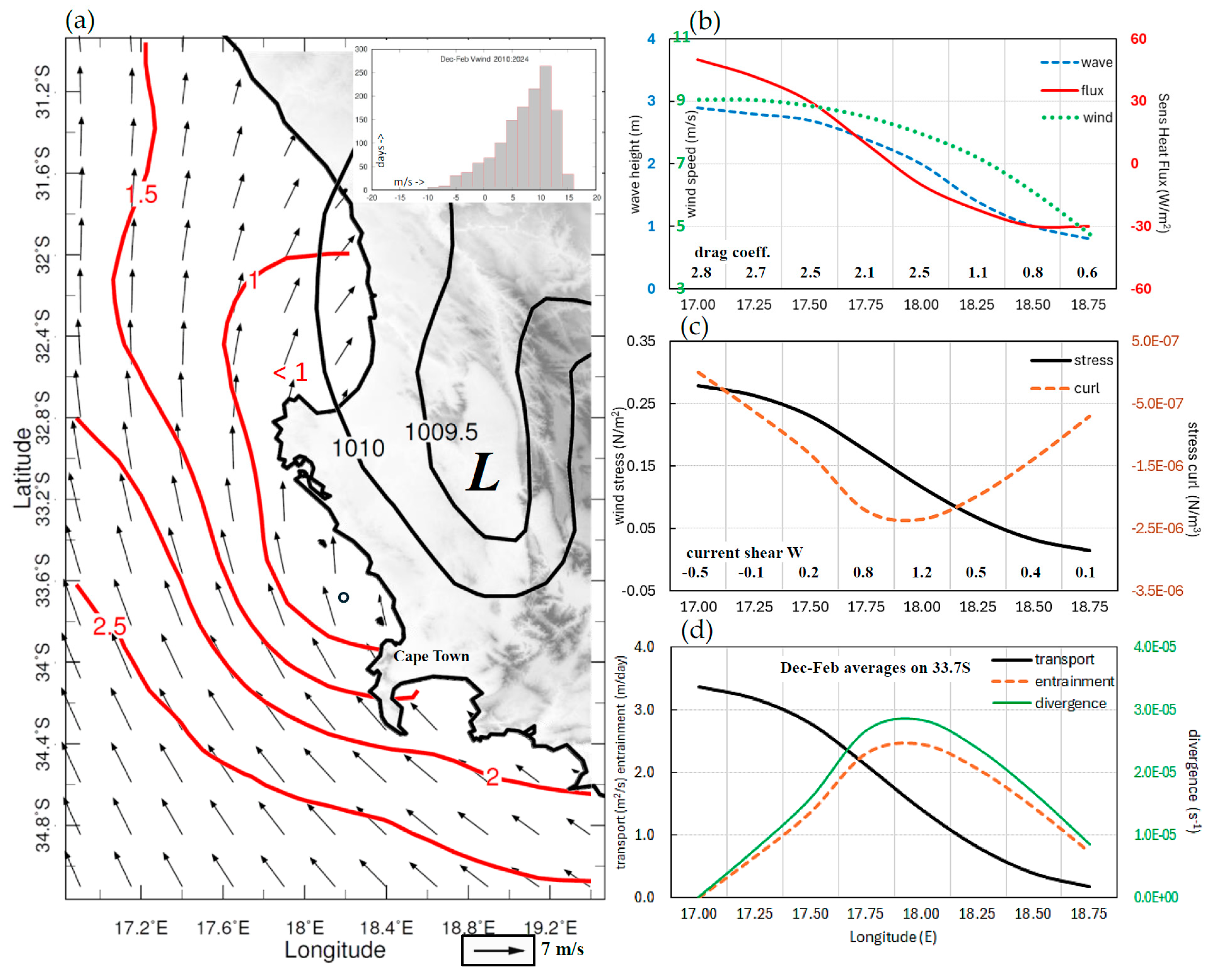
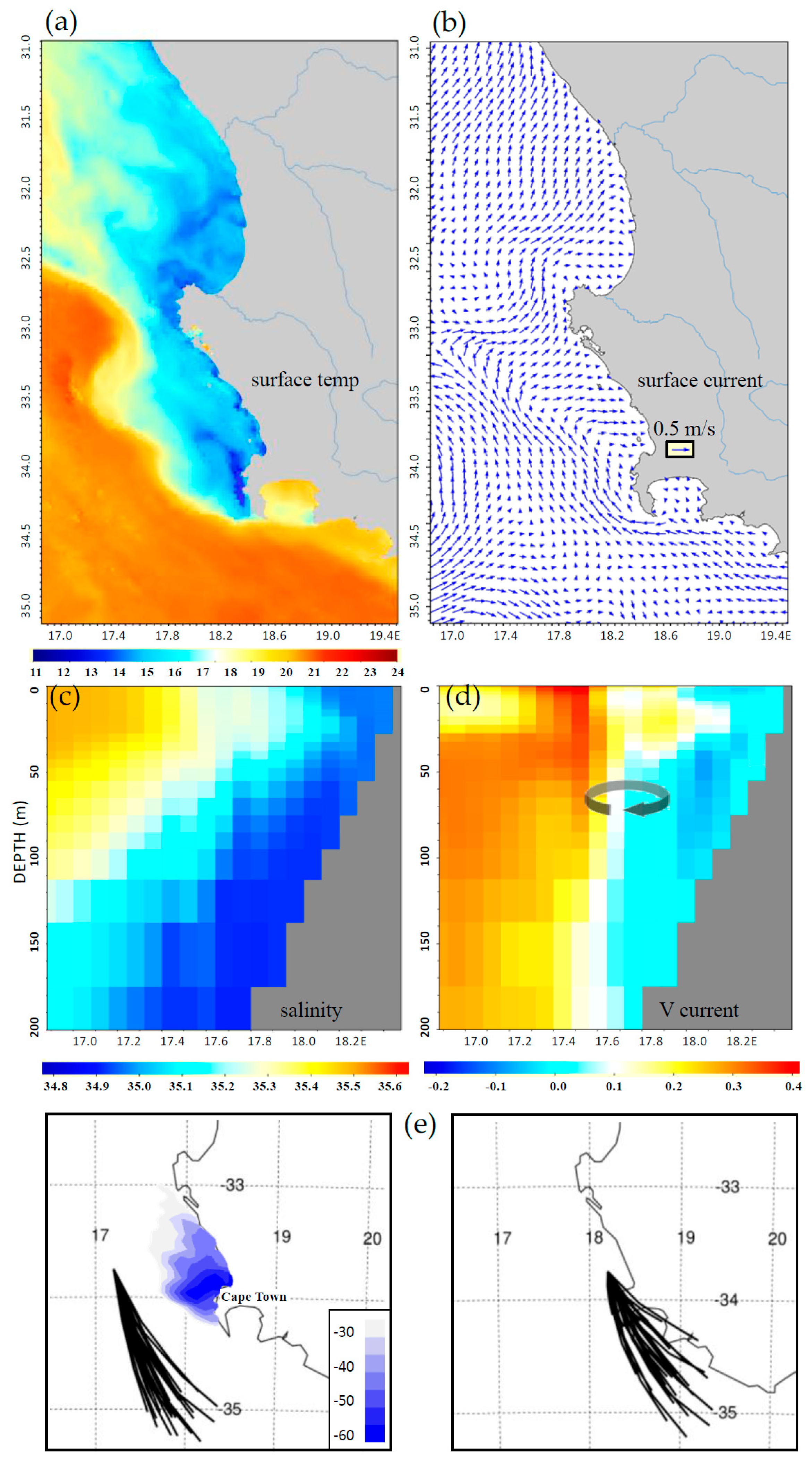
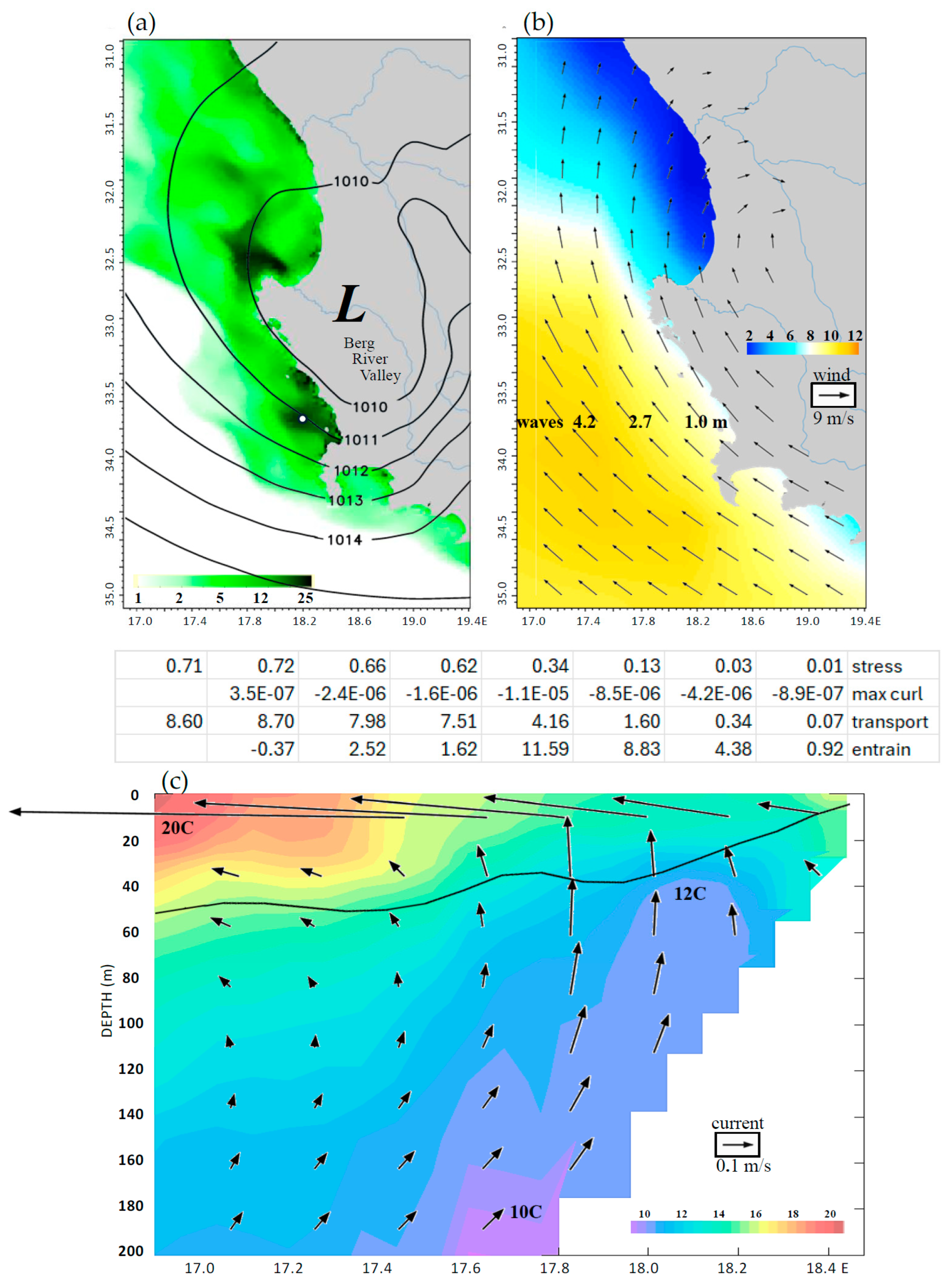
3.1. Summer Averages

Spatial context is provided in Figure 1a,b and Figure 2a. As can be seen, there is a convex NW–SE coast with the shelf edge ~100 km offshore. The northern interior comprises the low-lying Berg River Valley. There is a range of mountains > 1000 m along 19.4° E, and three capes protrude at 34.4° S, 34.1° S, and 32.9° S. Mid-latitude storms spawn 3 m waves that sweep in from ~210°. A plume of cool seawater < 14 °C spreads equatorward along the 200 m isobath (17.8° E). Inshore temperatures of ~16 °C suggest that upwelling is sluggish along the leeward coast to the north of Cape Town. Northwestward currents of 0.3 m/s along the shelf edge at 17.6° E contrast with weak flow that turns cyclonically toward the coast near 18.4° E, making a return current. The marine anticyclone generates December–February average surface winds of ~9 m/s with a depth of ~1 km, which promotes upstream channeling. A leeside thermal low develops over the Berg River Valley, and moderate winds along the coast to the north of Cape Town enable phytoplankton blooms, reflected in chlorophyll concentrations > 3 mg/m³. The V wind histogram (upper right, Figure 2a) exhibits a skewed distribution with 10 m/s southerlies most frequent during austral summer at the virtual buoy. Northerlies (−V) occur only 10% of the time in December–February, while +V > 7 m/s prevails ~2/3 of the time. Spring and autumn seasons (not shown) reflect moderate southerlies (~5 m/s), while winter has a Gaussian distribution with similar proportions of equatorward and poleward airflow.

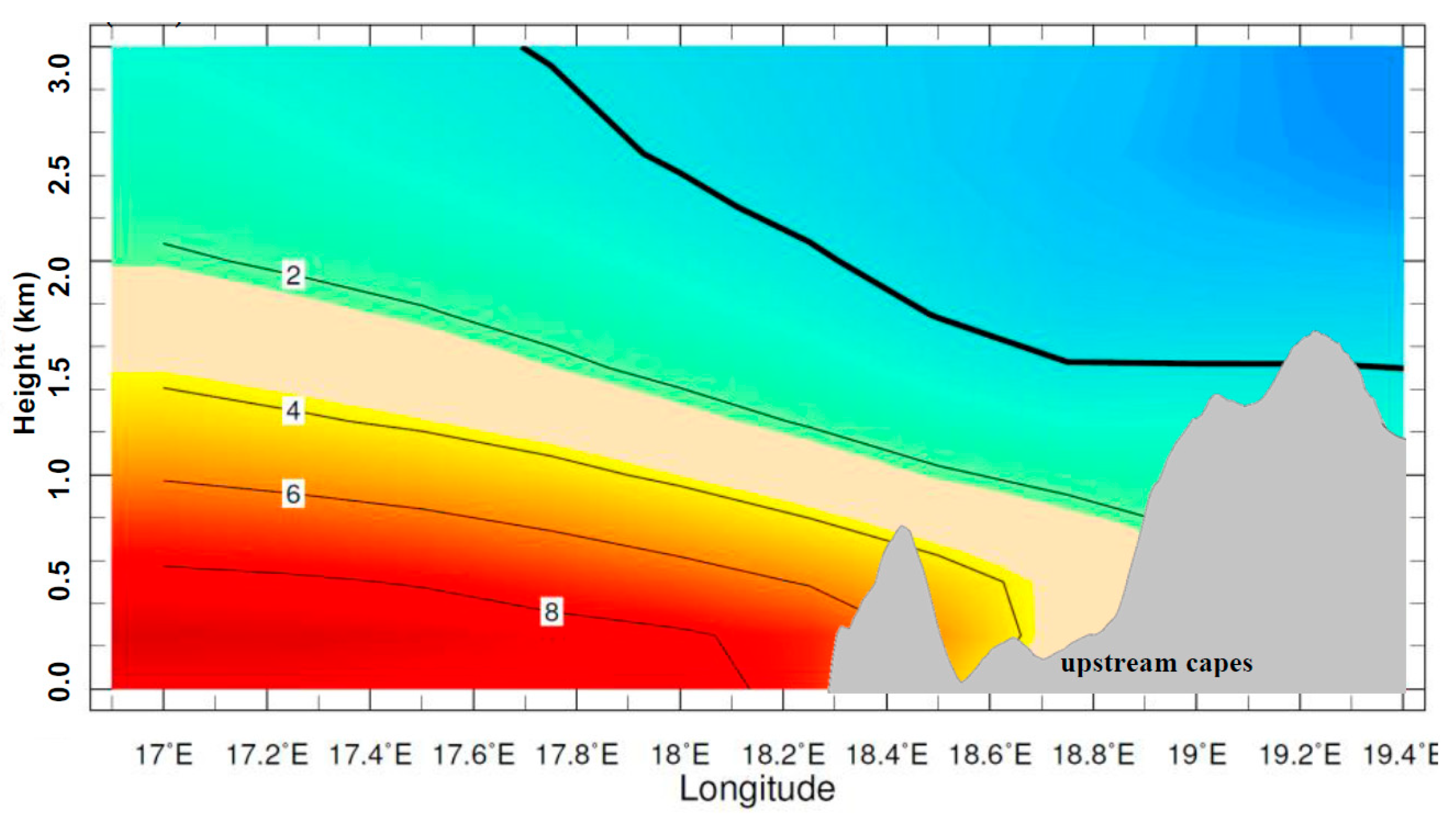
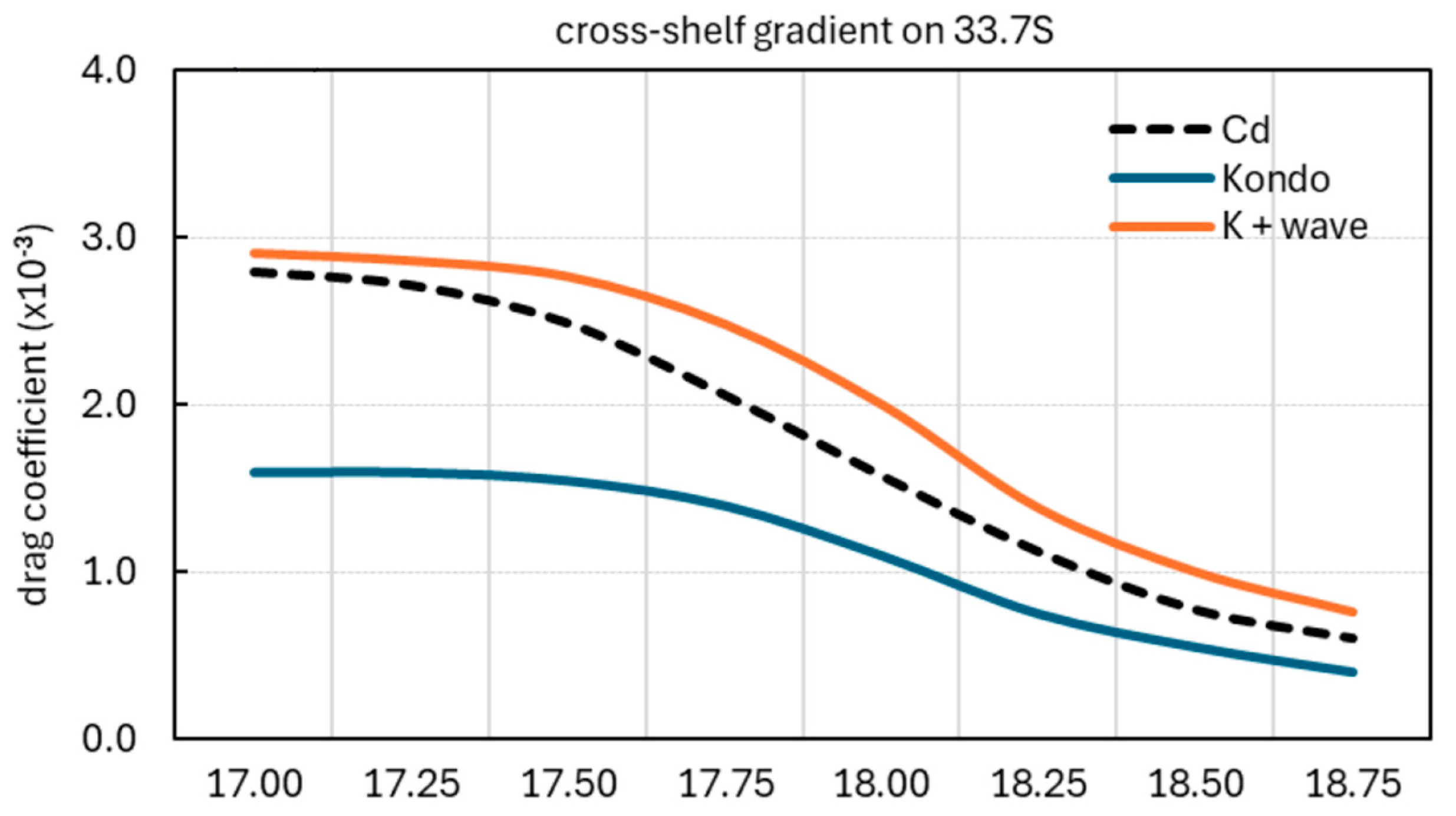
3.2. Cross-Shore Gradients

Focusing on cross-shelf gradients, data on wind, wave height, and Qh were used to estimate the drag coefficient, wind stress, curl (vorticity), Ekman transport, and entrainment (Figure 2b–d) along the section 33.7° S, from 16.9 to 18.7°E. From December to February, average wind speeds decrease shoreward from 9.1 to 4.5 m/s, wave heights from 2.9 to 0.8 m, and Qh from +50 W/m² to −30 W/m². Summing their standardized values as outlined above, the empirically derived drag coefficient (cf. [36]) diminishes from 2.8 to 0.6 × 10⁻³, decoupling wind stress from 0.27 to 0.02 N/m² at the coast. This affects offshore Ekman transport, which declines shoreward by 10-fold. Seawater mass divergence in the wind-mixed layer reaches a maximum ~50 km offshore (2.8 × 10⁻⁵ s⁻¹). The calculated austral summer average stress curl is most cyclonic at −2.4 × 10⁻⁶ N/m³ at 18° E, so vertical entrainment reaches 2.5 m/day in mid-shelf (200 m depth). The shoreward weakening of equatorward currents plays a supporting role, whereby cyclonic shear (∂V/∂x) induces uplift of ~1.2 m/day at 18° E. These values are significant [37] and depend on kinematic and thermal roughness effects on the drag coefficient and (consequently) the upper ocean. Inshore upwelling is much weaker at 0.6 m/day and is maintained less by mixed layer transport than by wind stress curl- and divergence-induced uplift. Decoupling of the longshore wind stress via negative Qh helps maintain higher SST and recirculating currents that favor phytoplankton blooms near the coast [37]. The steep shoreward decline of C_d would not apply during winter when onshore airflow, downwelling, and neutral Qh prevail. A constant air drag of ~1.5 × 10⁻³ [30] could be used to account for mechanical roughness from average winter wave heights of 3–4 m. Note that many of the curves in Figure 2b–d are derived from the drag coefficient’s influence on upwelling; this coefficient is a common denominator that instills circular dependencies.

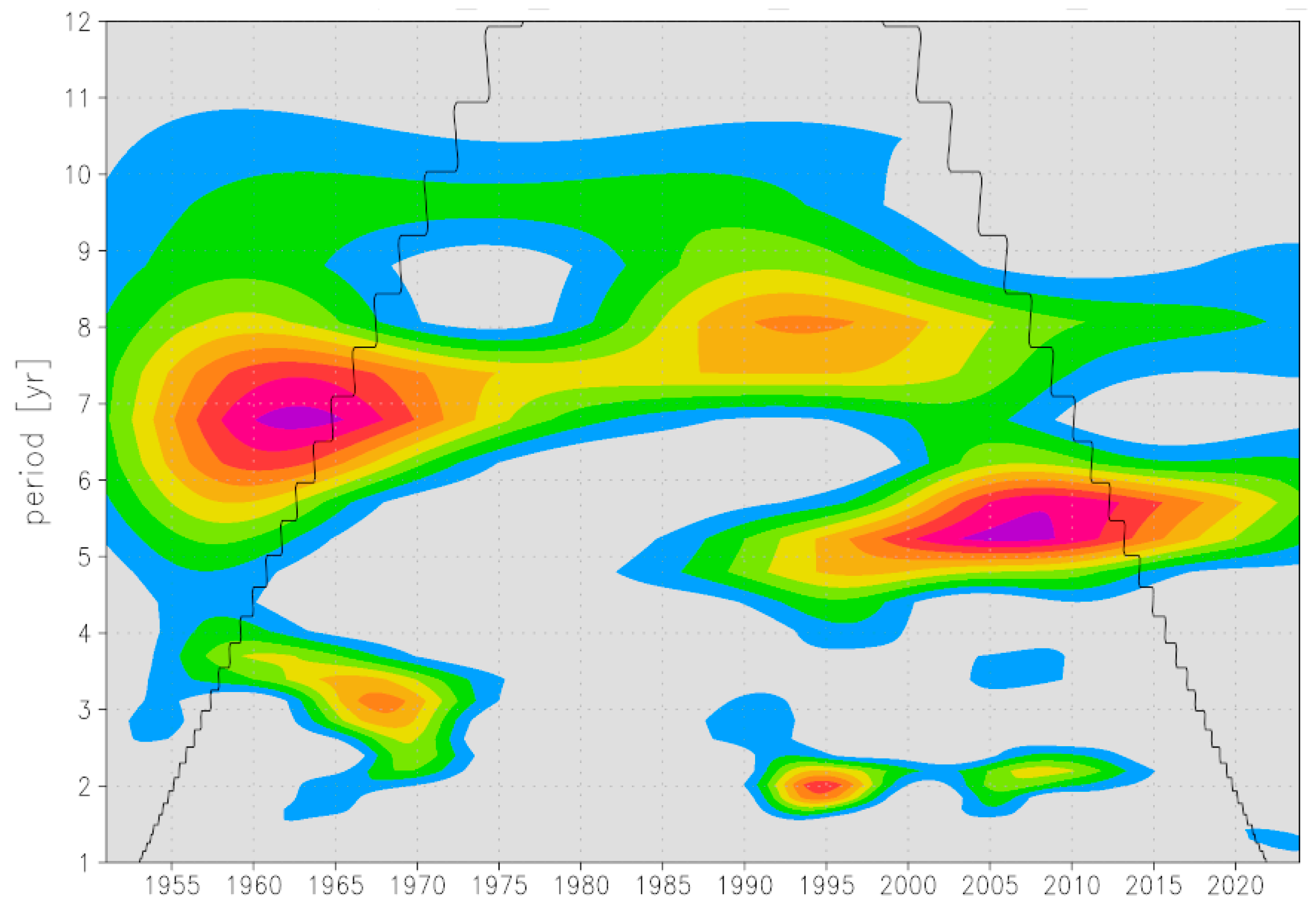
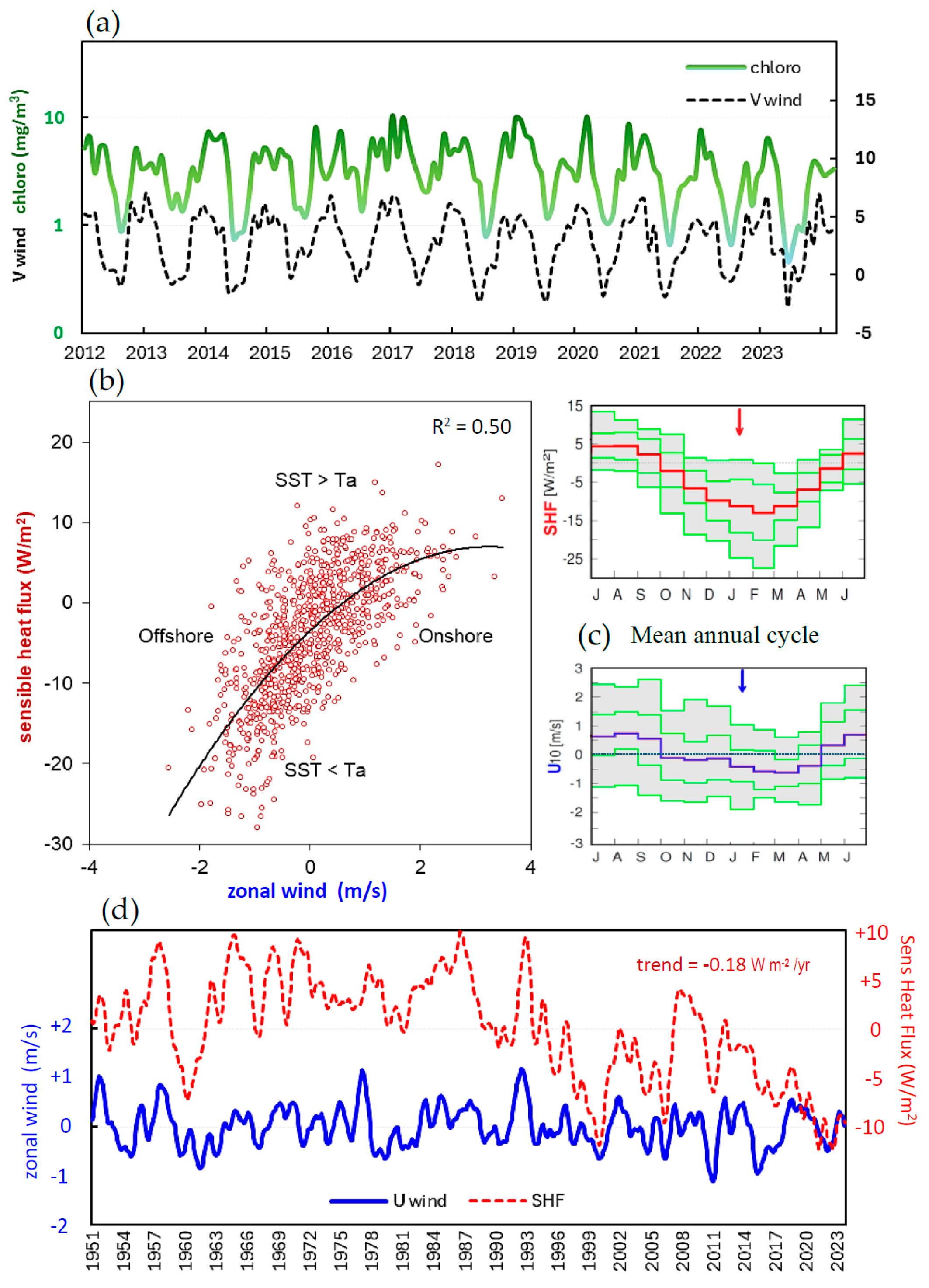
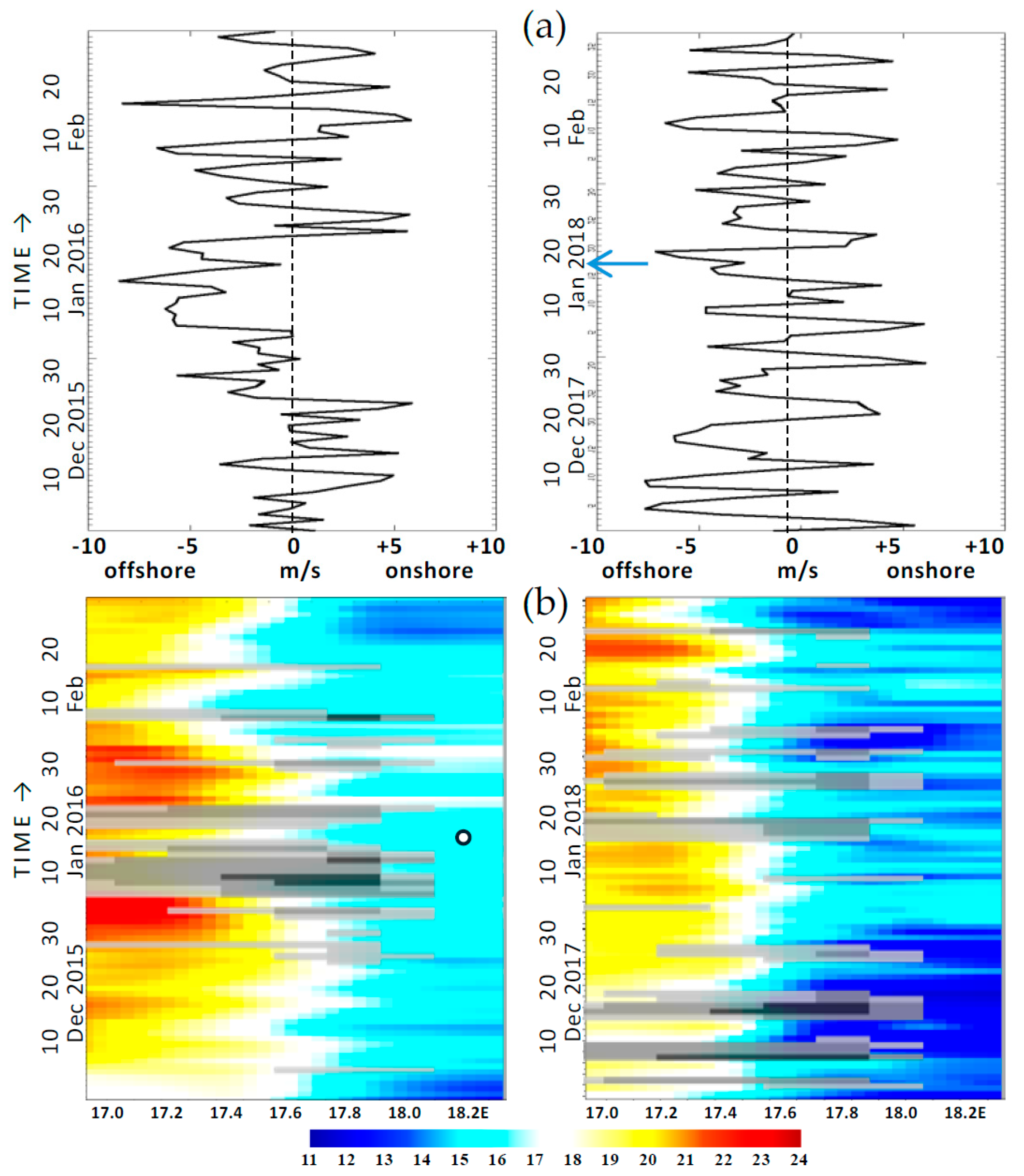
3.3. Temporal Characteristics

In this section, we explore monthly time series at the virtual buoy (33.7° S, 18.2° E). Figure 3a presents a graph of chlorophyll and meridional wind. These naturally share seasonal oscillations wherein a southerly wind (+V) drives upwelling and higher productivity a month later. A bimodal character prevails due to spring/autumn peaks between a summer plateau.

Figure 3b,c illustrate a positive correlation between zonal wind and Qh. Offshore winds (−U) advect warm air over cold water, leading to −Qh. The mean annual cycles suggest high amplitude for Qh, with most negative values in austral summer (December–March). Zonal winds stay close to zero: +2 m/s (from west) June–September and −2 m/s (from east) January–March. Of interest is the long-term filtered record (Figure 3d), which indicates the zonal (U) wind oscillates with Qh at a 5–8-year interval according to wavelet spectral analysis (cf. Appendix A). There is a significant downtrend of −0.18 Wm⁻²/year, which accounts for 38% of the variance, indicating that Ts is cooling faster than Ta.

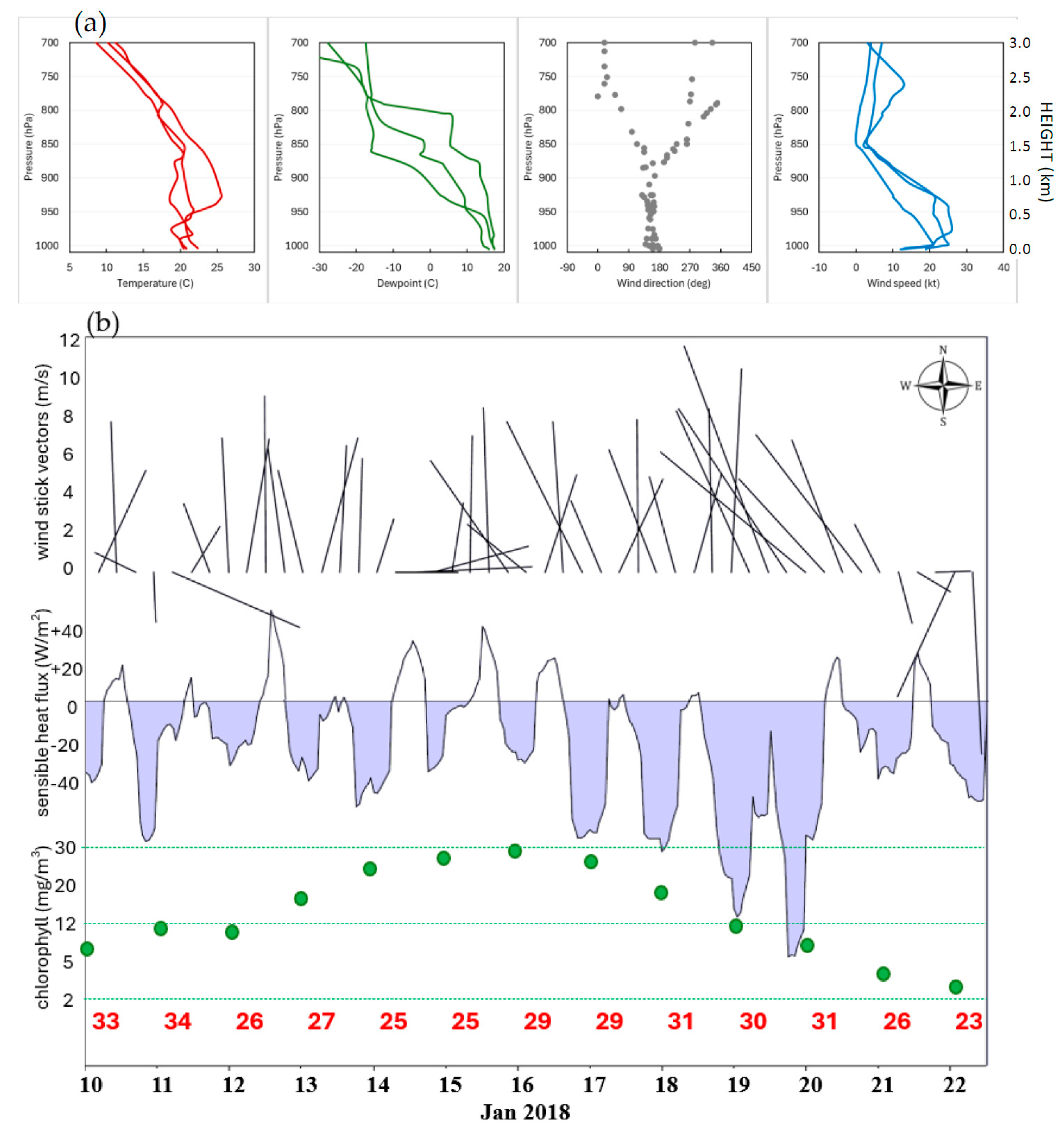
3.4. Case Study of January 2018

An analysis of active coastal upwelling was conducted, starting with the vertical atmospheric structure derived from Cape Town radiosonde profiles of 17–19 January (Figure 4a). Subtropical anticyclonic weather is evident in (i) near-constant air temperatures (1000–850 hPa), (ii) dry air aloft, (iii) 160° winds below 900 hPa, and (iv) a low-level jet > 20 kt from 975 to 925 hPa. Virtual buoy time series (Figure 4b) illustrates diurnal surges of southerly wind from 12 to 20 January. The Qh shows nocturnal dips under land breeze, with minimum values trending −90 W/m² from 17 to 20 January, as inland air temperatures exceeded 30 °C. Chlorophyll concentrations (a proxy for productivity) at the virtual buoy crested above 10 mg/m³ from 14 to 18 January. The wind sticks exhibit counterclockwise (inertial) rotation, as expected from sea breezes forcing near the Coriolis frequency.

Maps of multi-satellite SST and Hycom3 surface currents on 18 January 2018 are presented in Figure 5a,b. Coastal upwelling plumes emanate from the capes at 34.1° S and 32.9° S. The cold seawater (<13 °C) diffuses northward alongside warm waters (>22 °C) from the Agulhas Retroflection. Inshore temperatures remain near 15 °C. Surface currents are northwestward at ~0.4 m/s along the shelf edge but turn shoreward and weaken to 0.1 m/s north of Cape Town. Depth sections on 33.7° S of Hycom3 salinity and meridional currents are presented in Figure 5c,d. Salinity is a ‘tracer’ of coastal upwelling and shows a wedge of fresh water (<34.9 ppt) climbing up the shelf. V currents below the wind-mixed layer on 18 January are equatorward (+0.3 m/s offshore) and poleward (−0.1 m/s inshore) and generate cyclonic shear over the shelf. The reversal of flow nearshore is a regular feature (not an infrequent undercurrent). Back-trajectories of airflow arriving at the shelf edge and inshore on 18 January 2018 are presented in Figure 5e. Shelf-edge airflow remains over warm water, whereas inshore airflow passes over upstream capes that channel the longshore wind and impose diurnal cycling. This segregation may assure steep cross-shore gradients; however, both trajectories have similar lengths due to venturi acceleration. Contrasts derive from the impact of fetch: leeward of the capes, locally generated wind waves are absent, and Qh is markedly negative (Figure 5e); thus, air–sea interactions are decoupled to the north of Cape Town, and the lower atmosphere adjusts downstream as winds turn shoreward.

This case exhibited high chlorophyll concentrations inside the upwelling plumes (Figure 6a), which may relate to the surface air pressure gradient. The thermal low over the Berg River Valley spread seaward (Figure 6b) and guided longshore winds in a broad cyclonic arc. Simultaneously, there were sharp gradients in wave height from 4.2 to 1.0 m. Negative Qh values caused a steep shoreward decline of air drag and wind stress, resulting in cyclonic curl. Many of these features are captured by analyzing peak daily values during January 2018 (Figure 6c). The listing of cross-shore gradients reveals shoreward declines in stress (0.71–0.01 N/m²) and transport (8.7–0.07 m²/s) and mid-shelf maxima (17.8° E) in cyclonic curl (−1.1 × 10⁻⁵ N/m³) and vertical entrainment (11.6 m/day). The depth section on 33.7° S reflects 10–12 °C water climbing up the shelf at 17.8–18.0° E and accelerating offshore transport within the mixed layer occupied by warm waters and stormy seas at 16.9–17.3° E. The upwelling circulation (Figure 6c) is weakened by air–sea decoupling shoreward of 18°E, and offshore transport and vertical entrainment become subdued.

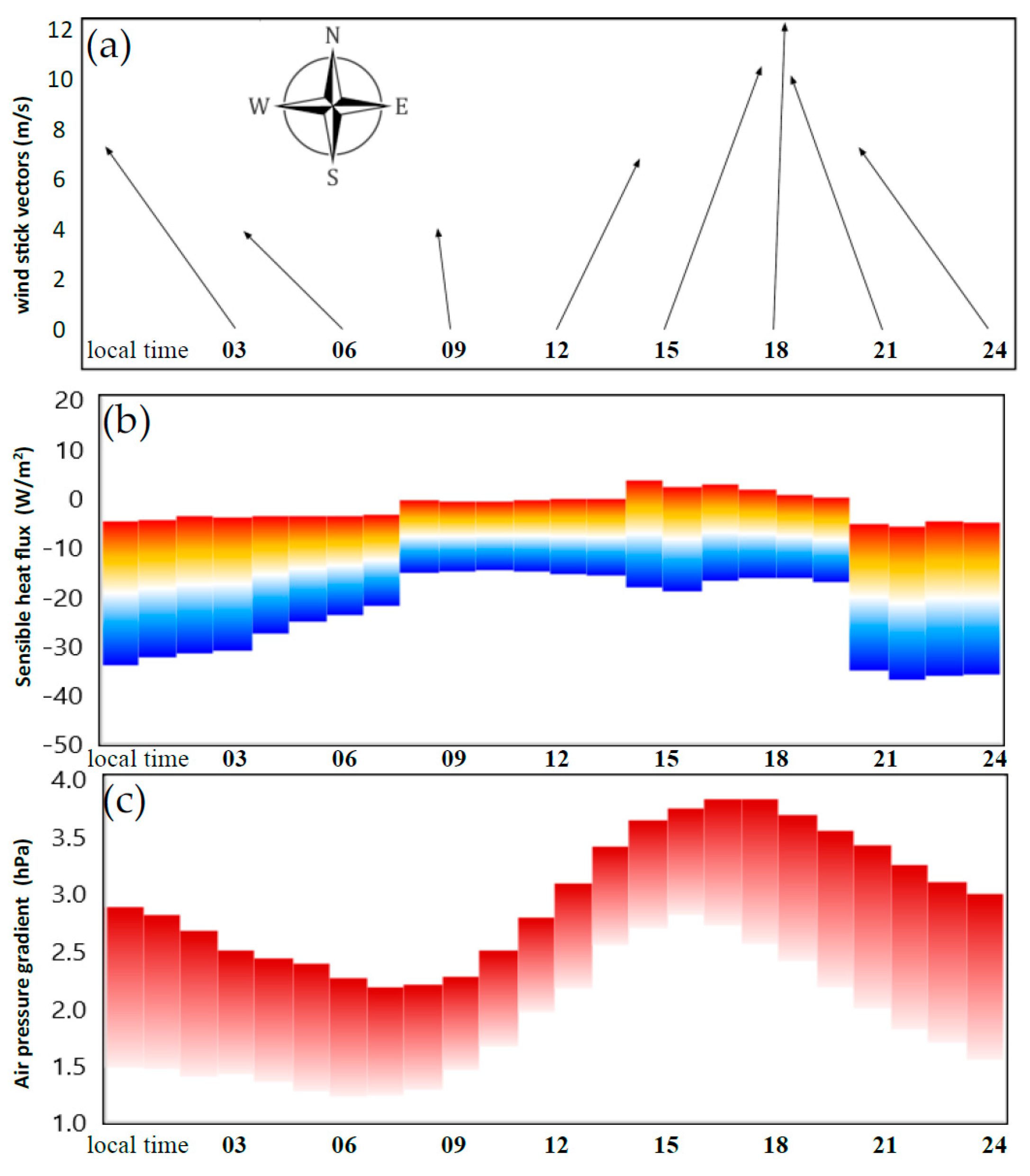
3.5. Variability and Diurnal Cycle

Summer southeasterly winds are known to segregate rough offshore and smooth inshore conditions, but weather pulsing could dissolve these contrasts. The daily U wind time series and Hovmoller plots of SST and V wind (Figure 7a,b) over the summers of 2016 and 2018 were evaluated. Spells of U < −5 m/s and V wind > 12 m/s pulse the coastal upwelling SST < 14 °C, yet the warm boundary SST ~ 20 °C remains at 17.4° E. In Jan 2016, there was a lengthy spell of southeasterly wind and moderate upwelling, while December–February 2018 saw frequent −U + V wind pulsing and SST < 12 °C. Although weather-induced fluctuations advect kinematic and thermal roughness back and forth across the shelf, the gradient remains steady.

The case study found inertial oscillations at the virtual buoy, which warrant analysis of the mean diurnal cycle in austral summer. Figure 8a illustrates that southeasterly winds weaken to 4 m/s and rotate offshore in the morning (03:00–06:00) and strengthen to 12 m/s and rotate onshore in the afternoon (15:00–18:00) due to land–sea breeze forcing. The mean diurnal cycle of Qh (Figure 8b) changes from negative −20 W/m² at night to neutral −5 W/m² during the day with abrupt transitions at sunrise and sunset. Thus, the air–sea momentum transfer is decoupled inshore at night. Diurnal amplitude naturally tends to flatten seaward and grow landward. The mean diurnal cycle of the air pressure gradient between the virtual buoy and the Berg River Valley is analyzed in Figure 8c. Cooling inland near sunrise (03:00–06:00) relaxes ∂P/∂x and subdues coastal winds, while warming inland near sunset (15:00–18:00) intensifies ∂P/∂x and coastal winds; the gradient is 2 hPa/50 km. The leeside thermal low plays an important role in channeling the airflow and stabilizing the coastal atmosphere north of Cape Town via nocturnal winds that conspire with the inertial oscillation.

4. Discussion

The results of this study provide insights into the interaction between atmospheric, oceanic, and biological processes along the southern African coast north of Cape Town. These findings complement a growing body of research that has sought to understand the mechanisms driving coastal upwelling, primary productivity, and fisheries dynamics in this region. Using observational and empirical methods, the study highlights the relationships between wind patterns, sea surface temperature (SST), and phytoplankton growth, with a focus on cross-shelf gradients in wind stress that drive shelf-edge upwelling.

The spatial variability in oceanographic and atmospheric conditions, as presented in Figure 1 and Figure 2, supports earlier studies [38] that have noted the role of capes along the convex NW–SE coastline in forming distinct upwelling plumes driven by accelerated winds juxtaposed with shadow zones, as seen elsewhere [31]. The study also corroborates findings [37,39] that link summertime wind stress curl to vertical entrainment, shelf-edge upwelling, and phytoplankton blooms (CHL > 3 mg/m³).

The cross-shelf gradients (Figure 2) are generated by the shoreward decline of wind stress, wave height, and sensible heat flux (Qh), which decouple air–sea momentum transfer. The rapid decrease in kinematic and thermal ‘roughness’ concentrates upwelling near the shelf edge (cf. [36]) and promotes recirculating currents and moderate SST inshore, which support phytoplankton blooms and fishery yields [38].

The observed decoupling of wind stress at the coast, driven by negative Qh, provides an important refinement to previous models of upwelling dynamics. The effect of wind stress curl on vertical entrainment (~2.5 m/day at mid-shelf) is a notable contribution to understanding the physical mechanisms that govern summertime nutrient diffusion and the trophic cascade, consistent with [40].

The temporal analysis of chlorophyll and wind data (Figure 3) reveals an interesting biannual seasonality, which echoes [41]. Moving to shorter timescales, diurnal variations in wind and Qh (Figure 8a,b) elucidate the role of land–sea interactions in upwelling productivity. The offshore–onshore shift in the coastal wind jet by land–sea breezes stimulates inertial oscillations [42] and helps to link short-term fluctuations in coastal upwelling to phytoplankton blooms. The decoupling of air–sea momentum transfer during the nocturnal land breeze aligns with [31].

The case study of January 2018 provides a vivid example of how wind stress curl and associated upwelling dynamics induce phytoplankton blooms. High chlorophyll concentrations underlie a cyclonic atmospheric circulation that steepens SST gradients and encourages poleward currents inshore, as noted in [40]. The cyclonic circulation swirls around a thermal low over the Berg River Valley, which pulses upwelling and primary productivity on weekly timescales [41].

The results here contribute to our understanding of coastal upwelling dynamics along the southern African coast north of Cape Town, emphasizing the role of air–sea interactions in primary production. The findings are consistent with recent research on wind-driven upwelling systems and provide new insights into the temporal and spatial variability of coastal productivity. The interplay between atmospheric circulation, wind stress, and upwelling dynamics remains a critical area of study for understanding the underlying mechanisms that influence regional marine ecosystems and fisheries. Further work on long-term variability and the role of mesoscale atmospheric features will help refine models of coastal productivity and enhance our ability to predict changes in marine resources under future climate conditions.

5. Conclusions

Coastal upwelling to the north of Cape Town in austral summer becomes amplified by cyclonic shear in the shallow southeasterly winds. The downstream effects of mountainous capes (Figure A1) alter air–sea interactions through a rapid shoreward decline of summertime kinematic and thermal roughness: (i) wind speeds decrease from 9.1 to 4.5 m/s, (ii) wave heights diminish from 2.9 to 0.8 m, and (iii) Qh decreases from +50 W/m² (17.0° E) to −30 W/m² (18.5° E), producing an ‘inshore decoupling’. These factors result in a drag coefficient that declines from 2.8 to 0.6 × 10⁻³ (Figure A2), consistent with earlier studies [42]. Thermal stability in the lower atmosphere alters the effectiveness of equatorward wind stress, which declines from 0.27 to 0.02 N/m² inshore. The calculated offshore Ekman transport is 10× greater at the shelf edge than at the coast, promoting the inshore retention of phytoplankton. Many features exhibit maxima at 18° E: (i) divergence of offshore transport, (ii) wind stress curl of −2.4 × 10⁻⁶ N/m³, (iii) current shear, and (iv) vertical entrainment. Decoupling of longshore wind stress over the inner shelf generates cyclonic recirculation that lengthens the residence time for biological productivity. Note that the air drag coefficient would become homogeneous during winter because of stormy onshore winds and downwelling; in this study, we have focused on summer.

Marine climate change is evidenced by the −0.18 W m⁻²/year decline in Qh to the north of Cape Town since 1950, which is related to a poleward shift in the South Atlantic anticyclone. Wavelet spectra in the Qh time series (Figure A3) reveal 5–8-year cycles in addition to the trend. Shallow southeasterly winds support a leeside thermal low in the Berg River Valley, forcing the pressure gradient seaward and widening the wind shadow for marine productivity, as noted in the case of January 2018. Further work will consider cross-shore gradients along the south coast (34° S, 25° E), extend recent studies [43,44], and consider processes driving the slow decline of sensible heat flux.