Design and Efficiency Analysis of High Maneuvering Underwater Gliders for Kuroshio Observation
Abstract
1. Introduction
2. Materials and Methods
2.1. Methodology and Simulation Framework
2.1.1. OpenProp
2.1.2. Integrated LBM–Lagrangian LES Multiphysics Framework
2.2. Numerical Calculation
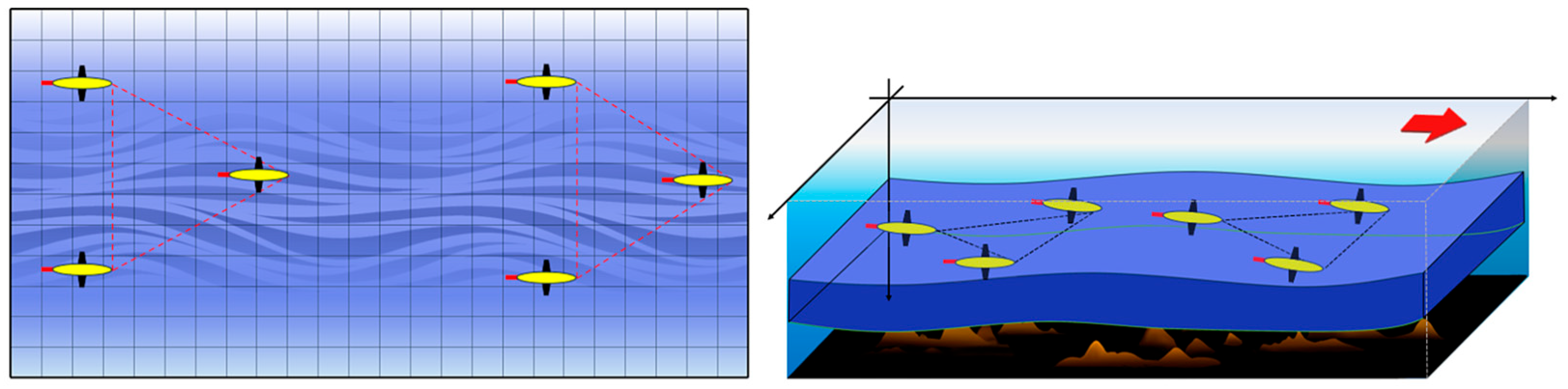
2.2.1. Application Scene
2.2.2. Establishment of Propeller Mechanical Model
2.2.3. Cavitation Initiation Analysis with Correlation Derivation
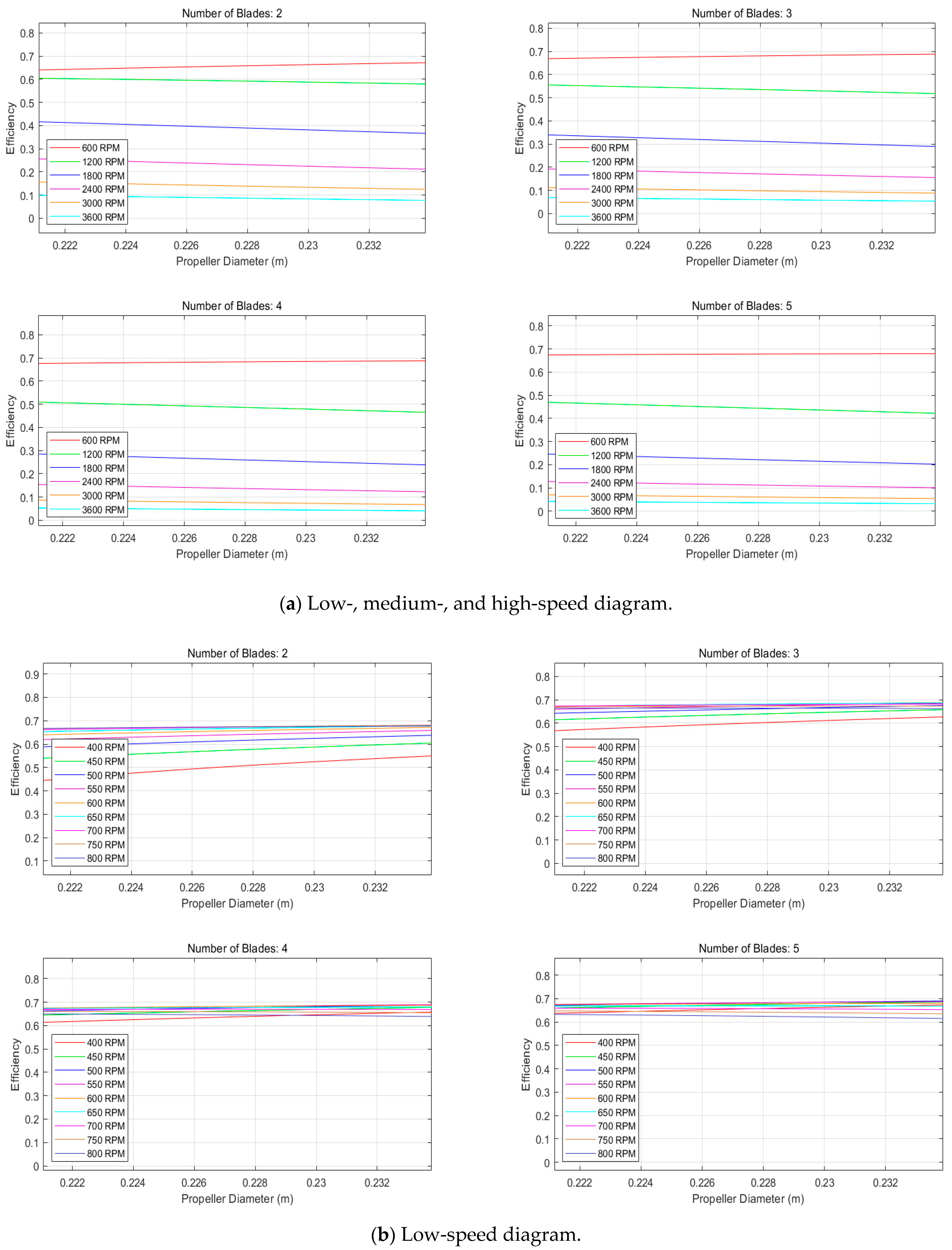
2.2.4. Screening and Optimization of Propeller Mechanical Geometric Parameters
3. Theory of Sound Field Solution
4. Simulation
4.1. Computational Simulation Environment Configuration
4.2. XFLOW Simulation
4.2.1. Simulation Parameter Setting
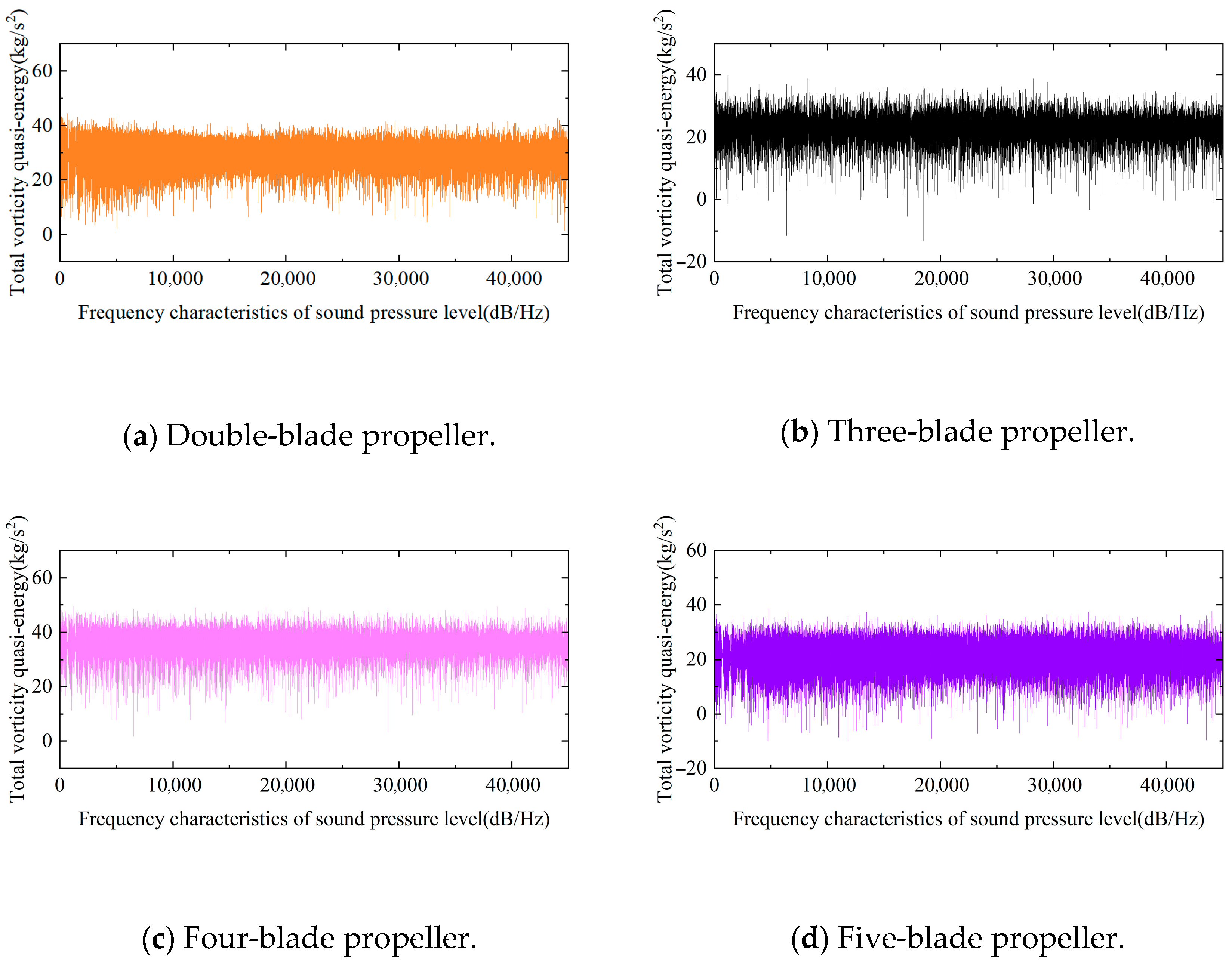
4.2.2. Numerical Results Analysis
4.3. Fluent Simulation
4.3.1. Meshing
4.3.2. Numerical Simulation
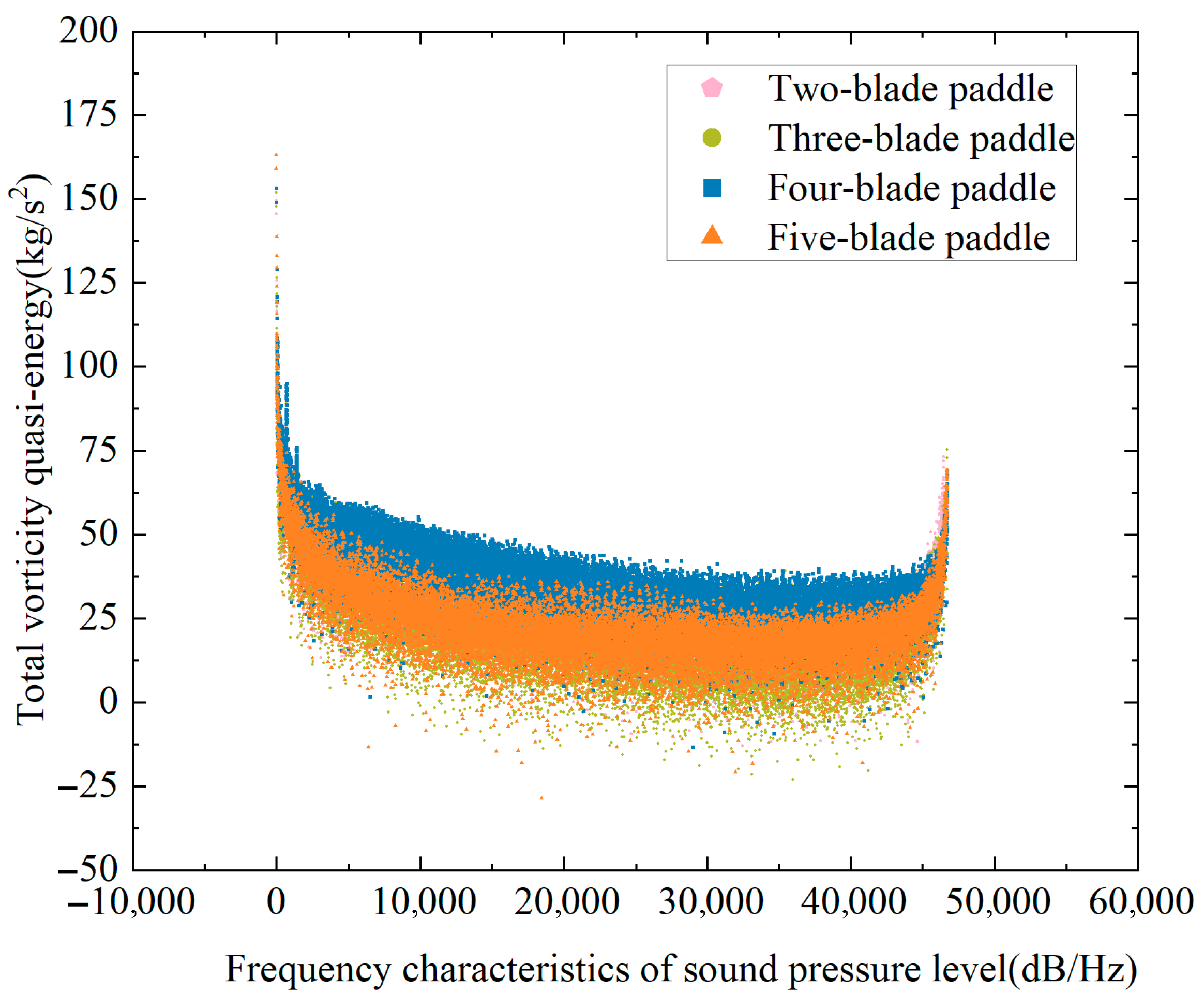
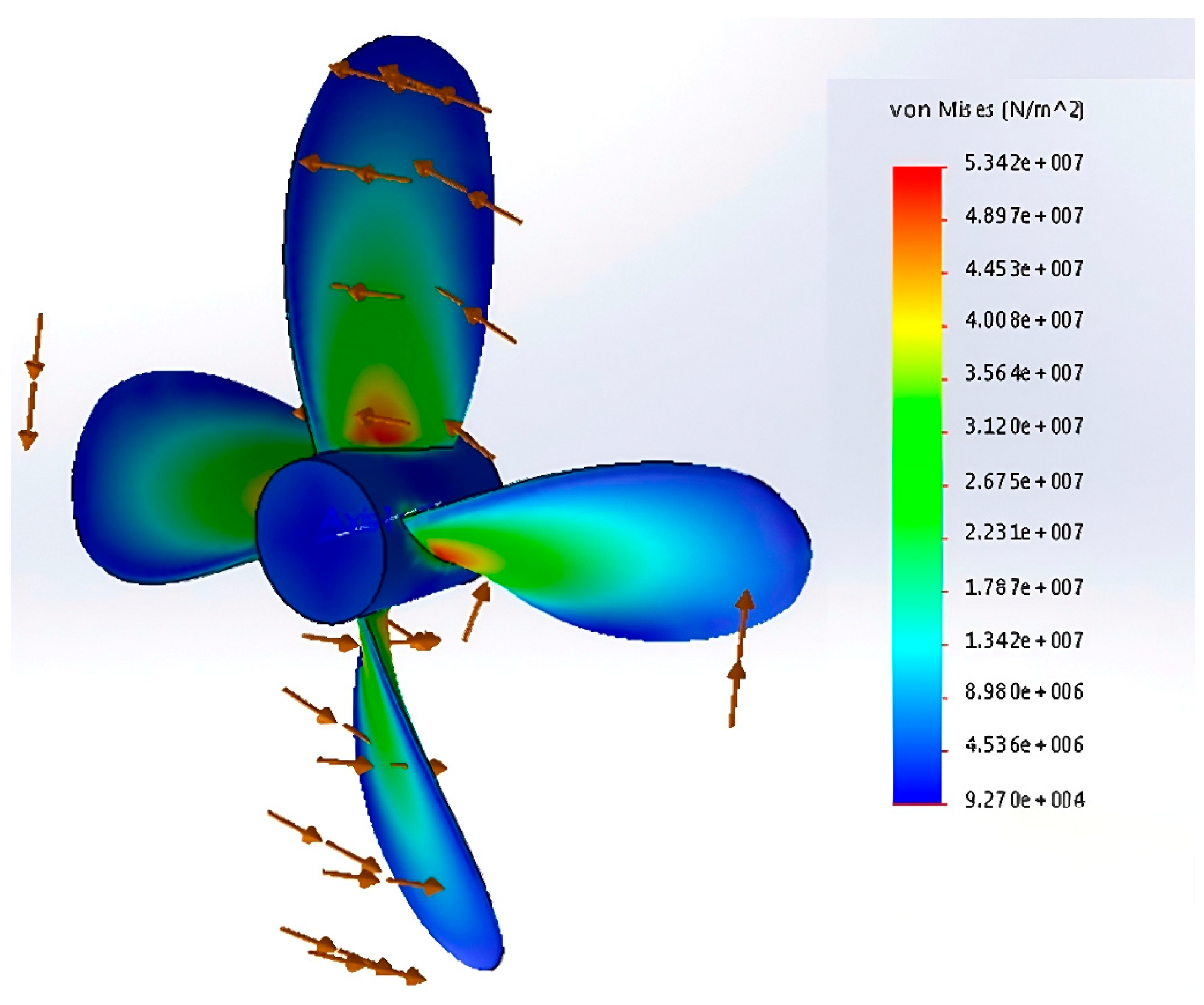
4.3.3. Analysis of Numerical Results
5. Test Verification
5.1. Test Object
5.2. Monitoring Equipment
5.3. Test Environment
5.4. Noise Evaluation Method
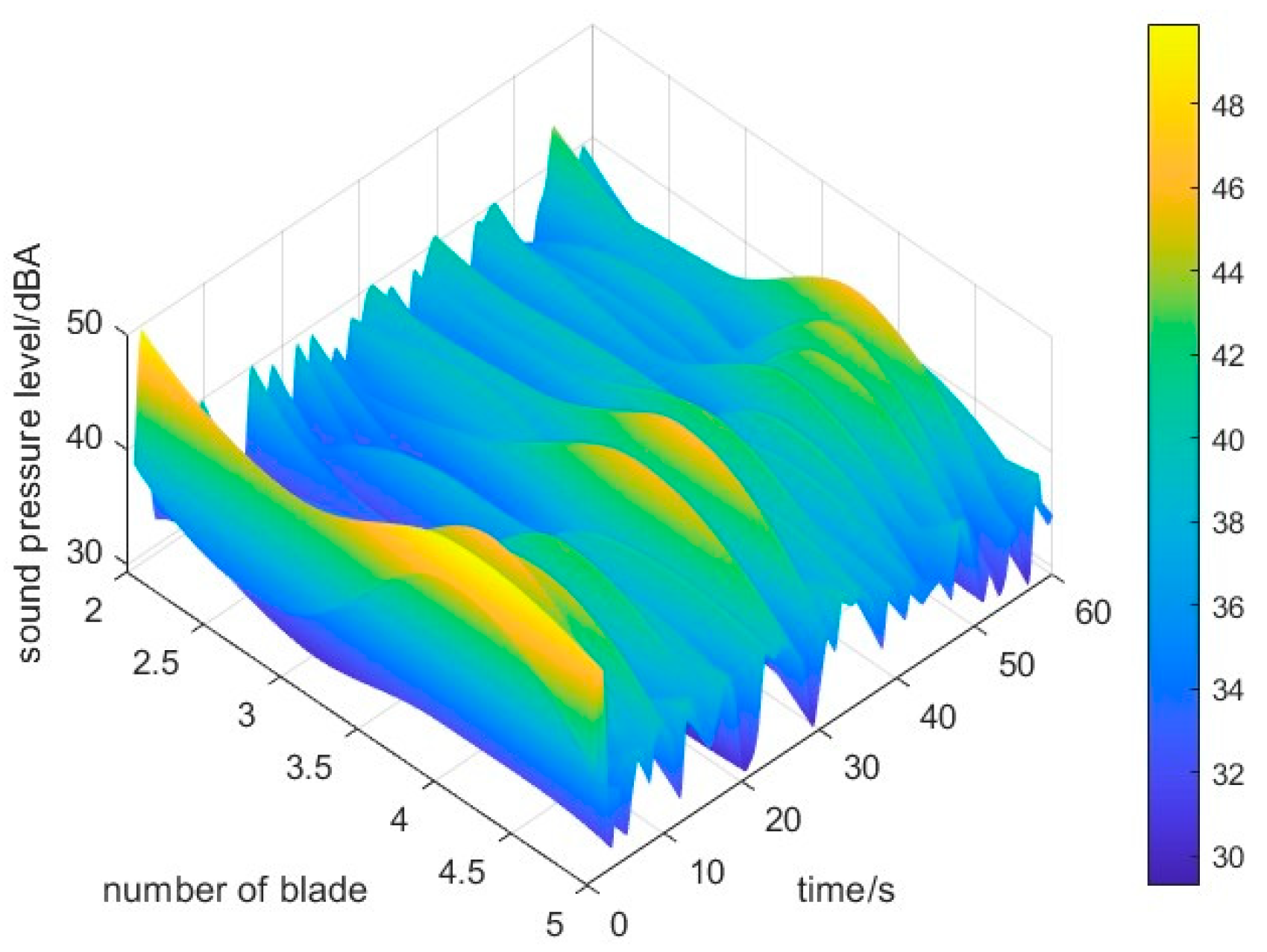
5.5. Test Results
5.6. Data Comparison
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, B.; Wang, J.; Zhang, R.; Wang, X.; Wan, X.; Yang, Y. Efficiency evaluation of underwater glider fleet based on Fuzzy-AHP-ADC model. Expert Syst. Appl. 2025, 271, 126685. [Google Scholar] [CrossRef]
- Ortolani, F.; Capone, A.; Dubbioso, G.; Pereira, F.A.; Maiocchi, A.; Di Felice, F. Propeller performance on a model ship in straight and steady drift motions from single blade loads and flow field measurements. Ocean Eng. 2020, 197, 106881. [Google Scholar] [CrossRef]
- Giulio, D.; Roberto, M.; Fabrizio, O.; Andrea, D.M. Numerical analysis of marine propellers low frequency noise during maneuvering. Part II: Passive and active noise control strategies. Appl. Ocean Res. 2022, 106, 102461. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, W.Z. Research on ground effect of ducted fans of VTOL UAVs. J. Unmanned Undersea Syst. 2023, 31, 942–948. [Google Scholar] [CrossRef]
- Zhang, Z.R.; Luo, K.; Qin, K. Design method for low specific speed axial flow pump for high-speed undersea vehicles. J. Unmanned Undersea Syst. 2024, 32, 130–138. [Google Scholar] [CrossRef]
- Zhao, X.Y.; Wu, T.L.; Lin, X.H.; Wu, J.G.; Zhang, M.G. Research on propeller cavitation suppression based on pump jet rectification mechanism. J. Unmanned Undersea Syst. 2022, 28, 410–419. [Google Scholar] [CrossRef]
- Cheng, H.Y.; Huang, J.L.; Han, C.Z.; Lei, T.T.; Ji, B. Investigation of the risk of cavitation erosion on propeller blade surface with different cavitation numbers. Eng. J. Wuhan Univ. 2023, 12, 1527–1535. [Google Scholar] [CrossRef]
- Tan, K.L.; Xie, W.; Liu, Z.Y.; Xie, X.C.; Wang, W.G.; Liu, Q. Research on the influence of propellers on ship maneuvering hydrodynamics under different speeds. Ocean Eng. 2024, 4, 141–149. [Google Scholar]
- Wen, X.F.; Cai, B.G.; Huang, J.X.; Zhou, R.P. Transient response of marine propulsion shafting during ship turning operation. Navig. China 2019, 42, 72–80. [Google Scholar]
- Wen, X.F.; Cai, B.G.; Wang, X.D. Dynamic simulation of ship propulsion shafting system under cyclic loading. Navig. China 2021, 44, 13–19. [Google Scholar]
- Zou, R.H.; Hu, W.J.; Wang, H.R. CFD Simulation of aerodynamic characteristics of ducted propeller and analysis of influence of structural parameters. Fluid Meas. Control 2024, 5, 7–10. [Google Scholar]
- Kim, N.; Kwon, J.H.; Kim, H.; Lee, D. Propeller blade structural reliability analysis considering mixed-mode fatigue crack growth. Eng. Fail. Anal. 2024, 158, 108014. [Google Scholar] [CrossRef]
- Cao, Q.; Wei, K.; Nie, Y.P.; Yan, Q.; Chen, Y.H. Aeroacoustic test system design and experimental research for counter-rotating propeller. Adv. Aeronaut. Sci. Eng. 2024, 15, 148–154. [Google Scholar] [CrossRef]
- Aram, S.; Mucha, P. CFD validation and analysis of turning maneuvers of a surface combatant in regular waves. Ocean Eng. 2024, 293, 116653. [Google Scholar] [CrossRef]
- Liu, Y.G.; Fu, W.A.; Wang, H.M.; Zeng, C.J. Research on abnormal monitoring of propeller vibration force during inspection of offshore wind turbine unmanned aerial vehicle. Autom. Instrum. 2024, 1, 93–97. [Google Scholar]
- Zheng, S.J.; Zhou, L.; Diao, F.; Ding, S.F.; Liu, R.F. Experimental study on hydrodynamic performance of two-way propeller in cavitation tunnel. J. Ship Mech. 2024, 28, 70–80. [Google Scholar] [CrossRef]
- Liu, K.; Liu, Y.Q.; Lin, H.; Xiao, J.H.; Peng, H.; Lu, X.J.; Lu, H.M. Research of trans-medium strategy for unmanned aerial-undersea vehicles. J. Unmanned Undersea Syst. 2024, 32, 396–410. [Google Scholar] [CrossRef]
- Zhou, J.; Ma, L.; Heng, H. Simulation Analysis of variable cross-section Linetype optimization for swim-out tube in UUVs. J. Unmanned Undersea Syst. 2024, 32, 147–151. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, G.L.; Guan, S.; Wang, Y.F.; Ding, J.H. Motion simulation of spatial sampling of mesoscale processes for underwater gliders. J. Unmanned Undersea Syst. 2022, 30, 474–484. [Google Scholar] [CrossRef]
- Zhang, H.W.; Wang, J.X. Fault-tolerant control of AUV thruster based on adaptive backstepping sliding mode. J. Unmanned Undersea Syst. 2021, 29, 420–427. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, X.P.; Wang, Q.; Luo, Z.N.; Wang, G.Q. Improved design of hovering efficiency of ducted propeller with large blade tip clearance based on grooved duct configuration. J. Aerosp. Power 2025, 150, 109226. [Google Scholar] [CrossRef]
- Zou, K.; Gui, M.H.; Lai, M.Y. Influence of appendages upon performance and propellers power imbalance analysis of a vessel with triple pods. Ship Ocean Eng. 2023, 6, 54–59. [Google Scholar] [CrossRef]
- Lu, D.S.; Sun, T.Z.; Zhang, G.Y. Numerical analysis of hydrodynamic characteristics of ducted propeller. Ship Boat 2023, 34, 102. [Google Scholar] [CrossRef]
- Pang, J.J.; Han, H. A calculation method of static balance of 3-blade propeller. CFHI Technol. 2023, 6, 47–51. [Google Scholar] [CrossRef]
- Oberai, A.A.; Roknaldin, F.; Hughes, T.J. Computation of trailing—Edge noise due to turbulent flow over an airfoil. AIAA J. 2002, 40, 2206–2216. [Google Scholar] [CrossRef]






| Variable Initialization | Parameter Value |
|---|---|
| Viscosity Model | k-ε SST Enhanced Wall Treatment (EWT) |
| Wall Boundary Formulations | |
| Flow Boundary Configuration | Pressure-Defined Flow Boundaries |
| Gauge Pressure Measurement | Standard Atmospheric Pressure |
| Pressure–Velocity Coupling Algorithm | Coupled |
| Pressure Gradient Resolution Scheme | Body Force Weighted |
| water flow velocity | 2 m/s |
| Ambient Temperature | 16 °C |
| Humidity Level | 60% |
| Two-Blade Propeller | Three-Blade Propeller | Four-Blade Propeller | Five-Blade Propeller | |
|---|---|---|---|---|
| XFLOW | 29.14 | 21.28 | 35.62 | 22.89 |
| FLUENT | 29.54 | 22.78 | 35.58 | 22.91 |
| Experiment | 36.23 | 34.85 | 39.01 | 35.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Z.; He, B.; Zhang, H.; Zhang, C.; Zhang, T.; Zhang, R. Design and Efficiency Analysis of High Maneuvering Underwater Gliders for Kuroshio Observation. Oceans 2025, 6, 48. https://doi.org/10.3390/oceans6030048
Tian Z, He B, Zhang H, Zhang C, Zhang T, Zhang R. Design and Efficiency Analysis of High Maneuvering Underwater Gliders for Kuroshio Observation. Oceans. 2025; 6(3):48. https://doi.org/10.3390/oceans6030048
Chicago/Turabian StyleTian, Zhihao, Bing He, Heng Zhang, Cunzhe Zhang, Tongrui Zhang, and Runfeng Zhang. 2025. "Design and Efficiency Analysis of High Maneuvering Underwater Gliders for Kuroshio Observation" Oceans 6, no. 3: 48. https://doi.org/10.3390/oceans6030048
APA StyleTian, Z., He, B., Zhang, H., Zhang, C., Zhang, T., & Zhang, R. (2025). Design and Efficiency Analysis of High Maneuvering Underwater Gliders for Kuroshio Observation. Oceans, 6(3), 48. https://doi.org/10.3390/oceans6030048







