Determination of Submerged Breakwater Efficiency Using Computational Fluid Dynamics
Abstract
1. Introduction
- Section 2.1 presents a detailed explanation of the ICFD method used for breakwater analysis, including a description of the theoretical background and its advantages over another method for solving fluid–structure interaction (FSI) problems, namely the ALE method.
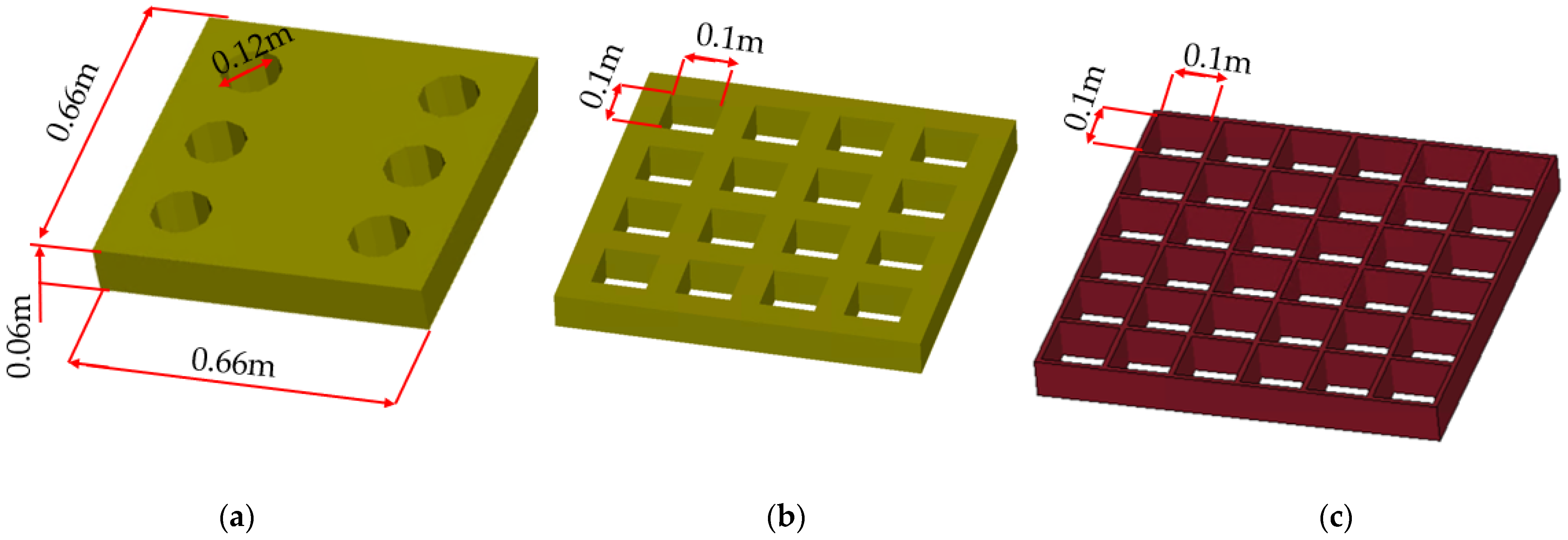
- Three possible topologies of breakwater systems with geometrical particulars are presented in Section 2.2.
- Section 3 details the numerical setup for assessing the most efficient topology, including comprehensive information about the mesh and boundary conditions of the breakwater system.
- Section 4 presents the results of both analyses, emphasising wave height reduction and drag estimation.
- The conclusion in Section 5 focuses on the findings obtained and points out the potential issues and/or limitations of the applied methods.
2. Material and Methods
2.1. ICFD
2.2. Breakwater Geometry
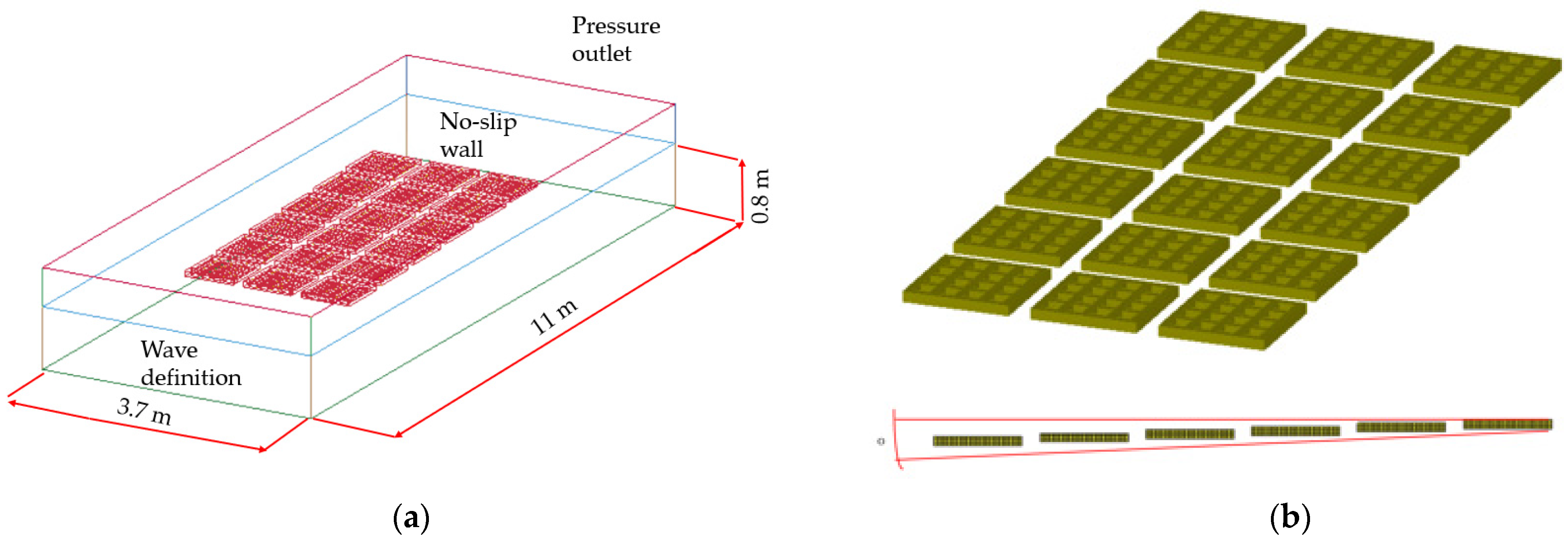
3. Numerical Setup
3.1. Mesh Particulars
3.2. Numerical Setup for Assessing Most Efficient Topology
3.3. Convergence Analysis
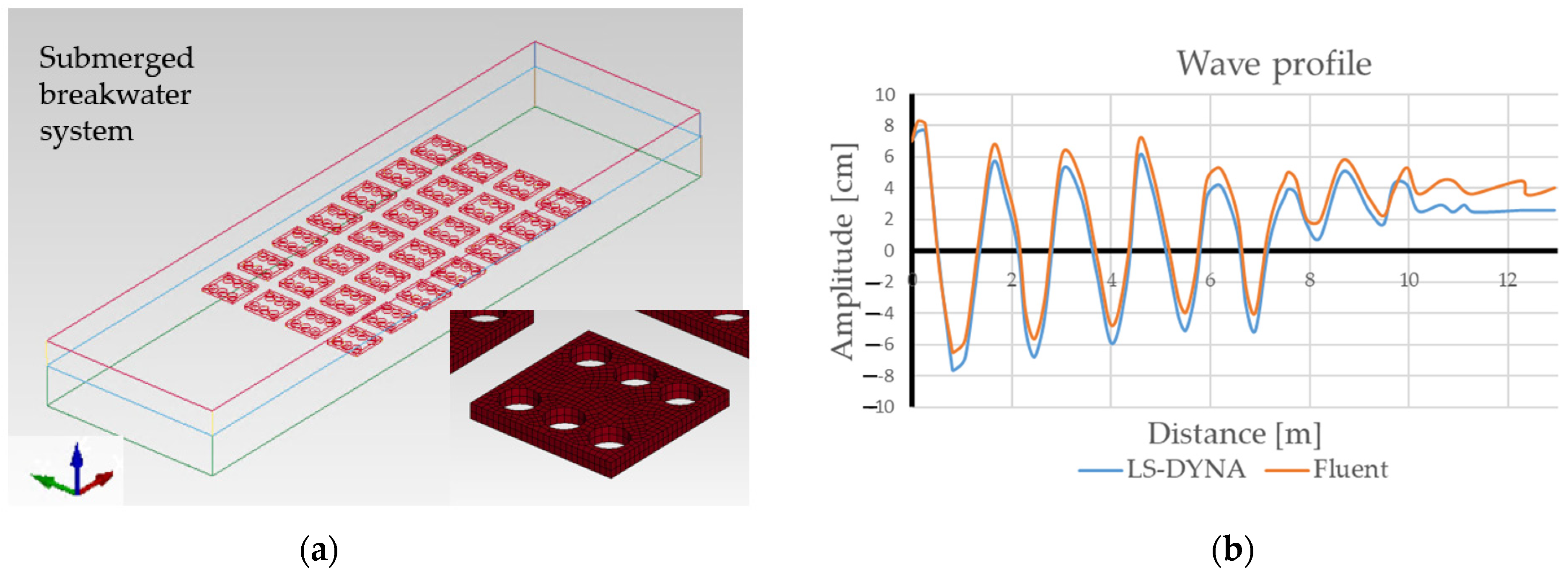
3.4. Numerical Setup for Submerged Breakwater System
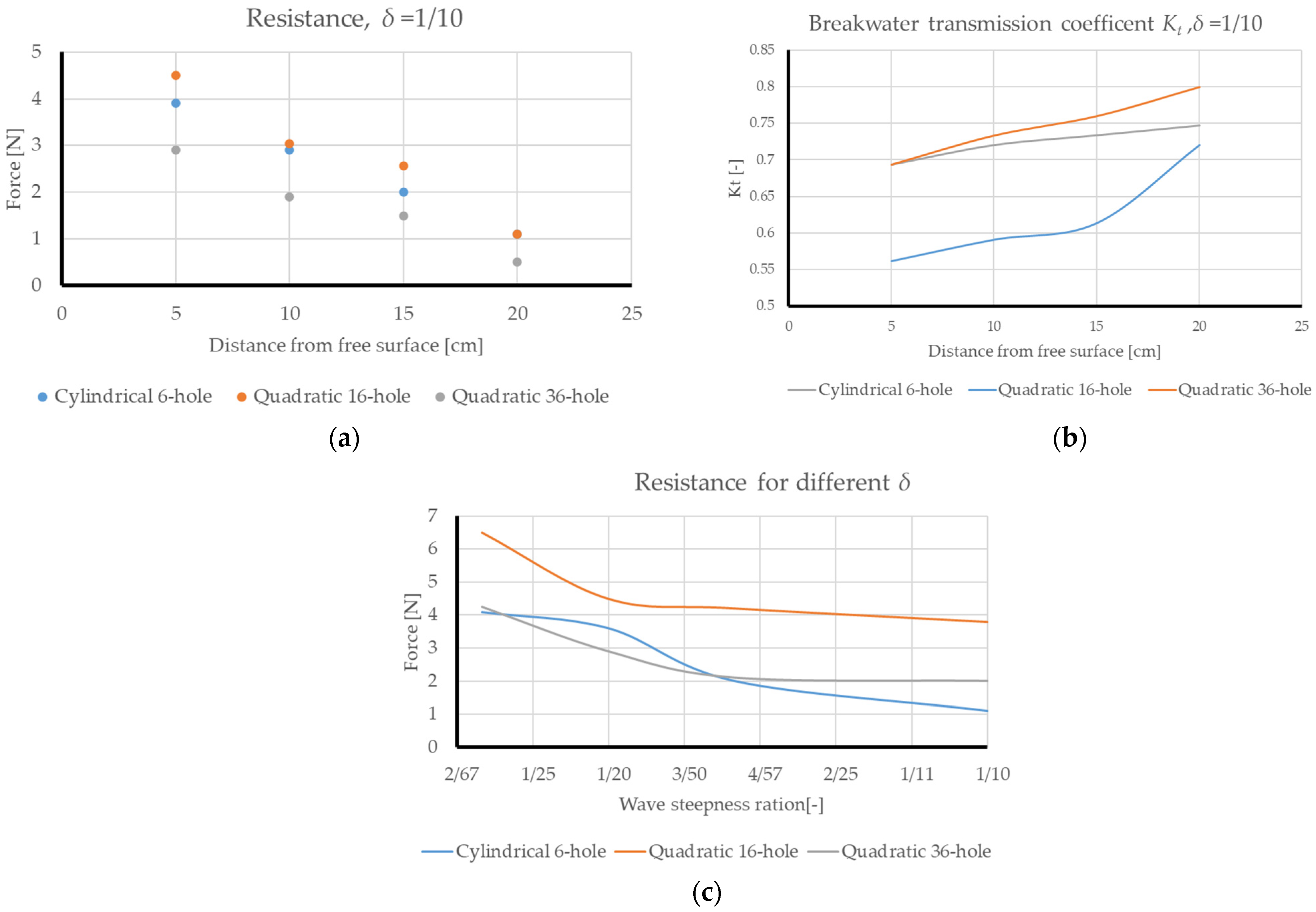
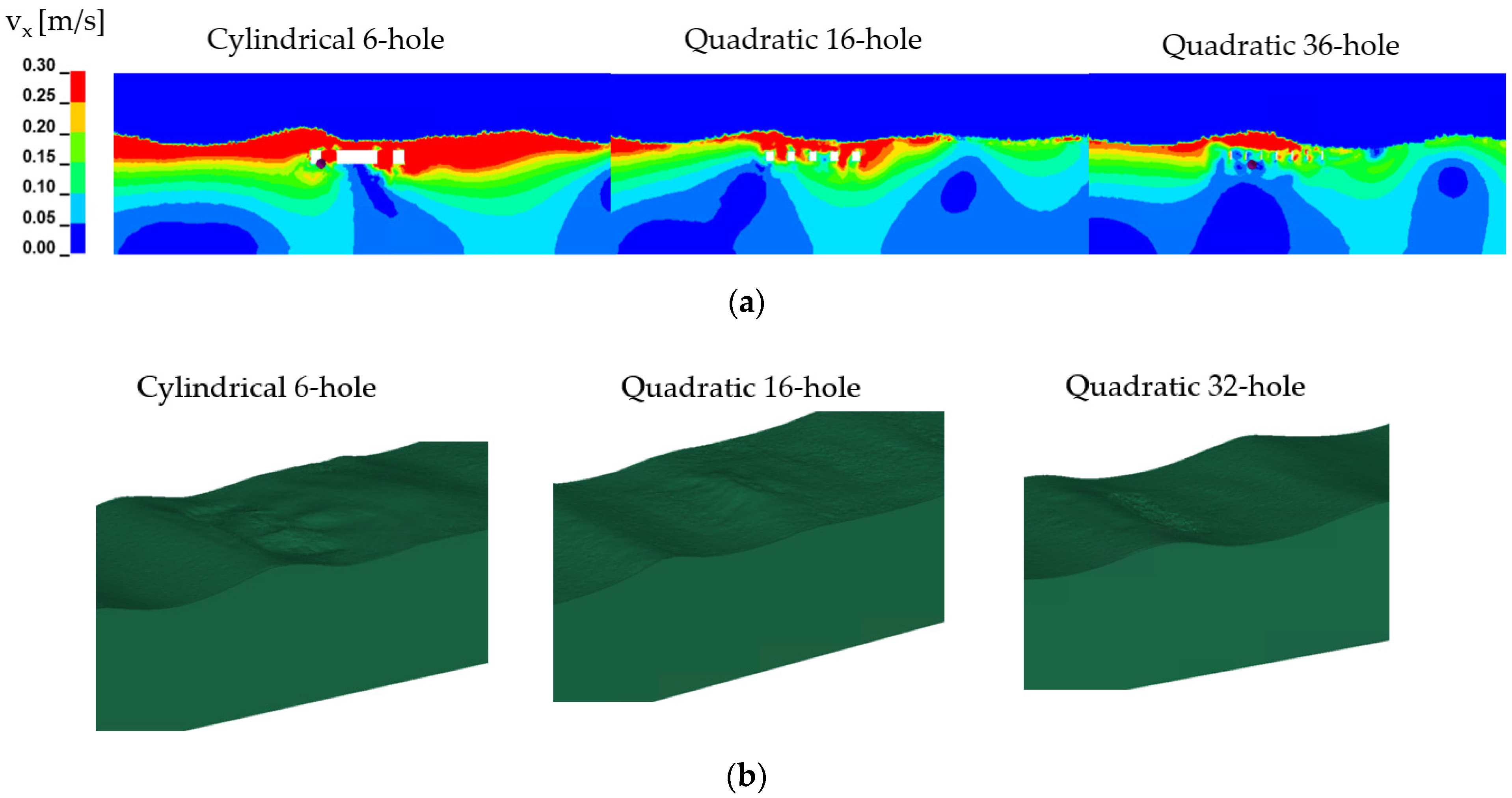
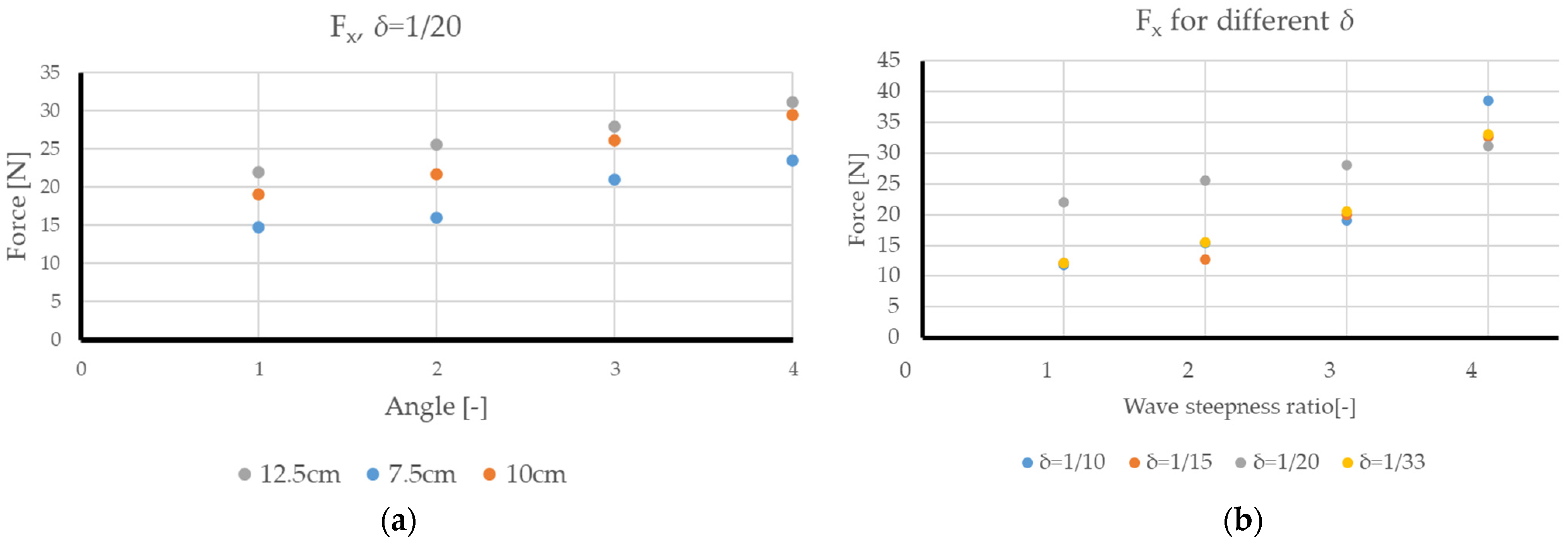
4. Results
4.1. Breakwater Efficiency
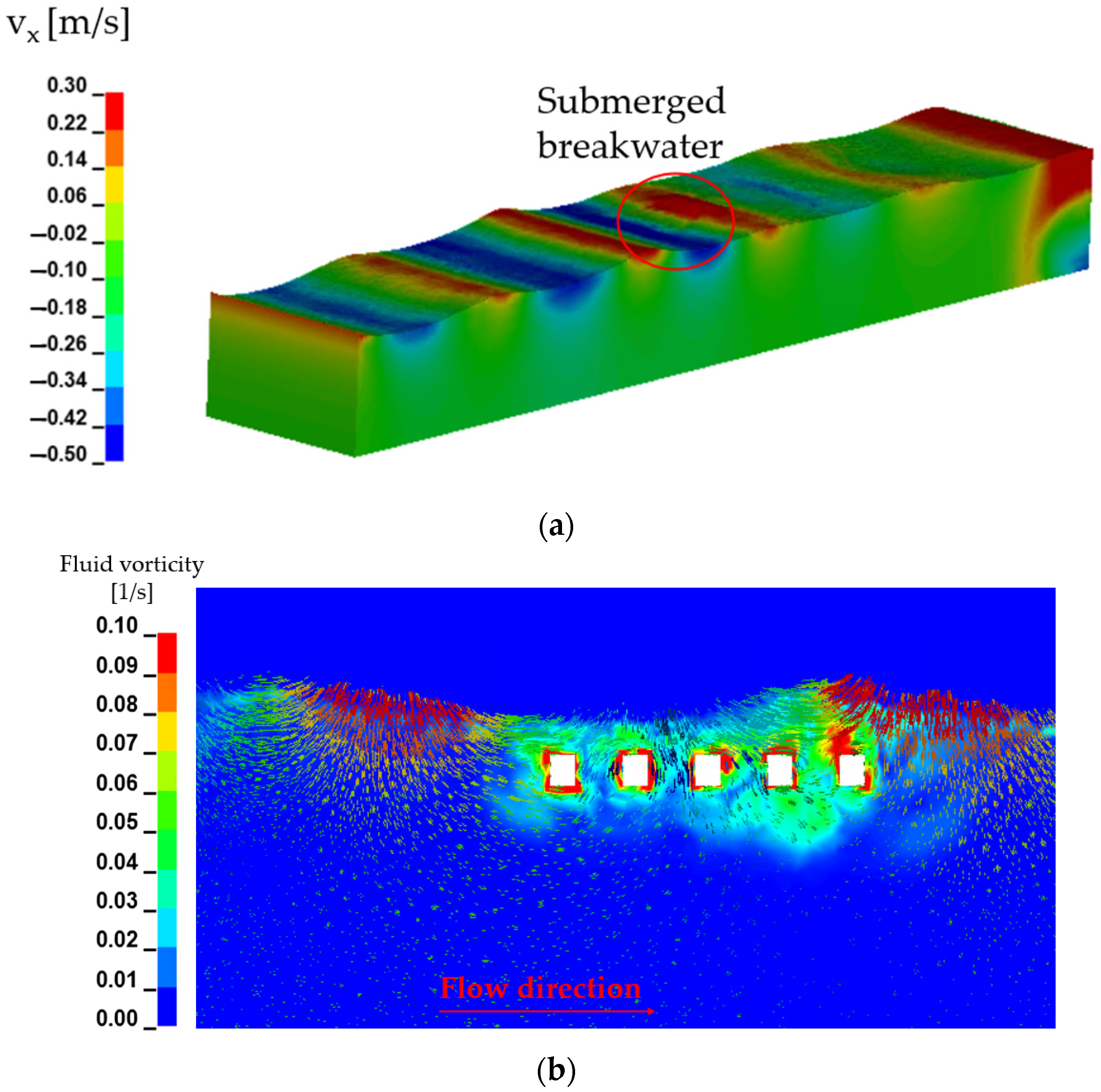
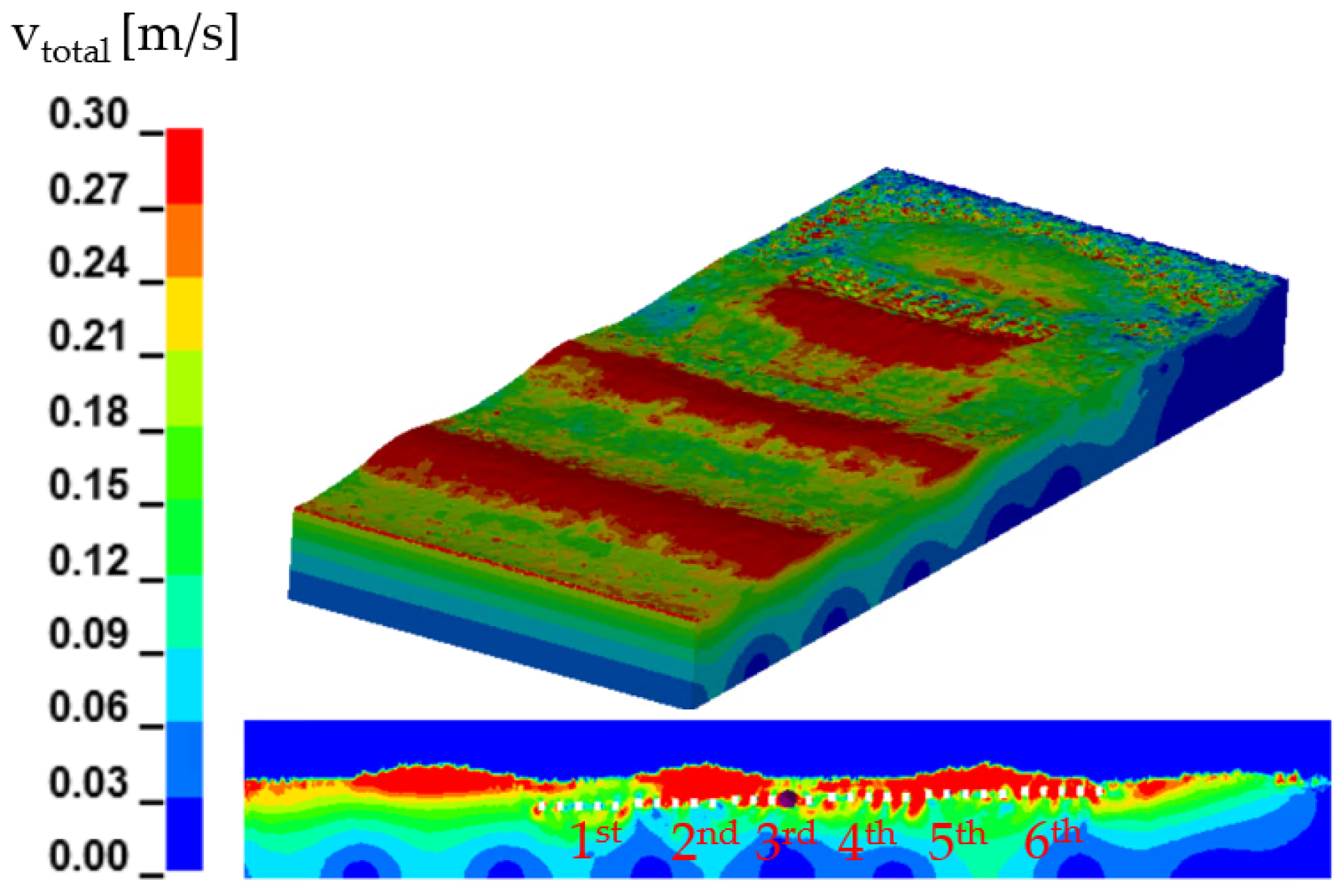
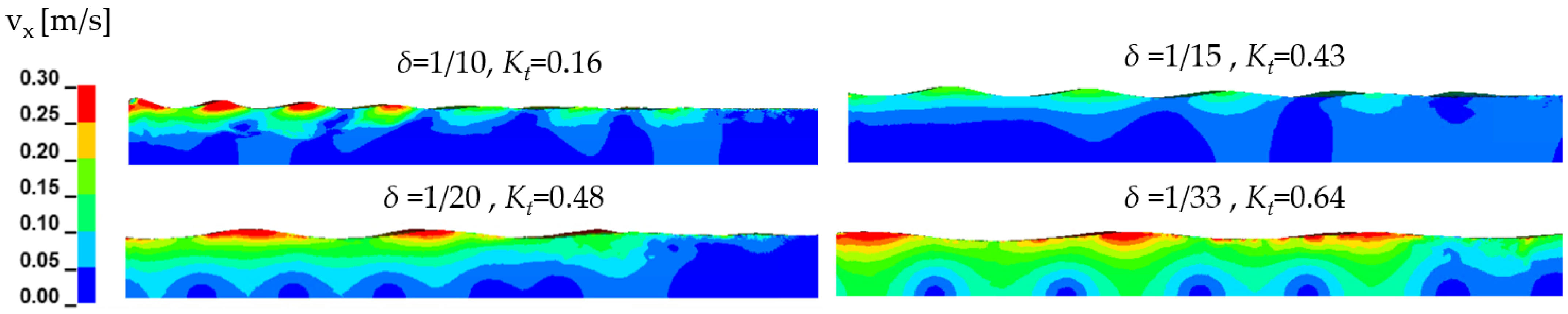
4.2. Submerged Breakwater System Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, Y.; Liu, M.; Chen, C.P.; Jiang, Y.P. Experimental study on the wave dissipation performance and mooring force of porous floating breakwater. IOP Conf. Ser. Earth Environ. Sci. 2018, 189, 022058. [Google Scholar] [CrossRef]
- Chybowski, L.; Grządziel, Z.; Gawdzińska, K. Simulation and Experimental Studies of a Multi-Tubular Floating Sea Wave Damper. Energies 2018, 11, 1012. [Google Scholar] [CrossRef]
- Coastal Engineering Manual-CEM. Coastal Engineering Manual Part II; US Army Coastal Engineering Research Centre: Washington, DC, USA, 2002. [Google Scholar]
- Matsunaga, N.; Hashida, N.; Uzaki, K.; Kanzaki, T.; Uragami, Y. Performance of Wave Absorption by a Steel Floating Breakwater with Truss Structure. In Proceedings of the Twelfth International Offshore and Polar Engineering Conference, Kitakyushu, Japan, 26–31 May 2002; pp. 768–772. [Google Scholar]
- Pena, E.; Ferreras, J.; Sanchez, F. Experimental study on wave transmission coefficient, mooring lines and module connector forces with different designs of floating breakwaters. Ocean Eng. 2011, 38, 1150–1160. [Google Scholar] [CrossRef]
- Ji, C.; Deng, X.; Cheng, Y. An experimental study of double-row floating breakwaters. J. Mar. Sci. Technol. 2018, 54, 359–371. [Google Scholar] [CrossRef]
- Kim, N.H.; Young, Y.L.; Yang, S.B.; Park, K.I. Wave damping analysis in a porous seabed. KSCE J. Civ. Eng. 2006, 10, 305–310. [Google Scholar] [CrossRef]
- Chalmoukis, I.A.; Leftheriotis, G.A.; Dimas, A.A. Large-Eddy Simulation of Wave Attenuation and Breaking on a Beach with Coastal Vegetation Modelled as Porous Medium. J. Mar. Sci. Eng. 2023, 11, 519. [Google Scholar] [CrossRef]
- Setiyawan. Transmission Coefficient (kt) and Reflection Coefficient (kr) on Breakwater Type Cube. Int. J. Innov. Res. Adv. Eng. 2018, 5, 158–166. [Google Scholar] [CrossRef]
- Ji, C.; Cheng, Y.; Yang, K.; Oleg, G. Numerical and experimental investigation of hydrodynamic performance of a cylindrical dual pontoon-net floating breakwater. Coast. Eng. 2017, 129, 1–16. [Google Scholar] [CrossRef]
- Syed, S.A.; Mani, J.S. Performance of rigidly interconnected multiple floating pontoons. J. Nav. Archit. Mar. Eng. 2004, 1, 3–17. [Google Scholar] [CrossRef][Green Version]
- Cheng, X.; Liu, C.; Zhang, Q.; He, M.; Gao, X. Numerical Study on the Hydrodynamic Characteristics of a Double-Row Floating Breakwater Composed of a Pontoon and an Airbag. J. Mar. Sci. Eng. 2021, 9, 983. [Google Scholar] [CrossRef]
- Fitriadhy, A.; Faiz, M.A.; Abdullah, S.F. Computational fluid dynamics analysis of cylindrical floating breakwater towards reduction of sediment transport. J. Mech. Eng. Sci. 2017, 11, 3072–3085. [Google Scholar] [CrossRef]
- He, M.; Gao, X.; Xu, W.; Ren, B.; Wang, H. Potential application of submerged horizontal plate as a wave energy breakwater: A 2D study using the WCSPH method. Ocean Eng. 2019, 185, 27–46. [Google Scholar] [CrossRef]
- Guo, W.; Zou, J.; He, M.; Mao, H.; Liu, Y. Comparison of hydrodynamic performance of floating breakwater with taut, slack, and hybrid mooring systems: An SPH-based preliminary investigation. Ocean Eng. 2022, 258, 111818. [Google Scholar] [CrossRef]
- He, M.; Liang, D.; Ren, B.; Li, J.; Shao, S. Wave interactions with multi-float structures: SPH model, experimental validation and parametric study. Coast. Eng. 2023, 184, 104333. [Google Scholar] [CrossRef]
- Lloyd, C.; O’Doherty, T.; Mason-Jones, A. Development of a wave-current numerical model using Stokes 2nd Order Theory. Int. Mar. Energy J. 2019, 2, 1–14. [Google Scholar] [CrossRef]
- Huang, L.; Ren, K.; Li, M.; Tukovic, Z.; Cardiff, P.; Thomas, G. Fluid-structure interaction of a large ice sheet in waves. Ocean Eng. 2019, 182, 102–111. [Google Scholar] [CrossRef]
- Ge, G.; Zhang, W.; Xie, B.; Li, J. Turbulence model optimization of ship wake field based on data assimilation. Ocean Eng. 2024, 295, 116929. [Google Scholar] [CrossRef]
- Wiesent, L.; Geith, M.; Wagner, M. Simulation of Fluid-Structure Interaction between injection medium and balloon catheter using ICFD. In Proceedings of the 11th European LS-DYNA Conference, Salzburg, Austria, 9–11 May 2017. [Google Scholar]
- ICFD Theory Manual, Incompressible Fluid Solver in LS-DYNA; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2014.
- Maâtoug, M.A.; Ayadi, M. Numerical simulation of the second-order Stokes theory using finite difference method. Alex. Eng. J. 2016, 55, 3005–3013. [Google Scholar] [CrossRef][Green Version]
- Farkas, A.; Parunov, J.; Katalinić, M. Wave Statistics for the Middle Adriatic Sea. J. Marit. Transp. Sci. 2016, 52, 33–47. [Google Scholar] [CrossRef]
- Zorović, D.; Mohović, R.; Mohović, Đ. Towards Determining the Length of the Wind Waves of the Adriatic Sea. Naše More 2003, 50, 145–150. [Google Scholar]
- Perin, B.; Verdrel, P.; Bordenave, P.; Grippon, E.; Belloc, H.; Caldichoury, I. Computational Fluid Dynamic of NACA0012 with LS-DYNA® (ALE & ICFD) and Wind Tunnel Tests. In Proceedings of the 14th International LS-DYNA Users Conference, Detroit, MI, USA, 12–14 June 2016. [Google Scholar]
- Connell, K.; Cashman, A. Development of a numerical wave tank with reduced discretization error. In Proceedings of the International Conference on Electrical, Electronics, and Optimisation Techniques (ICEEOT), Chennai, India, 3–5 March 2016. [Google Scholar] [CrossRef]
- da Silva, C.B. The behavior of subgrid-scale models near the turbulent/nonturbulent interface in jets. Phys. Fluids 2009, 21, 081702. [Google Scholar] [CrossRef]
- Calero, L.; Blanco, J.M.; Izquierdo, U.; Esteban, G. Performance Assessment of Three Turbulence Models Validated through an Experimental Wave Flume under Different Scenarios of Wave Generation. J. Mar. Sci. Eng. 2020, 8, 881. [Google Scholar] [CrossRef]
- Šimun, S.; Smiljko, R. Development of wave dampers using computational fluid dynamics. In Proceedings of the 24th Numerical Towing Tank Symposium, Zagreb, Croatia, 15–18 October 2022; pp. 168–174. [Google Scholar]






| Model Name | Number of ICFD Elements | Number of Solid Elements | |
|---|---|---|---|
| Cylindrical holes | δ = 1/10, T = 1.75 s | 206 k | 500 |
| δ = 1/15, T = 3.75 s | 206 k | 500 | |
| δ = 1/20, T = 5 s | 206 k | 500 | |
| δ = 1/33, T = 7.5 s | 206 k | 500 | |
| Quadratic 16 holes | δ = 1/10, T = 1.75 s | 206 k | 1284 |
| δ = 1/15, T = 3.75 s | 206 k | 1284 | |
| δ = 1/20, T = 5 s | 206 k | 1284 | |
| δ = 1/33, T = 7.5 s | 206 k | 1284 | |
| Quadratic 36 holes | δ = 1/10, T = 1.75 s | 206 k | 2148 |
| δ = 1/15, T = 3.75 s | 206 k | 2148 | |
| δ = 1/20, T = 5 s | 206 k | 2148 | |
| δ = 1/33, T = 7.5 s | 206 k | 2148 |
| Model Name | Number of ICFD Elements | Number of Solid Elements | Real-World Time | |
|---|---|---|---|---|
| 7.5 cm amplitude, 1.5 m wavelength, δ = 1/20, T = 3.75 s | Angle 1 | 435 k | 22 k | 12 h, 29 min |
| Angle 2 | 435 k | 33 k | 12 h, 43 min | |
| Angle 3 | 435 k | 45 k | 13 h, 13 min | |
| Angle 4 | 435 k | 60 k | 13 h, 50 min | |
| 10 cm amplitude, 2 m wavelength, δ = 1/20, T = 5 s | Angle 1 | 284 k | 22 k | 3 h, 50 min |
| Angle 2 | 284 k | 33 k | 3 h, 55 min | |
| Angle 3 | 284 k | 45 k | 4 h, 6 min | |
| Angle 4 | 284 k | 60 k | 4 h, 15 min | |
| 12.5 cm amplitude, 2.5 m wavelength, δ = 1/20, T = 6.25 s | Angle 1 | 197 k | 22 k | 2 h, 58 min |
| Angle 2 | 197 k | 33 k | 3 h | |
| Angle 3 | 197 k | 45 k | 3 h, 2 min | |
| Angle 4 | 197 k | 60 k | 3 h, 12 min | |
| 12.5 cm amplitude, 1.25 m wavelength, δ = 1/10, T = 3.1 s | Angle 1 | 197 k | 22 k | 4 h, 3 min |
| Angle 2 | 197 k | 33 k | 4 h, 15 min | |
| Angle 3 | 197 k | 45 k | 4 h, 54 min | |
| Angle 4 | 197 k | 60 k | 8 h, 21 min | |
| 12.5 cm amplitude, 1.875 m wavelength, δ = 1/15, T = 6.25 s | Angle 1 | 197 k | 22 k | 4 h, 45 min |
| Angle 2 | 197 k | 33 k | 6 h, 40 min | |
| Angle 3 | 197 k | 45 k | 7 h, 3 min | |
| Angle 4 | 197 k | 60 k | 7 h, 14 min | |
| 12.5 cm amplitude, 3.6 m wavelength, δ = 1/33, T = 9 s | Angle 1 | 197 k | 22 k | 5 h, 46 min |
| Angle 2 | 197 k | 33 k | 6 h, 36 min | |
| Angle 3 | 197 k | 45 k | 6 h, 42 min | |
| Angle 4 | 197 k | 60 k | 7 h, 24 min |
| δ = 1/20 | Model Name | Centreline Kt [-] | Cut 1 Kt [-] | Cut 2 Kt [-] | Cut 3 Kt [-] |
|---|---|---|---|---|---|
| 7.5 cm amplitude | Angle 1 | 0.34 | 0.36 | 0.33 | 0.4 |
| Angle 2 | 0.3 | 0.32 | 0.29 | 0.33 | |
| Angle 3 | 0.07 | 0.09 | 0.067 | 0.16 | |
| Angle 4 | 0.04 | 0.05 | 0.032 | 0.12 | |
| 10 cm amplitude | Angle 1 | 0.46 | 0.48 | 0.45 | 0.53 |
| Angle 2 | 0.33 | 0.35 | 0.32 | 0.42 | |
| Angle 3 | 0.22 | 0.24 | 0.21 | 0.33 | |
| Angle 4 | 0.15 | 0.17 | 0.14 | 0.28 | |
| 12.5 cm amplitude | Angle 1 | 0.53 | 0.55 | 0.53 | 0.6 |
| Angle 2 | 0.28 | 0.29 | 0.27 | 0.46 | |
| Angle 3 | 0.2 | 0.22 | 0.19 | 0.37 | |
| Angle 4 | 0.13 | 0.15 | 0.12 | 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rudan, S.; Sviličić, Š. Determination of Submerged Breakwater Efficiency Using Computational Fluid Dynamics. Oceans 2024, 5, 742-757. https://doi.org/10.3390/oceans5040042
Rudan S, Sviličić Š. Determination of Submerged Breakwater Efficiency Using Computational Fluid Dynamics. Oceans. 2024; 5(4):742-757. https://doi.org/10.3390/oceans5040042
Chicago/Turabian StyleRudan, Smiljko, and Šimun Sviličić. 2024. "Determination of Submerged Breakwater Efficiency Using Computational Fluid Dynamics" Oceans 5, no. 4: 742-757. https://doi.org/10.3390/oceans5040042
APA StyleRudan, S., & Sviličić, Š. (2024). Determination of Submerged Breakwater Efficiency Using Computational Fluid Dynamics. Oceans, 5(4), 742-757. https://doi.org/10.3390/oceans5040042







