Abstract
This research focuses on integrating seakeeping indices into the trajectory planning of a mother ship in order to minimize risks during UAV (unmanned aerial vehicle) takeoff and landing in challenging sea conditions. By considering vessel dynamics and environmental factors, the proposed trajectory planning algorithm computes optimal paths that prioritize the stability and safety of the ship, mitigating the impact of adverse weather on UAV operations. Specifically, the new adaptive weather routing model presented is based on a genetic algorithm. The model uses the previously evaluated response amplitude operators (RAOs) for the reference ship at different velocities and encounter angles, along with weather forecast data provided by the global wave model (GWAM). Preliminary evaluations confirm the effectiveness of the presented model in significantly improving the reliability of autonomous UAV operations from a mother ship across all encountered sea state conditions, particularly when compared with a graph-based solution. The current results clearly demonstrate that it is possible to achieve appreciable improvements in ship seakeeping performance, thereby making UAV-related operations safer.
1. Introduction
The field of autonomous navigation, situated at the convergence of robotics, artificial intelligence, and transport engineering, offers significant potential to transform transportation in numerous sectors. Leveraging state-of-the-art technologies about sensors, algorithms for machine learning, and complex control systems, guidance, control, and navigation (GNC) systems allow vehicles to function and make choices on their own, eliminating the need for direct human control. Ranging from autonomous cars to drones and ships, these technologies stand on the brink of altering the conventional methods of movement and goods transportation.
In the context of UAV operations on a mother ship, integration and coordination between the unmanned aerial vehicles (UAVs) and the vessel become paramount. The mother ship serves as a mobile base of operations, providing a stable platform for launching and recovering UAVs in various maritime environments. However, the challenges inherent in conducting these operations at sea necessitate careful consideration of factors such as vessel motion, deck dynamics, and environmental conditions.
During launch and recovery procedures, the UAVs must navigate the dynamic environment of the mother ship deck with precision and agility. This requires sophisticated control systems that can adapt to the vessel motion and compensate for any disturbances induced by waves, wind, or other external forces. Furthermore, the UAVs must be equipped with robust sensing capabilities to accurately assess the relative motion between the aircraft and the ship, enabling them to make real-time adjustments to their flight path and trajectory.
For UAV recovery operations, the mother ship typically employs a variety of systems and mechanisms to safely retrieve the aircraft upon completion of their mission. This may include the use of recovery nets, landing pads, or even autonomous landing systems that guide the UAVs to a designated touchdown area on the ship deck. In addition to ensuring the safety of the UAVs themselves, these systems must also take into account the safety of personnel and equipment on board the vessel, particularly in rough sea conditions where precision and stability are critical.
By integrating seakeeping criteria into the trajectory planning process, this research aims to reduce the dangers associated with the landing and departure operations of UAVs, optimizing the route followed by the mother ship in order to maximize stability and reduce exposure to motions during navigation in adverse marine conditions.
Through a combination of advanced algorithms, the goal is to enable autonomous UAV operations from a mother ship platform that are safe, efficient, and capable of supporting a wide range of maritime missions.
The suggested method relies on a new adaptive weather routing system made to find the best route, improving how well ships perform in various sea conditions. This model focuses on particular factors that keep ships steady, ensuring that it picks routes that make the most of the ship’s abilities in the ever-changing sea conditions. Within this framework, this research explores the application of a genetic algorithm-based planning methodology.
The algorithm is applied to a designated mother ship, serving as the benchmark vessel, to investigate the impact of selected seakeeping variables and vessel speed on the optimal route selection for launch and recovery operations. Consequently, the primary objective of this study is to develop an adaptive weather routing model with the following aims: (i) improve the vessel seakeeping performance across varying sea states; (ii) increase safety in autonomous launch and recovery procedures, particularly in adverse weather conditions; and (iii) conduct a comprehensive sensitivity analysis to verify the influence of individual seakeeping parameters on the optimal route determination. A campaign of numerical results is considered to prove the effectiveness of the proposed procedure, with a comparative analysis with a Djikstra-based algorithm being used to evaluate the effectiveness of each model in facing the intricate challenges posed by adverse marine conditions.
Although the existing literature on weather routing mainly concentrates on route changes to optimize fuel consumption, the impact of weather routing on fuel savings can be considered only marginal, as discussed in previous papers [1,2]. For this reason, this paper focuses on the seakeeping performance impact in weather routing, taking into account some specific parameters useful for improving the takeoff and landing operations of UAVs. The proposed procedure is a genetic-based optimization algorithm to overcome graph-based solutions and consider seakeeping performance as nonlinear constraints.
The key contributions of the paper are: (i) development of an adaptive weather routing system introducing a new model that enhances ship performance in various sea state conditions by optimizing the route of the mother ship, focusing on reducing ship motions; (ii) application of a genetic algorithm-based planning methodology to optimize the trajectory of the ship, taking into account seakeeping performance limits as constraints; (iii) the limits are defined in order to improve UAV takeoff and landing operations; and (iv) a comprehensive sensitivity analysis is conducted to verify the influence of individual seakeeping index on optimal route determination.
2. Literature Review
Understanding the intricacies of weather routing is foundational to appreciating the complexities and solutions in the operations of unmanned aerial vehicles (UAVs) on a mother ship, where the seamless integration and coordination between UAVs and the vessel are paramount. Within this framework, ship weather routing (SWR) emerges as an important operational-level decision tool, entailing the determination of the optimal route for a vessel navigating from an originating port to a designated final port, taking into account variable weather conditions such as winds, waves, and sea currents.
In recent years, there has been a proposal to adopt the term environmental routing as a more apt descriptor as it encompasses environmental factors in the pursuit of the most efficient or economical route. For example, in [3], authors highlight that the terms environmental routing and weather routing are often used interchangeably, but the latter can be considered as a subset of the former. Weather conditions, such as winds, waves, and currents, constitute elements of the environment where ships operate, significantly impacting their performance. It is important to clarify that in this context, environmental routing pertains to the prevailing weather conditions and environmental factors (such as sea depth and designated areas necessitating specific fuel usage) in which ships navigate, distinct from the environmental performance of a voyage itself. The selection of a route optimizing vessel performance, such as minimizing ship emissions, can be addressed as part of the green ship routing problem [4].
In the context of weather routing, risk can be considered in several ways, which is contingent upon the concerns of the ship operator seeking to mitigate adverse weather-related impacts. For instance, in [5], authors identify wind as a primary safety hazard during voyages and aim to reduce the risk of prolonged exposure to high-wind areas. However, their utilization of multicriteria optimization may inadvertently prolong total sailing time, which could serve as an alternative objective in ship weather routing. Ref. [6] assesses safety risk based on the probability of encountering waves exceeding 4 m in height. In [7], navigation risk is evaluated according to the sailing conditions outlined in the International Maritime Organization (IMO) guidelines for navigators. The determination of weather conditions, such as wave height, length, and wind, that constitute a safety risk is contingent upon several factors specific to the voyage, including ship type, condition, and geographical region. These environmental considerations can be integrated into ship weather routing models by minimizing fuel consumption as it is feasible to estimate fuel consumption in areas affected by adverse weather conditions. A comprehensive analysis of risk assessment models in narrow maritime waterways is presented in [8], focusing on accident frequency and severity, albeit without exploring the influence of weather. Alternatively, risk definitions may concentrate on the financial implications of a voyage, such as assessing the risk of failing to reach the next port within a specified timeframe, potentially resulting in contractual penalties [9], or increased operating costs due to heightened fuel consumption in adverse weather conditions [10].
Weather routing not only addresses the risk of maritime incidents but also plays a crucial role in boosting the reliability of maritime services and reducing the operating costs of voyages. For example, although it is not the unique factor in preventing container losses at sea, it significantly aids in this effort. Economically, navigating through adverse weather conditions can lead to heightened fuel consumption and the possibility of voyage delays, potentially incurring additional demurrage charges [11]. Environmentally, lower fuel consumption results in decreased emissions of CO2 and SOx. Nonetheless, it is important to recognize potential environmental tradeoffs; for example, even with reduced fuel consumption, emissions of particulate matter may increase due to engines operating at lower loads [12]. In [13], various strategies aimed at optimizing vessel operations to reduce carbon emissions are reviewed, identifying weather routing as a key operational alternative.
Nevertheless, route planning presents considerable challenges due to the intricate and diverse nature of environments. This issue is frequently articulated as an optimization problem, wherein the most efficient trajectory traverses a series of predetermined waypoints, taking into account obstacles, potential traffic, constraints arising from the ship behavior in rough seas, and the characteristics of the encountered sea conditions. A foundational approach to solving such complex, multi-stage decision-making problems was introduced in [14], where the author provided a mathematical framework for optimizing decisions across different fields, introducing optimization techniques for problems involving sequential decisions.
The extensive body of literature on 2D path planning problems benefits from interdisciplinary exchanges with the robotics and automotive sectors, sharing algorithms and resolution strategies. These methodologies can be categorized into several groups: variational methods, optimal control strategies, geometric methodologies, graph optimization techniques, artificial potential field frameworks, and nature-inspired optimization algorithms.
Variational methods for path planning are intuitively appealing but become challenging in complex scenarios, particularly when coupled with flight dynamics constraints [15,16]. Optimal control strategies, designing closed-loop algorithms that converge to locally sub-optimal trajectories, may struggle to find a global optimum and require extensive computational resources when dealing with nonlinear optimization algorithms [17,18,19,20].
Geometric approaches to path planning, which define paths as sequences of segments, arcs, or template curves, include solutions such as Dubins’ car problem [21] or clothoid curves [22]. These methods usually need to be integrated with other algorithms to manage obstacles and no-fly zones [23,24].
Graph optimization, employing edges designed through geometric methods, requires discretizing environments into grids and often utilizes visibility graphs, Voronoi diagrams, rapidly exploring random trees (RRTs), tangent graphs, sparse tangential networks (SPARTANs), and roadmaps [25,26,27,28,29,30,31,32,33,34,35,36,37]. Algorithms such as Dijkstra’s, A*, and D* algorithms are commonly employed to find the shortest paths [38,39,40].
Artificial potential field techniques, while effective for real-time guidance, become problematic with increased obstacles or “potential sources”, necessitating strategies to circumvent emerging singularities [41,42].
Lastly, nature-inspired optimization methods enable the design of complex models based on flight dynamics, optimizing sequences of feasible maneuvers to reach target points. These methods, while sophisticated, are computationally demanding and typically suited for offline optimization [43,44,45,46,47].
Concurrently, the literature on ship weather routing presents various approaches, broadly categorized into exact methods, heuristic approaches, and multi-objective evolutionary methods. Early works typically employed exact methods, while recent studies have leaned towards heuristics. This overview outlines these approaches and highlights key objective functions, such as economic concerns, climate considerations, and regional fairness.
One of the earliest techniques is the isochrone method, devised by James in 1957 [48], which prioritizes minimizing travel time and facilitates manual route planning. Subsequent advancements, like those by Hagiwara and Spaans in 1987 [49], incorporated fuel consumption considerations and computerized the method. The calculus of variations method, introduced by Haltiner et al. [50], provides an analytical approach to weather routing, determining both the ship path and engine power. In Chen et al. [51], five improved methods are proposed and compared to investigate the most effective enhancement strategy for achieving robustness and practicality in real-time applications. Papadakis [52] develops general methodologies for the minimal time routing problem of a vessel moving in stationary or time-dependent environments.
Commonly employed methods include multi-objective genetic algorithms, which probabilistically tackle a discretized nonlinear optimization problem, utilizing the ship course and velocity profile represented by parametric curves. Most existing weather route optimization methods generate the optimal route to minimize fuel oil consumption; however, in the work of Pennino et al. [1,2], a new adaptive weather routing model was presented based on Dijkstra’s shortest path algorithm, which aims to select the optimal route that maximizes the ship performance during navigation. Szłapczynska and Smierzchalski [5] introduced a multi-criteria evolutionary weather routing algorithm, employing an iterative population development process to yield a Pareto-optimal set of solutions. Wei and Zhou [53] devised a three-dimensional (3D) dynamic programming approach based on De Wit’s original work [54], focusing on optimizing ship speed and heading angle during route planning. Zaccone et al. [55] developed a 3D dynamic-programming-based method for ship voyage optimization, aiming to select the optimal path and speed profile considering expected weather conditions along the route. Another technique for weather routing optimization is pathfinding. Padhy et al. [56] applied the Dijkstra algorithm to address the ship routing problem, while Veneti [57] proposed an enhanced solution based on the time-dependent bi-objective shortest path algorithm. This improved method optimizes conflicting objectives, such as fuel consumption and expected risk, along the route. Huu [58] also proposed a weather routing method to obtain the optimal fuel route based on the Dijkstra algorithm and neural network.
Other methods, including dynamic programming approaches by Motte and Calvert [59], and those utilizing shortest path algorithms by Montes [60], Panigrahi et al. [61], and Mannarini et al. [62], have also been explored. van Dooren et al. [63] reformulated an optimal control problem using convex functions to convert it into a convex optimization problem, which they initially solved assuming that environmental conditions were constant over time, and then addressed the problem under time-varying conditions. In [64], the authors enhance the original FOPSO (fractional order particle swarm optimization) algorithm by introducing adaptive coefficients in the fractional order velocity update formula to avoid local optima and premature convergence.
Evolutionary approaches like genetic algorithms (GAs) offer efficient solutions to pathfinding problems by accommodating a wide range of constraints and objectives. For instance, Walther et al. [65] proposed a GA optimizing fuel costs while supporting variable ship speed. Wang et al. [66] introduced a real-coded GA, albeit with limitations around waypoint flexibility. Similarly, simulated annealing algorithms, such as the one introduced by Yuankui et al. [67], have been utilized to minimize vessel travel time.
Multi-objective evolutionary methods enable the simultaneous optimization of multiple objectives. Tsou [68] and Azariadis [69] combined evolutionary algorithms with modified A* algorithms to optimize routes considering safety and economic factors. Li and Zhang [70] proposed a GA focusing on minimizing turning variation and fuel consumption, with fixed vessel orientations at the start and end positions. Other studies, like those by Szlapczynska [71,72] and Vettor and Guedes Soares [73], applied multi-objective evolutionary algorithms to minimize passage time, fuel consumption, and route risk. Zhao et al. [74] introduce a hybrid multicriteria ship route planning method that combines enhanced particle swarm optimization with genetic algorithms to optimize meteorological risk, fuel consumption, and navigation time.
Several problems exist that are similar to the vessel weather routing problem. One of them is the path planning of unmanned aerial vehicles (UAVs). Arantes et al. [75], for example, used a genetic algorithm (GA) to plan the paths of drones and mention no-fly zones and obstacles that were similar to the land masses in the weather routing problem. They included the position uncertainty of the aircraft due to turbulence, which does not occur in the weather routing problem. The multi-population genetic algorithm is combined with a visibility graph maintaining all feasible paths for the drone, which would not be possible for the weather routing problem because of the much larger solution space. Hasircioglu et al. [76] also used a GA to plan paths offline for UAVs. The GA uses three different mutation operators that update, insert, and delete control points visited by the UAV. Hence, there are no operators that are specific to the case of UAV path planning. Ragusa et al. [77] also investigate a GA for “micro aerial vehicles”. However, for the problem of weather routing, intersections are infeasible, which is different than in the approach of Ragusa et al. In their approach, intersections are allowed, and the algorithm focuses on minimizing the degree of intersection with obstacles. Furthermore, the routes used by Ragusa et al. have fewer waypoints than in the case of ship routing because the routes are much shorter and need fewer waypoints.
Recent research activities have examined cooperative path-following control algorithms for an unmanned surface vessel and unmanned aerial vehicles (USV-UAVs) that simplify design complexity and transmission requirements. In [78], the research focuses on reducing communication overhead and increasing fault tolerance in sensor systems by presenting an adaptive control strategy that adjusts based on sensor faults and varying data transmission needs. In [79], a cooperative path control strategy is explored that simplifies design complexity and minimizes command transmission between USVs and UAVs.
Certainly, up to now, the problem of planning the ship voyage by adapting the route to weather conditions has not been addressed by linking it to the trajectory planning of UAVs. The goal of this work is to leverage weather routing techniques to enable the safest possible takeoff and landing from the mother ship.
3. Modeling of Ship Behavior in Seaways
The performance of a ship during operations can markedly differ when transitioning from calm waters to navigating through waves up to the conditions of a storm. Influenced by environmental elements, predominantly waves, wind, and occasionally currents, a ship undergoes increased and dynamic loading. This typically leads to an increase in resistance, which consequently reduces the vessel forward speed and decreases the efficiency of the propulsion system. The lack of efficiency is largely due to altered water flow around the propeller, which can lead to the propeller emergence and ventilation, along with oscillatory movements of the ship hull across all six degrees of freedom. These movements can potentially create unsafe conditions for both the crew and the cargo, necessitating either a course alteration or a deliberate reduction in speed.
During the navigation of a mother ship, various weather and sea conditions can significantly affect the safety of UAV landing and takeoff operations. Pitch, roll, and heave motions, vertical plane movements, and water on the deck can create adverse conditions that make UAV landing and takeoff challenging and hazardous. To address this challenge, an adaptive weather routing model has been specifically designed to assist the mother ship in identifying safe routes during various weather and sea conditions. This model takes into account weather forecasts and the specific characteristics of the ship to determine optimal routes that minimize the risk of UAV operations. By using this approach, the mother ship can navigate more safely and reliably, avoiding adverse weather conditions that could compromise the stability of the ship and the safety of UAV operations. Additionally, the adaptive weather routing model allows the mother ship to dynamically adapt to changing weather and sea conditions along the route, ensuring that landing and takeoff operations are conducted safely and efficiently at any time and in any location.
Seakeeping Performances Index
The present evaluation assesses seakeeping performance using five key reference criteria: (i) pitch motion amplitude, (ii) heave motion amplitude, (iii) roll motion amplitude, (iv) probability of green water on deck, and (v) vertical plane movement. This determination follows a specified equation.
where is the RMS, root mean square, of the pitch motion amplitude; is the root mean square of the heave motion amplitude; is the root mean square of the roll motion amplitude; is the RMS of the vertical acceleration; and is the probability of green water on deck. The denominators represent the relevant limit values. This relation is structured to ensure the optimal seaworthiness performance for the ship by minimizing the complement of the criteria once their adherence is confirmed. The limit value of the pitch amplitude is based on NATO STANAG Standardization Agreement 4154 criteria, while the RMS of roll amplitude and green water on deck probability comply with the NORDFORSK 1987 criteria, as detailed in Table 1. The limit values for the RMS of the heave motion amplitude and the vertical plane motion, not being covered in the previously reported regulatory references, have been hypothesized by assuming 10% of the draft as the limit value for the heave. Obviously, all limit values can be adjusted according to the needs.

Table 1.
General operability limiting criteria for ships.
A seakeeping analysis for a displacing ship in rough seas is commonly performed in the frequency domain. The response spectrum for the six ship motions is obtained from the following equations.
where are the frequency transfer functions and the modulus of these transfer functions is defined as the response amplitude (RAO). The absolute wave frequency is indicated with is the encounter wave frequency, represents the vessel speed, and is the encounter angle between the ship heading and the prevailing sea state direction. denotes the wave spectrum, while is defined as:
where k is the wave number. In this paper, the JONSWAP [80] spectrum is applied, thanks to its reliability to resemble wind-generated sea state conditions, and it is defined as follows:
where is the Bretschneider [81] spectral density function, whose expression is a function of the significant height; is the angular spectral peak frequency; and is the peak enhancement factor that expresses, less than a constant, the ratio between the maxima of the JONSWAP to the corresponding Bretschneider spectrum.
The root mean square (RMS) of the pitch motion amplitude is calculated using the following equation, which relies on the ship response amplitude operator.
where , also commonly referred to as , is the pitch motion transfer function. is the wave spectrum, and is the encounter wave frequency that satisfies the Doppler shift equation depending on the absolute wave frequency and the factor ; the vessel speed is denoted by , and , as indicated previously, denotes the encounter angle between the ship heading and the prevailing sea state direction. is the wave number satisfying the deep water condition. Similarly, the root mean square (RMS) of the heave motion amplitude is calculated using the following equation.
where , also commonly referred to as , is the heave motion transfer function. The root mean square (RMS) of the roll motion amplitude is defined by the following equation.
where , also commonly referred to as , is the roll motion transfer function. Regarding the probability of green water on the forward deck structures, its determination follows a similar approach.
where is the swell-up coefficient equal to one, is the zero spectral moment of the ship relative motion with respect to the sea surface, and is the freeboard at the ship forward perpendicular. In the end, the root mean square of the relative vertical acceleration is obtained by combining the heave, pitch and roll motions at the ship forward perpendicular.
where is the longitudinal distance (fwd+) of the ship forward perpendicular from its center of mass; is the transverse distance (stbd+), equal to zero since the considered point lies on the diametral plane; and is the wave number satisfying the deep water condition.
To conduct a comprehensive analysis of the ship seaworthiness, the Motion module of Maxsurf was utilized. This module calculates and analyzes the ship response to user-defined sea conditions. Input data included initial velocity and various heading angles. The Motion module played a crucial role in defining response amplitude operators (RAOs) for roll, pitch, and heave motions, essential for evaluating seakeeping criteria along the optimized route. Additionally, added resistance values were computed by Motion, aiding in determining speed reduction due to varying sea states. In particular, by assuming an engine brake horsepower and total propulsion efficiency, the effective power was derived and, consequently, the ship resistance as well. By adding the values of added resistance provided by the Motion module to the resistance, it was possible to determine the speed reduction in various sea conditions, which is crucial for assessing the impact of sea conditions on the ship performance.
The indices were selected based on the type of ship and the specific service which it is intended for. The objective is to enhance safety in the launch and landing operations of autonomous drones. The developed code provides the ability to identify the motions and, consequently, the indices to analyze and consider according to specific needs. Therefore, the indices can be modified and adapted based on the specific needs of the ship and the priorities dictated by the service it must perform.
4. GA-Based Weather Routing
In this study, an optimization methodology employing the genetic algorithm was utilized. Genetic algorithms are an optimization technique inspired by the principles of natural selection and biological evolution. These algorithms simulate the process of natural evolution by generating a population of candidate solutions to a problem and evolving these solutions over successive generations. Each candidate solution, often referred to as an individual, is evaluated using a fitness function that measures its quality or performance concerning the optimization objective. The key principles of genetic algorithms include selection, crossover, and mutation. Selection involves choosing the fittest individuals from the current population to participate in the creation of the next generation. Crossover, or recombination, combines pairs of selected individuals to produce offspring that inherit characteristics from both parents. Mutation introduces random changes to individual solutions, promoting diversity and preventing premature convergence to local optima. In this paper, we refer to an implementation in Matlab of NSGA-II [82].
In the context of optimizing the ship trajectory, the genetic algorithm was implemented to find the most efficient route considering various sea states and ship responses.
Consider and being the departure and target points, respectively. Let be the search space and be the set of waypoints, which are the passage points of the trajectory such that , and .
Defining waypoints solely by their coordinates without considering the order and relative positions among them can result in inefficient and impractical routes. This approach can cause the trajectory to intersect itself or loop back to previously traversed points, leading to unnecessary detours and an overall suboptimal path.
In order to achieve a more effective solution for route planning, it is advantageous to employ a local reference system for defining the coordinates of each waypoint. Each point can be described in terms of its direction and distance relative to the preceding waypoint rather than using absolute coordinates. This method simplifies the definition of constraints on the distances between waypoints and the changes in direction, thereby preventing the generation of inefficient trajectories with intersections or backward movements. Using a local reference system ensures a more structured and feasible approach for defining the path from the starting point to the destination.
Consider as the local search space in which the design variables , are defined on. The position of the -th waypoint can be computed as follows:
where , with and being computed in order to consider a vision cone whose axis is the line joining the points and (see Figure 1).
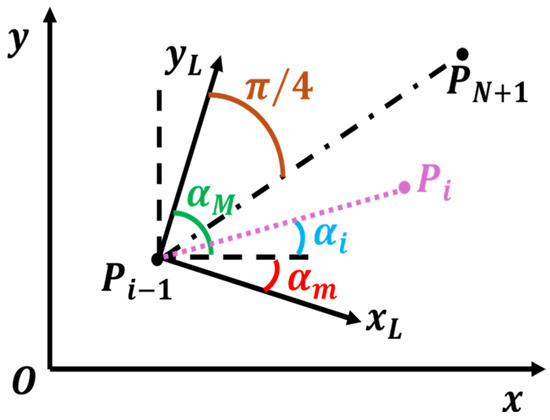
Figure 1.
Local reference system for waypoint definition.
The objective function is defined as the sum of all distances between consecutive waypoints:
where indicates the arc distance between two points.
The optimization procedure seeks to minimize the objective function while ensuring that the resulting route adheres to constraints related to the ship performance and safety in varying sea conditions by calculating the seakeeping performance index (SPI) for various sea states along the route. Routes with SPI values exceeding a critical threshold are penalized, encouraging the selection of safer and more efficient paths. This iterative process continues until an optimal or satisfactory route is found, balancing the tradeoffs between route efficiency and seakeeping performance.
The proposed adaptive weather routing procedure operates through a series of well-defined steps:
- (1)
- Input data reception—Initially, the procedure receives crucial input data, including weather information, vessel details (such as dimensions, response amplitude operators, and added resistance values), initial speed, and specific coordinates for the departure and arrival points of the trip.
- (2)
- Trajectory optimization process—For each considered trajectory in the optimization problem, the following steps are performed:
- (a)
- Waypoint definition—The coordinates of waypoints are computed.
- (b)
- Speed reduction estimation—Using the meteorological data, the procedure estimates the reduction in speed that the ship will experience in various sea states. This step is essential for understanding how weather conditions affect the vessel’s speed.
- (c)
- JONSWAP sea spectrum calculation—The JONSWAP sea spectrum is computed based on the received meteorological data. This spectrum characterizes the energy distribution of sea waves, which is crucial for further analysis.
- (d)
- Vessel response evaluation—With the JONSWAP spectrum, the vessel dynamic response to different combinations of heading angles and speeds is computed. The response in terms of roll, heave, and pitch motions can computed by simulation to predict the behavior of the vessel in open sea under various conditions.
- (e)
- SPI function determination—The values about each criterion along the trajectory can be computed and used to determine the overall value of the SPI function.
- (f)
- Fitness evaluation—The objective function is evaluated and the fitness is computed taking into account the constraint on the SPI.
- (3)
- Optimal route provision—After the optimization process is complete, the procedure provides the optimal route. This route is the safest and most efficient for the ship, taking into account expected weather and sea conditions and the vessel’s specific characteristics.
A flowchart of the proposed adaptive weather routing procedure is summarized in Figure 2.
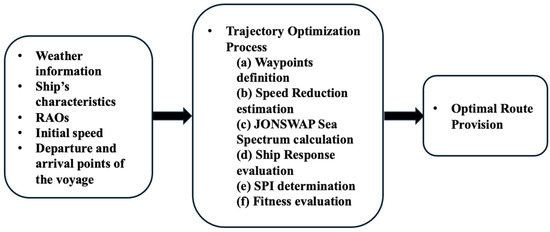
Figure 2.
Flow chart: code structure.
5. Input Data
The reference ship is a vessel that serves as a UAV mother ship, and its main characteristics are detailed in Table 2.

Table 2.
Main details of the UAV mother ship.
The response operator details of the above ship was ascertained by defining the representative model using Maxsurf 2023 Update 7 software. Maxsurf is an integrated naval architecture used to design, analyze, and build different types of vessels. The detailed analysis of the vessel’s seaworthiness was conducted using the Maxsurf Motion module, which computes and analyzes the ship response in user-defined sea conditions. It is well known for simulating the dynamic response of the ship to various forces and effects. For the relevant vessel, the Motion module played a key role in defining the RAOs for the rolling, pitching, and heaving motions that enabled the assessment of the seakeeping criteria over segments of the optimized route.
The selected route is in the North Atlantic Ocean, one of the most important shipping zones in the world, being the corridor where all the infrastructure of Western Europe’s key ports has been regularly and significantly upgraded to keep up with current and anticipated increases in shipping. Weather conditions in this area can vary through the seasons and affect the final outcomes. The coordinates of the departure point are 14.4° N 46.3° W, and the target is at 30.8° N 24.6° W. Figure 3 presents the selected route to be followed, showing the great circle distance between points. The great circle route is 1549 nm long, and the rhumb-line route is 1555 nm long. Although the great circle is shorter, it requires the captain to correct the heading frequently. On the other hand, rhumb-line, although a little longer, does not require changes in the absence of wind and sea current, making it more practical.
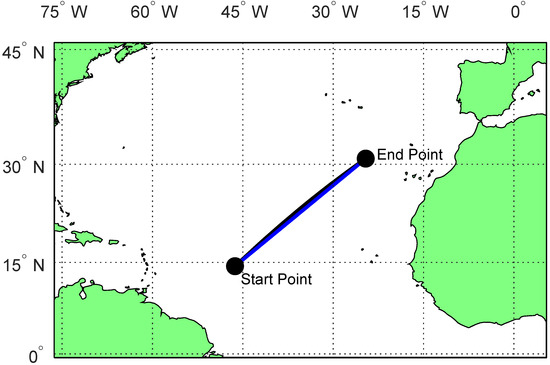
Figure 3.
Reference route.
The daily operational meteorological forecast data are a good estimation of the reference scenario needed to test the functionality of the adaptive weather routing algorithm. These data are crucial for assessing the various scenarios that the algorithm must handle. With this objective, several software packages are available, with different resolutions, domains (from regional to global), and qualities. These applications are validated by the agreements that shipping companies have with meteorological institutes to ensure the data are both current and accurate.
Currently, the community adheres to the standardization established by the World Meteorological Organization, which mandates that all information be presented in the self-explanatory GRIB (GRIdded Binary) format. This standardization facilitates the reading and utilization of input data, significantly easing the integration process into weather routing systems. In the current analysis, data are obtained from the third-generation global wave model (GWAM), abbreviated as GWAM, initially developed in the mid-1980s by an international group of wave modelers [83]. This model is extensively recognized and utilized by research institutions worldwide due to its ability to explicitly solve the wave transport equation without assuming the wave spectrum’s shape. The GWAM can be applied to any regional or global grid, tailored to specific topographic data sets, with adjustable grid resolutions in space and time. The wave propagation analysis can be performed on latitudinal–longitudinal or Cartesian grids, making it highly adaptable to various geographical contexts. The outputs of the GWAM model, which are essential to the route optimization process, include the significant wave height, the mean wave period, and the prevailing sea state direction.
In this study, the GRIB files were downloaded with a time step of 3 h and a duration of 7 days for each sequence from 17 March to 24 March 2024, with 0.25° × 0.25° grid spacing. An example of the meteorological images that depict changes in environmental conditions during a certain period in the selected patch can be seen in Figure 4, which contains a photo series of GRIB files showing the trend of the significant wave height from 03:00 UTC on 17 March 2024 up to 00:00 UTC on 18 March 2024. In particular, the significant wave height is defined as:
where the wind wave component is denoted by while the swell component is indicated as . GRIB files can be easily read using open-source software like XyGrib v1.2.6 or, as in this case, imported into Matlab 2023a to be used as the input for subsequent simulations. The parameters of interest extracted include: the significant height, the prevailing direction, and the mean period of the wind wave surface; and also the significant height, the prevailing direction, and the mean period of the swell wave surface. These data represent the environmental factors used as the input in the optimization procedure, giving us the possibility to use either a single-peak spectrum, such as the JONSWAP spectrum, or a two-peak spectrum, such as the Torsethaugen spectrum [84]. By modifying the encounter sea state direction and accounting for speed variations caused by changes in added resistance, the encounter frequency is varied, which subsequently impacts the ship’s response to rough seas.
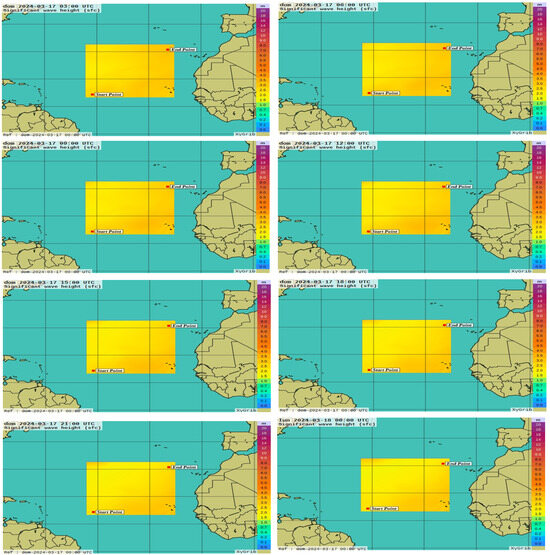
Figure 4.
Time trend of the significant wave height from 03:00 UTC on 17 March 2024 up to 00:00 UTC on 18 March 2024.
6. Case Study
After input data definition, the route optimization algorithm was initiated, testing three different starting speed values of 5, 10, and 15 knots, corresponding to Froude numbers of 0.15, 0.3, and 0.45, respectively.
To prove the effectiveness of the proposed solution, it was compared with a Dijkstra-based route planner [1,2].
The genetic algorithm, unlike Dijkstra’s algorithm, does not rely on a fixed grid of points but looks for waypoints defining the course between start and end points. The location of the waypoints is optimized in relative polar coordinates as defined above. The results shown in this section were obtained using the parameters in Table 3. In particular, the optimization process involves 100 epochs with a population size of 100 individuals, resulting in a total of 10,000 objective function evaluations. Being the solution that depended on a probabilistic evolution, the process was repeated 10 times to be sure that an optimal solution was found. No stopping criterion was considered to maintain a constant number of objective function evaluations.

Table 3.
Main genetic algorithm parameters.
To compare the proposed optimization process with an alternative solution available in the literature, a technique using the Dijkstra algorithm was investigated, known for its speed in yielding results. The Dijkstra algorithm identifies the shortest path between two points with known coordinates by maximizing a non-negative cost function, in this case the seakeeping performance index (SPI). Before assessing the ship performance, it is necessary to set up a network of nodes between the start and endpoint to define a region that constrains the ship’s route. This network, described in detail in [1,2], is a special form of a Dijkstra graph consisting of nodes and arcs, and it is defined following the steps reported in Lee et al. [85]. Specifically, the central point of the great circle is determined along with a set of center points along a rhumb line perpendicular to the great circle. Subsequently, a network of nodes is generated, considering a series of perpendicular rhumb lines in the first half of the great circle and a similarly occurring series in the second half. Each node is characterized by static information, such as geographic coordinates, and a dynamic grid with meteorological data, which are periodically updated. Once the network of nodes is defined, arcs connecting adjacent grid points are created, and a cost function based on the SPI values at the ends of the arcs is assigned to determine the optimal route. The algorithm is iteratively updated by changing the starting point based on elapsed time and the path already travelled by the ship.
Figure 5a,b provide the optimal paths with reference to FN = 0.15. In both cases, the great circle route is highlighted in black, the optimal route is represented in blue, and the black circles represent the departure and arrival points.
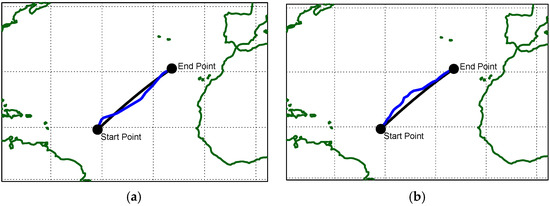
Figure 5.
Minimum distance (great circle) and optimal route detection, FN = 0.15: (a) genetic algorithm; (b) Dijkstra algorithm.
To evaluate the performance of the optimization procedure, several performance indices can be defined, taking into account the seakeeping criteria considered in Section 3 as follows:
where the subscript GC indicates the values related to the great circle trajectory, with GA being the genetic procedure result and D being the Dijkstra-based procedure resulting path.
Table 4 provides the values of the indices, revealing a significant performance improvement given by the proposed genetic procedure. Opting for the optimized trajectory over the great circle results in an overall improvement exceeding 57%, notably enhancing vertical plane movement and green water on deck probability management, thereby positively impacting navigation safety. On the other hand, the optimized route results in an increased travelled distance of about 3.8% with respect to the great circle route, equal to 59 nautical miles. However, the comparison with the Dijkstra-based procedure allows for an appreciation of the good performance of the proposed optimizer, with a loss in terms of trajectory length (and consequently fuel consumption) of only 0.9%.

Table 4.
Results of optimal route detection, FN = 0.15.
Figure 6a,b and Table 5 provide the results obtained with FN = 0.30. They confirm the obtained improvements, even if in this case the increase in the path length is 3.7%. The genetic-based route shows a 7.3% increase in the travelled distance compared with the great circle route, equal to 114 nautical miles.
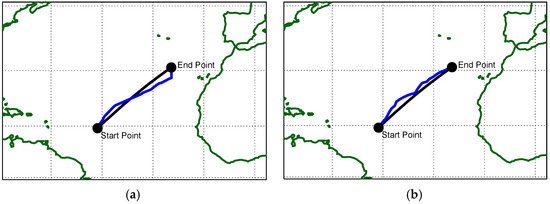
Figure 6.
Minimum distance (great circle) and optimal route detection, FN = 0.30: (a) genetic algorithm; (b) Dijkstra algorithm.

Table 5.
Results of optimal route detection, FN = 0.30.
Finally, Figure 7a,b and Table 6 provide results obtained with FN = 0.45. They confirm the improvements obtained using the proposed procedure. Furthermore, the analysis of the optimized routes reveals a 5.3% increase in distance traveled compared with the great circle route, equal to 82 nautical miles, while the Dijkstra-based results indicate only a 43 nautical mile increase over the great circle route, equivalent to 2.8%.
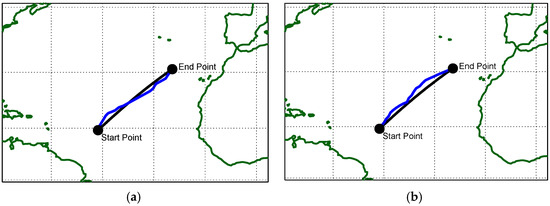
Figure 7.
Minimum distance (great circle) and optimal route detection, FN = 0.45: (a) genetic algorithm; (b) Dijkstra algorithm.

Table 6.
Results of optimal route detection, FN = 0.45.
The developed code was also applied by reversing the travel direction, therefore inverting the departure and arrival coordinates. Obviously, the results differ because the marine conditions encountered when traveling in the opposite direction vary. The outcomes are presented for a Froude number of 0.15 in Figure 8a,b and Table 7, demonstrating that the optimized trajectory compared with the great circle results in an overall improvement of more than 84%, particularly in the management of roll and pitch motions. However, the optimized route leads to an increased travel distance of about 3.7%, equivalent to 56.6 nautical miles. Meanwhile, the Dijkstra algorithm results in a smaller improvement in seakeeping indices and also an increased travel distance of 4.7%, approximately equal to 73 nautical miles.
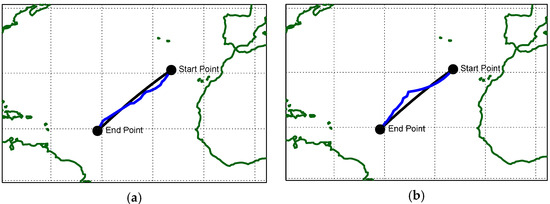
Figure 8.
Minimum distance (great circle) and optimal route detection, FN = 0.15: (a) genetic algorithm; (b) Dijkstra algorithm.

Table 7.
Results of optimal route detection, FN = 0.15.
The results for FN = 0.30, presented in Figure 9a,b and Table 8, indicate an improvement in this case as well. The SPI index improved by 45.4% compared with 19.7% for the Dijkstra algorithm, with a 7.7% increase in travel distance, equivalent to 120.5 nautical miles.
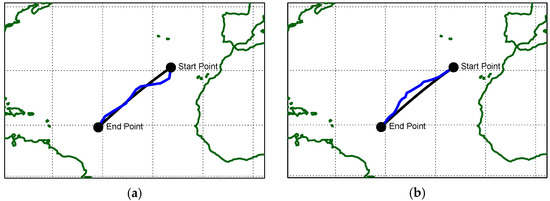
Figure 9.
Minimum distance (great circle) and optimal route detection, FN = 0.30: (a) genetic algorithm; (b) Dijkstra algorithm.

Table 8.
Results of optimal route detection, FN = 0.30.
Finally, the case for FN = 0.45 is presented in Figure 10 and Table 9. In this instance, the overall index improves by approximately 27%, with a notable reduction in roll motion. The increase in direction is only 1.1%, corresponding to 16.8 nautical miles, and the increase in distance is less than that obtained using the Dijkstra algorithm.
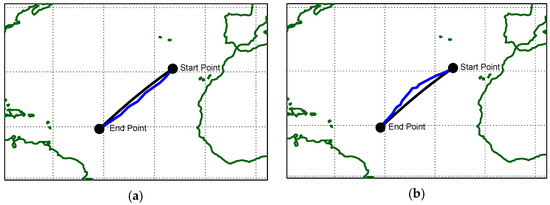
Figure 10.
Minimum distance (great circle) and optimal route detection, FN = 0.45: (a) genetic algorithm; (b) Dijkstra algorithm.

Table 9.
Results of optimal route detection, FN = 0.45.
The analysis of the results obtained through the application of the genetic and Dijkstra algorithms, in the context of weather routing, highlights that both algorithms are valuable tools for improving ship performance in adverse marine conditions. While Dijkstra’s algorithm quickly identifies optimal routes due to its predefined grid, the genetic algorithm, unrestricted by a grid, takes about 40 min to produce a solution, but it excels in optimizing seakeeping criteria. This comparison underlines a tradeoff between time efficiency and solution quality, suggesting that the choice between the algorithms should be based on specific project needs, use, and priorities.
Route optimization could be used at the design stage, considering a usual route and the most likely meteorological and marine conditions in the area, so that hydrodynamic performance can be used for optimizing the hull shape [86]. More commonly, a course optimization system can be used both for planning the ship’s path and during navigation. In this case, the initial condition response spectra can be obtained from measurements of ship motions in the time domain which, as seen in [87,88], can be easily obtained from low-cost measurement systems such as common smartphones. Indeed, these devices are generally equipped with several built-in sensors, providing raw data with a high sampling rate, and a GNSS receiver, which provides the device’s position and velocity in a global context.
7. Conclusions
This paper focuses on the integration of seakeeping indices into the trajectory planning of a mother ship dedicated to the launch and recovery operations of an autonomous drone. It aims to adapt seakeeping indices to minimize risks during UAV takeoff and landing in challenging sea conditions by considering vessel dynamics and environmental factors. The proposed trajectory planning algorithm computes optimal paths prioritizing ship stability and safety, thereby mitigating the adverse effects of weather on UAV operations.
The proposed genetic-based procedure, without the restriction of a predefined grid, increases the computational burden to produce a solution, but it is able to find a notable advantage in optimizing seakeeping criteria.
Based on the results obtained, the current outcomes are encouraging for continuing further research activities to make landing and takeoff operations safer. The developed algorithm can be integrated on board by modifying and varying the seakeeping indices to be considered, depending on the service the ship must perform and the utility and importance of using a specific index according to the specific ship mission. This approach can provide valuable support to navigation for both crewed and autonomous ships, thus achieving safer and more efficient navigation.
Future developments will focus on enhancing the model by integrating additional seakeeping indices, tailored to the specific needs of the ship and its mission. These indices will serve as constraints to refine trajectory planning under various conditions. The implemented model will be validated through onboard experimental tests to verify its effectiveness and assess its impact on the ship’s seakeeping and consequently on the safety of UAV landing and takeoff operations; more generally, the model’s contribution to safer and more efficient maritime navigation for any type of ship will be assessed. Additionally, the goal of the tests is to define a simulation model of ship-drone dynamics in rough seas, entirely developed in the time domain, in such a way as to define a robust cooperative path-following control algorithm.
Author Contributions
Conceptualization, E.D., S.P. and A.S.; methodology, S.R.B., E.D. and S.P.; software, S.R.B., E.D., S.I. and S.P.; formal analysis, S.R.B. and S.I.; writing—original draft preparation, S.R.B., S.I. and S.P.; writing—review and editing, E.D. and A.S.; supervision, E.D. and A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the research project—ID:P2022XER7W “CHEMSYS: Cooperative Heterogeneous Multi-drone SYStem for disaster prevention and first response” granted by the Italian Ministry of University and Research (MUR) within the PRIN 2022 PNRR program, funded by the European Union through the PNRR program.
Data Availability Statement
The data presented in this study are available on request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pennino, S.; Gaglione, S.; Innac, A.; Piscopo, V.; Scamardella, A. Development of a new ship adaptive weather routing model based on seakeeping analysis and optimization. J. Mar. Sci. Eng. 2020, 8, 270. [Google Scholar] [CrossRef]
- Pennino, S.; Scamardella, A. Weather Routing Model for Ship Motions Reduction and Fuel Saving. In Proceedings of the NAV 2022, International Conference on Ships and Maritime Research, Genoa and La Spezia, Italy, 15–17 June 2022. [Google Scholar]
- Christiansen, M.; Fagerholt, K.; Nygreen, B.; Ronen, D. Maritime transportation. In Handbooks in Operations Research and Management Science; Elsevier: Amsterdam, The Netherlands, 2017; Volume 14, pp. 189–284. [Google Scholar]
- Kontovas, C.A. The green ship routing and scheduling problem (GSRSP): A conceptual approach. Transp. Res. Part D Transp. Environ. 2014, 31, 61–69. [Google Scholar] [CrossRef]
- Szłapczynska, J.; Smierzchalski, R. Multicriteria optimisation in weather routing. Mar. Navig. Saf. Sea Transp. 2009, 3, 393–400. [Google Scholar]
- Delitala, A.M.; Gallino, S.; Villa, L.A.; Lagouvardos, K.; Drago, A. Weather routing in long-distance Mediterranean routes. Theor. Appl. Climatol. 2010, 102, 125–137. [Google Scholar] [CrossRef]
- Fabbri, T.; Vicen-Bueno, R.; Hunter, A. Multi-criteria weather routing optimization based on ship navigation resistance, risk and travel time. In Proceedings of the 2018 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 12–14 December 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Li, Y. An overview of the DSRC/WAVE technology. In Quality, Reliability, Security and Robustness in Heterogeneous Networks: 7th International Conference on Heterogeneous Networking for Quality, Reliability, Security and Robustness, QShine 2010, and Dedicated Short Range Communications Workshop, DSRC 2010, Houston, TX, USA, 17–19 November 2010; Revised Selected Papers 7; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Fisher, M.L.; Rosenwein, M.B. An interactive optimization system for bulk-cargo ship scheduling. Nav. Res. Logist. (NRL) 1989, 36, 27–42. [Google Scholar] [CrossRef]
- Lindstad, H.; Asbjørnslett, B.E.; Jullumstrø, E. Assessment of profit, cost and emissions by varying speed as a function of sea conditions and freight market. Transp. Res. Part D Transp. Environ. 2013, 19, 5–12. [Google Scholar] [CrossRef]
- Gershanik, V.I. Weather routing optimisation–challenges and rewards. J. Mar. Eng. Technol. 2011, 10, 29–40. [Google Scholar] [CrossRef]
- Zis, T.; North, R.J.; Angeloudis, P.; Ochieng, W.Y.; Bell, M.G.H. Evaluation of cold ironing and speed reduction policies to reduce ship emissions near and at ports. Marit. Econ. Logist. 2014, 16, 371–398. [Google Scholar] [CrossRef]
- Armstrong, V.N. Vessel optimisation for low carbon shipping. Ocean Eng. 2013, 73, 195–207. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957; 340p. [Google Scholar]
- Dasgupta, B.; Gupta, A.; Singla, E. A variational approach to path planning for hyper-redundant manipulators. Robot. Auton. Syst. 2009, 57, 194–201. [Google Scholar] [CrossRef]
- Shukla, A.; Singla, E.; Wahi, P.; Dasgupta, B. A direct variational method for planning monotonically optimal paths for redundant manipulators in constrained workspaces. Robot. Auton. Syst. 2013, 61, 209–220. [Google Scholar] [CrossRef]
- la Cour-Harbo, A.; Bisgaard, M. State-control trajectory generation for helicopter slung load system using optimal control. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009. [Google Scholar]
- Harada, M.; Nagata, H.; Simond, J.; Bollino, K. Optimal trajectory generation and tracking control of a single coaxial rotor UAV. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar]
- Xu, N.; Cai, G.; Kang, W.; Chen, B.M. Minimum-time trajectory planning for helicopter uavs using computational dynamic optimization. In Proceedings of the 2012 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Seoul, Republic of Korea, 14–17 October 2012; IEEE: Piscataway, NJ, USA, 2012. [Google Scholar]
- Dai, S.-L.; He, S.; Ma, Y.; Yuan, C. Distributed cooperative learning control of uncertain multiagent systems with prescribed performance and preserved connectivity. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 3217–3229. [Google Scholar] [CrossRef] [PubMed]
- Dubins, L.E. On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents. Am. J. Math. 1957, 79, 497–516. [Google Scholar] [CrossRef]
- Babel, L. Coordinated target assignment and UAV path planning with timing constraints. J. Intell. Robot. Syst. 2018, 94, 857–869. [Google Scholar] [CrossRef]
- Liu, P.; Yu, H.; Cang, S. Geometric analysis-based trajectory planning and control for underactuated capsule systems with viscoelastic property. Trans. Inst. Meas. Control. 2017, 40, 2416–2427. [Google Scholar] [CrossRef]
- Duan, H.; Zhao, J.; Deng, Y.; Shi, Y.; Ding, X. Dynamic discrete pigeon-inspired optimization for multi-UAV cooperative search-attack mission planning. IEEE Trans. Aerosp. Electron. Syst. 2020, 57, 706–720. [Google Scholar] [CrossRef]
- Scherer, S.; Singh, S.; Chamberlain, L.; Elgersma, M. Flying fast and low among obstacles: Methodology and experiments. Int. J. Robot. Res. 2008, 27, 549–574. [Google Scholar] [CrossRef]
- Scholer, F.; la Cour-Harbo, A.; Bisgaard, M. Configuration space and visibility graph generation from geometric workspaces for uavs. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Portland, OR, USA, 8–11 August 2011. [Google Scholar]
- Scholer, F.; la Cour-Harbo, A.; Bisgaard, M. Generating approximative minimum length paths in 3D for UAVs. In Proceedings of the 2012 IEEE Intelligent Vehicles Symposium, Alcala de Henares, Spain, 3–7 June 2012; IEEE: Piscataway, NJ, USA, 2012. [Google Scholar]
- Maini, P.; Sujit, P.B. Path planning for a UAV with kinematic constraints in the presence of polygonal obstacles. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Bortoff, S.A. Path planning for UAVs. In Proceedings of the 2000 American Control Conference, Chicago, IL, USA, 28–30 June 2000; ACC (IEEE Cat. No. 00CH36334). IEEE: Piscataway, NJ, USA, 2000; Volume 1. [Google Scholar]
- Pehlivanoglu, Y.V. A new vibrational genetic algorithm enhanced with a Voronoi diagram for path planning of autonomous UAV. Aerosp. Sci. Technol. 2012, 16, 47–55. [Google Scholar] [CrossRef]
- Lin, Y.; Saripalli, S. Path planning using 3D dubins curve for unmanned aerial vehicles. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Yang, J. Real-Time Trajectory Planning for Ground and Aerial Vehicles in a Dynamic Environment; University of Central Florida: Orlando, FL, USA, 2008. [Google Scholar]
- Véras, L.G.; Medeiros, F.L.; Guimarães, L.N. Rapidly exploring Random Tree* with a sampling method based on Sukharev grids and convex vertices of safety hulls of obstacles. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419825941. [Google Scholar] [CrossRef]
- Liu, Y.-H.; Arimoto, S. Proposal of tangent graph and extended tangent graph for path planning of mobile robots. In Proceedings of the 1991 IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; IEEE Computer Society: Piscataway, NJ, USA, 1991. [Google Scholar]
- Cover, H.; Choudhury, S.; Scherer, S.; Singh, S. Sparse tangential network (SPARTAN): Motion planning for micro aerial vehicles. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Babel, L. Curvature-constrained traveling salesman tours for aerial surveillance in scenarios with obstacles. Eur. J. Oper. Res. 2017, 262, 335–346. [Google Scholar] [CrossRef]
- Yan, F.; Liu, Y.-S.; Xiao, J.-Z. Path planning in complex 3D environments using a probabilistic roadmap method. Int. J. Autom. Comput. 2013, 10, 525–533. [Google Scholar] [CrossRef]
- Musliman, I.A.; Rahman, A.A.; Coors, V. Implementing 3D network analysis in 3D-GIS. Int. Arch. ISPRS 2008, 37, 913–918. [Google Scholar]
- de Heer, H.D.; Balcazar, H.G.; Castro, F.; Schulz, L. A path analysis of a randomized promotora de salud cardiovascular disease–prevention trial among at-risk Hispanic adults. Health Educ. Behav. 2012, 39, 77–86. [Google Scholar] [CrossRef] [PubMed]
- Carsten, J.; Ferguson, D.; Stentz, A. 3D Field D: Improved Path Planning and Replanning in Three Dimensions. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–13 October 2006; IEEE: Piscataway, NJ, USA, 2006. [Google Scholar]
- Eun, Y.; Bang, H. Cooperative control of multiple unmanned aerial vehicles using the potential field theory. J. Aircr. 2006, 43, 1805–1814. [Google Scholar] [CrossRef]
- Kitamura, Y.; Tanaka, T.; Kishino, F.; Yachida, M. 3-D path planning in a dynamic environment using an octree and an artificial potential field. In Proceedings of the 1995 IEEE/RSJ International Conference on Intelligent Robots and Systems, Human Robot Interaction and Cooperative Robots, Pittsburgh, PA, USA, 5–9 August 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 2. [Google Scholar]
- Roberge, V.; Tarbouchi, M.; Labonte, G. Fast genetic algorithm path planner for fixed-wing military UAV using GPU. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2105–2117. [Google Scholar] [CrossRef]
- Chai, R.; Tsourdos, A.; Savvaris, A.; Chai, S.; Xia, Y. Solving constrained trajectory planning problems using biased particle swarm optimization. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1685–1701. [Google Scholar] [CrossRef]
- Dever, C.; Mettler, B.; Feron, E.; Popovic, J.; McConley, M. Nonlinear trajectory generation for autonomous vehicles via parametrized maneuver classes. J. Guid. Control. Dyn. 2006, 29, 289–302. [Google Scholar] [CrossRef][Green Version]
- Frazzoli, E.; Dahleh, M.A.; Feron, E. Real-time motion planning for agile autonomous vehicles. J. Guid. Control. Dyn. 2002, 25, 116–129. [Google Scholar] [CrossRef]
- Blasi, L.; Barbato, S.; D’Amato, E. A mixed probabilistic–geometric strategy for UAV optimum flight path identification based on bit-coded basic manoeuvres. Aerosp. Sci. Technol. 2017, 71, 1–11. [Google Scholar] [CrossRef]
- James, R.W. Application of Wave Forecasts to Marine Navigation; New York University: New York, NY, USA, 1957. [Google Scholar]
- Hagiwara, H.; Spaans, J.A. Practical weather routing of sail-assisted motor vessels. J. Navig. 1987, 40, 96–119. [Google Scholar] [CrossRef]
- Haltiner, G.; Hamilton, H.; Arnason, G. Minimal-time ship routing. J. Appl. Meteorol. 1962, 1, 1–7. [Google Scholar] [CrossRef][Green Version]
- Chen, Y.; Tian, W.; Mao, W. Strategies to improve the isochrone algorithm for ship voyage optimisation. Ships Offshore Struct. 2024, 1–13. [Google Scholar] [CrossRef]
- Papadakis, N. Minimal Time Vessel Routing Problem. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1988. [Google Scholar]
- Wei, S.; Zhou, P. Development of a 3D Dynamic Programming Method for Weather Routing. In Methods and Algorithms in Navigatiom, 1st ed.; Taylor & Francis Group: Abingdon, UK, 2011. [Google Scholar]
- de Wit, C. Proposal for Low Cost Ocean Weather Routeing. J. Navig. 1990, 43, 428–439. [Google Scholar] [CrossRef]
- Zaccone, R.; Ottaviani, E.; Figari, M.; Altosole, M. Ship voyage optimization for safe and energy-efficient navigation: A dynamic programming approach. Ocean Eng. 2018, 153, 215–224. [Google Scholar] [CrossRef]
- Padhy, C.P.; Sen, D.; Bhaskaran, P.K. Application of wave model for weather routing of ships in the North Indian Ocean. Nat. Hazards 2007, 44, 373–385. [Google Scholar] [CrossRef]
- Veneti, A.; Makrygiorgos, A.; Konstantopoulos, C.; Pantziou, G.; Vetsikas, I.A. Minimizing the fuel consumption and the risk in maritime transportation: A bi-objective weather routing approach. Comput. Oper. Res. 2017, 88, 220–236. [Google Scholar] [CrossRef]
- Huu, K.D. Research on Ship Weather Routing Method Based on Dijkstra Algorithm and Neural Network. In Proceedings of the 2024 International Conference on Industrial Engineering, Applications and Manufacturing, ICIEAM, Sochi, Russia, 20–24 May 2024. [Google Scholar]
- Motte, R.H.; Calvert, S. On the selection of discrete grid systems for on-board micro-based weather routeing. J. Navig. 1990, 43, 104–117. [Google Scholar] [CrossRef]
- Montes, A.A. Network Shortest Path Application for Optimum Track Ship Routing. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 2005. [Google Scholar]
- Panigrahi, J.K.; Padhy, C.P.; Sen, D.; Swain, J.; Larsen, O. Optimal ship tracking on a navigation route between two ports: A hydrodynamics approach. J. Mar. Sci. Technol. 2012, 17, 59–67. [Google Scholar] [CrossRef]
- Mannarini, G.; Pinardi, N.; Coppini, G.; Oddo, P.; Iafrati, A. VISIR-I: Small vessels-least-time nautical routes using wave forecasts. Geosci. Model Dev. 2016, 9, 1597–1625. [Google Scholar] [CrossRef]
- van Dooren, S.; Duhr, P.; Onder, C.H. Convex modelling for ship speed optimisation. Ocean Eng. 2023, 28815, 11594. [Google Scholar] [CrossRef]
- Du, W.; Li, Y.; Zhang, G.; Wang, C.; Zhu, B.; Qiao, J. Ship weather routing optimization based on improved fractional order particle swarm optimization. Ocean. Eng. 2022, 24815, 110680. [Google Scholar] [CrossRef]
- Walther, L.; Shetty, S.; Rizvanolli, A.; Jahn, C. Comparing two optimization approaches for ship weather routing. In Operations Research Proceedings 2016: Selected Papers of the Annual International Conference of the German Operations Research Society (GOR), Helmut Schmidt University, Hamburg, Germany, 30 August–2 September 2016; Springer: Berlin/Heidelberg, Germany, 2018; pp. 337–342. [Google Scholar]
- Wang, H.-B.; Li, X.-G.; Li, P.-F.; Veremey, E.I.; Sotnikova, M.V. Application of real-coded genetic algorithm in ship weather routing. J. Navig. 2018, 71, 989–1010. [Google Scholar] [CrossRef]
- Yuankui, L.; Yingjun, Z.; Feixiang, Z. Minimal time route for wind-assisted ships. Mar. Technol. Soc. J. 2014, 48, 115–124. [Google Scholar] [CrossRef]
- Tsou, M.-C. Integration of a geographic information system and evolutionary computation for automatic routing in coastal navigation. J. Navig. 2010, 63, 323–341. [Google Scholar] [CrossRef]
- Azariadis, P. On using density maps for the calculation of ship routes. Evol. Syst. 2017, 8, 135–145. [Google Scholar] [CrossRef]
- Li, G.; Zhang, H. A Bézier curve based ship trajectory optimization for close-range maritime operations. In Proceedings of the ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering, American Society of Mechanical Engineers, Trondheim, Norway, 25–30 June 2017. [Google Scholar]
- Szlapczynska, J. Multiobjective approach to weather routing. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2007, 1, 273–278. [Google Scholar]
- Szlapczynska, J. Multi-objective weather routing with customised criteria and constraints. J. Navig. 2015, 68, 338–354. [Google Scholar] [CrossRef]
- Vettor, R.; Soares, C.G. Development of a ship weather routing system. Ocean Eng. 2016, 123, 1–14. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, Y.; Zhang, Z.; Wang, H. Multicriteria ship route planning method based on improved particle swarm optimization–genetic algorithm. J. Mar. Sci. Eng. 2021, 9, 357. [Google Scholar] [CrossRef]
- Arantes, M.D.S.; Arantes, J.D.S.; Toledo, C.F.M.; Williams, B.C. A hybrid multi-population genetic algorithm for UAV path planning. In Proceedings of the Genetic and Evolutionary Computation Conference 2016, Denver, CO, USA, 20–24 July 2016; ACM: New York, NY, USA, 2016; pp. 853–860. [Google Scholar]
- Hasircioglu, I.; Topcuoglu, H.R.; Ermis, M. 3-D path planning for the navigation of unmanned aerial vehicles by using evolutionary algorithms. In Proceedings of the 10th Annual Conference on Genetic and Evolutionary Computation 2008, Atlanta, GA, USA, 12–16 July 2008; pp. 1499–1506. [Google Scholar]
- Ragusa, V.R.; Mathias, H.D.; Kazakova, V.A.; Wu, A.S. Enhanced genetic path planning for autonomous flight. In Proceedings of the Genetic and Evolutionary Computation Conference 2017, Berlin, Germany, 15–19 July 2017; pp. 1208–1215. [Google Scholar]
- Li, J.; Zhang, G.; Zhang, X.; Zhang, W. Integrating Dynamic Event-Triggered and Sensor-Tolerant Control: Application to USV-UAVs Cooperative Formation System for Maritime Parallel Search. IEEE Trans. Intell. Transp. Syst. 2023, 25, 3986–3998. [Google Scholar] [CrossRef]
- Li, J.; Zhang, G.; Zhang, W.; Shan, Q.; Zhang, W. Cooperative Path Following Control of USV-UAVs Considering Low Design Complexity and Command Transmission Requirement. IEEE Trans. Intell. Veh. 2024, 9, 715–724. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurement of Wind Wave Growth and Swell Decay during the Joint North Sea Wave Project (JONSWAP). Ergaenzungsheft Dtsch. Hydrogr. Z. Reihe A 1973, 12, 1–95. [Google Scholar]
- Bretschneider, C.L. The generation and decay of wind waves in deep water. Trans. Am. Geophys. Union 1952, 33, 381–389. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Komen, G.J.; Cavaleri, L.; Donelan, M.; Hasselmann, K.; Janssen, P.A.E.M.; Hasselmann, S. Dynamics and Modelling of Ocean Waves; Cambridge University Press (CUP): Cambridge, UK, 1994. [Google Scholar]
- Torsethaugen, K. A two-peak wave spectral model. In Proceedings of the 12th International Conference on Offshore Mechanics and Arctic Engineering, Glasgow, UK, 20–24 June 1993; Volume 2, pp. 175–180. [Google Scholar]
- Lee, H.; Kong, G.; Kim, S.; Kim, C.; Lee, J. Optimum Ship Routing and It’s Implementation on the Web. In Computer Vision; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2002; Volume 2402, pp. 125–136. [Google Scholar]
- Grigoropoulos, G.J. Hull Form Optimization for Hydrodynamic Performance. Mar. Technol. Mar. Technol. 2004, 41, 167–182. [Google Scholar] [CrossRef]
- Pennino, S.; Scamardella, A. Motions Assessment Using a Time Domain Approach for a Research Ship in Antarctic Waters. J. Mar. Sci. Eng. 2023, 11, 558. [Google Scholar] [CrossRef]
- Pennino, S.; Angrisano, A.; Della Corte, V.; Ferraioli, G.; Gaglione, S.; Innac, A.; Martellato, E.; Palumbo, P.; Piscopo, V.; Rotundi, A.; et al. Sea state monitoring by ship motion measurements onboard a research ship in the antarctic waters. J. Mar. Sci. Eng. 2021, 9, 64. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).