Global Chlorophyll Concentration Distribution and Effects on Bottom Reflectance of Coral Reefs
Abstract
1. Introduction
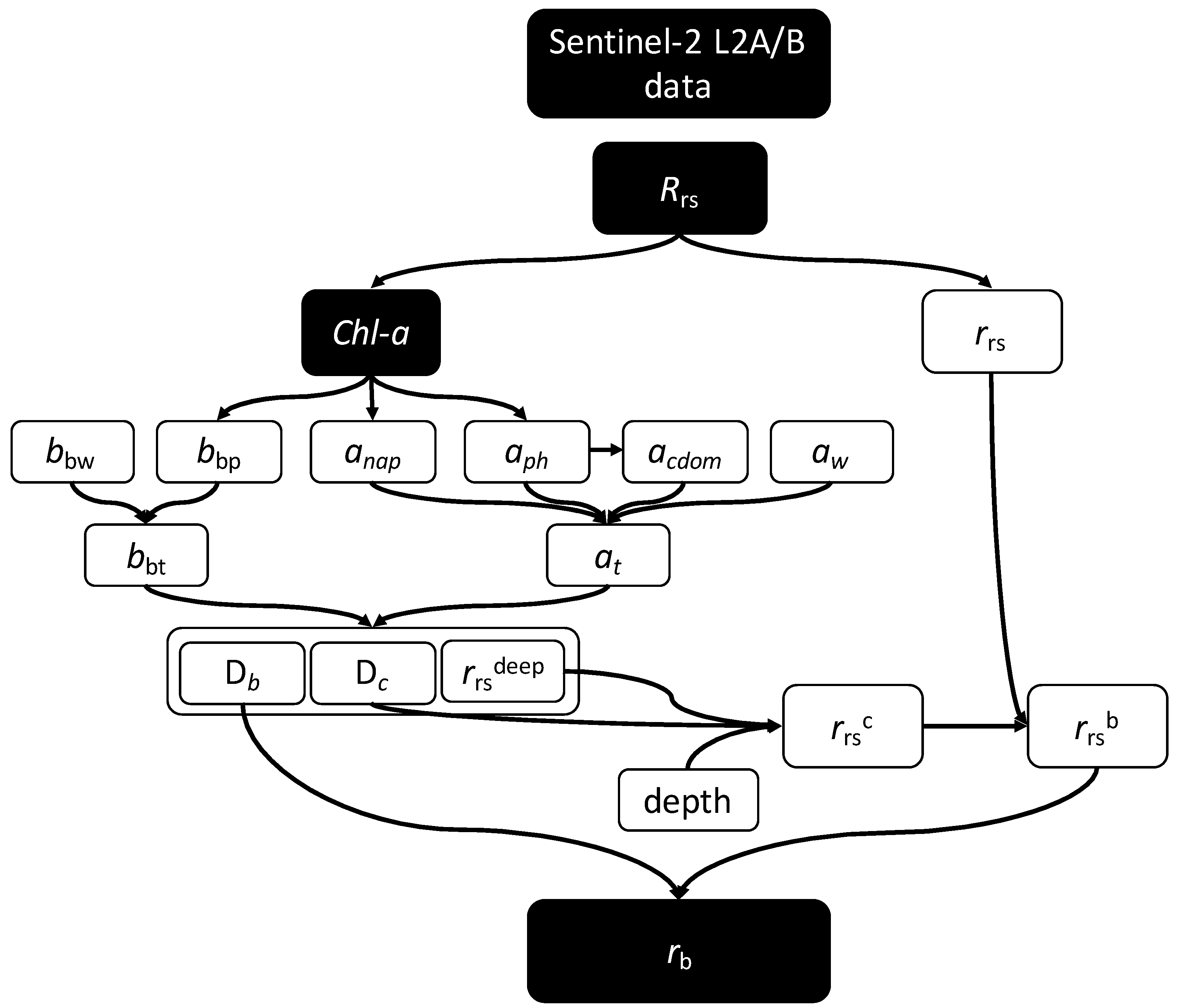
2. Materials and Methods
2.1. Satellite Data
2.2. Chl-a Calculation
2.3. Bottom Reflectance Calculation
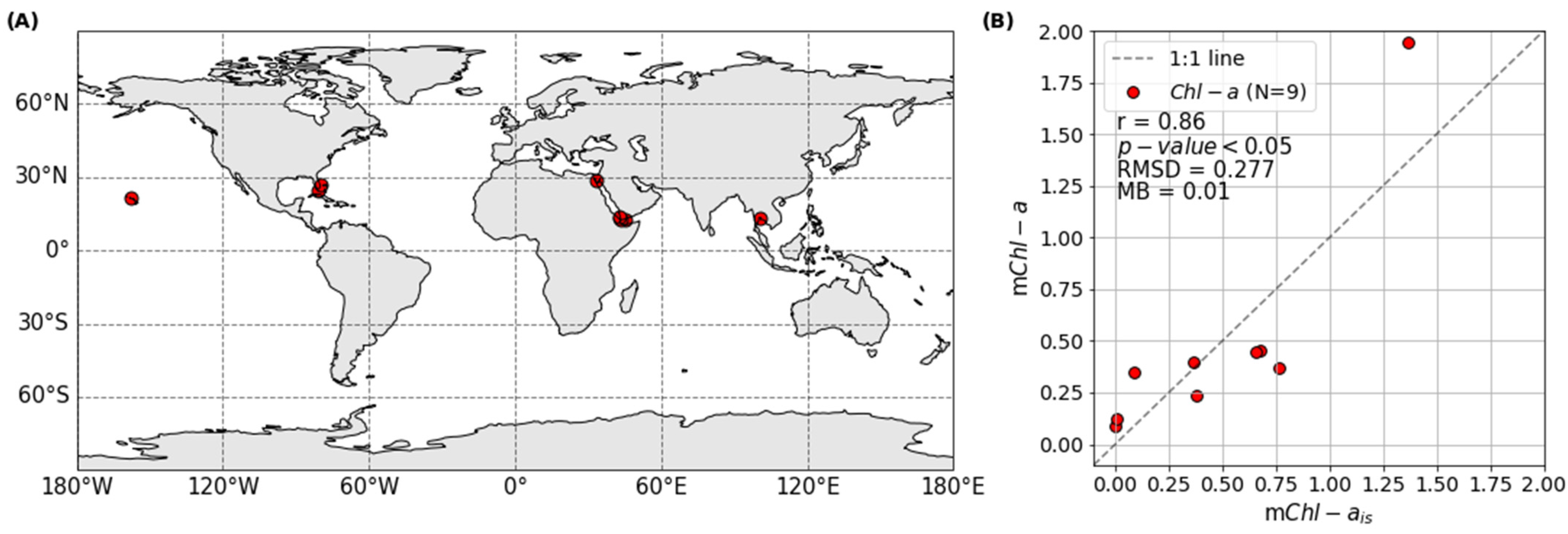
2.4. Satellite-Derived mChl-a Validation
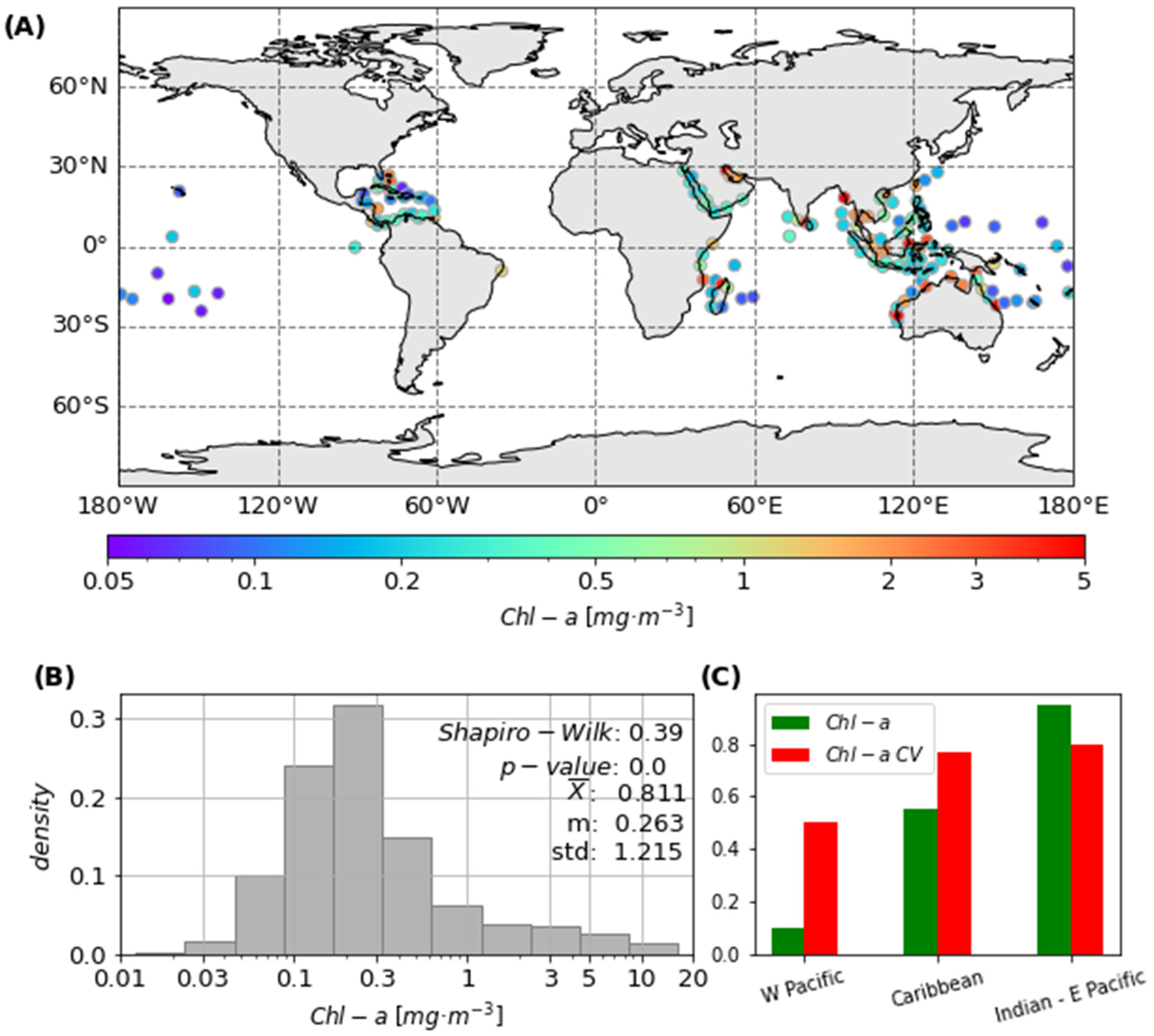
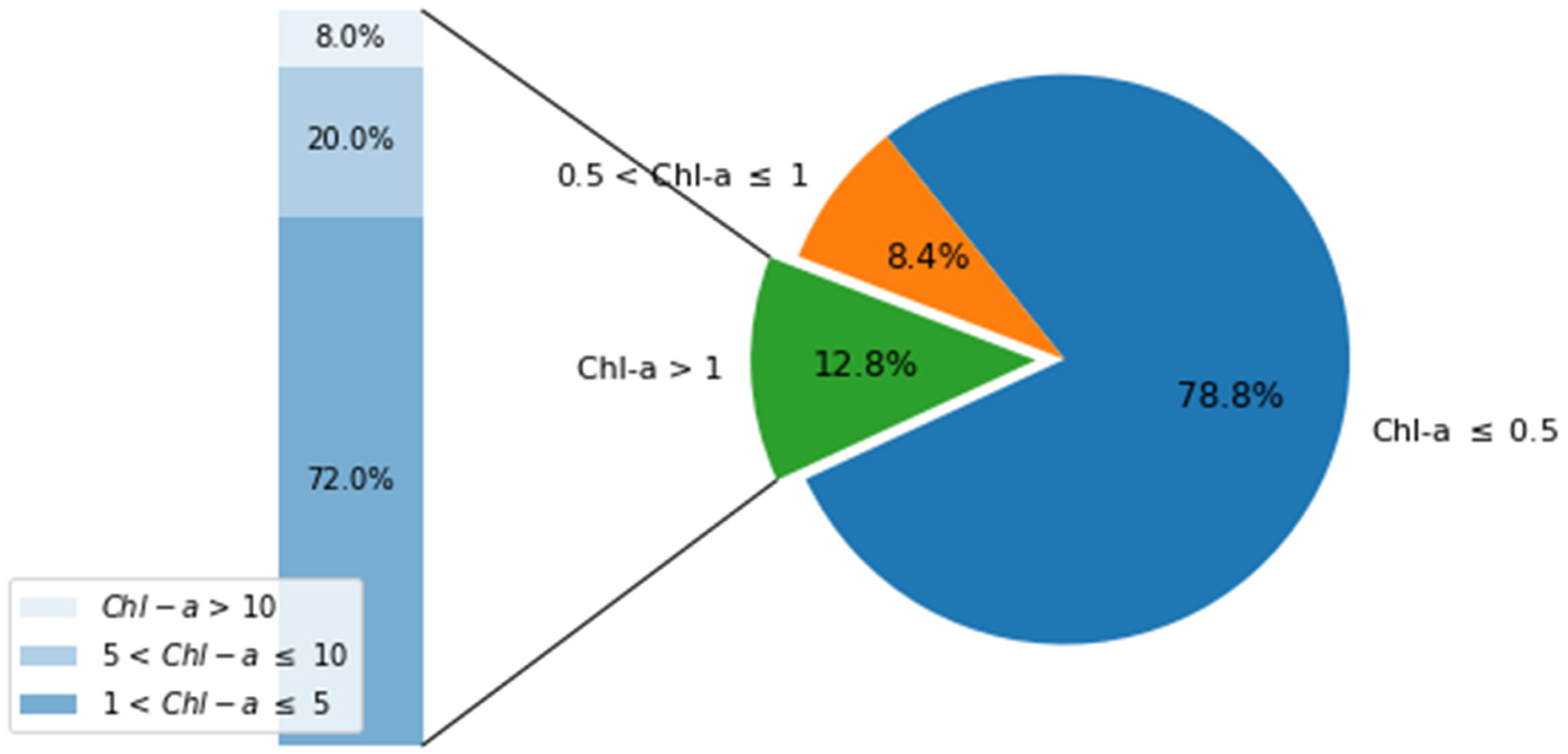
2.5. Satellite-Derived Chl-a Spatial Distribution Variability
2.6. Sensitivity Analysis
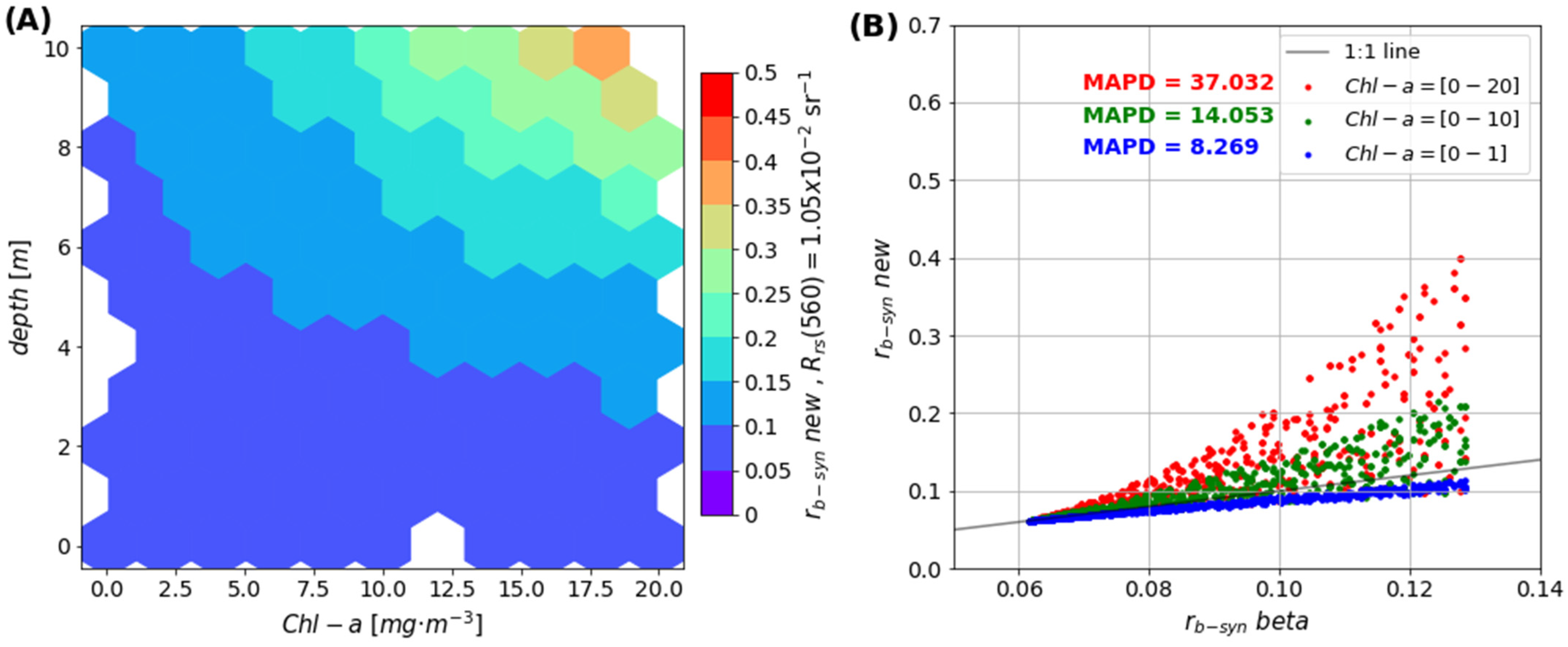
2.7. Comparison of rb-sat new vs. rb-sat beta
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mulhall, M. Saving the rainforests of the sea: An analysis of international efforts to conserve coral reefs. Duke Environ. Law Policy Forum. 2009, 19, 321–351. [Google Scholar]
- Where are Corals Found? NOAA Coral Reef Conservation Program. National Oceanic and Atmospheric Administration (NOAA). Available online: http://coralreef.noaa.gov/aboutcorals/coral101/corallocations/ (accessed on 19 December 2023).
- Spalding, M.D.; Grenfell, A.M. New estimates of global and regional coral reef areas. Coral Reefs 1997, 16, 225–230. [Google Scholar] [CrossRef]
- Spalding, M.D.; Ravilious, C.; Green, P.E. World Atlas of Coral Reefs; University of California Press: Berkley, CA, USA, 2001; Volume 39. [Google Scholar] [CrossRef]
- Pendleton, L.; Wilson, M.A.; Farber, S.; Colgan, C.S.; Lipton, D.; Kasperski, S.; Dismukes, D.E.; Barnett, M.L.; Darb, K.A.R.; Jin, D.; et al. The Economic and Market Value of Coasts and Estuaries: What’s at Stake? (Pendleton LH, ed.). Restore America’s Estuaries; 2010; Volume 182. Available online: https://repository.library.noaa.gov/view/noaa/10108/noaa_10108_DS1.pdf (accessed on 28 September 2023).
- Schill, S.; Knowles, J.; Rowlands, G.; Margles, S.; Agostini, V.; Blyther, R. Coastal Benthic Habitat Mapping to Support Marine Resource Planning and Management in St. Kitts and Nevis. Geogr. Compass 2011, 5, 898–917. [Google Scholar] [CrossRef]
- Stolt, M.; Bradley, M.; Turenne, J.; Payne, M.; Scherer, E.; Cicchetti, G.; Shumchenia, E.; Guarinello, M.; King, J.; Boothroyd, J.; et al. Mapping Shallow Coastal Ecosystems: A Case Study of a Rhode Island Lagoon. J. Coast. Res. 2011, 27, 1–15. [Google Scholar] [CrossRef]
- Barbier, E.B.; Koch, E.W.; Silliman, B.R.; Hacker, S.D.; Wolanski, E.; Primavera, J.; Granek, E.F.; Polasky, S.; Aswani, S.; Cramer, L.A.; et al. Coastal ecosystem-based management with nonlinear ecological functions and values. Science 2008, 319, 321–323. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C. Applying data fusion techniques for benthic habitat mapping and monitoring in a coral reef ecosystem. ISPRS J. Photogramm. Remote Sens. 2015, 104, 213–223. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, H.; Li, X.; Wang, J.; Cao, W.; Li, D.; Lou, X.; Fan, K. An exponential algorithm for bottom reflectance retrieval in clear optically shallow waters from multispectral imagery without ground data. Remote Sens. 2021, 13, 1169. [Google Scholar] [CrossRef]
- Xu, Y.; Vaughn, N.R.; Knapp, D.E.; Martin, R.E.; Balzotti, C.; Li, J.; Foo, S.A.; Asner, G.P. Coral bleaching detection in the hawaiian islands using spatio-temporal standardized bottom reflectance and planet dove satellites. Remote Sens. 2020, 12, 3219. [Google Scholar] [CrossRef]
- Dubinsky, Z.; Stambler, N. Coral Reefs: An Ecosystem in Transition; Springer Science and Business Media LLC: Dordrecht, The Netherlands, 2011. [Google Scholar] [CrossRef]
- Hu, C.; Lee, Z.; Franz, B. Chlorophyll a algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. Ocean. 2012, 117, C01011. [Google Scholar] [CrossRef]
- Angal, A.; Xiong, X.; Shrestha, A. Cross-calibration of MODIS reflective solar bands with sentinel 2A/2B MSI instruments. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5000–5007. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Werdell, P.J. Chlorophyll algorithms for ocean color sensors—OC4, OC5 & OC6. Remote Sens. Environ. 2019, 229, 32–47. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Fabina, N.S.; Knapp, D.E.; Asner, G.P. The sensitivity of multi-spectral satellite sensors to benthic habitat change. Remote Sens. 2020, 12, 532. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral Remote Sensing for Shallow Waters. I. A Semianalytical. Model. Appl. Opt. 1998, 37, 6329–6338. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Knapp, D.E.; Lyons, M.; Roelfsema, C.; Phinn, S.; Schill, S.R.; Asner, G.P. Automated global shallowwater bathymetry mapping using google earth engine. Remote Sens. 2021, 13, 1469. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters: 2 Deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831. [Google Scholar] [CrossRef]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef]
- Lee, Z.; Weidemann, A.; Arnone, R. Combined effect of reduced band number and increased bandwidth on shallow water remote sensing: The case of world view 2. IEEE Trans Geosci Remote Sens. 2013, 51, 2577–2586. [Google Scholar] [CrossRef]
- Lee, Z.; Lubac, B.; Werdell, J.; Arnone, R. An Update of the Quasi-Analytical Algorithm (QAA_v5). 2009, IOCCG software report. Available online: http://www.ioccg.org/groups/Software_OCA/QAA_v5.pdf (accessed on 19 August 2023).
- Bricaud, A.; Morel, A.; Babin, M.; Allali, K.; Claustre, H. Variations of light absorption by suspended particles with chlorophyll a concentration in oceanic (case 1) waters: Analysis and implications for bio-optical models. J. Geophys. Res. Ocean. 1998, 103, 31033–31044. [Google Scholar] [CrossRef]
- Morel, A.; Maritorena, S. Bio-optical properties of oceanic waters: A reappraisal. J. Geophys. Res. Ocean. 2001, 106, 7163–7180. [Google Scholar] [CrossRef]
- Smith, R.C.; Baker, K.S. Optical properties of the clearest natural waters (200–800 nm). Appl. Opt. 1981, 20, 177–184. [Google Scholar] [CrossRef]
- Werdell, P.J.; Bailey, S.; Fargion, G.; Pietras, C.; Knobelspiesse, K.; Feldman, G.; McClain, C. Unique data repository facilitates ocean color satellite validation. EOS Trans. AGU 2003, 84, 377–387. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Campolongo, F.; Saltelli, A.; Cariboni, J. From screening to quantitative sensitivity analysis. A unified approach. Comput. Phys. Commun. 2011, 182, 978–988. [Google Scholar] [CrossRef]
- Owen, A.B. On Dropping the First Sobol’ Point. Springer Proc. Math. Stat. 2022, 387, 71–86. [Google Scholar] [CrossRef]
- Saltelli, A. Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun. 2002, 145, 280–297. [Google Scholar] [CrossRef]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Li, J.; Yu, Q.; Tian, Y.Q.; Becker, B.L.; Siqueira, P.; Torbick, N. Spatio-temporal variations of CDOM in shallow inland waters from a semi-analytical inversion of Landsat-8. Remote Sens. Environ. 2018, 218, 189–200. [Google Scholar] [CrossRef]
- Reichstetter, M.; Fearns, P.; Weeks, S.; McKinna, L.; Roelfsema, C.; Furnas, M. Bottom Reflectance in Ocean Color Satellite Remote Sensing for Coral Reef Environments. Remote Sens. 2015, 7, 16756–16777. [Google Scholar] [CrossRef]
- Birkeland, C. Caribbean and Pacific Coastal marine system: Similarities and differences. Nat. Resour. 1990, 26, 3–12. [Google Scholar]
- Kidd, R.; Sander, F. Influence of Amazon River discharge on the marine production system off Barbados, West Indies. J. Mar. Res. 1981, 37, 669–682. [Google Scholar]
- Bienfang, P.K.; Szyper, J.P.; Okamoto, M.Y.; Noda, E.K. Temporal and spatial variability of phytoplankton in a subtropical ecosystem. Limnol. Oceanogr. 1984, 29, 527–539. [Google Scholar] [CrossRef]
- Tranter, D.J.; Leech, G.S. Factors influencing the standing crop of phytoplankton on the Australian Northwest Shelf seaward of the 40 m isobath. Cont. Shelf Res. 1987, 7, 115–133. [Google Scholar] [CrossRef]
- Slijkerman, D.M.E.; de León, R.; de Vries, P. A baseline water quality assessment of the coastal reefs of Bonaire, Southern Caribbean. Mar. Pollut. Bull. 2014, 86, 523–529. [Google Scholar] [CrossRef] [PubMed]
- Otero, E.; Carbery, K.K. Revista de Biología Tropical Chlorophyll a and turbidity patterns over coral reefs systems of La Parguera Natural Reserve, Puerto. J. Trop. Biol. 2005, 53, 25–32. Available online: http://www.redalyc.org/articulo.oa?id=44920889003 (accessed on 15 July 2023).
- Racault, M.-F.; Raitsos, D.E.; Berumen, M.L.; Brewin, R.J.; Platt, T.; Sathyendranath, S.; Hoteit, I. Phytoplankton phenology indices in coral reef ecosystems: Application to ocean-color observations in the Red Sea. Remote Sens. Environ. 2015, 160, 222–234. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Raitsos, D.E.; Pradhan, Y.; Hoteit, I. Comparison of chlorophyll in the Red Sea derived from MODIS-Aqua and in vivo fluorescence. Remote Sens. Environ. 2013, 136, 218–224. [Google Scholar] [CrossRef]
- Barbini, R.; Colao, F.; De Dominicis, L.; Fantoni, R.; Fiorani, L.; Palucci, A.; Artamonov, E.S. Analysis of simultaneous chlorophyll measurements by lidar fluorosensor, MODIS and SeaWiFS. Int. J. Remote Sens. 2004, 25, 2095–2110. [Google Scholar] [CrossRef]
- Boss, E.; Picheral, M.; Leeuw, T.; Chase, A.; Karsenti, E.; Gorsky, G.; Taylor, L.; Slade, W.; Ras, J.; Claustre, H. The characteristics of particulate absorption, scattering and attenuation coefficients in the surface ocean; Contribution of the Tara Oceans expedition. Methods Oceanogr. 2013, 7, 52–62. [Google Scholar] [CrossRef]
- Werdell, P.J.; Proctor, C.W.; Boss, E.; Leeuw, T.; Ouhssain, M. Underway sampling of marine inherent optical properties on the Tara Oceans expedition as a novel resource for ocean color satellite data product validation. Methods Oceanogr. 2013, 7, 40–51. [Google Scholar] [CrossRef]
- Ghaemi, M.; Abtahi, B.; Gholamipour, S. Spatial distribution of nutrients and chlorophyll a across the Persian Gulf and the Gulf of Oman. Ocean Coast. Manag. 2021, 201, 105476. [Google Scholar] [CrossRef]
- Polikarpov, I.; Saburova, M.; Al-Yamani, F. Diversity and distribution of winter phytoplankton in the Arabian Gulf and the Sea of Oman. Cont. Shelf Res. 2016, 119, 85–99. [Google Scholar] [CrossRef]
- Dupouy, C.; Wattelez, G.; Fuchs, R.; Murakami, H.; Frouin, R. The colour of the Coral Sea. In Proceedings of the 12th International Coral Reef Symposium, Cairns, Australia, 9–13 July 2012. [Google Scholar] [CrossRef]
- Wattelez, G.; Dupouy, C.; Mangeas, M.; Lefèvre, J.; Touraivane Frouin, R. A statistical algorithm for estimating chlorophyll concentration in the New Caledonian lagoon. Remote Sens. 2016, 8, 45. [Google Scholar] [CrossRef]
- Rubio-Cisneros, N.T.; Herrera-Silveira, J.; Morales-Ojeda, S.; Moreno-Báez, M.; Montero, J.; Pech-Cárdenas, M. Water quality of inlets’ water bodies in a growing touristic barrier reef Island “Isla Holbox” at the Yucatan Peninsula. Reg. Stud. Mar. Sci. 2018, 22, 112–124. [Google Scholar] [CrossRef]
- Silva, B.J.; Ibánhez, J.S.P.; Pinheiro, B.R.; Ladle, R.J.; Malhado, A.C.; Pinto, T.K.; Flores-Montes, M.J. Seasonal influence of surface and underground continental runoff over a reef system in a tropical marine protected area. J. Mar. Syst. 2022, 226, 103660. [Google Scholar] [CrossRef]
- Barroso, H.d.S.; Lima, I.d.O.; Bezerra, A.D.A.; Garcia, T.M.; Tavares, T.C.L.; Alves, R.S.; Junior, E.F.d.S.; Teixeira, C.E.P.; Viana, M.B.; Soares, M.O. Distribution of nutrients and chlorophyll across an equatorial reef region: Insights on coastal gradients. Ocean Coast. Res. 2023, 71 (Suppl. 2), e23002. [Google Scholar] [CrossRef]
- Cazzaniga, I.; Bresciani, M.; Colombo, R.; Della Bella, V.; Padula, R.; Giardino, C. A comparison of Sentinel-3-OLCI and Sentinel-2-MSI-derived Chlorophyll-a maps for two large Italian lakes. Remote Sens. Lett. 2019, 10, 978–987. [Google Scholar] [CrossRef]
- Smith, B.; Pahlevan, N.; Schalles, J.; Ruberg, S.; Errera, R.; Ma, R.; Giardino, C.; Bresciani, M.; Barbosa, C.; Moore, T.; et al. A Chlorophyll-a Algorithm for Landsat-8 Based on Mixture Density Networks. Front. Remote Sens. 2021, 1, 623678. [Google Scholar] [CrossRef]
- Tran, M.D.; Vantrepotte, V.; Loisel, H.; Oliveira, E.N.; Tran, K.T.; Jorge, D.; Mériaux, X.; Paranhos, R. Band Ratios Combination for Estimating Chlorophyll-a from Sentinel-2 and Sentinel-3 in Coastal Waters. Remote Sens. 2023, 15, 1653. [Google Scholar] [CrossRef]
- Gregg, W.W.; Conkright, M.E. Decadal changes in global ocean chlorophyll. Geophys. Res. Lett. 2002, 29, 20-1–20-4. [Google Scholar] [CrossRef]
- Gregg, W.W.; Conkright, M.E. Recent trends in global ocean chlorophyll. Geophys. Res. Lett. 2005, 32, 1–5. [Google Scholar] [CrossRef]
- Vantrepotte, V.; Loisel, H.; Mélin, F.; Desailly, D.; Duforêt-Gaurier, L. Global particulate matter pool temporal variability over the SeaWiFS period (1997–2007). Geophys. Res. Lett. 2011, 38, 1–5. [Google Scholar] [CrossRef]
- Bonelli, A.G.; Vantrepotte, V.; Jorge, D.S.F.; Demaria, J.; Jamet, C.; Dessailly, D.; Mangin, A.; D’Andon, O.F.; Kwiatkowska, E.; Loisel, H. Colored dissolved organic matter absorption at global scale from ocean color radiometry observation: Spatio-temporal variability and contribution to the absorption budget. Remote Sens. Environ. 2021, 265, 112637. [Google Scholar] [CrossRef]
- Jönsson, B.F.; Salisbury, J.; Atwood, E.C.; Sathyendranath, S.; Mahadevan, A. Dominant timescales of variability in global satellite chlorophyll and SST revealed with a MOving Standard deviation Saturation (MOSS) approach. Remote Sens. Environ. 2023, 286, 113404. [Google Scholar] [CrossRef]
- Pittman, N.A.; Strutton, P.G.; Johnson, R.; Matear, R.J. An Assessment and Improvement of Satellite Ocean ColorAlgorithms for the Tropical Pacific Ocean. J. Geophys. Res. Ocean. 2019, 124, 9020–9039. [Google Scholar] [CrossRef]
- Nababan, B.; Rosyadi, N.; Manurung, D.; Natih, N.M.; Hakim, R. The Seasonal Variability of Sea Surface Temperature and Chlorophyll-a Concentration in the South of Makassar Strait. Procedia Environ. Sci. 2016, 33, 583–599. [Google Scholar] [CrossRef]
- Sachoemar, S. Variability Of Sea Surface Chlorophyll-a, Temperature and Fish Catch Within Indonesian Region Revealed By Satellite Data. Mar. Res. Indones. 2015, 37, 75–87. [Google Scholar] [CrossRef]
- Susanto, D.R.; Marra, J. Effect of the 1997/98 El Niño on Chlorophyll-a Variability Along the Southern Coasts of Java and Sumatra. Oceanography 2005, 18, 124–127. [Google Scholar] [CrossRef]
- Yu, Y.; Xing, X.; Liu, H.; Yuan, Y.; Wang, Y.; Chai, F. The variability of chlorophyll-a and its relationship with dynamic factors in the basin of the South China Sea. J. Mar. Syst. 2019, 200, 103230. [Google Scholar] [CrossRef]
- Vantrepotte, V.; Mélin, F. Inter-annual variations in the SeaWiFS global chlorophyll a concentration (1997-2007). Deep. Res. Part I Oceanogr. Res. Pap. 2011, 58, 429–441. [Google Scholar] [CrossRef]
- Ali, K.A.; Flanagan, D.C.; Brandt, M.E.; Ortiz, J.D.; Smith, T.B. Semi-analytical inversion modelling of Chlorophyll a variability in the U.S. Virgin Islands. Front. Remote Sens. 2023, 4, 1172819. [Google Scholar] [CrossRef]


| Units | Definition | |
|---|---|---|
| acdom(λ) | m−1 | Absorption coefficient of chromophoric dissolved organic mater |
| anap(λ) | m−1 | Absorption coefficient of non-algal particles |
| aph(λ) | m−1 | Absorption coefficient of phytoplankton pigments |
| at(λ) | m−1 | Absorption coefficient of the total (aw + acdom + aph + anap) |
| aw(λ) | m−1 | Absorption coefficient of pure seawater |
| bbp(λ) | m−1 | Backscattering coefficient of suspended particles |
| bbt(λ) | m−1 | Backscattering coefficient of the total, bbw + bbp |
| bbw(λ) | m−1 | Backscattering coefficient of pure seawater |
| Chl-a | mg·m−3 | Chlorophyll-a concentration |
| Db | Distribution function that relates the vertically averaged diffuse attenuation coefficient for upwelling radiance from bottom reflectance to at and bt | |
| Dc | Distribution function that relates the vertically averaged diffuse attenuation coefficient for upwelling radiance from water-column scattering to at and bt | |
| rrs | sr−1 | Below-surface remote sensing reflectance |
| rrsb | sr−1 | Below-surface remote sensing reflectance from bottom reflection |
| rrsc | sr−1 | Below-surface remote sensing reflectance from water column scattering |
| rrsdeep | Below-surface remote sensing reflectance when the water depth is infinite | |
| rb | Bottom reflectance | |
| Rrs | sr−1 | Above-surface remote sensing reflectance |
| Dataset | Chl-a [mg·m−3] | Rrs(560) [sr−1] | Depth [m] |
|---|---|---|---|
| rb-syn new | range = [0–20] | 0.0105 (fixed) | range = [0–10] |
| rb-syn new (0–1) | range = [0–1] | range = [0.009–0.012] | range = [0–10] |
| rb-syn new (0–10) | range = [0–10] | range = [0.009–0.012] | range = [0–10] |
| rb-syn new (0–20) | range = [0–20] | range = [0.009–0.012] | range = [0–10] |
| rb-syn beta | 0.5 (fixed) | range = [0.009–0.012] | range = [0–10] |
| Region | N | Year | Mean Depth [m] | mChl-ais [mg·m−3] | mChl-ais std [mg·m−3] | mChl-a [mg·m−3] | mChl-a std [mg·m−3] |
|---|---|---|---|---|---|---|---|
| Aden | 7 | 2001 | 0 | 0.382 | 0.017 | 0.234 | 0.081 |
| East Gulf of Thailand | 15 | 2003 | 0 | 1.369 | 1.973 | 1.945 | 2.761 |
| Eritrea | 4 | 2001 | 0 | 0.678 | 0.087 | 0.453 | 0.152 |
| Florida Keys | 293 | 2011, 2016–2021 | 1.49 | 0.087 | 0.169 | 0.345 | 0.758 |
| Gulf of Suez | 85 | 2001 | 0 | 0.367 | 0.327 | 0.395 | 0.134 |
| Gulf of Tadjoura | 10 | 2001 | 0 | 0.762 | 0.044 | 0.372 | 0.107 |
| Hawaii | 1 | 2017 | 0 | 0.002 | - | 0.086 | 0.039 |
| Southeast Florida | 10 | 2007, 2012, 2017 | 4.24 | 0.004 | 0.002 | 0.123 | 0.045 |
| Western Yemen | 77 | 2001 | 0 | 0.657 | 0.123 | 0.446 | 0.176 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonelli, A.G.; Martin, P.; Noel, P.; Asner, G.P. Global Chlorophyll Concentration Distribution and Effects on Bottom Reflectance of Coral Reefs. Oceans 2024, 5, 210-226. https://doi.org/10.3390/oceans5020013
Bonelli AG, Martin P, Noel P, Asner GP. Global Chlorophyll Concentration Distribution and Effects on Bottom Reflectance of Coral Reefs. Oceans. 2024; 5(2):210-226. https://doi.org/10.3390/oceans5020013
Chicago/Turabian StyleBonelli, Ana G., Paulina Martin, Phillip Noel, and Gregory P. Asner. 2024. "Global Chlorophyll Concentration Distribution and Effects on Bottom Reflectance of Coral Reefs" Oceans 5, no. 2: 210-226. https://doi.org/10.3390/oceans5020013
APA StyleBonelli, A. G., Martin, P., Noel, P., & Asner, G. P. (2024). Global Chlorophyll Concentration Distribution and Effects on Bottom Reflectance of Coral Reefs. Oceans, 5(2), 210-226. https://doi.org/10.3390/oceans5020013












