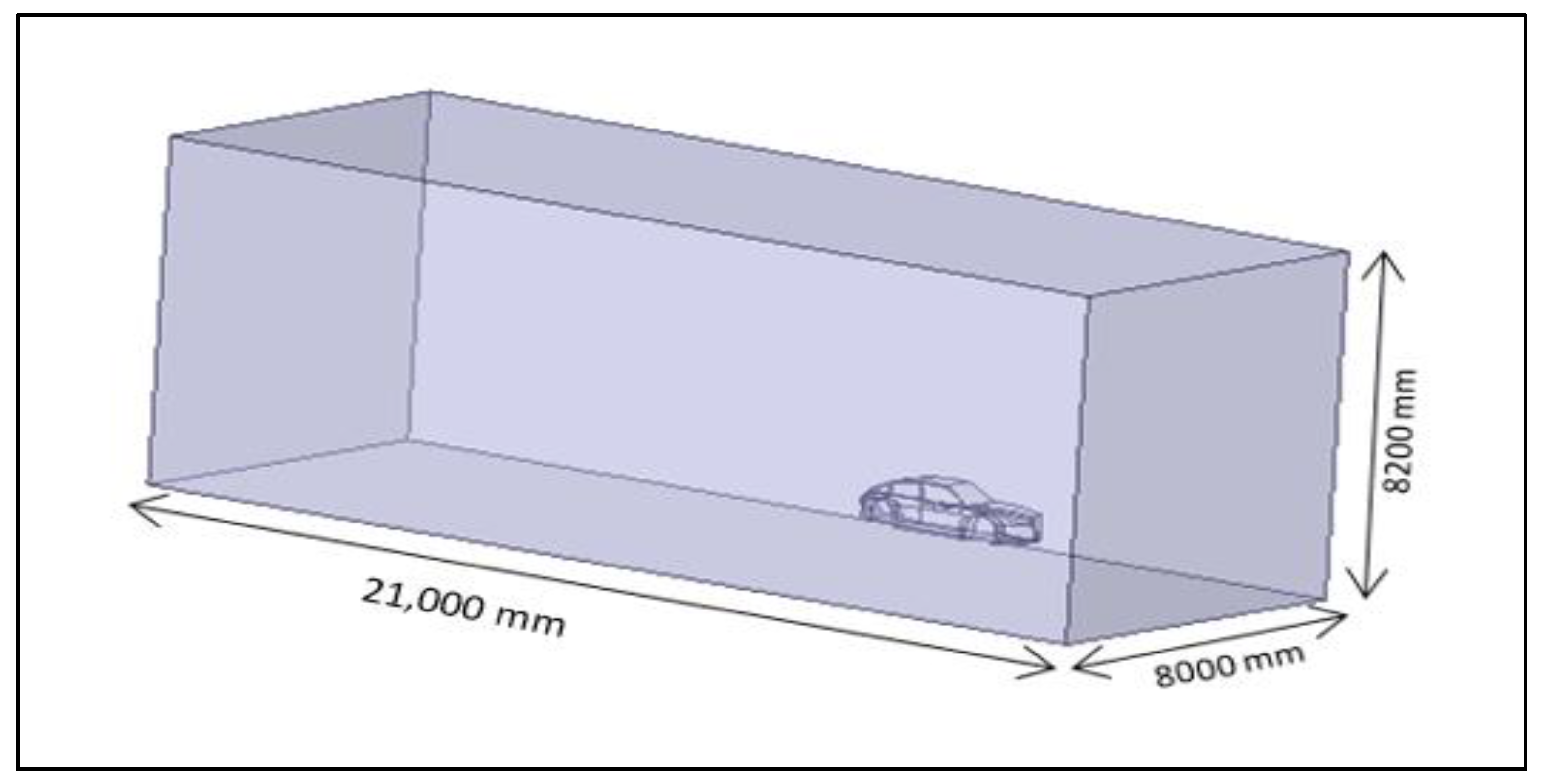
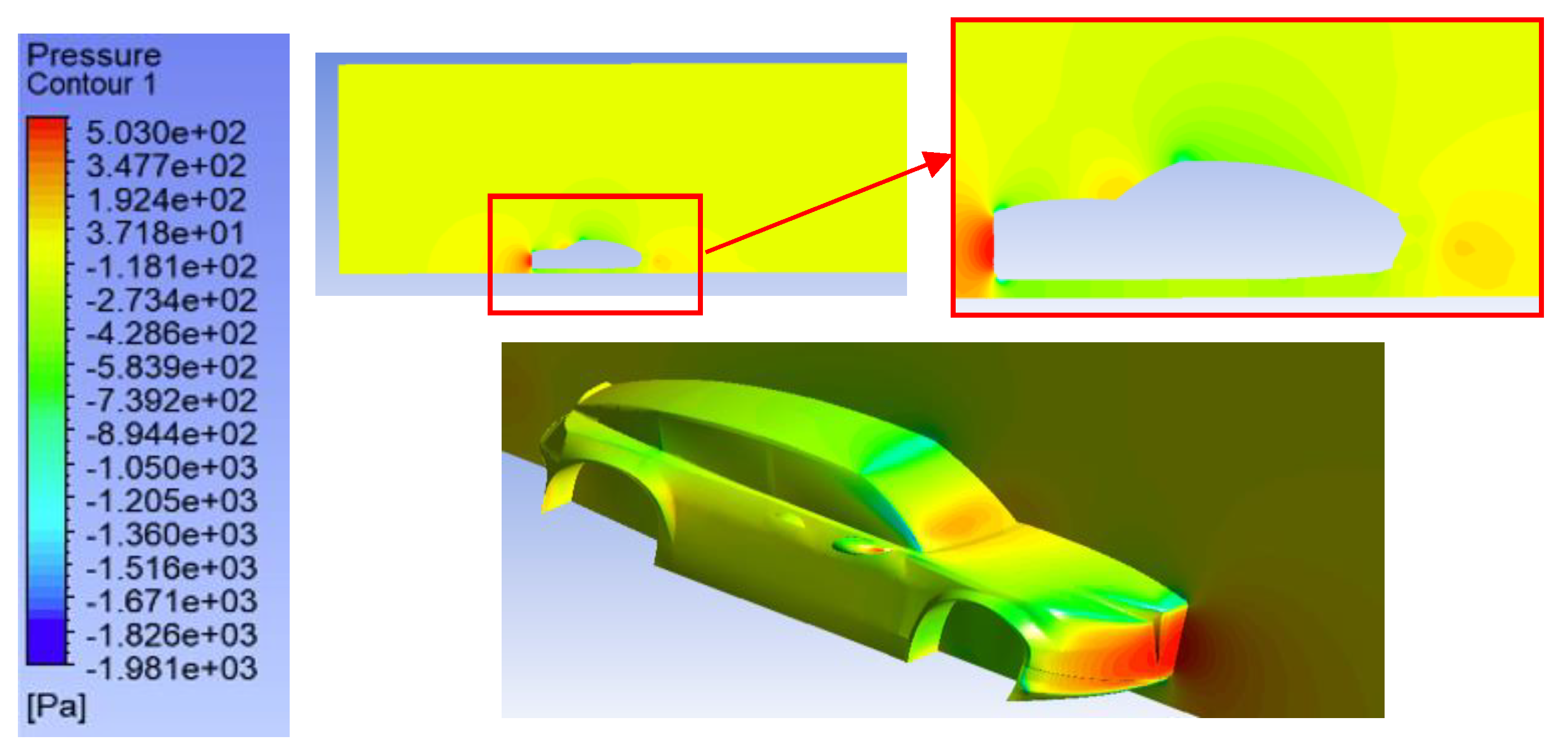
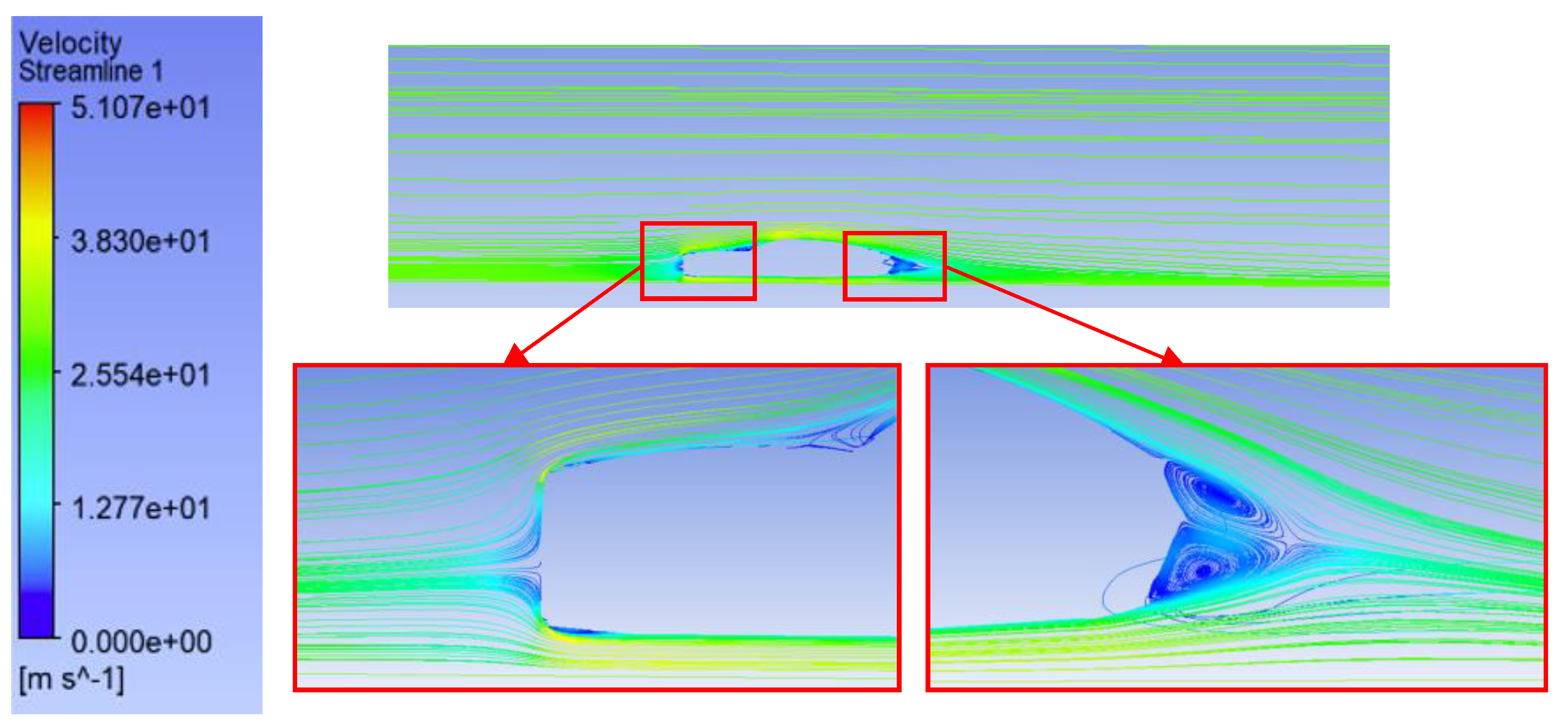
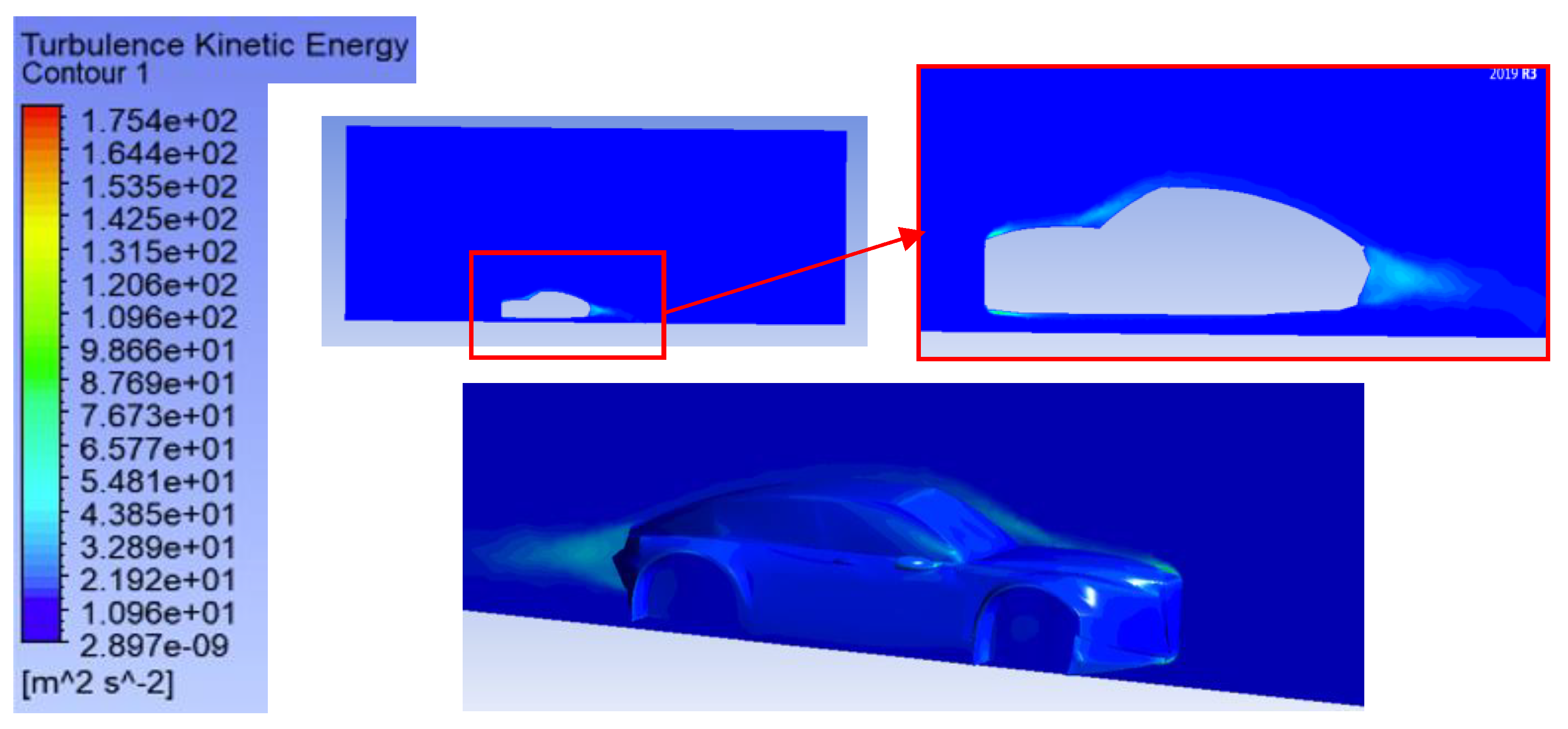
1. Introduction
In automotive technology, increasing the energy performance of vehicles has become a substantial challenge, whether the powertrain is internal combustion or otherwise. Aerodynamic optimization is one of the primary levers to arrive at this, as the drag explains a substantial part of resistance to movement, particularly at high accelerations. Ensuring reduced drag results in a direct reduction in energy or fuel consumption, stability, and general performance of the vehicle. Therefore, the performance of a vehicle is determined mostly by its aerodynamic performance, especially the drag and lift coefficients. Various research studies have been carried out to examine different approaches that can be used to reduce these unwanted outcomes and maximized overall efficiency.
Various research works have identified various methods to reduce the unwanted effects and enhance the aerodynamic efficiency of vehicles. These optimization and simulation tools are commonly applied to engineering such as genetic algorithms in production and maintenance planning [
1], mixed finite element methods in fluid dynamics [
2], and isogeometric analysis [
3]. Rear diffusers have been effective in the previous case, in recovery of pressure and reduction of drag, when the angle and length of the rear diffuser are well managed to reduce the frequency of the wake turbulence [
4,
5]. The rear shape and pillar geometry of the vehicle also affect the stability in crosswind conditions [
6], and optimization schemes with a combination of statistical, neural network, and genetic algorithms have been demonstrated to minimize aerodynamic drag and noise reduction at the same time [
7].
Active aerodynamic systems including dynamic spoilers and blowing control are introduced to reduce the drag and increase energy efficiency [
8,
9]. The underbody design with fairings and curved diffusers improves the lift behavior and reduces drag [
4,
8]. The flow stabilization and pressure distribution are enhanced by the optimal positioning of wheels and the application of deflectors [
10,
11,
12] has shown that the specific CFD model to be used (in this case the type of mesh and turbulence model) affects the aerodynamic outcome to a great extent, and that a good trade-off of accuracy to computational cost is a hybrid RANS-LES model. Experiments in wind tunnels confirm that an appropriate mix of underbody diffusers, active systems, and front-end optimizations can dramatically decrease drag and increase stability [
4,
13,
14,
15], and small things like exhaust pipe placement can affect aerodynamic performance by up to 41% [
16], the significance of the overall optimization of the vehicle.
Other researchers have focused on the front part of the vehicle. Ref. [
17] optimized the nose shape of a Formula Student car using the adjoint method such that the drag of the vehicle was reduced by 27% as well as reducing the fuel consumption by 27%. Experimental data confirm their work, which indicates dramatic enhancement in aerodynamic performance because of their decreased wake. Also, ref. [
18] suggests an organization of parametric optimization of aerodynamic shapes in ANSYS DesignXplorer and Fluent. Modifiable parameters of geometric properties are defined through quantification of the individual properties and construction of response models is performed by simulating various configurations with the use of a design of experiments (DoE). This multi-objective-based method is most effective in terms of reducing drag and managing lift and fewer simulations are needed in this compared to the conventional way of doing it and so the overall performance of the aerodynamics is also optimized.
Researchers have applied their investigation to sports vehicles and race cars (such as Formula SAE) for proving the significance of front-installed aerodynamic features like front wings and spoilers in controlling lift and drag [
19,
20]. Vehicle energy efficiency benefits substantially from both changes made to windshield angles at front and rear positions [
21] and the application of frontal deflectors [
22].
The application of deflectors under the front bumper has been examined using both scaled models and Kriging optimization techniques to prove their capability of guiding airflow and decreasing drag [
23]. Vehicle drag decreased by 13.18% while lift decreased by 13.93% after testing multiple passenger vehicle configurations through bumper modification [
24]. Various recent studies show that the front windshield angle together with the hood slope plays a vital function in wake development and vehicle performance [
25,
26].
Finally, researchers have conducted multiple investigations into different shapes which minimize aerodynamic losses. The research investigates the front vehicle area by analyzing the bumper together with the hood and windshield regions. The investigation conducted by [
27] discovered that elevating front bumper incline angles together with modifying hood curvature diameters leads to decreases in drag coefficient values. Scientists have achieved significant improvements in the aerodynamics by optimizing the lateral design of the front bumper according to research [
28]. The influence of front shape upon drag has also been shown in experimental work upon agricultural vehicles, although the maximum difference is a comparatively small 3 percent [
29].
Numerous past research studies on the issue of vehicle aerodynamic have been dedicated towards the enhancement of airflow in the rear and underbody of the vehicle, including the optimization of the rear diffuser, the underfloor flow, and the rear spoiler. As an illustration, a number of studies on front grille and hood geometry have shown that it is possible to potentially reduce the value of the drag coefficient to as low as 26% by redesigning the frontal area and profile of the bonnet.
The vast majority of these investigations, however, were based on simplified geometries or focused on one aerodynamic goal (usually reducing drag), without a systematic examination of how front-end shape distortions affect the total vehicle stability, specifically using the lift coefficient (Cl) in realistic driving. The merits of such works are that it clearly shows the possibility of drag reduction. However, they also have significant drawbacks such as limited coverage of parameters, they do not consider front bumper inclination effects, and simultaneous consideration of both drag and lift performance, and need to be applicable only to modern vehicle design.
Judging by this review, the gap in the research can be defined as the lack of a comprehensive and systematic study on the impact of front bumper inclination angle, which would combine both indicators of aerodynamic performance, drag and lift, in the framework of multi-objective optimization that would be appropriate in the aerodynamics of electric vehicles. Whereas a few studies have examined the hood or bumper lip individually due to structural or styling considerations, it has not been used in studies to examine the combined aerodynamic effect of front bumper tilt on Cd and Cl at the same time.
Here, the current work suggests an efficient and repeatable methodology comprising parametric geometrical modeling of the front bumper, fully automated CFD, response surface analysis (RSM), and multi-objective optimization by ANSYS DesignXplorer. Such a strategy successfully fills in the gap in research as it allows for the improvement of drag and lift ratios simultaneously, offers a framework that is directly applicable to the automotive industry, and suggests improving the general picture of the aerodynamic impact of the front-end geometry in electric vehicles.
The article is divided into the following sections:
Section 2 provides the geometric model, namely, a brief description of the vehicle model, and describes the different types of bumpers used at the front. The simulation methodology as described in
Section 3 consists of two methods: the basic analysis of a typical CFD simulation conducted in ANSYS Fluent, and a parametric optimization run carried out with DesignXplorer. In
Section 4, the findings of the two phases are discussed and the aerodynamic performance of the various configurations are compared with the best solution indicated.
Section 5 also closes the study and provides some possible future research directions.
5. Conclusions
The paper presented an organized and thorough approach to studying the impact of front bumper inclination on electric vehicle aerodynamics performance and how it can be improved. The novelty of the work consists in such an experiment that it establishes an elementary but characteristic geometry and attention to a frontal area that is highly critical to drag.
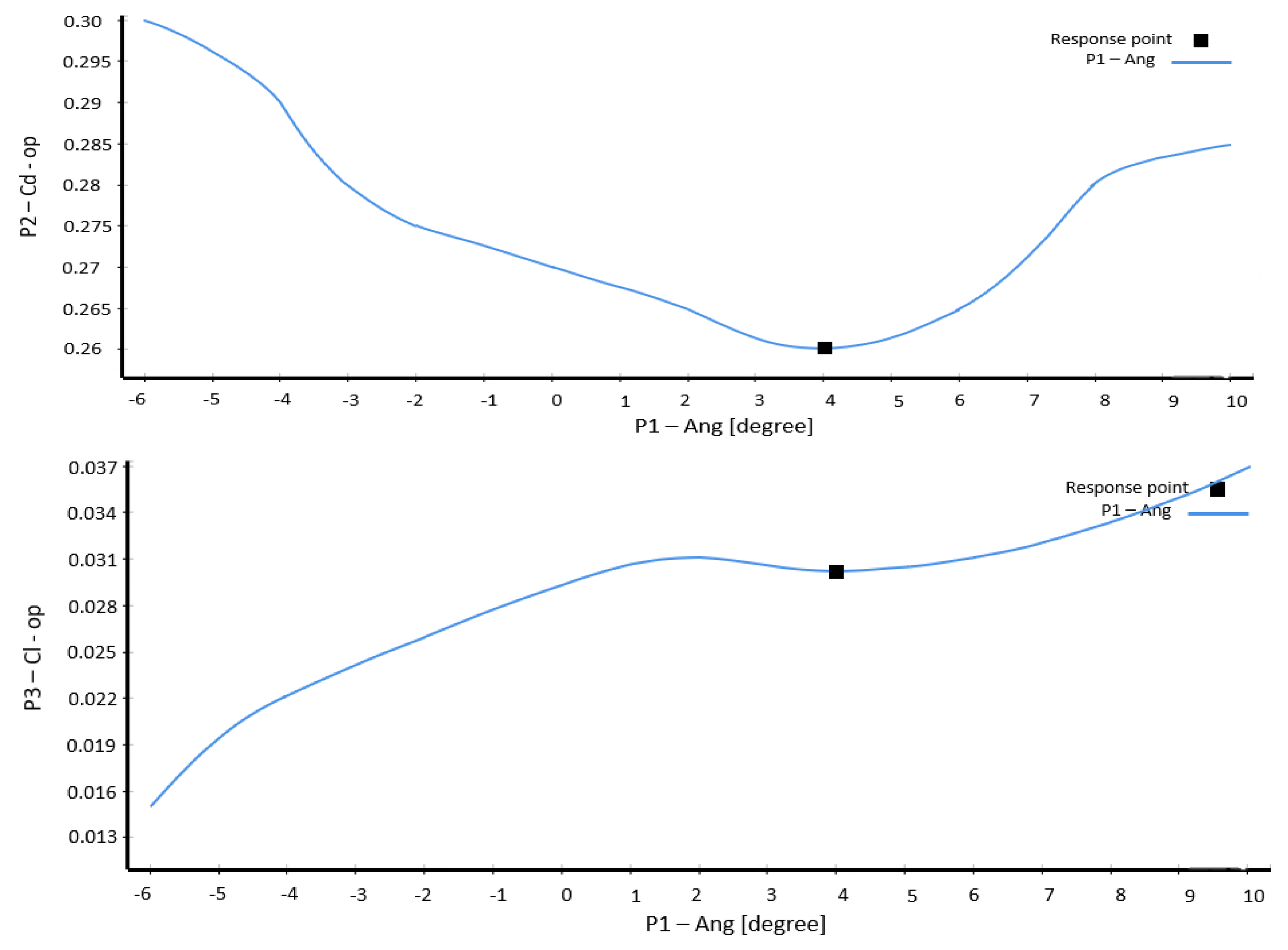
A first set of CFD calculations was performed on four different front bumper set-ups of the angle (−4°, 0°, 4°, 8°). Every configuration had characteristic aerodynamic tendencies. The −4° gradient decreased the lift but gave increased drag (Cd = 0.29), whereas the 0° angle gave a neutral but less than ideal flow (Cd = 0.27, Cl = 0.029). The angle (4°) became best because it has the least amount of drag (Cd = 0.26) and controlled lift (Cl = 0.030). On the other hand, the 8° angle produced an increased lift (Cl = 0.033) and drag (Cd = 0.28), which adds compromise to vehicle stability.
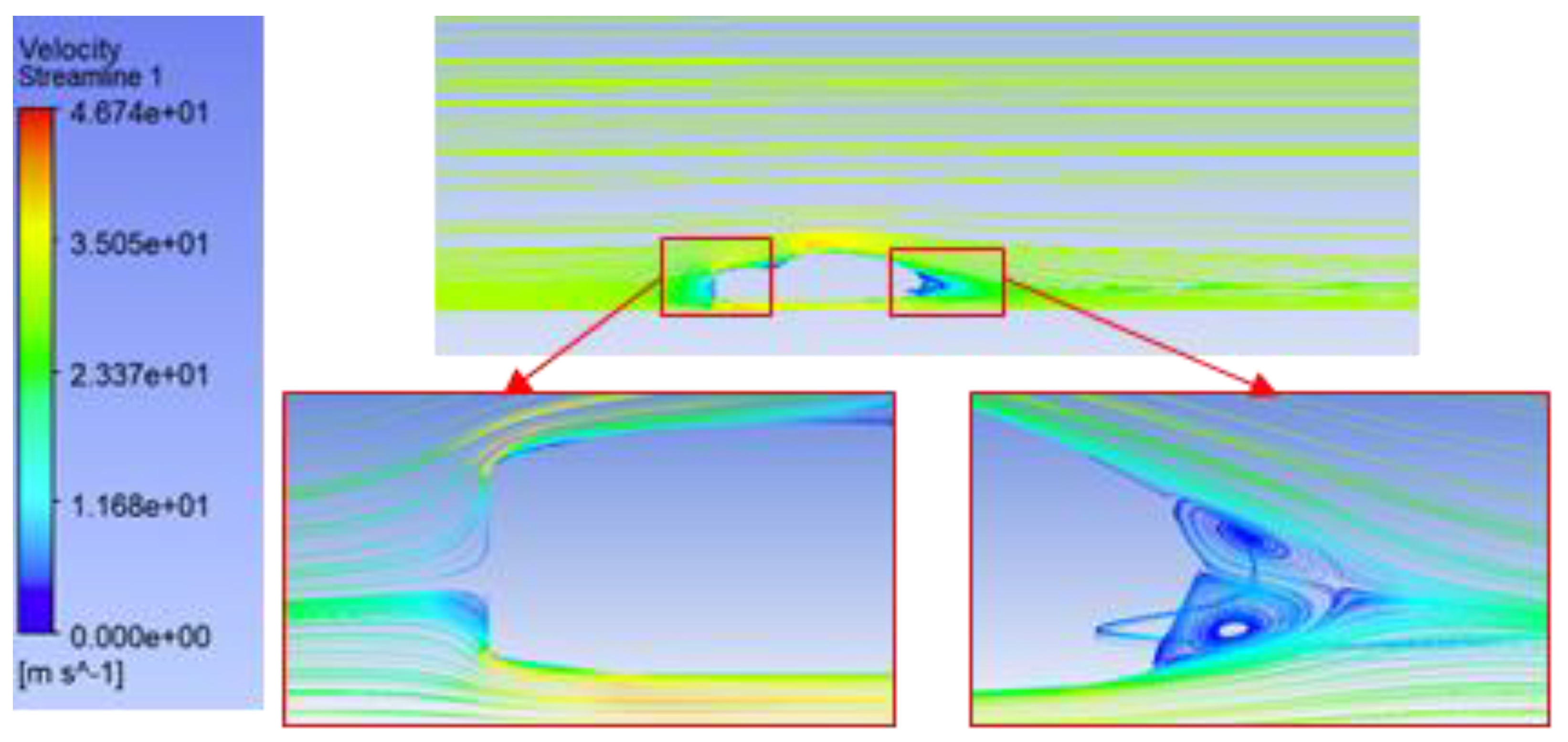
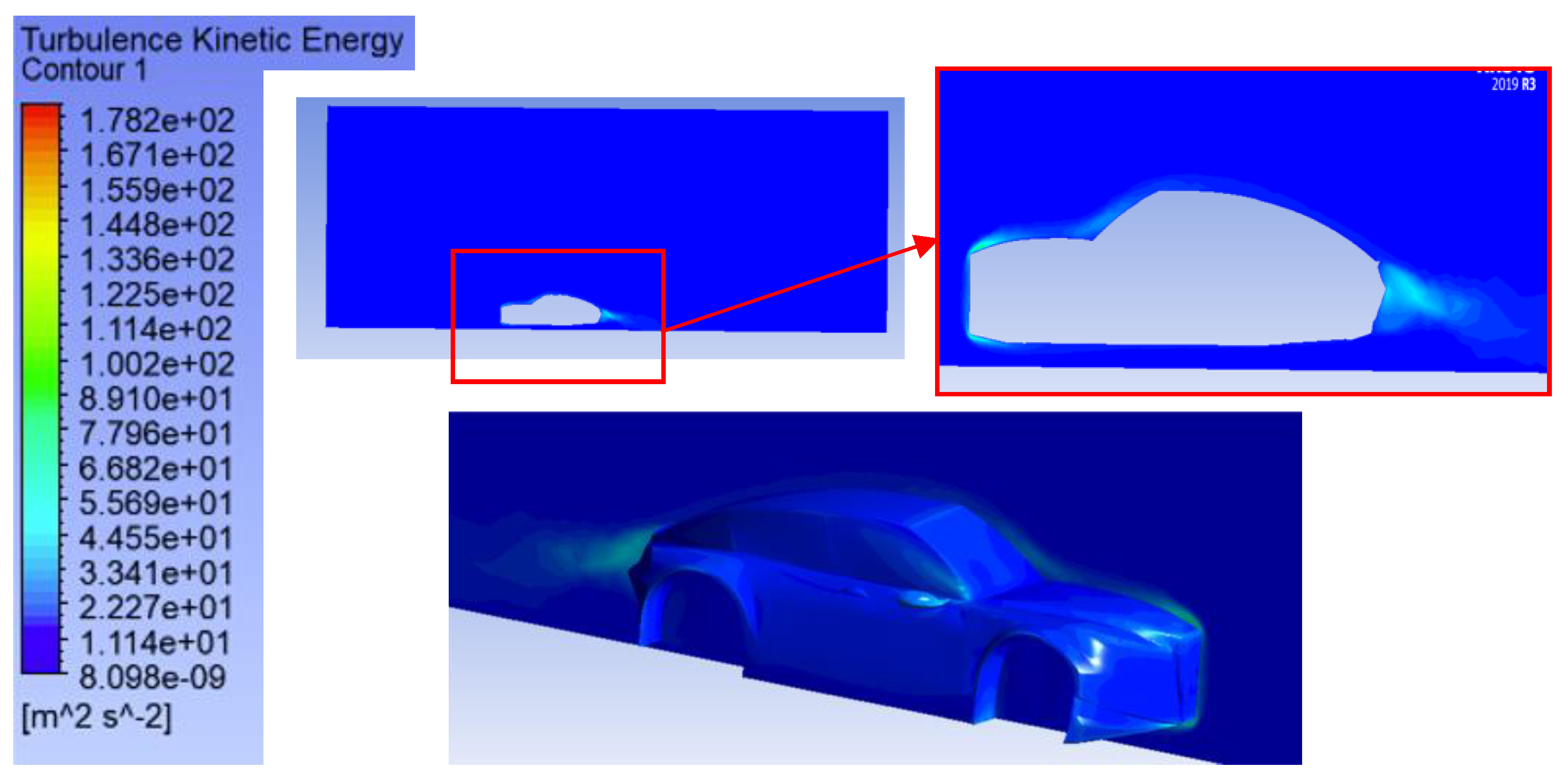
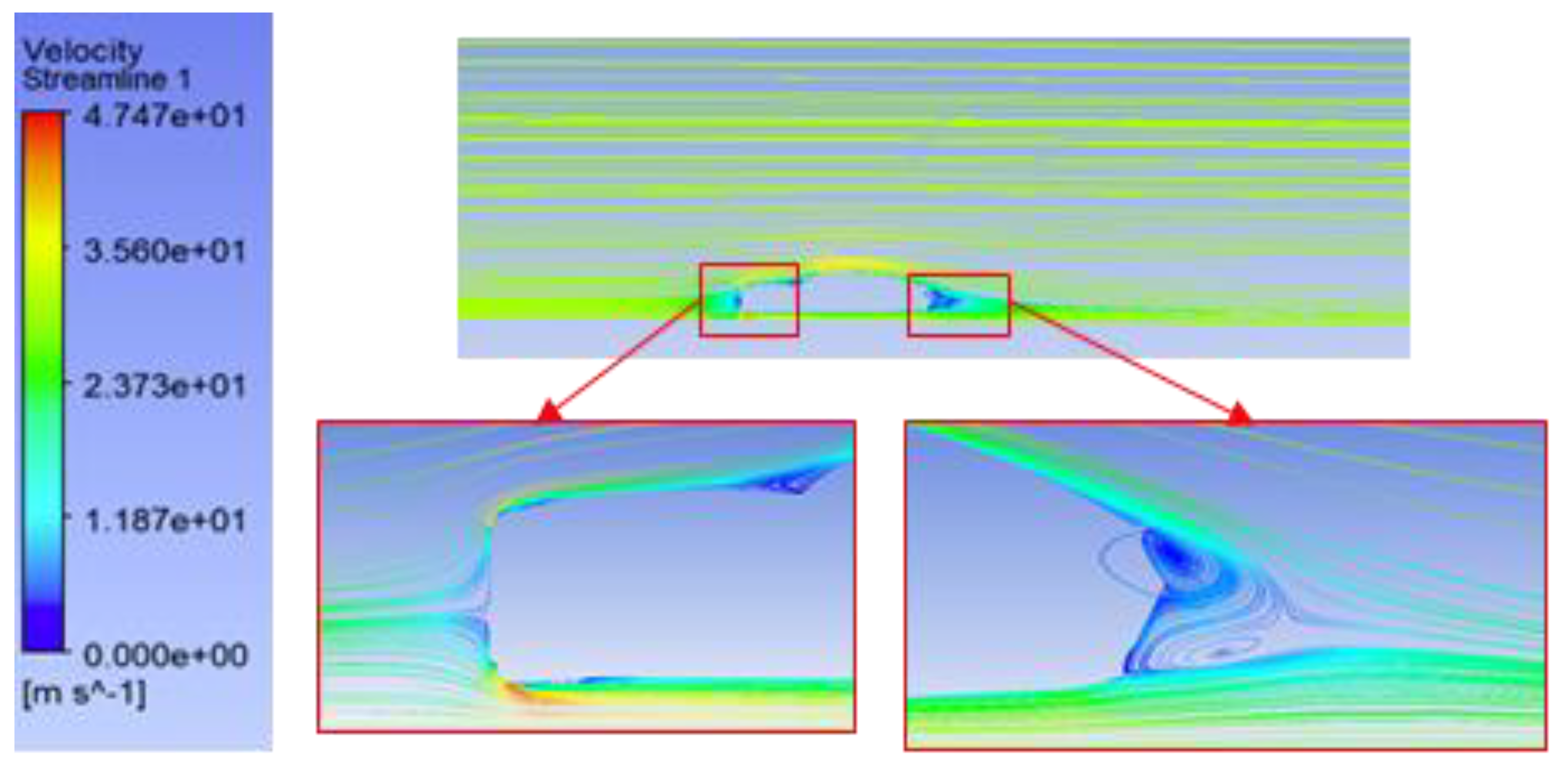
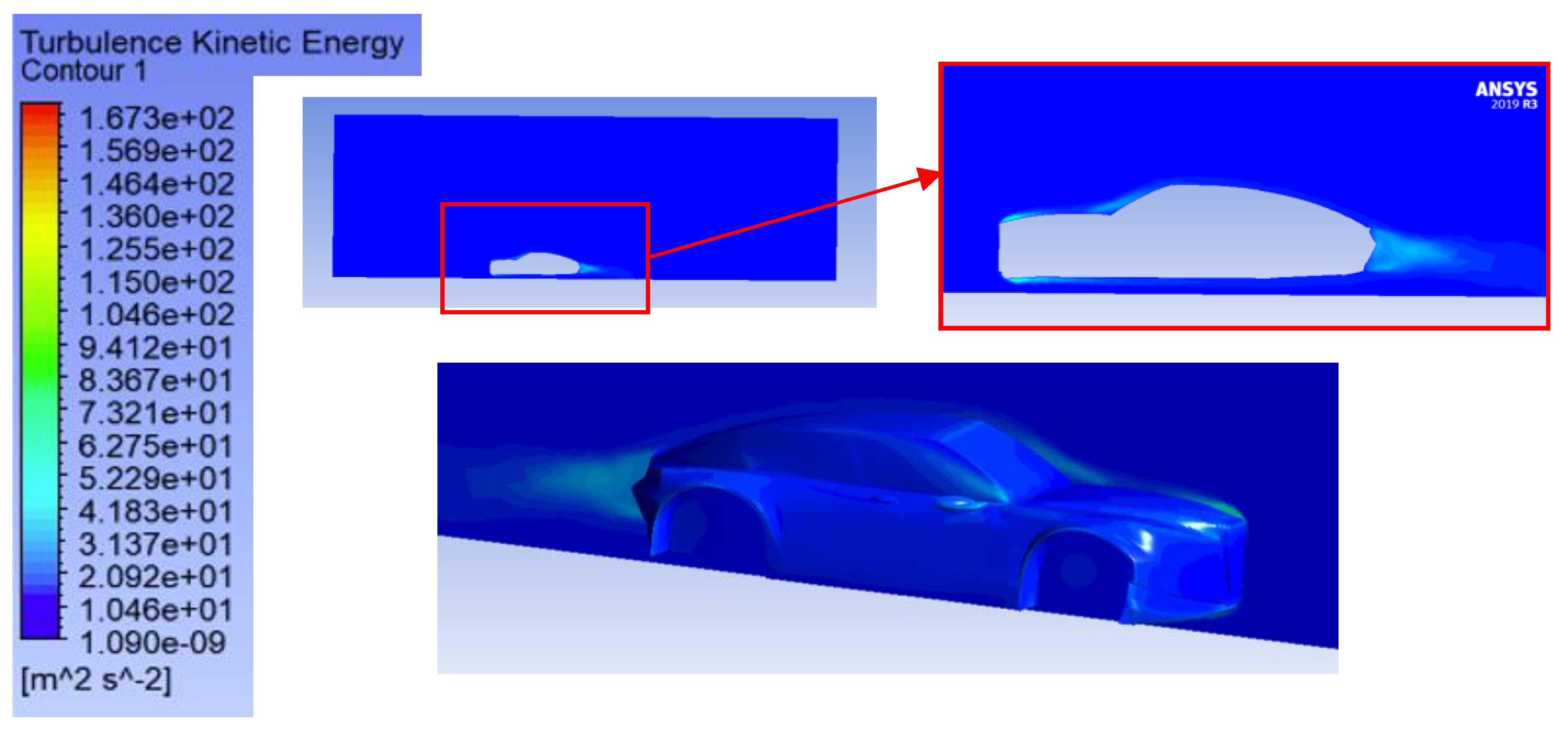
This has to do directly with the aerodynamic influence of the front bumper shape: by altering the angle of inclination, the airflow is directed around the body in a more desirable formation, eliminating areas of separation and the voluminous gap behind the car. The 4° case is an optimum distribution that reduces front pressure and minimizes backward turbulence. Therefore, an easy geometric modification to accomplish a considerable drag decrease has been found beneficial in the study, which could mean saving on energy or gaining on the range with the use of electric vehicles.
To validate the scientific accuracy of observations made in the fixed cases and extending the analysis to a larger variety of configurations, a parametric optimization strategy was also incorporated by means of ANSYS DesignXplorer. To this end, it was decided that the geometric parameterization could be applied in ANSYS Workbench directly, so that once a certain angle on the front bumper has been achieved, it can be continually varied, without the need to use the CAD environment again. The angle of inclination was set as an input parameter in the geometry module and mapped onto a meshing module on one hand and on the other as an alternate parameter to the CFD simulation module. Transparent simulations in Fluent were prepaid to each automatically produced configuration and aerodynamic outputs were captured after each simulation. The information was then applied in constructing a quadratic response surface of a relationship between angle value and the aerodynamic performances (Cd, Cl in anticipation to predict and optimize future settings).
The quality of this statistical model was confirmed by residual analysis, local sensitivity, and global robustness diagnostics. The multi-objective optimization gave an optimal solution through 3.9998° at a drag coefficient of 0.2601 and a lift coefficient of 0.0302. This solution is also Pareto optimal; this proves that it is a trade-off non-dominated between the two objectives: drag and aerodynamic stability.
This work represents a twofold contribution in the sense that it shows that a local geometric change to the bumper can make a measurable difference in the overall aerodynamic efficiency of an electric vehicle, and second, that a reproducible computational procedure should be proposed to provide a workflow through parametric modeling of geometry, an automatic simulation, and optimization. This can easily be translated to other parts of the body like the hood, grille, or underbody.
Moreover, the results of this study surpass the scientific interest and indicate the practical prospects of real-world optimization of the aerodynamics of electric vehicles. The created methodology can be directly adopted by the automotive engineers to optimize the front-end geometry, reduce the aerodynamic drag, and improve the overall energy efficiency. To ensure that the numerical result is verified in future work, it is proposed to use wind tunnel testing and experiments with scaled models to verify the accuracy of the presented CFD-based predictions. Such viewpoints open the way to the industrial implementation of the suggested aerodynamic optimization solution in the actual design of a vehicle.
Finally, future work will focus on including the impact of crosswind and unsteady conditions will need to be included, as well as a range gain being assessed directly using a standardized driving cycle, the development of a simplified digital twin of the vehicle which can be tested swiftly on a numerical platform, and extrapolation of the method to more realistic industrial design applications that must take into consideration manufacturing or styling limits.