Efficiency-Oriented Gear Selection Strategy for Twin Permanent Magnet Synchronous Machines in a Shared Drivetrain Architecture

Abstract

This article presents a gear selection methodology for electric vehicle powertrains employing two identical Permanent Magnet Synchronous Machines (PMSMs) arranged in a twin-drive configuration. Both machines are coupled through a shared output shaft and operate with coordinated torque–speed characteristics, enabling efficient utilization of the available gear stages. The proposed approach establishes a control-oriented drivetrain framework that incorporates mechanical dynamics together with real-time thermal states and loss mechanisms. Unlike conventional strategies, which rely mainly on static or speed-based shifting rules, the method integrates detailed thermal and electromagnetic loss modeling directly into the gear-shifting logic. By accounting for the dynamic thermal behavior of PMSMs under variable load conditions, the strategy aims to reduce cumulative drivetrain losses, including electromagnetic, thermal, and mechanical, while maintaining high efficiency. The methodology is implemented in a MATLAB/Simulink R2024a and LabVIEW 2024Q2 co-simulation environment, where thermal feedback and instantaneous efficiency metrics dynamically guide gear selection. Simulation results demonstrate measurable improvements in energy utilization, particularly under transient operating conditions. The resulting efficiency maps are broader and flatter, as the motors’ operating points are continuously shifted toward zones of optimal performance through adaptive gear ratio control. The novelty of this work lies in combining real-time loss modeling, thermal feedback, and coordinated gear management in a twin-motor system, validated through experimentally motivated efficiency maps. The findings highlight a scalable and dynamic control framework suitable for advanced electric vehicle architectures, supporting intelligent efficiency-oriented drivetrain strategies that enhance sustainability, thermal management, and system performance across diverse operating conditions.

1. Introduction

The electrification of vehicle powertrains has led to increasingly complex drive architectures emphasizing efficiency [1,2], reliability [3], and control flexibility [4]. Among these, twin-drive systems employing two identical Permanent Magnet Synchronous Machines (PMSMs) operating in parallel are notable for torque sharing [5], fault tolerance [6], and enhanced dynamic performance [7]. Such systems are particularly attractive for electric buses and high-performance passenger cars, where scalability and redundancy are critical [8,9].

However, twin-drive architectures present significant integration challenges in transmission coupling and gear ratio coordination [10]. While gear shifting in conventional ICE vehicles primarily depends on speed and load [11,12], in electric drivetrains, especially with twin PMSMs, thermal behavior and loss mechanisms are decisive for both efficiency [13,14] and durability [15]. Since both machines drive a common shaft, synchronized gear selection is essential to ensure smooth torque blending and prevent efficiency degradation [16,17]. In addition, cumulative heating and interdependent electromagnetic losses necessitate a coordinated control strategy [18,19].

This study proposes a gear selection methodology [20] tailored for twin-drive systems, embedding detailed thermal and loss models into the shifting logic [21,22]. By utilizing real-time thermal feedback and efficiency metrics, the framework dynamically selects gear ratios to minimize drivetrain losses while satisfying torque demand [23]. The approach is implemented in a MATLAB/Simulink and LabVIEW co-simulation environment [24,25], enabling integrated evaluation of electrical, thermal, and mechanical interactions. Simulation results demonstrate improved energy utilization under transient and repeated load conditions [26,27,28,29,30,31,32,33,34,35,36].

The novelty lies in integrating real-time loss modeling, thermal feedback, and multi-gear coordination within a twin-motor setup [28,37]. Unlike conventional speed-based rules, the proposed strategy offers a scalable solution for advanced EVs, enhancing efficiency, sustainability [29,38], and thermal management [30,39]. The contribution is reinforced by rigorous mathematical modeling and a structured methodology [40,41]. Twenty-two systematically derived equations formalize the control logic, encompassing battery state-of-charge, converter dynamics, and power-flow constraints [31,32]. These formulations strengthen reproducibility and robustness across diverse operating conditions [33,34].

Overall, the framework [35,42] transforms gear shifting from [36,43] a static concept into a simulation-ready [36,44], application-oriented solution for electric drivetrains [45,46]. The article is organized as follows: Section 2 analyzes the dynamics of dual transmissions; Section 3 details the gear-shifting process in a dual-gearbox architecture; Section 4 formalizes effective output states; Section 5 presents a temperature-aware shifting strategy; Section 6 validates the approach in co-simulation; Section 7 compares efficiency across gears and thermal states; Section 8 discusses practical implications; and Section 9 concludes with the main contributions.

2. Dynamic Behavior of Dual Transmission Units in Synchronized Output Configurations

In electric vehicle propulsion systems, particularly those applied in heavy-duty transport such as electric buses, innovative drivetrain architectures are required to ensure both high efficiency and mechanical reliability [2,6,21]. One such architecture employs two identical PMSMs, each driving a separate multi-speed gearbox [1,5]. These gearboxes are coupled via a differential, which merges their outputs into a single driveline. This configuration introduces unique opportunities and challenges for gear coordination and torque distribution, especially when the objective is to optimize operational efficiency [7,20].

Each PMSM is connected to a four-speed gearbox, capable of independently adjusting the torque–speed characteristics through discrete gear ratios. These ratios are typically arranged in a geometric sequence to maintain near-constant power output and efficient motor operation across the vehicle’s speed range [3,13]. When operating independently, each gearbox provides four distinct output speeds corresponding to the selected gear. However, when the outputs are combined through a differential, the number of potential output states expands significantly [4,14].

The differential plays a crucial role in this configuration. It averages the rotational speeds of the two input shafts (from the gearboxes) and transmits the combined torque to a single output shaft, typically the main drive axle of the bus. Importantly, the differential allows the two gearboxes to engage different gear states simultaneously, provided the speed difference remains within mechanical tolerance. The resulting combined output gear ratio is not additive or arithmetic but governed by the harmonic mean of the two individual gear ratios [16,24].

Mathematically, the equivalent gear ratio i_eq at the differential output is given by:

$${\mathrm{i}}_{\mathrm{e}\mathrm{q}}={\displaystyle \frac{2}{\frac{1}{{\mathrm{i}}_{\mathrm{A}}}+\frac{1}{{\mathrm{i}}_{\mathrm{B}}}}}$$

(1)

where i_A and i_B are the selected gear ratios from the two gearboxes, respectively. This expression reflects the physical reality that rotational speed contributions combine reciprocally, and not linearly. The harmonic mean is particularly appropriate here because gear ratios represent inverse relationships between speed and torque.

Unlike conventional single-gearbox systems, the combined output from two gearboxes coupled via a differential does not yield a set of equivalent gear ratios that follow geometric or arithmetic progressions. Instead, the result is a nonlinear distribution of output states, with up to sixteen unique combinations in a dual four-speed configuration. These states cannot be predicted by a simple ratio or multiplier, as their spacing is irregular and depends on the relative values of the selected gear ratios. This nonlinearity has significant implications for control strategies and efficiency optimization. Because the output states are unevenly spaced, gear selection algorithms must account for the states of both machines simultaneously. Predictive logic or real-time optimization is required to select gear combinations that maximize system-level efficiency. Moreover, transitions between certain gear combinations can cause abrupt changes in output speed or torque if not carefully synchronized, an especially critical issue in heavy vehicles such as electric buses, where passenger comfort and component durability are paramount.

In summary, integrating two identical PMSM-driven gearboxes through a differential generates a wide set of operating points for an electric bus drivetrain. The harmonic mean governs the relationship between the individual gearbox outputs and the collective drivetrain behavior, introducing additional complexity that requires accurate modeling and intelligent control. When leveraged effectively, this architecture can provide substantial efficiency gains and operational flexibility for next-generation electric mobility systems. Figure 1 illustrates a twin PMSM drive system prior to measurement and testing. The setup is shown in the preparation phase, with both machines mechanically coupled and ready for evaluation.

Special attention is devoted to verifying the inverter units that control each PMSM, ensuring correct wiring, communication, and parameter configuration. At this stage, the system is not yet energized, as preliminary checks are conducted to confirm operational safety and data acquisition readiness. This step is essential for validating the synchronization logic between the dual drives and the common transmission path. In parallel, the temperature sensors and monitoring interfaces are inspected to confirm their operational integrity. The objective is to guarantee that thermal feedback and loss measurements can be reliably acquired once the testing procedure begins.

Figure 2 illustrates a twin PMSM drive system prior to measurement. At this stage, the focus is on verifying the operation of the automated (robotized) transmission system.

The transmission is mechanically coupled to the shared output shaft of both PMSMs, and its actuator control is tested for responsiveness and accuracy. Engineers are verifying the synchronization between gear selection commands and the mechanical engagement of the gear stages.

Ensuring smooth and reliable shifting is essential before full system operation commences. Electrical interfaces and communication between the inverter controllers and the transmission unit are also under inspection. This verification phase is critical to prevent shifting delays or errors during dynamic load testing.

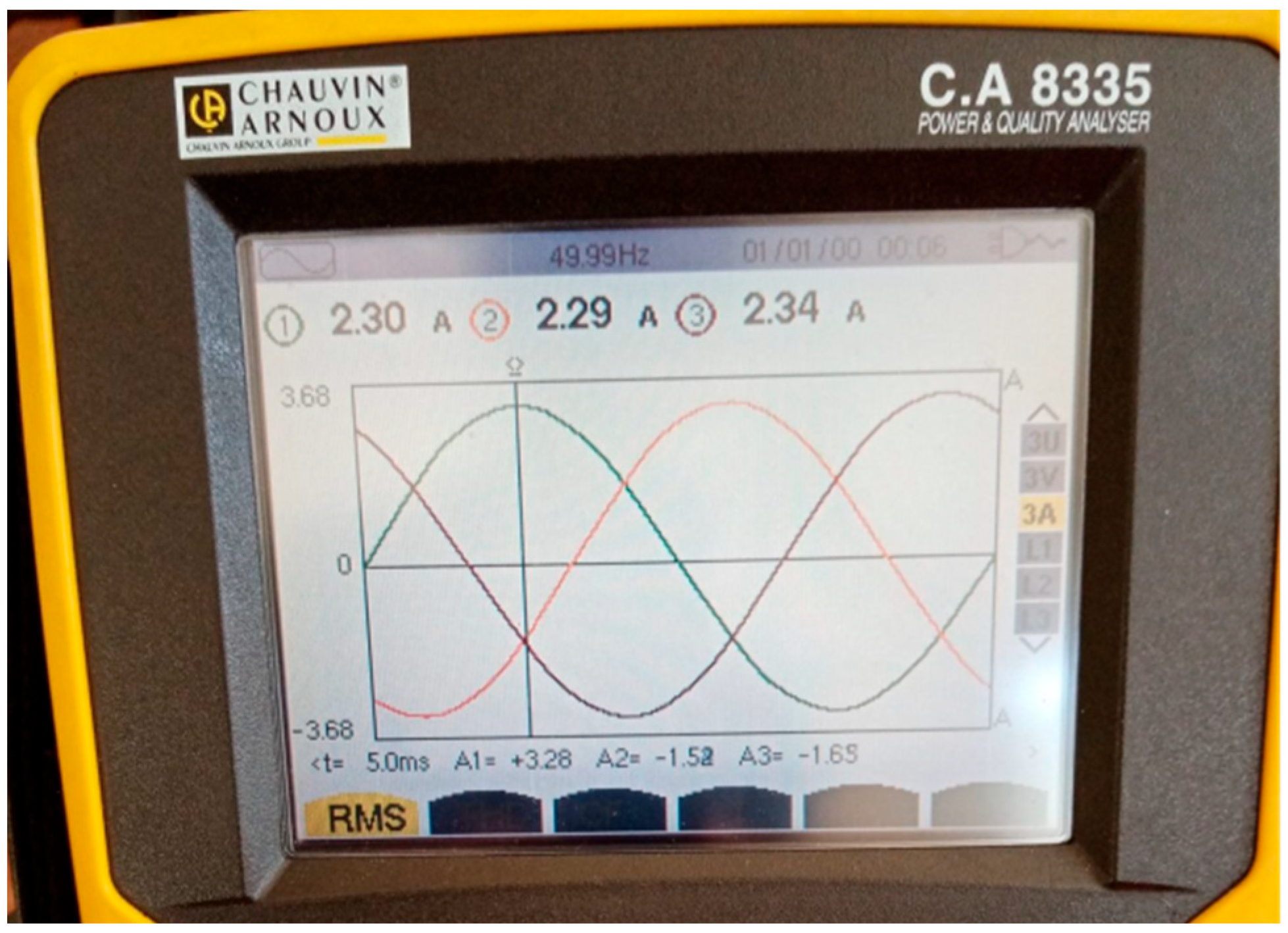
Before commencing the load tests (Figure 3), the system was operated at low rotational speed to verify readiness. This preliminary run allowed the drivetrain components to be inspected under minimal stress. During this phase, a power quality analyzer monitored the electrical parameters, confirming correct inverter output and signal stability. These checks established safe operating conditions prior to applying the full load to the twin PMSM system.

3. Gear Shifting Process in a 16-State Dual-Gearbox Differential Drive

In a drivetrain composed of two identical 4-speed gearboxes, each driven by an individual PMSM (Permanent Magnet Synchronous Machine) and connected to a common differential, the total number of unique output states is 16. These states arise from the combinatorial pairing of gear positions in the two gearboxes:

$$4\left(\mathrm{g}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{l}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{l}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{A}\right)·4\left(\mathrm{g}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{l}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{l}\mathrm{s}\right)=16\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s}$$

(2)

Each output state corresponds to a specific pair of gear selections: one from gearbox A and one from gearbox B. The effective output speed is determined by the harmonic mean of the individual gear ratios, and not all transitions between states result in linear or proportionally increasing speeds.

3.1. Shifting Strategies and Redundant States

The drivetrain can follow different shifting strategies depending on the operating range. In a sequential approach, the system begins from the low-speed, high-torque state (A1–B1), progresses through intermediate states such as (A2–B1) or (A1–B2), and ultimately transitions to (A2–B2) for higher speed. At the upper operating range, the shift from (A3–B3) to (A4–B4) yields the maximum gear ratio, corresponding to the lowest torque and highest vehicle speed.

In practice, however, efficiency-based shifting often outperforms strict sequential operation. Here, the controller dynamically selects among available gear states by considering real-time operating conditions, including load demand, vehicle speed, torque requirements, efficiency maps, traffic and safety constraints, and acceleration limits. This adaptive strategy allows the drivetrain to operate closer to optimal efficiency while maintaining vehicle performance and safety.

Certain gear states, such as (A2–B2) and (A3–B1), may produce nearly identical effective gear ratios due to harmonic averaging. These states are functionally interchangeable, and the controller can prioritize the state that provides better thermal performance or higher energy efficiency. Such redundancy enhances operational flexibility and allows fine-tuned optimization.

3.2. Special Modes and Control Implications

Although not part of the sixteen forward-driving states, reversing and neutral modes are integral to the control framework. Reversing is achieved by inverting motor rotation, while neutral can be realized by disengaging one gearbox. Both require dedicated synchronization logic to ensure stability and prevent mechanical stress.

To manage all possibilities, the controller maintains a gear-state matrix or lookup table covering all sixteen valid combinations and their corresponding harmonic mean ratios. Shifting decisions are then informed by a wide range of real-time inputs, including desired acceleration or deceleration, battery state-of-charge, motor temperature, road gradient, passenger load, and the need to prevent torque spikes or vibrations. This ensures that each shift is both mechanically safe and efficiency-oriented.

3.3. Summary of the Dual-Gearbox Shifting Framework

The dual-gearbox differential system provides a total of sixteen distinct operating states, each achieved through coordinated transitions between the gear pairs of subsystems A and B. These operating states are not arbitrary but governed by harmonic mean logic, which defines the effective gear ratio emerging from the interaction of the two parallel gearboxes. As a result, the framework introduces an additional layer of computational complexity compared to conventional single-gearbox drivetrains, since the controller must continuously evaluate the harmonic outcome of potential gear combinations.

Each shift must be executed under dynamically varying operating conditions, requiring not only precise synchronization of speed and torque but also the integration of torque-shaping or transient torque reduction strategies to prevent mechanical shock. In this sense, gear transitions serve as a coupled electromechanical process, where the thermal, electromagnetic, and mechanical domains intersect. Effective management of this process ensures smooth and efficient transitions, minimizes the risk of torque imbalance, and prevents resonance phenomena or drivetrain oscillations that could otherwise degrade performance.

When properly implemented, the shifting framework significantly enhances overall drivetrain functionality. It allows the system to exploit the full range of available gear states, adapt flexibly to different load conditions, and maintain optimal operation across the entire vehicle speed range. Beyond efficiency gains, the approach contributes to improved drivability, passenger comfort, and component longevity, establishing a foundation for advanced control strategies in next-generation electric drivetrains.

3.4. Simplification of Dual-Gearbox Shifting: From 16 to 4 Levels

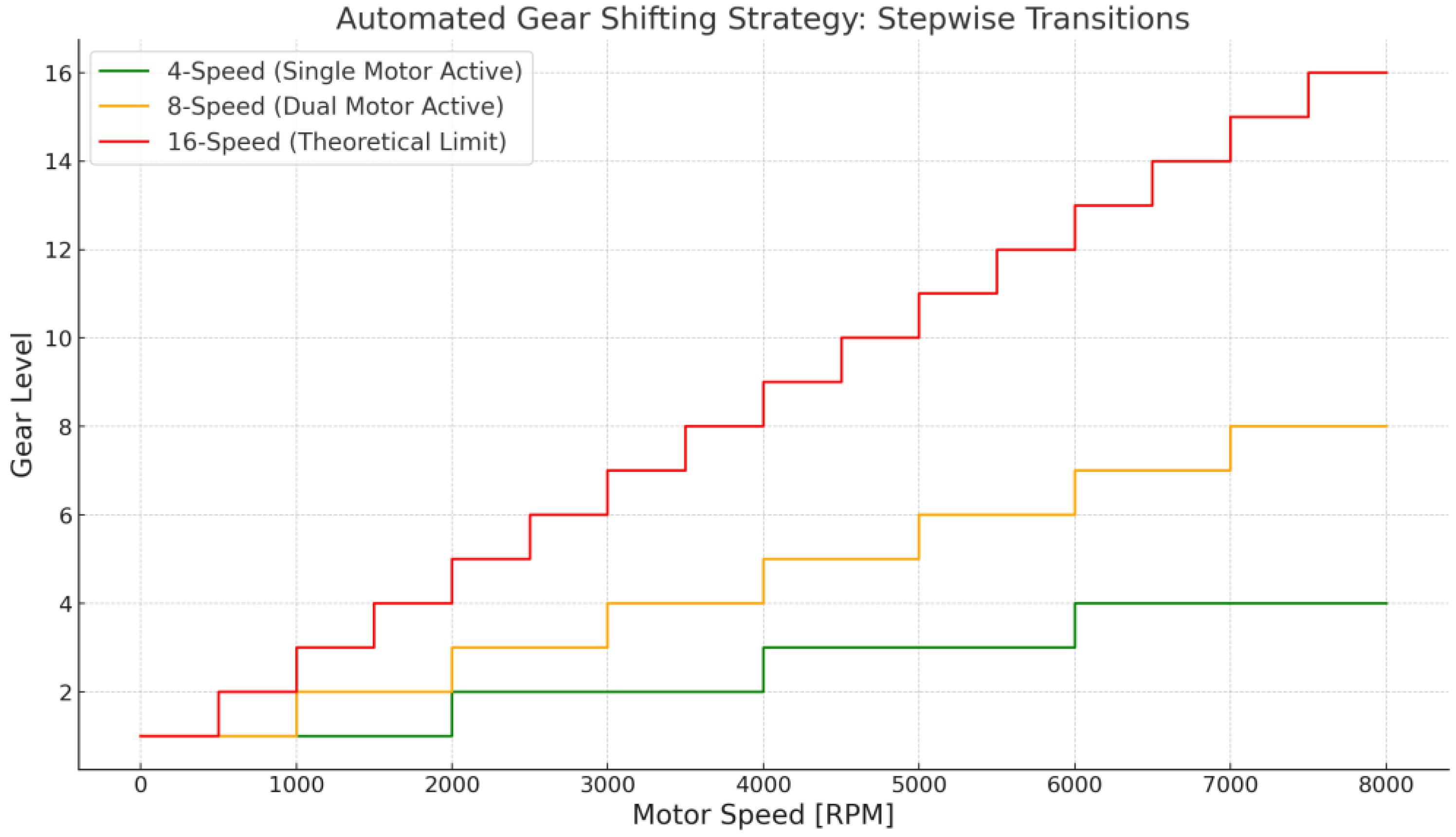
This figure compares automated gear-shift transitions in a dual-gearbox system, showing the difference between the original 16-level shifting strategy (blue) and the simplified 4-level mapping (green) as a function of motor speed.

The Figure 4 illustrates a stepwise automated gear shifting strategy for an electric drivetrain architecture featuring two identical electric motors, each connected to a multi-speed transmission. The horizontal axis represents motor speed in revolutions per minute (RPM), while the vertical axis denotes the gear level engaged at a given speed.

Green Curve: 4-Speed Mode (Single Motor Active):

Represents the physically implemented gear levels when only one motor drives the vehicle. This mode minimizes complexity and energy consumption under light-load conditions by limiting operation to four distinct gear states. Each step corresponds to a gear shift point triggered by motor speed.

Orange Curve: 8-Speed Mode (Dual Motor Active):

Shows the gear engagement strategy when both motors are active, enabling the use of eight combined gear states. This mode provides enhanced performance and torque availability while allowing thermal load distribution between the motors. The gear shift logic is extended to accommodate intermediate gear levels formed by dual motor coordination.

Red Curve: 16-Speed Mode (Theoretical Limit):

Depicts the theoretical maximum resolution of gear combinations resulting from a 4 × 4 dual gearbox system (i.e., 16 possible combinations). Although not all of these are practically achievable due to mechanical, thermal, and speed limitations, the curve serves as a reference for optimal operating envelope design and loss minimization strategies.

This figure emphasizes the hierarchical abstraction of gear states from a mathematical model (16-speed) to a practical, real-time control implementation (4- and 8-speed modes). It also highlights the potential of stepwise gear engagement to optimize drivetrain efficiency and performance in electric vehicle applications through intelligent gear state management.

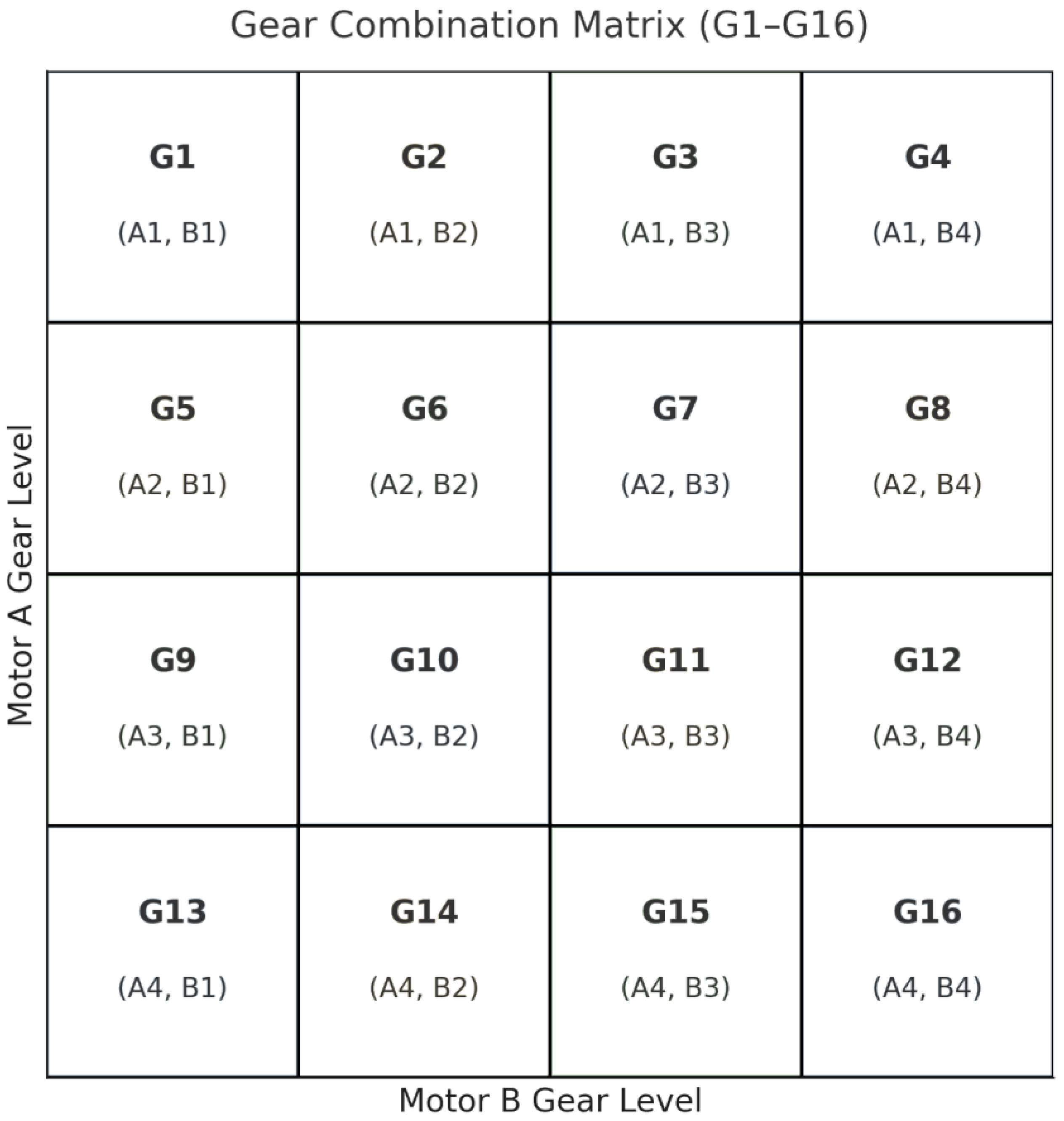
The gear combination matrix shown in Figure 5 defines the sixteen theoretically possible gear states (G1–G16) that arise from the interaction of two electric machines, Motor A and Motor B, each operating a dedicated four-speed gearbox. The matrix is structured such that the vertical axis represents the gear levels of Motor A (A1–A4), while the horizontal axis denotes the gear levels of Motor B (B1–B4). Each cell corresponds to a specific gear pairing (e.g., G1 = A1–B1, G2 = A1–B2, G16 = A4–B4), which in turn determines a distinct effective gear ratio at the differential output.

These combinations provide the mathematical basis for automated gear selection in dual-motor electric drivetrains. In real-world operation, advanced control algorithms dynamically traverse the matrix to identify gear states that maximize drivetrain efficiency, limit thermal stress, and enable smooth torque blending. Although all sixteen combinations are theoretically valid, practical constraints—such as motor speed boundaries, synchronization requirements, and redundancy in effective ratios—inevitably reduce the number of gear states available under real driving conditions.

To mitigate this complexity, gear states exhibiting comparable performance or nearly identical ratios can be clustered into eight or even four representative virtual states, depending on whether one or both motors are active. For instance, single-motor operation reduces the system to four effective gear levels, while dual-motor operation allows eight, offering a balance between control complexity and performance. The matrix, therefore, functions not only as a descriptive representation but also as a decision space for intelligent gear selection strategies that integrate instantaneous vehicle demands, torque distribution, and thermal feedback, thereby improving adaptability, efficiency, and robustness of the overall powertrain.

The gear combination matrix illustrates all 16 theoretical gear pairings formed by two 4-speed gearboxes in a dual-motor electric drivetrain. It serves as a foundational structure for optimizing gear selection, enabling the system to reduce complexity by clustering these combinations into 8 or 4 effective shift states based on motor usage, thereby enhancing drivetrain efficiency and control flexibility.

4. Harmonic Mean Formulas for Dual Gearbox Output States

The formulas presented above define the equivalent gear ratios for all sixteen possible gear pairings in a dual four-speed gearbox system coupled through a differential. Each pairing, such as (A1, B2) or (A3, B4), corresponds to a unique combination of gear selections from the two individual gearboxes.

The resulting output gear ratio of the system is determined by applying the harmonic mean of the two selected gear ratios. This formulation reflects the physical principle of a differential, which averages rotational speeds rather than combining torque or mechanical ratios linearly. The harmonic mean is particularly well-suited to this context, as it inherently accounts for the inverse relationship between gear ratios and rotational speed. Formally, if i_A and i_B denote the gear ratios selected in Gearbox A and Gearbox B, respectively, the effective output ratio is obtained as their harmonic mean.

These formulations demonstrate that the system does not yield a linear or geometric progression of output states. Instead, the distribution of equivalent gear ratios is inherently non-uniform and nonlinear, governed by the reciprocal interactions of the selected gear ratios [3]. This nonlinearity produces a versatile yet complex shifting pattern, which must be systematically managed by the control unit to guarantee smooth transitions and efficient operation [4].

Overall, the harmonic mean model is indispensable for accurately simulating and controlling the drivetrain behavior of electric buses and other vehicles employing dual synchronized gearboxes with differential coupling. It enables precise mapping of gear transitions, rigorous evaluation of energy efficiency, and effective torque balancing within a multistate power delivery system [46].

4.1. Gear Shifting Process

In a dual-gearbox electric drive system, each motor operates its own multi-speed gearbox, and their outputs are merged through a differential. This configuration yields sixteen distinct gear combinations, arising from the independent selection of four gear levels in each gearbox [13,14]. The gear-shifting process requires carefully controlled transitions between these combinations to guarantee smooth torque delivery [15,27], synchronization of rotational speeds, and maximized powertrain efficiency [37,38]. Because the effective output speed is determined by the harmonic mean of the selected gear ratios, each shift necessitates precise mathematical coordination between the two gearboxes and the central control unit [41,42]. To prevent mechanical stress and to ensure seamless operation under varying driving conditions, accurate timing and synchronization are indispensable [43].

The dynamic response and coordination logic of this architecture can be further reinforced by advanced real-time control techniques and predictive modeling strategies. In particular, mathematical gear-shift algorithms and adaptive engagement control frameworks provide the means to anticipate transient conditions, optimize state transitions, and maintain stability across a wide range of operating scenarios.

$${\mathrm{i}}_{\mathrm{e}\mathrm{q}}(\mathrm{A}1,\mathrm{B}1)={\displaystyle \frac{2}{\frac{1}{4.0}+\frac{1}{4.0}}}$$

(3)

$${\mathrm{i}}_{\mathrm{e}\mathrm{q}}(\mathrm{A}1,\mathrm{B}2)={\displaystyle \frac{2}{\frac{1}{4.0}+\frac{1}{2.5}}}$$

(4)

$${\mathrm{i}}_{\mathrm{e}\mathrm{q}}(\mathrm{A}1,\mathrm{B}3)={\displaystyle \frac{2}{\frac{1}{4.0}+\frac{1}{1.6}}}$$

(5)

$${\mathrm{i}}_{\mathrm{e}\mathrm{q}}(\mathrm{A}1,\mathrm{B}4)={\displaystyle \frac{2}{\frac{1}{4.0}+\frac{1}{1.0}}}$$

(6)

$${\mathrm{i}}_{\mathrm{e}\mathrm{q}}(\mathrm{A}2,\mathrm{B}1)={\displaystyle \frac{2}{\frac{1}{2.5}+\frac{1}{4.0}}}$$

(7)

$${\mathrm{i}}_{\mathrm{e}\mathrm{q}}(\mathrm{A}2,\mathrm{B}2)={\displaystyle \frac{2}{\frac{1}{2.5}+\frac{1}{2.5}}}$$

(8)

$${\mathrm{i}}_{\mathrm{e}\mathrm{q}}(\mathrm{A}2,\mathrm{B}3)={\displaystyle \frac{2}{\frac{1}{2.5}+\frac{1}{1.6}}}$$

(9)

$${\mathrm{i}}_{\mathrm{e}\mathrm{q}}(\mathrm{A}2,\mathrm{B}4)={\displaystyle \frac{2}{\frac{1}{2.5}+\frac{1}{1.0}}}$$

(10)

$${\mathrm{i}}_{\mathrm{e}\mathrm{q}}(\mathrm{A}3,\mathrm{B}1)={\displaystyle \frac{2}{\frac{1}{1.6}+\frac{1}{4.0}}}$$

(11)

$${\mathrm{i}}_{\mathrm{e}\mathrm{q}}(\mathrm{A}3,\mathrm{B}2)={\displaystyle \frac{2}{\frac{1}{1.6}+\frac{1}{2.5}}}$$

(12)

$${\mathrm{i}}_{\mathrm{e}\mathrm{q}}(\mathrm{A}3,\mathrm{B}3)={\displaystyle \frac{2}{\frac{1}{1.6}+\frac{1}{1.6}}}$$

(13)

$${\mathrm{i}}_{\mathrm{e}\mathrm{q}}(\mathrm{A}3,\mathrm{B}4)={\displaystyle \frac{2}{\frac{1}{1.6}+\frac{1}{1.0}}}$$

(14)

$${\mathrm{i}}_{\mathrm{e}\mathrm{q}}(\mathrm{A}4,\mathrm{B}1)={\displaystyle \frac{2}{\frac{1}{1.0}+\frac{1}{4.0}}}$$

(15)

$${\mathrm{i}}_{\mathrm{e}\mathrm{q}}(\mathrm{A}4,\mathrm{B}2)={\displaystyle \frac{2}{\frac{1}{1.0}+\frac{1}{2.5}}}$$

(16)

$${\mathrm{i}}_{\mathrm{e}\mathrm{q}}(\mathrm{A}4,\mathrm{B}3)={\displaystyle \frac{2}{\frac{1}{1.0}+\frac{1}{1.6}}}$$

(17)

$${\mathrm{i}}_{\mathrm{e}\mathrm{q}}(\mathrm{A}4,\mathrm{B}4)={\displaystyle \frac{2}{\frac{1}{1.0}+\frac{1}{1.0}}}$$

(18)

4.2. Harmonic Averaging Strategy for Efficiency-Oriented Gear Control

This relationship does not follow a linear or exponential rule. Instead, the equivalent gear ratio is derived from the inverse of the sum of the reciprocals of the selected individual gear ratios. Mathematically, it is governed by a harmonic mean rather than by direct proportionality [46]. As a consequence, successive gear states cannot be related through a constant multiplier, the resulting sequence is neither arithmetic nor geometric, and the gear ratio values do not increase or decrease uniformly since the ratios between them are not constant.

In dual-electric motor drivetrains with two synchronized multi-speed gearboxes, the system can theoretically generate sixteen unique gear ratio combinations by independently selecting one of four gear positions in each gearbox. These combinations yield distinct output ratios defined by the harmonic mean of the individual gear ratios. While this internal flexibility is advantageous, practical implementation often necessitates simplifying the drivetrain interface to a reduced number of user-facing or control-level gear states—typically four.

In a dual-gearbox electric drive system, each motor operates its own multi-speed gearbox, and their outputs are merged through a differential [13,14]. This configuration produces sixteen possible gear combinations, resulting from the independent selection of four gear levels in each gearbox [15,27]. The shifting process involves carefully controlled transitions between these combinations to ensure smooth torque delivery [37,38], synchronization of rotational speeds, and optimal system efficiency [41,42]. Because the effective output speed is determined by the harmonic mean of the selected gear ratios, each shift requires precise mathematical coordination between the two gearboxes and the central control unit [43]. Synchronization is particularly critical to avoid mechanical stress and to maintain seamless operation across varying driving conditions. These coordination challenges motivate the adoption of real-time control strategies and predictive shift planning, as reflected in recent research on gear engagement modeling [13,14], adaptive shift strategies [15,27], and dynamic torque control [37,38].

To achieve a practical yet efficient implementation, a classification and gear-state mapping strategy is introduced [41]. The sixteen harmonic gear combinations are systematically analyzed across thermal, torque, and speed domains to evaluate their efficiency characteristics [42,43]. Based on observed similarities in output behavior and performance, these combinations are clustered into four functionally equivalent groups, each representing a virtual gear level. Each group contains multiple internal gear pairings that deliver comparable drive performance under dynamic load conditions. The control system continuously monitors real-time vehicle parameters—motor temperatures, load, speed, and requested torque—and selects the most efficient internal gear pair within the corresponding virtual gear cluster [27,38]. This approach allows the system to dynamically reconfigure internal gear states while presenting four consistent external shift levels to the driver or supervisory controller. In doing so, the drivetrain achieves a balance between high-resolution energy optimization and manageable system complexity [15,37]. Moreover, the strategy supports adaptive behavior under thermal fluctuations and load variation, as the virtual gear levels can dynamically map to different internal combinations in response to changing conditions [13,41].

Importantly, this structured reduction from sixteen to four gear states is not a limitation but a functional simplification enabled by intelligent control [42]. It preserves the advantages of high-resolution torque–speed matching while streamlining system logic and maintaining predictable driving behavior [14,43]. Such an architecture is particularly advantageous in commercial electric vehicle applications—such as buses and delivery fleets—where minimizing energy losses, reducing thermal stress, and extending component lifetime are operational priorities [27,38]. The proposed gear abstraction strategy, therefore, provides a practical solution to the inherent complexity of multi-speed twin-drive systems, supported by rigorous mathematical foundations and offering scalable implementation potential [37,41].

4.3. Input–Output Parameter Matrix for Adaptive Gear Shifting in Electric Drives

The configuration presented in

Table 1. Measurement and Control Framework for Efficiency Mapping and Gear Actuation in Electric Powertrains.

Parameter Number	Input Parameter	Description (Input)	Unit	Parameter Number	Output Parameter	Description (Output)	Unit
1	t_run	runtime	s	13	t_run	runtime	s
2	t_meas	Measurement and calculating timestamp	ms	14	t_meas	Measurement and calculating timestamp	ms
3	f_sampling	sampling frequency	μs	15	t_proc	processing time	s
4	U_DC	DC lin voltage (battery)	V	16	T_motor	Motor airgap torque calculated	Nm
5	U_AC	Motor terminal voltage	V	17	T_shaft	Motor shaft torque calculated	Nm
6	I_motor	Motor current	A	18	T_gearbox input	Calculated	Nm
7	S_motor	Motor speed	rpm	19	T_gearbox output	Calculated	Nm
8	T_motor	Motor temperature	°C	20	Efficiency	Calculated	ratio
9	f_inverter	Inverter output frequency	Hz	21	Motor fundamental frequency	Calculated	Hz
10	f_switching	Switching frequency	kHz	22	Efficiency map	Calculated Speed, Torque	rpm, Nm
11	Gear_req	Gear shift request	ratio	23
12	Phase equivalent circuit diagram of an electric machine with resistances and reactances	resistances, reactances, coil and main field inductances	Ω, H (Henry)	24	Gear shift	Measured and calculated the output shaft	ratio

outlines a real-time data acquisition and control framework for an electric drivetrain system, with a focus on efficiency-aware gear shifting in multi-motor applications. The framework synchronously captures and processes both electrical and mechanical parameters within defined time intervals. Each operational cycle begins with the recording of runtime (t_run) and the measurement timestamp (t_meas), which serve as temporal references for acquired and computed signals. The processing time (t_proc) refers to the total execution duration of the simulation within the software environment, representing the computational effort required to complete a model run under specified solver and step-size settings. The sampling frequency (f_sampling) defines the rate at which continuous signals are discretized into digital data.

In measurement systems, this parameter determines the temporal resolution of acquired signals and directly affects the ability to capture dynamic phenomena without aliasing, as constrained by the Nyquist–Shannon theorem. In software environments, it specifies the computational update rate for simulations and control algorithms, thereby influencing numerical accuracy, stability, and processing load. Within such execution environments, it is essential to harmonize real-time operation, processing time, sampling intervals, and measurement cycles with the underlying computational framework. Each parameter has a distinct role, and their interaction directly governs the fidelity, reliability, and stability of the simulation or control process.

Real-time operation refers to the capability of the software or control system to execute tasks within strict temporal constraints that match the dynamics of the physical process being modeled. If deadlines are missed, the system can no longer represent the true dynamics accurately, which may result in delayed responses or control errors. Processing time denotes the actual computational duration required to complete one simulation or control cycle. It depends on model complexity, solver configuration, and hardware performance. When processing time exceeds the available cycle window dictated by real-time requirements, data cannot be updated on time, leading to delays, jitter, or even instability in closed-loop control. Sampling time (or sampling frequency) specifies how often continuous-time signals are discretized and updated for numerical computation. An appropriately chosen sampling rate ensures that system dynamics are captured without aliasing and that fast transients are represented faithfully. A rate that is too low causes information loss, whereas an excessively high rate increases computational load unnecessarily.

Measurement cycles define the frequency and timing of acquiring sensor data or simulated outputs. They are critical for ensuring that feedback information remains consistent with the actual physical state of the system. If measurement updates are misaligned with sampling or processing cycles, the control algorithm may operate on outdated or inconsistent data. When these cycles are properly synchronized and harmonized, the digital system can accurately replicate the physical process. Effective synchronization ensures that measurement data are acquired at the correct instants, computations are completed within the real-time window, and control signals are applied without delay. Such alignment minimizes latency, reduces the risk of aliasing or phase lag, and guarantees numerical stability as well as dynamic consistency. Conversely, a lack of synchronization may result in missed deadlines, data loss, jitter in control actions, or inaccurate representation of dynamic states. These problems can reduce efficiency, increase thermal stress in electric drives, or even destabilize system behavior. Ultimately, the coordination of real-time execution, processing time, sampling intervals, and measurement periods forms the foundation for reliable, reproducible, and physically valid results. This requirement is particularly critical in the co-simulation of electric drives, where electromagnetic, thermal, and mechanical subsystems must interact seamlessly. By aligning timing cycles, the software environment ensures that complex coupled phenomena are captured with sufficient resolution while maintaining computational efficiency.

On the input side, the system monitors the DC-link voltage from the battery (U_DC), the AC terminal voltage of the motor (U_AC), the phase current (I_motor), and the motor speed (S_motor) in revolutions per minute. The thermal behavior is also tracked via the motor temperature (T_motor), while the inverter’s output frequency (f_inverter) and the applied switching frequency (f_switching) provide insights into the modulation and control strategy. A gear shift request (Gear_req) acts as a high-level control signal to initiate changes in transmission state. The electrical machine is further characterized by its equivalent phase circuit, including resistances and reactances, and the associated coil and main field inductances, which help model the motor’s dynamic performance under varying load conditions. On the output side, the system computes the motor’s electromagnetic torque (T_motor), the actual shaft torque (T_shaft), and the torque transferred to and from the gearbox (T_gearbox input, T_gearbox output). The real-time efficiency (Efficiency) is determined as a dimensionless ratio, and the complete efficiency map (Efficiency map) is generated across the torque–speed plane, facilitating deeper analysis and visualization. Additionally, the fundamental frequency of the motor (Motor fundamental frequency) is derived to support frequency-domain diagnostics. The resulting gear shift (Gear shift) is measured and calculated based on the gearbox output shaft behavior. An important output is also the updated runtime of the sub-process, which reflects the elapsed duration from the gear shift initiation to the stabilized output response. This closed-loop measurement–control system enables adaptive gear selection based on motor behavior, thermal state, and load conditions. It supports advanced drivetrain control algorithms that optimize energy conversion while reducing thermal stress, making it particularly suitable for electric vehicles equipped with twin or multi-motor architectures.

5. Temperature-Aware, Efficiency-Oriented Shift Strategy for Dual-Gearbox Electric Drive Systems

In a 16-state dual-gearbox electric drivetrain where two PMSM-driven 4-speed gearboxes operate in coordination via a differential, a robust gear selection strategy must go beyond mechanical logic. To ensure peak performance, motor thermal behavior must be integrated into the shifting algorithm. Since the efficiency of PMSMs varies not only with torque and speed but also with temperature, each gear combination must be evaluated dynamically in relation to thermal limits.

Assuming that the motor control system accounts for temperature increments of 5 °C, and that motor thermal models update the torque-speed efficiency map accordingly at each step, the system must manage multiple thermal states per gear combination. For example, over a practical temperature range of 0 °C to 100 °C, this results in 21 thermal states. With 16 gear ratio combinations available, this leads to:

$$16\mathrm{g}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}·21\mathrm{t}\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{s}=336\mathrm{u}\mathrm{n}\mathrm{i}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{y}\mathrm{m}\mathrm{a}\mathrm{p}\mathrm{s}$$

(19)

Each of these 336 maps represents a distinct operating scenario, and the gear selection algorithm must identify the combination that not only maintains the output shaft in its optimal torque-speed region, but also prevents overheating, reduces thermal cycling, and prolongs motor lifespan.

This temperature-aware strategy continuously evaluates:

• Motor temperature feedback from thermal sensors;
• Predicted thermal drift based on load and ambient conditions;
• Real-time performance of each motor-gear pairing;

The system then selects the gear state that maximizes combined efficiency while minimizing thermal stress, ensuring that the motor operates within its most favorable thermal and electrical conditions. Such an approach enhances reliability, drives smoothness, and energy efficiency, especially in demanding applications like electric buses, where both continuous power delivery and long-term component protection are critical.

By blending thermal modeling, harmonic gear computation, and efficiency mapping, this advanced shift logic represents a key step toward intelligent, thermally robust electric vehicle drivetrains.

In a dual-motor electric drivetrain featuring two 4-speed gearboxes linked via a differential, gear shifting must be managed not only for performance and efficiency, but also for thermal stability. Each combination of gear selections, 16 in total, produces a unique harmonic mean output ratio. However, in real-world operation, the torque-speed efficiency of Permanent Magnet Synchronous Motors (PMSMs) is strongly affected by their temperature, which in turn alters the optimal gear selection criteria.

To manage this, an adaptive thermal model is implemented in the control unit. For every 5 °C increment in motor temperature, a new efficiency map is applied to reflect changing losses, magnet behavior, and copper resistance. Assuming a nominal operating range of 0 °C to 100 °C, this would yield 21 thermal states, and when paired with the 16 gear combinations, a total of (depending on how much calculation is needed):

$$16\mathrm{g}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}·37\mathrm{t}\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{s}=592\mathrm{u}\mathrm{n}\mathrm{i}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{y}\mathrm{m}\mathrm{a}\mathrm{p}\mathrm{s}$$

(20)

Motor thermal class limits often exceed 100 °C for example, a typical Class F or Class H motor may allow safe operation up to 155–180 °C winding temperatures.

Therefore, the system must account for a broader temperature range, e.g., −20 °C to 160 °C, resulting in more than 36 thermal steps (with 5 °C resolution).

Each of these maps defines a distinct relationship between torque, speed, thermal state, and efficiency. The gear shift logic must dynamically evaluate which gear combination offers the best compromise between performance, efficiency, and thermal load, using predictive models to avoid overheating, limit derating, and optimize long-term durability.

This advanced strategy is particularly vital in electric buses, which experience highly variable loads, extended operating hours, and frequent low-speed, high-torque demand. By integrating temperature feedback, motor class constraints, and harmonic-based gear computation, the system ensures that gear shifts support not only driving performance but also thermal protection and energy conservation, making the drivetrain smarter, safer, and more sustainable.

6. Temperature-Aware, Efficiency-Oriented Gear Shifting in Dual-Gearbox Electric Drivetrains

In modern electric drivetrain architectures, especially those employed in heavy-duty applications such as electric buses, dual-motor configurations with separate gearboxes offer both flexibility and performance optimization opportunities. A representative system consists of two identical PMSMs, each connected to a 4-speed mechanical gearbox. The outputs of these gearboxes are merged via a differential, enabling up to 16 unique gear combinations depending on the selected gear in each branch.

The resulting output gear ratio is not a simple mechanical sum but is determined by the harmonic mean of the two individual gear ratios. This reflects the physical role of the differential in averaging rotational speeds. However, selecting the optimal gear combination is not merely a matter of mechanical matching. To maximize energy efficiency and ensure thermal safety, the shift logic must incorporate motor temperature as a dynamic control parameter.

Electric motors, particularly PMSMs, exhibit efficiency and performance variations depending on their internal temperature. Factors such as copper resistance, magnetic saturation, and iron losses change as the machine heats up. Therefore, an efficiency-oriented shift strategy must continuously adapt to temperature-dependent performance curves. In the proposed method, this is done by recalculating the optimal gear state every 5 °C of motor temperature change. Within a standard operating range of 0 °C to 100 °C, this results in 21 thermal intervals, which, when applied to all 16 gear combinations, yield a total of 336 distinct torque-speed-efficiency states.

Nonetheless, this is not the full picture. Real-world applications, particularly in public transportation, require drivetrain operation outside the 0–100 °C range. Cold-start conditions may involve ambient temperatures below zero, while sustained operation under load may push motor temperatures near or beyond 155 °C, depending on the thermal class of the motor insulation (e.g., Class F or H). When accounting for this extended range, for example, from −20 °C to 160 °C, the number of temperature intervals increases significantly, leading to a total of more than 590 distinct operating states that must be considered by the control system.

Each of these combined gear-temperature states defines a unique efficiency landscape. As a result, the control logic must make shifting decisions not only based on driver demand and vehicle speed, but also on motor temperature, anticipated thermal rise, and real-time efficiency feedback. This enables the drivetrain to remain within optimal thermal and electrical boundaries, prevents unnecessary motor derating, and reduces long-term wear and energy loss.

The aim of the current research phase has been to investigate and quantify these interdependencies through a combination of simulation and empirical testing. Simulation models have been used to explore the interactions between gear states, motor temperature, and drive efficiency. These results are being compared with measurements collected from physical test rigs and vehicle prototypes. The objective is to validate the harmonic mean-based gear modeling approach under real-world thermal conditions and to develop a robust, temperature-aware shifting strategy that maximizes both efficiency and motor protection in dual-motor electric bus drivetrains.

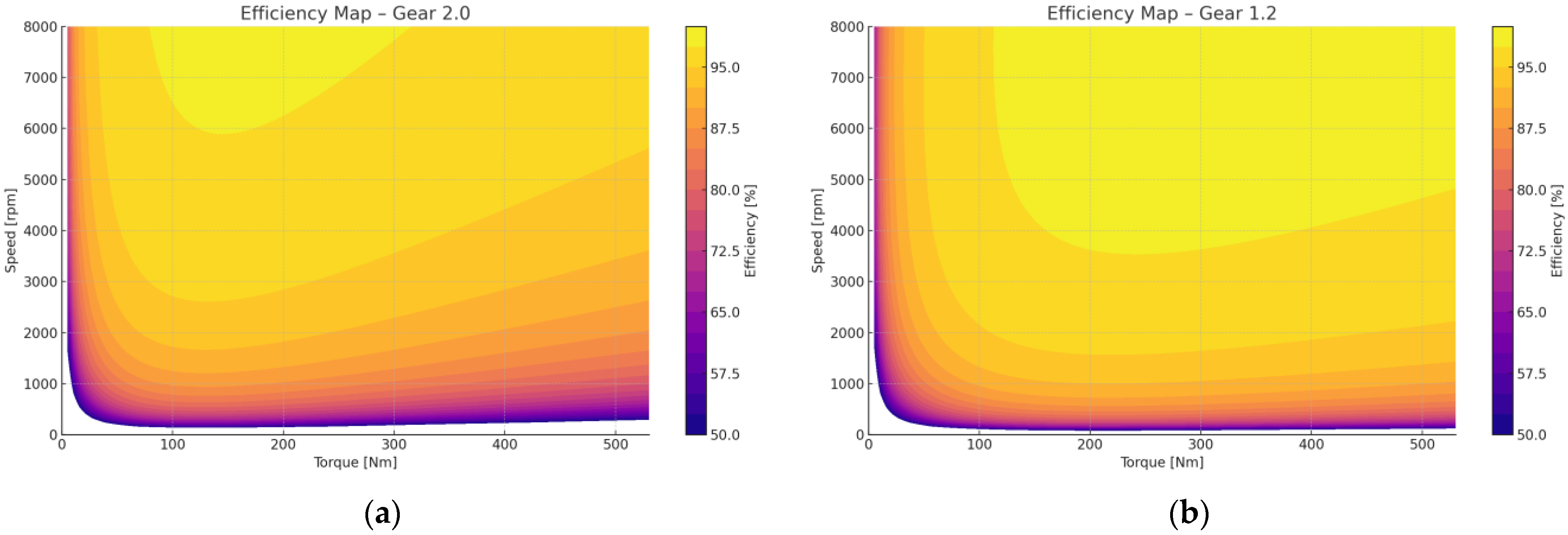
7. Comparative Analysis of the Efficiency Characteristics of a High-Performance Synchronous Machine

This study presents a comparative analysis of the efficiency characteristics of a high-performance synchronous machine under various fixed gear ratios. Four discrete gear stages—4.5:1, 3.0:1, 2.0:1, and 1.2:1—were examined using detailed loss modeling based on machine parameters, including copper loss, iron loss (speed-dependent), mechanical losses, and inverter losses. The baseline efficiency map without gear reduction served as a reference case, showing the native performance of the machine across its rated torque-speed range.

The introduction of gear ratios significantly alters the motor’s operating domain, effectively reshaping the efficiency landscape. Each gear stage compresses or stretches the torque and speed demands on the machine, enabling operation closer to regions of high efficiency. The highest attainable efficiency was observed in the 1.2:1 gear configuration, due to lower torque requirements at higher rotational speeds, which reduced copper losses.

The 4.5:1 gear stage provided excellent efficiency at high torque and low speed, making it suitable for launch and climbing conditions. The 3.0:1 and 2.0:1 gears showed balanced behavior, favoring mid-range operating points such as urban driving or steady acceleration. The contour plots clearly illustrated how the efficiency peak shifts with each gear, supporting the strategic use of multi-speed transmissions in electric drivetrains.

Removing the color scale in the final comparative plots improved visual clarity, emphasizing contour shapes and efficiency gradients across operating regions. The results confirm that appropriate gear ratio selection can substantially enhance energy utilization in electric powertrains by keeping the machine within its optimal efficiency envelope.

Furthermore, the mapping approach used here, based on physical parameter modeling and real torque-speed transformations, provides a useful framework for real-time gear selection logic. These maps may serve as a foundation for optimization algorithms or thermal-aware control strategies that aim to minimize total drivetrain losses under dynamic load conditions.

In conclusion, integrating gear stages into synchronous machine (rated data: Table 1) operation enables significant flexibility and performance tuning. The findings highlight the value of multi-speed drivetrains in applications requiring both high efficiency and broad operating ranges, such as commercial electric vehicles or automated guided systems.

The investigated electric machine is designed for high-performance operation (

Table 2. Data for selected synchronous machines.

Name	Value	Unit of Measure
Rated battery voltage	640	V
Rated torque	205	Nm
Rated power	155	kW
Rated current	232	A
Rated speed	7220	RPM
Peak torque	530	Nm
Peak performance	277.8	kW
Peak current	691.9	A
Maximum speed	8000	RPM

Synchronous machine manufacturer. https://ph.parker.com/us/en/product/gvm-global-vehicle-motors-for-mobile-applications/gvm210300dpwaabpb1g (the access date: 20 May 2021).

). It has a rated battery voltage of 640 V, with a rated torque of 205 Nm and a rated power of 155 kW. Under nominal conditions, the motor draws a rated current of 232 A at a rated speed of 7220 rpm. In transient operation, the machine is capable of delivering a peak torque of 530 Nm and a peak power of 277.8 kW, which corresponds to a peak current of 691.9 A. The maximum achievable rotational speed is 8000 rpm, allowing the drive to operate efficiently across a wide load and speed range.

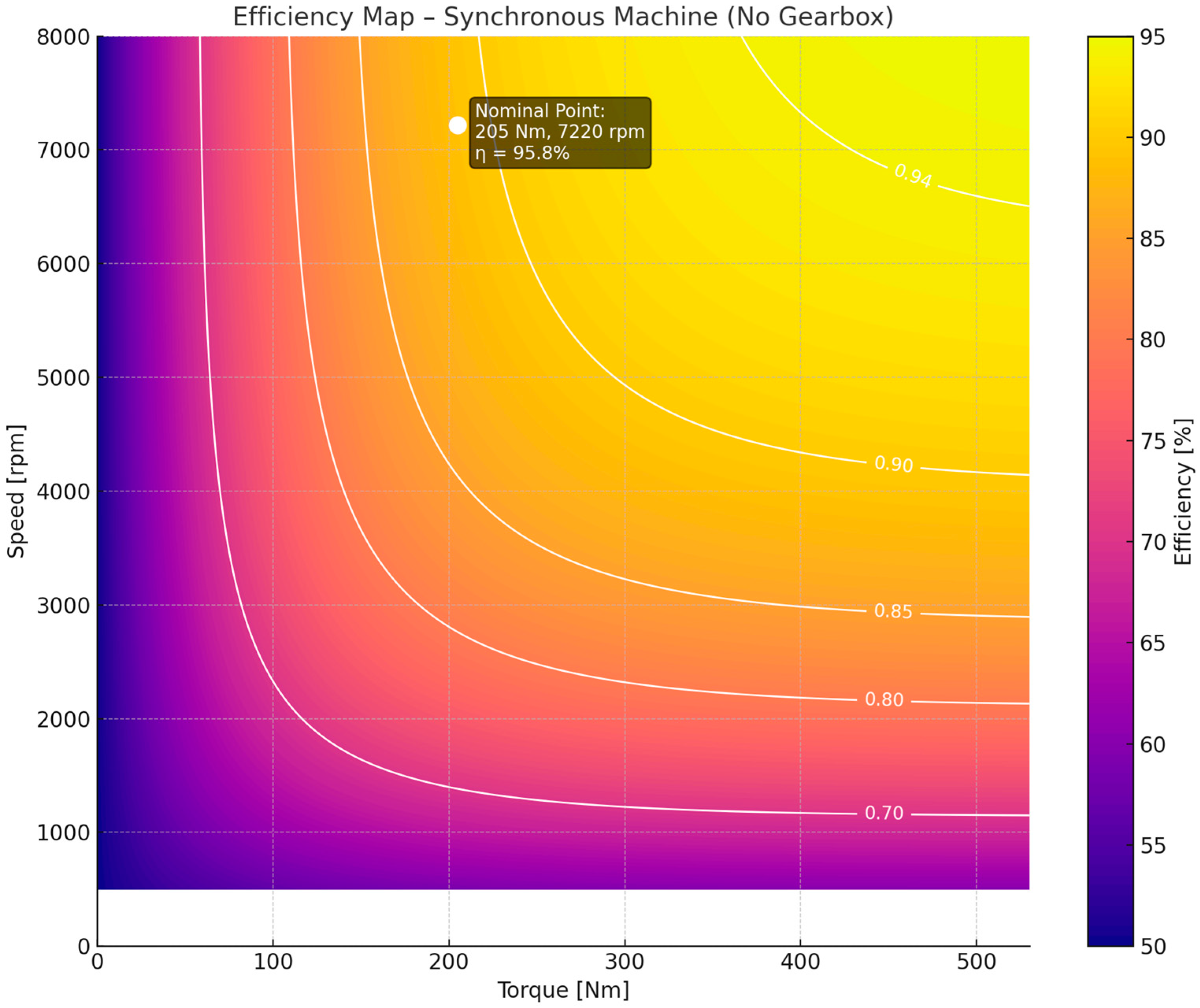
In addition, an efficiency map of the motor (Figure 6) was calculated, where the nominal operating point is explicitly indicated to highlight the reference condition for performance evaluation.

This efficiency map illustrates the performance of the synchronous machine across the full torque–speed operating range (Figure 6). It identifies regions of elevated efficiency and delineates areas where losses become significant. The nominal operating point (205 Nm, 7220 rpm, η = 95.8%) is indicated as a benchmark for assessing the machine’s energy conversion performance.

The integration of four discrete gear ratios (Figure 7 and Figure 8)—4.5:1, 3.0:1, 2.0:1, and 1.2:1—effectively enhances the efficiency map of the synchronous machine by shifting its operating points toward regions of higher energy conversion efficiency. Each gear ratio modifies the torque-speed relationship at the motor shaft, allowing the machine to operate closer to its optimal efficiency range under varying load and speed conditions.

The low gear (4.5:1) compresses the speed range and boosts torque, enabling high efficiency at low speeds where the base motor map would otherwise suffer from increased losses. Conversely, the high gear (1.2:1) reduces torque demands at high speed, minimizing copper losses and maximizing efficiency during cruising or highway driving. Intermediate gears (3.0:1 and 2.0:1) bridge the performance gap between low-speed torque-rich scenarios and high-speed light-load conditions, expanding the motor’s usable high-efficiency envelope.

Collectively, the four gear stages flatten and widen the overall efficiency distribution. Instead of a single efficiency peak, the drivetrain now offers multiple high-efficiency regions across different speed and torque domains. This enables more frequent operation within favorable conditions, ultimately leading to better energy utilization and thermal performance throughout the drive cycle.

Theorem 1.

In an electric drivetrain architecture consisting of two identical synchronous machines, each coupled to a multi-speed gearbox and connected to a common output shaft via a differential, the theoretical set of sixteen harmonic gear combinations can be reduced to four virtual output levels by applying a mapping strategy based on efficiency clustering. The drivetrain control unit can maintain optimal operational efficiency by dynamically selecting internal gear pairings within these four groups, without compromising performance or thermal stability.

Proof of Theorem 1.

In a dual-motor drivetrain, each synchronous machine operates its own four-speed gearbox, and when coupled through a differential, the system provides sixteen gear ratio combinations. The effective output ratio is determined as the harmonic mean of the two selected gear ratios.

In practice, automotive control systems benefit from reducing these sixteen states to a smaller set, such as four, to improve robustness, shift coordination, and computational efficiency. Many of the harmonic combinations produce comparable torque, speed, and efficiency; thus, by evaluating performance under varying load and thermal conditions, they can be clustered into four groups. Each group defines a virtual gear level, within which the controller dynamically selects the most efficient internal pairing.

Because the two synchronous machines operate in a coordinated, torque-balanced manner, transitions between internal states remain smooth as long as the effective ratio stays within the chosen virtual level. Hence, the original sixteen gear states can be systematically reduced to four practical output levels through harmonic modeling, efficiency evaluation, and real-time control. This approach preserves high-resolution optimization while presenting a simplified, stable interface to the vehicle system. □

8. Discussion

To fully leverage the flexibility of a 16-state dual-gearbox electric drive system, where each PMSM-driven gearbox can operate independently across four discrete gear levels, a dedicated shift logic must be implemented to ensure the drivetrain operates within its most efficient torque-speed envelope. The core objective of this strategy is to dynamically select gear combinations that maximize overall system efficiency, particularly under varying load conditions, gradients, and vehicle speeds.

Since the effective gear ratio is determined by the harmonic mean of the two selected gear ratios, the control system must evaluate not only individual gear states, but also the resulting equivalent ratio and its interaction with the combined efficiency maps of the motors and gearboxes. This involves constructing a real-time lookup matrix or optimization table where each of the 16 possible gear states is mapped to expected motor efficiency, torque availability, and mechanical constraints.

The shift strategy continuously monitors the drivetrain’s operating point and selects the gear combination that maintains the output shaft speed and torque within the highest efficiency region of the motors’ performance curves. This approach avoids suboptimal transitions, minimizes unnecessary shifting, and ensures smooth torque delivery—particularly important in heavy-duty applications such as electric buses, where passenger comfort and energy conservation are paramount.

By integrating predictive control, torque balancing, and energy-aware decision-making, the system transitions fluidly between gear states, adapting to both driver demand and environmental conditions. The result is a smart, harmonics-aware drivetrain that extracts maximum performance with minimum energy loss, enabling next-generation electric mobility with optimal drive quality and range efficiency.

9. Conclusions

The investigation of temperature-aware, efficiency-oriented gear shifting for dual-gearbox electric drivetrains has underscored the importance of harmonizing mechanical, electrical, and thermal domains in advanced EV architectures. By modeling the effective gear ratio through the harmonic mean of two independently shifted gearboxes, the drivetrain attains a high degree of operational flexibility. However, this flexibility must be rigorously managed to ensure that each gear combination remains within thermally safe and energetically optimal boundaries.

Incorporating motor temperature as a real-time parameter into the gear-shift strategy substantially enhances drivetrain reliability and performance. Capturing a broad temperature spectrum—from sub-zero start-up conditions to severe thermal stress near insulation limits—necessitates the generation of hundreds of distinct torque–speed–efficiency maps. These maps directly inform the control logic, enabling the selection of gear states that minimize energy losses, mitigate overheating, and extend component lifetime.

The present phase of the research has successfully established the theoretical framework and, through simulation supported by preliminary measurements, demonstrated the feasibility of the proposed approach. Consequently, this study provides the foundation for the deployment of intelligent shift strategies in electric buses and other heavy-duty applications, where energy efficiency, thermal resilience, and drive smoothness are paramount. Future work will focus on integrating predictive control algorithms and extending the measurement program under dynamic driving scenarios.

10. Patents

A part of the present study is based on the invention described in Hungarian Patent P1900265/24, titled “Gear Switching Method for Vehicles Powered by an Electric Motor Which Is Coupled to an Automatic or Automatized Mechanical Gear Shift” by Dr. Sándor Simonyi [24].

The patent, published on 1 March 2021 and granted on 21 February 2022, outlines a control strategy for optimizing gear transitions in electric vehicles through the use of an efficiency-based, harmonically balanced shift method. This concept serves as the foundation for the simulation and measurement methodology discussed in this paper.

A part of the research presented in this paper is derived from the invention described in Hungarian Patent P1800232/21, titled “Procedure for Efficient Operation of Electric Motors Used in Vehicles with a Drive Train Consisting of Two Electric Motors and a Gear-Box”, authored by Dr. Sándor Simonyi [25].

The patent, published on 30 December 2019 and granted on 21 January 2022, introduces a method for maintaining optimal efficiency of electric motors operating in a dual-motor, multi-speed transmission configuration. The concept focuses on dynamic torque distribution and gear selection based on thermal and load conditions, forming a theoretical foundation for the control algorithms analyzed and tested in this study.

Procedure for Efficient Operation of Electric Motors Used in Vehicles with a Drive Train Consisting of Two Electric Motors and a Gear-Box. Hungarian Patent P1800232/21, B60K 1/00, Published: 30 December 2019; Granted: 21 January 2022. Authored by Dr. Sándor Simonyi.