A Graph-Theoretic Approach for Exploring the Relationship Between EV Adoption and Charging Infrastructure Growth
Abstract
1. Introduction
2. Literature Review
2.1. Impact of Charging Infrastructure and Other Factors on EV Adoption
2.2. Application of Graph Model to Charging Infrastructure
2.3. Gaps Found in the Literature
- Most of the existing literature examines EV adoption and its relationship with other factors in one to three cities, resulting in limited data diversity. This study, however, analyzes 137 counties across six U.S. states, enhancing the analysis and demonstrating the role of states in clustering counties within the correlation networks.
- The use of graph models has mostly been limited to optimizing the placement of charging stations within specific areas. In contrast, this study contributes by applying a graph model to explore patterns in both EV adoption and CI growth networks under two scenarios of Early Adoption and Late Adoption, build a correlation network, and cluster counties accordingly.
- Existing studies rarely examine how the relationship between EV adoption and CI growth varies across different adoption scenarios (e.g., Early Adoption vs. Late Adoption) or under varying temporal granularities and lags. This limits our understanding of the timing and directionality of influence between the two. Our study addresses this by incorporating multiple time granularities and adoption phases to uncover nuanced structural and causal patterns.
3. Methodology
3.1. Data Collection
3.1.1. EV Data
3.1.2. CI Data
3.2. Proposed Graph-Theoretic Approach: Correlation Network
3.3. Early Versus Late Adoption
3.3.1. Early Adoption
3.3.2. Late Adoption
3.4. Different Time Granularities
3.5. Causality Relationships Between EVs and CIs
- Early Adoption Scenario: This hypothesis tests whether the growth of EV adoption leads to subsequent growth in CI. The null hypothesis is the following: EV adoption growth does not Granger-cause CI growth.
- Late Adoption Scenario: This hypothesis tests whether the growth of CI drives EV adoption. The null hypothesis is the following: CI growth does not Granger-cause EV adoption.
4. Results
4.1. Early Adoption of EV
4.2. Late Adoption of EV
4.3. Causal Relationships Between EV Adoption and CI Growth
5. Limitations and Future Work
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Atabani, A.; Badruddin, I.A.; Mekhilef, S.; Silitonga, A.S. A review on global fuel economy standards, labels and technologies in the transportation sector. Renew. Sustain. Energy Rev. 2011, 15, 4586–4610. [Google Scholar] [CrossRef]
- United States Environmenta Agency (EPA). Inventory of U.S. Greenhouse Gas Emissions and Sinks; Createspace Independent Publishing Platform: North Charleston, SC, USA, 2018.
- U.S. Environmental Protection Agency. Fast Facts on Transportation Greenhouse Gas Emissions; US Environmental Protection Agency: Washington, DC, USA, 2015.
- Alternative Fuels Data Center (A.F.D.C.). Electric Vehicle Benefits and Considerations; US Department of Energy: Washington, DC, USA, 2022; Volume 8.
- Chen, R.; Meng, Q.; Yu, J.J. Optimal government incentives to improve the new technology adoption: Subsidizing infrastructure investment or usage? Omega 2023, 114, 102740. [Google Scholar] [CrossRef]
- Archsmith, J.; Muehlegger, E.; Rapson, D.S. Future paths of electric vehicle adoption in the United States: Predictable determinants, obstacles, and opportunities. Environ. Energy Policy Econ. 2022, 3, 71–110. [Google Scholar] [CrossRef]
- Burra, L.T.; Al-Khasawneh, M.B.; Cirillo, C. Impact of charging infrastructure on electric vehicle adoption: A synthetic population approach. Travel Behav. Soc. 2024, 37, 100834. [Google Scholar] [CrossRef]
- Pamidimukkala, A.; Kermanshachi, S.; Rosenberger, J.M.; Hladik, G. Evaluation of barriers to electric vehicle adoption: A study of technological, environmental, financial, and infrastructure factors. Transp. Res. Interdiscip. Perspect. 2023, 22, 100962. [Google Scholar] [CrossRef]
- Kamis, A.; Abraham, P.S. Predictive models of electric vehicle adoption in the United States: Charging ahead with renewable energy. Transp. Res. Interdiscip. Perspect. 2024, 24, 101041. [Google Scholar] [CrossRef]
- Nicholas, M.; Hall, D.; Lutsey, N. Quantifying the electric vehicle charging infrastructure gap across US markets. Int. Counc. Clean Transp. 2019, 20, 1–39. [Google Scholar]
- Ledna, C.; Muratori, M.; Brooker, A.; Wood, E.; Greene, D. How to support EV adoption: Tradeoffs between charging infrastructure investments and vehicle subsidies in California. Energy Policy 2022, 165, 112931. [Google Scholar] [CrossRef]
- White, L.V.; Carrel, A.L.; Shi, W.; Sintov, N.D. Why are charging stations associated with electric vehicle adoption? Untangling effects in three United States metropolitan areas. Energy Res. Soc. Sci. 2022, 89, 102663. [Google Scholar] [CrossRef]
- Khan, H.A.U.; Price, S.; Avraam, C.; Dvorkin, Y. Inequitable access to EV charging infrastructure. Electr. J. 2022, 35, 107096. [Google Scholar] [CrossRef]
- Debnath, R.; Bardhan, R.; Reiner, D.M.; Miller, J. Political, economic, social, technological, legal and environmental dimensions of electric vehicle adoption in the United States: A social-media interaction analysis. Renew. Sustain. Energy Rev. 2021, 152, 111707. [Google Scholar] [CrossRef]
- Babic, J.; Carvalho, A.; Ketter, W.; Podobnik, V. A data-driven approach to managing electric vehicle charging infrastructure in parking lots. Transp. Res. Part D Transp. Environ. 2022, 105, 103198. [Google Scholar] [CrossRef]
- Illmann, U.; Kluge, J. Public charging infrastructure and the market diffusion of electric vehicles. Transp. Res. Part D Transp. Environ. 2020, 86, 102413. [Google Scholar] [CrossRef]
- Haidar, B.; Rojas, M.T.A. The relationship between public charging infrastructure deployment and other socio-economic factors and electric vehicle adoption in France. Res. Transp. Econ. 2022, 95, 101208. [Google Scholar] [CrossRef]
- Ou, S.; Lin, Z.; He, X.; Przesmitzki, S.; Bouchard, J. Modeling charging infrastructure impact on the electric vehicle market in China. Transp. Res. Part D Transp. Environ. 2020, 81, 102248. [Google Scholar] [CrossRef]
- Chen, R.; Fan, R.; Wang, D.; Yao, Q. Effects of multiple incentives on electric vehicle charging infrastructure deployment in China: An evolutionary analysis in complex network. Energy 2023, 264, 125747. [Google Scholar] [CrossRef]
- Langfelder, P.; Horvath, S. WGCNA: An R package for weighted correlation network analysis. BMC Bioinform. 2008, 9, 559. [Google Scholar] [CrossRef] [PubMed]
- Putnik, G.; Costa, E.; Alves, C.; Castro, H.; Varela, L.; Shah, V. Analysing the correlation between social network analysis measures and performance of students in social network-based engineering education. Int. J. Technol. Des. Educ. 2016, 26, 413–437. [Google Scholar] [CrossRef]
- Moni, M.A.; Liò, P. Network-based analysis of comorbidities risk during an infection: SARS and HIV case studies. BMC Bioinform. 2014, 15, 333. [Google Scholar] [CrossRef]
- Malisetty, S.; Ali, H.H.; Rastegari, E.; Siu, K.C. An innovative comparative analysis approach for the assessment of laparoscopic surgical skills. Surgeries 2023, 4, 46–57. [Google Scholar] [CrossRef]
- Thelagathoti, R.K.; Ali, H.H. A Correlation Network Model for Analyzing Mobility Data in Depression Related Studies. In Proceedings of the 16th International Conference on Health Informatics (HEALTHINF 2023), Lisbon, Portugal, 16–18 February 2023; pp. 416–423. [Google Scholar]
- Kim, S.; Thapa, I.; Ali, H.H. A Robust Network Model for Studying Microbiomes in Precision Agriculture Applications. In Proceedings of the 24th International Conference on Computational Science (ICCS 2024), Malaga, Spain, 2–4 July 2024; Springer: Cham, Switzerland, 2024; pp. 58–71. [Google Scholar]
- Gagarin, A.; Corcoran, P. Multiple domination models for placement of electric vehicle charging stations in road networks. Comput. Oper. Res. 2018, 96, 69–79. [Google Scholar] [CrossRef]
- Arkin, E.M.; Carmi, P.; Katz, M.J.; Mitchell, J.S.; Segal, M. Locating battery charging stations to facilitate almost shortest paths. Discret. Appl. Math. 2019, 254, 10–16. [Google Scholar] [CrossRef]
- Funke, S.; Nusser, A.; Storandt, S. Placement of loading stations for electric vehicles: No detours necessary! J. Artif. Intell. Res. 2015, 53, 633–658. [Google Scholar] [CrossRef]
- Funke, S.; Nusser, A.; Storandt, S. Placement of Loading Stations for Electric Vehicles: Allowing Small Detours. In Proceedings of the 26th International Conference on Automated Planning and Scheduling (ICAPS 2016), London, UK, 12–17 June 2016; AAAI Press: Washington, DC, USA, 2016; pp. 131–139. [Google Scholar]
- Agarwal, P.K.; Pan, J.; Victor, W. An efficient algorithm for placing electric vehicle charging stations. In Proceedings of the 27th International Symposium on Algorithms and Computation (ISAAC 2016), Sydney, Australia, 12–14 December 2016; Schloss-Dagstuhl-Leibniz Zentrum für Informatik: Wadern, Germany, 2016. [Google Scholar]
- Altundogan, T.G.; Yildiz, A.; Karakose, E. Genetic algorithm approach based on graph theory for location optimization of electric vehicle charging stations. In Proceedings of the 2021 Innovations in Intelligent Systems and Applications Conference (ASYU), Elazig, Turkey, 6–8 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar]
- Nigro, N. State EV Registration Data. Available online: https://www.atlasevhub.com/materials/state-ev-registration-data/ (accessed on 6 May 2024).
- Alternative Fueling Station Locator. Available online: https://afdc.energy.gov/stations (accessed on 6 May 2024).
- Newman, M.E.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
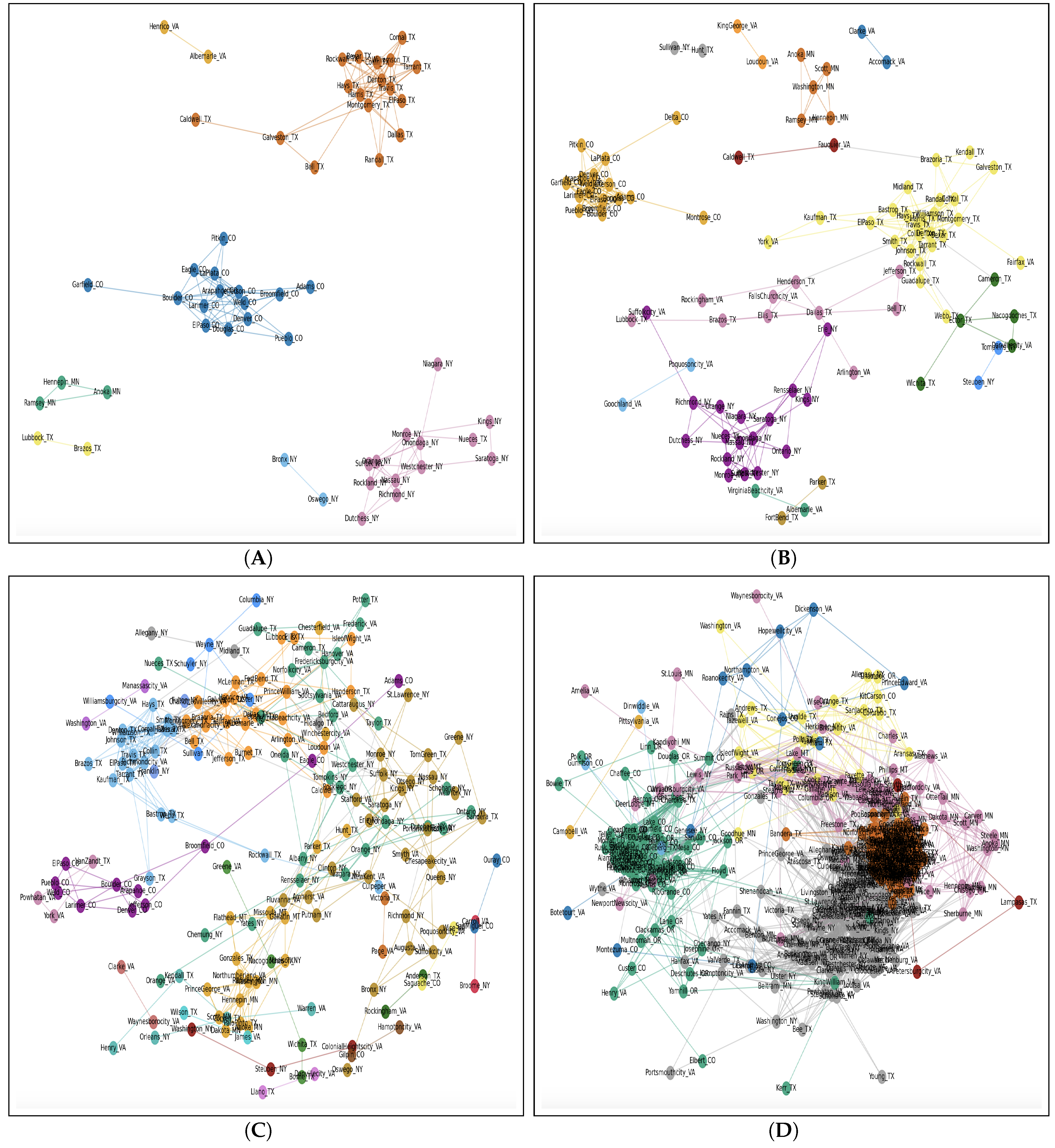
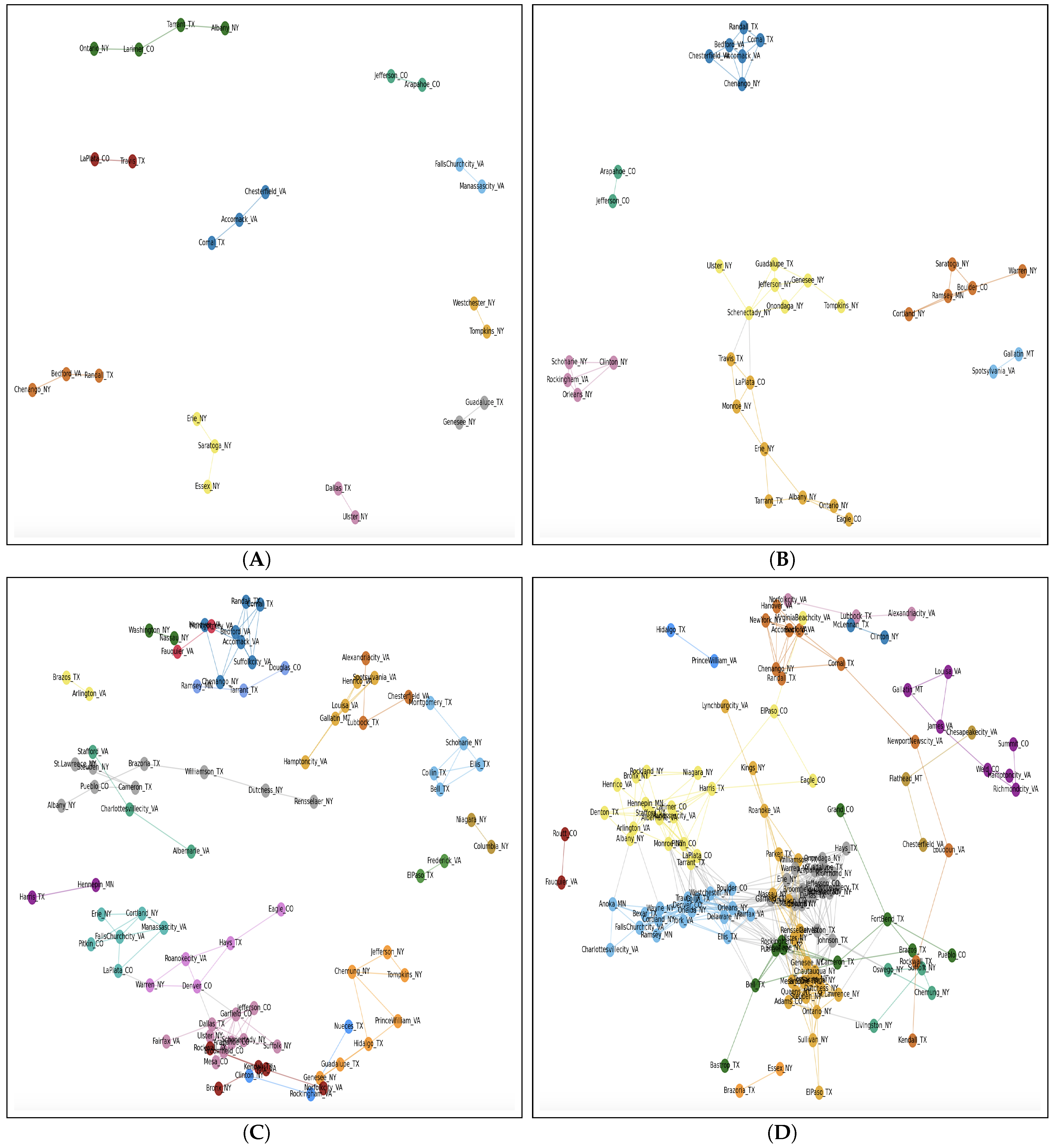
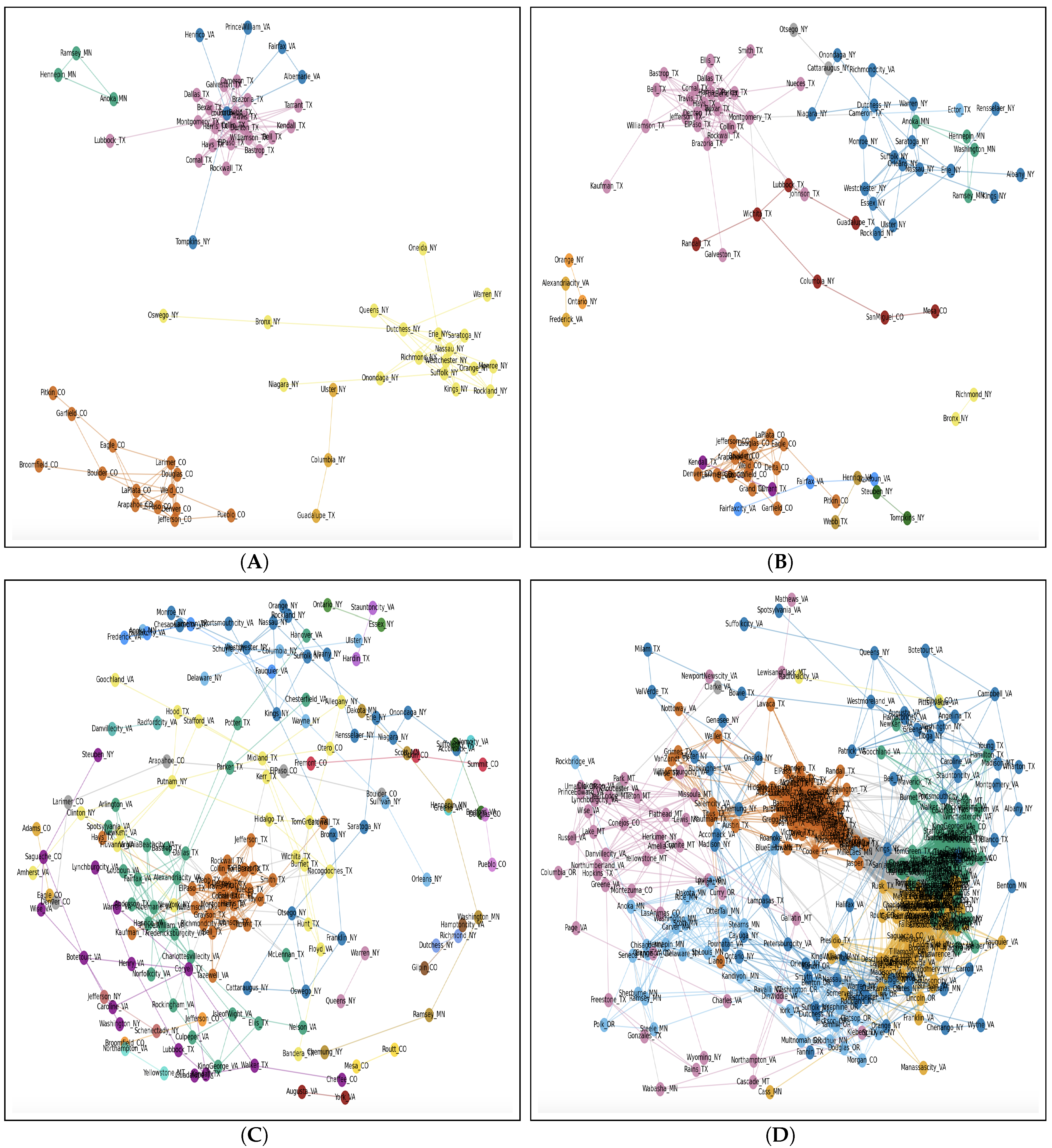
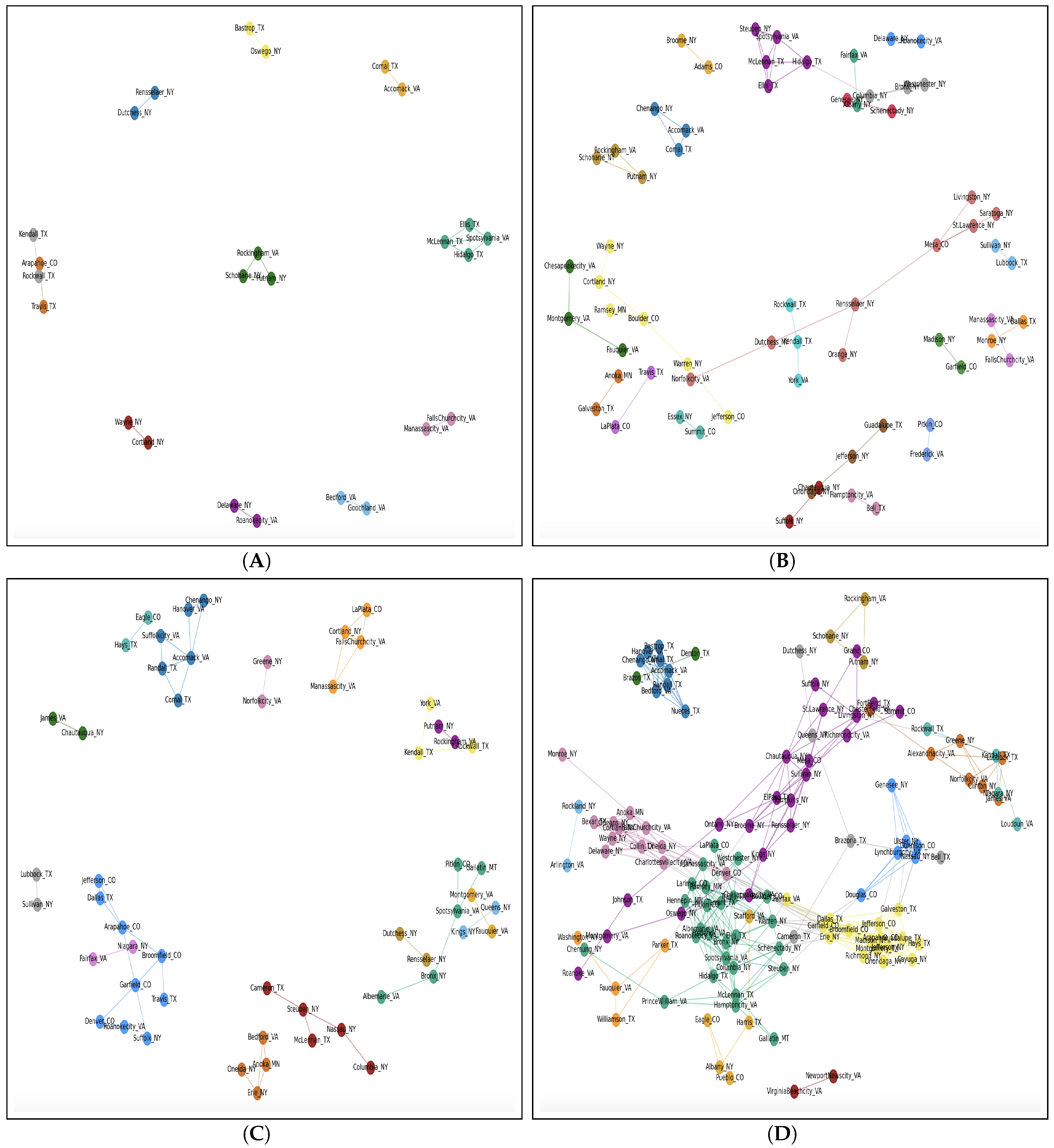
| No | State | # of Completed Counties |
|---|---|---|
| 1 | Colorado | 20 |
| 2 | Minnesota | 3 |
| 3 | Montana | 2 |
| 4 | New York | 48 |
| 6 | Texas | 30 |
| 7 | Virginia | 34 |
| 8 | Total | 137 |
| Granularity | EV vs. DC | EV vs. Level 2 | EV vs. ALL |
|---|---|---|---|
| Monthly | 0.1772 | 0.2205 | 0.2305 |
| Bi-monthly | 0.0972 | 0.1345 | 0.1416 |
| Quarterly | 0.0715 | 0.0624 | 0.0543 |
| Bi-annually | 0.0123 | 0.0366 | 0.0214 |
| Granularity | EV vs. DC | EV vs. Level 2 | EV vs. ALL |
|---|---|---|---|
| Monthly | 0.1415 | 0.2529 | 0.2667 |
| Bi-monthly | 0.1806 | 0.1347 | 0.1824 |
| Quarterly | 0.0897 | 0.0737 | 0.0619 |
| Bi-annually | 0.0263 | 0.0368 | 0.0203 |
| Granularity\Lag | Half-Year | One-Year | Two-Year | Three-Year | Unique |
|---|---|---|---|---|---|
| monthly | 12 | 20 | 16 | 13 | 49 |
| Bi-monthly | 12 | 16 | 18 | 14 | 52 |
| quarterly | 17 | 19 | 17 | 15 | 57 |
| Bi-annual | 9 | 12 | 6 | 15 | 30 |
| Unique | 28 | 38 | 45 | 33 | 93 |
| Granularity\Lag | Half-Year | One-Year | Two-Year | Three-Year | Unique |
|---|---|---|---|---|---|
| monthly | 18 | 11 | 9 | 9 | 37 |
| Bi-monthly | 23 | 9 | 4 | 12 | 39 |
| quarterly | 15 | 6 | 4 | 8 | 27 |
| Bi-annual | 17 | 8 | 7 | 8 | 35 |
| Unique | 44 | 26 | 20 | 26 | 77 |
| State | EV → ALL | ALL → EV | Unique |
|---|---|---|---|
| New York | 36 | 26 | 40 |
| Texas | 15 | 23 | 26 |
| Virginia | 23 | 16 | 27 |
| Colorado | 16 | 8 | 18 |
| Minnesota | 2 | 2 | 2 |
| Montana | 1 | 2 | 2 |
| Unique | 93 | 77 | 115 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alrasheedi, F.S.; Ali, H.H. A Graph-Theoretic Approach for Exploring the Relationship Between EV Adoption and Charging Infrastructure Growth. Vehicles 2025, 7, 54. https://doi.org/10.3390/vehicles7020054
Alrasheedi FS, Ali HH. A Graph-Theoretic Approach for Exploring the Relationship Between EV Adoption and Charging Infrastructure Growth. Vehicles. 2025; 7(2):54. https://doi.org/10.3390/vehicles7020054
Chicago/Turabian StyleAlrasheedi, Fahad S., and Hesham H. Ali. 2025. "A Graph-Theoretic Approach for Exploring the Relationship Between EV Adoption and Charging Infrastructure Growth" Vehicles 7, no. 2: 54. https://doi.org/10.3390/vehicles7020054
APA StyleAlrasheedi, F. S., & Ali, H. H. (2025). A Graph-Theoretic Approach for Exploring the Relationship Between EV Adoption and Charging Infrastructure Growth. Vehicles, 7(2), 54. https://doi.org/10.3390/vehicles7020054







