Optimization of Adaptive Cruise Control Strategies Based on the Responsibility-Sensitive Safety Model
Abstract
1. Introduction
2. Methods
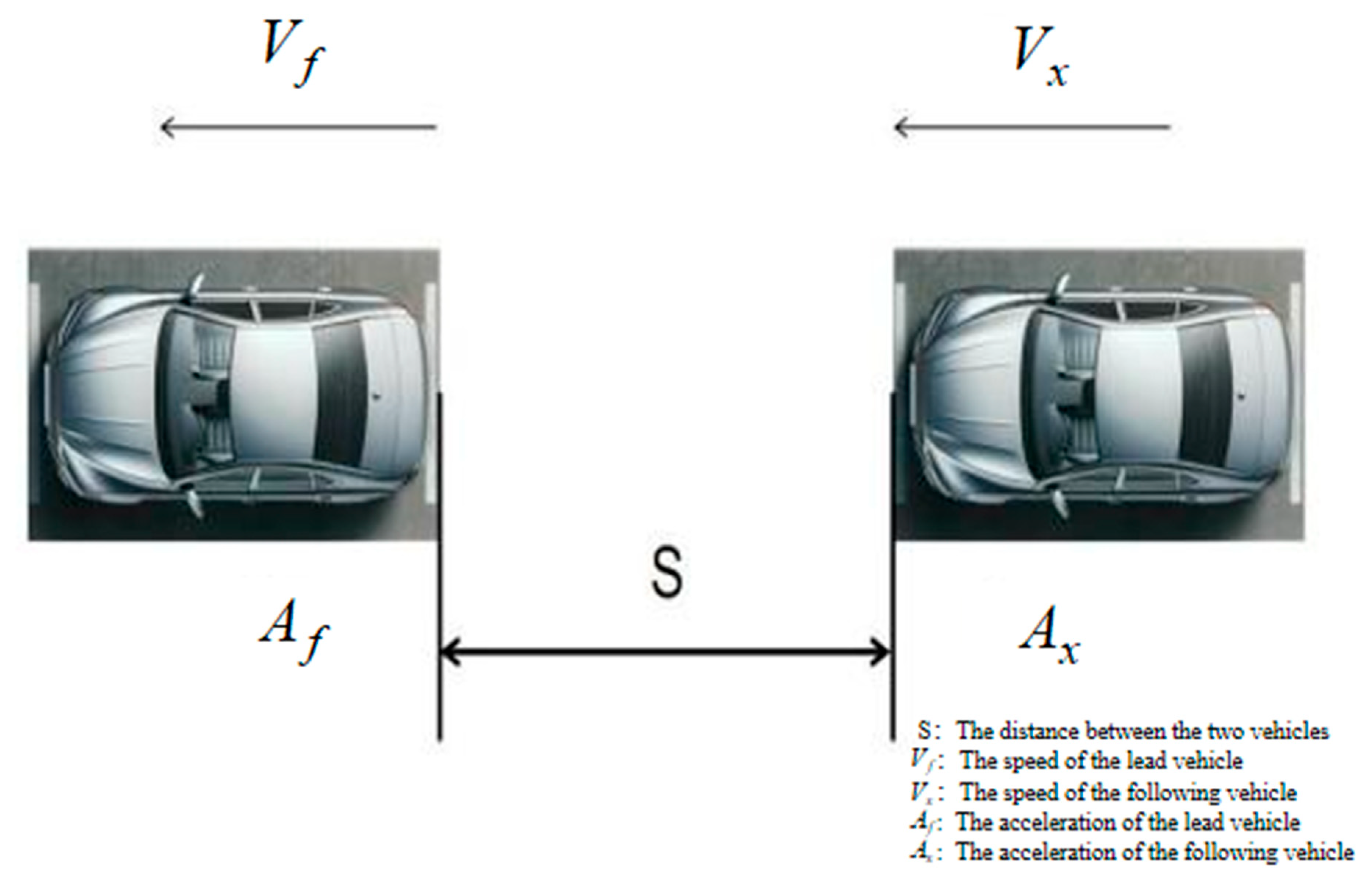
2.1. Following Cruise Framework Design
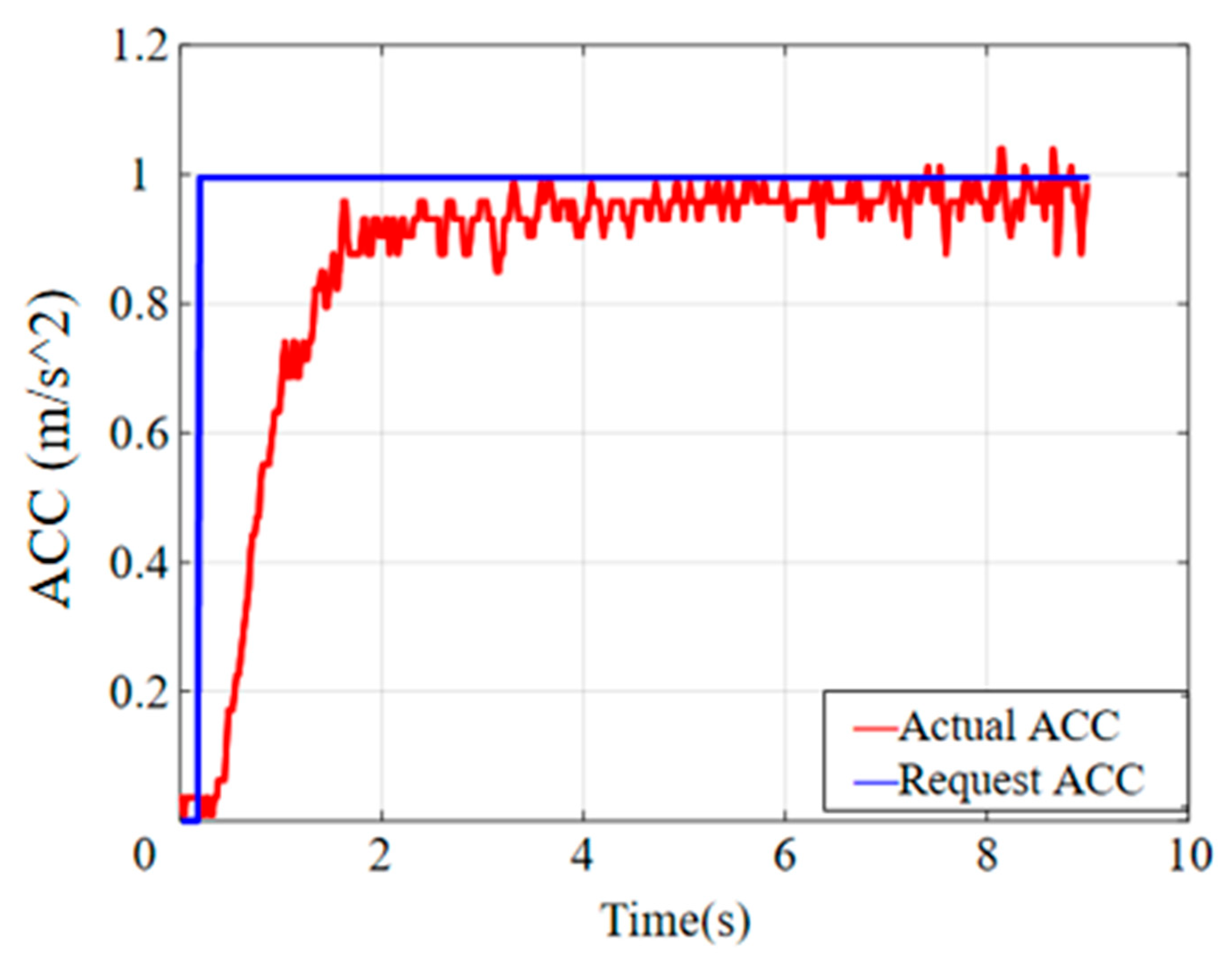
2.2. MPC Optimization Design
2.3. Integration of RSS into MPC
3. Surrogate Safety Measurements
3.1. Time to Collision
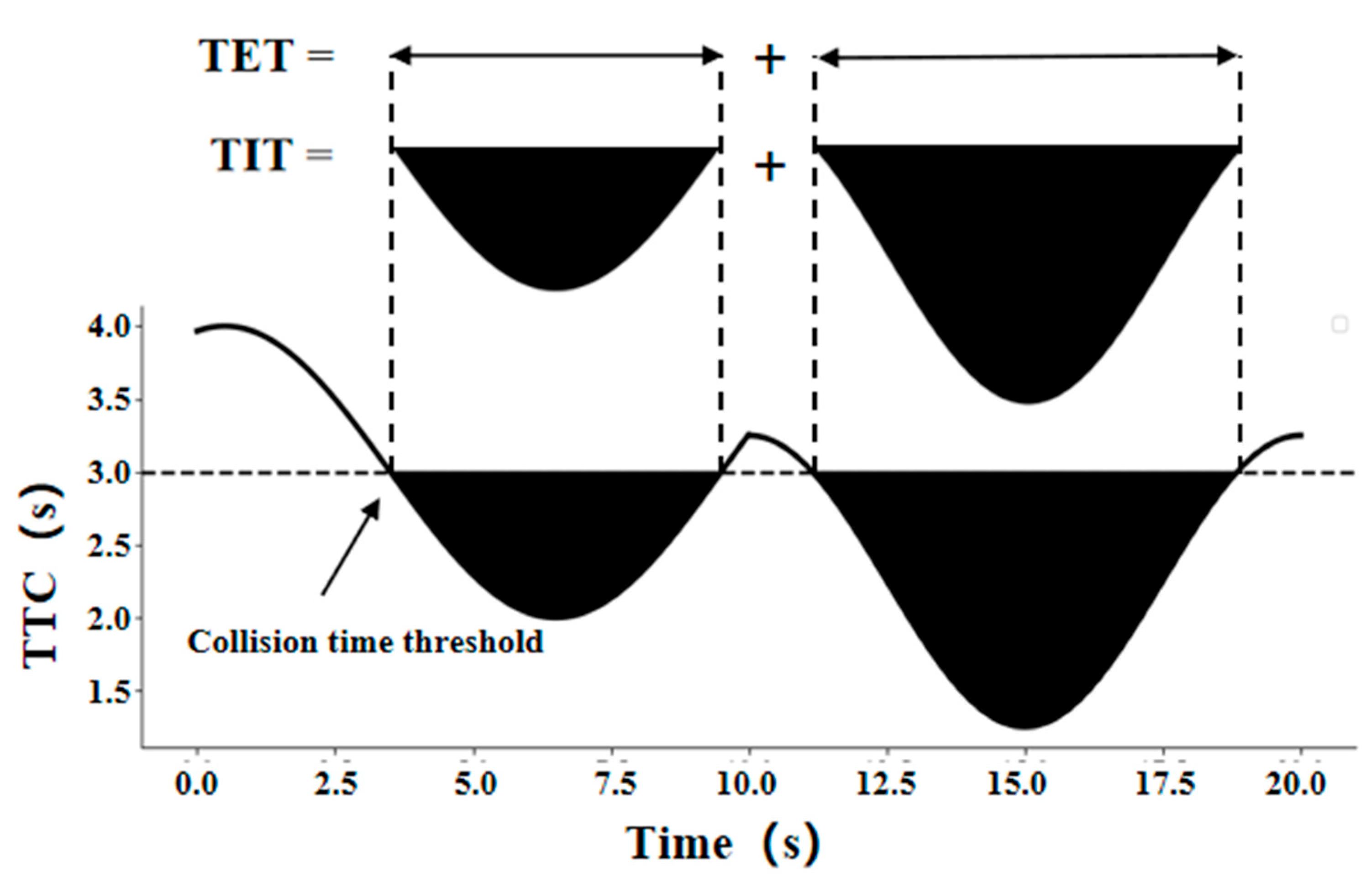
3.2. Time Exposed TTC and Time Integrated TTC
4. Results
4.1. Driving Data Collection
4.2. Related Experiments
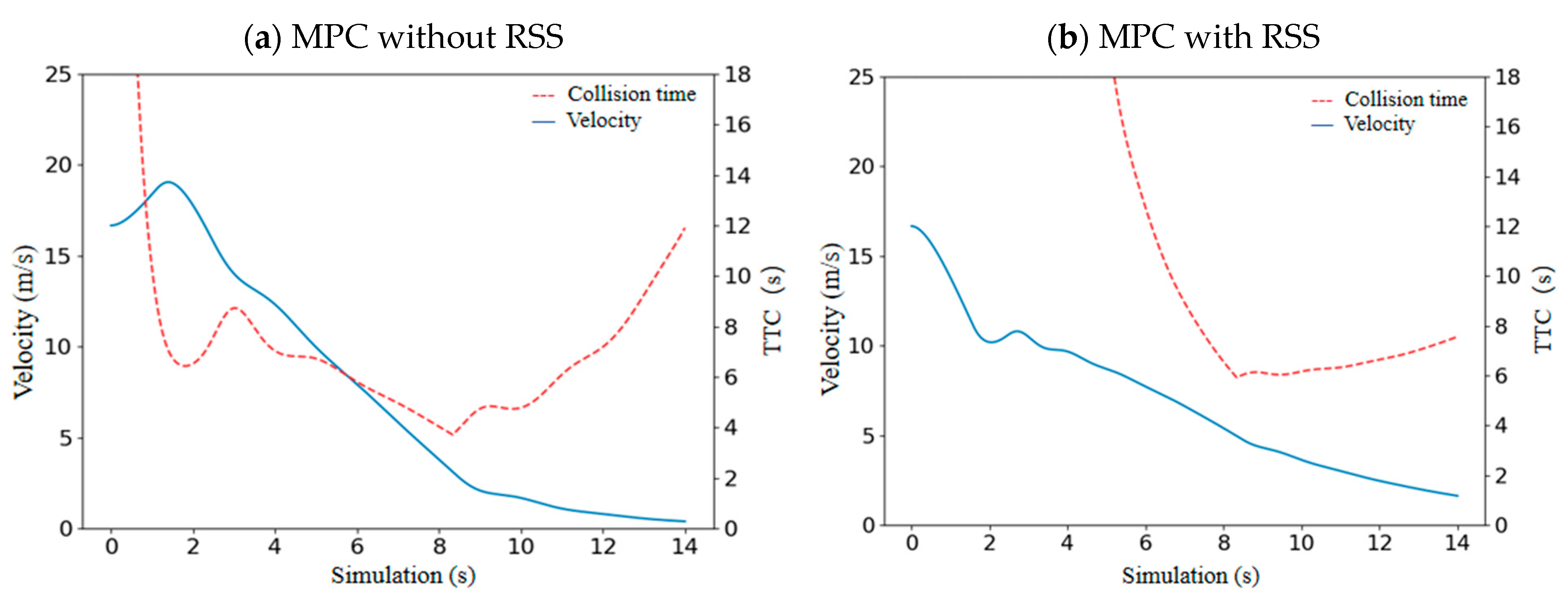
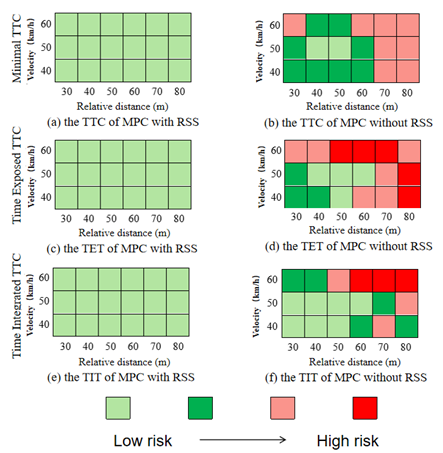
4.3. Safety Assessment Based on SSM
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Autonomous Vehicle Disengagement Reports 2018. California’s Department of Motor Vehicles (DMV). Available online: https://www.dmv.ca.gov/portal/dmv/detail/vr/autonomous/disengagement_report_2018 (accessed on 4 April 2019).
- Eustace, D. Emerging Transportation Safety and Operations: Practical Perspectives. Vehicles 2024, 6, 2251–2256. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Shammah, S.; Shashua, A. On a formal model of safe and scalable self-driving cars. arXiv 2017, arXiv:170806374. [Google Scholar]
- Hasuo, I. Responsibility-sensitive safety: An introduction with an eye to logical foundations and formalization. arXiv 2022, arXiv:2206.03418. [Google Scholar]
- Moser, D.; Schmied, R.; Waschl, H.; del Re, L. Flexible Spacing Adaptive Cruise Control Using Stochastic Model Predictive Control. IEEE Trans. Control. Syst. Technol. 2018, 26, 114–127. [Google Scholar] [CrossRef]
- Dang, R.; Wang, J.; Li, S.E.; Li, K. Coordinated Adaptive Cruise Control System with Lane-Change Assistance. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2373–2383. [Google Scholar] [CrossRef]
- Xiao, L.; Gao, F.; Wang, J. On Scalability of Platoon of Automated Vehicles for Leader Predecessor Information Framework. In Proceedings of the 2009 IEEE Intelligent Vehicles Symposium, Xi’an, China, 3–5 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1103–1108. [Google Scholar]
- Yanakiev, D.; Kanellakopoulos, I. Nonlinear Spacing Policies for Automated Heavy-Duty Vehicles. IEEE Trans. Veh. Technol. 1998, 47, 1365–1377. [Google Scholar] [CrossRef]
- Yang, L.; Mao, J.; Liu, K.; Du, J.; Liu, J. An adaptive cruise control method based on improved variable time headway strategy and particle swarm optimization algorithm. IEEE Access 2020, 8, 168333–168343. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, Y.; Liang, H. Effects of ACC and CACC Vehicles on Traffic Flow Based on an Improved Variable Time Headway Spacing Strategy. IET Intell. Transp. Syst. 2019, 13, 1365–1373. [Google Scholar] [CrossRef]
- Tawfeek, M.H.; El-Basyouny, K. A perceptual forward collision warning model using naturalistic driving data. Can. J. Civ. Eng. 2018, 45, 899–907. [Google Scholar] [CrossRef]
- Yu, W.; Zhao, C.; Wang, H.; Liu, J.; Ma, X.; Yang, Y.; Li, J.; Wang, W.; Hu, X.; Zhao, D. Online legal driving behavior monitoring for self-driving vehicles. Nat. Commun. 2024, 15, 408. [Google Scholar] [CrossRef] [PubMed]
- Winkler, S.; Werneke, J.; Vollrath, M. Timing of Early Warning Stages in A Multi Stage Collision Warning System: Drivers’ Evaluation Depending on Situational Influences. Transp. Res. Part F Psychol. Behav. 2016, 36, 57–68. [Google Scholar] [CrossRef]
- Crundall, D.; Kroll, V. Prediction and perception of hazards in professional drivers: Does hazard perception skill differ between safe and less-safe fire-appliance drivers? Accid. Anal. Prev. 2018, 121, 335–346. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, H.; Wang, W.; Liu, S.; Xiang, Y. Reducing the risk of rear-end collisions with infrastructure-to-vehicle (I2V) integration of variable speed limit control and adaptive cruise control system. Traffic Inj. Prev. 2016, 17, 597–603. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, H.; Wang, W.; Xing, L.; Liu, S.; Wei, X. Evaluation of the impacts of cooperative adaptive cruise control on reducing rear-end collision risks on freeways. Accid. Anal. Prev. 2017, 98, 87–95. [Google Scholar] [CrossRef] [PubMed]
- Al-Gabalawy, M.; Hosny, N.S.; Aborisha, A.S. Model predictive control for a basic adaptive cruise control. Int. J. Dyn. Control 2021, 9, 1132–1143. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, X.; Tarko, A. Modeling car-following behavior on urban expressways in Shanghai: A naturalistic driving study. Transp. Res. Part C Emerg. Technol. 2018, 93, 425–445. [Google Scholar] [CrossRef]
- Luo, L.H.; Liu, H.; Li, P.; Wang, H. Model predictive control for adaptive cruise control with multi-objectives: Comfort, fuel-economy, safety and car-following. J. Zhejiang Univ. Sci. A 2010, 11, 191–201. [Google Scholar] [CrossRef]

| Symbol | Value |
|---|---|
| Deceleration rate of front vehicle | |
| Velocity of front vehicle | (40, 50, 60) km/h |
| Initial distance | (30, 40, 50, 60, 70, 80) m |
| Initial (cruise) velocity | (40, 50, 60) km/h |
| RSS reaction time RSS maximum brake rate RSS minimum brake rate | 1 s |
| ACC time gap | 1 s |
| ACC default space ACC reaction time | 3.5 m 0.5 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, T.; Tang, Y.; Chen, R.; Zhao, S. Optimization of Adaptive Cruise Control Strategies Based on the Responsibility-Sensitive Safety Model. Vehicles 2025, 7, 28. https://doi.org/10.3390/vehicles7020028
Yu T, Tang Y, Chen R, Zhao S. Optimization of Adaptive Cruise Control Strategies Based on the Responsibility-Sensitive Safety Model. Vehicles. 2025; 7(2):28. https://doi.org/10.3390/vehicles7020028
Chicago/Turabian StyleYu, Tengwei, Yubin Tang, Renxiang Chen, and Shuen Zhao. 2025. "Optimization of Adaptive Cruise Control Strategies Based on the Responsibility-Sensitive Safety Model" Vehicles 7, no. 2: 28. https://doi.org/10.3390/vehicles7020028
APA StyleYu, T., Tang, Y., Chen, R., & Zhao, S. (2025). Optimization of Adaptive Cruise Control Strategies Based on the Responsibility-Sensitive Safety Model. Vehicles, 7(2), 28. https://doi.org/10.3390/vehicles7020028





