Abstract
This work focuses on the design of a hybrid proton exchange membrane fuel cell (PEMFC) solution for any micro vehicle such as an unmanned aerial vehicle (UAV). A hydrogen fuel cell can provide extended operation, low emissions, and a highly efficient form of energy storage compared with alternative methods, while a battery can be used as an additional energy storage system to support the transient and higher loads required by the UAV, which are not suitable for normal fuel cell operation. The choice of hydrogen storage is one of the main challenges in using hydrogen as an energy carrier. The current study discusses a range of hydrogen storage technologies and provides a methodology for selection for a given application. A sizing design methodology for a hybrid fuel cell system is proposed. Then, it is applied to a case study to demonstrate its implementation.
1. Introduction
Interest in micro vehicles, such as UAVs, has seen a dramatic increase following recent innovations in the industry. Today, the use of UAVs has increased dramatically in many civil applications and in the transport sector. Typical propulsion systems range from internal combustion engines (ICEs) to battery energy storage technologies. With modern-day concerns surrounding climate change and an increase in the regulation of greenhouse gases, there is incentive for companies to move away from traditional ICE systems to alternative renewable fuel sources. Batteries such as lithium–ion offer a solution to this problem if they can be recharged. However, as they have an energy density about a hundred times lower than gasoline, they do not provide a feasible solution when optimising for range or for in heavy-duty UAV operations due to the mass of batteries that would be required for sustained flight.
One solution to this problem is to hybridise a hydrogen fuel cell with an additional energy storage unit. The hydrogen fuel cell provides a high energy density and efficient power source that overcomes the problems associated with batteries. In addition, the hydrogen fuel cell can be considered a clean energy system as it has very low emissions. Within the hybrid setup, the fuel cell is used as the primary energy source, and the additional energy storage system, typically a battery or a supercapacitor, acts as an energy buffer system. The typical use case would be in applications where the load is dynamic or where peak powers are required for sections of the mission length. The advantages of hybridising include the ability to downsize components, causing a reduction in size, which in turn results in improved system efficiency and optimised endurance between refuels.
This solution is particularly effective in portable applications, which has led to research into its use in road vehicles where the fuel cell and battery have been hybridised [1,2]. However, the reduction in size and the energy efficiency of this solution have been a concern [3]. A micro gas turbine [4] or a supercapacitor [5] could also be combined with the fuel cell system. The hybrid system can be used for off-grid applications [6] or emergency/back-up portable power generation [7,8,9] to supply power to a load when mains power is insufficient. In the case of underwater vehicles, the use of a hybrid fuel cell system to generate power from a high purity hydrogen source would reduce fuel recharging time. It also describes the crushing and minimisation of exhaust gases by recycling unreacted gas to provide heat [10,11].
The use of a hybrid propulsion system for unmanned aerial vehicles, based on either a proton exchange membrane fuel cell or a solid oxide fuel cell in combination with a battery and electric motors, has been the subject of many recent studies [12,13,14].
The focus of this paper is on the sizing and selection of generating sets. It is intended to address the design of the power system for an application that requires a precise design in terms of power and range. As an aerial vehicle’s performance hinges on the weight of the aircraft, limitations on weight and volume will be considered, and optimising the UAV’s performance based on these factors will be discussed. Although the power sharing and electrical control strategies between the power units are important, they are not discussed in this paper as they have been addressed in numerous other studies [15,16,17,18]. The methodology laid out will be best suited for applications with simple discrete power profiles repeated on a cyclic basis. These are typical for many applications from communication systems to portable electronic devices.
The main components of a hybrid fuel cell system are the fuel cell stack, fuel supply, oxidant supply, auxiliaries (such as humidifiers, heat exchangers, pumps, etc.), the additional energy storage system, and an electronic regulation system that controls the flow of electrical power over different loads.
One of the most important considerations when designing a hydrogen fuel cell system is the fuel storage method, as this in turn affects the weight and energy capacity of the UAV. Several storage methods are discussed, ranging from tried and tested solutions, such as compressed gaseous hydrogen, to new and innovative solutions, including complex hydrides. The effect on the UAV’s performance is investigated, and a method for selecting the best storage type suited to an application is provided.
2. Methodology
2.1. The Sizing/Design Methodology
In this section, based on the mission requirements and the performance dynamics of the UAV, a methodology for component sizing and selection is established. A flow chart illustrating the steps of the sizing/design process is given in Figure 1.
2.2. Mission Requirements
The mission profile and requirements, detailing the basic characteristics of both the UAV and the mission, should be established in the early stages of UAV design. A simple mission would consist of five flight phases: take-off, climb, cruise, descent, and landing. The UAV characteristics would include take-off weight, take-off distance, operating altitude, rate of climb or descent, and endurance. Once these factors have been determined, a constraint analysis can be carried out to provide an initial estimate of the power requirements of the mission. From this, a map of the power profile can be produced, from which components can be sized. The power requirements of all onboard electrical equipment must also be considered. This includes the fuel-cell balance of the plant and any onboard avionics (flight control system, receiver, etc.).
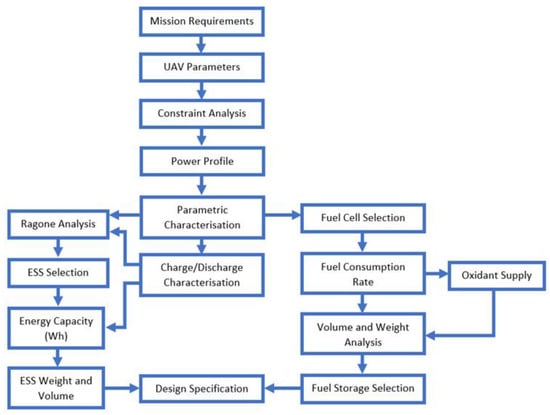
Figure 1.
Flow chart illustrating steps in the sizing/design methodology.
2.3. Constraint Analysis
This analysis looks at the power-to-weight constraints with respect to wing loading and gives an indication of the power required for certain wing loading conditions. These constraints include take-off distance, rate of climb, cruise airspeed, and stall characteristics. Additional constraints may be considered if necessary, such as service ceiling or turn rate requirements, but only the four basic constraints are considered in this analysis.
The wing loading (W/S) is a design parameter that is optimised for each flight phase. The constraint equations are a set of functions that provide the thrust-to-weight ratios required to meet the wing loading requirements. It is worth noting that thrust loading is defined as the ratio of thrust to weight, while W/S is the weight to wing area of the aerial vehicle. The W/S is usually given in kg/m2, which becomes the mass of the wing area.
As electric motors are rated in power, these thrust-to-weight ratios can then be converted into power requirements. For the purposes of this study, the constraint equations for a conventional fixed-wing aerial vehicle given by Gudmundsson [19] have been considered.
2.3.1. Take-Off Distance Constraint
The constraint that gives the required thrust-to-weight ratio, , for the ground run at take-off is given by Equation (1).
where T is the thrust, W is the weight of the UAV, and W/S is the wing loading ratio. The VTO is the take-off velocity, g is the gravitational acceleration, SG is the ground run, μ is the ground friction coefficient, is the drag coefficient at take-off, is the drag coefficient at lift, and q is the dynamic pressure at identified altitude.
The take-off velocity can be determined using Equation (2).
where ρ is the density at identified altitude.
2.3.2. Cruise Speed Constraint
Cruise flight consists of a steady level flight at the speed at which the aerial vehicle is experiencing minimum drag at a specific altitude. This constraint is defined by Equation (3).
where is the minimum drag coefficient and k is the lift-induced drag constant.
2.3.3. Rate of Climb Constraint
From the thrust-to-weight constraint, the rate of climb (RoC) can be achieved as shown by the following expression:
where is the climb speed.
The best rate of climb can be determined through an analysis of energy changes and resolving forces about the direction of flight. During climb, any excess power required to overcome drag can be used to increase the kinetic or potential energy of the aerial vehicle. In steady climbing flight, the rate of climb is given by Equation (5).
The and
Where is propulsive efficiency at true airspeed and D is the drag force. is the power at propeller shaft.
The power available is dependent on multiple factors including altitude, flight speed, etc. The airspeed at which maximum excess power is available represents the shortest time to climb to cruise altitude.
2.3.4. Conversion of Thrust to Power
As electric motors are rated in power, it is necessary to convert the thrust-to-weight ratios given by the constraint equations to power-to-weight ratios. This can be achieved by using Equation (6).
where is the propeller efficiency.
2.4. The Power Profile
It is important to define the drone’s application in order to determine the power requirements for each of the subsystems, with the additional energy storage system (ESS) providing peak power and the PEMFC providing lower base-load power. To preserve the lifetime of the fuel cell, it is best for it to provide a constant level of power under optimum conditions. When the power provided by the fuel cell falls below the drone’s requirements, any excess power from the fuel cell is used to charge the auxiliary ESS. The nature of the power profile will help to define the technological requirements of the auxiliary ESS.
A generic cyclic power profile is shown in Figure 2. Using this power profile, several parameters need to be defined in order to estimate the requirements of the ESS.
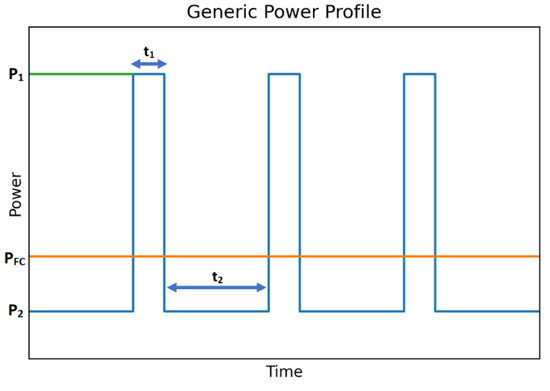
Figure 2.
Generic cyclic power profile.
- ■
- P1 = Peak power;
- ■
- P2 = Base power;
- ■
- t1 = Time at peak power;
- ■
- t2 = Time at base power.
Considering the design of the proposed hybrid power system, the power between the battery and the fuel cell can be regulated, which would add another degree of freedom in the process of optimising the FC and ESS sizing.
For example, the fuel cell power, PFC, can be proportional to the average power demand, PAVERAGE. This would add another degree of freedom to the FC and ESS sizing optimisation process. To simplify the process, it was assumed that PFC ≡ PAVERAGE, and the PAVERAGE has been expressed in Equation (7).
In view of what has been shown in Figure 2, the power that can be considered as additional energy eligible for ESS is the difference between the peak power and the average power evaluated for the PEMFC. This can be interpreted as follows, using Equation (8).
If the power required by the fuel cell auxiliary systems are not taken into account within the power profile, then the power required by the balance-of-plant (BOP) can simply be added onto the PAVERAGE to give the power required by the fuel cell.
2.5. Degree of Hybridisation
Where there are loads of cyclic nature, the rate of charge and discharge of the additional ESS system needs to be accounted for. If the rate of discharge is higher than the rate of charge, the additional ESS may not be able to sustain the high load periods.
For analysis purposes, it is useful to consider non-dimensional parameters that allow the range of power profiles to be extended. For example, the following non-dimensional parameters can be defined to find the charge and discharge limits.
where F is the power ratio and t is the time ration. The DOH (degree of hybridisation) represents the ratio of power provided by the additional ESS at peak power to the maximum power required.
From Equation (11), we can see that a low value of DOH represents a relatively low required power output from the additional energy storage system, while high DOH represents a high required power output from the additional ESS. It is useful to express this in terms of F and t to see how the difference between maximum and minimum power loads and the time spent at those loads affect the degree at which it is required to hybridise the system. This can be shown in a graphical representation, as shown in Figure 3.
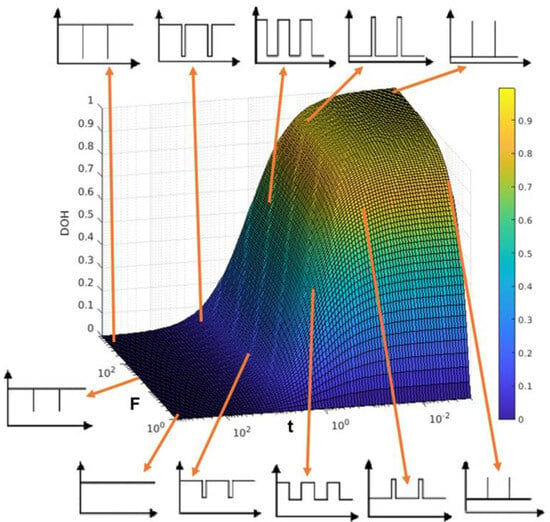
Figure 3.
A plot of DOH against F and t, showing a range of possible power profiles.
The plot axes of F and t have been set to a logarithmic scale to show the variation of the power profile types at the extremes. It can be seen that the DOH is highest when the values of F are highest and t is lowest. This indicates that a larger additional ESS system is required when peak loads occur over shorter periods of time.
The DOH is at its lowest when t is at its highest, as the longer period of peak power increases the value of the average power and therefore increases the size of the fuel cell required, which reduces the requirement for our additional storage system and therefore reduces the degree to which our system is hybridised.
The value of DOH also decreases with F, which can be understood as the power difference between peak and base power decreases, the power required from the auxiliary power system also decreases and less hybridisation is required.
For a cyclic power profile such as shown in Figure 2, the amount of energy discharged from the additional ESS can be calculated by Equation (12), and the amount of energy discharged by the fuel cell can be determined by Equation (13).
where n is the number of cycles over the total operational period and ttotal is the time taken over the total operational period.
2.6. Charge and Discharge Considerations
The time spent by the system either charging or discharging the additional ESS is dependent on the power profile. This is important, as the type of additional ESS selected should be suited to handle the time spent at charge and discharge and the rates of charge and discharge.
The case where time spent at discharge is higher than the time spent charging is known as ‘charge limited’, whereas the case where time spent at charge is higher than that of discharge is known as ‘discharge limited’ and can be determined from the power profile by Equation (14) and Equation (15), respectively.
For the case of ‘charge limited’, the average power, , can be written as follows:
While, for the case of ‘discharge limited’, the average power, , can be written as follows:
Considering the share point between the two boundary domains, it can be written:
This can be put in terms of DOH, F, and t, as shown by Equation (17).
Once the limitations of the system are known, the characteristic time can be determined and, from that, a Ragone analysis can be used to determine the best additional ESS technology to use.
2.7. Hydrogen Storage Technologies
Hydrogen is a promising energy carrier; however, the method of storing hydrogen presents a substantial challenge and is still the subject of ongoing research. As an aspect of hydrogen storage [20], high-pressure gas storage and the control of the rapid filling process of hydrogen into fuel cells [21] or the effect of refuelling parameters on the storage density of compressed hydrogen storage [22] are interesting topics for many researchers. Researchers have also compared compressed and liquid hydrogen as fuels for fuel cells in terms of energy efficiency, environmental impact, and cost [23]. High-surface-area hydrogen storage [24] and nanoporous hydrogen storage adsorbents [25] have also been studied by others. On the other hand, the material investigation of bipolar plates in contact with hydrogen and the search for a suitable durable material for fuel cells has been studied [26].
While the use of sustainable fuels is seen as a key solution to reducing emissions in the aviation sector [27], efforts have been made to use metal hydride systems for hydrogen storage and delivery [28]. Different methods for hydrogen storage also reported in the literature include high-pressure and cryogenic liquid storage, adsorptive storage on high-surface-area adsorbents, chemical storage in metal hydrides and complex hydrides, and storage in boranes.
Taking into account what has been carried out to date and the storage solutions commercially available at the time, this current study discussion has been taken forward. For a mission requiring a high energy capacity (either for high-powered or long endurance missions), the fuel and oxidiser storage sub systems will dominate the overall size of the fuel cell system. Within aerospace applications, there are strict constraints when it comes to weight and storage volume. It is then important to select a fuel storage type based on mission type, while considering parameters such as gravimetric and volumetric densities and fuel consumption rates, as well as the technological limitations of each storage method.
In this paper, various forms of commercially available hydrogen storage methods are considered. These range from tried and tested methods such as compressed gaseous hydrogen to more experimental forms such as metal and chemical hydrides. The gravimetric and volumetric densities are given in Table 1. It is important to note that these values are estimates for the whole storage system, including balance of plant, fuel tanks, etc. This makes it more useful from an engineering design perspective as the whole storage mass can be estimated based on the amount of fuel required.

Table 1.
Hydrogen storage system (HSS) specification.
Compressed hydrogen is a reliable solution that has reached a higher level of technological maturity compared with other storage methods. However, it has relatively low volumetric densities, so, where there are limitations in storage volume, this may not be a feasible solution. Metal hydrides offer a high volumetric density but, due to the high atomic weight of the metal alloy, they have a relatively low gravimetric density, which can be problematic where weight is a stringent limitation, such as in aerospace applications.
Liquid hydrogen achieves promising gravimetric and volumetric densities through the cryogenic storage of hydrogen to achieve a liquid phase. This occurs at 21 K (−252 °C) and provides significant improvement of mass and volume density at lower pressures. The main disadvantages are that, firstly, it is an inefficient method of storing hydrogen, with 40% of the energy content of hydrogen being lost to achieve the low temperatures required. In addition, a helium refrigeration cycle is required to keep the hydrogen at these low temperatures. Although the cylinders are heavily insulated, some heat leaking in from the environment is unavoidable due to the low phase change enthalpy of hydrogen from a liquid to gaseous state, which causes the liquid hydrogen to evaporate, which then increases the pressure within the tank. To avoid failure of the cryogenic tank, this pressure is monitored, and the hydrogen is vented when the pressure reaches 1 MPa. This brings about significant losses in hydrogen; as a result, this storage method is rarely applied [29].
However, due to recent advancements in insulative materials, there has been a reduction in hydrogen loss, but it can still occur at a rate of approximately 1% of fuel stored per day.
A viable alternative to low volumetric densities of compressed hydrogen, the gravimetric densities of metal hydrides, and the issues presented by the storage of liquid hydrogens, chemical hydrides, such as magnesium hydride, sodium borohydride, and lithium amide, have been studied. Chemical hydrides store hydrogen through the covalent or ionic bonding within a chemical lattice structure (usually metallic or boron). It has viable operating temperatures and pressures, and volumetric and gravimetric densities exceeding that of liquid hydrogen. The disadvantage is its capacity to store hydrogen, and the limitation in the rate at which it can release hydrogen through a process known as dehydrogenation. This makes it best suited for small UAVs or other low-power applications. This storage method is still in development, and improvements are continuously being made to improve upon its current drawbacks.
3. Results and Discussion
3.1. Mission Requirements
Fixed-wing drones provide utility in cases where endurance and range are required (e.g., healthcare, agriculture, and commercial industries), typically for monitoring, surveillance, payload delivery, and photography. When building a UAV, the choice of power system is a major consideration as it determines the performance variables, such as airspeed, endurance, and altitude. Endurance is the main concern for many applications as it enables the aerial vehicle to operate over larger distances.
Fuel cells compliment the fixed-wing architecture when optimising for endurance. For applications in defence, it can also provide stealth characteristics as it only produces low-grade noise when compared with an ICE.
The sizing design methodology is then applied to a medium weight UAV. The application of the UAV will be payload delivery, so the only loads considered are those imposed by the different phases of flight. Once a performance profile has been mapped, a process will be used to determine the best power architecture and to investigate the effect of different hydrogen storage methods on endurance.
A 2 kg payload with a 7 h endurance is considered. These requirements are typical for healthcare UAVs, as medical payloads often need to be delivered to hard-to-reach locations such as disaster zones or rural areas with limited road access.
3.2. UAV Parameters
The UAV selected is the Eagle Plus 3.5 m, as it meets the requirements set by the mission. Its vertical take-off and landing (VTOL) capability allows for take-off and landing without the requirement of a runway, allowing for quick deployment in a variety of situations. The required parameters are provided in Table 2.

Table 2.
UAV parameters.
3.3. Power Profile and Application
The first step is to define the power profile of the drone over the duration of the mission. The motor loads during cruise flight and take-off are the main power requirements that need to be considered.
As the application does not require any complex electronics, the power profile should be simple with no cyclic characteristics. The power profile for a mission duration of 7 h (25,200 s) is illustrated in Figure 4.
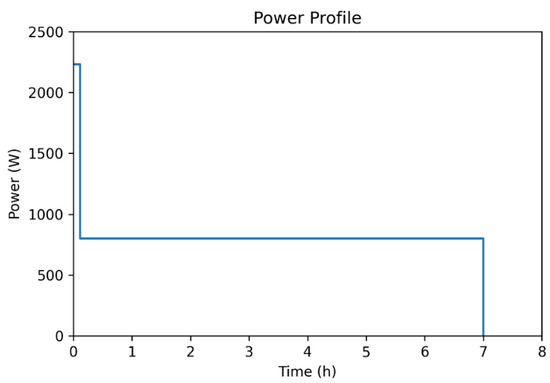
Figure 4.
Power profile for the identified mission.
The profile parameters consist of a period during take-off and climb, where the required power is P1 = 2232 W and the duration time is t1 = 400 s (~7 min). The power required during cruise is P2 = 801 W and the duration time is t2 = 24,800 s (~6 h and 53 min).
This yields a PAVERAGE = 823.7 W across the mission. As the fuel cell auxiliary systems are not included in the power profile, a balance of plant power consumption rate of 43% is assumed as it is typical for PEM fuel cells. This gives the power required by the fuel cell, PFC = 1453 W (1453 W − 823.7 W = 629.3 W). Where the percentage of the auxiliary power has been calculated (629.3 W/1453 W = 43.3%), the power of the additional energy storage system is the difference between the peak power, P1, and the average power, PAVERAGE, which gives us a value for Padd.ESS = 1408.3 W (2232 W − 823.7 W = 1408.3 W).
The energy capacity of the additional storage system (Eadd.ESS) can then be calculated with a value of 156.5 Wh (1408.3 W × 400 s = 156.5 Wh), similarly for the energy capacity of the fuel cell (EFC) with a value of 10.17 kWh (1453 W × (400 s + 24,800 s) = 10.17 kWh).
Whether the system is charge-limited or discharge-limited will affect the type of additional ESS required, as charge-limited will require high discharge over a long period of time and the time spent charging the additional ESS will be limited. Therefore, an additional ESS capable of charging in a short time is required. If the system is discharge-limited, the time spent discharging will require a high power output over a short period of time, and the time available for charging will be long. Therefore, the rate of power output must be prioritised over the time available for charging.
To calculate whether the system is charge or discharge limited, Equations (14) and (15) can be used:
As PAVERAGE < 1516.5 W, additional ESS is discharge-limited; therefore, it will be required to handle high loads of power over short periods of time, and recharge time will not be a priority. The advantage of having a discharge-limited system is that, as the additional ESS is not limited in charge time and if there are any unexpected transient loads, the ESS should assist in handling them without any additional load on the fuel cell.
3.4. Component Selection
3.4.1. Additional Energy Storage System
To find the best technology suited as an additional ESS for the system, we first need to define our characteristic time. In our case our characteristic time will be the same value as t1: 400 s or 0.111 h.
There are three technologies that suite our characteristic time: combustion engines, gas turbines, and Li-ion batteries. As Li-ion batteries are lighter, and any additional current produced by our fuel cell can be used to charge them (making them reusable at no extra cost), Li-ion batteries have been selected to be used.
To estimate the required rated capacity for a Li-ion battery, the following formula can be used:
Considering a typical value for Li-ion efficiency and taking the discharge limit to be 80% of full discharge, this gives us the following parameters: ESS efficiency = 0.9; discharge limit = 124.8 Wh.
Using these values, a rated capacity of 52.73 Wh is calculated. The weight and volume of this component can then be computed using the calculated value of the rated capacity. Using a value for specific energy of 160 Wh/kg, a value for the battery mass of 0.34 kg is obtained, and using a value of 300 Wh/L, an approximate volume of 0.176 L (1.76 × 10−4 m3) is estimated.
Batteries with these specifications can be found in numerous companies, some examples include Farnell, Panasonic, EGO, and Shorai.
3.4.2. Fuel Cell Selection
As UAVs are considered transport applications, PEM fuel cells are the clear choice due to their lightweight portable nature and feasible operating temperatures.
From the discussion in Section 3.3, a calculated fuel cell power requirement is 1453 W. It is always best to oversize the system for unexpected conditions. Fuel cells that can meet these capacities can be found in companies such as Intelligent Energy (Loughborough, UK), Ballard Power Systems (Burnaby, BC, Canada), and HES Energy Systems (Singapore), depending on specific requirements [30]. For the system of this case study, the 1500 W Fuel Cell from Aerostak, called the Aerostak A-1500, is selected. It has a mass of 2.8 kg, a volume of 2.25 L (2.25 × 10−3 m3), and an efficiency of 0.53.
3.4.3. Hydrogen Storage Selection
As the different hydrogen storage methods are limited in their ability to provide fuel, it is first required to calculate the fuel consumption rates needed by the hydrogen storage system to deliver fuel at the specified power output. As the required power load on the fuel cell is 1453 W, and with an efficiency value for Aerostak of 53%, the fuel consumption rate will be equivalent to a 2750 W fuel cell. To calculate the fuel consumption rate, Equation (19) can be used,
where yields for 82.25 g/h, LHV is the lower heating value of hydrogen, and ηFC is the fuel cell electrical efficiency.
The maximum duration-to-weight and duration-to-volume ratios are calculated to be 3673 sKg−1 and 1800 sL−1, respectively, assuming the fuel cell operates for the entire 7 h mission. For such a mission scenario, the liquid hydrogen storage method can meet the gravimetric and volumetric density constraints; however, it comes with its own limitations. Given the mass constraints, if an alternative mode of hydrogen storage is required to overcome the limitations of liquid hydrogen as a storage technology, then the mission length would need to be shortened to below 7 h. As such, a shorter mission length of 5 h and 3 h will be considered to evaluate whether it is feasible to use other forms of hydrogen storage. Complex and metal hydrides will also be investigated and, even though they may not yet be available in commercial forms for this application, the purpose is to show what may be possible using future hydrogen storage technologies.
The mass of hydrogen (in kilograms) used for 7 h, 5 h, and 3 h can be calculated using Equation (20) for each type of storage system.
Using this result, the mass and volume for each of the different storage systems is estimated for each of the mission lengths. The results are provided in Figure 5.
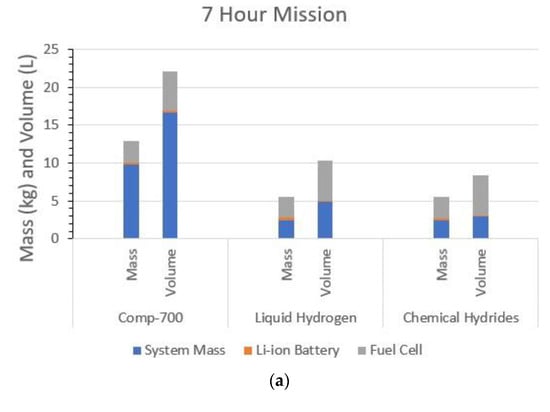
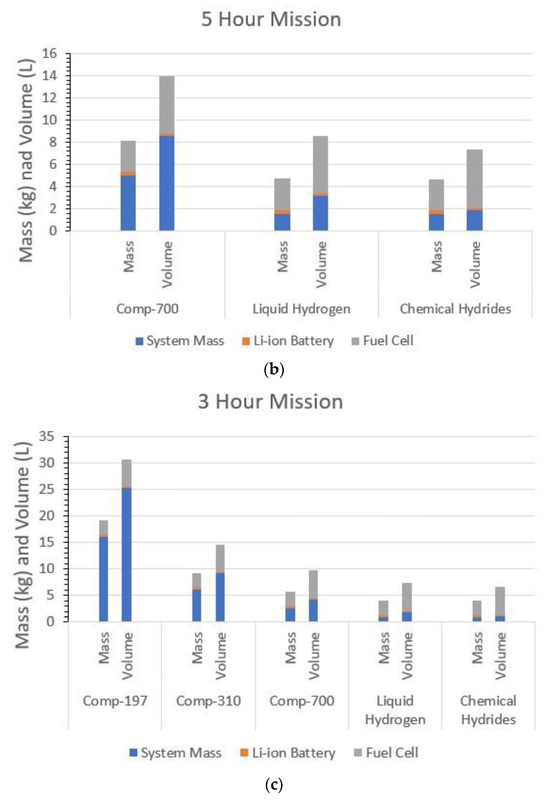
Figure 5.
Mass and volume balance analysis of hybrid fuel cell system: (a) 7 h mission, (b) 5 h mission, and (c) 3 h mission.
For longer mission lengths, the larger the fuel store required, the higher the fuel storage system mass will be. This increase in weight will need to be countered by a corresponding increase in lift in order for the aerial vehicle to achieve flight; as such, the power output of the motor needs to be increased in order to attain the lift force required. The power required by the fuel cell is related to the weight of the aerial vehicle by a square root relationship; as such, the power required increases exponentially as the endurance increases. Therefore, the achievable endurances depend on the gravimetric densities of the storage types. This can be seen in Figure 5, where for the 7 h and 5 h missions, Comp-197 and Comp-310 are excluded, as well as metal hydrides, for all the mission lengths for this reason.
The achievable endurances for the fuel storage system mass for each of the storage methods are illustrated in Figure 6. The mass capacity is set to 6.86 kg (dashed line), which is the total capacity for the energy system (10 kg) minus the fuel cell and battery masses.
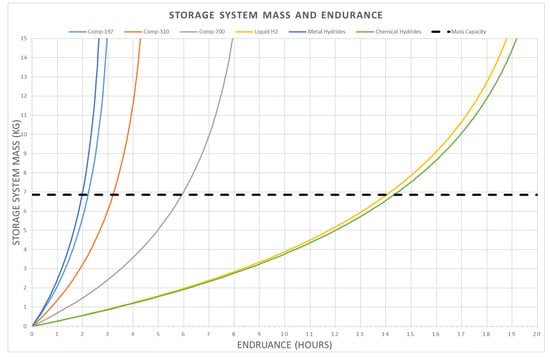
Figure 6.
Fuel storage system mass effect on UAV endurance. The dashed line shows the mass capacity (6.86 kg) set in our calculation to achieve the specified energy system.
This graph gives us an idea of what is achievable with the different storage methods in terms of a given capacity. The metal hydrides and comp-197 hydrogen yield an endurance of approximately 2–2.5 h, which is typical for most battery-powered UAVs in a fixed-wing configuration.
Comp-310, which is the most readily available hydrogen storage format in commercial form, gives an endurance of approximately 3 h 15 min. Comp-700 significantly increases endurance to around 6 h; however, it is difficult to find storage in this form for drone application.
Liquid hydrogen shows a significant improvement in endurance, with a theoretical value of 14.2 h; however, it is important to note that this does not take into consideration fuel loss due to the nature of the technology.
Chemical hydrides provide comparative endurance to liquid hydrogen; however, they are still in experimental stages, so it will be difficult to find suitable commercial options for the intended application.
It is important to note that the relationship between fuel mass and endurance is not linear but, as the mass of the fuel storage system increases, the endurance per unit mass decreases until it eventually plateaus. This indicates that, depending on the type of storage used, there are theoretical limits to the use of these technologies in an aerospace application due to differences in the gravimetric densities of the fuel storage systems.
4. Conclusions
In this paper, a methodology was established and applied to the design of a fuel cell as the main power system for a UAV, with the inclusion of an additional energy storage system to support peak loads. The first step was establishing a power profile, which was achieved by assessing the consumption needs of the components of the UAV. Then, the individual requirements of the fuel cell and additional ESS were determined based on the power profile. The energy devices were then selected based on these requirements. For our use case, this was a Li-ion battery as the additional ESS, with a capacity of 125 Wh, which was sourced from Panasonic, and a PEM fuel cell for the main ESS, with a power requirement of 1453 W. This was sourced from the company Aerostak, the model being the A-1500. The Li-ion battery was selected due to its charge/discharge characteristics, and the PEM fuel cell was selected for its suitability to transport applications.
Several hydrogen storage methods were then assessed, primarily considering the gravimetric and volumetric densities and practical maturity of the different solutions. In the end, a liquid hydrogen storage method was selected, with a total ESS mass of 5.57 kg. However, as using liquid hydrogen presented numerous problems, including high fuel losses, the need for a separate cooling system, and it being an inefficient method of storing hydrogen, two other mission lengths of 5 h and 3 h were looked at.
A trade-off between total mass of the UAV and its endurance was then established, showing the relationship between the amount of fuel stored and the endurance of the aerial vehicle as non-linear, and, in fact, the endurance of the aerial vehicle plateaued with an increase in mass. This led to the conclusion that, for an increase in flight time, an exponentially increasing amount of fuel would be required. The limits of endurance for different storage types could then be obtained by comparing them to the maximum take-off weight of the UAV. A maximum endurance of approximately 14.4 h was established using a chemical hydride fuel supply. However, as this storage method was still in its experimental stages and was not available commercially for this kind of application, this value was theoretical and its purpose was to show what will likely be possible in the future. An endurance of 14.2 h was given for the use of liquid hydrogen; however, this did not account for any fuel loss that may occur in storage due to boil-off throughout the mission. Endurances of 6 h, 3.2 h, and 2.3 h were possible using comp-700, comp-310, and comp-197 hydrogen storages, respectively.
The case study in this report demonstrated how the methodology can be applied to a real-world scenario. In addition to fixed-wing UAVs, this methodology can be applied to multiple scenarios, including rotary-wing UAVs and larger aerial vehicles, once a performance profile has been established. As the market for hydrogen-powered aerial vehicles grows, the aim of this report is to provide designers with a methodology for sizing a fuel cell as the main power unit and selecting the most appropriate storage methods for their application, which will deliver energy efficiency and range benefits in an environmentally friendly manner.
Author Contributions
Conceptualization, Z.A. methodology, Z.A.; visualization, A.F.; validation, C.K. and M.C.; analysis, C.K. and M.C.; writing—original draft preparation, C.K. and M.C.; writing—review and editing, M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bethoux, O. Hydrogen Fuel Cell Road Vehicles: State of the Art and Perspectives. Energies 2020, 13, 5843. [Google Scholar] [CrossRef]
- Fakhreddine, O.; Gharbia, Y.; Derakhshandeh, J.F.; Amer, A.M. Challenges and Solutions of Hydrogen Fuel Cells in Transportation Systems: A Review and Prospects. World Electr. Veh. J. 2023, 14, 156. [Google Scholar] [CrossRef]
- Fletcher, T.; Ebrahimi, K. The Effect of Fuel Cell and Battery Size on Efficiency and Cell Lifetime for an L7e Fuel Cell Hybrid Vehicle. Energies 2020, 13, 5889. [Google Scholar] [CrossRef]
- Seitz, A.; Nickl, M.; Troeltsch, F.; Ebner, K. Initial Assessment of a Fuel Cell—Gas Turbine Hybrid Propulsion Concept. Aerospace 2022, 9, 68. [Google Scholar] [CrossRef]
- Xun, Q.; Liu, Y.; Holmberg, E. A Comparative Study of Fuel Cell Electric Vehicles Hybridization with Battery or Supercapacitor. In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy,, 20–22 June 2018; pp. 389–394. [Google Scholar] [CrossRef]
- Ma, S.; Lin, M.; Lin, T.; Lan, T.; Liao, X.; Maréchal, F.; Van Herle, J.; Yang, Y.; Dong, C.; Wang, L. Fuel cell-battery hybrid systems for mobility and off-grid applications: A review. Renew. Sustain. Energy Rev. 2021, 135, 110119. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, Y.; Chen, Q. Energy Management Strategy of Fuel-Cell Backup Power Supply Systems Based on Whale Optimization Fuzzy Control. Electronics 2022, 11, 2325. [Google Scholar] [CrossRef]
- Cigolotti, V.; Genovese, M.; Fragiacomo, P. Comprehensive Review on Fuel Cell Technology for Stationary Applications as Sustainable and Efficient Poly-Generation Energy Systems. Energies 2021, 14, 4963. [Google Scholar] [CrossRef]
- Xing, H.; Stuart, C.; Spence, S.; Chen, H. Fuel Cell Power Systems for Maritime Applications: Progress and Perspectives. Sustainability 2021, 13, 1213. [Google Scholar] [CrossRef]
- Cai, Q.; Brett, D.J.L.; Browning, D.; Brandona, N.P. A sizing-design methodology for hybrid fuel cell power systems and its application to an unmanned underwater vehicle. J. Power Sources 2010, 195, 6559–6569. [Google Scholar] [CrossRef]
- Sezgin, B.; Devrim, Y.; Ozturk, T.; Eroglu, I. Hydrogen energy systems for underwater applications. Int. J. Hydrogen Energy 2022, 47, 19780–19796. [Google Scholar] [CrossRef]
- Rostami, M.; Dehghan Manshadi, M.; Farajollahi, A.H.; Marefati, M. Introducing and evaluation of a new propulsion system composed of solid oxide fuel cell and downstream cycles; usage in Unmanned Aerial Vehicles. Int. J. Hydrogen Energy 2022, 47, 13693–13709. [Google Scholar] [CrossRef]
- Farajollahi, A.H.; Rostami, M.; Marefati, M. A hybrid-electric propulsion system for an unmanned aerial vehicle based on proton exchange membrane fuel cell, battery, and electric motor. Energy Sources Part A Recovery Util. Environ. Eff. 2021, 44, 934–950. [Google Scholar] [CrossRef]
- Wang, B.; Zhao, D.; Li, W.; Wang, Z.; Huang, Y.; You, Y.; Becker, S. Current technologies and challenges of applying fuel cell hybrid propulsion systems in unmanned aerial vehicles. Prog. Aerosp. Sci. 2020, 116, 100620. [Google Scholar] [CrossRef]
- Gyu Gang, B.; Kwon, S. Design of an energy management technique for high endurance unmanned aerial vehicles powered by fuel and solar cell systems. Int. J. Hydrogen Energy 2018, 43, 9787–9796. [Google Scholar] [CrossRef]
- Verstraete, D.; Lehmkuehler, K.; Gong, A.; Harvey, J.R.; Brian, G.; Palmer, J.L. Characterisation of a hybrid, fuel-cell-based propulsion system for small unmanned aircraft. J. Power Sources 2014, 250, 204–211. [Google Scholar] [CrossRef]
- Corcau, J.I.; Dinca, L. Fuel Cell/Battery Hybrid Electric System for UAV. In Proceedings of the 2023 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Venice, Italy, 29–31 March 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Bayrak, Z.U.; Kaya, U.; Oksuztepe, E. Investigation of PEMFC performance for cruising hybrid powered fixed-wing electric UAV in different temperatures. Int. J. Hydrogen Energy 2020, 45, 7036–7045. [Google Scholar] [CrossRef]
- Gudmundsson, S. General Aviation Aircraft Design: Applied Methods and Procedures; Butterworth-Heinemann: Oxford, UK, 2014; pp. 57–59. [Google Scholar]
- Rajangam, P. Hydrogen Fuel Cells as Green Energy. In Cases on Green Energy and Sustainable Development; Yang, P., Ed.; IGI Global: Hershey, PA, USA, 2020; pp. 291–323. [Google Scholar] [CrossRef]
- Li, M.; Bai, Y.; Zhang, G.; Song, Y.; Jiang, S.; Grouset, D.; Zhang, M. Review on the research of hydrogen storage system fast refueling in fuel cell vehicle. Int. J. Hydrogen Energy 2019, 44, 10677–10693. [Google Scholar] [CrossRef]
- Sapre, S.; Vyas, M.; Pareek, K. Impact of refueling parameters on storage density of compressed hydrogen storage Tank. Int. J. Hydrogen Energy 2021, 46, 16685–16692. [Google Scholar] [CrossRef]
- Ye, M.; Sharp, P.; Brandon, N.; Kucernak, A. System-level comparison of ammonia, compressed and liquid hydrogen as fuels for polymer electrolyte fuel cell powered shipping. Int. J. Hydrogen Energy 2022, 47, 8565–8584. [Google Scholar] [CrossRef]
- Deng, Q.W.; Ren, G.Q.; Li, Y.J.; Yang, L.; Zhai, S.L.; Yu, T.; Sun, L.; Deng, W.Q.; Li, A.; Zhou, Y.H. Hydrogen and CO2 storage in high surface area covalent triazine–based frameworks. Mater. Today Energy 2020, 18, 100506. [Google Scholar] [CrossRef]
- Hirscher, M.; Zhang, L.; Oh, H. Nanoporous adsorbents for hydrogen storage. Appl. Phys. A 2023, 129, 112. [Google Scholar] [CrossRef]
- Forouzanmehr, M.; Reza Kashyzadeh, K.; Borjali, A.; Ivanov, A.; Jafarnode, M.; Gan, T.H.; Wang, B.; Chizari, M. Detection and Analysis of Corrosion and Contact Resistance Faults of TiN and CrN Coatings on 410 Stainless Steel as Bipolar Plates in PEM Fuel Cells. Sensors 2022, 22, 750. [Google Scholar] [CrossRef]
- Cabrera, E.; de Sousa, J.M.M. Use of Sustainable Fuels in Aviation—A Review. Energies 2022, 15, 2440. [Google Scholar] [CrossRef]
- Lototskyy, M.V.; Davids, M.W.; Tolj, I.; Klochko, Y.V.; Sekhar, B.S.; Chidziva, S.; Smith, F.; Swanepoel, D.; Pollet, B.G. Metal hydride systems for hydrogen storage and supply for stationary and automotive low temperature PEM fuel cell power modules. Int. J. Hydrogen Energy 2015, 40, 11491–11497. [Google Scholar] [CrossRef]
- Eberle, U.; Felderhoff, M.; Schuth, F. Chemical and Physical Solutions for Hydrogen Storage. Angew. Chem. 2009, 48, 6608–6630. [Google Scholar] [CrossRef]
- Verstraete, D.; Gong, A.; Lu, D.D.C.; Palmer, J.L. Experimental investigation of the role of the battery in the AeroStack hybrid, fuel-cell-based propulsion system for small unmanned aircraft systems. Int. J. Hydrogen Energy 2015, 40, 1598–1606. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).