Abstract
Although research has shown that through the additional rigidity introduced in the secondary suspension, traction rods can affect the vertical dynamic performance of railway vehicles, this topic has been less studied by researchers in the field. In this paper, the effect of a traction rod on the vertical vibration behavior of a carbody of a railway vehicle is analyzed, using the results obtained through numerical simulations. Numerical simulation applications are developed based on a vehicle model, where the vehicle carbody is modeled using a free-free equivalent beam Euler–Bernoulli, and the bogie chassis and wheelsets are represented by rigid bodies linked together by Kelvin-Voigt systems that model the secondary suspension and the primary suspension. The novelty element of this paper is found in the model of the traction rod. This includes traction rod damping, which has been neglected in previous research. The stiffness and damping of the traction rod are represented by a longitudinal Kelvin–Voigt system integrated into a secondary suspension model. The effect of the traction rod on the vertical vibration behavior of the vehicle carbody is analyzed based on the power spectral density of the acceleration, the root mean square of acceleration, and the ride comfort index, for three cases for analysis: a ‘without traction rod’ case, a ‘with traction rod—with damping’ case, and a ‘with traction rod—without damping’ case. The conclusions of the paper highlight the influence of the stiffness and damping of the traction rod on the vibration level of the carbody, especially in its middle. Depending on the stiffness of the traction rod, significant increases in the ride comfort index are obtained, which at high velocities can exceed 300%. Damping of the traction rod reduces the ride comfort index by up to 10%.
1. Introduction
The assessment of the vibration behavior of railway vehicles is a problem that can be approached both theoretically and experimentally [1,2,3]. Research based on theoretical approaches has been developed with the help of the results obtained through numerical simulations [4,5], and experimental approaches use the results of tests carried out in the laboratory on scale experimental models [6,7,8,9,10,11] and on special test vehicles [12,13], or the results of tests carried out on the line [14].
Numerical simulation applications are useful tools for estimating the railway vehicles’ vibration behavior and optimizing their dynamic performance regarding ride quality and ride comfort from the design phase, and then for investigating problems that occur during operation. In relation to experimental tests, which are costly and involve a large consumption of time and resources, numerical simulations have the advantage that they allow investigation of the vehicle’s vibration behavior, even in extreme situations that cannot be highlighted in real test conditions [15,16,17,18].
However, in the development of theoretical research into the evaluation of the vibration behavior of railway vehicles based on numerical simulation results, there are challenges in the stage of mechanical modeling of the vehicle–track system [19,20,21,22,23,24,25,26,27]. This becomes a difficult task when both the vibration characteristics of the railway vehicle and the combined effect due to several sources of vibration found at the wheel–rail contact point must be considered [28,29,30,31,32,33]. In the case of the railway vehicle, the difficulties are related to the modeling of a complex mechanical system, with a specific behavior of vibrations, which includes both rigid modes of vibration and flexible modes of vibration, independent or coupled to each other. At the point of wheel–rail contact, there are several sources of excitation of the vibrations of the railway vehicle: the irregularities of the rolling surfaces and the constructive discontinuities of the rail, and the undulating wear of the rolling surfaces of the wheel or the deviations from the circular shape of the wheel (eccentricity, ovality, polygonalization, plane place, or flattening) [34,35,36,37,38,39]. If the mechanical model of the vehicle–track system considers all these factors that can influence the vibration behavior of railway vehicles, complex mathematical and numerical models, which require very long simulation times, are produced.
In general, the mechanical model is obtained via a simplified representation of the real technical system vehicle track, based on the elimination of secondary effects and the retaining of only the significant ones, in accordance with the specific aspects of the studied problem and the precision required of the results. Useful qualitative and even quantitative information regarding the basic characteristics of railway vehicle vibrations can also be obtained based on simple models. To obtain reliable results, it is necessary to adopt complex models, which consider several important factors that influence the vibration behavior of the vehicle. For example, the vibration behavior of the railway vehicle is largely determined by the suspension. Consequently, the precision of the numerical simulation results will be closely related to the complexity of the suspension model [20,21,22]. Or, when it comes to assessing the vibration comfort performance of the railway vehicle, the accuracy of the results depends significantly on the modeling of the carbody. Previous research has highlighted that at high velocities, the ride comfort performance of railway vehicles, as evaluated using the results obtained with models of said vehicles, in which the carbody is modeled by a “rigid carbody”-type model, are overestimated. In such research, it is important to use a ‘flexible carbody’-type model [40,41].
Another major factor that influences the vertical vibration behavior of the railway vehicle is the traction rod, which ensures the transmission of forces in the longitudinal direction between the carbody and the bogie [42]. Although there is a lot of research that addresses the problem of vertical vibrations and their effect on the dynamic behavior of the railway vehicle, either in terms of ride quality or ride comfort, the influence of the traction rod is a very understudied issue. To the knowledge of the authors, the only papers that address this research topic are the ones described below.
Ma and Song introduced the stiffness of the traction rod into the model of a subway vehicle to analyze its influence on the vertical dynamic performance of a vehicle [43]. The conclusions of the study highlight that the additional stiffness introduced by the traction rod leads to an increase in the stiffness of the secondary suspension, which can have the effect of amplifying some undesirable phenomena, such as wear and deformation of the wheels, and can reduce ride comfort.
Starting from the theory that bogies can be used as a dynamic vibration absorber to reduce the vertical bending vibrations of the carbody of railway vehicles, as proposed by Tomioka and Takigami [13], a team of researchers recently conducted two studies [44,45]. These had as their study object the traction rod effect on the dynamic behavior of the carbody of high-speed railway vehicles, and the identification of the possibility of improving ride comfort by optimizing the stiffness of the traction rod, respectively. The originality of these studies is the representation of the traction rod in the vehicle model. More precisely, as a novelty compared to the original research, in which the stiffness of the traction rod was represented by an elastic element with linear characteristics, in these latest studies, the traction rod is represented as a non-linear element.
As can be seen from the brief description of these studies, all consider only the stiffness of the traction rod and the bushings at the two ends of the traction rod, neglecting its damping.
In this paper, the effect of the traction rod on the vertical vibration behavior of the railway vehicle carbody is analyzed, considering the damping of the traction bar. The problem is investigated using results obtained through numerical simulations developed based on a vehicle model of the rigid–flexible coupled type, with seven degrees of freedom, in which the rigid modes of the vertical vibration of the carbody (bounce and pitch), the first mode of vertical bending, and the rigid modes of vertical vibration of the bogies (bounce and pitch) were considered. The stiffness and damping of the traction rod are represented in the vehicle model by a longitudinal Kelvin–Voigt system integrated into the secondary suspension model. The vertical vibration behavior of the railway vehicle carbody is evaluated based on the power spectral density of the acceleration, the root mean square of acceleration, and the ride comfort index, comparing three cases (‘without traction rod’, ‘with traction rod—with damping’, and ‘with traction rod—without damping’). For each of these cases, a dedicated model of secondary suspension is adopted. In the first case, the secondary suspension is modeled by a vertical Kelvin–Voigt system, and in the second case, by two Kelvin–Voigt systems, one vertical and one longitudinal. In the third case, the secondary suspension model includes a vertical Kelvin–Voigt system and a longitudinal elastic element. In this context, the physical implications of these three study scenarios are analyzed from the point of view of the influence of the stiffness and damping of the traction bar on the level of vertical vibrations of the carbody and on ride comfort. The results presented for the case “without traction rod” and the case “with traction rod—without damping” are qualitatively comparable with the results from the specialized literature [45], which have already been verified based on experimental tests carried out in the laboratory on a scale model.
The novelty of the presented study consists of the model of the traction rod, which is integrated into the model of the secondary suspension of the vehicle. Unlike previous research, in the model of the traction rod, both the stiffness of the bar and its damping are represented.
2. The Railway Vehicle Model and Equations of Motion
2.1. Description of the Railway Vehicle Model
To study the effect of the traction rod on the vertical vibrations of the railway vehicle carbody, the mechanical model presented in Figure 1 is adopted. It consists of the vehicle carbody, modeled by a free–free equivalent beam of the Euler–Bernoulli type, and the chassis of the two bogies and the four wheelsets, represented by rigid bodies, linked together by Kelvin–Voigt systems that model the primary suspension and the secondary suspension of the vehicle (see Figure 2).
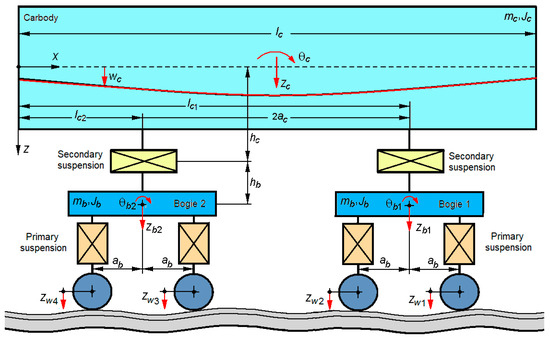
Figure 1.
The mechanical model of the railway vehicle.
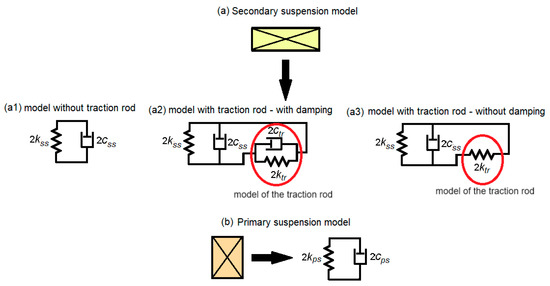
Figure 2.
Vehicle suspension model: (a) secondary suspension model; (b) primary suspension model.
The secondary suspension of a bogie is modeled by a Kelvin–Voigt vertical system with stiffness 2kss and damping 2css (Figure 2(a1)), for which the case ‘without traction rod’ is obtained. For the case ‘with traction rod—with damping’, a longitudinal Kelvin–Voigt system with stiffness 2ktr and damping 2ctr is integrated into the secondary suspension model, through which the elasticity and damping of the traction rod is modeled (Figure 2(a2)). The distance from this system to the neutral axis of the carbody is denoted by hc, and the distance to the center of gravity of the bogie is denoted by hb. For the case ‘with traction rod—without damping’, the traction rod is modeled by an elastic element with stiffness 2ktr (Figure 2(a3)). The primary suspension of a wheelset is modeled by a vertical Kelvin–Voigt system with stiffness 2kps and damping 2cps (Figure 2b).
The following vertical vibration modes of the carbody are considered: bounce, pitch, and the first vertical bending mode. The vertical displacement of the carbody corresponding to the bounce, denoted by zc, and the pitch rotation angle of the carbody, denoted by θc, are highlighted in Figure 1. The vertical displacement of the section of the carbody located at the distance x from the reference system at time t, is denoted wc(x,t). This displacement results from the overlap of the displacements corresponding to the three modes of vibration of the carbody—the bounce, the pitch and the first mode of vertical bending, corresponding to the relation
where lc is the length of the carbody, Tc is the time coordinate of the first vertical bending mode, and Xc is the eigenfunction of the vertical bending mode described by the relation
with
that verifies the characteristic equation
where ωc is the natural angular frequency of the first vertical bending mode of the carbody; ρc = mc/lc represents the mass of the beam per unit length; EcIc is the bending stiffness, where Ec is the longitudinal modulus of elasticity; and Ic is the moment of inertia of the cross-section of the beam.
The vibration modes of the two bogies are bounce and pitch. The vertical displacement corresponding to the bounce is denoted by zb1,2, and the rotation angle at the pitch is denoted by θb1,2.
The railway vehicle is running on a track with vertical irregularities, marked next to each axle with zw1…4. It is specified that since the natural frequencies of the vertical vibration of the vehicle are much lower than the natural frequencies of the wheelset–track system, the perfectly rigid track hypothesis is adopted.
2.2. The Motion Equations
The motion equations of the vehicle are written for the complex case ‘with traction rod—with damping’, from which the equations for the simpler cases ‘without traction rod’ and ‘with traction rod—without damping’ can then be derived.
The Euler–Bernoulli beam theory is used to derive the general form of the motion equation of the carbody. This is of the following form:
where δ(.) is Dirac’s delta function, μ is the structural damping coefficient, lc1,2 fixes the supporting points of the carbody on the secondary suspension, Fss1,2 represents the forces in the secondary suspension, and Ftr1,2 are the longitudinal forces in the traction rods.
Distances lc1,2 are determined depending on the length of the carbody lc and the longitudinal base of the secondary suspension 2ac,
The vertical forces of the secondary suspension and the longitudinal forces in the traction rods are of the following form:
Applying the modal analysis method [46] from the general Equation (5), the motion equations of the bounce, the pitch and the first vertical bending mode of the carbody are obtained:
where mmc represents the modal mass of the carbody, cmc is modal damping of the carbody, and kmc is modal stiffness of the carbody,
The bounce and pitch equations of the two bogies are deduced with the help of the fundamental laws of mechanics, taking into account that they are acted upon by the inertia forces during bounce and pitch, the forces from the secondary suspension corresponding to the two bogies (Fss1,2), the forces from the traction rods (Ftr1,2), and the forces of the primary suspension corresponding to the four wheelsets (Fps1…4):
The forces of the secondary suspension and the forces in the traction rods were defined above (see Equations (7) and (8)), and the forces of the primary suspension are of the following form:
The motion equations of the carbody and the two bogies form the following system
where q is the vector of displacement coordinates, and zw is the vector of inhomogeneous terms:
M, C şi K are the inertia, damping, and stiffness matrices. These are in the following form:
The following notations can be found in matrices C and K:
The vectors P and R are of the following form:
For the cases ‘without traction rod’ and ‘with traction rod—without damping’, the matrices C and K change their form.
It is observed that in all three cases, ‘without traction rod’, ‘with traction rod’—with damping’, and ‘with traction rod—without damping’, the vibrations of bounce, pitch, and vertical bending of the carbody are coupled with the bogie bounce. The difference between the cases ‘without traction rod’ and ‘with traction rod’ consists of the way in which the pitch vibrations of the bogies are manifested. In the case ‘without traction rod’, these are independent vibrations. In the case ‘with traction rod’, the pitch vibrations of the bogies are transmitted to the carbody through the traction rods (Figure 3). The pitch vibrations of the bogies are coupled with the pitch and vertical bending vibrations of the carbody, and through them with the bounce vibrations of the carbody.
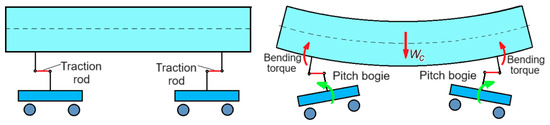
Figure 3.
Transmission of the pitch bogies to the carbody through the traction rods.
3. Evaluation of the Vertical Vibration Behavior of the Railway Vehicle Carbody
The power spectral density of acceleration, the root mean square of acceleration, and the ride comfort index are used to evaluate the vertical vibration behavior of the railway vehicle carbody.
The power spectral density of acceleration of the carbody at some point x, placed on the longitudinal axis of the carbody, is described by the relation
where G(ω) represents the power spectral density of the vertical irregularities of the track, and is the frequency response function of the acceleration of the vehicle carbody.
The power spectral density of the vertical irregularities of the track is defined by the relation [47]:
where V is the velocity of the vehicle, Ω is the wave number, Ωc = 0.8246 rad/m, Ωr = 0.0206 rad/m, and A is a constant that depends on the quality of the track; for a good-quality track, A = 2.119 × 10−7 radm; for a low-quality track, A = 6.124 × 10−7 radm.
The frequency response function of the carbody acceleration is calculated with the relation
where , , are the partial frequency response functions of the acceleration of the carbody corresponding to the vibration modes of the carbody, respectively: bounce, pitch and vertical bending. Details on how to calculate the partial frequency response functions are presented in Appendix A.
Relation (20) is particularized for the calculation of the power spectral density of the acceleration in the middle of the carbody (for x = lc/2), denoted by Gcm(ω), or above the secondary suspension corresponding to one of the two bogies (for x = lc1,2), denoted by Gc1,2(ω):
where is the frequency response function of the acceleration at the middle of the carbody, and is the frequency response function of the acceleration of the carbody above the secondary suspension, which is calculated with the following relations:
The root mean square of acceleration of the carbody is calculated as a function of the power spectral density of the acceleration, defined according to the relations above. Thus, at some point x located on the longitudinal axis of the carbody, the root mean square of acceleration is
where the power spectral density of the acceleration is given by relation (18). In the middle of the carbody and above the secondary suspension, the root mean square of acceleration is calculated with the following relations:
where Gcm(ω) and Gc1,2(ω) are defined by relations (23) and (24).
According to the mean comfort method, described in the UIC 513R leaflet [48] and the standard of railway applications EN 12299 [49], the quantification of vibration comfort is carried out using the ride comfort index (NMV) and a conventional scale that connects the values of this index and the sensation of comfort (see Figure 4).
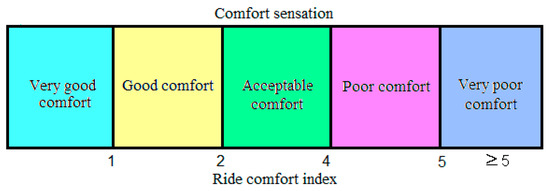
Figure 4.
The significance of the ride comfort index.
For the assessment of ride comfort in vertical vibrations, the partial ride comfort index is defined according to the relation [50]:
where ac is the root mean square of acceleration of the carbody, 95 represents the quantile of order 95%, and Wab is an acceleration weighting filter resulting from the product of two filters Wab = Wa × Wb, where Wa is a passband filter and the filter Wb considers human sensitivity to vertical vibrations within the frequency interval of 4 Hz and 12 Hz.
The frequency weighting function of the filter Wa are of the following form:
where s = iω (with i2 = −1), f1 = 0.4 Hz, f2 = 100 Hz, and Q1 = 0.71.
The Wb filter has the following frequency weighting function:
where f3 = 16 Hz, f4 = 16 Hz, f5 = 2.5 Hz, f6 = 4 Hz, Q2 = 0.63, Q4 = 0.8 and K = 0.4.
The vertical carbody accelerations are assumed to have a Gaussian distribution with zero mean. In these conditions, the partial ride comfort index is obtained with the general relation
where represents the quantile of the standard Gaussian distribution with the probability of 95% and Hab(ω) = Ha(ω) × Hb(ω), where Ha(ω) and Hb(ω) are the frequency weighting function corresponding to the filters Wa and Wb.
The frequency weighting functions of the Wa and Wb filters are represented in Figure 5a, and the frequency weighting function of the Wab filter is represented in Figure 5b.

Figure 5.
The frequency weighting functions (a) of the filters Wa and Wb; and (b) of the filter Wab.
For the calculation of the ride comfort indices at the middle of the carbody NMVm and above to the support points of the carbody on the secondary suspension NMV1,2, in relation (31) the power spectral density of the acceleration of the carbody Gc(x,ω) is replaced by the spectral density of power Gcm(ω) defined by relation (21), respectively, with Gc1,2(ω), according to relation (22).
4. Numerical Analysis of the Effect of the Traction Rod on the Vertical Vibration Behavior of the Railway Vehicle Carbody
4.1. Parameters of the Railway Vehicle Numerical Model
Table 1 presents the reference parameters of the railway vehicle for the numerical simulations.

Table 1.
Parameters of the numerical model of the railway vehicle.
4.2. Numerical Simulation Results and Discussion
In this section, the results obtained through numerical simulations are presented, based on which the effect of the traction bar on the vertical vibration behavior of the railway vehicle carbody is analyzed. To evaluate the vertical vibration behavior of the carbody, the power spectral density of the carbody acceleration, the root mean square of the carbody acceleration and the partial ride comfort index, calculated at the middle of the carbody and above the secondary suspension of the first bogie (bogie 1), are used. To analyze the effect of the traction rod, the cases ‘without traction rod’ and ‘with traction rod—with damping’ are considered, and to highlight the effect of the damping of the traction rod, the cases ‘with traction rod—with damping’ and ‘with traction rod—without damping’ are considered.
Figure 6 shows the power spectral density of the acceleration of the carbody, at a velocity of 200 km/h, for the cases ‘without traction rod’ and ‘with traction rod’—with damping’. For the case ‘with traction rod’, three values of the stiffness of the traction rod are considered, respectively: the reference value (ktr = 10 MN/m) and two analysis values (ktr = 15 MN/m and ktr = 20 MN/m).
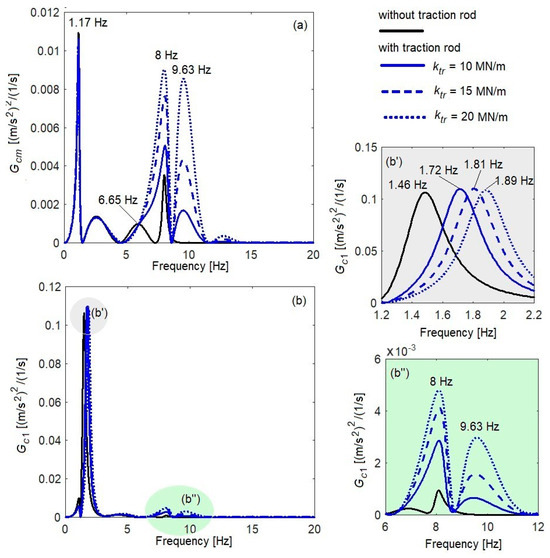
Figure 6.
The influence of the stiffness of the traction rod on the power spectral density of the acceleration: (a) in the middle of the carbody; (b) above the secondary suspension of bogie 1.
Series of maxima and minima are evident on the power density spectrum of the acceleration. The maxima correspond to the natural frequencies of the vehicle vibration modes. In the middle of the carbody, the peaks corresponding to the natural frequencies of carbody bounce (1.17 Hz), the vertical bending of the carbody (8 Hz), and the bogie bounce (6.65 Hz) are highlighted. The peak corresponding to the natural frequency of the bogies’ pitch (9.63 Hz) appears only in the case ‘with traction rod’. In this case, pitch vibrations of the bogies are transmitted through the traction bar to the carbody. The peaks of the natural frequencies of the bounce and vertical bending of the carbody and the bogie pitch are also observed on the spectrum of the power density of the acceleration above the secondary suspension, but here, these vibration modes have a less significant weight. In this case, the spectrum of the acceleration power spectral density is dominated by the peak corresponding to the natural frequency of the carbody pitch, which is at 1.46 Hz for the case ‘without traction rod’. For the case ‘with traction rod’, the natural frequency of the pitch vibrations of the carbody changes according to the stiffness of the traction rod, respectively, being 1.72 Hz for the reference value of the stiffness of the traction rod, 1.81 Hz for ktr = 15 MN/m, and 1.89 Hz for ktr = 20 MN/m.
The minima of the power spectral density of the acceleration are produced by the antiresonance effect due to the geometric filtering effect of the wheelbase of the carbody and the wheelbase of the bogie. These minima occur at geometric filtering frequencies. When the geometric filtering frequencies overlap with one of the natural frequencies of the vehicle’s vibration modes, their influence is significantly reduced. The effect of geometric filtering has been highlighted in numerous studies of vertical vibrations of the railway vehicles [50,51,52]. As can be seen in the diagrams in Figure 6, geometric filtering has a more important effect at the middle of the carbody, because here, both the filtering effect produced by the bogie wheelbase and the geometric filtering effect produced by the carbody wheelbase are cumulated. The geometric filtering effect above the secondary suspension is less effective than in the middle of the carbody, because only the bogie wheelbase is produced. On the other hand, geometric filtering effect is velocity dependent. As a result of the geometric filtering effect, the vibration level of the carbody does not increase continuously as the velocity increases [52], as will be shown later.
As for the influence of the traction rod on the vertical vibration level of the carbody, it manifests especially at the natural frequency of the vertical bending of the carbody and the natural frequency of the pitch vibrations of the bogie. Increasing the stiffness of the traction rod results in significant increases in the vibration level at both natural frequencies, and this is best highlighted in the middle of the carbody (diagram a). For example, at the natural frequency of the vertical bending of the carbody, comparing the case ‘without traction rod’ and the case ‘with traction rod’, an increase in the power spectral density of the acceleration is registered as 43.34% for ktr = 10 MN/m. If the traction rod stiffness is 15 MN/m, the power spectral density of the acceleration increases is 115.29%, and for kxc = 20 MN/m, it is 154.95%. At the natural frequency of the bogie pitch, increasing the traction rod stiffness from 10 MN/m to 20 MN/m leads to an increase of about 400% in the power spectral density of the acceleration.
The influence of the damping of the traction rod on the vertical vibration level of the carbody at a velocity of 200 km/h is highlighted in Figure 7. The case ‘with traction rod’, with a traction rod stiffness of 20 MN/m, and the cases ‘without damping’ and ‘with damping’ (with ctr = 25 kNs/m) were considered.
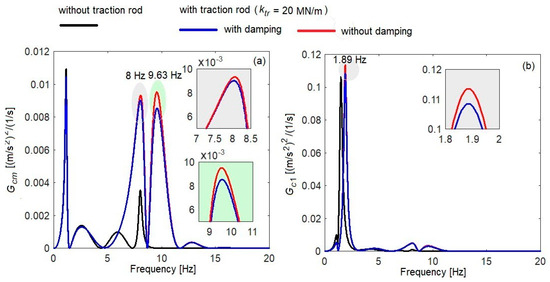
Figure 7.
The influence of traction rod damping on the power spectral density of the acceleration: (a) in the middle of the carbody; (b) above the secondary suspension of bogie 1.
The increase in the power spectral density for the case ‘without damping’ is highlighted in the natural frequencies of the vertical bending of the carbody and the bogie pitch (diagram a), and at the natural frequency of the carbody pitch (diagram b). In the middle of the carbody, at 8 Hz, there is an increase in the power spectral density of acceleration of 3.3%, and, at 9.63 Hz, the increase is 11.8%. Above the secondary suspension, at a frequency of 1.89 Hz, the increase in the power spectral density of the acceleration is 4.7%. The increase in the power spectral density of the acceleration in the case ‘with traction rod—without damping’ also depends on the stiffness of the traction rod, as shown in Figure 8.
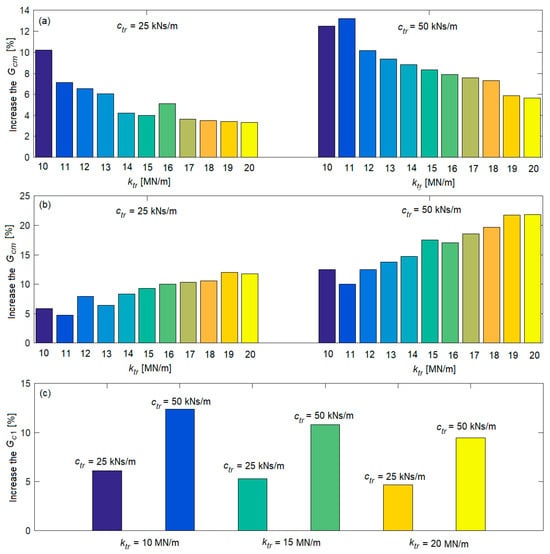
Figure 8.
The increase in the power spectral density of the acceleration in the ‘with traction rod—without damping’ case: (a) in the middle of the carbody at the natural frequency of the vertical bending of the carbody; (b) in the middle of the carbody at the natural frequency of the bogie pitch; (c) above the secondary suspension of bogie 1 at the natural frequency of the carbody pitch.
Diagrams (a) and (b) in Figure 8 show the increase in the power spectral density of the acceleration at the natural frequencies of the vertical bending of the carbody (8 Hz) and the pitch of the bogie (9.63 Hz) for several values of the stiffness of the traction rod between 10 MN/m and 20 MN/m, for the case ‘with traction rod—without damping’ in relation to the case ‘with traction rod—with damping’ with ctr = 25 kNs/m and ctr = 50 kNs/m. It is observed that if the damping of the traction rod is not considered, the increase in the power spectral density of the acceleration at the frequency of 8 Hz can reach up to 10.2% (for ktr = 10 MN/m) in relation to the case ‘with damping’ for ctr = 25 kNs/m, respectively, up to 13.2% (for ktr = 11 MN/m) for ctr = 50 kNs/m. At a frequency of 9.63 Hz, the maximum increase in the power spectral density of the acceleration in the case ‘without damping’ in relation to the case ‘with damping’ is 12% (for ktr = 19 MN/m) for ctr = 25 kNs/m and of 21.8% (for ktr = 20 MN/m) for ctr = 50 kNs/m. At the natural frequency of the pitch vibrations of the carbody (diagram c), the highest increase in the power spectral density of the acceleration (12.36%) is recorded for a traction rod stiffness of 10 MN/m and a traction rod damping of 50 kNs/m.
In Figure 9 and Figure 10, the power spectral density of the acceleration at the natural frequency of the vertical bending of the carbody and the natural frequency of the bogie pitch, respectively, in the velocity range between 10 km/h and 200 km/h in correlation with traction rod stiffness is represented. The general tendency is for the carbody vibration level to increase with the velocity at both natural frequencies, but the increase is not continuous due to the geometric filtering effect. Depending on the velocity, the diagrams show a succession of maxima of the power spectral density of the acceleration; these correspond to a situation wherein geometric filtering has no effect. The minima appear at geometric filtering velocities. The geometric filtering effect is more intense in the area of low velocities, where more geometric filtering velocities are concentrated, an aspect highlighted in diagrams (a’) and (b’). The influence of the stiffness of the traction rod on the level of vertical vibrations of the carbody is dependent on the velocity and on the geometric filtering effect, respectively. The largest increases in the power spectral density of the acceleration due to the traction rod occur at high velocities, when geometric filtering has no effect. For example, at the vertical bending frequency of the carbody, in the middle of the carbody (Figure 9), at a velocity of 121 km/h, there is an increase in the power spectral density of 19%, prompted by increasing the stiffness of the traction rod from 10 MN/m to 20 MN/m; at a velocity of 158 km/h, the increase is 28.8%. At the pitch frequency of the bogie, in the middle of the carbody (Figure 10), when increasing the traction rod stiffness from 10 MN/m to 20 MN/m at a velocity of 147 km/h, the increase in the power spectral density is 432.8%; at a velocity of 190 km/h, the increase is 422.7%.

Figure 9.
Power spectral density of acceleration at the vertical bending frequency of the carbody (a) and (a’) in the middle of the carbody; (b) and (b’) above the secondary suspension of bogie 1.
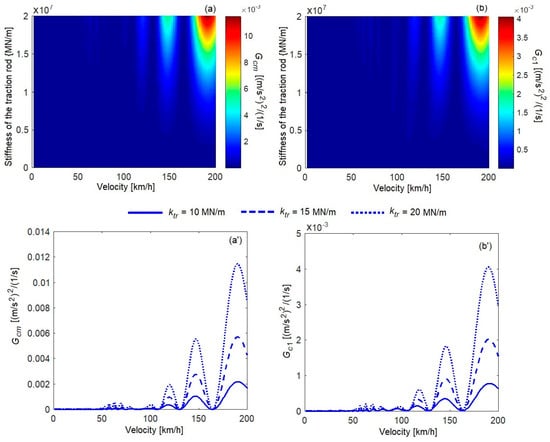
Figure 10.
Power spectral density of acceleration at the pitch frequency of the bogie: (a) and (a’) at the middle of the carbody; (b) and (b’) above the secondary suspension of bogie 1.
Figure 11 shows the root mean square of acceleration of the carbody at its middle and above the secondary suspension of the first bogie, over a velocity range between 10 km/h and 200 km/h, in correlation with the stiffness of the traction rod. Here, too, the general tendency of the root mean square to increase with velocity is noticeable, which is not continuous due to the geometric filtering effect. The influence of the traction rod on the root mean square of acceleration manifests itself at velocities higher than 100 km/h and, particularly in the middle of the carbody, where significant increases in the vibration level are recorded for the values of traction rod stiffness greater than 10 MN/m. For example, the diagrams of Figure 12 show the root mean square of the acceleration at velocities of 160 km/h, 180 km/h, and 200 km/h for the case ‘without traction rod’ and for the case ‘with traction rod—with damping’, with three values of the stiffness of the traction rod. Table 2 shows the increase in the root mean square of the acceleration for the case ‘with traction rod—with damping’ in relation to the case ‘without traction rod’.
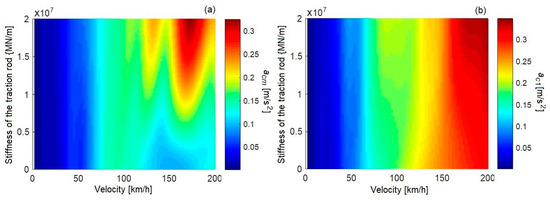
Figure 11.
The root mean square of acceleration: (a) at the middle of the carbody; and (b) above the secondary suspension of bogie 1.
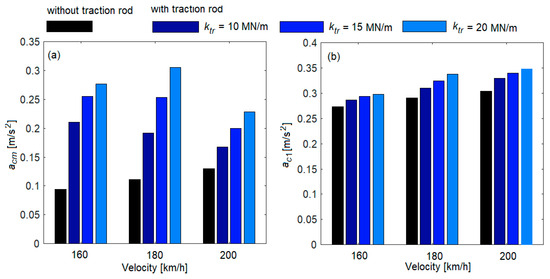
Figure 12.
Example of the influence of the traction rod stiffness on the root mean square of acceleration: (a) at the middle of the carbody; and (b) above the secondary suspension of bogie 1.

Table 2.
The increase in the root mean square of acceleration due to the traction rod.
To analyze the influence of the traction rod damping on the root mean square of acceleration, in Figure 13, the cases ‘without traction rod’ and ‘with traction rod’ (for ktr = 20 MN/m) were considered, both ‘with damping’ and ‘without damping’, for the velocities analyzed above.
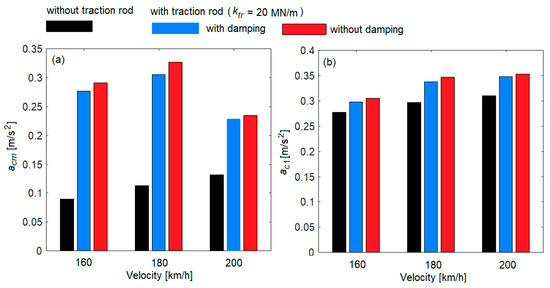
Figure 13.
The influence of the traction rod damping on the root mean square of acceleration: (a) in the middle of the carbody; and (b) above the secondary suspension of bogie 1.
Comparing the cases ‘with damping’ and ‘without damping’, it is observed that if the damping of the traction rod is not considered, the increase in the root mean square of acceleration can reach up to 6.9% in the middle of the carbody, respectively, to 2.81% above the secondary suspension, at a velocity of 180 km/h. This increase, however, depends on the velocity, as shown in Figure 14, in which the percentage increase in the root mean square of acceleration for the case ‘without damping’ compared to the case ‘with damping’ is presented. It is observed that in the middle of the carbody, the increase in the root mean square of acceleration reaches 8.9%, while above the secondary suspension, this increase is less important, not exceeding 2.9%.

Figure 14.
Increase in the root mean square for the case ‘without damping’ compared to the case ‘with damping’: (a) in the middle of the carbody; and (b) above the secondary suspension of bogie 1.
Based on the following figures, the influence of the traction rod on ride comfort is analyzed based on the partial ride comfort index for vertical vibrations. Figure 15 shows the ride comfort index calculated for the velocity range 10... 200 km/h in correlation with the stiffness of the traction rod. The ride comfort index increases with speed, but not monotonically, due to the geometric filtering effect, similar to the root mean square acceleration. The effect of the traction rod on the ride comfort index keeps the same trend as the root mean square; it is important at velocities above 100 km/h for traction rod stiffnesses between 10 MN/m and 20 MN/m. Here, significant increases in the ride comfort index are observed both in the middle of the carbody and above the secondary suspension. For example, Figure 16 shows the ride comfort indices at velocities of 160 km/h, 180 km/h and 200 km/h, for the case ‘without traction rod’ and for the case ‘with traction rod—with damping’ with three values of the traction rod stiffness: 10 MN/m, 15 MN/m and 20 MN/m. For these cases, the percentage increases in the ride comfort index due to the traction rod were calculated (see Table 3).
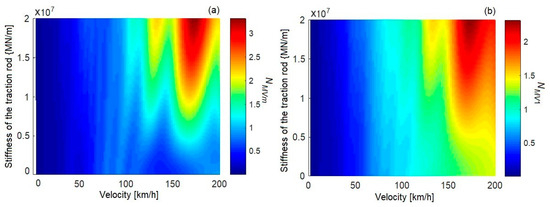
Figure 15.
The ride comfort index: (a) in the middle of the carbody; and (b) above the secondary suspension of bogie 1.
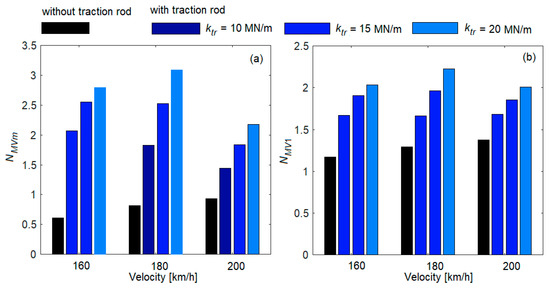
Figure 16.
Example of the influence of the traction rod stiffness on the ride comfort index: (a) in the middle of the carbody; and (b) above the secondary suspension of bogie 1.

Table 3.
Increased ride comfort index due to the traction rod.
The influence of traction rod damping on ride comfort is highlighted in the diagrams in Figure 17, where ride comfort indices are presented for the case ‘without traction rod’ and for the case ‘with traction rod’, both ‘with damping’ and ‘without damping’ for ktr = 20 MN/m at velocities of 160 km/h, 180 km/h and 200 km/h.
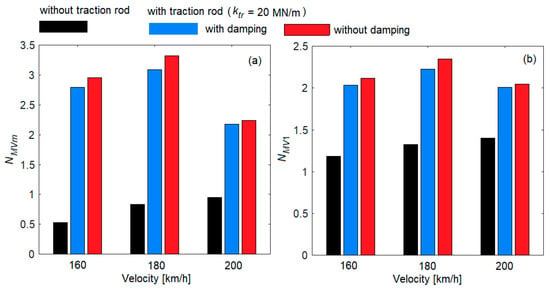
Figure 17.
The influence of the traction rod damping on ride comfort index: (a) in the middle of the carbody; and (b) above the secondary suspension of bogie 1.
If we compare the case ‘with traction rod—without damping’ and the case ‘with traction rod—with damping’, the ride comfort index in the middle of the carbody increases without damping the traction rod by 5.6% at a velocity of 160 km/h, by 3.3% at a velocity of 180 km/h, and by 3.1% at 200 km/h. Above the secondary suspension, the ride comfort index increases by 4.2% at 160 km/h, 5.3% at 180 km/h, and 1.95% at 200 km/h. Depending on the velocity, these increases can reach almost 10% in the middle of the carbody and 6% above the secondary suspension, as shown in Figure 18.
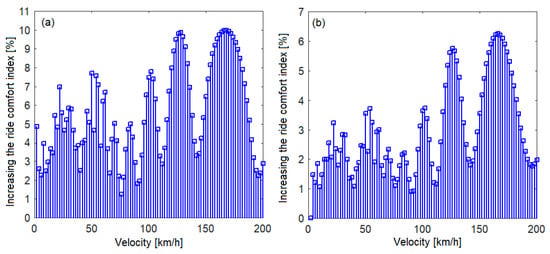
Figure 18.
Increase in the ride comfort index for the case ‘without damping’ compared to the case ‘with damping’: (a) in the middle of the carbody; and (b) above the secondary suspension of bogie 1.
5. Conclusions
In this paper, the effect of the traction rod on the vertical vibration behavior of a railway vehicle carbody—evaluated based on the power spectral density of the carbody acceleration, the root mean square of the carbody acceleration, and the ride comfort index—was analyzed. In this context, a parametric study was carried out regarding the vertical vibration level of the carbody at its middle and above the secondary suspension, according to the stiffness and damping of the traction rod, in correlation with the velocity. To this end, the results of the numerical simulations obtained for the cases ‘with traction rod—with damping’ and ‘with traction rod—without damping’ were used, which were compared with the results of the numerical simulations for the case ‘without traction rod’. The results for the case ‘without traction rod’ and the case ‘with traction rod—without damping’ are qualitatively comparable to those in the literature review. Numerical simulation applications were developed based on a theoretical rigid–flexible vehicle model, where the traction rod is represented in an original way by a longitudinal Kelvin–Voigt system integrated into the secondary suspension model.
After analyzing the results of the numerical simulations, the following conclusions were drawn:
- The effect of the traction rod on the power density spectrum of the carbody acceleration was highlighted on the one hand by increasing the natural frequency of the pitch vibrations of the carbody without significant changes in the vibration level, and on the other hand by increasing the level of vibrations of the carbody at the natural frequencies corresponding to the carbody vertical bending and the bogie pitch. Increasing the vibration level of the carbody at these frequencies correlated with traction rod stiffness, traction rod damping, and velocity.
- The effect of the traction rod on the root mean square of the acceleration is particularly pronounced in the middle of the carbody at velocities above 100 km/h. Depending on the stiffness of the traction rod and velocity, there were significant increases in the root mean square of the carbody acceleration that reached almost 200%. In the absence of traction rod damping, significant increases in the root mean square (of between 0.47% and 8.9%) in the middle of the carbody were obtained, which varied depending on the velocity.
- The ride comfort index at vertical vibration is significantly influenced by the stiffness of the traction rod. Significant increases in the ride comfort index that exceed 300% in the middle of the carbody and 70% above the secondary suspension, respectively, were obtained, depending on the velocity and the stiffness of the traction rod. The lack of traction rod damping causes significant increases in the ride comfort index, which can reach up to almost 10% in the middle of the carbody and 6% above the secondary suspension, depending on the velocity.
The above conclusions, which highlight the influence of the stiffness and damping of the traction rod on the vibration level of the carbody, will be useful in future research focusing on the evaluation of vibration behavior, or the evaluation of the ride quality and ride comfort of railway vehicles.
Author Contributions
Conceptualization, M.D.; methodology, M.D.; software, M.D. and I.I.A.; validation, M.D. and I.I.A.; formal analysis, M.D. and I.I.A.; investigation, M.D. and I.I.A.; resources, M.D. and I.I.A.; writing—original draft preparation, M.D.; writing—review and editing, M.D. and I.I.A.; supervision, M.D.; project administration, M.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a grant of the Ministry of Research, Innovation and Digitization, CCCDI—UEFISCDI, project number PN-III-P2-2.1-PED-2021-0319, within PNCDI III”.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
For the calculation of the partial frequency response functions of the carbody acceleration corresponding to the three modes of vibration, bounce, pitch, and vertical bending, respectively, it is considered that the vertical irregularities of the track are harmonic with the amplitude zw0. Relative to the middle of the carbody, the vertical irregularities of the track are described along the four wheelsets by the harmonic functions
where ω = 2πV/Λ represents the angular frequency given by the vertical irregularities of the track with wavelength Λ.
Considering that the response of the vehicle to the harmonic irregularities of the track is also harmonic, with the same frequency, the coordinates that describe the displacements of the carbody and bogies can be written according to the general relation
where Qk is the displacement amplitude, and αk is the phase of the coordinate k compared to the vertical irregularities of the track relative to the carbody middle.
In the system of Equation (17), the complex quantities associated with the real quantities are introduced (for i2 = −1):
with , , ,
where , , , , , , , are the complex amplitudes:
The system of Equation (17), which is a system of second-order differential equations with ordinary derivatives, turns into a system of inhomogeneous algebraic equations
where the vectors Q and B, respectively, and the matrices M and A are of the form
in which the notations were entered:
The system of Equation (A5) results in the frequency response functions of the acceleration of the vehicle carbody, corresponding to the three modes of vibration: bounce, pitch, and vertical bending,
References
- Huang, C.; Zeng, J.; Luo, G.; Shi, H. Numerical and experimental studies on the car body flexible vibration reduction due to the effect of car body-mounted equipment. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 2018, 232, 103–120. [Google Scholar] [CrossRef]
- Diana, G.; Cheli, F.; Collina, A.; Corradi, R.; Melzi, S. The development of a numerical model for railway vehicles comfort assessment through comparison with experimental measurements. Veh. Syst. Dyn. 2002, 38, 165–183. [Google Scholar] [CrossRef]
- Sharma, S.K.; Sharma, R.C.; Lee, J.; Jang, H.L. Numerical and experimental analysis of DVA on the flexible-rigid rail vehicle carbody resonant vibration. Sensors 2022, 22, 1922. [Google Scholar] [CrossRef]
- Li, T.; Su, Q.; Shao, K.; Liu, J. Numerical analysis of vibration responses in high-speed railways considering mud pumping defect. Shock Vib. 2019, 2019, 707909. [Google Scholar] [CrossRef]
- Tomioka, T.; Takigami, T.; Suzuki, Y. Numerical analysis of three-dimensional flexural vibration of railway vehicle car body. Veh. Syst. Dyn. 2006, 44, 272–285. [Google Scholar] [CrossRef]
- Dumitriu, M.; Mazilu, T.; Apostol, I.I. Scale models to verify the effectiveness of the methods to reducing the vertical bending vibration of the railway vehicles carbody: Applications and design elements. Appl. Sci. 2023, 13, 2368. [Google Scholar] [CrossRef]
- Melero, M.; Nieto, A.J.; Morales, A.L.; Palomares, E.; Chicharro, J.M.; Ramiro, C.; Pintado, P. Experimental analysis of constrained layer damping structures for vibration isolation in lightweight railway vehicles. Appl. Sci. 2022, 12, 8220. [Google Scholar] [CrossRef]
- Suzuki, E.; Watanabe, K.; Hoshino, H.; Yonezu, T.; Nagai, M. A study of Maglev vehicle dynamics using a reduced-scale vehicle model experiment apparatus. J. Mech. Syst. Transp. Logist. 2010, 3, 196–205. [Google Scholar] [CrossRef]
- Kamada, T.; Hiraizumi, T.; Nagai, M. Active vibration suppression of lightweight railway vehicle body by combined use of piezoelectric actuators and linear actuators. Veh. Syst. Dyn. 2010, 48, 73–87. [Google Scholar] [CrossRef]
- Takigami, T.; Tomioka, T.; Hansson, J. Vibration suppression of railway vehicle carbody with piezoelectric elements (A study by using a scale model of Shinkansen). J. Adv. Mech. Des. Syst. Manuf. 2007, 1, 649–660. [Google Scholar] [CrossRef][Green Version]
- Takigami, T. Investigation into suppressing the bending vibration of railway vehicle carbody with piezoelectric elements. Railw. Technol. Avalanche 2005, 9, 54–60. [Google Scholar]
- Sugahara, Y.; Takigami, T.; Kazato, A.; Koganei, R.; Sampei, M. Suppression of vertical vibration in railway vehicles by damping force control of primary suspension using an LQG controller. J. Syst. Des. Dyn. 2008, 2, 251–262. [Google Scholar] [CrossRef][Green Version]
- Tomioka, T.; Takigami, T. Reduction of bending vibration in railway vehicle carbodies using carbody–bogie dynamic interaction. Veh. Syst. Dyn. 2010, 48, 467–486. [Google Scholar] [CrossRef]
- Takigami, T.; Tomioka, T. Bending vibration suppression of railway vehicle carbody with piezoelectric elements (Experimental results of excitation tests with a commuter car). J. Mech. Syst. Transp. Logist. 2008, 1, 111–121. [Google Scholar] [CrossRef]
- Uehan, F. Recent research and development on numerical simulation techniques in railway dynamics. Q. Rep. RTRI 2020, 61, 86–89. [Google Scholar] [CrossRef] [PubMed]
- Polach, O.; Berg, M.; Iwnicki, S. Simulation. In Handbook of Railway Vehicle Dynamics; CRC Taylor & Francis Group: London, UK, 2006; pp. 359–421. [Google Scholar]
- Evans, J.; Berg, M. Challenges in simulation of rail vehicle dynamics. Veh. Syst. Dyn. 2009, 47, 1023–1048. [Google Scholar] [CrossRef]
- Schupp, G. Simulation of railway vehicles: Necessities and applications. Mech. Based Des. Struct. Mach. 2003, 31, 297–314. [Google Scholar] [CrossRef]
- Dumitriu, M. Modeling of railway vehicles for virtual homologation from dynamic behavior perspective. Appl. Mech. Mater. 2013, 371, 647–651. [Google Scholar] [CrossRef]
- Dumitriu, M.; Apostol, I.I.; Stănică, D.I. Influence of the suspension model in the simulation of the vertical vibration behavior of the railway vehicle car body. Vibration 2023, 6, 512–534. [Google Scholar] [CrossRef]
- Bruni, S.; Vinolas, J.; Berg, M.; Polach, O.; Stichel, S. Modelling of suspension components in a rail vehicle dynamics context. Veh. Syst. Dyn. 2011, 49, 1021–1072. [Google Scholar] [CrossRef]
- Graa, M.; Nejlaoui, M.; Houidi, A.; Affi, Z.; Romdhane, L. Modeling and control of rail vehicle suspensions: A comparative study based on the passenger comfort. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 260–274. [Google Scholar] [CrossRef]
- Mazilu, T.; Gheți, M.A. Theoretical assessment of vertical interaction between a wheelset and track: Influence of the track damping model. In Proceedings of the International Conference on Structural Dynamic, EURODYN 2020, Athens, Greece, 23–26 November 2020; Volume 2, pp. 2667–2679. [Google Scholar]
- Mazilu, T.; Arsene, S.; Cruceanu, I.C. Track model with nonlinear elastic characteristic of the rubber rail pad. Mater. Plast. 2021, 58, 84–98. [Google Scholar]
- Bhardawaj, S.; Sharma, R.C.; Sharma, S.K. A survey of railway track modelling. Int. J. Veh. Struct. Syst. 2019, 11, 508–518. [Google Scholar] [CrossRef]
- Zhai, W.; Zhu, S. Track design, dynamics and modelling. In Handbook of Railway Vehicle Dynamics, 2nd ed.; CRC Taylor & Francis Group: London, UK, 2019; pp. 307–344. [Google Scholar]
- Grossonia, I.; Powrie, W.; Zervos, A.; Bezina, Y.; Le Pen, L. Modelling railway ballasted track settlement in vehicle-track interaction analysis. Transp. Geotech. 2021, 26, 100433. [Google Scholar] [CrossRef]
- Jing, L.; Wang, K.; Zhai, W. Impact vibration behavior of railway vehicles: A state-of-the-art overview. Acta Mech. Sin. 2021, 37, 1193–1221. [Google Scholar]
- Xu, L.; Zhai, W.; Gao, J.; Meacci, M.; Chen, X. On effects of track random irregularities on random vibrations of vehicle–track interactions. Probab. Eng. Mech. 2017, 50, 25–35. [Google Scholar] [CrossRef]
- Cheli, F.; Corradi, R. On rail vehicle vibrations induced by track unevenness: Analysis of the excitation mechanism. J. Sound Vib. 2011, 330, 3744–3765. [Google Scholar] [CrossRef]
- Dumitriu, M. Analysis of the dynamic response in the railway vehicles to the track vertical irregularities. Part II: The numerical analysis. J. Eng. Sci. Technol. Rev. 2015, 8, 32–39. [Google Scholar] [CrossRef]
- Dumitriu, M.; Cruceanu, I.C. Effect of vertical track irregularities on the vibration of railway bogie. UPB Sci. Bull. Ser. D Mech. Eng. 2019, 81, 67–78. [Google Scholar]
- Lei, X.; Noda, N.A. Analyses of dynamic response of vehicle and track coupling system with random irregularity of track vertical profile. J. Sound Vib. 2002, 258, 147–165. [Google Scholar] [CrossRef]
- Shan, W.; Wu, P.; Wu, X.; Zhang, F.; Shi, H. Effect of wheel polygonization on the axle box vibrating and bolt self-loosening of high-speed trains. IOP Conf. Ser. J. Phys. Conf. Ser. 2019, 1213, 052044. [Google Scholar]
- Peng, B.; Iwnicki, S.; Shackletona, P.; Crosbee, D.; Zhao, Y. The influence of wheelset flexibility on polygonal wear of locomotive wheels. Wear 2019, 432–433, 102917. [Google Scholar]
- Liu, K.; Jing, L. A finite element analysis-based study on the dynamic wheel-rail contact behaviour caused by wheel polygonization. Proc. Inst. Mech. Eng. 2020, 234, 1285–1298. [Google Scholar]
- Mazilu, T.; Dumitriu, M.; Tudorache, C.; Sebesan, M. Wheel/rail interaction due to the polygonal wheel. UPB Sci. Bull. Ser. D Mech. Eng. 2011, 3, 95–108. [Google Scholar]
- Mazilu, T. A dynamic model for the impact between the wheel flat and rail. UPB Sci. Bull. Ser. D Mech. Eng. 2007, 69, 45–58. [Google Scholar]
- Mazilu, T. Geometric model of a railway wheel with irregular contour. Adv. Intell. Syst. Comput. 2016, 356, 155–166. [Google Scholar]
- Dumitriu, M.; Dihoru, I.I. Influence of bending vibration on the vertical vibration behaviour of railway vehicles carbody. Appl. Sci. 2021, 11, 8502. [Google Scholar] [CrossRef]
- Dumitriu, M. On the critical points of vertical vibration in a railway vehicle. Arch. Mech. Eng. 2014, 61, 115–140. [Google Scholar] [CrossRef]
- Spiryagin, M.; Wu, Q.; Wolfs, P.; Spiryagin, V. Design of powered rail vehicles and locomotives. In Handbook of Railway Vehicle Dynamics, 2nd ed.; CRC Taylor & Francis Group: London, UK, 2019; pp. 116–165. [Google Scholar]
- Ma, W.; Song, R. Analyses of the additional stiffness function of the traction bar on the vertical dynamics performance of subway vehicle. Electr. Rev. 2012, 88, 39–43. [Google Scholar]
- Bokaeian, V.; Rezvani, M.A.; Arcos, R. Nonlinear impact of traction rod on the dynamics of a high-speed rail vehicle carbody. J. Mech. Sci. Technol. 2020, 34, 4989–5003. [Google Scholar]
- Bokaeian, V.; Arcos, R.; Rezvani, M.A. A numerical and scaled experimental study on ride comfort enhancement of a high-speed rail vehicle through optimizing traction rod stiffness. J. Mech. Sci. Technol. 2021, 27, 2548–2563. [Google Scholar]
- Meirovitch, L. Elements of Vibration Analysis; McGraw-Hill International Edition: New York, NY, USA, 1986; pp. 235–238. [Google Scholar]
- C 116; Interaction between Vehicles and Track, RP 1, Power Spectral Density of Track Irregularities, Part 1: Definitions, Conventions and Available Data. UIC: Utrecht, The Netherlands, 1971.
- UIC 513R.; Guidelines for Evaluating Passenger Comfort in Relation to Vibration in Railway Vehicles. International Union of Railways: Paris, France, 1994.
- EN 12299; Railway Applications. Ride Comfort for Passengers. Measurement and Evaluation. British Standard: London, UK, 1999.
- Gong, D.; Gu, Y.J.; Song, Y.J.; Zhou, J. Study on geometry filtering phenomenon and flexible car body resonant vibration of articulated trains. Adv. Mater. Res. 2013, 787, 542–547. [Google Scholar]
- Gong, D.; Zhou, J.; Sun, W.J. On the resonant vibration of a flexible railway car body and its suppression with a dynamic vibration absorber. J. Vib. Control 2013, 19, 649–657. [Google Scholar]
- Zhou, J.; Wenjing, S. Analysis on geometric filtering phenomenon and flexible car body resonant vibration of railway vehicles. J. Tongji Univ. 2009, 37, 1653–1657. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).