Machine-Learning-Based Digital Twins for Transient Vehicle Cycles and Their Potential for Predicting Fuel Consumption
Abstract
1. Introduction
- Physical-based models: the system physics is described with mathematical equations. Extensive know-how and a theoretical background are usually required to obtain reliable and useful models. A trade-off between CPU consumption and model details is frequently found. These models can range from a detailed subsystem of the engine using 3D CFD to study an accurate solution that then is extrapolated to the whole engine [18,19] to a 1D/0D model offering a lower computational cost, but also lower details of the problem’s physics for reducing fuel consumption [11,16,17,20,21].
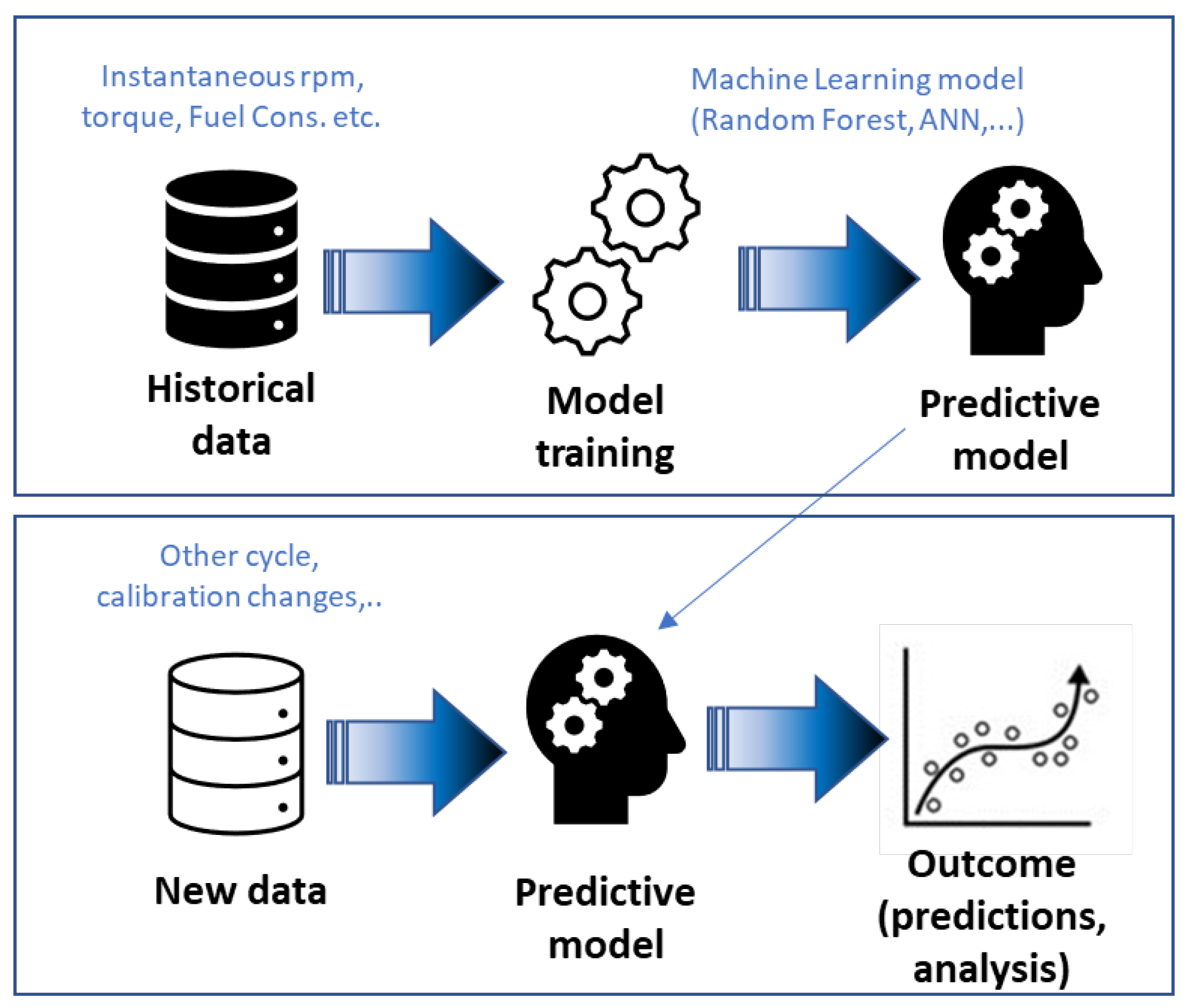
- Empirical data models: Such models are data driven, not physics based. Test data are used to create an abstract mapping of the system and to select the variables to be studied. A crescent field of investigation involves the use of Artificial Intelligence (AI). AI uses computer codes to perform cognitive functions, such as perceiving, reasoning, learning, and problem solving. It is used in, for example, robotics and autonomous vehicles, computer vision, language, virtual agents, and machine learning. AI machine learning involves the use of AI tools to analyze very large data sets. Machine-learning algorithms detect patterns and learn how to make predictions and recommendations by processing data and experiences. In this way, a machine learning model can be considered a digital twin: a nonphysical model that has been designed to accurately reflect an artificial or physical system, wherein sensors are placed to acquire a variety of data about the system performance (see Figure 1).
2. Methodology
2.1. Vehicle Characteristics
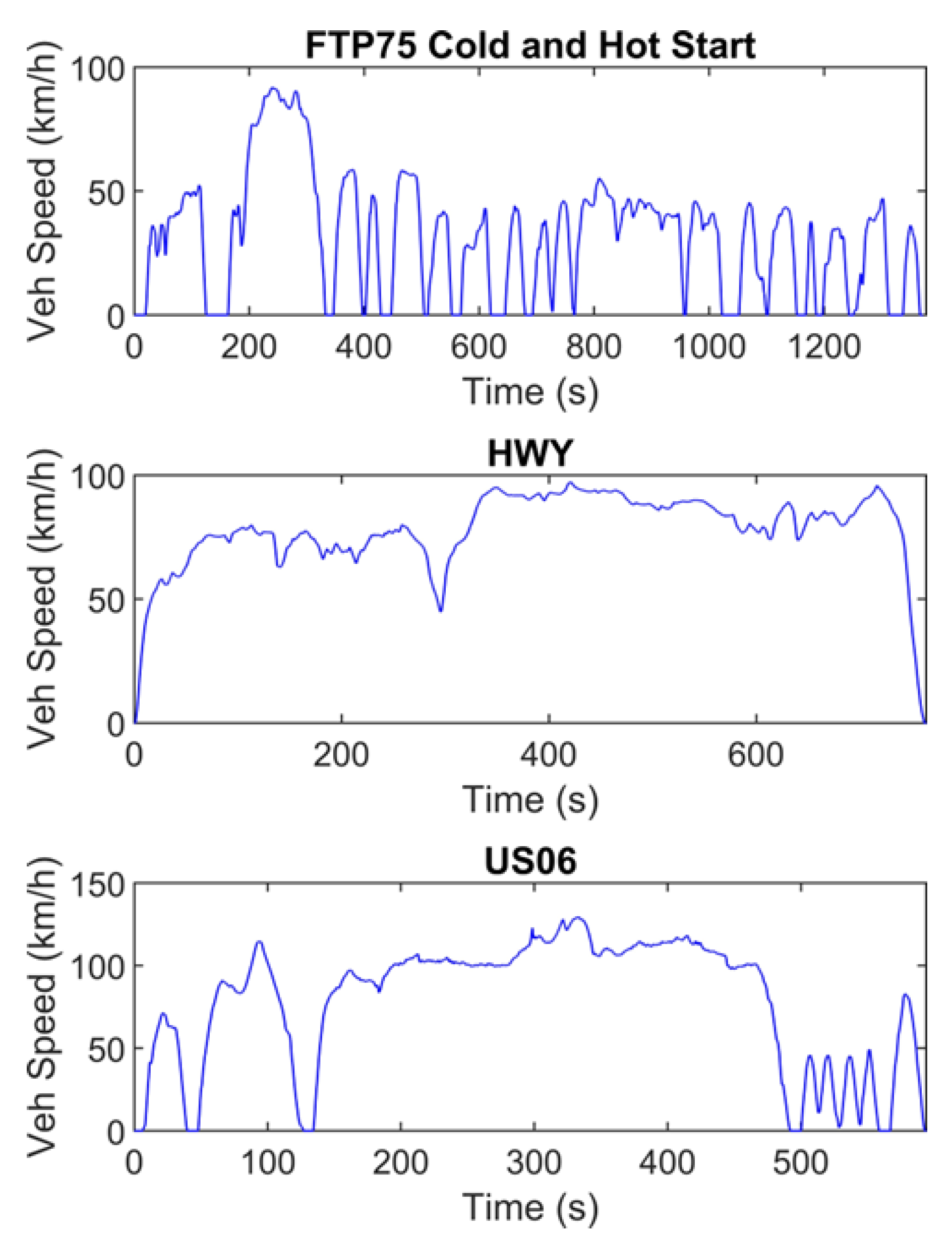
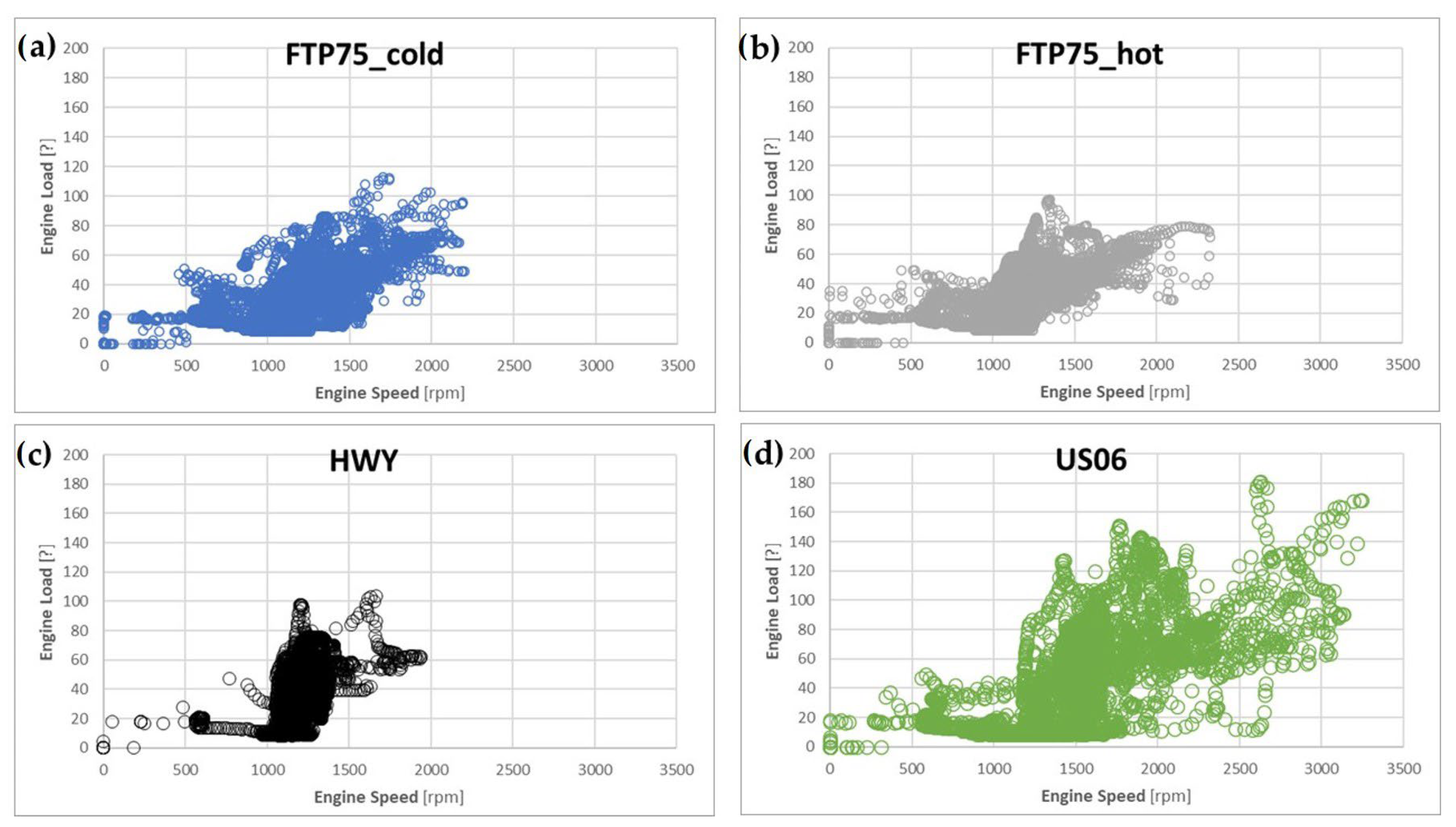
2.2. Cycle Characteristics
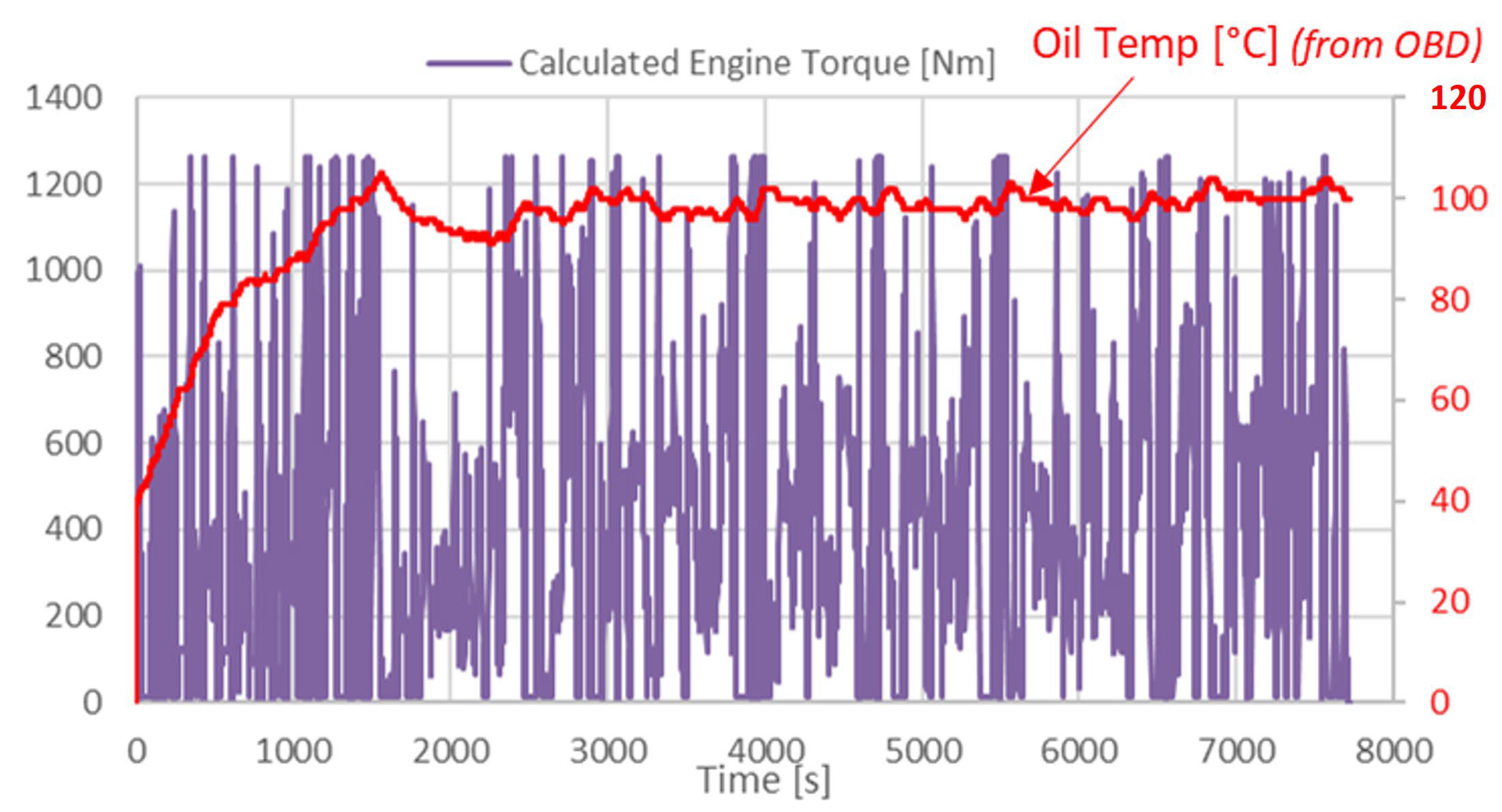
RDE Truck Test
2.3. Machine Learning Models
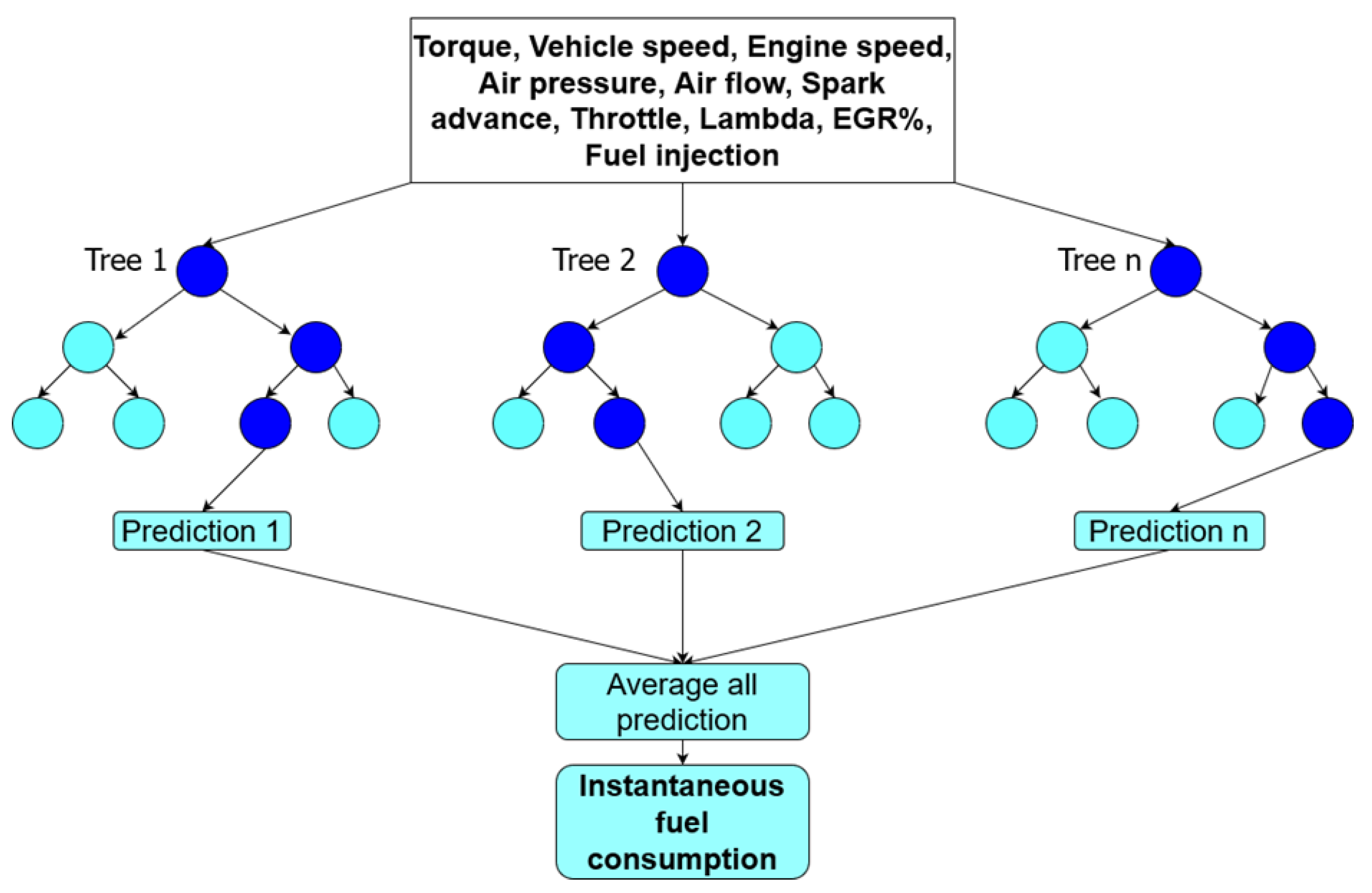
- Random Forest: The Random Forest method uses bootstrapping to create subsets of the original dataset containing a random portion of all the elements. The method involves a combination of multiple tree predictors (see Figure 8) that aggregates the results, casting the most popular outcome and thus reducing variation compared to normal decision trees. To find the threshold that best separates the data, random subsets of features are used. Many trees will be trained in a weaker way and each of them will produce a different prediction. However, these weaker predictions tend to cancel out each other, and the stronger predictions tend to dominate. For regression tasks, the mean or average prediction of the individual trees is used [34].
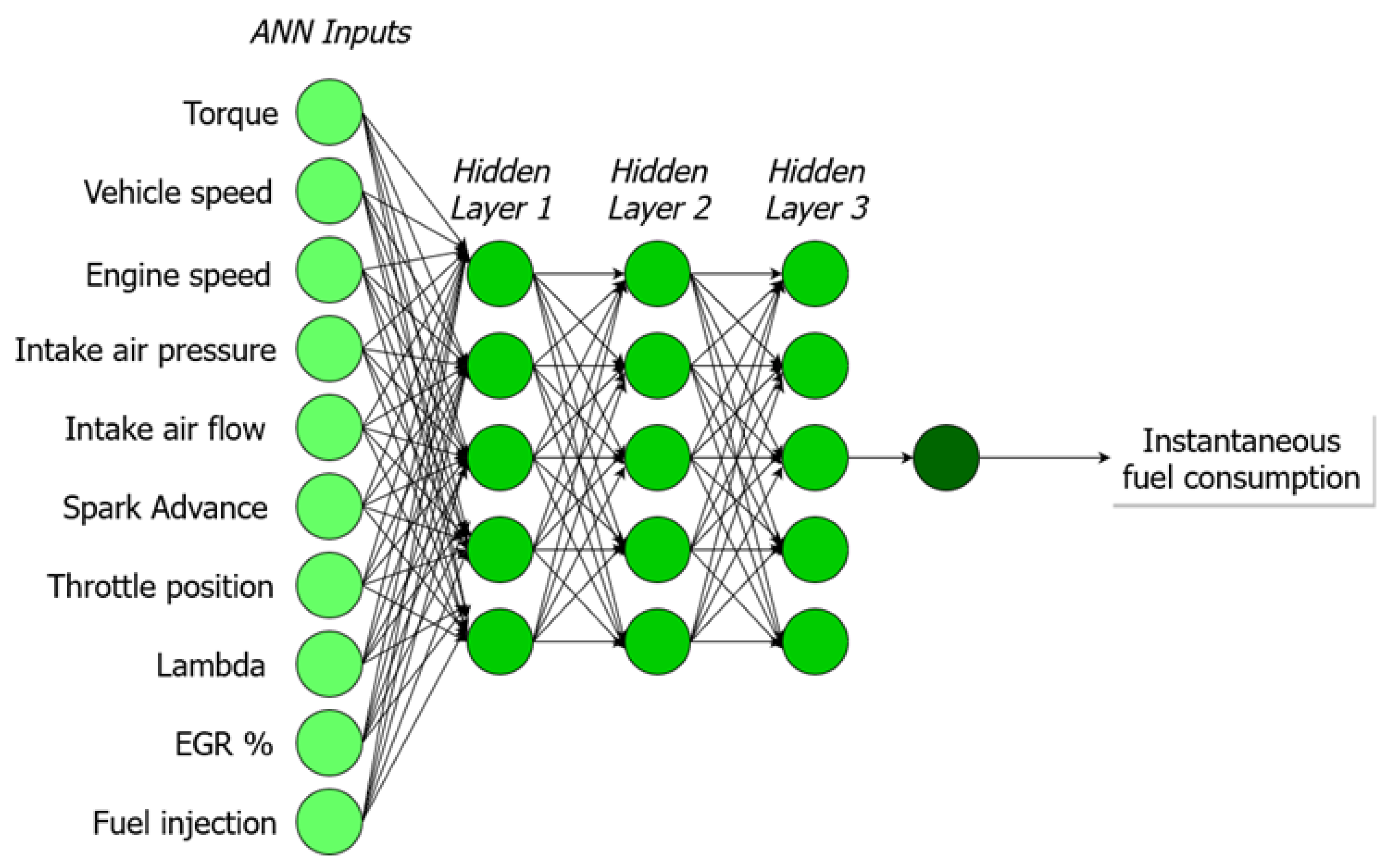
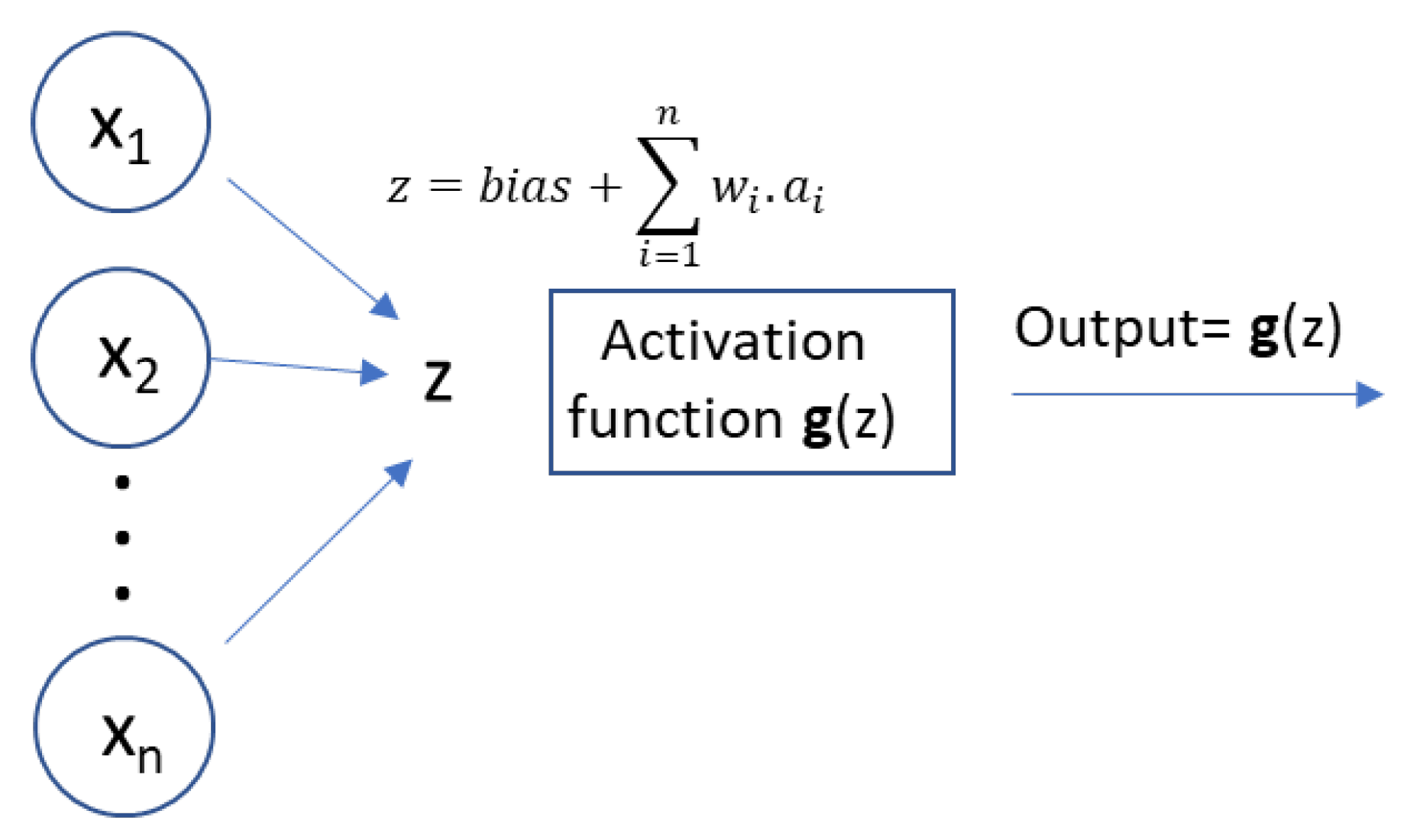
- Artificial Neural Network: An ANN is a group of interconnected artificial neurons interacting with one another in a concerted manner, loosely reproducing the interaction of neurons in a biological brain (see Figure 9). Each artificial neuron has several inputs and produces a single output which can be sent to multiple other neurons, meaning it exhibits a high degree of connectivity, which is also called multilayer perceptrons. In this work, multilayer perceptrons with 3 hidden layers and up to 20 neurons per layer were trained to predict the instantaneous fuel consumption of a given vehicle during the vehicle test cycle. Hidden layer selection has been used by other authors to predict fuel consumption in light-duty vehicles [35,36,37,38,39,40]. In the present study, the backpropagation (BP) method was used to train the neural network. This is common practice of fine-tuning the weights of a neural net based on the error rate obtained in previous epoch (iteration). Proper tuning of the weights ensures lower error rates, making the model reliable by increasing its generalization.
- R2: R-squared value is used to measure the goodness of fit or best-fit line. The higher R2, the better the regression model, as most of the variation in actual values from the mean value is explained by the regression model.
- Mean Squared Error (MSE): Measures the average squared error of the model predictions. For each data point, the squared difference between the predictions and the target is calculated and used for the averages. The lower the MSE, the better the model. MSE is calculated as:
3. Results
3.1. Truck RDE
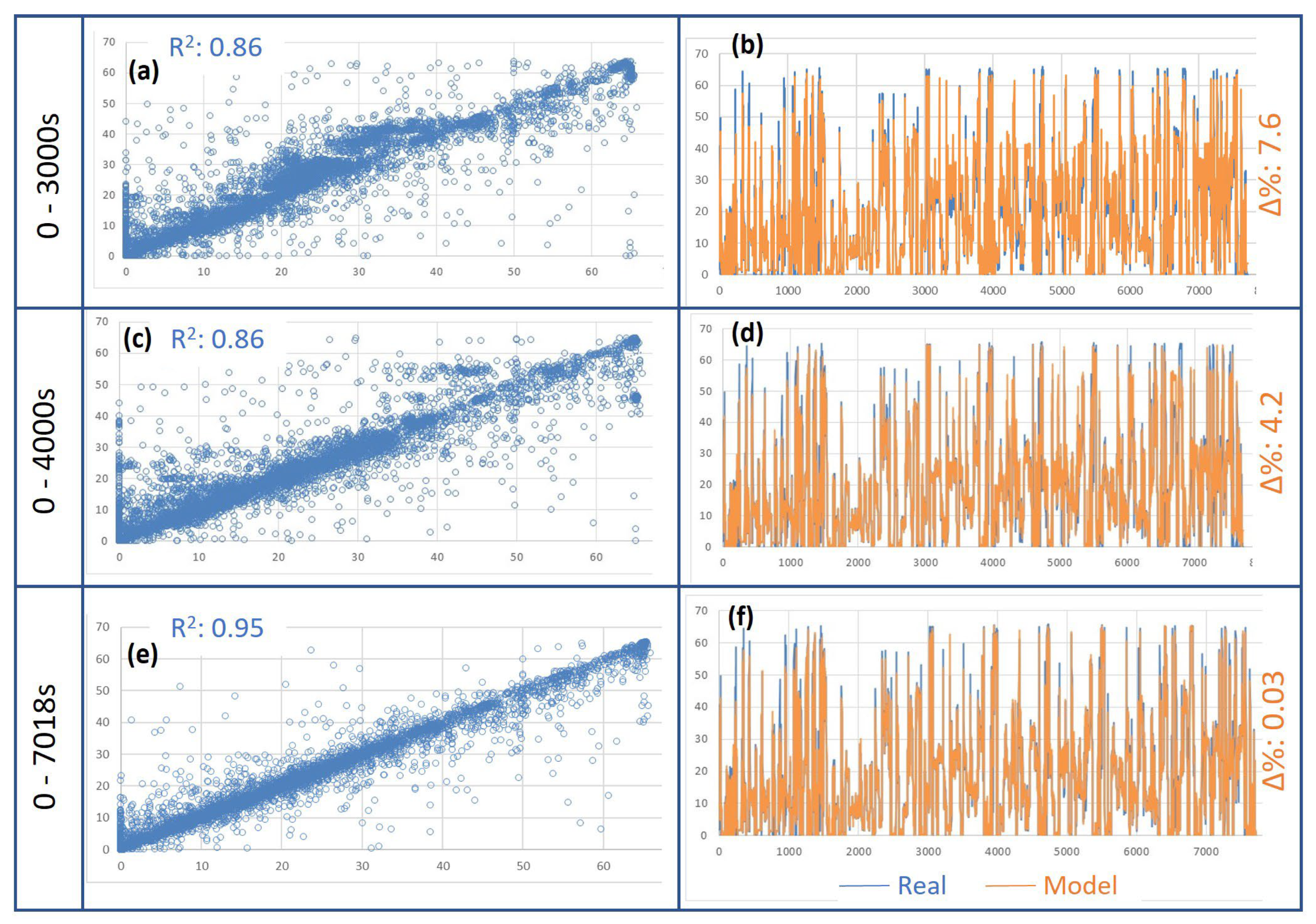
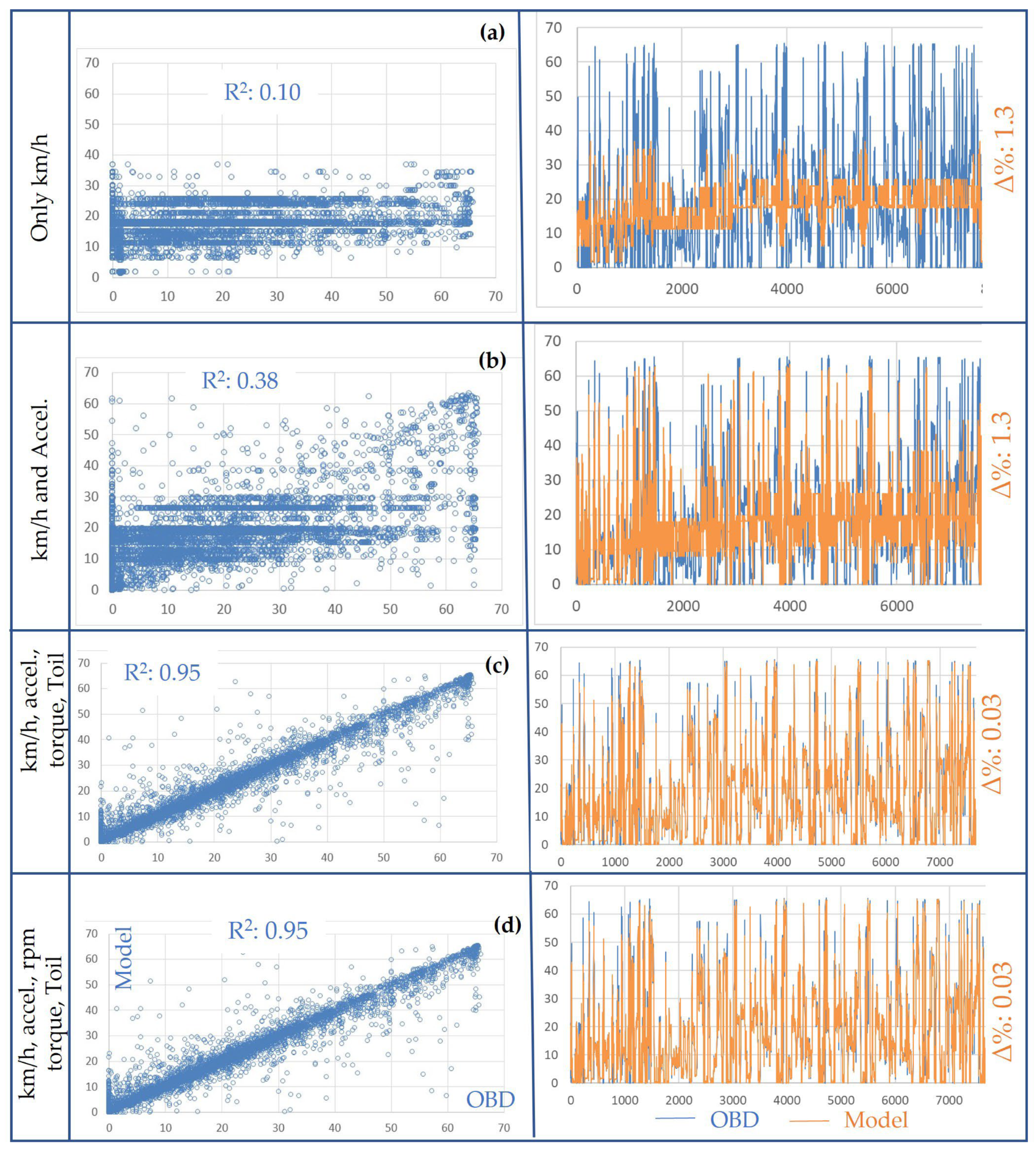
- For only the truck speed, the model’s performance was, of course, very poor. The R2 was 0.06 but the accumulated cycle error for the fuel consumption, ∆%, was only +1.3%. One should be careful when analyzing the model’s performance. The total error was (almost by chance) very low, but the model very poorly represented the actual truck, as indicated by Figure 14a.
- When including the truck acceleration, calculated from the OBD truck speed, the model’s performance increased significantly. The R2 remained low, but the spiky fuel rate was reproduced relatively well by the model. See Figure 14b.
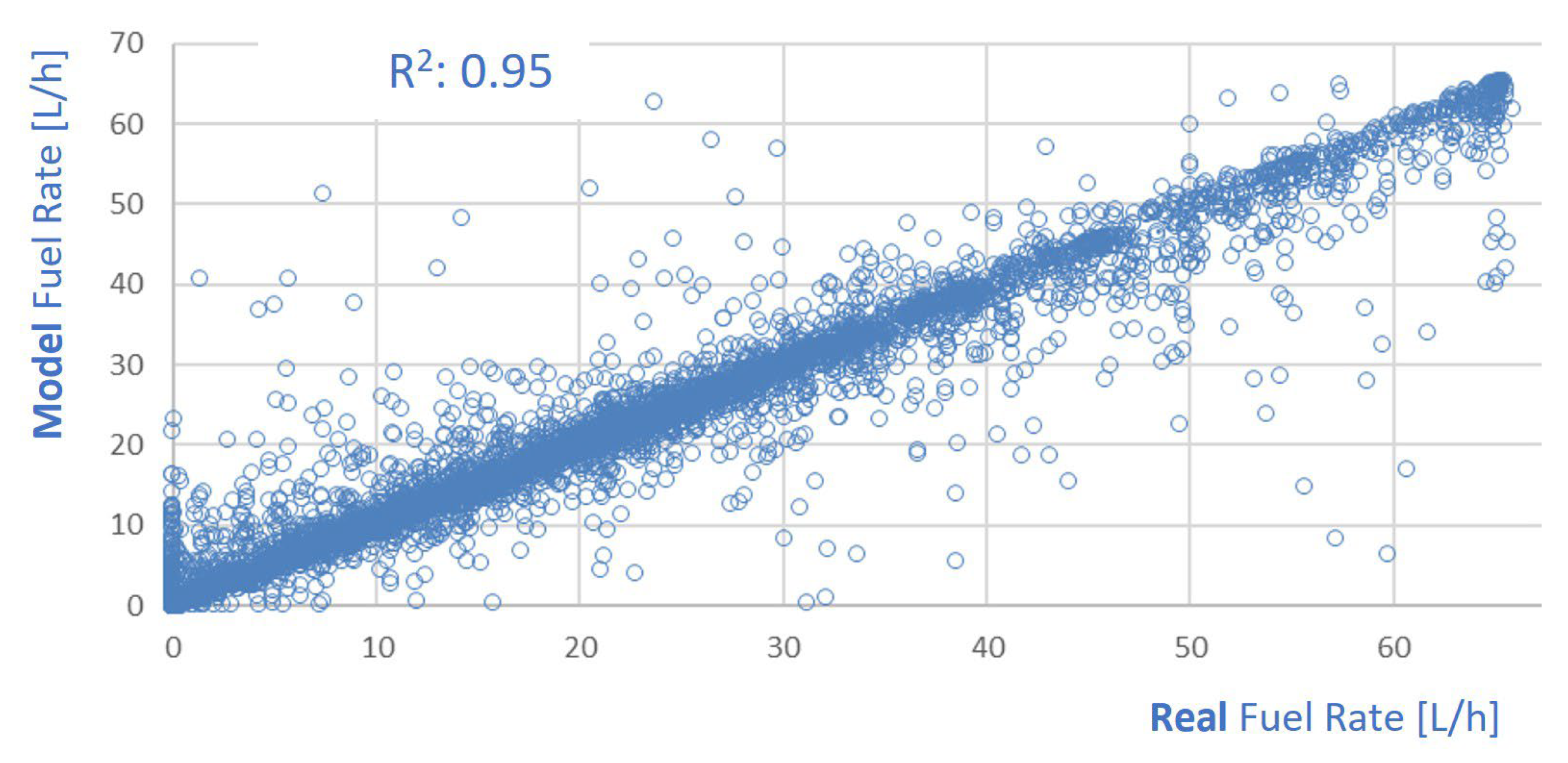
- When including the engine torque and oil temperature, the model’s performance was very good. The R2 increased to 0.95 and the ∆% was only 0.03. See Figure 14c.
- Due to the low variation in the engine rpm during the test, including the rpm led to almost no difference in the model’s performance. See Figure 14d.
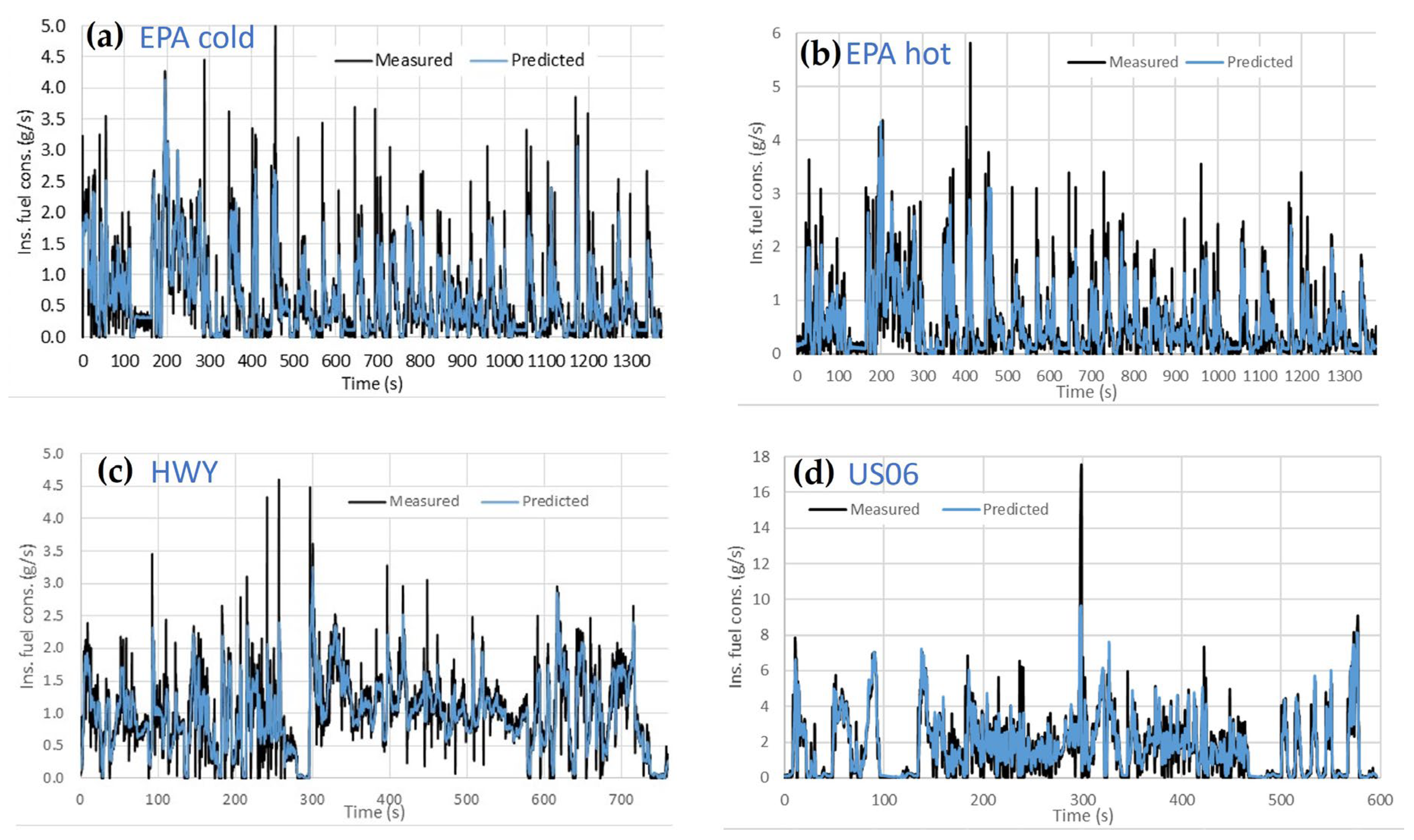
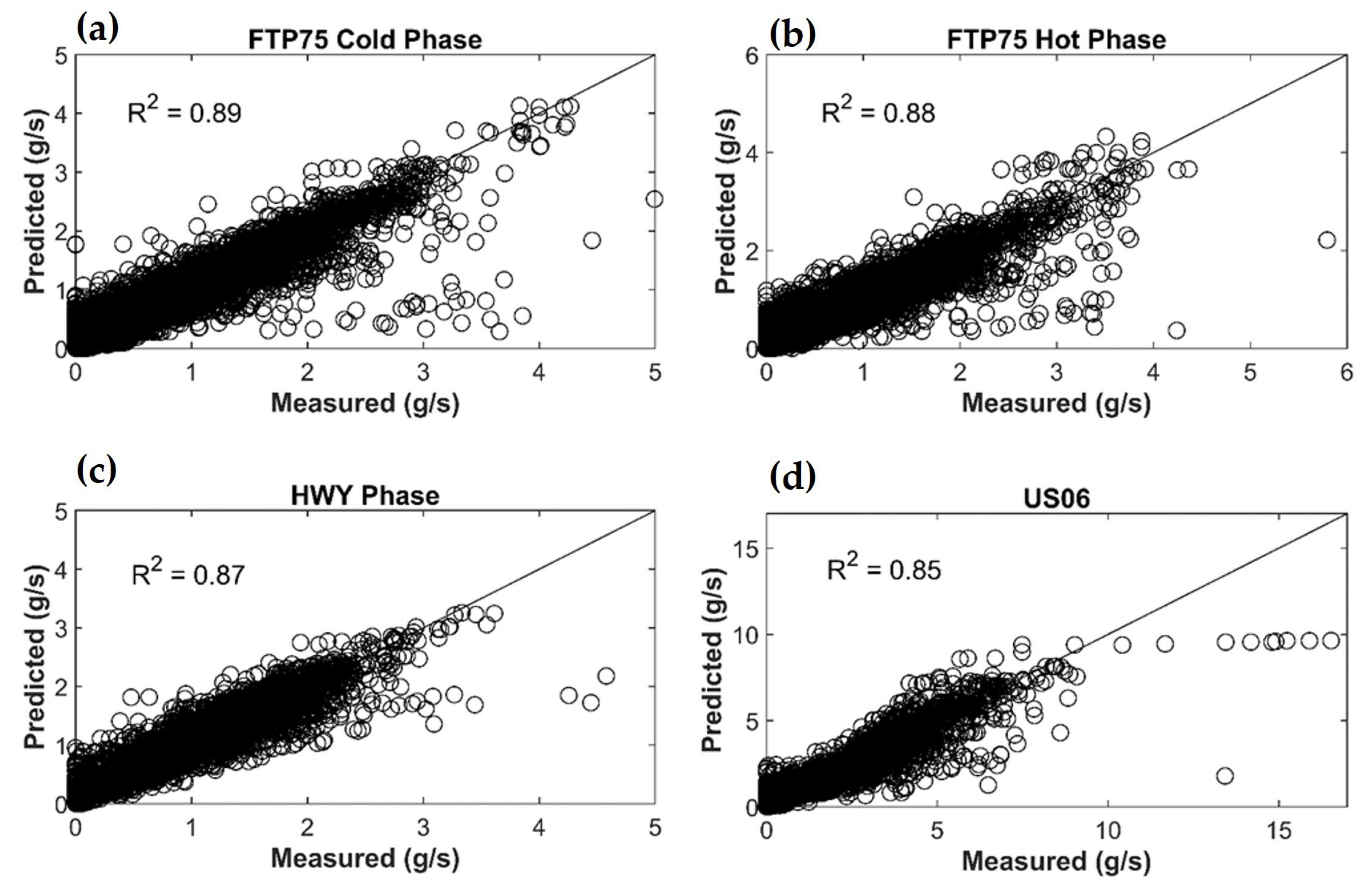
3.2. SUV
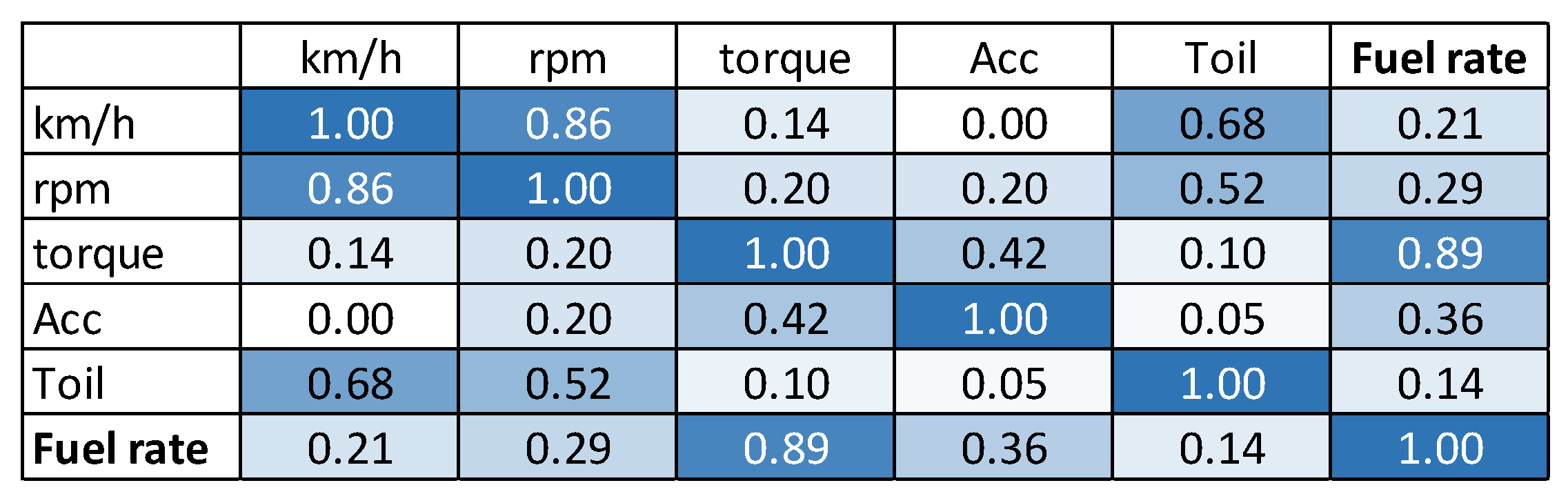
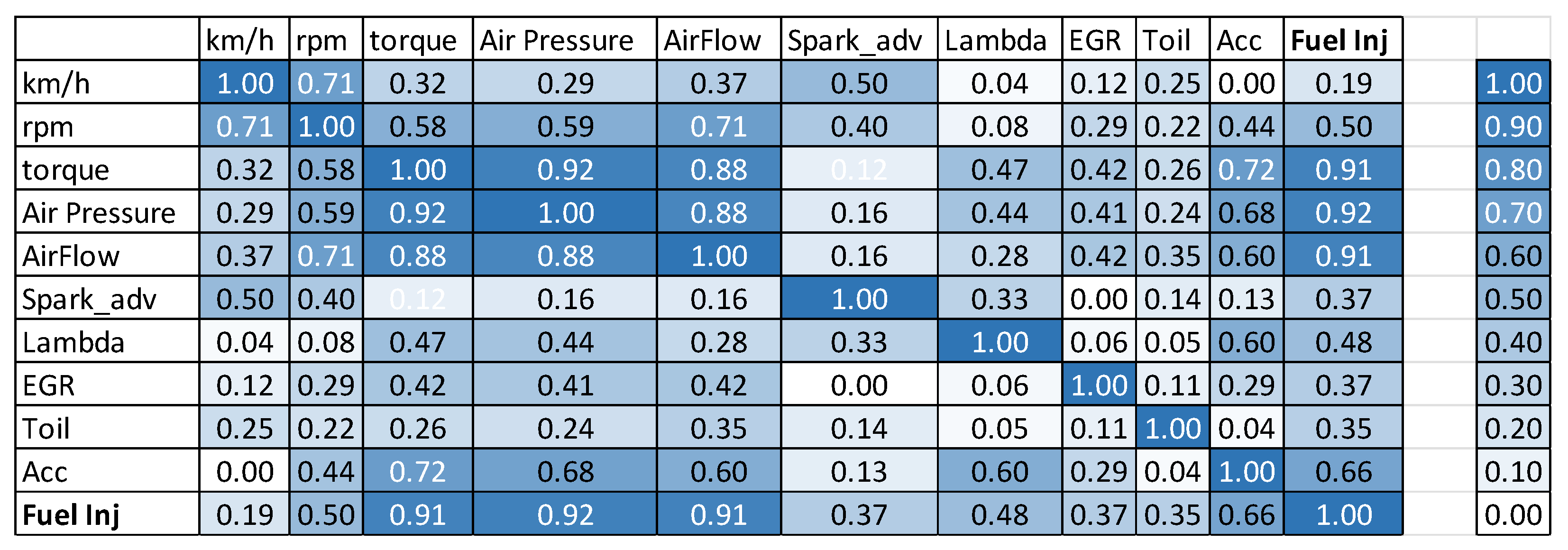
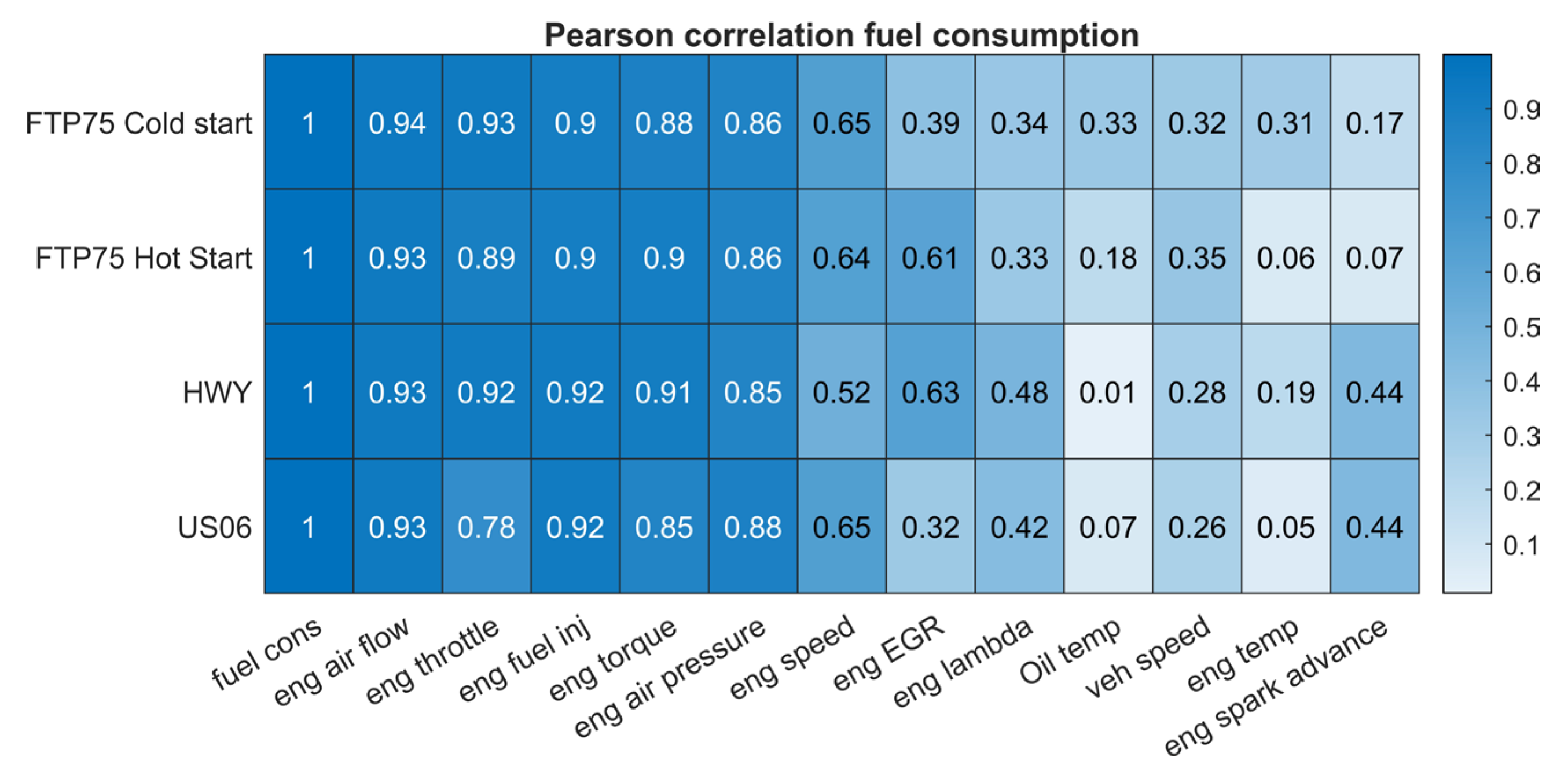
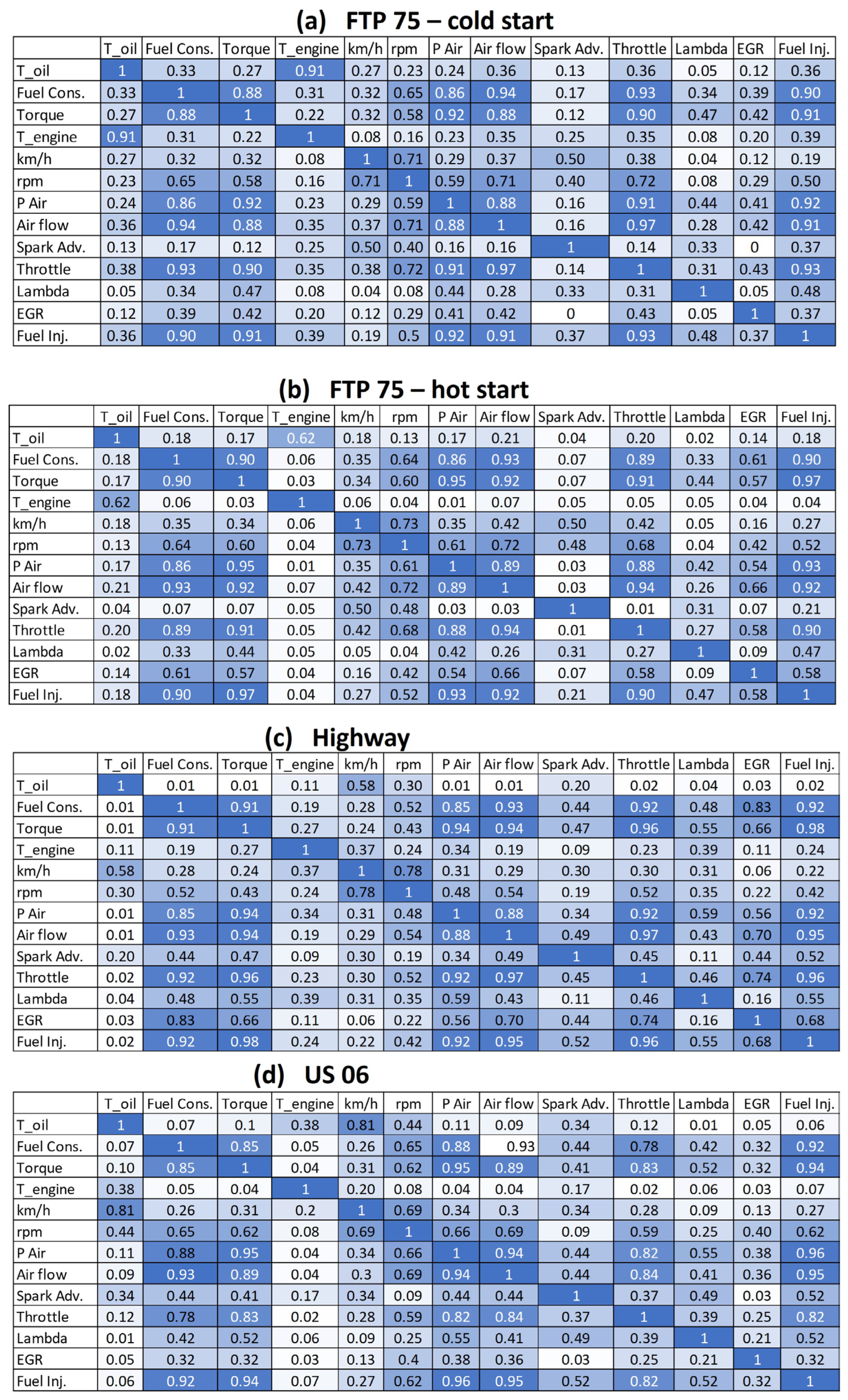
- From the external vehicle instrumentation: The fuel consumption with the mass flow meter (target variable), engine coolant temperature and engine oil temperature.
- From the Engine Control Unit (ECU): the engine torque, vehicle speed, engine speed, intake air pressure, air flow, spark advance, throttle, EGR percentage and lambda.
- −
- The air flow, air pressure and engine torque were obviously the major influences on the instantaneous fuel consumption.
- −
- Some correlated parameters, such as the engine air pressure and air flow, were probably able to be omitted, with only engine torque needing to be used instead.
- −
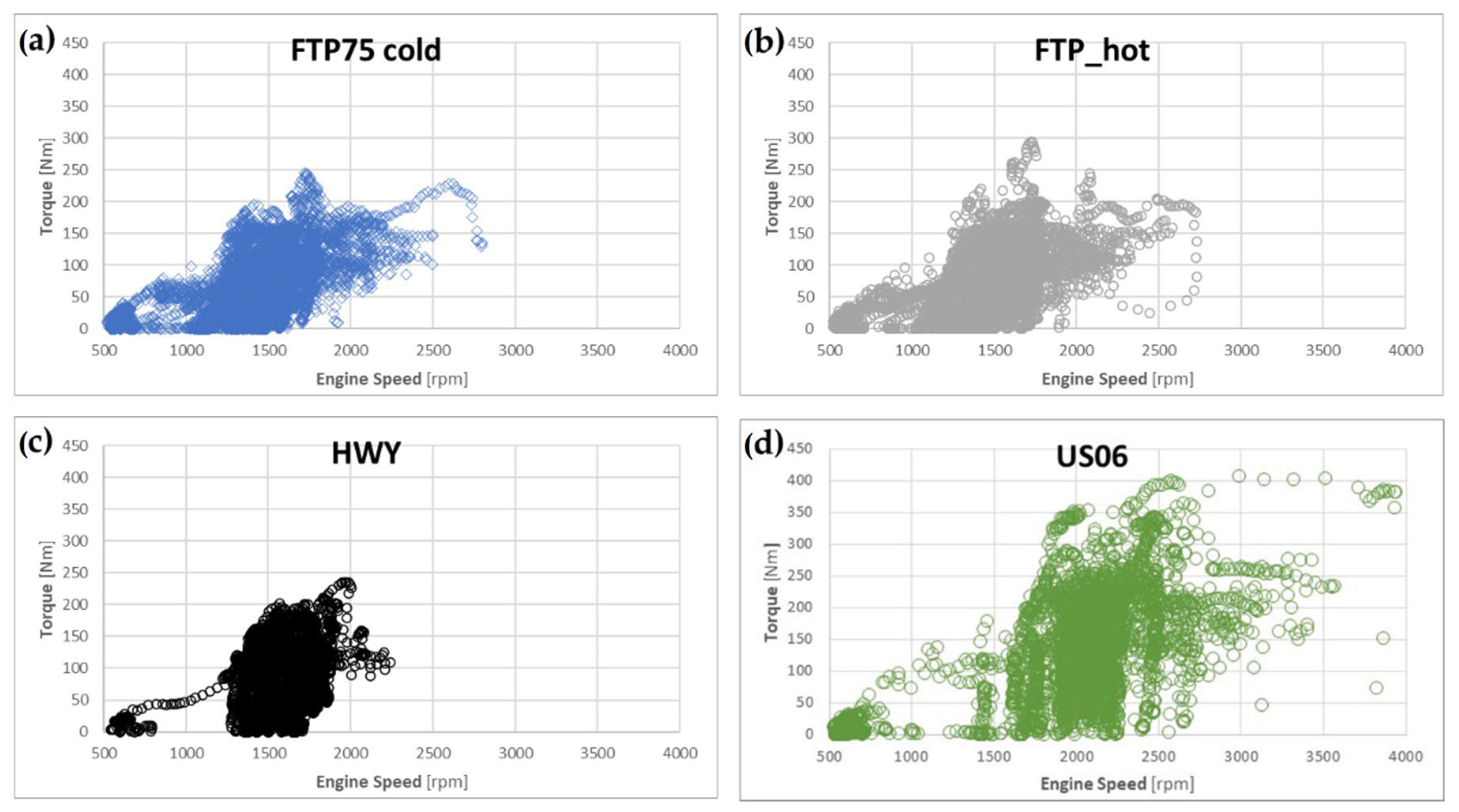
- While the oil temperature had a relatively high influence in the FTP75 cold and hot start cycles, its influence was negligible in the highway and US06 cycles, in which the engine was already hot and the engine loading was much more severe.
- −
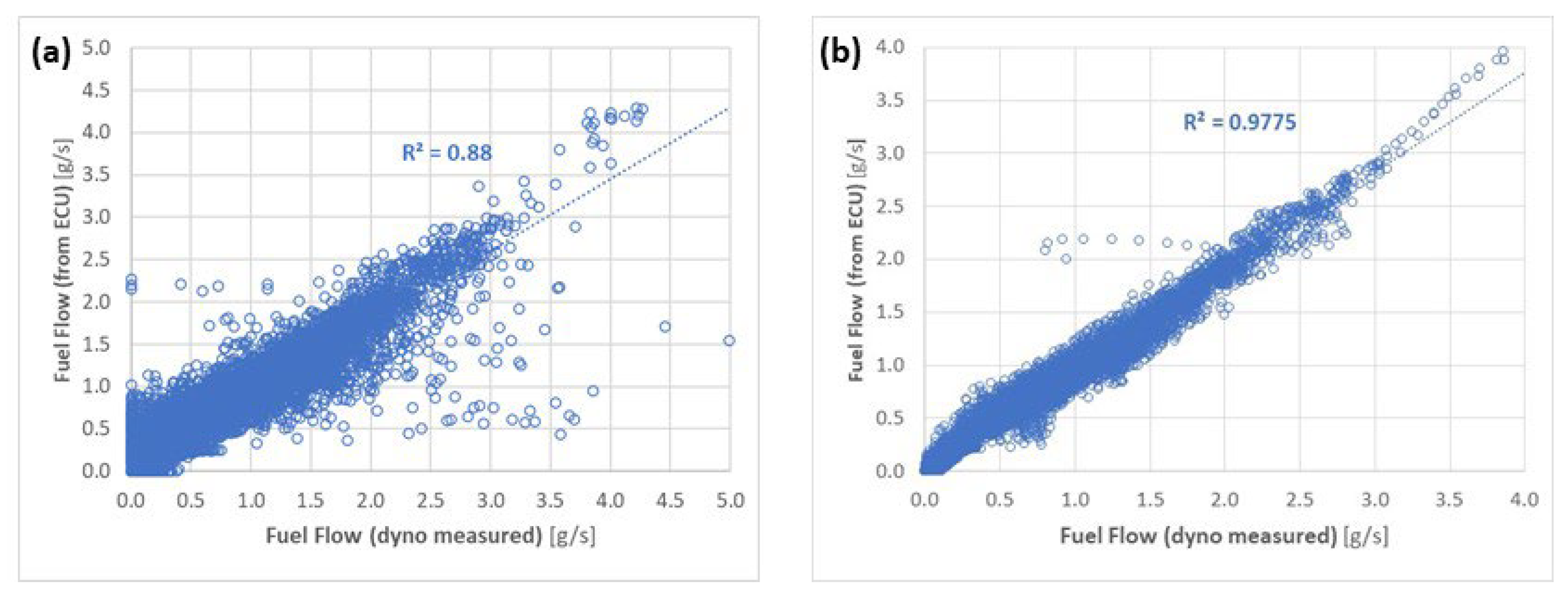
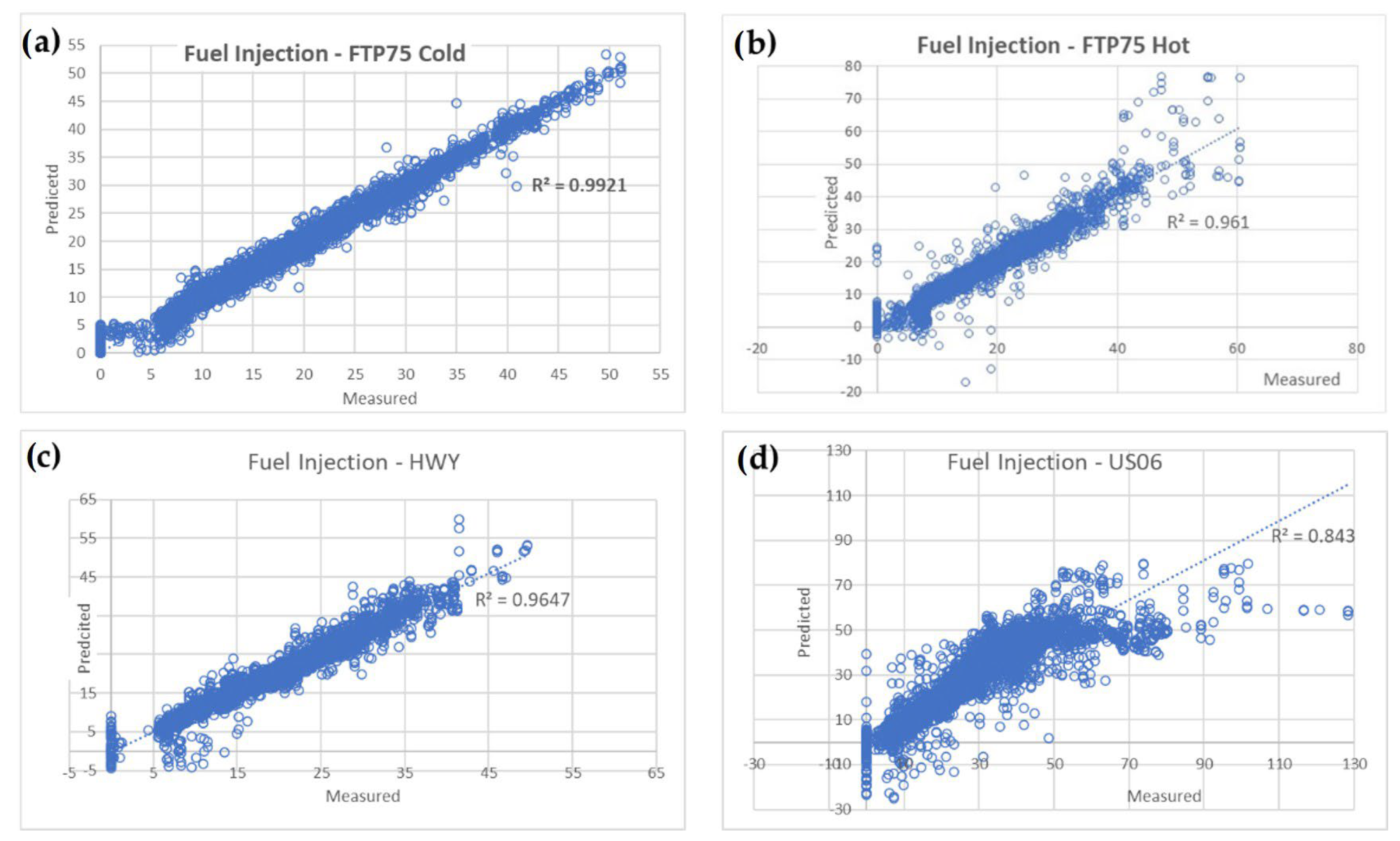
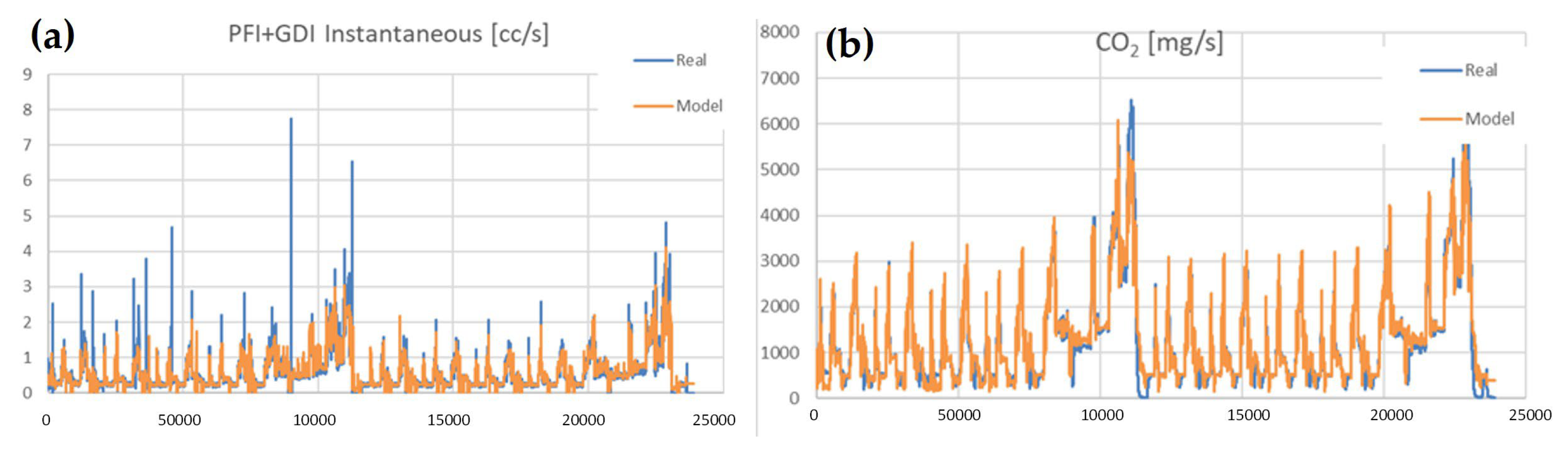
- The fuel injection, read from the ECU, obviously correlated well with the measured fuel consumption. As mentioned earlier, this creates the opportunity to use only the vehicle ECU data (or the truck/bus OBD data) instead of much more expensive dynamometer or specific measurement equipment. This will be explored further in Section 3.4.
3.3. Light Truck
3.4. Using Only ECU Data for the Light Truck Test
4. Discussion
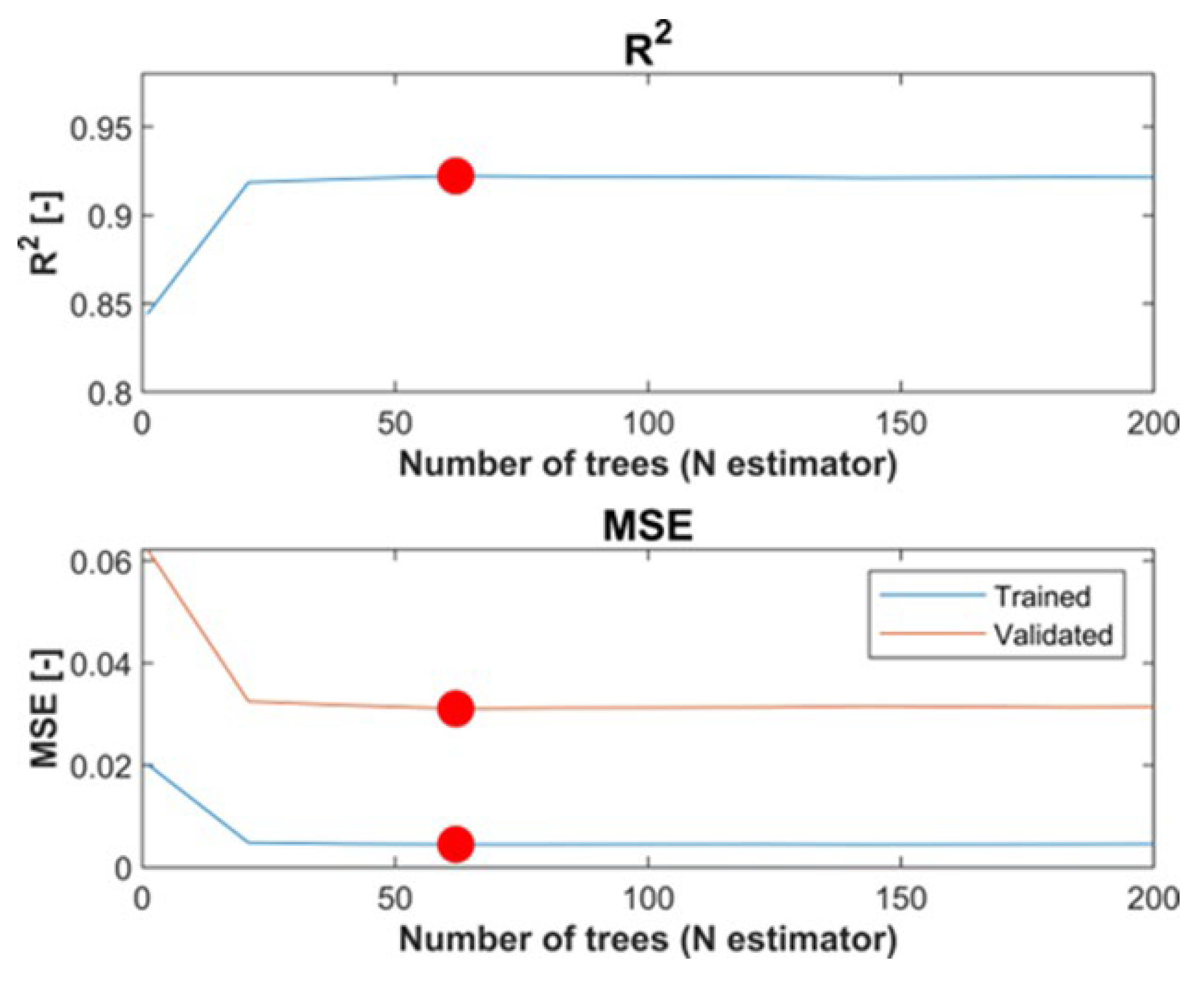
4.1. Optimizing Number of Trees in Random Forest
4.2. Optimizing Number of Neurons in the ANN Model
4.3. Future Work
5. Conclusions
- Modern vehicles have a myriad of sensors that are read in real time by the ECU/OBD. With the use of a datalogger, such data can be easily read and used by AI models, allowing for much cheaper tests and simulations.
- In this work, two machine learning models were trained and used to predict the fuel consumption of three vehicles during different transient cycles.
- The machine learning models were able to predict the instantaneous fuel consumption during transient emission cycles without needing to be programmed specifically for this problem.
- The variables chosen as input for training the models were key to achieving better model performance.
- The Artificial Neural Network model showed a better fit in predicting the fuel consumption for the four emission tests, being in all cases under the 2% error. However, compared with the simpler Random Forest model, the improvement in its model fitness came at a considerable expense regarding the CPU time. This amounted to a few minutes versus several hours for the Random Forest and ANN models, respectively.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tseregounis, S.; McMillan, M.; Olree, R. Engine Oil Effects on Fuel Economy in GM Vehicles—Separation of Viscosity and Friction Modifier Effects; SAE Technical Paper 982502; SAE: Warrendale, PA, USA, 1998. [Google Scholar]
- Bartz, W. Fuel Economy Improvement by Engine and Gear Oils. In Tribology for Energy Conservation; Elsevier: Amsterdam, The Netherlands, 1998; pp. 13–24. [Google Scholar]
- Hoshino, K.; Kawai, H.; Akiyama, K. Fuel Efficiency of SAE 5W-20 Friction Modified Engine Oil; SAE Technical Paper 982506; SAE: Warrendale, PA, USA, 1998. [Google Scholar]
- Taylor, R.I.; Coy, R.C. Improved fuel efficiency by lubricant design: A review. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2000, 214, 1–15. [Google Scholar] [CrossRef]
- Carvalho, M.; Seidl, P.; Belchior, C.; Sodre, J. Lubricant viscosity and viscosity improver additive effects on diesel fuel economy. Tribol. Int. 2010, 43, 12. [Google Scholar]
- Macián, V.; Tormos, B.; Ruíz, S.; Ramírez, L. Potential of low viscosity oils to reduce CO2 emissions and fuel consumption of urban buses fleets. Transp. Res. Part D Transp. Environ. 2015, 39, 76–88. [Google Scholar] [CrossRef]
- Dam, W.; Both, J.; Parsons, G. Taking Heavy Duty Diesel Engine Oil Performance to the Next Level, Part 1: Optimizing for Improved Fuel Economy; SAE Technical Paper 2014-01-2792; SAE: Warrendale, PA, USA, 2014. [Google Scholar]
- Carvalho, M.; Richard, K.; Goldmints, I.; Tomanik, E. Impact of Lubricant Viscosity and Additives on Engine Fuel Economy; SAE Technical Paper 2014-36-0507; SAE: Warrendale, PA, USA, 2014. [Google Scholar]
- Tormos, B.; Ramírez, L.; Johansson, J.; Björling, M.; Larsson, R. Fuel consumption and friction benefits of low viscosity engine oils for heavy duty applications. Tribol. Int. 2017, 110, 23–34. [Google Scholar] [CrossRef]
- Devlin, M.T. Common Properties of Lubricants that Affect Vehicle Fuel Efficiency: A North American Historical Perspective. Lubricants 2018, 6, 68. [Google Scholar] [CrossRef]
- Taylor, R.I.; Morgan, N.; Mainwaring, R.; Davenport, T. How Much Mixed/Boundary Friction is there in an Engine-and where is it? Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 234, 1563–1579. [Google Scholar] [CrossRef]
- Yamamoto, K.; Hiramatsu, T.; Hanamura, R.; Moriizumi, Y.; Heiden, S. The Study of Friction Modifiers to Improve Fuel Economy for WLTP with Low and Ultra-Low Viscosity Engine Oil; SAE Technical Papers 2019-01-2205; SAE: Warrendale, PA, USA, 2019. [Google Scholar]
- Tormos, B.; Pla, B.; Bastidas, S.; Ramírez, L.; Pérez, T. Fuel economy optimization from the interaction between engine oil and driving conditions. Tribol. Int. 2019, 138, 263–270. [Google Scholar] [CrossRef]
- Yoshida, S.; Yamamori, K.; Hirano, S.; Sagawa, T.; Okuda, S.; Miyoshi, T.; Yukimura, S. The Development of JASO GLV-1 Next Generation Low Viscosity Automotive Gasoline Engine Oils Specification; SAE Technical Paper 2020-01-1426; SAE: Warrendale, PA, USA, 2020. [Google Scholar]
- Tormos, B.; Jiménez, A.J.; Fang, T.; Mainwaring, R.; L-Garcia, E. Numerical Assessment of Tribological Performance of Different Low Viscosity Engine Oils in a 4-Stroke CI Light-Duty ICE; SAE Technical Papers (2022-01-0321); SAE: Warrendale, PA, USA, 2022. [Google Scholar]
- Tomanik, E.; Profito, F.J.; Tormos, B.; Jiménez, A.J.; Zhmud, B. Powertrain Friction Reduction by Synergistic Optimization of the Cylinder Bore Surface and Lubricant Part 1: Basic Modelling; SAE Technical Paper No. 2021-01-1214; SAE: Warrendale, PA, USA, 2021. [Google Scholar]
- Zhmud, B.; Tomanik, E.; Jiménez, A.J.; Profito, F.; Tormos, B. Powertrain Friction Reduction by Synergistic Optimization of Cylinder Bore Surface and Lubricant-Part 2: Engine Tribology Simulations and Tests; SAE Technical Paper No. 2021-01-1217; SAE: Warrendale, PA, USA, 2021. [Google Scholar]
- Zeman, J.; Papadimitriou, L.; Watanabe, K.; Kubo, M.; Kumagai, T. Model Ing and Optimization of Plug-In Hybrid Electric Vehicle Fuel Economy; SAE Technical Papers (2012-01-1018); SAE: Warrendale, PA, USA, 2012. [Google Scholar] [CrossRef]
- Lujan, J.; Climent, H.; Novella, R.; Rivas-Perea, M. Influence of a low pressure EGR loop on a gasoline turbocharged direct injection engine. Appl. Therm. Eng. 2015, 89, 432–443. [Google Scholar] [CrossRef]
- Li, Y.; Chen, H.; Tian, T. A Deterministic Model for Lubricant Transport within Complex Geometry under Sliding Contact and Its Application in the Interaction between the Oil Control Ring and Rough Liner in Internal Combustion Engines; SAE Technical Papers No. 2008-01-1615; SAE: Warrendale, PA, USA, 2008. [Google Scholar] [CrossRef]
- Tormos, B.; Martin, J.; Blanco-Cavero, D.; Jimenez-Reyes, A. One-Dimensional Modeling of Mechanical and Friction Losses Distribution in a Four-Stroke Internal Combustion Engine. J. Tribol. 2020, 142, 11703. [Google Scholar] [CrossRef]
- Tomanik, E.; Tomanik, V.V.; Morais, P. Use of Tribological and AI Models on Vehicle Emission Tests to Predict Fuel Savings through Lower Oil Viscosity; SAE Technical Paper (2021-36-0038); SAE: Warrendale, PA, USA, 2021. [Google Scholar]
- Sarker, I.H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar] [CrossRef]
- Hien, N.L.H.; Kor, A.L. Analysis and prediction model of fuel consumption and carbon dioxide emissions of light-duty vehicles. Appl. Sci. 2022, 12, 803. [Google Scholar] [CrossRef]
- Katreddi, S.; Thiruvengadam, A. Trip based modeling of fuel consumption in modern heavy-duty vehicles using artificial intelligence. Energies 2021, 14, 85–92. [Google Scholar] [CrossRef]
- Gong, J.; Shang, J.; Li, L.; Zhang, C.; He, J.; Ma, J. A Comparative Study on Fuel Consumption Prediction Methods of Heavy-Duty Diesel Trucks Considering 21 Influencing Factors. Energies 2021, 14, 8106. [Google Scholar] [CrossRef]
- He, Y.; Rutland, C.J. Application of artificial neural networks in engine modelling. Int. J. Engine Res. 2005, 5, 281–296. [Google Scholar] [CrossRef]
- Cruz-Peragon, F.F.; Espadafor, J.; Palomar, J.; Dorado, M. Combustion faults diagnosis in internal combustion engines using angular speed measurements and artificial neural networks. Energy Fuels 2008, 22, 2972–2980. [Google Scholar] [CrossRef]
- Ziółkowski, J.; Oszczypała, M.; Małachowski, J.; Szkutnik-Rogoż, J. Use of Artificial Neural Networks to Predict Fuel Consumption on the Basis of Technical Parameters of Vehicles. Energies 2021, 14, 2639. [Google Scholar] [CrossRef]
- Perrotta, F.; Parry, T.; Neves, L. Application of machine learning for fuel consumption modelling of trucks. In Proceedings of the 2017 IEEE International Conference on Big Data, Boston, MA, USA, 11–14 December 2017; pp. 3810–3815. [Google Scholar]
- Du, Y.; Wu, J.; Yang, S.; Zhou, L. Predicting vehicle fuel consumption patterns using floating vehicle data. J. Environ. Sci. China 2017, 59, 24–29. [Google Scholar] [CrossRef]
- Parlak, A.; Islamoglu, Y.; Yasar, H.; Egrisogut, A. Application of artificial neural network to predict specific fuel consumption and exhaust temperature for a diesel engine. Appl. Therm. Eng. 2006, 26, 824–828. [Google Scholar] [CrossRef]
- Downloadable Dynamometer Database—Argonne National Laboratory. Available online: https://www.anl.gov/es/downloadable-dynamometer-database (accessed on 22 March 2023).
- Overview of the ANL Chassis Dynamometer Test Facilities and Methodology. Available online: https://anl.app.box.com/s/5tlld40tjhhhtoj2tg0n4y3fkwdbs4m3 (accessed on 22 March 2023).
- Ho, T. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; pp. 278–282. [Google Scholar]
- Hosamani, B.R.; Ali, S.A.; Katti, V. Assessment of performance and exhaust emission quality of different compression ratio engine using two biodiesel mixture: Artificial neural network approach. Alex. Eng. J. 2021, 60, 837–844. [Google Scholar] [CrossRef]
- Roy, S.; Banerjee, R.; Bose, P. Performance, and exhaust emissions prediction of a CRDI assisted single cylinder diesel engine coupled with EGR using artificial neural network. Appl. Energy 2014, 119, 330–340. [Google Scholar] [CrossRef]
- Bhowmik, S.; Paul, A.; Panua, R.; Ghosh, S.; Debroy, D. Performance-exhaust emission prediction of diesosenol fueled diesel engine: An ANN coupled MORSM based optimization. Energy 2018, 153, 212–222. [Google Scholar] [CrossRef]
- Babu, D.V.; Thangarasu, A. Ramanathan, Artificial neural network approach on forecasting diesel engine characteristics fueled with waste frying oil biodiesel. Appl. Energy 2020, 263, 114612. [Google Scholar] [CrossRef]
- Togun, N.; Baysec, S. Prediction of torque and specific fuel consumption of a gasoline engine by using artificial neural networks. Appl. Energy 2010, 87, 349–355. [Google Scholar] [CrossRef]


| N3 Class Truck 18-Ton Euro 6 | SUV * 2016 Mazda CX-9 | Light Truck * 2017 Ford F-150 |
|---|---|---|
| 7.0-L, I6 | 2.5 L I4 | 3.5 L, V6 |
| CI, TDI | SI TDI | SI, PFI and DI |
| 210 kW | 186 kW | 280 kW |
| 1150 Nm | 420 Nm | 637 Nm |
| 9-speed manual | 6-speed automatic | 10-speed automatic |
| FTP75 | Highway | US06 | |
|---|---|---|---|
| Stop and Go Urban Traffic | Free-Flow Traffic at Highway Speeds | Higher Speed, Harder Acceleration & Braking | |
| Engine startup | Cold and warm | Warm | Warm |
| Top speed (km/h) | 90 | 97 | 129 |
| Average Speed (km/h) | 34 | 77.7 | 77.9 |
| Max. accel. (m/s2) | 1.47 | 1.43 | 3.78 |
| Distance | 17.7 | 16.6 | 8 |
| Time (min) | 23 | 12.73 | 12.9 |
| Stops | 23 | None | 4 |
| Idling time (%) | 18 | None | 7 |
| Training | Overall Cycle | |||
|---|---|---|---|---|
| R2 | MSE | R2 | MSE | |
| Random Forest | 0.92 | 0.004 | 0.97 | 0.011 |
| ANN | 0.95 | 0.041 | 0.95 | 0.042 |
| Measured [g] | Model Error [%] | ||
|---|---|---|---|
| Random Forest | ANN | ||
| Cold Start | 832.9 | 0.1 | 0.1 |
| Hot Start | 745.3 | 1.4 | 0.7 |
| HWY | 750.4 | 2.4 | −0.2 |
| US06 | 995.7 | −7.9 | −0.2 |
| Measured [g] | Model Error [%] | ||
|---|---|---|---|
| Random Forest | ANN | ||
| Cold Start | 1019.5 | 0.25 | −0.08 |
| Hot Start | 924.8 | 6.50 | −1.21 |
| HWY | 881.0 | −0.20 | −1.78 |
| US06 | 1194.4 | −10.4 | −1.56 |
| SUV | Light Truck | |
|---|---|---|
| Number of Trees | 62 | 41 |
| R2 | 0.92 | 0.88 |
| MSE training | 0.004 | 0.003 |
| MSE validation | 0.031 | 0.075 |
| Hidden Neurons | Accumulated Pred. vs. Measured [%] | Avg Absolute Error [%] | |||||
|---|---|---|---|---|---|---|---|
| Layer 1 | Layer 2 | Layer 3 | Cold Start | Hot Start | HWY | US06 | |
| 1 | 1 | 2 | 0.10 | 0.76 | −0.82 | −0.89 | 0.65 |
| 2 | 7 | 0.08 | 0.66 | −0.15 | −0.19 | 0.27 | |
| 3 | 11 | −0.02 | 0.48 | −0.72 | −0.63 | 0.46 | |
| 14 | 1 | 0.10 | 0.75 | −0.87 | −0.89 | 0.65 | |
| 2 | 1 | 6 | −0.59 | −0.03 | 0.57 | 0.03 | 0.31 |
| 11 | −0.12 | 0.33 | −0.43 | −0.90 | 0.44 | ||
| 4 | 18 | 0.05 | 0.72 | −0.78 | −0.53 | 0.52 | |
| 8 | 19 | 0.19 | 0.66 | −0.35 | −0.43 | 0.40 | |
| 13 | 9 | −0.22 | 0.33 | −0.76 | −0.53 | 0.46 | |
| 5 | 2 | −0.08 | 0.71 | 0.19 | −0.49 | 0.37 | |
| 7 | 2 | −0.14 | 0.72 | −0.18 | −0.20 | 0.31 | |
| 7 | 2 | 6 | 0.03 | 0.71 | 0.41 | −0.59 | 0.43 |
| 9 | 11 | −0.29 | −0.02 | 0.76 | −0.11 | 0.30 | |
| 15 | 15 | 7 | −0.90 | −0.51 | 0.58 | −0.41 | 0.60 |
| 19 | 10 | −0.07 | −0.49 | 0.54 | −0.91 | 0.50 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomanik, E.; Jimenez-Reyes, A.J.; Tomanik, V.; Tormos, B. Machine-Learning-Based Digital Twins for Transient Vehicle Cycles and Their Potential for Predicting Fuel Consumption. Vehicles 2023, 5, 583-604. https://doi.org/10.3390/vehicles5020032
Tomanik E, Jimenez-Reyes AJ, Tomanik V, Tormos B. Machine-Learning-Based Digital Twins for Transient Vehicle Cycles and Their Potential for Predicting Fuel Consumption. Vehicles. 2023; 5(2):583-604. https://doi.org/10.3390/vehicles5020032
Chicago/Turabian StyleTomanik, Eduardo, Antonio J. Jimenez-Reyes, Victor Tomanik, and Bernardo Tormos. 2023. "Machine-Learning-Based Digital Twins for Transient Vehicle Cycles and Their Potential for Predicting Fuel Consumption" Vehicles 5, no. 2: 583-604. https://doi.org/10.3390/vehicles5020032
APA StyleTomanik, E., Jimenez-Reyes, A. J., Tomanik, V., & Tormos, B. (2023). Machine-Learning-Based Digital Twins for Transient Vehicle Cycles and Their Potential for Predicting Fuel Consumption. Vehicles, 5(2), 583-604. https://doi.org/10.3390/vehicles5020032







