1. Introduction
One of the main global problems in recent years is climate change (global warming). According to the report of the United States Environmental Protection Agency (EPA), the transportation sector is responsible for the largest share of greenhouse gas emissions (29% of 2019 greenhouse gas emissions) [
1]. Therefore, authorities and environmental agencies establish strict limitations for automotive manufacturers concerning carbon dioxide gas emissions. Currently, the automotive industry mainly depends on fossil fuels, although world oil reserves have been estimated at 50 years of contemporary consumption [
2]. Thus, the transportation industry is being asked for the implementation of a decarbonization program or at least the reduction of greenhouse gas emissions [
3,
4]. The realization of these tasks with the conventional propulsion system is challenging. Hybridization of the existing driving system with an additional energy source, such as batteries or supercapacitors, is one solution [
5]. The combination of electric and conventional propulsion systems allows for the significant reduction of greenhouse CO
emissions. In spite of the popularity of this solution, it is impossible to reach zero carbon emissions. Hydrogen as an energy carrier for the propulsion of vehicles is seen as a solution for sustainable green mobility [
6] with higher energy density than electric batteries, with water as the only exhaust product.
Lately, the implementation of fuel cell vehicles in the transportation sector has emerged as a solution [
7]. Hydrogen as an energy carrier makes it possible to have tank-to-wheel carbon-free propulsion and allows it to cover basic driving requirements. In the fuel cell system, hydrogen gas combined with oxygen from ambient air produces electricity, which is used for the propulsion, heat, and pure water [
8]. However, the fuel cell system as the only power supply has lower power density and slower power response when compared with ICE [
7]. The usage of an additional energy storage system composed of batteries or super-capacitors coupled with such a system allows us to tackle this issue and creates several benefits. This solution makes it possible for energy recovery from braking, a more flexible energy supply, prolongs the life of the fuel cell system, and minimizes the consumption of hydrogen [
9]. In addition, fuel cells (FCs) are three times more efficient than the ICE and are advantageous in terms of driving range and refueling time compared with pure battery electric vehicles (BEV) [
10,
11,
12]. In many cases, the fuel cell system is designed to provide the average power demand while an additional energy source is used to provide the transient power demand to supplement the insufficient power of FC during power-starving phases such as acceleration or climbing [
13].
The possible configurations of a fuel cell vehicle (FCV) are (1) FCV—a pure fuel cell vehicle (without additional electrical energy storage), and (2) FCHEV—a fuel cell hybrid electric vehicle (solution with a battery or super-capacitor coupled with the fuel cell through DC/DC converter) [
14]. The second one is also referred to as the Series hybrid-fuel cell configuration [
15]. As mentioned above, due to the delayed power response of FC, the implementation of batteries or super-capacitors may increase the efficiency of the FC stack and allow regenerative braking. FC vehicles with super-capacitors are more efficient in absorbing regenerative power than batteries due to the high power density of super-capacitors and providing it during power starving phases. However, the energy density of super-capacitors is much lower than that of batteries. The realization of these solutions can be found in the Honda FCX Clarity and Toyota Mirai [
16].
Since FCHEV has two on-board energy storage devices, the problem of energy management arises. An energy management system (EMS) aims to reduce fuel usage while preserving the battery state of charge (SOC) and extending the battery life [
17,
18]. The key role of EMS for FCHEV is to decide on the power splitting for energy sources at any given time while maintaining the vehicle driveability constraints [
18]. The equivalent consumption minimization strategy (ECMS) is one of the most widely used EMS and it is based on the conversion of electrical energy in the energy storage sources into equivalent fuel consumption and minimization of the cost function. The latter is composed of the instantaneous fuel consumption and equivalent fuel consumption of the electric drive [
18,
19]. In this strategy, all energy of the vehicle comes directly or indirectly from hydrogen. The charging and discharging of batteries or super-capacitors should be equivalent to hydrogen consumption according to the set of equivalence factors. The energy consumption of both the electric drive and FC system should be equivalent to hydrogen consumption in order to minimize the system’s instantaneous fuel utilization [
20]. The calculation of the equivalent fuel consumption of batteries is performed by assuming that SOC variation is virtually compensated by the FC system. This principle was first introduced by Paganelli et al. [
21], who presented an algorithm for the EMS of HEV that chooses the power split between an electric motor and an engine to minimize fuel consumption. As a result, 17.5% of fuel reduction was achieved in the simulation. Concerning the implementation of ECMS on FCHEV, several works were carried out by researchers. Paganelli et al. [
22] proposed an ECMS control strategy for real-time application of an instantaneous power split between a fuel cell and an electrical accumulator in a charge-sustaining fuel cell hybrid vehicle and allowing the overall minimization of hydrogen consumption while meeting the driver demand. Han et al. [
23] studied the performance of a dynamic programming control strategy, comparing it with Pontryagin’s minimum principle and ECMS. Liu et al. [
20] proposed ECMS to solve the power allocation problem of FCHEV in order to reduce hydrogen energy consumption and prolong battery life. As a result, the optimal output power of FC was obtained by using ECMS, and the battery output power was smoothed, achieving the best power distribution between the battery and the super-capacitor. Bassam et al. [
24] simulated different control strategies, including ECMS on hybrid fuel cell/battery passenger vessels. An optimized proportional-integral (PI) controller-based energy management strategy was presented. They made a comparative analysis with the original PI controller, ECMS, and state-based energy management strategies in terms of hydrogen consumption and FC stresses with no additional hardware changes. Li et al. [
25] designed an ECMS strategy for the FCHEV powered by a fuel cell, battery and super-capacitor. FC system operates at its best efficiency zone and the battery is used as a long-term energy buffer, while the super-capacitor supplies the peak power. Kamal et al. [
26] presented a comparative analysis of the performance of different energy management strategies, including ECMS simulation over the UDDS driving cycle.
In this context, the present paper aims to compare three control strategies; namely, rule-based, optimization-based equivalent consumption minimization strategy, and the real control strategy used in Toyota Mirai. In the first part of the paper, the modeling, simulation, and validation of FCHEV based on the Toyota Mirai (1st generation) vehicle are presented. For this purpose, various subsystems of the vehicle are developed with mathematical relations, and proper block diagrams are constructed by means of backward modeling approaches. The obtained results are compared with experimental data from the open-source Argonne National Laboratory database [
27,
28]. In the second part, the ECMS control strategy is implemented and replaced Toyota Mirai’s real control strategy in order to optimize hydrogen consumption and compare with the results obtained using experimental and rule-based energy management strategies over various driving cycles. Finally, the hydrogen economy optimization windows are determined and proper conclusions are made concerning the performance of control strategies for different driving patterns.
2. Methodology
For the Toyota Mirai, the fuel cell stack works as a primary power source, while the battery works as an auxiliary source or power buffer [
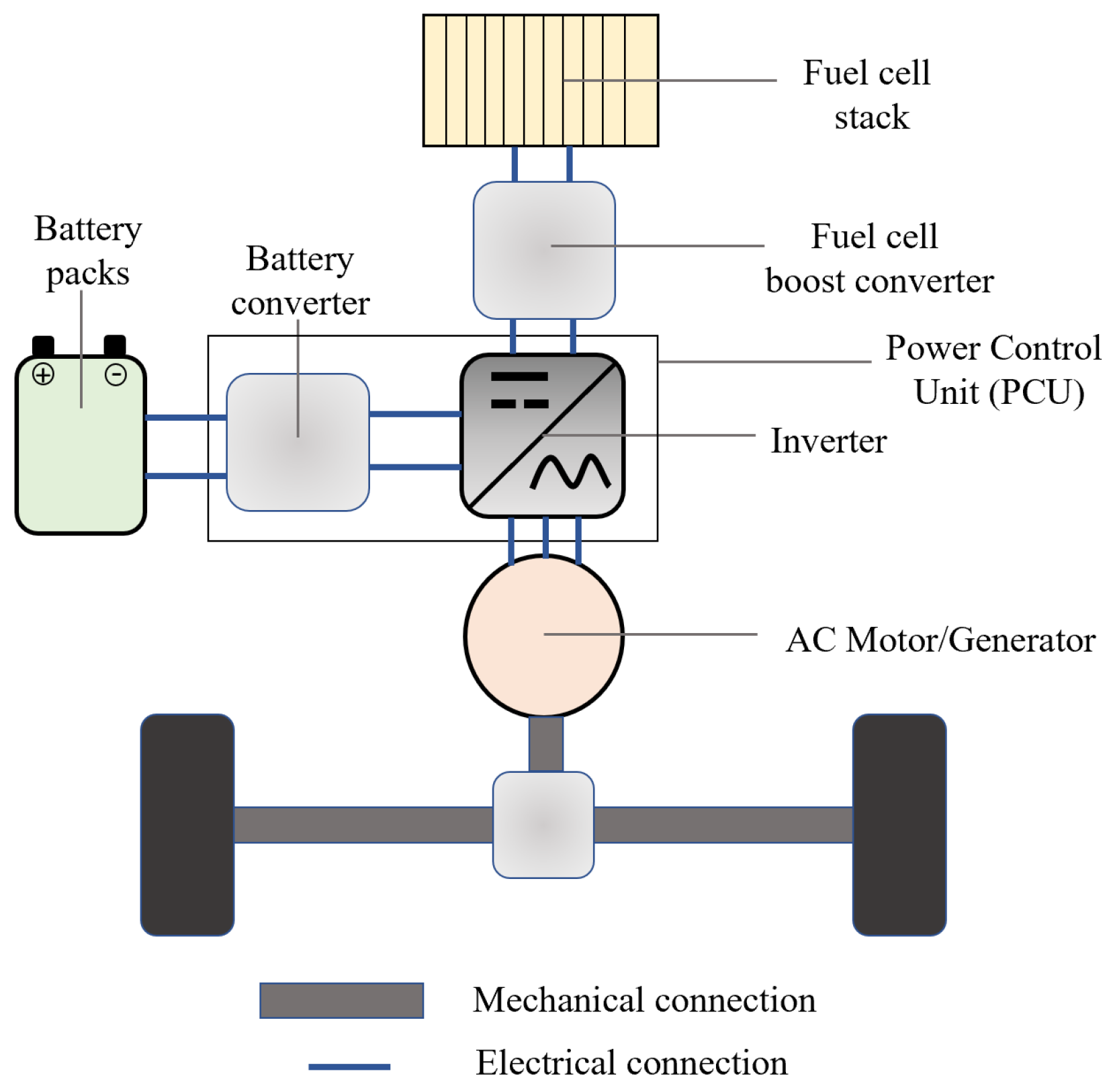
29]. The backward modeling technique is employed during this research, meaning that input parameters for the model come from the driving cycle, which are WLTC, NEDC, UDDS, JC08, HWY, and US06 in our case, and the output parameters are hydrogen consumption and battery SOC, while in reality, the situation is inverse. In this research paper, the total system is subdivided into several subsystems, which are the vehicle, speed reducer, electric machine, power control unit, battery, boost converter, fuel cell system, and hydrogen tanks. The general configuration of the system is provided in
Figure 1.
2.1. Vehicle Dynamics Subsystem
This subsystem aims at calculating the angular velocity and torque of a driving axle given the acceleration and velocity request from the driving cycle [
32]. The equations of this block are the equations of the longitudinal dynamics of a vehicle. The total tractive force at a tire-ground contact is the sum of all resistance forces and the inertia force due to acceleration [
32,
33].
where
—torque of the wheels, [Nm];
—wheel angular velocity, [rad/s];
—wheel angular acceleration, [rad/s
];
g—gravity constant, [m/s
];
—radius of the wheel, [m];
—rotational inertia of the wheel, [kgm
];
—air density, [kg/m
];
v—vehicle speed, [m/s];
—vehicle frontal area, [m
];
—aerodynamic drag coefficient, [-];
—rolling resistance coefficient, [-];
M—FCHEV’s total mass with full load, [kg];
—road inclination, [deg];
—longitudinal acceleration, [m/s
].
The values of vehicle and powertrain parameters are listed in
Table 1. The impact of the lateral dynamics is not taken into account, and the additional torque due to the inertia of rotating parts is considered separately for each part of the vehicle and included in the mathematical model of the corresponding part.
2.2. Speed Reducer Subsystem
This subsystem calculates the torque and speed request for the electric motor given the torque and speed of the wheels and the reduction ratio. The Toyota Mirai FCHEV is equipped with a single-speed reducer ratio. Therefore, the electric machine torque will be equal to
where
—reduction ratio, [-];
—speed reducer efficiency, [-];
—electric machine angular velocity, [rad/s];
—electric machine angular acceleration, [rad/s
].
2.3. Electric Machine Subsystem
Transmission system power request and electric machine efficiency can be used to compute power supply to an electric machine.
where
—power required by batteries and fuel cell system, [W];
—electric machine inertia, [kgm
];
—electric machine efficiency, [-];
—auxiliary power, [W].
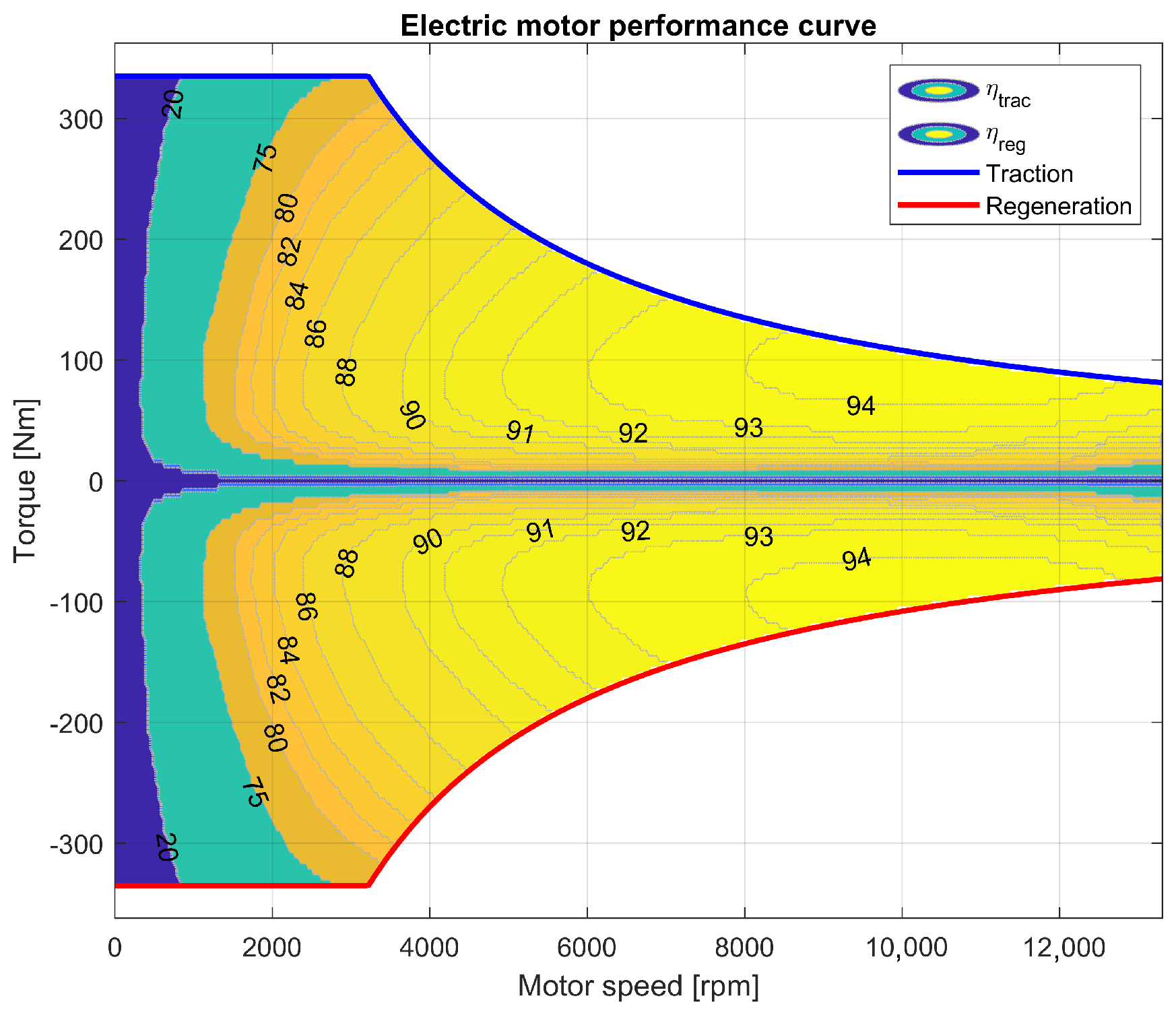
Electric machine efficiency depends on its torque and speed, and is graphically represented in the electric machine efficiency map. An AC synchronous motor with a maximum power of 113 kW and maximum torque of 335 Nm is used in the 2014 Toyota Mirai FCHEV [
34]. Due to the unavailability of this motor efficiency map, a similar motor with almost the same peak power and torque is considered, specifically, a YASA P400 R SERIES AC synchronous motor’s efficiency map [
35] is used, and the parameters are re-scaled to fit the peak torque and speed [
36]. The final representation of the efficiency map and torque curve of the electric machine is illustrated in
Figure 2.
2.4. Fuel Cell System Model
The full onboard fuel cell system is made of a fuel cell stack and auxiliary systems such as hydrogen, air, water, coolant, and electrical supply circuits [
29]. The full model requires additional computing time since it includes intricate internal dynamic responses [
37]. Due to the intricacy of the FC model, this paper focuses mostly on the power distribution of the bus rather than the precise FC conversion process. Consequently, a simple efficiency graph, which is obtained from the experimental results, is used for the simulation.
The experimental data, publicly available from the Argonne National Laboratory [
28], were used to establish the FC model. The curves for the hydrogen flow rate, FC stack efficiency, FC system efficiency, and polarization curve have been reconstructed from the experimental data. The experimental operating points and the dependence of FC stack and system efficiency, and hydrogen flow rate on the FC output power have the form illustrated in
Figure 3.
Consequently, this dependence can be approximated with polynomials of the sixth degree for FC stack efficiency, the fifth degree for FC system efficiency, and the second degree for hydrogen flow rate, as shown in Equations (
8)–(
10).
where
.
where
.
where
.
By using the FC polarisation curve (
Figure 3d), the fuel cell stack current can be determined. The dependence of the stack voltage and stack current can be approximated with the polynomial of the fifth degree:
where
.
2.5. Battery Model
A nickel metal hydride battery pack with a capacity of 6.5 Ah is used in the 2014 Toyota Mirai as an additional to the FC power source [
34]. By integrating a battery pack into the propulsion system, regenerative braking is made possible, and the vehicle’s autonomy is increased. From the standpoint of energy management, the majority of batteries are modeled using a Thevenin equivalent circuit model [
32,
33]. The data from the 2004 Toyota Prius, experimentally obtained by Idaho National Laboratory (INL) and made publicly available through their website [
38], which has the closest battery data, are used.
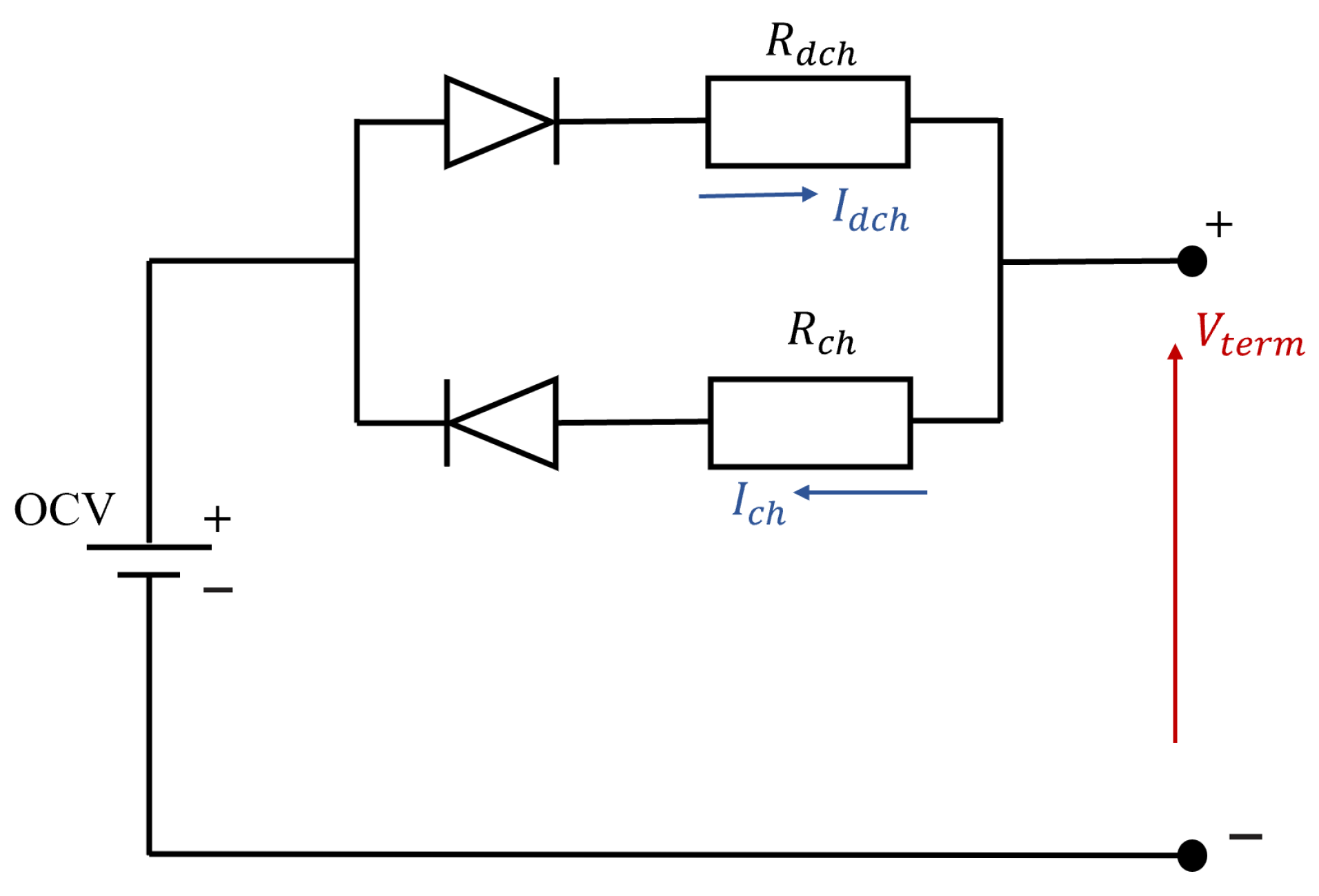
The battery cell characteristics are maintained while being adjusted to the battery pack nominal parameters given by Toyota Mirai datasheets. An ideal voltage source, internal charging, and discharging resistances are the three elements of this model (
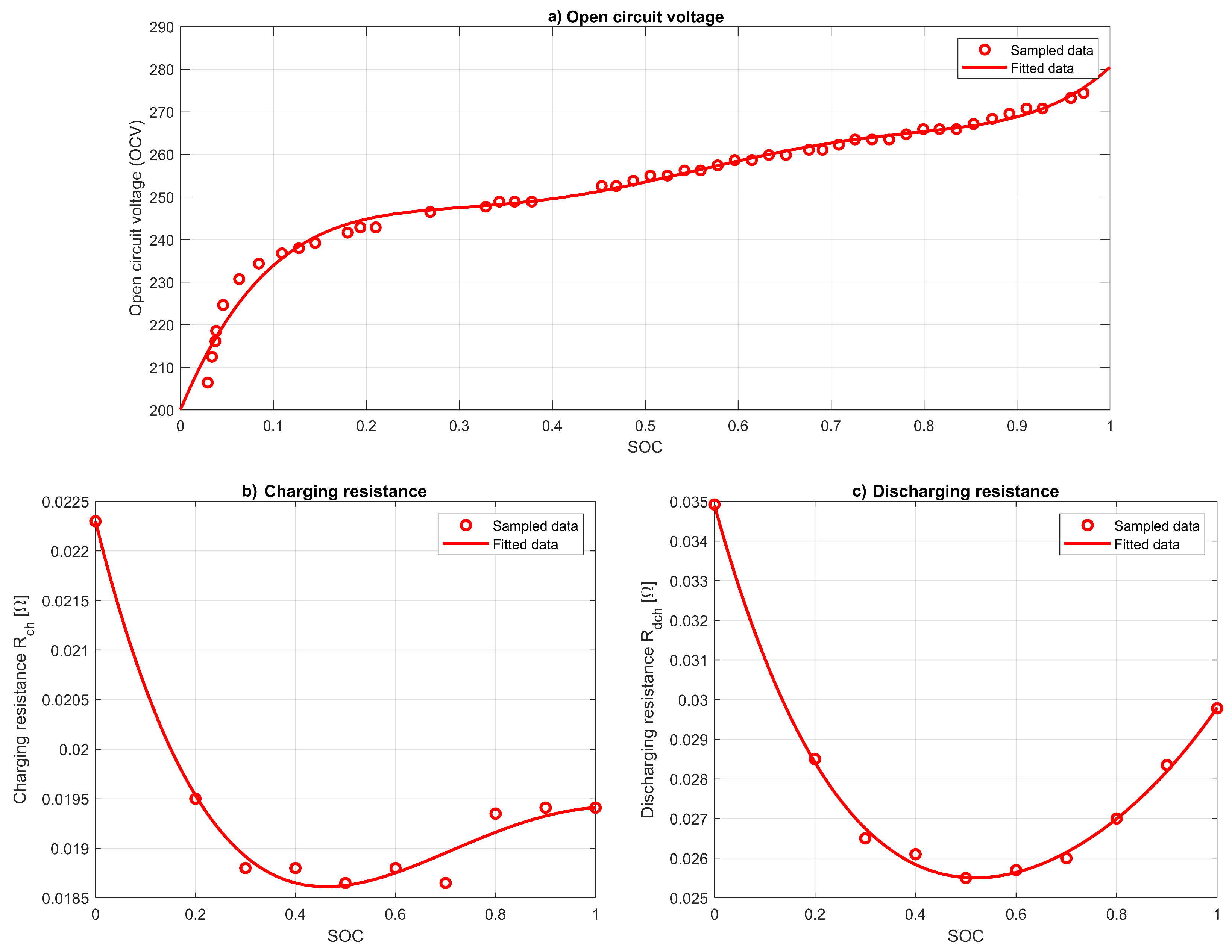
Figure 4). The open circuit voltage (OCV) of the battery is represented by the ideal voltage source and is dependent on the SOC of the battery (
Figure 5a). The terminal voltage, battery internal charging, and discharging resistances are represented as
,
, and
, respectively, and are also the functions of the battery SOC.
Figure 5b,c demonstrate this dependence. The charging and discharging currents are
and
, respectively. Internal resistances and open circuit voltage depend on SOC and temperature. In this work, the dependence on temperature is not taken into account and the temperature is assumed to be constant. These relations can be approximated with the polynomial of the fifth degree for battery OCV, and fourth degree for battery charging and discharging resistances.
where
.
where
.
where
.
The coefficient of correlation (
) in all the above equations is within 0.80–0.95, which indicates the acceptable correspondence between the equations and experimental data. The nominal parameters of the battery pack used in the simulation are represented in
Table 2.
By knowing the power required from the battery
, its charging and discharging currents and battery SOC can be formulated from energy and charge conservation principles as follows [
18,
32]:
where
—power required from batteries, [W];
k—coefficient that takes into account Peukert’s effect (ranges between 1 and 1.2 for NiMH batteries [
39]);
—battery state of charge at instant time t;
—battery state of charge one step time before;
—the battery capacity represented in Coulomb, [C].
Table 2.
Specifications of Toyota Mirai FCHEV battery pack [
38,
40].
Table 2.
Specifications of Toyota Mirai FCHEV battery pack [
38,
40].
| Parameters | Unit | Value |
|---|
| Type | - | Air-cooled Nickel Metal Hydride |
| Nominal capacity | kWh | 1.6 |
| Nominal voltage | V | 245 |
| Capacity | Ah | 6.5 |
| Number of series connections | - | 34 |
| Number of parallel connections | - | 1 |
2.6. Boost Converter and Inverter Model
In our case, a boost converter must be integrated in order to step-up the voltage of the fuel cell stack because the voltage that should be given to the AC synchronous motor is approximately 650 V, but the voltage of the FC stack is roughly its nominal value (245 V) [
41]. These subsystems’ average 95% efficiency is taken into account in the model.
2.7. Energy Management Strategy (EMS) Model
There is flexibility in the power distribution between the fuel cell stack and battery because there are two energy sources. For the optimal realization of EMS, hydrogen consumption should be reduced while battery operates in charge-sustaining mode. The main logic of the power control unit is to force the fuel cell stack to work at high-efficiency points along the optimum operating line in order to reduce hydrogen consumption while the battery supplies the differential power since the efficiency of the fuel cell stack is not constant and strongly depends on power. The value of the SOC of the battery has an impact on the power splitting as well. Only when the SOC exceeds a predetermined threshold value is the battery allowed to supply power.
By using experimental data from the Argonne National Laboratory [
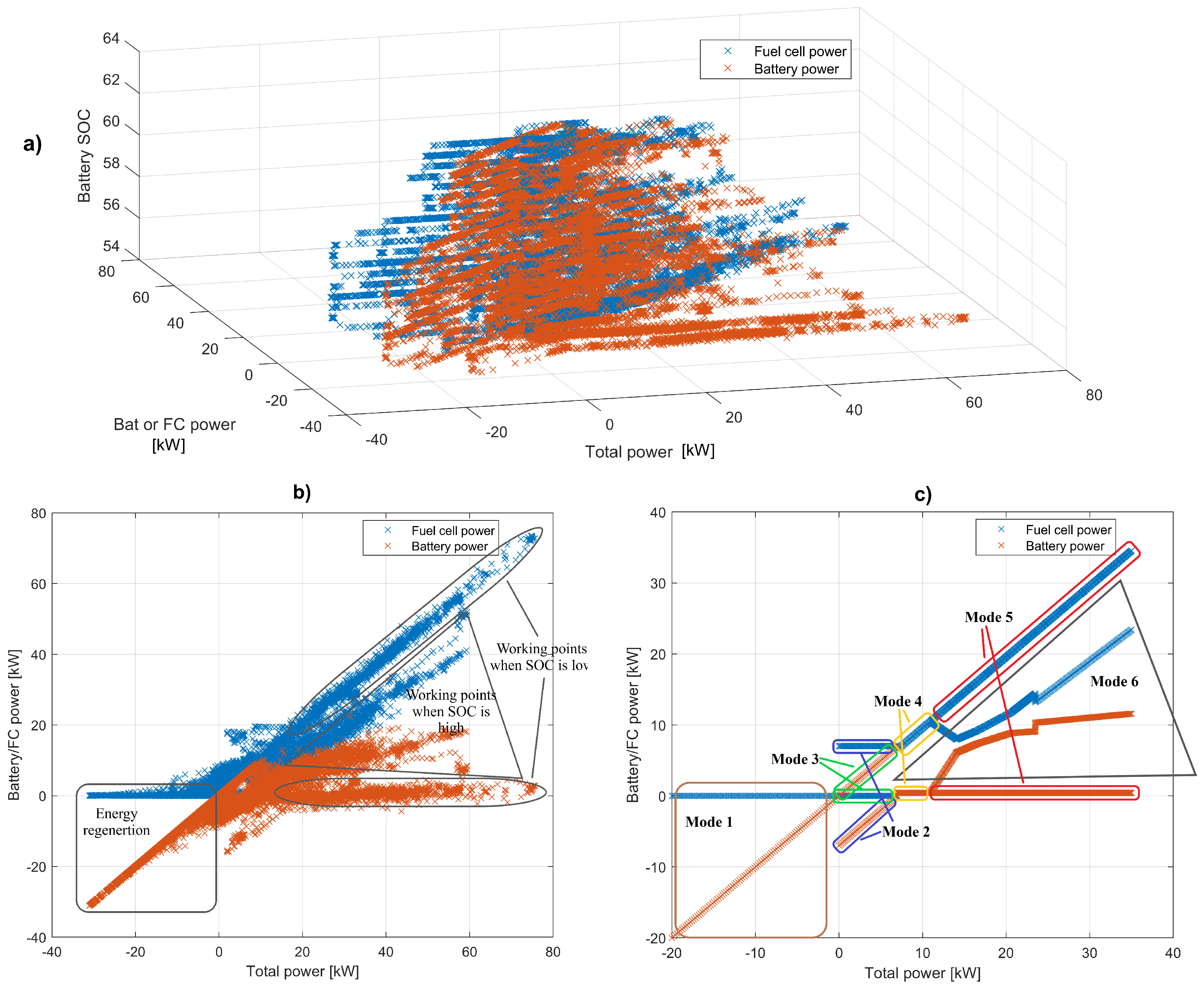
28], it is possible to approximate the Toyota Mirai’s (1st generation FCHEV) energy management strategy. The choice of power distribution between a fuel cell stack and the battery is heavily influenced by the state of charge (SOC) and the power required by an electric machine. The working points of the FC and battery over WLTC driving cycles are represented as a function of the electric machine’s required power and battery SOC, which are illustrated in
Figure 6a and as a function of required power only (the planar projection of
Figure 6a), which is illustrated in
Figure 6b. In
Figure 6b, the low values or the high values of SOC mean the values, lower or higher or equal than 57%, respectively. Experimental EMS is reconstructed by means of a rule-based strategy and approximated by means of a linear regression procedure (
Figure 6c). The FC and battery working point location depends on the EM required power and battery SOC and is assumed to be divided into six different modes. However, as
Figure 6a illustrates, the real control strategy could be more complex and presumably represented by fuzzy-logic rules.
Mode 1—Regenerative braking.
FCHEV works in Mode 1 during the energy regeneration phase, when EM supplies negative power and the braking energy is stored in batteries.
Mode 2—Load Shift.
FCHEV operates in Mode 2 at low power requests (0 <
< 7 kW) and low SOC (<57%). Since the FC efficiency is extremely small at low power outputs (lower than 7 kW), it provides constant power output, while the differential power charges the batteries.
Mode 3—Only battery.
Mode 3 is used at low power requests (0 <
< 7 kW) and high SOC (≥57%). The battery provides all the required power, while the FC is turned off.
Mode 4—FC driving. Low power.
In mode 4, the battery powers only the auxiliary devices, while the FC provides the traction power for any values of the battery SOC in the interval of
between 7 and 11 kW.
Mode 5–FC driving. High power and low SOC.
FCHEV operates in Mode 5 at high power requests (
> 11 kW) and low SOC (<57%). All the power requests are provided by the FC, whereas the battery supplies the auxiliary power.
Mode 5—FC driving. High power and high SOC.
Mode 6 is activated at high power request (
> 11 kW) and at high values of SOC (≥57%). Both battery and FC provide the power with a proportion that is assumed to be described by complex linear equations:
The coefficient of correlation () in all the above equations is within 0.80–0.95, which is interpreted as a good correspondence between the equations and experimental data.
3. Simulation Results with Rule-Based Control Strategy
The performance of FCHEV using the rule-based control strategy is numerically evaluated in this section. This was performed on the basis of simulations over WLTC, NEDC, UDDS, US06, HWY, and JC08 driving cycles. To focus on the influence of the control strategy, the variation of the temperature of the powertrain components was not considered in this work. The present model was validated by comparing the simulation results from the MATLAB/Simulink environment with the experimental data from ANL. The ambient temperature indicated in the experimental data of ANL is 22
C (72
F). The reconstructed rule-based control strategy parameters shown in
Figure 6c have been used to simulate the performance of the vehicle.
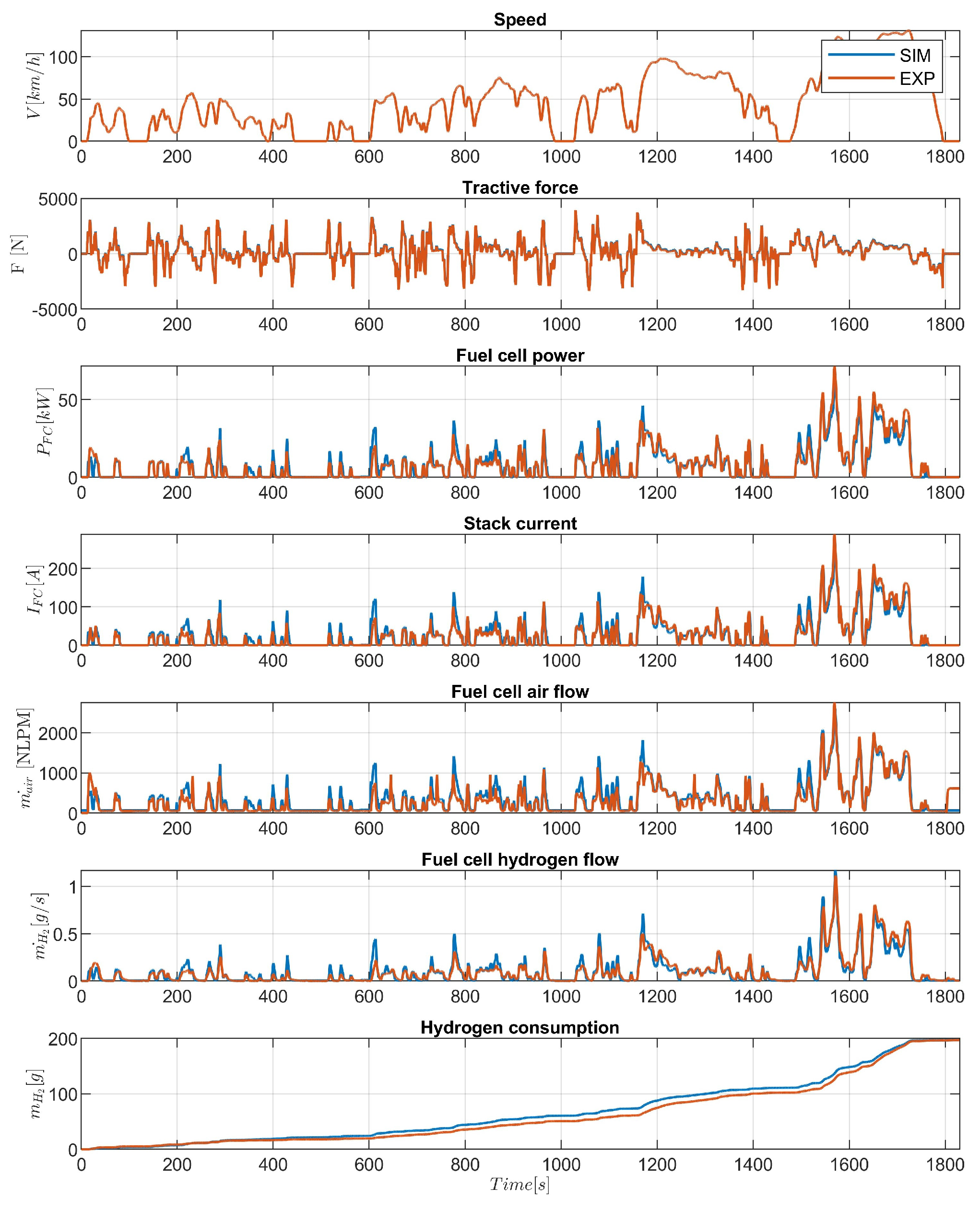
Figure 7 and
Figure 8 illustrate speed, tractive force, fuel cell power, fuel cell stack current, fuel cell air flow rate, fuel cell hydrogen flow rate, cumulative hydrogen consumption, electric machine power, battery power, battery current and battery state of charge time history for WLTC, NEDC, UDDS, JC08, US06, and HWY driving cycles. Red lines present the experimental data profile (from ANL data), while blue lines show the simulated.
Table 3 summarizes the data for hydrogen consumption and the final value of the battery state of charge and provides information about simulated and experimental cumulative hydrogen consumptions, expressed in grams.
Due to the difference in the simulated and experimental final battery SOC, the corresponding compensation in terms of hydrogen is considered. It was found through an iterative calculating procedure that 0.9 grams of hydrogen equate to the energy content in 1 percent of battery SOC.
The WLTC driving cycle showed the lowest change in the final value of battery SOC, which was found to be 1%, and the highest difference is for the JC08 and US06 cycles, being 10%.
Table 3 shows that the highest match between the simulated and experimental data is for the WLTC driving cycle, with a difference of just 0.5%. On the other hand, the UDDS and HWY driving cycles showed the greatest difference between the simulated and experimental overall hydrogen consumption data; 18.1% for UDDS and 16.1% for HWY, respectively. The moderate difference, which is slightly less than 7%, has been noted for JC08 and US06 cycles. The model was actually calibrated by looking at the complete driving cycle, where at low speeds offsets are higher, and lower at high speeds. However, at the driving cycle level, the energy of the simulation and experiments correspond. There are several factors that cause the deviation between simulated and experimental data. One of them is the effect of backward modeling and quasi-static simulation. This methodology does not fully reflect the dynamic behavior since it relies on maps, which are often built during steady-state laboratory testing, neglecting the transients. Another reason is the differences in rules used in EMS (
Figure 2) and the EM efficiency map (
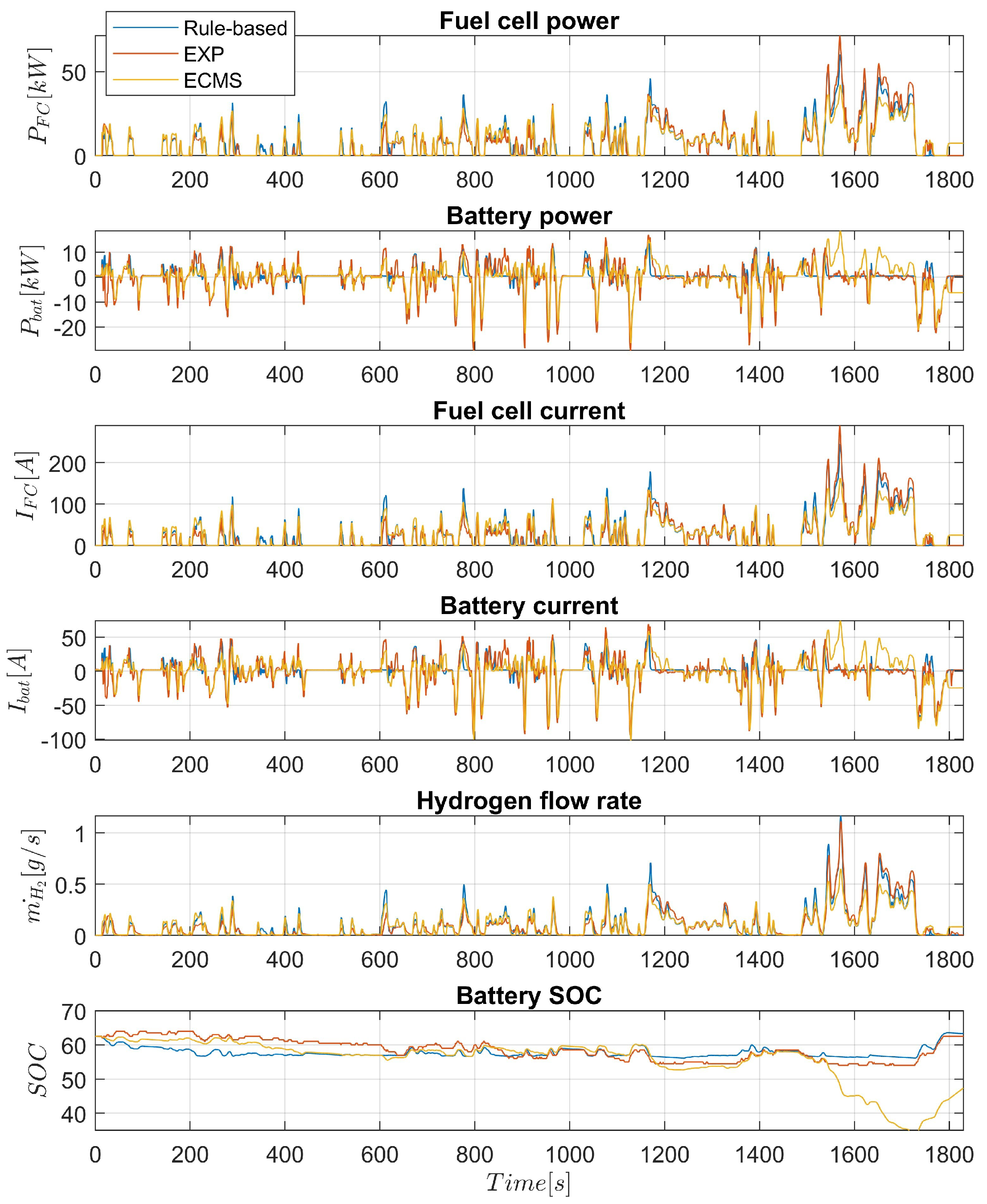
Figure 6) that do not correspond to the Toyota Mirai EM. Finally, the effect of the dependence of the Peukert coefficient on the discharging current can be highlighted. The derived numerical findings are comparable, and the general shape of the fuel cell and battery parameters are well-reproduced with sufficient accuracy. Given the driving pattern, this mathematical model is used to simulate FCHEV and estimate hydrogen consumption for the comparison of results for the equivalent consumption minimization strategy (ECMS), and the rule-based and experimental control strategies.
5. Conclusions
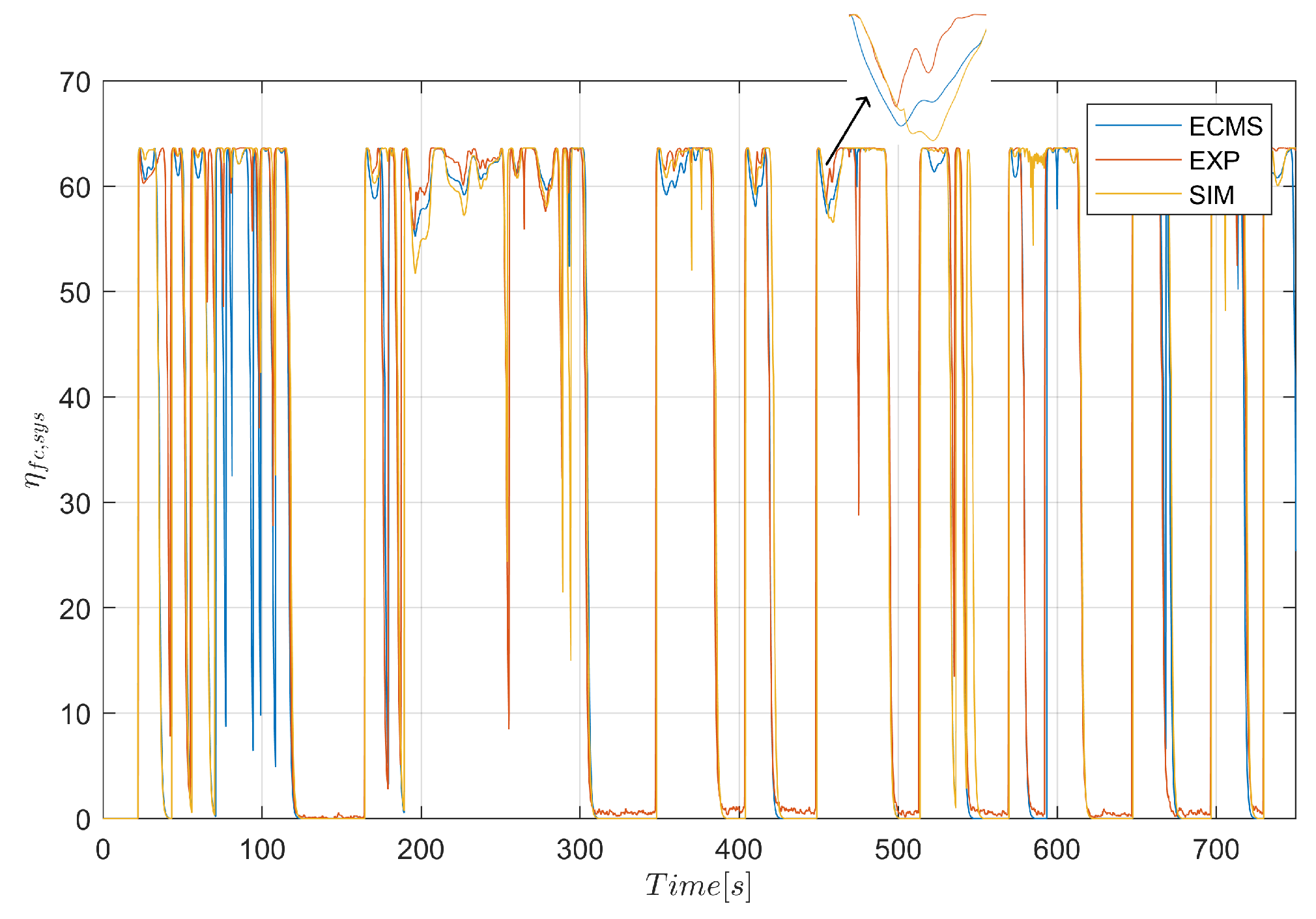
In this paper, a full MATLAB/Simulink model of the FCHEV has been developed and validated, simulating all vehicle components over several driving cycles. This model has been found to be rapid and to produce results that are reliable and steady. In order to determine the ideal power split between the fuel cell and battery, an ECMS control method for fuel cell vehicles was developed and put to the test in the Toyota Mirai FCHEV. The design of the FCHEV energy management strategy involved reconstructing the experimental EMS using a linear regression approach and approximating it with rules-based EMS, which consists of six distinct modes of operation. For the WLTC cycle, the modeled and experimental data matched perfectly with a difference of just 0.5%, whereas the UDDS and HWY driving cycles had the largest differences of nearly 18% and 16%, respectively. In conclusion, this model performs well for low-load driving cycles such as WLTC, NEDC, JC08, and US06, with an error of less than or about equal to 10%.
The ECMS control strategy has been simulated in the Toyota Mirai FCHEV to optimize the power split between power sources. Instantaneous fuel cell and equivalent battery hydrogen consumptions have been calculated from an approximated hydrogen consumption polynomial. The penalty function that incorporates battery SOC was taken into account while defining the objective function. For all driving cycles, it was found that the ECMS controller outperforms the rule-based strategy, with a minimum fuel consumption reduction of 0.4% for UDDS and a maximum of 15.6% for WLTC. The ECMS controller, on the other hand, proves to perform worse than a real controller for NEDC, UDDS, and JC08 cycles, with a contrary effect of fuel economy, increasing up to 17.6% for UDDS, 13.6% for JC08, and 1.4% for NEDC cycles, while the fuel economy reduction was observed to be 15.2%, 17.5%, and 19.6%, respectively, for the WLTC, US06, and HWY driving cycles. The temperature of the components affects the performance of the powertrain, which can be considered in future work.