Abstract
The recovery of kinetic energy (KER) in electric vehicles was analyzed and characterized. Two main systems were studied: the use of regenerative brakes, and the conversion of potential energy. The paper shows that potential energy is a potential source of kinetic energy recovery with higher efficiency than the traditional system of regenerative brakes. The study compared the rate of KER in both cases for a BMWi3 electric vehicle operating under specific driving conditions; the results of the analysis showed that potential energy conversion can recover up to 88.2%, while the maximum efficiency attained with the regenerative brake system was 60.1%. The study concluded that in driving situations with sudden and frequent changes of vehicle speed due to traffic conditions, such as in urban routes, the use of regenerative brakes was shown to be the best option for KER; however, in intercity routes, driving conditions favored the use of potential energy as a priority system for KER.
1. Introduction
Recovery energy constitutes one of the main goals in energy conversion systems to improve performance. In the case of electric vehicles, the recovery of kinetic energy losses started with the car racing tests, specifically in Formula One [1,2,3,4,5,6,7,8], which represented an excellent testing bench for commercial applications [9,10,11].
Kinetic energy recovery has become one of the focus points of researchers, designers, and manufacturers in the electric vehicle industry [12,13,14,15,16,17,18,19,20,21,22,23]. Since part of the energy used in propelling electric vehicles is lost during driving, the recovery of a percentage of these losses improves the efficiency of the energy taken from the battery and extends the driving range [24,25,26,27,28,29,30,31,32,33,34].
Electric vehicles use regenerative brakes as the current method of recovering kinetic energy losses while decelerating because of brake activation, a fact that is common in urban routes where traffic jams force the use of brakes to slow down or stop the vehicle. This option, however, is not the only one to recover kinetic energy losses, especially in intercity routes where traffic jams rarely happen, and where braking occurs occasionally.
The alternative to the regenerative brake in kinetic energy recovery is the use of the so called “potential energy loss” (PEL) that happens when the vehicle slows down without activating the braking system. In this case, the reduction of speed generates a kinetic energy loss that can be transformed into electricity and recharge the battery [34,35].
Two situations arise as representative of kinetic energy loss with no braking activation: slowing down due to the entering of a zone of speed limitation, and the descending segments of the route. In the first case, the reduction of vehicle speed may happen in a short time, and thus the amount of kinetic energy recovery is limited; the second option, however, can be prolonged, making kinetic energy recovery profitable.
In effect, a route descent generates a reduction in potential energy in the vehicle and thus its conversion into kinetic energy to maintain the energy balance. The increase of kinetic energy also makes the vehicle speed increase, although part of the kinetic energy gain is used in compensating the increase in the drag force. In case the balance between kinetic energy gain and the increase of energy waste due to drag forces is positive, the electric vehicle increases its speed progressively; if the driver does not want the vehicle speed to increase, either for security reasons or due to route speed limitations, the cruise control should activate the kinetic energy recovery system [36,37,38] or dissipate the excess of energy as heat [39].
Cruise control at descent segments produces an energy deliver that can be transformed into electricity by reversing the electric engine of the vehicle and converting it into an electric generator. The current so produced is, therefore, used to recharge the battery. This way of using the kinetic energy loss represents a feasible means of energy recovery, thus improving the performance of the system, increasing the efficiency of energy conversion, and extending the driving range of the electric vehicle.
The paper is divided in two different sections; first, the theoretical analysis of the problem with the development of specific algorithms; and second, the experimental tests where all data from running tests in an electric vehicle are included. The tests are divided in two sections: one corresponding to the urban route, and the other to the intercity route. This second section also includes a comparison between the theoretical approach and experimental data as well as the analysis of the comparison.
2. Theoretical Foundations
Kinetic energy losses are defined from the classical equation of kinematics:
where m is the mass of the vehicle, and vf and vi are the initial and final speed of the kinetic energy variation process, respectively.
In case the energy losses are converted into electricity, the following equation should be used:
I and V are, respectively, the output voltage and current of the electric engine when playing the role of electric generator, and ηg is the efficiency of the energy conversion process.
Provided the electric generator supplies a constant voltage, and considering the generated current depends on the rank of kinetic energy, Equation (2) should be reformulated as in
where different steps in the kinetic energy loss process are considered for time intervals of Δt.
In case the time interval is sufficiently short,
represents the average value of the vehicle speed at the segment j.
Equation (4) is useful in flat terrain where no changes of route elevation occur, or they are negligible, and the variation of kinetic energy is associated with a reduction of vehicle speed due to braking or simply to a releasing of the accelerator pedal. However, if the route is descending, the kinetic energy variation can be associated with the changes in the route elevation; thus,
At the route descent, two different situations arise, namely, cruise control engaged or disengaged; in the first case, the cruise control maintains constant the vehicle speed; therefore, the drag force is maintained constant too. In this situation, the loss of potential energy due to the descending level of the route is transformed into kinetic energy that is converted into electricity at the generator; the amount of electric current injected into the battery is given by
where α is the slope of the road, is the average vehicle speed during the descent, and ηg is the efficiency of the electric motor acting as an electric generator.
Assuming the duration of the descent is t, which is given by Equation (7), the amount of charge injected into the battery is
where d is the travelled distance during the descent.
The amount of charge from Equation (8) can be expressed, in terms of battery capacity, as Equation (9), where ΔC represents the relative capacity increase, and Cn is the nominal capacity of the battery, currently provided by the manufacturer.
Since the battery capacity is not a fixed value but a variable one that depends on the discharge rate, Equation (9) should be rewritten in terms of real capacity, Cr:
where fC is the capacity correction factor defined as [40]
tD is the theoretical discharge time at the operating discharge rate, and tref is the discharge time for standard discharge conditions [41,42,43].
Combining Equations (8), (10) and (11),
Since the driving range is directly related to the battery capacity, the capacity increase can be transformed into a driving range extension through the following equation:
where ζrate is the energy rate of the electric vehicle, in Wh/km.
The electric energy rate can be obtained from the analysis of the dynamic conditions under which the electric vehicle is running. From the classical expressions of dynamics, namely, Equations (14) and (15), where ξ is the energy consumption, P is the required power, t is the time of operation, and F is the propelling force, we can establish
Since the cruise control maintains constant the vehicle speed, the acceleration is null; therefore, Equation (16) is converted into
Applying the definition for energy rate,
Using Equation (7), it results in
Combining Equations (13) and (19), we obtain
or in terms of generated current,
Equation (21) provides a useful expression to obtain the enlargement of the driving range for the electric vehicle as a function of characteristics parameters.
Assuming the dynamic conditions are constant as well as vehicle parameters and battery characteristics, the only two variables that arise from Equation (21) are the generated current and the slope of the route, which can be easily obtained from the appropriate sensors, namely, an inclinometer for the slope and an ammeter for the current. The other parameters involved in the enlargement of the driving range can be taken from a data base.
An alternative situation occurs if the cruise control is disengaged; in such a case, the vehicle speed can no longer be constant—either increasing or decreasing depending on dynamic driving conditions. A vehicle speed increase happens when the electric engine continues pulling the vehicle at the same or similar rate, while vehicle speed diminishes if the driver releases the accelerator and leaves the vehicle to run under inertial forces.
In this latter case, there is a minimum value for the slope of the route that makes the electric vehicle run, since the drag and rolling forces continue acting on the vehicle movement, reducing its speed until the vehicle is completely stopped. In this situation, the kinetic energy recovery can only be applied if the following condition is fulfilled:
or in terms of variation of the altitude of the route,
where z is the altitude of the route, and sub-indexes i and f account for initial and final state, respectively, of the specific segment.
The conditions expressed in Equation (22) or Equation (23) indicate the amount of potential energy that must be devoted to compensate the energy waste due to drag and rolling forces; therefore, the kinetic energy recovery can be obtained from
It can be noticed that the kinetic energy recovery depends on the slope of the road segment and on the travelled distance on the segment.
Converting the kinetic energy recovery into increases in driving range, we have
or in terms of generated current,
3. Experimental Tests
Two types of tests were run: one in urban routes at the city of Madrid, Spain, and another in an intercity route, north of Madrid, Spain. The urban route was extended for a travelled distance of 12.4 km, and the intercity route for a one-way distance of 53.3 km. The test electric vehicle was a BMWi3, the characteristics of which were taken from the official data sheet of the manufacturer [44,45].
The physical diagram of the experimental device is shown in Figure 1. The figure represents the layout of the system with the different components and sub-systems. Sensors provide specific information about the operating voltage of the battery and electric motor, as well as the current extracted from the battery. The power sensor gives the power used by the electric motor to propel the vehicle.

Figure 1.
Layout of the power system for the tested electric vehicle.
Tests on the intercity route were run on the way back and forth to verify the validity of the results. The urban route was considered only for the regenerative brakes, while the intercity route was devoted to kinetic energy recovery from variations of potential energy along the route. The intercity route was divided into three segment categories according to the route profile: flat terrain, ascent, and descent. Segments were classified as flat terrain, ascent, or descent depending on the slope of the road; for slopes in the range (−1°, 1°), the segment was considered to be flat terrain, while above and below these values, the segment was classified as ascent for positive values of the slope and descent for negative values.
For simplicity, all segments belonging to any of the aforementioned categories were grouped; Table 1 summarizes the travelled distance for any of the three categories.

Table 1.
Distribution of travelled distance at the intercity route according to segment category.
3.1. Urban Route
The vehicle studied was equipped with a regenerative braking system, which takes advantage of braking moments to charge the vehicle battery with the kinetic energy losses. Tests were carried out for the purpose of evaluating the maximum capacity of kinetic energy recovery. To do this, data were taken from the vehicle’s control system, which provides information on the vehicle’s speed and instantaneous power. In order to obtain data on the maximum use of kinetic energy, the vehicle was allowed to brake only with the use of the regenerative braking system; that is, at no time were the electric vehicle’s conventional brakes activated. It was observed that the regenerative braking system was deactivated at a speed of 6 km/h.
Electric vehicle speed was taken from the vehicle speedometer and from GPS data. Since the car speedometer had a margin of error, an adjustment in the profile of vehicle speed was necessary to match speedometer values and GPS data. In our case, the deviation between the GPS signal and speedometer values was in the range of 2–5 km/h.
Using expression from the theoretical section, the power evolution with time was calculated and compared to the values provided by the electric vehicle control unit (EVCU). The results of the comparison can be seen in Figure 2, Figure 3, Figure 4 and Figure 5.
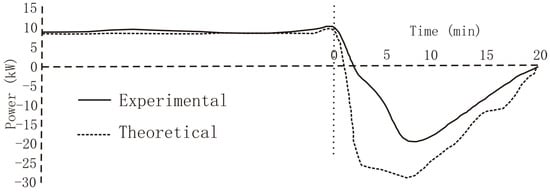
Figure 2.
Evolution with time of the kinetic energy power.
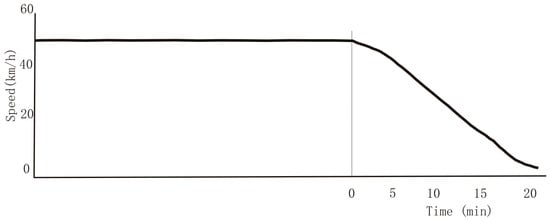
Figure 3.
Vehicle speed evolution with time.
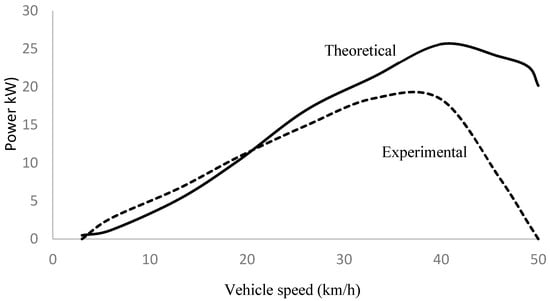
Figure 4.
Evolution with time of the regenerative braking power (test 1).
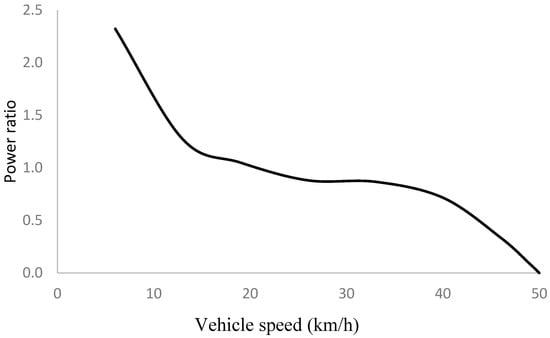
Figure 5.
Theoretical to experimental power ratio of the kinetic energy recovery system (regenerative braking system).
Analyzing the curves of Figure 2 we realized there were two different sections, one to the left of the vertical dotted line, with positive power values, and one to the right with negative power values; the left hand section shows that the regenerative braking system was not activated, since the vehicle speed was not reduced; however, in the right hand section the regenerative braking system was activated and was recharging the battery, so it is the one that interested us.
It can also be noticed that theoretical curve covers a larger area than the experimental, which means the regenerative braking system used only a fraction of the predicted kinetic energy recovery.
Figure 3 shows how the vehicle speed evolved with time. We realize the vehicle speed was maintained constant as long as the regenerative braking was not working, which means there was no kinetic energy losses. When the vehicle started reducing its velocity, regenerative braking was activated, and it initiated energy recovery from the reduction of kinetic energy due to a reduction of velocity.
Since the regenerative braking system was only activated when there was an effective reduction of vehicle speed and thus of kinetic energy, we represented the section where the regenerative braking is activated, the right hand section of Figure 2, to analyze the effectiveness of the kinetic energy recovery system (Figure 3).
To evaluate the real performance of the regenerative braking system, we calculated the kinetic energy losses from the experimental data provided by the EVCU as well as the energy recovery from the regenerative braking system, resulting in the following value:
This value represents the average efficiency of the regenerative braking system.
As stated before, we observed that the theoretical prediction of kinetic energy recovery by the regenerative braking system does not match experimental values, a clear sign of the inefficiency of the process. To evaluate how the efficiency of the regenerative braking system evolved with kinetic energy loss, we correlated the ratio of theoretical to experimental values of kinetic energy recovery power as a function of the vehicle speed. Figure 4 shows the results of the correlation.
The power factor shown in Figure 5 was correlated to a third degree polynomial function of the following type:
This correlation function has a regression coefficient of R2 = 0.9955, which indicates excellent agreement.
To verify the validity of the correlation we applied the power factor to the theoretical predictions, and the resulting values were drawn against experimental data, obtaining the following results shown in Figure 6. We realize there was very good agreement between theoretical predictions and experimental data, with accuracy higher than 98%.
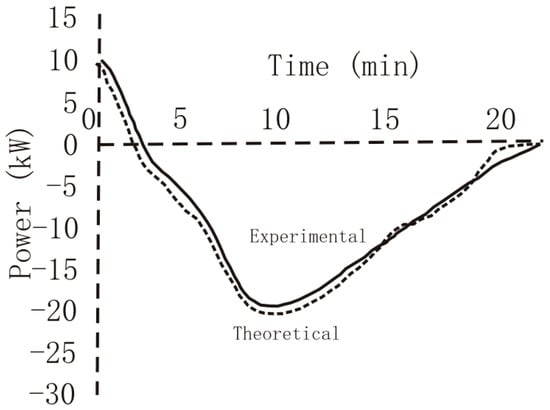
Figure 6.
Simulated evolution with time of the power of the kinetic energy.
Evaluations of the regenerative braking system were conducted for three additional urban routes, the results of which are graphically represented in Figure 7.
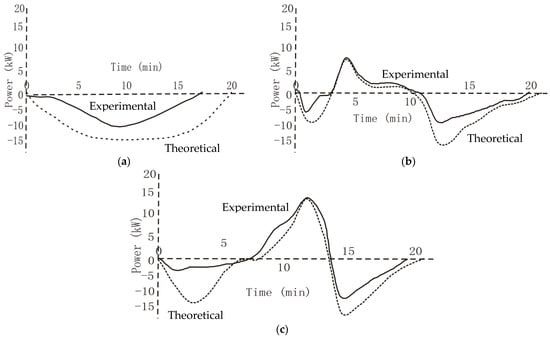
Figure 7.
Evolution with time of the power of the regenerative braking (tests 2, 3, and 4) (a–c).
Solid lines in Figure 7 represent experimental data, while dotted lines correspond to theoretical predictions.
As in the first test, we noticed a difference in performance between theoretical predictions and experimental values, which were the result of the inefficiency of the regenerative braking system. The same correlation process was applied to tests 2, 3, and 4 with similar results to those obtained for test 1, with slight differences in the coefficient values of the third degree polynomial function in Equation (28); therefore, the algorithm of Equation (28) was taken as a reference to determine the ratio between theoretical predictions and experimental results for the regenerative braking power as a function of the vehicle speed.
The efficiency of the regenerative braking system for tests 1 through 4 is shown in Table 2.

Table 2.
Efficiency of the regenerative braking system.
Averaging the values from Table 2, we obtained an efficiency for the regenerative braking system of 60.1%. We observed that all values were within 95% accuracy, which proved the validity of the results.
It must be noted that all carried out tests were developed using pure electric breaks with no activation of mechanical brakes at any time.
The average speed during the urban routes was set to 30 km/h, although the resulting value from experimental data was 28 km/h. The slight difference was due to errors in the speedometer, as has been mentioned before, of around 2.5 km/h on average. If we take into account the band error, the experimental data fell within the set up range.
An additional test was run using mechanical brakes together with the regenerative braking system to reduce vehicle speed; the efficiency in recovering kinetic energy losses was 22.8%, much lower than the value obtained with the use of regenerative braking only. The difference was due to the conversion of kinetic energy at the conventional brakes into heat.
Using data from the experimental test, we determined the energy rate, including the kinetic energy recovery; the results are shown in Table 3.

Table 3.
Energy rate.
Now using data from the technical data sheet for the tested electric vehicle [44,45], and applying results from the experimental tests, we could obtain the global energy recovery. Since our tests lasted for 20 min, the resulting recovery power is given by
where PEV is the power recovery data given by the manufacturer, ηKERS is the average efficiency of the energy recovery system, and f is the factor that account for the relative operational time related to the hourly period.
Comparing the results obtained in Equation (29) with those from Figure 5 and Figure 6, we observed that there was good agreement, which indicates the accuracy of the testing method.
If we apply these results to the determination of the driving range of the tested electric vehicle, using the battery energy capacity provided by the manufacturer [44,45], we obtain the results shown in Table 4.

Table 4.
Electric vehicle driving range.
We realize there is a significant increase in the driving range in the case of using the regenerative braking system up to 42.8% and 122 km.
3.2. Intercity Route
In this section, we studied and analyzed the kinetic energy recovery due to changes in the elevation of the route. In this case, the variation of potential energy because of the changes in the elevation was transformed into electricity since the vehicle speed and therefore the kinetic energy was maintained constant.
To do so the following condition must be fulfilled:
where m is the mass of the vehicle, ρ the air density, Cx the aerodynamic coefficient of the vehicle, A its front area, v the vehicle speed, μ the rolling coefficient, and α the slope of the road.
Replacing characteristics values for the BMWi3, which were taken from the technical data sheet [44,45], the minimum slope from which the kinetic energy recovery is feasible could be obtained. Table 5 shows the minimum slope of the road as a function of the vehicle speed.

Table 5.
Minimum slope of the road for feasible recovery energy.
We considered negative values of the slope of the route segments, since they are the only ones where there is kinetic energy recovery. To facilitate the evaluation, we used a route where most of the segments have negative slopes, so the amount of kinetic energy recovery would increase, thus minimizing the error in the calculation of the efficiency in the kinetic energy recovery process.
The orographic profile of the testing route can be seen in Figure 8.
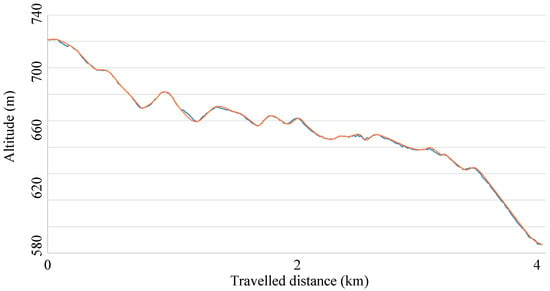
Figure 8.
Orographic profile of the testing route (descending segments). Blue line in Figure 8 corresponds to orographic profile supplied by the cartographic information of the region. Red line represents the theoretical approach of the profile used by the simulation.
The vehicle speed was set up at 77 km/h activating the cruise control unit. The dissipated power was calculated through the following expression:
Following the orographic profile, using data from official data sheet for the electric vehicle [44,45], taking values for measuring parameters, and applying Equation (31), we calculated the energy used as a function of the slope of the route; the results of the calculation are presented in Figure 9.
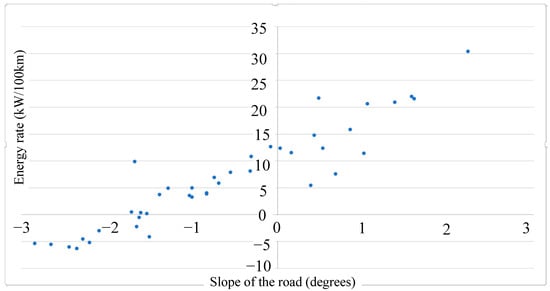
Figure 9.
Testing route energy rate vs. slope of the road.
The route was divided into 43 segments, each one characterized by the travelled distance, the slope of the segment, the change in road elevation, and the average speed of the electric vehicle. The energy rate at every segment is represented by a point in Figure 10. We observed that the kinetic energy recovery system was activated for slope values above −1.6°, when the energy rate became positive.
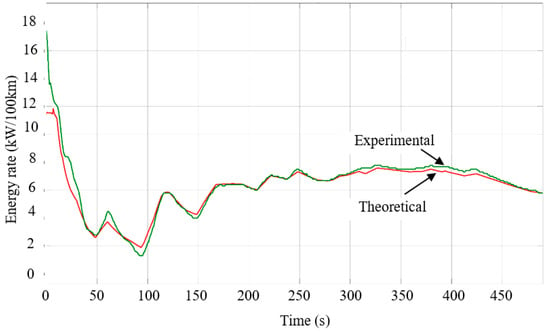
Figure 10.
Comparative results of theoretical predictions and experimental data.
From the mathematical definition of average energy rate,
where ξ+ and ξ− are the energy used and recovered, respectively, and d is the travelled distance; using data from experimental tests and applying Equation (32), we determined the average energy recovery rate.
The average energy recovery rate was used for simulating the energy rate for the whole route, and the results were compared to the experimental data obtained directly from the electric vehicle control unit. Figure 9 shows the results of the comparative analysis between the theoretical prediction from the simulation process and experimental data from direct measurements.
Dealing only with route segments with negative slopes, the energy recovery rate increased, as shown in Figure 11.
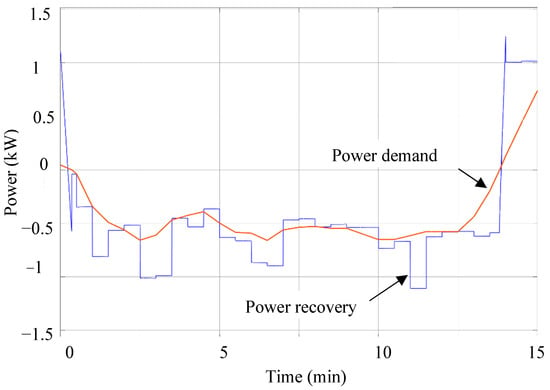
Figure 11.
Power demand (red) and recovery (blue) at the intercity testing route for negative slope segments.
To determine the efficiency of the kinetic energy recovery system, we calculated the available energy for recovery and the energy recovery itself and applied the following expression:
Sub-indexes rec and av account for recovery and available.
Values in Equation (34) have determined integrating the curves for available and recovery in Figure 11 for the whole time lapse.
To verify the validity of the calculation, we determined the energy associated with the drag and rolling forces during the energy recovery process. Since the electric vehicle operates at zero acceleration, the dynamic conditions statement can be expressed as:
Because the electric vehicle is under mechanical equilibrium, F = 0, and taking into account that the last term of the equation corresponds to the recovery energy, we can establish
Equation (36) indicates that only the drag and rolling forces intervene in the calculation of the available energy, as stated before.
Converting force into energy,
where the efficiency of the kinetic energy recovery system (KERS) was included to match real operating conditions.
Applying the MATLAB-Simulink simulation to the process, we obtained
a value that matches the previous result within 99.2% accuracy.
Two additional tests were run on similar driving conditions in alternative intercity routes of likely orographic profiles; the results of these additional tests gave energy recovery rates of 86.8% and 88.2%, slightly above the previous result. Averaging the three values, we obtained a characteristic average rate for the kinetic energy recovery of 86.7%. Table 6 shows the deviation from the average value at any case.

Table 6.
Efficiency of the kinetic energy recovery system.
The driving range was extended at the testing intercity routes by using the conversion process of potential energy reduction into kinetic energy; applying the same procedure as for the urban route to the entire intercity route,
which represents an extension of 98.6 km for the BMWi3 tested electric vehicle, considering the reference energy rate of 14.04 kWh/100 km provided by the manufacturer.
This extended range, however, may change with the route configuration, since the efficiency of the kinetic energy recovery system depends on the used system, regenerative braking or potential into kinetic energy conversion, which should be applied to different segments of the route, regenerative braking for the flat and ascent segments, and potential to kinetic energy conversion for the descending ones.
4. Conclusions
It was proven that kinetic energy recover can be attained, either by using the regenerative braking system or through the conversion into kinetic energy of the potential energy reduction.
The efficiency of the kinetic energy recovery system from the conversion into kinetic energy of the potential energy reduction is higher than using a regenerative braking system. The first method produced an average efficiency of the energy recovery rate of 86.7%, while for the regenerative braking, the efficiency was only 60.1%.
The high value of the efficiency of the energy recovery process through the conversion of potential energy variation into kinetic energy is valid only if applied to a route segment with a negative slope; in case the method is applied to an entire route with flat, ascent, and descent segments, the efficiency drops to 48.5%, a lower value compared to the regenerative braking system.
The regenerative braking system is more suitable for urban routes where sudden and frequent reduction of vehicle speed occurs due to traffic conditions. On the contrary, kinetic energy recovery from the reduction of potential energy should be used in intercity routes where braking barely happens and where changes in the route elevation, and thus of the potential energy, are more frequent.
According to what has been previously stated, in intercity routes it is more efficient to use the regenerative braking system with flat and ascending terrain, and the conversion process or potential energy reduction into kinetic energy with descending terrain.
The use of the energy recovery system extends the driving range of the electric vehicle in a significant way, up to 42.8% in urban routes when using regenerative braking system and up to 34.5% in intercity routes if the conversion system of potential energy variation into kinetic energy is applied.
The extension percentage for intercity routes may change if the configuration of the route is modified, since the efficiency of the kinetic energy recovery system depends on the type of system used for the recovery, regenerative braking, or energy conversion. Because the two systems should be applied at different segments of the route, the configuration is critical, hence the global efficiency and the resulting driving range extension.
Author Contributions
Conceptualization, C.A.-D.; methodology, C.A.-D. and H.C.; software, H.C.; validation, C.A.-D. and H.C.; formal analysis, C.A.-D. and H.C.; investigation, C.A.-D. and H.C.; resources, C.A.-D. and H.C.; data curation, C.A.-D. and H.C.; writing—original draft preparation, C.A.-D.; writing—review and editing, C.A.-D.; visualization, C.A.-D.; supervision, C.A.-D.; project administration, C.A.-D.; funding acquisition, None. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Provided by Carlos Armenta-Déu on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Boretti, A. Kinetic Energy Recover Systems for Racing Cars; SAE: Warrendale, PA, USA, 2013. [Google Scholar] [CrossRef]
- Limebeer, D.J.; Perantoni, G.; Rao, A.V. Optimal control of formula one car energy recovery systems. Int. J. Control. 2014, 87, 2065–2080. [Google Scholar] [CrossRef]
- Yoshida, M.; Kita, M.; Atarashi, H. Development of Hybrid System for Formula One. Honda R&D Technical Review F1 Special (The Third Era Activities). 2009, pp. 225–238. Available online: https://www.hondarandd.jp/summary.php?sid=23&lang=en (accessed on 25 April 2022).
- Kawamura, T.; Atarashi, H.; Miyoshi, T. The Development of a Low Viscosity, Highly Efficient Lubricant for Sport Motorcycle Applications (2011-32-0513). In Design of Racing and High-Performance Engines 2004–2013; Fehan, D.R., Ed.; SAE International: Warrendale, PA, USA, 2013. [Google Scholar] [CrossRef]
- Turner, J.W.G.; Pearson, R.J. High Power Density Motor for Racing Use (2011-39-7221). In Design of Racing and High-Performance Engines 2004–2013; Fehan, D.R., Ed.; SAE International: Warrendale, PA, USA, 2013. [Google Scholar] [CrossRef]
- Watson, H.C.; Gauci, A.; Yousuff, F.; Boretti, A. A Theoretical and Experimental Study of Resonance in a High Performance Engine Intake System: Part I (2006-01-3653). In Design of Racing and High-Performance Engines 2004–2013; Fehan, D.R., Ed.; SAE International: Warrendale, PA, USA, 2013. [Google Scholar] [CrossRef]
- Sopan, K.M.; Ramrao, S.P.; Yashwant, S.A.; Gokul, I.; Nivrutti, D.S.A. Kinetic Energy Recovery System. Int. Res. J. Eng. Technol. 2018, 5. [Google Scholar]
- Daidzic, N.E. Adopting a kinetic energy recovery system for helicopters. Prof. Pilot 2013, 47, 78–84. [Google Scholar]
- Rymaniak, Ł.; Fuć, P. Powertrain technology transfer between F1 and the automotive industry based on Mercedes-Benz. Combust. Engines 2018, 172, 3–13. [Google Scholar]
- Harris, S. From Race to Renewables. Engineer Online. 17 February 2014. Gale Academic OneFile. Available online: https://link.gale.com/apps/doc/A358872779/AONE?u=anon~483b3bca&sid=googleScholar&xid=55cce8f9 (accessed on 25 April 2022).
- Gunatilake, W.A.D.N.; Herath, B.G.H.M.M.B.; Bowatta, B.G.C.T.; Jayaweera, N.D.; De Silva, C.M.S.P. Design and development of kinetic energy recovery system for motor vehicles. Int. J. Multidiscip. Res. Rev. 2016, 9, 1–17. [Google Scholar]
- Ershad, N.F.; Mehrjardi, R.T.; Ehsani, M. Development of a kinetic energy recovery system using an active electromagnetic slip coupling. IEEE Trans. Transp. Electrif. 2019, 5, 456–464. [Google Scholar] [CrossRef]
- Farrokhzadershad, N. Development of Dual Shaft Electric Motor with Independent Input-Output Torque-Speed for Vehicle Kinetic Energy Recovery Systems. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2018. [Google Scholar]
- Krithika, V.; Subramani, C. A comprehensive review on choice of hybrid vehicles and power converters, control strategies for hybrid electric vehicles. Int. J. Energy Res. 2018, 42, 1789–1812. [Google Scholar] [CrossRef]
- Li, Z.; Khajepour, A.; Song, J. A comprehensive review of the key technologies for pure electric vehicles. Energy 2019, 182, 824–839. [Google Scholar] [CrossRef]
- Harshavarthini, S.; Divya, M.; Bongarla, R.; Priya, C.H.; Balaji, R. A critical investigation on regenerative braking energy recovering system on HEV based on electric and natural extracted fuel. Mater. Today Proc. 2021. [Google Scholar] [CrossRef]
- Guruvareddiyar, G.; Ramaraj, R. Super Capacitor Based Energy Recovery System from Regenerative Braking used for Electric Vehicle Application. In Proceedings of the 2019 IEEE International Conference on Clean Energy and Energy Efficient Electronics Circuit for Sustainable Development (INCCES), Krishnankoil, India, 18–20 December 2019; pp. 1–3. [Google Scholar]
- Ehsani, M.; Singh, K.V.; Bansal, H.O.; Mehrjardi, R.T. State of the art and trends in electric and hybrid electric vehicles. Proc. IEEE 2021, 109, 967–984. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhang, H.; Xin, Y. Research on control strategy of hydraulic regenerative braking of electrohydraulic hybrid electric vehicles. Math. Probl. Eng. 2021, 2021, 5391351. [Google Scholar] [CrossRef]
- Feng, J. Brake energy recovery system for electric vehicle. Int. J. Ambient Energy 2022, 43, 942–945. [Google Scholar] [CrossRef]
- Yu, W.; Wang, R. Development and performance evaluation of a comprehensive automotive energy recovery system with a refined energy management strategy. Energy 2019, 189, 116365. [Google Scholar] [CrossRef]
- Liu, W.; Qi, H.; Liu, X.; Wang, Y. Evaluation of regenerative braking based on single-pedal control for electric vehicles. Front. Mech. Eng. 2020, 15, 166–179. [Google Scholar] [CrossRef]
- Ji, F.; Pan, Y.; Zhou, Y.; Du, F.; Zhang, Q.; Li, G. Energy recovery based on pedal situation for regenerative braking system of electric vehicle. Veh. Syst. Dyn. 2020, 58, 144–173. [Google Scholar] [CrossRef]
- Qiu, C.; Wang, G. New evaluation methodology of regenerative braking contribution to energy efficiency improvement of electric vehicles. Energy Convers. Manag. 2016, 119, 389–398. [Google Scholar] [CrossRef]
- Heydari, S.; Fajri, P.; Rasheduzzaman, M.; Sabzehgar, R. Maximizing regenerative braking energy recovery of electric vehicles through dynamic low-speed cutoff point detection. IEEE Trans. Transp. Electrif. 2019, 5, 262–270. [Google Scholar] [CrossRef]
- Lin, Z.; Zhanqun, S.; Yuegang, L.; Jing, K. A study of energy recovery system during braking for electric vehicle. In Proceedings of the 6th International Conference on Applied Science 2016, Engineering and Technology (ICASET), Qingdao, China, 29–30 May 2016. [Google Scholar]
- Ruan, J.; Walker, P.; Zhu, B. Experimental verification of regenerative braking energy recovery system based on electric vehicle equipped with 2-speed DCT. In Proceedings of the 7th IET International Conference on Power Electronics, Machines and Drives (PEMD 2014), Manchester, UK, 8–10 April 2014. [Google Scholar]
- Rakov, V. Determination of optimal characteristics of braking energy recovery system in vehicles operating in urban conditions. Transp. Res. Procedia 2020, 50, 566–573. [Google Scholar] [CrossRef]
- Taleghani, H.; Hassan, M.K.; Abdul Rahman, R.Z.; Che Soh, A. Improving regenerative braking strategy using genetic algorithm for electric vehicles. J. Mech. Eng. (JMechE) 2018, 1, 121–130. [Google Scholar]
- Xu, G.; Li, W.; Xu, K.; Song, Z. An intelligent regenerative braking strategy for electric vehicles. Energies 2011, 4, 1461–1477. [Google Scholar] [CrossRef]
- KA, A. Improving Braking Energy Recovery Efficiency of Electric Vehicle Equipped with a Super capacitor. Int. Res. J. Eng. Technol. 2018, 5, 513–517. [Google Scholar]
- Xu, L.; He, X.; Shen, X. Improving energy recovery rate of the regenerative braking system by optimization of influencing factors. Appl. Sci. 2019, 9, 3807. [Google Scholar] [CrossRef]
- Walsh, J.; Muneer, T.; Celik, A.N. Design and analysis of kinetic energy recovery system for automobiles: Case study for commuters in Edinburgh. J. Renew. Sustain. Energy 2011, 3, 013105. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, L.; Ehsani, M. Investigation of the effectiveness of regenerative braking for EV and HEV. SAE Int. J. Passenger Cars 1999, 108, 3184–3190. [Google Scholar]
- Śliwiński, C. Kinetic energy recovery systems in motor vehicles. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Scientific Conference on Automotive Vehicles and Combustion Engines (KONMOT 2016), Krakow, Poland, 22–23 September 2016; Volume 148, p. 012056. [Google Scholar]
- Akhegaonkar, S.; Nouvelière, L.; Glaser, S.; Holzmann, F. Smart and green ACC: Energy and safety optimization strategies for EVs. IEEE Trans. Syst. Man Cybern. Syst. 2016, 48, 142–153. [Google Scholar] [CrossRef]
- Guo, J.; Li, W.; Wang, J.; Luo, Y.; Li, K. Safe and Energy-Efficient Car-Following Control Strategy for Intelligent Electric Vehicles Considering Regenerative Braking. IEEE Trans. Intell. Transp. Syst. 2021, 23, 7070–7081. [Google Scholar] [CrossRef]
- Kozica, E. Look Ahead Cruise Control: Road Slope Estimation and Control Sensitivity; IEEE: Manhattan, NY, USA, 2005. [Google Scholar] [CrossRef]
- Michaelides, E.E. Thermodynamics and energy usage of electric vehicles. Energy Convers. Manag. 2020, 203, 112246. [Google Scholar] [CrossRef]
- Armenta-Deu, C.; Carriquiry, J.P.; Guzman, S. Capacity correction factor for Li-ion batteries: Influence of the discharge rate. J. Energy Storage 2019, 25, 100839. [Google Scholar] [CrossRef]
- Jeff, S. How to Read Battery Discharge Curves, Battery Power Tips. 2021. Available online: https://www.batterypowertips.com/how-to-read-battery-discharge-curves-faq/ (accessed on 25 April 2022).
- Neeraj, K.S. Know Your Lithium-Ion Cells, Cell Specifications Performance Parameters. EV Battery, EVreporter. 4 February 2021. Available online: https://evreporter.com/know-your-lithium-ion-cells/ (accessed on 25 April 2022).
- Neeraj, K.S. Capacity Testing of Rechargeable Lithium-Ion Cells. EVreporter. 20 February 2021. Available online: https://evreporter.com/capacity-testing-of-rechargeable-lithium-ion-cells/ (accessed on 25 April 2022).
- Technical Data Sheet. BMWi3. Technical Specifications. BMW i3 (I01): Engines Technical Data|BMW.am. Available online: https://www.bmw.am/en/all-models/bmw-i/i3/2021/bmw-i3-technical-data.html#tab-0 (accessed on 21 April 2022).
- Technical Data Sheet. BMWi3. Available online: https://www.press.bmwgroup.com/global/article/attachment/T0284828EN/415571 (accessed on 21 April 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).