The Sensitivity in Consumption of Different Vehicle Drivetrain Concepts Under Varying Operating Conditions: A Simulative Data Driven Approach
Abstract
1. Introduction
2. State of the Art
2.1. Vehicle Consumption Modelling
2.2. Secondary Demand Model
2.3. Studies Concerning Range/Consumption
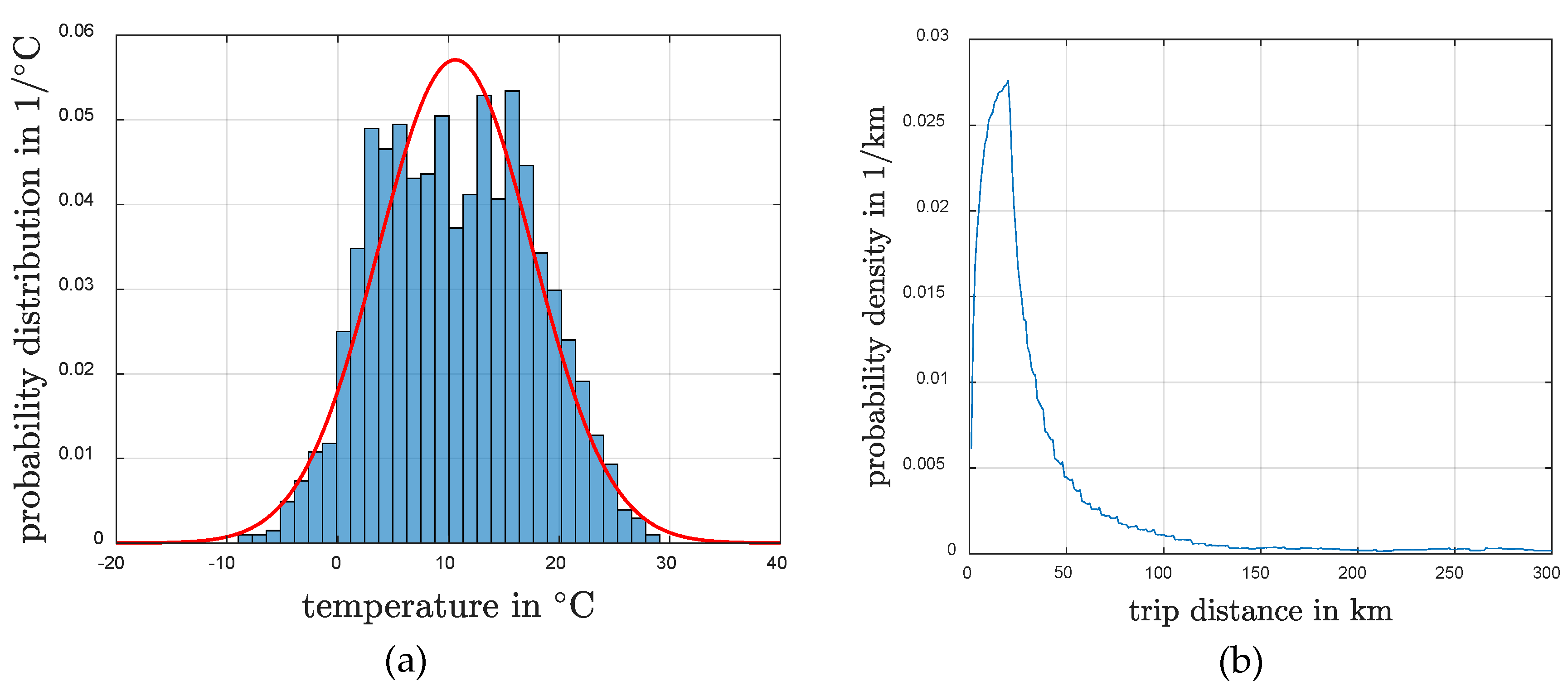
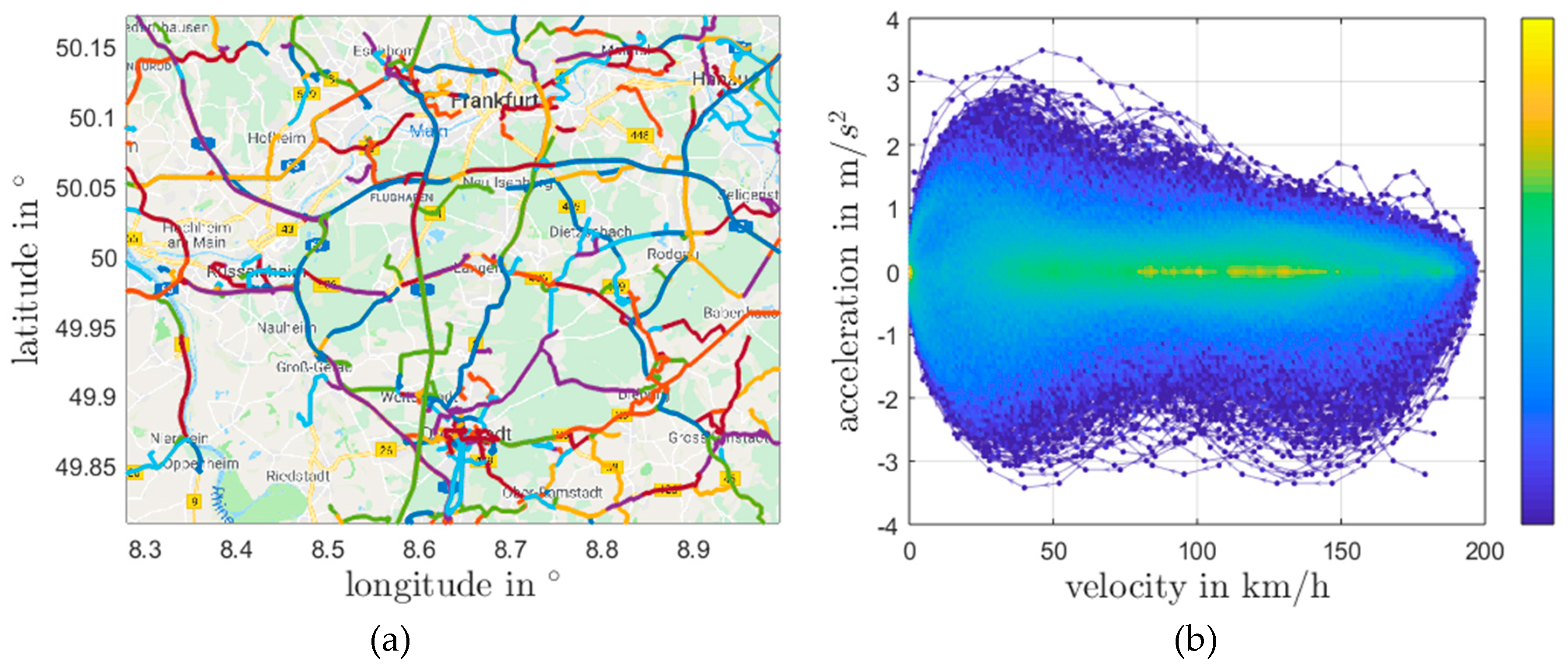
3. Data Basis for the Evaluation of Vehicle’s Consumption
- The mean velocity:where v is the vehicle velocity and t is the time.
- The variance of the velocity signal:
- The variance of the longitudinal acceleration:where a is the longitudinal acceleration of the vehicle.
- The normalized energy demand for the air drag over the evaluation time:where is the total traveled distance.
- The normalized energy demand for the rolling resistance over the evaluation time:where describes the time periods of cruising or acceleration situations.
- The normalized energy demand for the acceleration resistance over the evaluation time:
4. Vehicle Model
4.1. Primary Consumption Model
4.2. Secondary Consumption Model
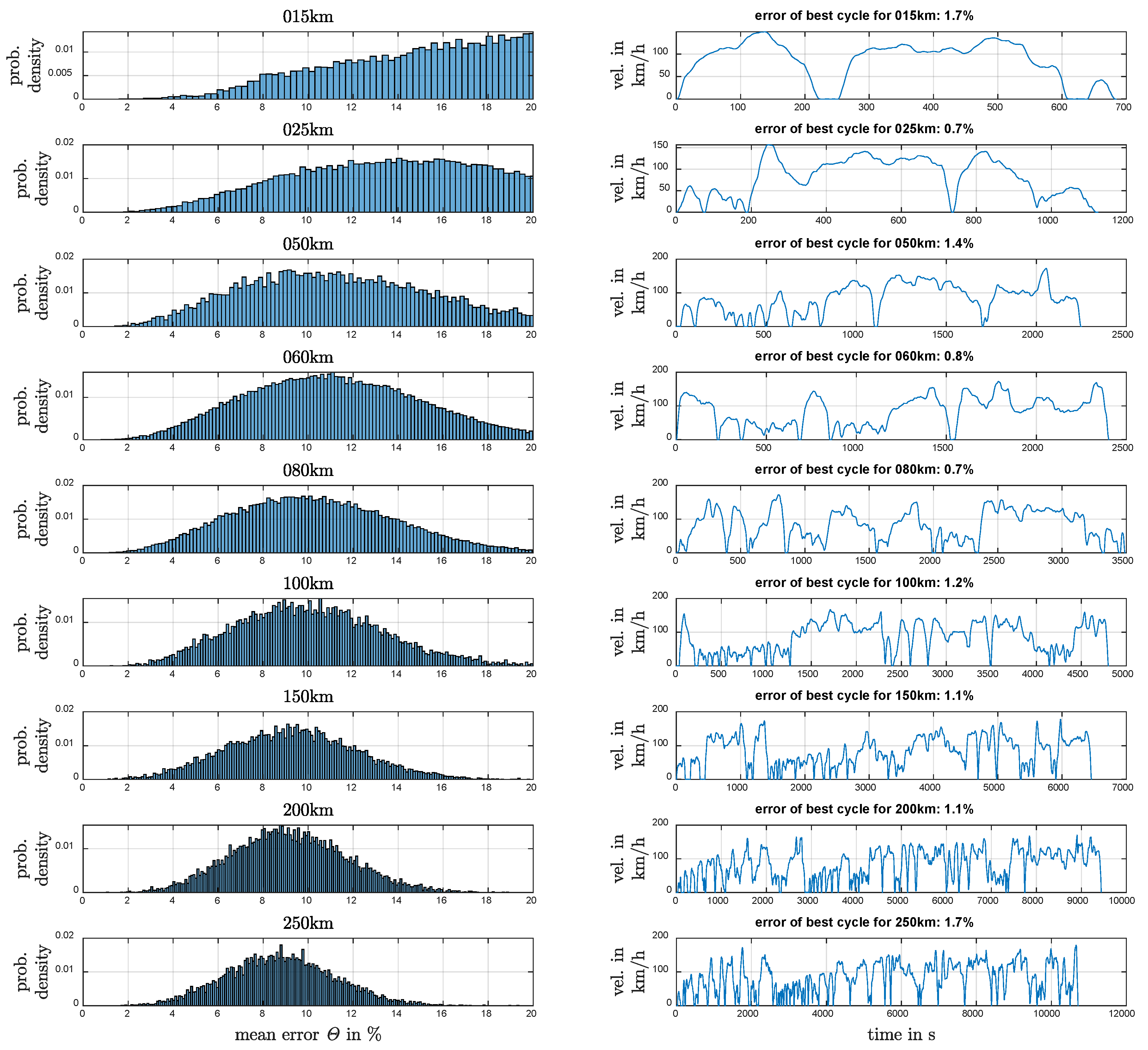
5. Results
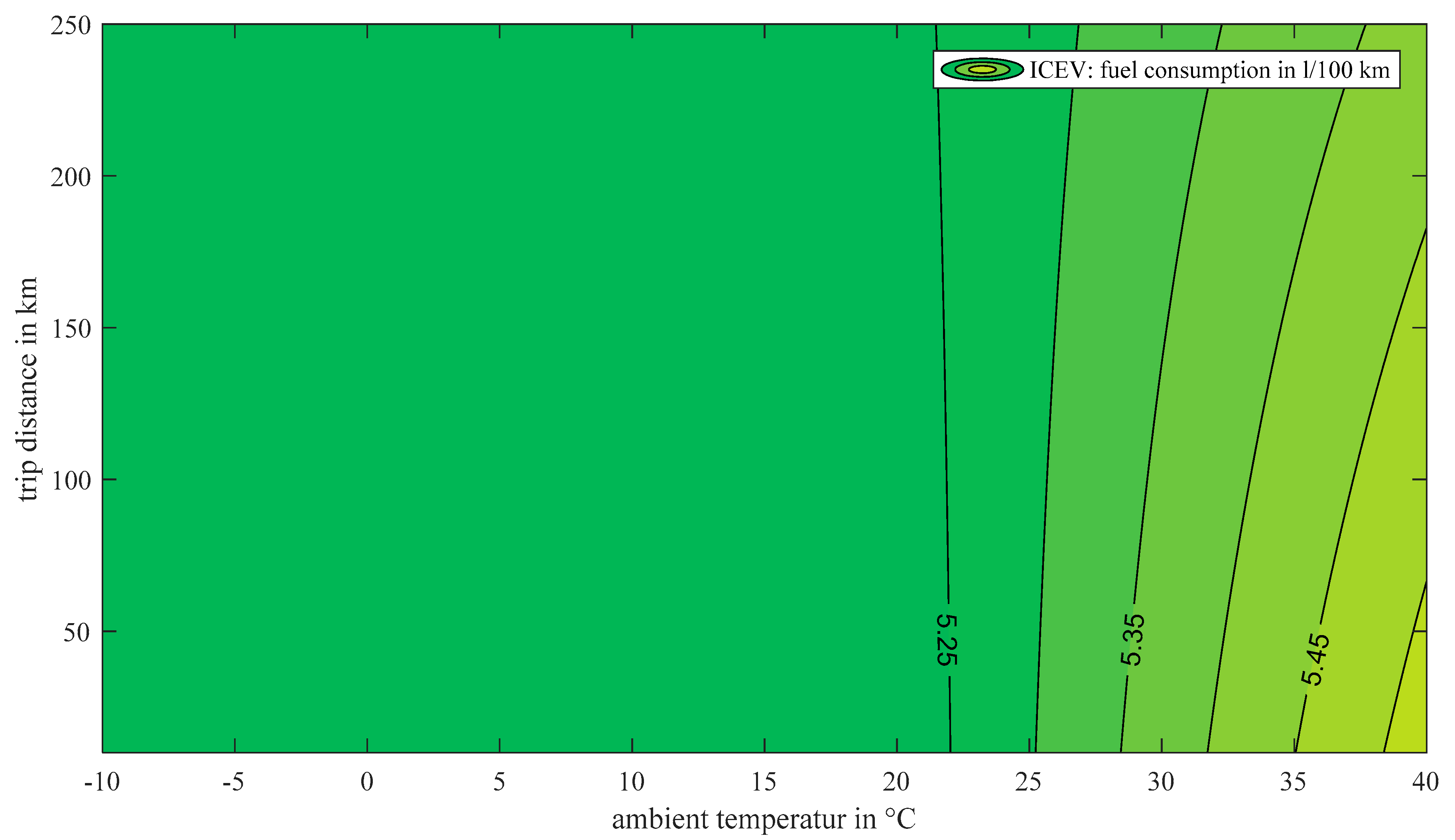
5.1. Internal Combustion Engine Vehicle
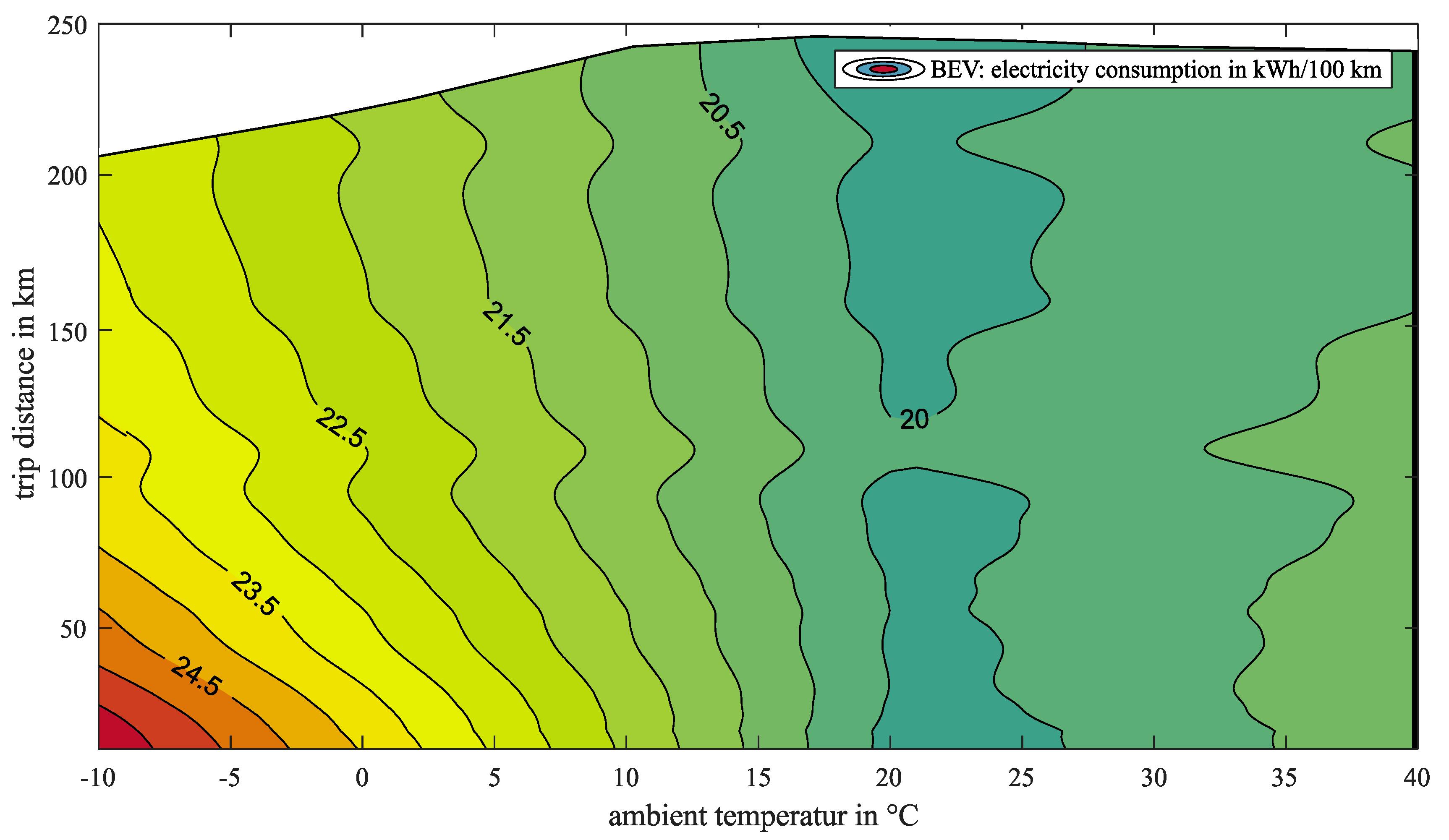
5.2. Battery Electric Vehicle
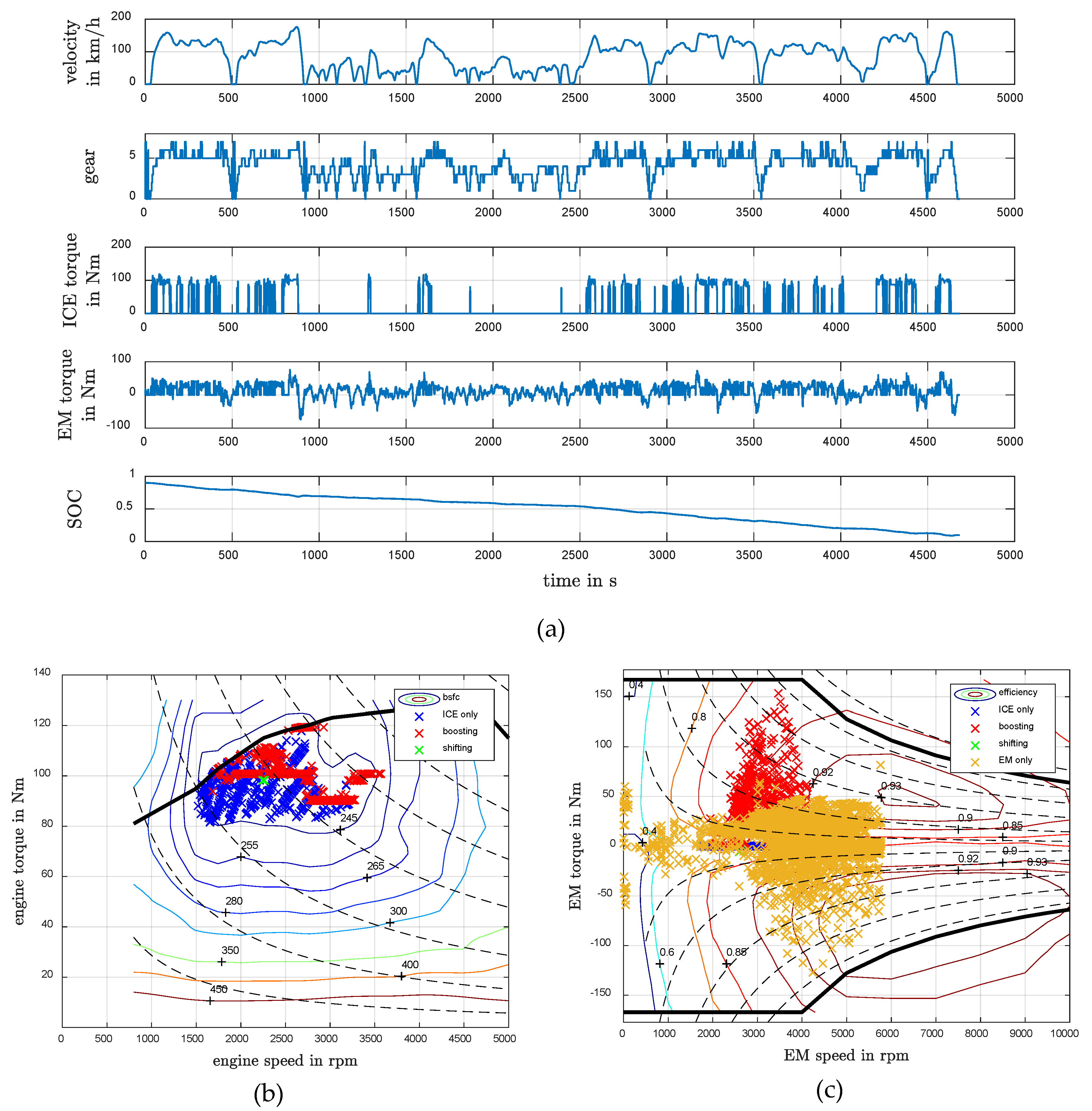
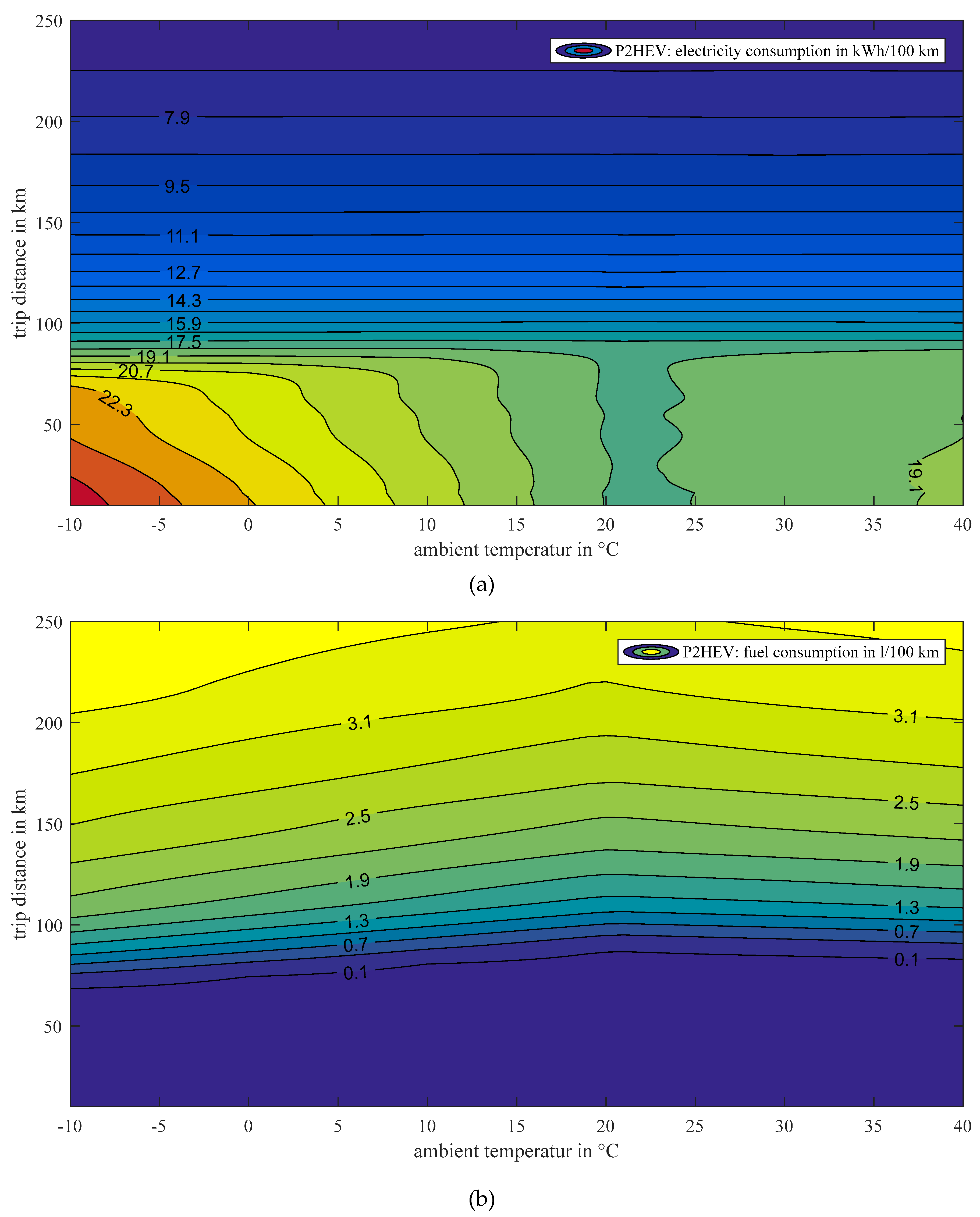
5.3. Plug-In Hybrid Electric Vehicle
6. Summary
Author Contributions
Funding
Conflicts of Interest
References
- European Union. Comission Regulation (EU), 2017 (2017/1151). Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=celex:32017R1151 (accessed on 12 October 2018).
- Mitschke, M.; Wallentowitz, H. Dynamik der Kraftfahrzeuge; 5., überarb. u. erg. Aufl. 2014; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2014. [Google Scholar]
- Sundaravadivelu, K.; Shantharam, G.; Prabaharan, P.; Raghavendra, N. Analysis of vehicle dynamics using co-simulation of AVL-CRUISE and CarMaker in ETAS RT environment. In Proceedings of the 2014 International Conference on Advances in Electrical Engineering (ICAEE), Vellore, India, 9–11 January 2014; pp. 1–4. [Google Scholar]
- Srinivasan, P.; Kothalikar, U.M. Performance Fuel Economy and CO2 Prediction of a Vehicle using AVL Cruise Simulation Techniques. SAE Int. 2009. 2009-01-1862. [Google Scholar]
- Orofino, L.; Amante, F.; Mola, S.; Rostagno, M.; Villosio, G.; Piu, A. An Integrated Approach for Air Conditioning and Electrical System Impact on Vehicle Fuel Consumption and Performances Analysis: DrivEM 1.0. SAE Trans. J. Passeng. Cars Mech. Sys. J. 2007, 116, 678–686. [Google Scholar]
- Eckert, J.J.; Corrêa, F.C.; Santiciolli, F.M.; Costa, E.D.S.; Dionísio, H.J.; Dedini, F.G. Parallel Hybrid Vehicle Power Management Co-Simulation. SAE Int. 2014. 2014-36-0384. [Google Scholar]
- Rinderknecht, S.; Esser, A.; Jardin, P. Relevance of Multidimensional Real-Driving Optimization for the Development of a Battery-Electric Vehicle 5.0. In Proceedings of the International VDI Congress, Bonn, Germany, 27–28 June 2018; VDI Verlag GmbH: Düsseldorf, Germany, 2018. [Google Scholar]
- Basler, A. Eine Modulare Funktionsarchitektur zur Umsetzung einer Gesamtheitlichen Betriebsstrategie für Elektrofahrzeuge; KIT Scientific Publishing: Karlsruhe, Germany, 2015. [Google Scholar]
- Huang, D.; Wallis, M.; Oker, E.; Lepper, S. Design of Vehicle Air Conditioning Systems Using Heat Load Analysis. SAE Int. 2007. 2007-01-1196. [Google Scholar]
- Titov, G.; Lustbader, J.A. Modeling Control Strategies and Range Impacts for Electric Vehicle Integrated Thermal Management Systems with MATLAB/Simulink. In Proceedings of the WCXTM 17: SAE World Congress Experience, Detroit, MI, USA, 4–6 April 2017; SAE International400 Commonwealth Drive: Warrendale, PA, USA, 2017. [Google Scholar]
- Liu, K.; Wang, J.; Yamamoto, T.; Morikawa, T. Exploring the interactive effects of ambient temperature and vehicle auxiliary loads on electric vehicle energy consumption. Appl. Energy 2018, 227, 324–331. [Google Scholar] [CrossRef]
- Fiori, C.; Ahn, K.; Rakha, H.A. Power-based electric vehicle energy consumption model: Model development and validation. Appl. Energy 2016, 168, 257–268. [Google Scholar] [CrossRef]
- Yuksel, T.; Michalek, J.J. Effects of regional temperature on electric vehicle efficiency, range, and emissions in the United States. Environ. Sci. Technol. 2015, 49, 3974–3980. [Google Scholar] [CrossRef] [PubMed]
- Deutscher Wetterdienst. WESTE-XL. Available online: https://www.dwd.de/DE/leistungen/weste/westexl/weste_xl.html (accessed on 12 October 2018).
- infas; DLR. Mobilität in Deutschland 2008. Available online: http://www.mobilitaet-in-deutschland.de/pdf/MiD2008_Abschlussbericht_I.pdf (accessed on 12 October 2018).
- Esser, A.; Zeller, M.; Foulard, S.; Rinderknecht, S. Stochastic Synthesis of Representative and Multidimensional Driving Cycles. SAE Int. J. Alt. Power. 2018, 7, 263–272. [Google Scholar] [CrossRef]
- OpenStreetMap. Available online: www.openstreetmap.org (accessed on 12 October 2018).
- Wipke, K.B.; Cuddy, M.R.; Burch, S.D. ADVISOR 2.1: A user-friendly advanced powertrain simulation using a combined backward/forward approach. IEEE Trans. Veh. Technol. 1999, 48, 1751–1761. [Google Scholar] [CrossRef]
- An, J.; Binder, A. Operation Strategy with Thermal Management of E-Machines in Pure Electric Driving Mode for Twin-Drive-Transmission (DE-REX). In Proceedings of the 2017 IEEE Vehicle Power and Propulsion Conference (VPPC), Belfort, France, 14–17 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- An, J.; Binder, A. Permanent magnet synchronous machine design for hybrid electric cars with double e-motor and range extender. Elektrotech. Inftech. 2016, 133, 65–72. [Google Scholar] [CrossRef]
- Paganelli, G.; Delprat, S.; Guerra, T.M.; Rimaux, J.; Santin, J.J. Equivalent Consumption Minimization Strategy for Parallel Hybrid Powertrains. In Proceedings of the IEEE Vehicular Technology Conference, Birmingham, AL, USA, 6–9 May 2002. [Google Scholar]
- Serrao, L.; Onori, S.; Rizzoni, G. ECMS as a realization of Pontryagin’s minimum principle for HEV control. In Proceedings of the IEEE American Control Conference, St. Louis, MO, USA, 10–12 June 2009. [Google Scholar]
- Rinderknecht, S.; Esser, A.; Schleiffer, J.-E.; Eichenlaub, T. Comparative Real-Driving Optimization of Drivetrain Concepts regarding the Ecological Impact—A Big Data Approach for the Fleet. In Proceedings of the eDSIM Conference, Darmstadt, Germany, 25–26 September 2018. [Google Scholar]
- Beetz, K.; Kohle, U.; Eberspach, G. Beheizungskonzepte für Fahrzeuge mit Alternativen Antrieben. ATZ Automobiltechnische Zeitschrift 2010, 112, 246–249. [Google Scholar] [CrossRef]
- Großmann, H. Pkw-Klimatisierung. Physikalische Grundlagen und Technische Umsetzung; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
| Criteria | Profile | Single Cycle | Error |
|---|---|---|---|
| 23.067 | 22.987 | 0.3% | |
| 150.481 | 150.233 | 0.1% | |
| 0.2084 | 0.2105 | 1.0% | |
| 577.369 | 582.641 | 0.9% | |
| 0.584 | 0.587 | 0.5% | |
| 0.1223 | 0.1236 | 0.1% | |
| θ | 0.66% |
| Main Parameters | ICEV | BEV | PHEV |
|---|---|---|---|
| ICE power in kW | 96 | ~ | 85 |
| EM power in kW | ~ | 300 | 120 |
| Battery capacity in kWh | ~ | 60 | 20 |
| Number of gears | 7 | 1 | 7 |
| Total mass in kg | 1109 | 1635 | 1358 |
| Necessary starting torque in Nm | 1656 | 2442 | 2028 |
| Typical electrical power rating of HVAC system in W [24] | 400–2000 | 6000 | 3500 |
| HVAC Technology | ICEV | BEV | PHEV |
|---|---|---|---|
| Heat exchanger heating | ✓ | ✕ | ✓ |
| PTC element heating | (✓) | ✓ | ✓ |
| Heat pump heating | ✕ | (✓) | ✕ |
| Heat pump cooling | ✓ | ✓ | ✓ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jardin, P.; Esser, A.; Givone, S.; Eichenlaub, T.; Schleiffer, J.-E.; Rinderknecht, S. The Sensitivity in Consumption of Different Vehicle Drivetrain Concepts Under Varying Operating Conditions: A Simulative Data Driven Approach. Vehicles 2019, 1, 69-87. https://doi.org/10.3390/vehicles1010005
Jardin P, Esser A, Givone S, Eichenlaub T, Schleiffer J-E, Rinderknecht S. The Sensitivity in Consumption of Different Vehicle Drivetrain Concepts Under Varying Operating Conditions: A Simulative Data Driven Approach. Vehicles. 2019; 1(1):69-87. https://doi.org/10.3390/vehicles1010005
Chicago/Turabian StyleJardin, Philippe, Arved Esser, Stefano Givone, Tobias Eichenlaub, Jean-Eric Schleiffer, and Stephan Rinderknecht. 2019. "The Sensitivity in Consumption of Different Vehicle Drivetrain Concepts Under Varying Operating Conditions: A Simulative Data Driven Approach" Vehicles 1, no. 1: 69-87. https://doi.org/10.3390/vehicles1010005
APA StyleJardin, P., Esser, A., Givone, S., Eichenlaub, T., Schleiffer, J.-E., & Rinderknecht, S. (2019). The Sensitivity in Consumption of Different Vehicle Drivetrain Concepts Under Varying Operating Conditions: A Simulative Data Driven Approach. Vehicles, 1(1), 69-87. https://doi.org/10.3390/vehicles1010005





