Non-Invasive Assessment of Heat Comfort in Dairy Calves Based on Thermal Signature

Abstract

Infrared thermography (IRT) is explored as a non-invasive method for indirectly measuring parameters related to animal performance and welfare. This study investigates a feature extraction method termed the “thermal signature” (TS), a descriptor vector derived from the temperature matrix of an animal’s body surface, representing the percentage distribution of temperatures within predefined ranges. The TS, combined with environmental data, serves as a predictor attribute for machine learning-based classifier models to assess heat stress levels. The methodology was applied to a dataset collected from two groups of five dairy calves housed in a climate-controlled chamber and exposed to two artificial heat waves over 13 days. Data, including IRT measurements, respiratory rate (RR), rectal temperature (RT), and environmental variables, were collected five times daily (from 6 a.m. to 10 p.m., every four hours). Classifier models were developed using random forest (RF), support vector machine (SVM), artificial neural network (ANN), and K-nearest neighbor (KNN) algorithms. The RF models based on RR achieved the highest accuracies, 94.1% for two heat stress levels and 80.3% for three heat stress levels, using TS configurations with six temperature ranges. The integration of TS with machine learning-based models demonstrates promising results for developing or enhancing classifiers of heat stress levels in dairy calves.

1. Introduction

The rearing of Holstein dairy cattle in tropical countries such as Brazil poses significant challenges due to heat stress caused by high ambient temperatures throughout the year [1,2]. While numerous studies have focused on heat stress in adult animals [3,4], investigations targeting the pre-weaning and rearing phases remain scarce [5]. These stages are critical for herd replacement and require specialized management practices, given the high incidence of disease associated with low immunity in the early months of life. Environmental conditions—such as air temperature, humidity, and solar radiation—when exceeding the thermal comfort zone, can induce heat stress [6]. This condition compromises animal welfare, reduces productivity, adversely affects health, and in extreme cases, can lead to death [7]. In this context, monitoring body temperature can not only support the management of heat stress but also assist in the early detection of inflammatory diseases [8].

Traditionally, thermal comfort indices have been used to characterize the thermal conditions based on environmental variables to indicate heat stress levels, such as the temperature, wet bulb temperature, and humidity index (THI) [9,10]. However, these indices do not consider the fact that the individual animal’s adaptive physiological responses, such as respiratory rate and core body temperature, are reliable indicators of stress. Although the physiological parameters are also reliable indicators of heat stress, their conventional assessment methods include manual and visual collection, which require careful and meticulous investigation and are often invasive and stressful, making them impractical for large-scale application [11,12].

Heat stress triggers several physiological effects in dairy cows, including increased body temperature, respiratory rate, and peripheral blood flow [13,14], indicating that skin temperature serves as a reliable indicator of heat stress [5,15,16].

An alternative approach to assess heat stress is the evaluation of body-surface temperature, which reflects peripheral microcirculatory activity and provides indirect insights into internal thermoregulatory responses. Microcirculation on the body surface is a parameter that has been researched for the diagnosis of thermal stress using data extracted from infrared thermography [17]. Infrared thermography is a tool for measuring heat transfer through radiation naturally emitted by bodies, without the need for physical contact (non-invasive) which can be obtained by cameras or through a thermographic matrix [18].

Indirect physiological measurements usually require mathematical models to describe the relationships between the variables involved. Biological systems involve complex relationships between variables, making modeling based on classical methods quite complex. In this regard, recent research on computational methods based on artificial intelligence (AI) techniques has achieved promising results in the development of predictive models for evaluating heat stress [19]. Thus, Rodrigues et al. [20] proposed a method referred to as the thermal signature to extract features from infrared thermography images. This technique considers the full range of temperatures within regions of interest in an image, generating a descriptor vector that represents the percentage distribution of pixel temperatures across predefined intervals.

The proposed methodology in Rodrigues et al. [20] improves the robustness and reliability of the analysis by integrating the complete thermal profile, as opposed to depending on discrete temperature measurements or averages. Accordingly, the objective of this study is to develop and evaluate a machine learning-based classifier for heat stress in dairy calves by extracting and selecting optimal features from thermographic images of key body-surface areas—integrated with environmental data—using a balanced, climate chamber-generated dataset to identify the most informative thermal signatures and the best classifier architecture for accurate stress-level discrimination.

2. Materials and Methods

The experiment to obtain data was carried out at the Fernando Costa Campus of the University of São Paulo (USP) in Pirassununga, SP, located at 21°59′46″ S 47°25′33″ W and an approximate altitude of 627 m. The city has an average temperature and precipitation of 21.5 °C and 1395 mm, respectively, with rainy summers and dry winters. The work was approved by the Brazilian Animal Use Ethics Committee with protocol 6957201219 (ID 001415). Data collection was carried out in the Climatic Chamber of the Department of Animal Reproduction, belonging to the School of Veterinary Medicine and Animal Science of the University of São Paulo, from 1 September 2020 to 15 October 2020.

Data collection was carried out during the confinement of 10 weaned Holstein calves, purebred by origin, with an average weight between 120 and 140 kg. The installation (climatic chamber) in which the animals were housed had a concrete floor, feeding troughs, and drinking fountains. During the confinement period, the troughs were filled twice a day (7 a.m. and 3 p.m.), and water was provided ad libitum. The animals were fed a diet consisting of hay, silage, and concentrated feed formulas, with the quantities adjusted weekly based on daily feed intake scores. The experimental procedure for collecting data in a climatic chamber enables the simulation of heat waves and allows us to obtain a database with animals at different levels of heat stress, a fundamental factor for improving the performance of prediction models. Animals were continuously monitored by veterinary professionals, ensuring the exclusion of any clinical conditions in the animals.

The thermoneutral zone (TNZ) for young calves is bounded by the lower critical temperature and the upper critical temperature, reported as 10 °C and 26 °C, respectively [21].

The heat waves simulated in this study were based on a 30-year climate dataset from the Pirassununga, SP, region. Climate data from 1980 to 2013, provided by Xavier et al. [22], were analyzed by the Center for Meteorological and Climate Research Applied to Agriculture (CEPAGRI/UNICAMP, Campinas, São Paulo, Brazil) using the 90th-percentile method to identify extreme heat events. The intensity of the simulated heat wave was modeled after a real event from 1988, which lasted five days and reached a peak temperature of 35.7 °C. A 13-day interval between two heat waves was adopted, replicating the pattern observed that year.

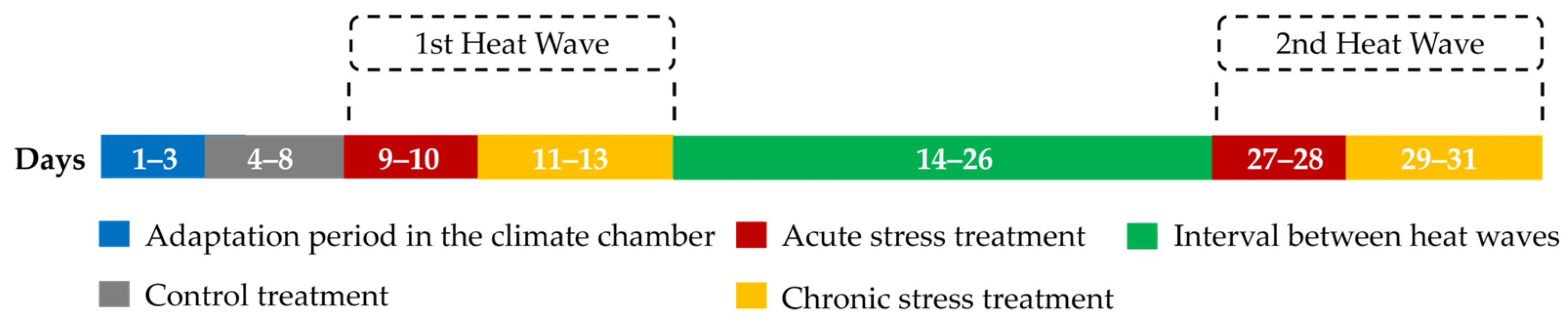
In the climate chamber, heat waves were reproduced with a gradual daily temperature increase: 30 °C at 10 a.m., 32 °C at noon, and 35.7 °C from 2 p.m. to 3:00 p.m. After 3:00 p.m., the system was turned off, allowing a natural cooling effect to simulate the environmental temperature drop typically observed at the end of the day. During the experimental period, the animals were submitted to three different treatments (control, acute stress, and chronic stress) according to Figure 1:

• Control treatment—ambient temperature: Carried out in the initial period of 5 days (after the animals’ 3-day adaptation period in the climatic chamber), with temperatures ranging from 22 °C to 31 °C (average of 26.8 °C) and relative humidity ranging from 30% to 80% (average of 54.4%).
• Acute and chronic stress treatments—stressful environment: Carried out to simulate heat waves, with temperatures varying between 30 °C and 35.7 °C from 10 a.m. to 3 p.m. over 5 days. The first two days were considered as acute stress treatment whilst the period from the third to fifth day represented the chronic stress treatment, thus obtaining a total period of five days for each heat wave.

Figure 1. Experimental stage timeline.

Figure 1. Experimental stage timeline.

Data collection was performed 5 times a day (from 6 a.m. to 10 p.m. every 4 h) in the control and chronic stress treatments. In the acute stress treatment, data were collected 9 times a day (from 6 a.m. to 10 p.m. every 2 h). During the experimental period, the animals underwent 3 days of adaptation in the climatic chamber, 5 days of control treatment, and two heat waves separated by an interval of 13 days. The simulation of two heat waves separated by a 13-day interval was designed to reflect realistic environmental patterns based on historical climate data from the study region [21].

From a physiological perspective, this experimental approach enables the evaluation of both the acute effects of heat exposure and the animals’ adaptive or cumulative responses to repeated thermal challenges. The 13-day interval serves as a recovery period between stress events, allowing for the investigation of potential resilience mechanisms or delayed physiological effects that would not be detectable under continuous heat exposure.

2.1. Data Collection and Preprocessing

Monitoring of the installation’s local microclimate was carried out using a HOBO U12-012 Temp/RH/Light Data Logger (Onset Computer Corporation, Cape Cod, MA, USA), installed in the center of the climate chamber. This equipment carried out the automatic measurement and storage of dry bulb temperature (DBT), humidity (RH), and enthalpy (H) throughout the experiment, 24 h a day, every 15 min.

Physiological data collection was performed by measuring rectal temperature (RT), respiratory rate (RR), and infrared thermography (IRT). RT was measured with a digital clinical thermometer. The RR was measured by counting the time after every ten movements of the flank using a stopwatch, and the number of movements per minute was subsequently calculated. The IRT data were obtained with a TESTO 875-2i camera (TESTO, Titisee-Neustadt, Germany) with projection perpendicular to the animal and emissivity set at 0.98. IRT data were obtained from the following body regions: head (forehead, ear, and eye), ribs, and flank. From the processing of the IRT data, the maximum, average, and minimum temperatures and the thermal signature (TS) were determined.

To obtain the TS, each IRT data matrix, representing a temperature map of a specific anatomical region of the animal, was processed individually (1740 images per region). In the first step, the matrices were segmented based on predefined body regions. Subsequently, the total number of temperature cells across all matrices was determined, and the temperature values were grouped into ranges using the quantile method, in which each range corresponds to a specific quantile. To increase resolution in the most frequently occurring temperature region, the last quantile was further subdivided into additional sub-quantiles. As a result, the temperature intervals became asymmetrical, since they were designed to ensure that each range contained approximately the same number of temperature cells across the dataset. In the final step, the relative frequency (i.e., percentage distribution) of the temperature cells within each range was computed for each IRT data matrix. This yielded a descriptor vector in which each element represented the proportion of temperature cells within a given range. The TS is thus defined as this descriptor vector, capturing the temperature distribution within the segmented body region [20].

Figure 2 presents a diagram of IRT data processing to obtain the TS and surface temperatures (average, maximum, and minimum), using the IRT of the animal’s eye region as a reference. As shown in Figure 2, the feature extraction process from the IRT data was conducted in three stages: (i) generation of temperature matrices from the proprietary BMT image format using IRSoft software (vesion 3.1) provided by the camera manufacturer; (ii) extraction of a visible image file from the temperature matrices and identification of regions of interest (ROIs) using a Python (Google Colab web platform version 2024-04-15); and (iii) construction of a feature extraction dataset from the cropped ROIs, also performed on Google Colab using a Python script.

2.2. Computational Modeling

After the data were collected and analyzed, the models were built, programmed, simulated, and confronted. Figure 3 diagrammatically illustrates the methodology used in the development of classifier models. In this diagram, it can be seen that the predictive attributes (input) are composed of the characteristics extracted from the IRT data (thermal signature and surface temperatures) and environmental variables. The target attribute (class output) of the models is the thermal stress-level classification. RR and RT values were used as ground truth, and the classification thresholds were obtained from peer-reviewed scientific literature [21].

All modeling procedures were performed to classify heat stress levels based on respiratory rate (RR), using both two- and three-class systems, and rectal temperature (RT), using a two-class system. These classifications were established according to threshold values reported in the literature [21,23], as shown in

Table 1. Classification of animal heat stress levels based on threshold values.

Heat Stress Levels	RR-3-Classes (mov/min)	RR-2-Classes (mov/min)	RR-2-Classes (°C)
Comfort	RR < 50	RR < 50	RT ≤ 39.3
Alert	50 ≤ RR ≤ 65
Danger	RR > 65	RR ≥ 50	RT > 39.3

Physiological data: respiration rate (RR); rectal temperature (RT). Parameters (classes): number of classes used for heat stress-level classification.

.

The modeling process resulted in three final heat stress classification models: RR-3-Classes (Table 1), RR-2-Classes (with alert and danger grouped into a single class), and RT-2-Classes (Table 1). The RR-3-Classes and RR-2-Classes models classified animals into three and two heat stress levels, respectively, based on respiratory rate values. In contrast, the RT-2-Classes model classified animals into two heat stress levels using rectal temperature values.

Hyperparameters for each model were first optimized through grid search, and the models were then trained using ten-fold cross-validation. The modeling step was carried out in four phases: selection of the best ROI; selection of the best machine learning-based algorithm (RF—random forest; SVM—support vector machine; ANN—artificial neural network; or KNN—K-nearest neighbors); selection of predictive attributes from data extracted from the IRT data; and selection of predictive attributes from environmental data. At the end of the three phases, the best classifier model was obtained for each output attribute (RR-2-Classes, RR-3-Classes, and RT-2-Classes).

Classifier selections (models) were performed using the Friedman and Nemenyi tests [24]. The modeling steps were implemented using a Python script developed on the Google Colab web platform. The Friedman test was conducted on a set of accuracies from computational models to determine if there were significant differences among the algorithms. When the Friedman test yields a p-value close to 0, it indicates significant differences in performance among the algorithms. Subsequently, the Nemenyi test is performed to identify which pairs of algorithms differ significantly. The Nemenyi test compares the accuracy differences between each pair of algorithms. If the difference between two algorithms is less than the critical distance, they are considered equivalent; otherwise, they are deemed significantly different.

3. Results

3.1. Characterization of the Thermal Environment and Physiological Responses

The results of the statistical analysis addressed in this item guided the modeling step. It was possible to observe the trends of physiological and environmental variables and their relationships.

During the study, under heat wave conditions, the average DBT inside the climatic chamber was 29 °C, ranging from a minimum of 22 °C to a maximum of 37 °C. The average RH was 52%, with values ranging from 31% to 80%. The average H was 68 kJ kg⁻¹, with a minimum of 47 kJ kg⁻¹ and a maximum of 84 kJ kg⁻¹. The average THI was 76, with a minimum of 68 and a maximum of 85.

The mean air temperatures recorded in all treatments exceeded the upper critical limit for thermal comfort in calves. Specifically, mean values were 27 °C for the control treatment, 29 °C for the acute stress treatment, and 30 °C for the chronic stress treatment, while maximum temperatures reached 31 °C in the control treatment and 37 °C in both stress treatments.

The average RH observed during the study was 54% in the control treatment, 52% in the acute stress treatment, and 51% in the chronic stress treatment—all within the range of 50% to 70%, which is considered adequate for efficient heat exchange between the animal and the environment [21]. The maximum RH values, 80% in the control treatment, 73% in the acute stress treatment, and 72% in the chronic stress treatment, likely did not impair thermal dissipation, as they occurred around 6 a.m., when ambient temperatures were milder.

The average THI values recorded for the acute and chronic stress treatments were 77 and 78, respectively, while the maximum THI reached 78 in the control treatment and 85 in both stress treatments. These results indicate that the animals were exposed to considerable thermal stress during the heat waves, likely triggering significant physiological responses.

Table 2. Correlation between physiological and environmental variables.

		DBT	RH	H
Full Experiment	RR	0.36	−0.26	0.27
	RT	0.27	−0.20	0.22
1st Heat Wave	RR	0.28	−0.43	−0.02
	RT	0.21	−0.21	0.12
2th Heat Wave	RR	0.40	−0.20	0.36
	RT	0.32	−0.19	0.25

Environmental data: dry bulb temperature (DBT); relative humidity (RH); enthalpy (H). Physiological data: respiration rate (RR); rectal temperature (RT).

presents the correlations between physiological and environmental variables. Correlations were obtained by treatment (using the database of the entire experiment and the database of the first heat wave and the second heat wave separately), with the aim of refining the analysis for the data selection in the modeling stage. Thus, in Table 2, it is possible to observe a greater correlation between the data obtained in the second heat wave. It can be seen that the highest correlation (0.40) occurs between FR and DBT with the data from the second heat wave.

Table 3. Correlations between physiological variables.

		Full Data		1st Wave		2th Wave
		RR	RT	RR	RT	RR	RT
IRT Eye	Max	0.48	0.55	0.37	0.46	0.54	0.63
IRTFor	Max	0.36	0.38	0.27	0.31	0.42	0.43
	Avg	0.38	0.35	0.31	0.28	0.44	0.4
	Min	0.33	0.26	0.23	0.18	0.39	0.33
IRTEar	Max	0.38	0.49	0.28	0.43	0.45	0.55
	Avg	0.46	0.48	0.39	0.43	0.54	0.54
	Min	0.50	0.40	0.50	0.40	0.60	0.50
IRTRib	Max	0.45	0.39	0.32	0.29	0.49	0.45
	Avg	0.46	0.36	0.35	0.27	0.50	0.42
	Min	0.4	0.30	0.30	0.20	0.50	0.40
IRTFlan	Max	0.39	0.39	0.23	0.3	0.46	0.45
	Avg	0.41	0.36	0.29	0.29	0.47	0.41
	Min	0.40	0.30	0.30	0.20	0.40	0.30

Physiological data: respiration rate (RR); rectal temperature (RT); surface temperature obtained with infrared thermography technique (IRT); eye surface temperature (IRTEye); forehead surface temperature (IRTFor); ear surface temperature (IRTEar); rib surface temperature (IRTRib); flank surface temperature (IRTFlan). Parameters: (Avg) average; (Min) minimum; (max) maximum.

presents the correlations between the physiological variables and the maximum, average, and minimum temperatures extracted from the IRTs from ROIs. The results show that eye maximum surface temperature (IRTEye) is best correlated with RR and RT, presenting values of 0.48 and 0.55, respectively. Furthermore, IRT data obtained in the second heat wave were better correlated with physiological variables. Finally, it is important to highlight that the lowest correlations of RR and RT are observed in the database of the first heat wave with the minimum temperature of the forehead region (IRTFor) of the animals, presenting values of 0.23 and 0.18, respectively. Therefore, IRTEye was defined as the ROI to be used in the subsequent phases of computational modeling.

Table 4. Descriptive statistics of the physiological and environmental data selected for computational modeling.

	Variable		Average ± Standard Deviation	Min	Max
Physiological Data	RR (mov/min)		58.4 ± 19	23.4	151.5
	RT (°C)		39.2 ± 0.5	37.7	41.0
	IRTEye (°C)	Max	37.1 ± 0.8	34.6	39.4
	IRTEar (°C)	Max	37.1 ± 1.2	27.3	39.8
		Avg	36.2 ± 1.3	26.7	38.8
		Min	34.9 ± 1.7	25.8	38.3
Environmental Data	DBT (°C)		28.5 ± 3.4	21.6	35.9
	RH (%)		52.4 ± 10.7	31.3	80.3
	H (kJ/kg)		63.4 ± 7.3	47.1	84.2

Environmental data: dry bulb temperature (DBT); relative humidity (RH); enthalpy (H). Physiological data: respiration rate (RR); rectal temperature (RT); data temperature obtained with infrared thermography technique (IRT); eye surface temperature (IRTEye); ear surface temperature (IRTEar). Parameters: (Avg) average; (Min) minimum; (Max) maximum.

presents the descriptive statistics of the physiological and environmental data collected in the experimental stage and used in the computational modeling phase. The maximum RT of 41 °C indicates that there were periods in which the animals experienced a high level of heat stress, as this value exceeds the thermal comfort threshold for calves, which is reported in the literature as 39.3 °C [21].

3.2. Modeling and Performance of Heat Stress-Level Classifiers

In the second modeling phase, models were generated using four machine learning algorithms (RF, SVM, ANN, and KNN), and their performances were compared. In this phase, data obtained during the second heat wave of the experiment were used, as they showed a stronger correlation with the variables used to classify the level of heat stress. Figure 4 presents the significance analysis diagram based on the Friedman and Nemenyi tests, highlighting the model that achieved the best overall performance. The critical distance observed in this analysis was 1.106. Comparing the two algorithms with the best performance, RF and SVM, a difference of 0.12 (1.56–1.44) is obtained, indicating that there is no statistically significant difference between them (according to the vertical line that connects the two algorithms), since it is a value less than 1.106. Between the two algorithms with the best performance and the two worst placed, there was a significant difference, as observed in the diagram. Thus, RF and SVM performed better than ANN and KNN, so these algorithms were selected to proceed to the next modeling phases.

Figure 5 highlights the best-performing model and compares the effectiveness of predictive datasets based on thermal signatures ranges from IRT data and surface temperature metrics (No-TS: average, maximum, and minimum). The diagram also assesses whether input variation significantly affected model performance. It is observed that the three best predictive attributes for the RF algorithm were the TS vectors with ranges of four, three, and six (there is no statistically significant difference between them), and for the SVM algorithm, they were best for the ranges of six, four, and eight (there is no statistically significant difference between them and there is no statistically significant difference between the ten, No-TS, and three ranges), respectively. Accordingly, the most effective predictive attributes were selected for each algorithm to be used in the next phase: six-range TS for RF, and eight-range TS for SVM.

In the final modeling phase, different combinations of environmental datasets were evaluated as predictive attributes (datasets: DBT, RH, and H; DBT and RH; DBT and H; and DBT only). The best TS vectors identified in the previous phase for the RF and SVM algorithms (six ranges for RF and eight ranges for SVM) were retained as fixed predictive attributes. Figure 6 presents the significance analysis of the best models generated by varying the environmental input combinations, based on the results obtained in this phase. It is evident that, for both algorithms, there were statistically significant differences between the models generated using all environmental variables and those generated with one or more variables excluded. Accordingly, all environmental variables were retained for the development of the final models (RR-2-Classes, RR-3-Classes, and RT-2-Classes).

At the end of the modeling phase, the three best models were obtained using the TS from the eye region of the animals. The classification models based on respiratory rate (RR) were generated using the RF algorithm employing six-range TS (RR-2-Classes and RR-3-Classes). The best classification model based on rectal temperature (RT) was obtained using the SVM algorithm employing eight-range TS (RT-2-Classes).

Table 5. Confusion matrix of best classifier models based on RR and RT, both using 2 classes.

		Random Forest Classifier
		Comfort	Danger	Sensitivity
Classification RR-2-Classes	Comfort	414	69	85.7%
	Danger	34	1223	97.3%
	Precision	92.40%	94.70%	Accuracy
				94.1%
		SVM Classifier
		Comfort	Danger	Sensitivity
Classification RT-2-Classes	Comfort	707	160	81.5%
	Danger	155	718	82.2%
	Precision	82.0%	81.8%	Accuracy
				81.9%

Physiological data: respiration rate (RR); rectal temperature (RT).

presents the confusion matrices of the best classifier models of RR-2-Classes and RT-2-Classes. The RR-2-Classes model achieved its highest classification accuracy (94.7%) in the danger class. The RT-2-Classes classifier model obtained a general accuracy of 81.9%.

Table 6. Confusion matrix of best classifier models based on RR using 3 classes.

		Random Forest Classifier
		Comfort	Alert	Danger	Sensitivity
Classification RR-3-Classes	Comfort	426	28	29	88.2%
	Alert	39	262	158	57.1%
	Danger	18	70	710	89.0%
	Precision	88.2%	72.8%	79.2%	Accuracy
					80.3%

Physiological data: respiration rate (RR).

presents the confusion matrix of the best RR-3-Classes classifier model based on RF. It is possible to observe that the intermediate class (alert) presented lower precision and sensitivity with values of 72.8% and 57.1%, respectively. The comfort and danger classes showed an accuracy of 88.2% and 79.2% in that order.

4. Discussion

Statistical analyses were conducted to examine the relationships between physiological and environmental variables, involving the assessment of correlations between ground truth variables associated with heat stress (RT and RR) and variables extracted from thermographic images and environmental data. The descriptive statistical analysis, presented in Table 4, identified specific moments in which the animals presented high levels of heat stress, evidenced by the average values of maximum rectal temperature and maximum respiratory rate. It is important to highlight that during this analysis process, the animals were continuously monitored by veterinary professionals, ensuring the exclusion of any clinical conditions in the animals. These analyses guided the selection of variables for the subsequent modeling phase.

In a study with dairy calves exposed to heat stress (THI > 78), Laporta et al. [15] found a reduction in heart rate, rectal temperature, and ear skin temperature (−12 bpm, −2.5 °C, and −0.11 °C, respectively) in groups subjected to acclimatization during the postnatal period, demonstrating a relationship between skin temperature and other physiological parameters. These responses reflect a broader adaptive mechanism aimed at maintaining homeostasis. Other studies also support the association between physiological markers, such as rectal temperature, and heat stress resilience in calves [2,25,26].

The RF- and SVM-based models demonstrated superior performance in the construction of classifier models, presenting statistically significant differences in comparison to the other algorithms analyzed, as observed by the Friedman and Nemenyi tests. The best models obtained for the RF algorithm used as inputs attribute a TS with four, three, and six temperature ranges (there is no statistically significant difference between them). In the last modeling phase, it was observed that the removal of one or more environmental variables as an input attribute caused a significant reduction in the performance of the classifier models generated by the RF and SVM algorithms, based on the evaluation using the Friedman and Nemenyi method.

One of the main challenges in applying artificial intelligence to animal production systems is the construction of balanced datasets with a sufficient number of data points representing each environmental and physiological condition, along with the corresponding level of heat stress. Typically, methodologies for building such datasets involve labor-intensive and costly experiments, requiring data collection from groups of animals, usually of a single breed over multiple days and across different seasons. In this context, the use of climate-controlled chambers proves highly advantageous, as they allow the simulation of diverse environmental conditions, such as heat waves, and enable the development of balanced datasets. The models in this study were developed using data from 10 animals exposed to varying levels of thermal stress in a climate-controlled chamber, enabling precise control of ambient temperature. Different climatic conditions were simulated to expose the animals to a range of thermal stress levels, as recommended by Rodrigues et al. [20], to enhance classifier model performance.

The best models, obtained in our study and evaluated using metrics derived from confusion matrices, achieved accuracies of 94.1%, 80.3%, and 81.9% for classifying heat stress based on respiratory frequency at two and three stress levels, and rectal temperature at two stress levels, respectively. Analysis of the confusion matrices showed balanced class precision, with comparable accuracy rates across the models. In contrast, Rodrigues et al. [20] reported an accuracy of 90.1% for their best classifier model with two thermal stress levels in dairy cows, using thermal signature as the input. However, their model exhibited significantly higher accuracy for the “comfort” class, which had a larger number of training samples.

Previous studies have explored the use of infrared thermography and machine learning to assess heat stress in dairy cows and small ruminants [27,28,29,30]. Pacheco et al. [29] used IRT as the input to convolutional neural networks to build models designed to predict heat stress levels in dairy cows. Classification was based on RT and RR ranges. The highest accuracy achieved by the model that used RT values was 70.5%, while the model based on RR achieved a maximum accuracy of 76.3%. Furthermore, Pacheco et al. [31] used data derived from infrared thermography as the input to artificial neural networks to predict the level of heat stress in dairy cows, based on RT values, achieving a maximum accuracy of 84%. The superior accuracy achieved in our study can be attributed to the greater robustness of the thermal signature methodology used to extract features from infrared thermography (IRT) images. This method considers all ROIs within images, rather than specific points, thus making it more robust to measurement uncertainties.

The model with the highest performance obtained in the present work (with 94.1% accuracy) obtained a result very close to the best thermal stress classifier model for cattle found in the literature—94.35% [32] and 0.89 [33]. In this study, an imbalance in the data was observed, with 94.22% of observations classified as “comfort” situations. This imbalance possibly affected the accuracy of the model, making an accurate assessment difficult, especially in situations where the animals were under a high level of thermal stress (danger class). Future work should explore the scalability of the TS methodology across breeds and environmental conditions, as well as its integration into real-time monitoring systems for on-farm decision support.

5. Conclusions

This study demonstrated the potential of infrared thermography, combined with the proposed thermal signature (TS) feature extraction method, as a robust and non-invasive tool for classifying heat stress levels in dairy calves. The TS, which represents the distribution of surface temperatures across predefined ranges, was integrated with environmental data and used as the input for machine learning-based classification models. Among the algorithms evaluated, random forest and support vector machine achieved the highest performance, with classification accuracies of 94.1% and 94.0%, respectively, in the two-class classification task. These models significantly outperformed the others, as confirmed by the Friedman and Nemenyi statistical tests.

The experimental design, based on a climate-controlled chamber and balanced datasets across different heat stress conditions, enabled controlled exposure to artificial heat waves and the collection of high-quality, time-resolved physiological and environmental data. The integration of TS with environmental variables enhanced model accuracy, and the removal of any environmental input led to significant drops in performance. These findings support the critical role of combining surface temperature patterns and environmental context in predictive modeling.