1. Introduction
Several studies have shown adaptive test designs such as computerized adaptive tests (CATs; [
1,
2,
3,
4,
5,
6,
7]) or multistage tests (MST; [
8,
9,
10,
11,
12,
13]) are usually more efficient in terms of shorter test lengths, providing equal or even higher measurement precision and higher predictive validity, compared to linear fixed-length tests (LFTs; [
6,
7,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23]). The advantages of adaptive tests are particularly evident for more extreme abilities at the lower and upper end of the measurement scale [
6,
15,
24].
In situations with administration time constraints, CATs can be a good choice and should be considered. However, a decision in favor of adaptive tests also means that some disadvantages are taken for granted. Some will be explained in the following. It should become clear that MST designs, compared to CATs, do not share many of these disadvantages, which has probably also led to its popularity and use in educational measurement and, in particular, international large-scale assessments (ILSAs; e.g., [
16]). In recent years, several well-known programs, such as the Programme for International Student Assessment (PISA; [
25]), the Programme for The International Assessment of Adult Competencies (PIAAC; [
26]), Trends in the International Mathematics and Science Study collection cycle 2019 on computer-based assessment systems (eTIMSS, TIMSS; [
27]), or the National Assessment of Educational Progress (NAEP; [
28,
29]), applied MST designs and might have contributed to its popularity. Besides ILSAs, there are several other areas with successful applications in the past decade, such as psychological assessment (e.g., [
30]), or classroom assessments [
16]. It can be summarized that the application of adaptive testing currently has become an essential testing method (e.g., [
31,
32]).
In the following, we refer to MSTs and CATs in their more classical form, even if some contributions do not separate both designs so strictly from one another. Chang [
16], for example, stated that both designs could be regarded as sequential designs (see also [
33,
34,
35,
36] for dynamic multistage designs).
Here, CATs should therefore be understood as adaptive designs on the item level. Based on one or more item selection algorithms, the best-suited item is selected. The maximum of information is often defined with a success rate of
for this item. If the item pool is large enough for the desired measurement accuracy, the smallest number of items is required in CATs. Therefore, the efficiency is theoretically the largest if the item pool is large enough. Some indices to measure the amount of adaptation in practice were recently discussed by Wyse and McBride [
37].
In MSTs, the decision points are modules. These are collections of items with mostly related content (see also the comparison to testlets; [
6,
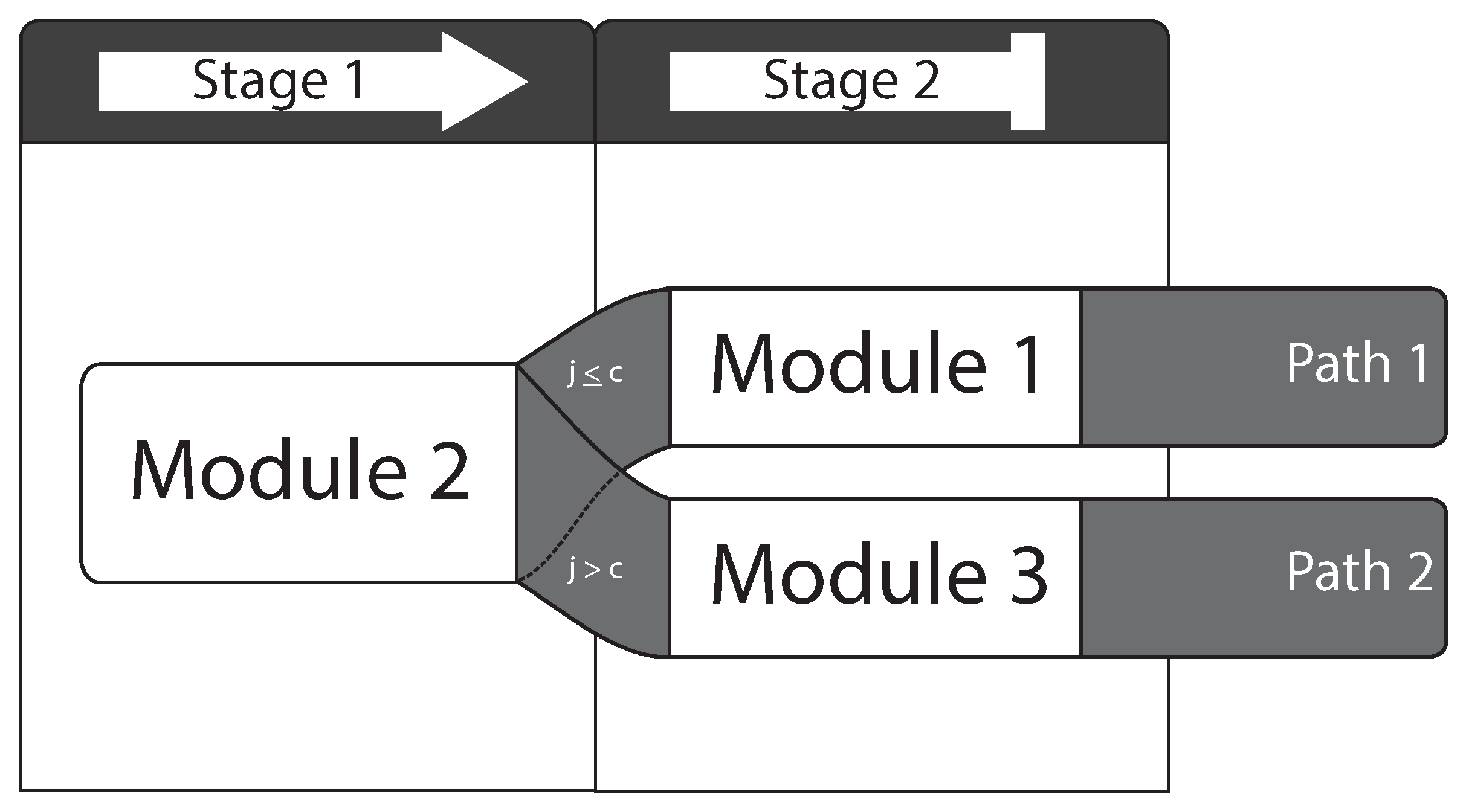
38]), certain mean item difficulties, and variances. At the start, test persons receive a routing module and, based on the performance in this module and performance-related prior information, if available, one or more additional modules. Each additional module in this routing process describes a stage in the MST design. Each stage consists of at least two modules (see
Figure 1 for an example). The specific combination of processed modules in the routing process is called a path. Different groups of modules, stages, and paths are called panels. Panels can be seen as parallel forms in LFTs. Routing in the MST context is branching from one to the next module, based on pre-specified rules.
As with all adaptive designs, the selection of items or modules is the central part of the design, and much research has been performed to serve different needs. In particular, in CATs, the item selection can become very complex. Additional considerations can refer to, e.g., content balancing or strategies to avoid overexposure and/or underexposure of items. Next to the desired purpose of that algorithm, there might also be some disadvantages, which can negatively impact the validity and the fairness of the test. In particular, in CATs, the item exposure control can become a challenging task [
13,
39].
Overexposure might be a problem if the information of those items processed more often is shared across test persons. This can threaten the validity of the test because the performance of the test persons can no longer be separable between ability and knowledge. Especially with high-stakes tests, it might be a major problem, where industry could quickly build up to collect the information of items [
40]. While simply increasing the item pool is not the solution [
39], additional algorithms must be considered. Concerning underexposure, economic considerations are probably more in the foreground, as the construction of items is very expensive. However, this can also lead to problems in parameter estimation if the sample size per item is low, which subsequently results in the inaccurate estimation of item parameters and the standard errors. Here, MST designs seem to show their advantages, as they can be designed and checked before they are applied. Hence, no additional algorithms are necessary.
1.1. Motivation
An essential factor in every test is the motivation of the test persons (see, e.g., [
41,
42,
43]). It has been reported that due to the better match of the item difficulty and the person’s ability, test persons, especially those with low abilities, are more motivated to proceed, sometimes less bored, and more committed during the test [
44,
45,
46,
47,
48,
49,
50]. On the other hand, there are several contributions concerning CATs that report negative psychological effects of the demanding item selection. Kimura [
51] stated that this could lead to negative test experiences as well as lower motivation, lower self-confidence, and increased test anxiety (see also [
52,
53,
54,
55,
56,
57,
58]). These psychological variables seem to be an important topic in testing since they could negatively affect the persons’ test performance [
56,
59,
60]. Motivation is a key factor in every low-stakes test such as ILSAs since unmotivated participants might influence the test results and thus the validity of the test (see, e.g., [
61]). It seems to be central and can be deduced from these contributions that the impact on motivation or boredom, but also anxiety, should not be ignored, as this can significantly influence the test results [
62,
63]. Finally, this contributes to standardization and thus to reliable results and more valid parameter estimates [
64,
65].
MST designs are conceptualized before the actual application. The items are explicitly assigned to modules, and every path of that design can be reviewed in advance. Therefore, these mentioned aspects can be verified before the application, and no additional algorithms are required during the actual application.
1.2. Test Anxiety
Increased test anxiety among test participants is another reported psychological effect in CATs [
60]. Due to the lack of the possibility to review items that have already been processed and, if necessary, changed by the test person, test anxiety might also be further increased [
66,
67,
68,
69,
70]. An item revision in CATs is not possible [
7,
71,
72], because the item selection in CATs is based on the responses already given. Hence, changing responses retrospectively may impact the measurement precision, which results in larger standard errors [
69,
73,
74,
75,
76,
77,
78]. Therefore, allowing item revision within CATs has been controversially discussed in the literature, even if some contributions encountered this measurement problem (see, e.g., [
66,
77,
79,
80,
81,
82]). While it can be argued that only a few persons might change their responses [
83], a lack of this ability appears to contribute to increased test anxiety. However, it is also reported that subsequent changes to given responses are mostly from wrong to processed correct [
83] and thus not only affect the psychological aspects, but also the validity of the test scores.
Several studies suggested methods to allow a (limited) item review in CATs while avoiding the negative effects of the lower measurement accuracy or the extension of the test at the same time [
68,
75,
77,
81,
82,
84]. However, the proposals can also be viewed critically. For example, Zwick and Bridgeman [
85] found that more experienced test persons may use the review options more often than others. This could again harm the validity of the test, while the absence of the item review affects all persons across the entire skill range equally [
60]. Next to the possibility of reprocessing the responses in CATs, this option can also be used to manipulate the test score [
84,
86]. Wainer [
76] described one of these strategies, in which a test person first gives only incorrect responses to continuously obtain easier items. At the end of the test, all given responses are then corrected, which results in large measurement errors. Kingsbury [
87] described a strategy in which test persons recognize whether a subsequent item is easier or more difficult than the one they have just worked on and obtain information about the given response. If the following item is easier, which hints that the prior response might be wrong, the response can be changed on this item; see also [
88]. In MSTs, all test persons have the same chance to review their given responses and change them before taking on a new module. It is, therefore, to be expected that test anxiety will be lower with MSTs.
1.3. Routing in Adaptive Designs
Item selection algorithms are one of the key factors in CATs, especially when it comes to maximizing the test economy and thus shortening the test length [
16]. Increasing the test efficiency can also be viewed critically, as we will discuss later. When choosing one of the selection algorithms, the optimization and the associated negative effects should be considered. Furthermore, the item selection is also related to considerations regarding under- and over-exposure, as well as considerations of the safety aspects. Some selection algorithms can be found in Chang [
16].
In this context, deterministic means that persons with the same performance in the same module
of
B modules with
in the same stage are routed to the same subsequent module. A decision base can be, e.g., the number of solved items (number-correct score; NC). Assuming a person
achieves a score
j in the module
, this person, given a cutoff value
c, is routed to an easier module in the cases
or
(that is, once again, performed deterministically by the test author) and, in the remaining cases, a more difficult module (see also [
6,
12]). In this simple case, the decision to route from one module to the next is only made based on the performance in the module currently being processed. This can easily be expanded by including the information from all previously processed modules in the decision. This type of routing should be referred to as the cumulative number-correct score (cNC; [
89,
90]). Since the information about the persons’ ability across modules is used, theoretically, a more valid routing is possible. In addition to the raw scores, the routing decision can also be made based on specifically processed items. Since item parameters are known, person parameters can be estimated a priori via the respective item combinations. This type of routing is referred to in the literature as item response theory (IRT)-based routing [
91]. The decision for a routing strategy in MST is linked to the efficiency of the proposed design and can also impact the precision of item parameter estimation [
6]. The available strategies can roughly be grouped into deterministic and probabilistic ones. Svetina et al. [
89] compared different routing strategies. The authors concluded that the IRT-based routing performed best, but the NC-based routing was not significantly worse when it came to the median of person parameter recovery rates. An additional argument for NC-based routing is that it is much easier to implement.
In the mentioned probabilistic routing, the routing rule
, respectively
, is expanded with an additional probability based on the performance
j. This means that routing into an easier module is not solely based on the cutoff value
c, but rather with a previously defined probability
, depending on the individual score
j of person
p. With the counter-probability
and the same score
j, the person is routed to a more difficult module. This type of routing is used, for example, in the PIAAC [
32,
92,
93]. In addition to the deterministic definition of the cutoff values
c, additional thresholds are defined for each decision stage and score.
A motivation to use probabilistic routing instead of exclusively deterministic is the possibility of being able to better control the exposure rate so that it is ensured across all proficiency levels that a minimum number of sufficient responses per item is guaranteed, even with difficult tasks (see, e.g., [
32,
93]).
To summarize: MSTs can be seen as a design with advantages from two perspectives. There are fully adaptive item-by-item designs such as CATs with a very high test economy [
14,
23,
94], on the one hand, and LFTs, on the other [
94]. MSTs allow for more efficient testing; test persons can review items within modules they have already worked on and change their responses if necessary. The design can be examined by the test authors concerning the item content regarding content balancing and security concerns, but also possible differential item functioning. Even overexposure and underexposure can be controlled more easily [
95]. While CATs are tied to the computer, MSTs can also be administered as paper-pencil tests [
19,
22,
30].
2. Item Parameter Estimation
Item parameter estimation in adaptive designs is an important topic and relates to the MST’s main component of this contribution. For the calibration of an item pool, with data obtained by an MST, an item response theory model such as the Rasch model (1PL; [
96]) is fitted. Item parameters are typically regarded as fixed, and persons are treated as either fixed or random (see, e.g., [
9,
97,
98,
99,
100], for a further discussion on this topic). Several methods are available, which will be briefly discussed in the following.
These are the marginal maximum likelihood method (MML; [
101,
102,
103]) and the conditional maximum likelihood method (CML; [
104,
105]). Various considerations can lead to choosing one of these estimation methods, such as the flexibility of that approach or more fundamental beliefs about the method.
The MML estimation method can also be applied in MST designs without leading to biased item parameter estimates (see, e.g., [
106,
107,
108]). The CML-based parameter estimation in MSTs, without severely biased item parameter estimates [
108], is only feasible by modifying the CML estimation method proposed by Zwitser and Maris [
109]. Besides the relatively newly proposed modification of the CML approach, the normal MML method and models with non-normal trait [
110] are available. It is frequently argued that the CML estimation method enables the estimation of item parameters independent of the distribution assumptions of the trait [
107,
108,
109,
111]. Comparisons between CML and MML estimation in MSTs showed biased item parameter estimates in MML if the distribution assumption deviates severely from the true distribution (see, e.g., [
109]). In our contribution, the estimation methods were systematically examined and compared. In this context, it seems very interesting that scaling the data using a multigroup model, in which the groups are represented by the respective paths in the MST design, seems to lead to severely biased parameter estimates [
106].
In the following, we only considered dichotomous item responses and utilized the 1PL model. In the 1PL model, the probability of solving item
i with difficulty
by person
p with ability
can be expressed as:
with
. Then, the likelihood
with responses
of the test person
p with ability
and the item difficulty
can be expressed as follows:
with
as the raw score of person
p with
. Equation (
2) can be seen as the starting point for the following approaches in parameter estimation. The likelihood for the response matrix
can be expressed as:
2.1. Marginal Maximum Likelihood Estimation
For the estimation in the parametric case (see Equation (
4)), a distribution
with probability density function
with a vector
containing the parameters of the latent ability distribution is introduced for person parameter
. It is assumed that the persons are a random sample from this population, e.g.,
. The random variable
is integrated out of the marginal log-likelihood function. For parameter estimation in MST designs, Glas [
108] and Zwitser and Maris [
109] stated that the distributional assumptions could be incorrect, and the estimated item parameter estimates can be severely biased. Therefore, the following simulation should shed some light on this.
Data collected based on the MST design have missing values due to the design. Mislevy and Sheehan [
112], referring to Rubin [
113], showed that MML provides consistent estimates in incomplete designs in general (see also [
106]). For MST designs, it can be shown that MML can also be applied to MST, following this justification [
106,
109]. Based on the likelihood function (
3), in the MML case, the likelihood for the observed data matrix
is the product of the integrals of the respective likelihood of the response patterns
.
with
the item score of item
i,
as the number of test persons with the raw score
r, and
as a parameters for the distribution
.
For model identification purposes, if a normal distribution is assumed, the mean is fixed to zero
, and
is freely estimated. Therefore, the marginal likelihood is no longer dependent on
(see Equation (
4)). The integral in Equation (
4) can be solved by, e.g., Gauss–Hermite quadrature by summing over a finite number of discrete quadrature points
with
and the corresponding weights
(see, e.g., [
101,
102]).
Marginal Maximum Likelihood with Log-Linear Smoothing
For the specification of the unknown latent ability distribution
in Equation (
4), both parametric and nonparametric strategies are available. Another interesting approach for the specification, which is flexible and parsimonious in terms of the number of parameters to be estimated, is the application of log-linear smoothing (LLS; [
110,
114,
115]). In IRT, this method was used, for example, by Xu and von Davier [
110]. They fitted an unsaturated log-linear model in the framework of a general diagnostic model (GDM; [
116]) to determine the discrete (latent) ability distribution
. The LLS model used here in the case of the 1PL can be described as
[
115,
117]. Here,
describes the logarithmic weighted quadrature points
. The intercept
is a normalization constant,
M the moments to be fitted, and
the dependent coefficients to be estimated. The central property of log-linear smoothing is the matching of the moments of the empirical distribution.
An interesting connection between the MML parameters’ estimation outlined above in
Section 2.1 using a nonparametric approach as described by Bock and Aitkin [
101] (also referred to as a Bock–Aitkin or the empirical histogram (EH) solution) and the LLS is that the former can be seen as a special case of the LLS method with
moments.
The LLS is integrated into the EM algorithm [
110] to estimate
since the number of expected persons (expected frequencies) at each quadrature point
is unobserved. An LLS with
moments is equivalent to a discretized (standard) normal distribution (exactly two parameters are necessary,
and
) (see [
117]). The specification of more than two moments allows, e.g., the specification of skewed latent variables [
118].
Casabianca and Lewis [
115] showed in detailed and promising simulation studies that the LLS method leads to better parameter recovery if the specified distribution deviates from the true empirical ones. By specifying up to four moments, bimodal distributions could be captured. It is also worth mentioning that there may be less effort for users to use this method since only the number of moments has to be specified.
2.2. Conditional Maximum Likelihood Estimation
Unlike the MML method, CML does not require assumptions for the distribution of the traits. Here, the person parameter is eliminated from the likelihood due to conditioning on the raw scores
, which is referred to as
minimal sufficient statistic for person parameter
[
96,
104,
105,
119] in Equation (
6). Therefore, only item parameters
, but no person parameter
, are estimated, which have to be determined afterwards. In the following, the likelihood for the response matrix
in the CML case is outlined following Equation (
3) again.
For the estimation of item parameter, the calculation of the elementary symmetric function (ESF)
of order
of
is the crucial part of the likelihood in CML. Different methods have been proposed, which differ mainly in accuracy and speed [
120,
121,
122].
There are
different possibilities to obtain the score
for a person with the ability
. The sum over these different possibilities results in
, with given item difficulty
, as well as the responses
for a given score
r.
The likelihood of the response vector
can be written as:
The likelihood in Equation (
6) can then be written using Equations (
3) and (
7) in the CML case as follows:
The resulting estimates
are consistent, asymptotically efficient, and asymptotically normally distributed [
99].
CML Approach of Zwitser and Maris (2015)
Glas [
108] stated that ignoring the MST design in the CML item parameter estimation process leads to severely biased estimates (see also [
107,
111]). Based on these results, it has long been recommended not to use the CML method for MST designs. The MML method offered an alternative, or the parameter of the items for each path or module could be estimated separately using the CML method [
123]. The latter has the major disadvantage that item parameters estimated in this way can no longer be compared. Recently, this CML estimation problem could be solved for deterministic routing while considering the respective MST design in the CML estimation process [
109]. To solve this problem, the symmetric function has to be modified, such that only those raw scores are considered, which can occur due to the specific MST design. This leads to consistent item parameter estimates. There are currently two R [
124] packages for this method:
dexterMST [
125] and
tmt [
126]. The modified CML estimate is outlined in the following. In the deterministic case, a person with score
j is routed from one module
to the next module based on a cut-score
c. Based on the design in
Figure 1, the probability of reaching a score of
in the modules
with ability
, and the number of solved items in the module
being less than or equal to the cut-score
c with
, can be described as follows:
The ESF as described above can be written as
and rearranged as
. Here, the ESF is first evaluated for each module separately and then for a specific path of the MST design. Zwitser and Maris [
109] proposed to partition the denominator of the likelihood into the sum of items
in the first module and
items in the second module. Equation (
9) can be factored as:
Inserting Equation (
10) into the common CML approach results in:
The probability of
being less than or equal to
c conditional on
:
Following Equations (
11) and (
12), we obtain:
and further:
Taking the same considerations from Equation (
14) for the following:
then it follows that:
Using Equations (
13), (
15) and (
16), Equation (
10) follows. Therefore, it can be concluded that after the integration of additional design information in the MST design, the CML item parameter estimation is justified.
3. Simulation Study
A Monte Carlo simulation was carried out to provide information on the influence of different trait distributions on the estimation of item parameters in MST designs. In addition to the different trait distributions (normal, bimodal, skewed, and
with
), the test length (
I = 15, 35, and 60 items), different MST designs, and sample sizes (
N = 100, 300, 500, and 1000) were considered. All conditions were simulated as MSTs, as well as fixed-length tests. The simulation and all conditions are explained in detail below. MST designs can be expanded to more modules, items within modules, and more stages. It is important to note that, branching on the item level as is the case with CATs, CML estimation is not possible. As stated by Zwitser and Maris [
109] for CATs, the information about the item parameters is bound in the design and thus not available for CML parameter estimation. Therefore, CAT designs were not considered here.
3.1. Data Generation
For all MST conditions, a two-stage design was used (see
Figure 1). All MST conditions started with the routing module
and were subsequently routed in one additional module. The module with easier items was the module
and the module with more difficult items
. The entire routing was based on the NC score. We chose deterministic routing for all multistage conditions because no additional random aspects influenced the routing process. The routing module in the test length condition
and
contained five items. The routing model in the condition with
contained ten items. The cutoff values for the routing into module
within the first two conditions were
and for the third condition
. Item parameters of all models were drawn from a uniform distribution
, whereby the item parameters for the routing module
were from
,
from
, and
from
. In the simulation, four different types of (standardized) distribution of
were considered (see
Figure 2;
skew as skewness and
kurt as the kurtosis parameter):
- (a)
(standard) normal (): ;
- (b)
bimodal (): ;
- (c)
skewed (): ;
- (d)
(): with one degree of freedom.
The skewed and bimodal distribution parameters were chosen following Casabianca and Lewis [
115]. This study also dealt with parameter recovery for MML with log-linear smoothing, but solely in LFT designs. The authors reported that they chose theses parameter based on their own work [
127], as well as other contributions that also dealt with simulation studies on the same or related topics (see, e.g., [
128,
129,
130,
131,
132,
133]).
In disciplines such as educational measurement, clinical psychology, or medicine, there are many situations where the resulting trait distribution might deviate from an assumed normal distribution (see, e.g., [
115,
129,
132,
134,
135]). A bimodal trait distribution might occur, e.g., in clinical and personality psychology, if one aspect of personality or psychopathology is low for most people and a few people high. One such reported dimension is, e.g., psychoticism, which tends to be positively skewed towards low scores [
136]. Furthermore, in situations where groups of persons are examined, in which a subgroup has psychopathological symptoms, distributions deviating from a normal distribution are expected and typically positively skewed [
137]. Areas of (large-scale) educational testing, as well as raw scores of state-wide tests tend to be non-normal distributed [
138,
139].
A bimodal distribution can be expected when two different groups of examinees are investigated, e.g., high versus low performer or schools with privileged versus underprivileged students [
140].
For the estimation, the following three different estimation approaches were used:
CML/CMLMST: CML estimation with consideration of the respective MST design in the MST condition (CMLMST);
MMLN: MML estimation, assuming that traits are normally distributed;
MMLS: MML estimation with log-linear smoothing up to four moments.
For each condition, 1000 datasets were generated, and the CML and MML estimation methods were applied. Thereby, 1000 replications
R were conducted in each cell. For the parameter estimation and the analysis of the simulation study, the open-source software R [
124] was used. For reasons of the comparability of the estimated item parameters across the different estimation methods, the estimated item parameters were centered after estimation.
3.2. Implementation in R
All introduced estimation methods were implemented in R packages. For the conventional CML estimation, there is a wide variety of packages available. In addition to the well-known
eRm with
eRm::RM() [
141], these are, for example, the R packages with the respective functions
psychotools with
psychotools::raschmodel(),
immer with
immer::immer_cml() and
tmt with the function
tmt::tmt_rm(), to name a few representatives [
126,
141,
142,
143]. All packages allow a user-friendly application, but they differ in terms of speed and the availability of further analysis options. With regard to CML parameter estimation in MST designs, two packages are currently available:
dexterMST with
dexterMST::fit_enorm_mst() and
tmt with the function
tmt::tmt_rm(). The two packages differ concerning the specification of the MST design to be taken into account. In
dexterMST, first, an MST project must be created with the function
dexterMST::create_mst_project(), then the the scoring rules used with
dexterMST::add_scoring_rules_mst() are handed over. Essentially, this is a list of all items, admissible responses, and assigned scores to each response when grading. For the estimation, the routing rules were set with
dexterMST::mst_rules() and with
dexterMST::create_mst_test(), then the actual test was carried out, created from the specified rules and the defined modules. Once these steps were executed, the actual data were added with
dexterMST::add_booklet_mst() to the created database. The actual parameter estimation was realized with
dexterMST::fit_enorm_mst(). Furthermore, in the
tmt package, the actual used MST design must be defined. For this purpose, a model language was developed that could be used to define the modules and routing rules. In the first section, the modules were defined, in the example below indicated as m1, m2 and m3. Subsequently, each path of the MST design with the respective rules was specified (in the example below with p1 and p2). In deterministic routing, the lower and upper limit of the raw scores must be specified for each module in each path. The parameter estimation was realized with
tmt::tmt_rm() with the specified design as an additional argument.
| model <- “ |
| m1 =~c(i01,i02,i03,i04,i05) |
| m2 =~c(i06,i07,i08,i09,i10) |
| m3 =~paste0(’i’,11:15) |
| |
| p1 := m2(0,2) + m1 |
| p2 := m2(3,5) + m3 |
| ” |
Furthermore, for MML parameter estimation, numerous packages are available. Some selected examples are
ltm with
ltm::rasch(),
sirt with
sirt::rasch.mml2() and
TAM with
TAM::tam.mml() or
mirt with mirt::mirt(), which also differ in functionality and speed [
144,
145,
146,
147]. In contrast to CML estimation, no further steps were necessary to obtained the unbiased estimates. The log-linear smoothing used here is available in the package
sirt [
145]. As already pointed out positively by Casabianca and Lewis [
115], only the desired number of moments needs to be specified additionally. This can also be emphasized as an advantage compared to the described CML estimation in MST designs, especially in cases with complex MST designs. To utilize the log-linear smoothing, the package
sirt with the function
sirt::rasch.mirtlc() is available. The model type (in our case,
modeltype = “MLC1”) and the trait distribution
distribution.trait = “codesmooth4” were passed as an additional argument (in this example, up to four moments). In the simulation described here, we utilized the R package
sirt [
145] for MML estimation and the R package
tmt [
126] for CML estimation.
3.3. Outcome Measures
To compare the different estimation methods under the different simulation conditions, we computed three criteria. The focus was the estimated item parameters
in each simulation condition. The computed quantities were the bias of the estimates, the accuracy measured with the root mean squared error (RMSE), and the average relative RMSE (RRMSE) as a summary of the bias and variability. The bias represents the absolute deviation of item parameter estimates from the true item parameter and is reported as the average absolute bias (ABIAS) overall replication in each condition.
For the evaluation of the overall accuracy of item parameter estimation, the RMSE was computed. The average RMSE was calculated as the square root of the squared differences between the estimated and true item parameters. The ABIAS and the ARMSE are reported, each as the average for each condition and in the MST case for each module separately.
The RRMSE is defined as follows:
where
is the average standard deviation of the item parameters of the CML method in the fixed-length condition, respectively CMLMST in the MST condition, and serves hereby as the reference.
5. Summary and Discussion
For the estimation of item parameters, alternative estimation methods are available.
While users of the CML method often emphasize that this method comes close to the idea of person-free assessment [
148] required for the postulation of specific objectivity [
150,
151] and that no distribution assumption for the person parameters are required, supporters of the MML method might highlight the flexibility of the approach.
When it comes to MST designs, there was only MML estimation available. If CML parameter estimation were applied, the estimated item parameters would be severely biased. Based on the contribution by Zwitser and Maris [
109], two implementations in R packages
dexterMST [
125] and
tmt [
126] are available for item parameter estimation using the CML method in MST designs.
The simulation study was carried out to investigate the influence of trait distributions on the estimation of item parameters. The results showed a differentiated picture. As the sample size increased and the number of items increased, the CMLMST method showed a comparatively small RMSE. As expected, the MMLN method led to a comparatively large RMSE in all non-normal distribution conditions. It is noteworthy that the MMLS estimation method provided the smallest RMSE across conditions. The results were very similar between MMLS and CMLMST, especially with increasing sample sizes and an increasing number of items, even though the MMLS method objectively led to a smaller RMSE. Based on the results, it seems favorable for MST designs to either use the CMLMST or MMLS estimation. Concerning the bias of the item parameter, the CMLMST method led to the smallest ABIAS independently of sample size and test length in nearly all MST conditions. However, in the decision for the CMLMST or MMLS method, it should be considered that the actual distribution used in the MMLS method was assumed to resemble the true population distribution, which may differ. This might be an advantage of the CMLMST method since no distribution assumption was made here.
There are also limitations associated with the present study that might limit the generalizability of the findings. In our research question, we were interested in the influence of the type of trait distribution on item parameter estimation. The number of items and the MST design were varied as additional factors. It would be interesting to systematically study the impact of using more complex MST designs in further studies and perhaps also consider Bayesian estimation methods (see, e.g., [
152]). It was noticeable in the results that for the 60-item condition with a
trait distribution, the difference in the RMSE among CML, MMLN, and MMLS was smaller than in the two other item conditions (15 and 35). Next to the different number of items, the MST design in the condition with 60 items differed in the size of the routing module with ten instead of five items. On the other hand, the difference between CML and MMLN seemed to increase with an increasing number of items, but the same size of the routing module. Therefore, it would be interesting to investigate more complex MST designs for item parameter estimation in future research.