1. Introduction
One primary goal of empirical studies in psychology and education is to compare cognitive outcomes across many groups. For example, the programme for international student assessment (PISA; [
1]) provides international comparisons of student performance for a large group of countries (72 countries in PISA 2015). A major obstacle to these comparisons is that cognitive tests often show differential item functioning (DIF; [
2]).
In this article, we investigate robust variants to the originally proposed Haebara linking method [
3] for many groups. We study a slight extension of robust Haebara linking that was proposed by He and Cui [
4] by using a more flexible class of loss functions. We use a two-parameter logistic model (2PL) item response model to introduce the methodology. It is shown that approximately unbiased group comparisons can be conducted with robust Haebara linking when group-specific subsets of items show DIF (i.e., partial invariance). Importantly, no additional steps for identifying items with DIF are needed; items that possess DIF are essentially treated as outliers [
5,
6] in the linking procedure.
The paper is structured as follows.
Section 2 describes the 2PL model under partial invariance that allows the presence of uniform DIF effects.
Section 3 introduces the robust Haebara linking method. It is argued that the proposed linking method can provide unbiased estimates in the presence of uniform DIF. In
Section 4, the proposed method is evaluated in a simulation study.
Section 5 presents an empirical example of PISA data. Finally,
Section 6 concludes with a discussion that focuses on limitations and potential gaps for future research.
2. 2PL Model with Partial Invariance: Presence of Uniform DIF Effects
In the following, we introduce the concept of partial invariance for multiple groups. For
G groups
,
I items
are administered. It is assumed that a unidimensional item response model holds in each group with group-specific item response functions (IRF)
, indicating the probability of a correct item response
, conditional on ability
. The IRFs in the 2PL model [
7] are given as
where
are group-specific item difficulties for item
i in group
g (
), and
are group-specific item loadings. In this article, we focus on the case of uniform DIF [
2] that presupposes that item loadings are invariant across groups, i.e.,
. Group-specific item difficulties are decomposed into
, where
indicates common item difficulties and
are denoted as uniform DIF effects. In Equation (
1),
denotes the logistic distribution function, and it is assumed that the abilities within each group
g are normally distributed with mean
and standard deviation
.
It is well known that not all DIF effects
and group means
can be simultaneously identified in the 2PL model [
8,
9]. To resolve the identification issue, the set of items for each group is partitioned into two distinct sets (see [
10]). More specifically, we assume that for each group
g, a subset of so-called anchor items
exists such that
for all
. The set of biased items is defined as
. Biased items are allowed to possess DIF effects
, which differs from zero. This situation is also referred to in the literature as partial invariance [
11,
12]. If there are no biased items, all item parameters are invariant, which is denoted as full invariance. One central argument in the DIF literature is that items with DIF effects have the potential to bias the estimated ability distributions (i.e., group means or group standard deviations) and should, therefore, not be included in group comparisons (e.g., [
1], for arguments in the PISA study, or [
13]). Biased estimates of group means can be particularly expected in the case that all DIF effects of items within a group have the same sign (i.e., unbalanced DIF).
In practice, it is not known which items serve as anchor items for group
g. The choice can be based on a substantive basis (e.g., considerations outside of psychometrics, see [
14]) or using psychometric methods. In this article, the identification of group means and group standard deviations is conducted using psychometric methods, namely linking methods (see [
15,
16,
17,
18,
19] for overviews). Linking methods rely on separate scalings for all groups. In more detail, the 2PL model is fitted for each group (under the assumption
), resulting in estimated item loadings
and estimated item intercepts
for all groups. In the second step, estimated parameters
are used to determine the vector of group means
and
standard deviations.
Alternatively, biased items could be determined by a statistical DIF detecting method prior to linking (see, e.g., [
12,
20,
21]). The linking method is then subsequently applied only on the anchor items. This approach relies on the somewhat arbitrary choice of a cutoff value for the DIF statistic. In this article, the proposed robust Haebara linking method does not require a prior determination of biased items, and in the next section, it is shown it can provide unbiased group mean estimates in the case of uniform DIF effects.
3. Haebara Linking
In this section, we introduce the robust Haebara linking method that determines group means
, group standard deviations
, common item slopes
, and common item difficulties
based on estimated item loadings
and estimated item intercepts
for all groups
g. A linking function
H is employed that minimizes the distances between group-specific IRFs and aligned common IRFs for computing unknown parameters
where
is a loss function, and
is a weighting function that fulfills
. In all subsequent analyses, we choose the standard normal density function as the weighting function
. Linking based on the function
H in Equation (
2) is referred to as robust Haebara linking and generalizes the originally proposed Haebara linking method for two groups [
3] that uses the loss function
. He and colleagues [
4,
22] considered the loss function
for two groups. Haebara linking for multiple groups was investigated in several articles [
10,
23,
24,
25]. In particular, it was shown in [
10] that the loss function
was efficient in handling the situation of partial invariance for multiple groups.
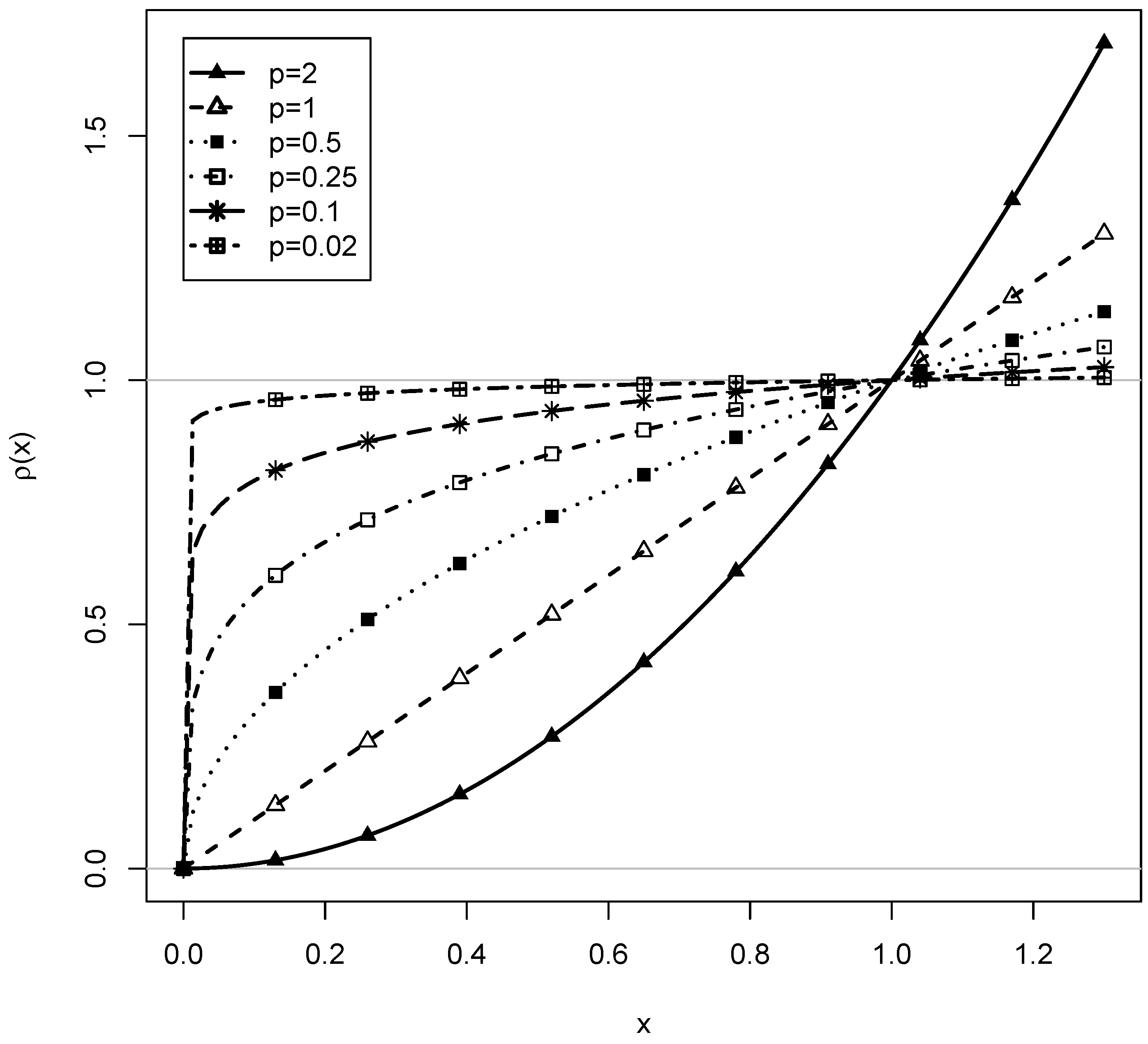
In this article, we consider the class of loss function
with nonnegative power values
p. In
Figure 1, the loss functions for different values of
p are shown. It can be seen that
and
put different weights for values near zero. In the limiting case of
,
is the step function that takes the value 0 if
x is zero, and 1 for all other
x values. With
for very small
p values (e.g.,
) in Equation (
2), the linking function essentially counts the number of events in which the group-specific IRF deviates from the aligned common IRF.
It should be noted that there are competitive linking methods to Haebara linking. The Stocking-Lord method [
26] minimizes the difference of the integrated squared difference of the sum of group-specific IRFs and the sum of aligned common IRFs. There are also alternative linking approaches that directly rely on estimated item parameters instead of IRFs, such as mean-mean linking [
17], Haberman linking based on regression modeling [
27], invariance alignment [
28], and distance-based measures (like
; [
29,
30]), to name a few. For Haberman linking and invariance alignment, robust alternatives were recently studied [
10,
31,
32,
33]. The linking approach is a two-step method as separate scalings are applied group-wise in the first step. However, it can be shown that one can reformulate the two-step estimation problem as a one-step estimation problem with side conditions [
34].
3.1. Estimation
In the minimization of the robust Haebara linking function
H defined in Equation (
2), the unknown parameters can be obtained by setting the first derivatives to 0, i.e.,
,
,
, and
. However, the loss function
is not differentiable for
, and the first derivative must be replaced by a subdifferential. Moreover, due to nondifferentiability of
, standard optimization algorithms that rely on derivatives cannot be used. However, in robust Haebara linking, the function
is replaced by a differentiable approximating function
using a small
(e.g.,
). Because
is differentiable, quasi-Newton minimization approaches can be used that are implemented in standard optimizers in R [
35]. The implementation of robust Haebara linking in the sirt [
36] package specifies a sequence of decreasing values of
in the optimization, each using the previous solution as initial values (see [
37] for a similar approach). It should be noted that alternative differentiable approximating function for the loss function
for values
p nearby zero have been employed [
38].
3.2. Estimated Group Means as a Function of DIF Effects
Next, we investigate the bias in estimated group means of robust Haebara linking for infinite sample sizes (i.e., the asymptotic bias). Assume that the vector of joint item parameters
and
and group standard deviations
are already identified. We now investigate the estimated group mean
and use the part in Equation (
2) that relates to the group mean
. The estimate
can be determined as
By using two Taylor approximations, we can formulate the estimated group mean
as a function of the true mean
and weighted DIF effects
. For
, we get (see
Appendix A; Equation (
A11))
where
, and
is the information function of item
i. The item-specific weights
consist of two factors. First, the factor
governs the influence of DIF effects. Items with large DIF effects
are down-weighted for
. Second, the factor
is the integrated information function with respect to
. The influence of this factor is largest for items with large item loadings
and item difficulties
that are located in the center of the ability distribution.
We now consider two important special cases of Equation (
4). For
, we obtain the Haebara linking proposed in [
3], and it holds that
All DIF effects are weighted according to their item information function. There is no down-weighting of large DIF effects because the weights only involve the integrated information functions. In the case of
(as proposed in [
4,
22]), it can be shown that the bias in estimated group means in robust Haebara linking is a weighted median of DIF effects (see Equation (
A15) in
Appendix A.5 and [
39]).
Finally, it is shown in
Appendix A.6 that the estimated group means can be estimated without an asymptotic bias in the limiting case that
p equals 0. For
, within each group, the linking function
H counts the number of items that show DIF. Hence, the number of noninvariant items is minimized within each group. The minimum within each group is given as
, i.e., the number of biased items within each group. In empirical applications of robust Haebara linking it can be expected that the bias decreases with decreasing values of
p. Obviously, the reasoning relies on asymptotic arguments, and it is of interest whether the property also holds true in moderately sized samples and to assess a potential loss of efficiency in using small values of
p in applications.
5. Empirical Example: PISA 2006 Reading Competence
In order to illustrate the choice of different values for the power
p in robust Haebara linking in the case of many groups, we analyzed the data from the PISA 2006 assessment [
45]. In this case, groups constitute countries. In this reanalysis, we included 26 OECD countries that participated in 2006 and focused on the reading domain (see [
46] for a similar analysis, but see also [
10,
39,
47] for findings using the same dataset). Reading items were only administered to a subset of the participating students, and we included only those students who received a test booklet with at least one reading item. This resulted in a total sample size of 110,236 students (ranging from 2010 to 12,142 between countries). In total, 28 reading items nested within eight testlets were used in PISA 2006. Six of the 28 items were polytomous and were dichotomously recoded, with only the highest category being recoded as correct. We used seven different analysis models to obtain estimates of the country means: a full invariance approach (concurrent scaling with multiple groups; FI), and robust Haebara linking using powers
, 1, 0.5, 0.25, 0.1, and 0.02. For all analyses, the 2PL model was estimated using student weights. Within a country, student weights were normalized to a sum of 5000, so that all countries contributed equally to the analyses. Finally, all estimated country means were linearly transformed such that the distribution containing all (weighted) students in all 26 countries had a mean of 500 (points) and a standard deviation of 100. Note that this transformation is not equivalent to the one used in officially published PISA publications.
In
Table 2, the country mean estimates obtained from the seven different analysis models are shown. Within a country, the range of country means differed between 0.4 (AUT, Austria) and 16.1 (KOR, South Korea) points (
,
) across the different models. These differences between the methods can be traced back to different amounts of country DIF. The model based on full invariance and Haebara linking with
appeared to be similar, resulting in a large correlation of estimated country means (
) and small absolute differences (
,
). In contrast, Haebara linking for
and
differed quite a lot, resulting in a correlation of
and non-negligible absolute differences between methods (
,
). Given that standard errors due to sampling of students in country means in PISA are typically about 3 points, in some cases, differences between different model estimates would provide different statements regarding statistical significance. Interestingly, the country mean estimate for South Korea (KOR) dropped from 560.5 (
) to 544.4 (
). The reason is that robust Haebara linking down-weights items with large DIF effects from the computation of country means. For South Korea, there are four items with large negative DIF effects (a relative advantage) and no items with large positive DIF effects (a relative disadvantage) that are most strongly down-weighted (see [
10]). Hence, it can be concluded the choice of a particular linking method has the potential to impact the ranking of countries in PISA (see also [
48,
49]).
6. Discussion
In this article, we investigated the performance of a slight extension of Haebara linking in many groups. By using a robust loss function family
(
) it was shown that the method efficiently handles the case of the presence of uniform DIF effects. Originally, Haebara linking has been proposed for
[
3] and has been robustified using
in [
22]. The linking method is robust insofar as it provides nearly unbiased estimates in the case of uniform DIF effects (but see [
28,
50] for an alternative robust linking method). Our analytical derivations give an intuition of the bias in estimated group means. The bias is determined as a function of weighted DIF effects per group where weights are given as integrated information functions. In the limiting case that
p tends to zero, the robust Haebara linking function essentially counts the number of deviant item response functions. In this sense, robust Haebara linking with a small
p maximizes the number of invariant items per group. We also showed analytically that in case
, robust Haebara linking provides unbiased group estimates under reasonable statistical assumptions. Our simulation study indicated that power values
p smaller than 1 had superior performance to
or
. More concretely, in the case of many groups,
p values of at most 0.25 were particularly advantageous. It should be noted that robust Haebara linking is always superior to a concurrent calibration approach if there exist biased items. If there were no biased items, the efficiency loss using Haebara linking is negligible (see [
10,
39,
44] for similar findings).
As it is true for all simulation studies, our study has some limitations. First, we restricted the number of groups to 9. For international large-scale assessments like PISA (e.g., [
1,
45]), the number of groups–countries in this case–are much larger, say 30, or even 50. On the other hand, we believe that the robust Haebara linking method could also be attractive in the case of two groups [
20] or a few groups [
51]. Second, we only used 20 dichotomous items in the simulation studies. The performance of robust Haebara linking with a very low or higher number of items could be a relevant topic of future research. Third, we restricted ourselves to dichotomous data. Robust Haebara linking could be extended to polytomous items (see, e.g., [
44]). Fourth, the performance proposed robust Haebara linking method was only assessed in the presence of uniform DIF (i.e., DIF effects in item intercepts). It could be expected that the linking approach can also be successfully applied in the presence of nonuniform DIF (i.e., DIF effects in item slopes; see, e.g., [
52]). The analytical derivations have to be adapted to a joint analysis of
. This probably complicates arguments a bit, but we suppose that unbiasedness can be also be shown in this situation when
p tends to zero. Nevertheless, in large-scale educational studies, uniform DIF does typically more frequently occur than nonuniform DIF [
1,
53].
In the simulation study, it was shown that robust Haebara linking shows desirable performance in the situation of partial invariance with uniform DIF effects. However, DIF effects could also be rather unsystematically distributed that cancel on average. This situation is sometimes referred to as approximate invariance (or random DIF, see [
31,
54,
55,
56,
57,
58]). It can be concluded that in the presence of approximate invariance, power values of
are probably optimal [
31,
32,
39], and the use of robust Haebara linking can lead to inferior statistical performance. We also did not compare linking and full invariance approaches with partial invariance approaches that allow that some item parameters are group-specific. The determination of which parameters should be estimated group-specific requires an additional step using DIF statistics. Unfortunately, a user-defined cutoff value for this DIF statistic is needed in this step. Previous research has shown that the partial invariance approach can only compete with robust or nonrobust linking approaches when the cutoff value is appropriately chosen [
10,
20,
39]. The partial invariance approach can be seen as an inferior implementation of a regularization based approach to the presence of DIF that statistically determines group-specific item parameters in a one-step approach (see, e.g., [
59,
60]).
It should be emphasized that robust Haebara linking is only robust with respect to violations of measurement invariance. It is not robust with respect to misspecifications in the item response model. For very large sample sizes, more flexible item response functions (e.g., B-spline functions) can be used for linking [
61]. Moreover, the estimation of linking constants could be probably made more robust to misspecifications in the IRT model if the first two moments of the trait distribution (i.e., the mean and the standard deviation) instead of item parameters or item response functions are aligned (see [
62] for such an approach).
It should be emphasized that we did not investigate the computation of standard errors in our linking approach. There is ample literature that derives standard error formulas for linking due to sampling of persons (e.g., [
44,
50,
63,
64,
65,
66,
67]) Alternatively, variability in estimated group means due to the selection of items has been studied as linking errors in the literature [
47,
68,
69,
70,
71,
72]. In future research, it would be interesting to accompany robust Haebara linking with error components that reflect these sources of uncertainty [
24,
64,
73]. We suppose that resampling procedures correctly reflect uncertainty due to persons and items in group mean estimates.
In this article, we focused on linking multiple groups for cross-sectional data. However, the approach can also fruitfully applied to longitudinal data in which the group to be linked constitute measurement waves [
74]. One can simply use estimated item parameters resulting from separate scalings of each wave as the input for a linking procedure (see, e.g., [
75,
76,
77,
78,
79,
80,
81,
82]).
Finally, we think that using separate estimation with subsequent linking has a number of advantages to concurrent calibration assuming full invariance (see [
44]). Often, computation times are substantially lower with separate estimation. In addition, it is often easier to diagnose potential estimation problems with separate estimation. Finally, concurrent calibration can only realize more efficient estimates if the model assumptions hold true. As one cannot be confident that there are no unmodelled DIF effects, there are likely only rare situations in which concurrent calibration should be preferred.