Filling in the Gaps: The Association between Intelligence and Both Color and Parent-Reported Ancestry in the National Longitudinal Survey of Youth 1997

1. Introduction

Among admixed African-European American descent groups, European genetic ancestry is associated with higher socioeconomic status (SES) and generally better social outcomes (Kirkegaard, Wang, and Fuerst, 2017) [1]. So too are skin color (or brightness) and other phenotypic indices of European ancestry (Hunter, 2007) [2]. Attempts to explain this pattern have come primarily from two contrasting paradigms: the discrimination model and the distributional model.

The discrimination models focus “on social and institutional practices that discriminate against members of one group (or favor members of another), thus tilting the playing field” (Rushton and Jensen, 2005, p. 281) [3]. In context to the association between racial phenotype and outcomes, the discrimination model comes in the form of “colorism”. The term “colorism” was first coined by Pulitzer Prize winner Alice Walker, who defined it as “prejudicial or preferential treatment of same-race people based solely on their color” (1983, p. 290) [4]). The concept of colorism has since been expanded to refer to color-based discrimination regardless of race (Dixon and Telles, 2017) [5]. According to contemporary colorism theorists, there is pervasive color-based discrimination that results in worse workplace and labor market-related outcomes and generally worse socioeconomic circumstances for darker-colored individuals (Marira and Mitra, 2013) [6]. These theorists place “primacy on the causal role of skin tone [discrimination] in engendering the colorism phenomenon” (Marira and Mitra, 2013, p., 103) [6]. Light skin color is viewed as “bodily capital” (Monk, 2015, p. 415) [7], which is conceived as a form of social capital, like beauty, that incurs advantages. According to this model, color-based discrimination directly results in associations between lighter color and better treatment. Insofar as it is acknowledged that measures of human capital, such as intelligence, covary with color in certain populations, these covariances are attributed to the indirect effects of color-based discrimination. For example, adverse discrimination is posited to result in cognitive inhibiting environments for darker colored individuals (Hailu, 2018) [8]. Moreover, insofar as associations between genetic ancestry and both socioeconomic outcomes and human capital traits are recognized, these are explained as indirect effects of phenotypic discrimination (Conley and Fletcher, 2017) [9].

In contrast to discriminatory models, distributional models account for outcome differences in terms of mean group characteristics. The characteristics could be “deep-rooted cultural values and family structures endemic to certain populations, as well as biological variables such as body type, hormonal levels, and personality and temperament” (Rushton and Jensen, 2005, pp. 281–282) [3]. Human capital (e.g., cognitive ability, knowledge, skill, experience, talent, etc.) models are a subset of distributional ones. Human capital models come in a number of forms depending on the specific groups in question. In context to admixed American groups, they come in the form of the cognitive human capital (i.e., cognitive capital/ability) and related models (e.g., racial ~ cognitive ability-socioeconomic (R~CA-S) hypothesis; Fuerst and Kirkegaard, 2016) [10]. According to these models, there are cognitive ability and other human capital differences between parental populations; these differences are transmitted vertically from parents to offspring. As a result, admixed groups have intermediate levels of skills and abilities. Moreover, individuals within admixed groups have different levels of skills and abilities depending on their admixture proportions. According to these models, socioeconomic differences are largely (but not entirely) downstream of human capital ones. Furthermore, associations with racial phenotype are secondary to associations with genetic ancestry. Some suggest that it is nearly impossible to disentangle genetic vs. cultural models of vertical transmission (e.g., Conley and Fletcher, 2017, p. 107) [11]. However, this concern is not directly relevant to the model in its general form, which does not specify whether the relations between ancestry and traits are mediated by either vertically transmitted genetic or cultural factors (Fuerst and Kirkegaard, 2016) [10,12].

Figure 1 shows the theoretical path model. The colorism model proposes that phenotype-based discrimination directly leads to social outcome differences. These differences, in turn, lead to differences in cognitive ability and other forms of human capital. Because racial phenotypes are correlated with genetic ancestry, both social outcomes and human capital traits will tend to be indirectly correlated with genetic ancestry in admixed populations. The racial ~ human capital model, on the other hand, posits that genetic and cultural factors are correlated with global ancestry both between and within self-identified racial groups. These genetic and cultural factors cause human capital differences and these trait differences are antecedent to social outcomes. Because genetic ancestry is correlated with racial phenotypes, both social outcomes and human capital traits will tend to be indirectly correlated with racial phenotype in admixed populations.

While human capital models may include a number of different forms of capital, cognitive capital (i.e., cognitive ability) is usually focused on, since, among other reasons, it is reliably measured (Fuerst and Kirkegaard, 2016) [10,12]. In this paper, we will also focus on cognitive ability. However, it is noted that the human capital model potentially applies to a wide range of traits that differ between the relevant populations.

It is unfortunate, but there has been relatively little research on the relationships between racial phenotypes and cognitive abilities. Huddleston and Montgomery (2010, p. 69) [13] note:

A great majority of the literature focuses on the intelligence gap between Blacks and Whites. Therefore, more research is needed on intragroup differences among Blacks and intelligence (Averhart and Bigler, 1997) [14]. Results from this research have huge implications for the skin tone hierarchy in the African American community. Despite the gap in the literature …

The authors go on to summarize research on the social correlates of color. That said, a small body of older research has investigated the association between intelligence scores and mostly phenotypic and genealogical indices of biogeographic (i.e., racial) ancestry [15]. However, this research has not been systematically meta-analyzed and narrative reports differ as to interpretations. More recently, Kirkegaard et al. (2019) [16] found that European genetic ancestry was associated with IQ among African and Hispanic Americans (respectively, r = 0.20, N = 227; r = 0.23, N = 328; Table S10-S11). Factors correlated with ancestry explained the full Black-White and most of the Hispanic-White differences in g. However, the analysis was based on a relatively small sample (about 1,400 children and youth in total). Nonetheless, these results have been replicated in a pre-registered study of European ancestry and cognitive ability among African and Hispanic Americans (r = 0.297, N = 193; Table 2) [17]. However, this was based on a convenience sample of individuals recruited online.

Additionally, replicating and extending the results of Lynn (2002) [18], Fuerst, Lynn, and Kirkegaard (2019) found that biracial status and color were associated with crystallized intelligence among African Americans [19]. This analysis was based on the nationally representative General Social Survey. However, the measure of cognitive ability, Wordsum, was only a 10-word vocabulary test. Moreover, the sample comprised adults, so it is possible that the crystallized intelligence differences were consequent of labor market-based discrimination. Additionally, Kreisman and Rangel (2015) examined the relationship between wages and skin tone among African American males using the same sample that we use here: the National Longitudinal Survey of Youth 1997 cohort (NLSY97) [20]. Their tables show that color is related to Armed Forces Qualification Test (AFQT) scores. However, the authors do not report coefficients and they only used a subset of the NLSY sample (males in the workforce).

Methods for disentangling the pathways in Figure 1 have been elaborated in other papers [10,12,16,19]. Generally, the race ~ cognitive ability model, at least in context to American admixed groups, predicts:

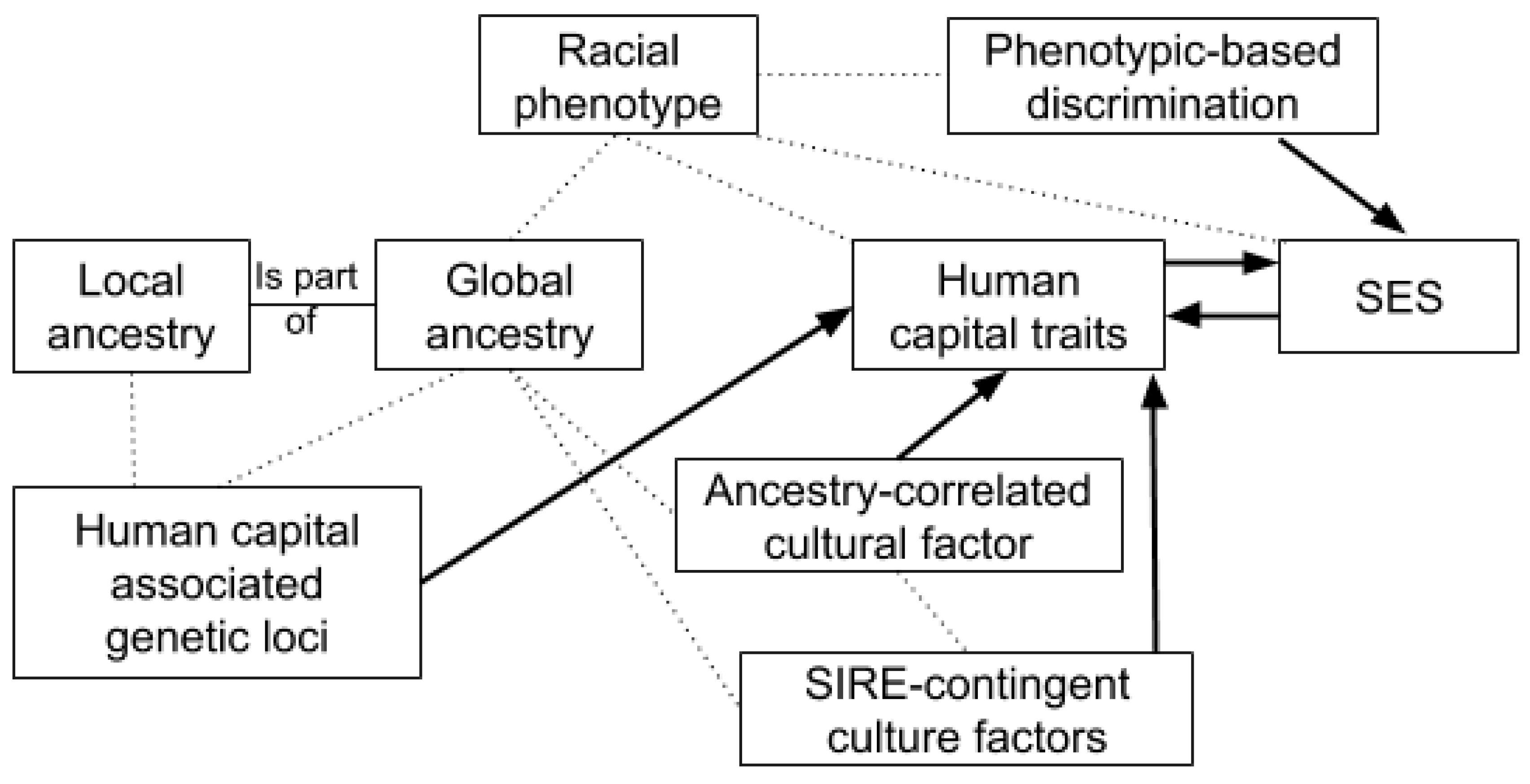
• There is an association between racial phenotype and cognitive ability within self-identified race/ethnic (SIRE) groups.
• There is an association between reported ancestry and cognitive ability within SIREs.
• The associations above are mediated by the relationship between genetic ancestry and cognitive ability.
• The associations between phenotype and cognitive ability can be identified prior to completing formal education and entering the labor market, since they are not a result of differences in educational attainment nor are they a result of labor market discrimination.
• The associations will be larger on the better measures of general cognitive ability, since the differences between racial groups are largely a result of g, which is the predictive backbone of tests of cognitive ability.
• The associations will not appear, to a substantial degree, between full siblings within families, which differ little in ancestry and not at all in shared environment. The potential for linkage between ancestry and skin color implies that there may be a small within-family residual effect. (Briefly: the simpler the genetic architecture of the traits, the less genetic linkage there will be between traits, and the lower the genetic correlation will be among full-siblings; skin color is a relatively simple, but still complex trait.)
• In a multivariate model with genetic ancestry, cognitive ability, color, and other race-related phenotypes, the latter will show little independent relation with cognitive ability. This is because color and other race-related phenotype act as proxies of ancestry, not vice versa.
• Admixture mapping will not show an association between genomic regions associated with conspicuous race-related phenotype and cognitive ability, as would be the case were the colorism model correct. However, it will still show a relationship between admixture and cognitive ability.

In this analysis, we attempt to fill in gaps in the literature by examining predictions 1 through 6. We focus on non-Hispanic White and Black Americans. We do this for two reasons. First, Hannon and Defina (2016) found that the Massey and Martin’s skin color scale, which is used in the NLSY survey, had little to no reliability among Hispanic Americans in the General Social Survey (ICC = 0.079, N = 88). [21]. This may simply have been due to sampling given the panel’s small sample size. However, the cause of the unreliability is not clear. As such, we are uncertain about the NLSY color scale’s reliability in context to Hispanics. Second, immigrant generation is a potential confound, since across generations migrants of the same ethnic stock may score differently owing to a host of factors, including linguistic bias in tests, migrant selectivity, etc. [20]. This problem is attenuated by restricting consideration to African and European Americans, who were predominantly natives in this cohort.

This analysis advances previous research in that we use a national sample, a good, multidimensional measure of cognitive ability, and in that we employ a sibling design. Moreover, it is the first, we are aware of, which looks at the correlation between color and IQ among siblings. Beyond this, we examine some psychometric characteristics of the group differences in cognitive ability. First, we examine sibling differential regression to the mean. This is done to see if the factors causing the Black-White difference have a similar effect across the cognitive spectrum (for logic see: Scarr, 1981; [22]). Second, using Multiple-group Confirmatory Factor Analysis (MGCFA), we examine whether measurement invariance (MI) holds between groups (Blacks and Whites), in addition to testing whether Spearman’s hypothesis, that group differences are due mainly to g, is tenable in these data. Finally, we examine absolute differences between full siblings along with full-sibling intraclass correlations. These analyses provide insight into the causes of group differences.

2. Materials and Methods

Data came from the National Longitudinal Survey of Youth 1997 cohort (NLSY97). The NLSY97 is a nationally representative panel study of 8,984 United States youths ages 12 to 16 in 1996. All analyses except for the MGCFA were conducted in SPSS 24. The dataset is freely available via the NLS Investigator at https://www.nlsinfo.org/investigator/.

2.1. Identified Race and Parent-Reported Ancestry

We limited the sample to non-Hispanic Whites (henceforth: Whites) and non-Hispanic Blacks (henceforth: Blacks). The race and ethnicity of the household adolescents were identified by an adult household member (the household informant) in wave 1. A single racial classification was picked from the NLSY list (White; Black or African-American; American Indian, Eskimo, or Aleut; Asian or Pacific Islander; or mixed race), which conforms to U.S. governmental classifications.

In the parent survey, the responding parent was asked, “What is your origin or descent?” and, “What is [spouse/partner’s name]'s origin or descent?” Multiple choices were permitted. If the responding parent reported that they or their spouse had descent from a European ethnic group, we coded the parents as having parent-reported European ancestry. If the responding parent reported that they or their spouse had “Black, African-American, or Negro,” “Haitian”, or “other African” descent, we coded the parents as having parent-reported African ancestry. Further, 20 White parents had some parent-reported African ancestry, while 88 Black parents had some reported European ancestry. For convenience, we call household informant-identified race “race” and parent-reported ancestry “ancestry”.

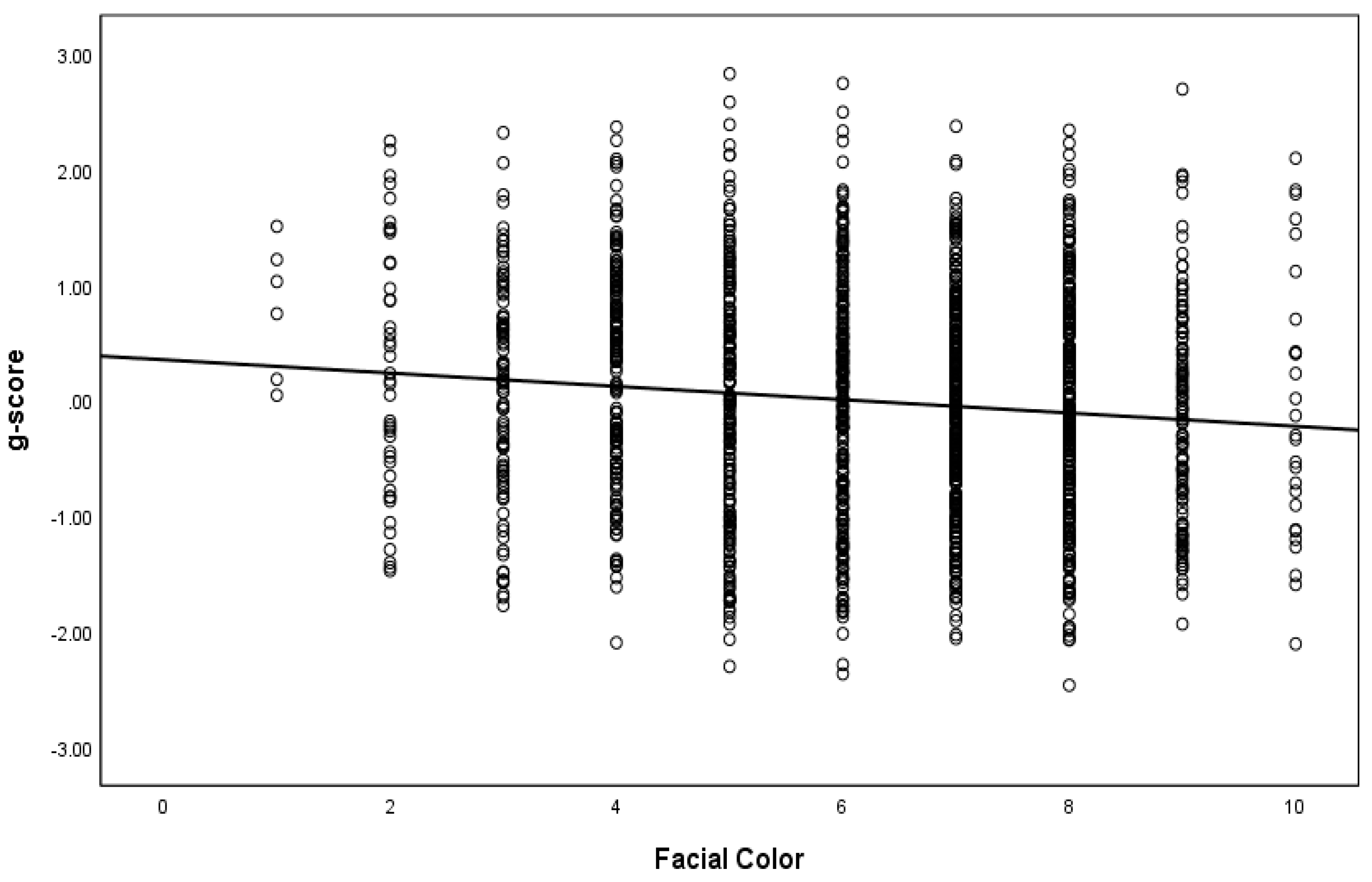
2.2. Color

In interview rounds 12–14, interviewers rated the individual’s facial color using a version of Massey and Martin’s skin color scale [23]. This was an 11-point scale with 0 being the lightest and 10 being the darkest. Rounds 12−14 took place in 2009 to 2011, when the now young adults (approximately ages 26 to 30 in 2010) had begun entering the workforce.

2.3. Cognitive Ability

In 1997−98 participants were given the computer-adaptive form of the Armed Services Vocational Aptitude Battery (CAT-ASVAB). This is a well validated cognitive battery used for selection by the U.S. Armed forces [24]. The 12 subtests are:

• General Science (Science/Technical): Knowledge of physical and biological sciences.
• Arithmetic Reasoning (Math): Ability to solve arithmetic word problems.
• Word Knowledge (Verbal): Ability to select the correct meaning of words presented in context and to identify the best synonym for a given word.
• Paragraph Comprehension (Verbal): Ability to obtain information from written passages.
• Numerical Operations (Speed): Ability to perform arithmetic computations.
• Coding Speed (Speed): Ability to use a key in assigning code numbers to words.
• Auto Information (Science/Technical): Knowledge of automobile technology.
• Shop Information (Science/Technical): Knowledge of tools and shop terminology and practices.
• Math Knowledge (Math): Knowledge of high school mathematics principles.
• Mechanical Comprehension (Science/Technical): Knowledge of mechanical and physical principles.
• Electronics Information (Science/Technical): Knowledge of electricity and electronics.
• Assembling Objects (Spatial): Ability to determine how an object will look when its parts are put together.

For the ASVAB subtests, we regressed out the effect of sex (dummy coded, Male = 1, Female = 0) and birth year. We computed g-scores for Whites and Blacks separately using principal axis factoring. Different analyses required different estimates of g.

For the mean difference, the full sample multivariate and the Method of Correlated Vector (MCV) analyses followed conventional methods and we calculated g separately for Whites and Blacks. We used listwise deletion since imputation could cause our subtest scores to be dependent on one another, which we did not want for the MCV analyses. Since both Black and White means were zero, to allow for comparisons between the racial groups we included the 1999 age-adjusted AFQT percentile scores. These were age-adjusted summary scores which were created by the National Longitudinal Survey staff and based on four subtests: MK, AR, WK, and PC.

2.4. Sibling Relations

The NLSY97 household roster reports biological relations between siblings. We identified full siblings. The NLSY subjects were considered full siblings if either identified the other as a full brother or sister and neither identified the other as something other than full brother or sister.

2.5. Demographic Controls in the Regression Analysis

In the initial multivariate analyses for color and g, following [19,20], we included controls for age, sex, region of residence during adolescence (dummy coded as: South = 1, non-South = 0), and interviewer race/ethnicity at the time of the color measure (in the form of three dummy coded variables: White = 1, non-White = 0; Black = 1, non-Black = 0; Hispanic = 1, non-Hispanic = 0).

3. Analytic Plan

3.1. Mean Differences

First, we examined mean differences by race and color/ancestry. The groups are: Whites with no African ancestry, Whites with African ancestry, Blacks with no European ancestry, Blacks with European ancestry, and Blacks by color classification (1 to 10, since no Blacks fell in the lightest category of 0). We treat Whites with no African ancestry vs. Whites with African ancestry and Blacks with no European ancestry vs. Blacks with European ancestry as two dichotomous-categorical variables. Based on the data available, we could not ascertain if Whites with African ancestry had more European ancestry than Blacks with European ancestry, so we could not safely treat these four groups as intervals in one continuous variable.

We created IQ-metric (M = 100, SD = 15) AFQT scores for ease of reading, while also providing the untransformed means and standard deviations. In computing these, we set Whites at 100 and used the total Black-White sample standard deviation. The total sample standard deviation was used, as we had several groups and subgroups, making the use of pooled standard deviations unwieldy. An alternative was to just use the White standard deviation; however, doing so was theoretically questionable in context to color differences among Blacks.

3.2. Method of Correlated Vectors

Second, we examined if there are Jensen Effects, that is, correlations between the vectors of g-loadings and the vectors of group differences, for 1) the Black-White subtest race differences, 2) the association between African ancestry and subtest scores among Whites, 3) the association between European ancestry and subtest scores among Blacks, and 4) the association between darker color and subtest scores among Blacks.

To do this, we used Jensen’s MCV (Jensen, 1998) [25]. This involves six steps. First, ASVAB subtests are corrected for the effect of age (birth year) and sex. Second, the g-loadings of the subtests are determined using principal axis factoring. In this case, we determined the g-loadings separately for Whites and Blacks. Third, the g-loadings are corrected for subtest reliabilities. The reliabilities are given by Moreno and Segall (1997) [24]. The reliability-corrected g-loadings constitute the first vector. Fourth, a vector of group differences is created (e.g., the mean subtest differences between races or the point-biserial correlation between subtest scores and ancestry). Fifth, this vector of group differences is corrected for subtest unreliability. Sixth, the two vectors are correlated.

For the MCV analysis of color, we used two alternative vectors of group differences: 1) the Pearson correlations between subtest scores and color and 2) the betas for color and subtest scores based on the full sample multivariate model (discussed in Section 3.3). Note also that we used the average Black-White g-loadings [25], calculated using the formula given by Hartmann et al. (2007) [26], in the context of the Black-White mean difference analysis, the White g-loadings in the context of the effect of African ancestry among Whites, and the Black g-loadings in the context of the effects of both European ancestry and color among Blacks.

3.3. Full African American Sample Multivariate Analysis for Color and Cognitive Ability

Third, we examined the association between color and g-scores among Blacks in a multivariate analysis. In this analysis, we controlled for the effects of age, sex, region, and interviewer race.

3.4. Sibling Sample Multivariate Analysis for Color and Cognitive Ability

Fourth, we examined the association between color and g among Blacks between and within families. We used a sibling average and sibling difference design e.g., [27,28,29,30]. To do this, we identified full sibling pairs which had both g and color scores. We identified 225 full sibling pairs, in addition to 814 singletons. In 24 cases (or 11%), there was more than one full sibling pair in a family. In these cases, we randomly picked one pair using a random number generator. Using, instead, the average of multiple sibling pair differences produced essentially the same results; as such, we only report the results based on the randomly picked sibling pair method.

For singletons, we look at the association between color and g controlling for sex (Male = 1, Female = 0), age (years and months old, calculated as below), and race of interviewer (White? Yes = 1, No = 0). Of interest is whether relationships between families of full siblings match up with those between singleton families. If this is found to be the case it would suggest that the full sibling subsample is representative of the full Black NLSY sample. This analysis is routinely carried out in behavioral genetic studies due to historical concerns about the representativeness of the family design datasets.

For each household with pairs of full siblings, we computed pair averages and pair differences for g, color, and age. The average is the sum of both sibling’s scores divided by two. The difference is the first sibling of the pair’s score minus the seconds. We additionally computed two sets of dummy variables for the sibling average analysis: sex (both male = 1, otherwise = 0; both female = 1, otherwise = 0) and interviewer race (both White = 1, otherwise = 0; both non-White = 1, otherwise = 0). For the sibling difference analysis, we computed one dummy variable for sex (same sex = 1; different sex = 0) and interviewer race (same interviewer race = 1, different interviewer race = 0). Note, to control for the effect of interviewer race, we used the dichotomously coded “Interviewer Race White” variable since this had the largest effect in both the full sample and the singleton analyses.

For this specific analysis to maximize the sample size, we include both Whites with African ancestry and Blacks. Additionally, prior to analysis, we impute missing ASVAB subtest scores by applying single deterministic imputations to the 12 subtest variables using the SPSS Impute Missing Data Values command, which uses fully conditional specification (FCS). To be clear, we used scores with imputations for this analysis, unlike those discussed in Section 3.1 to Section 3.3. We extract g-scores from the imputed data. To further correct for sex and age effects, since the sibling difference analysis is possibly sensitive to these variables, we regressed out of the g-scores the effects of sex and age (calculated as: age + month−1/12, e.g., so someone born in December 1977 would be (1997−1977) + ((12−1)/12) = 20.92 years old).

Note, we also ran the model using a between/within fixed effects design at the suggestion of a colleague. This did not produce interpretatively different results, since a fixed effects model is a variant of the same design we used here, so we only include the original design.

3.5. Differential Regression to the Mean

Regression to the mean refers to a broad class of phenomena in which imperfectly measured values if extreme when first measured will be less extreme when measured again. What is sometimes called familial regression to the mean is a type of this general phenomenon. It refers to when deviance from a population mean is incompletely passed on or inherited. The inherited portion of a trait deviation from the mean is the portion conditioned by additive genetics (and shared environment). Regression to the mean is simply the non-transmission of trait deviances. It occurs, for example, when very tall individuals have only somewhat tall siblings. This familial regression to the mean is exploited by biometricians to estimate heritability and other variance components, for example, in the case of regression-based methods like Defries-Fulker analysis. In both circumstances, the reason for the regression is the same: the “luck” factors which caused the extreme scores are not reproduced in the subsequent instance.

In the differential regression to the mean analyses, we compare the familial regression to the mean for White siblings and Black siblings. This comparison can be somewhat informative about the etiology of the differences. It can be informative since members of groups will regress to the mean of the group they belong with respect to the trait. Different causes of the mean difference in the trait will results in alternative regression patterns. A simple additive genetic (hereditarian) model predicts parallel regression lines, with the lower scoring group regressing to a lower mean across the full spectrum of the trait.

We examined differential regression to the mean. To do this, we roughly followed the method of Murray (1999) [31]. The following steps are taken: (1) We identify Black and White full siblings who both had g-scores; (2) we randomly assign one of the two as a reference sibling and the other as a comparison sibling using the excel RANDBETWEEN function (threefold); (3) we correct the g-scores for unreliability using the equation provided by Murray (1999), assuming a test-retest reliability of 0.95 for g; (4) we transform the g-scores into IQ-metric ones; (5) we calculate the means for the comparison and reference siblings separately by identified race; (6) we sort, highest to lowest, the Black and White sibling pairs by the reference sibling’s IQ; (7) we match Black and White sibling pairs on the reference sibling’s IQ (to the nearest IQ point); (8) we calculate the means of the matched reference and comparison siblings; and (9) we plot the sibling scores. When matching reference siblings, we use the first scores of each race (e.g., if there were five Black and three White pairs with an IQ of 92, we would match the first three pairs, by order of occurrence, and discard the last two pairs for Blacks).

3.6. MGCFA Assessment of MI and Spearman’s Hypothesis

We assessed MI using MGCFA. As we were unable to find a theoretical model for the 12-subtest version of the ASVAB (most published theory models were based on the 10 subtest ASVAB battery) we used exploratory factor analysis (EFA) to identify a best fitting model. This led to the following four non-g factors:

• Factor I (Technical): SI + AI + EI + MC + GS
• Factor II (Mathematical): NO + CS + MK
• Factor III (Verbal/Knowledge): PC + WK + GS
• Factor IV (Spatial): AR + AO + MC

Testing for MI proceeds by adding constraints to the initial configural model. The following steps are taken: First, the same number of indicators, latent variables, and patterns of constrained and estimated parameters are fitted in both groups (configural invariance), second, the factor loadings are constrained (metric or weak invariance), and third, an additional constraint is placed on the intercepts (scalar or strong invariance). The final step is usually to add a constraint on the residual variances (strict or full uniqueness invariance). If the model fit shows a meaningful decrement throughout the first through third steps, MI is rejected, but partial or approximate MI may still hold [32].

In addition to testing MI, we assessed Spearman’s hypothesis, which states, in the weak form, that the Black-White difference is primarily due to differences in the g factor and, in the strong form that the Black-White difference is entirely due to differences in g. This is in contrast with the contra hypothesis, according to which “there is no Black-White difference in g” but all differences relate to group factors [33]. Spearman’s hypothesis is of interest as it is seen as suggestive of the source of group differences in cognitive ability [34]. In order to investigate this hypothesis, a model in which latent factor variances are homogeneous should hold [35]. As such, we also assess whether constraining latent variances to equality is tenable.

3.7. Full Sibling Differences in Intraclass Correlations and Absolute Mean Differences

For the intraclass correlation and absolute difference analyses, we used the sample from Section 3.5. This was based on data with imputed ASVAB subtest scores. We used this data to maximize power. We computed the full sibling intraclass correlations (single measure, two way, mixed) along with the absolute average sibling differences.

4. Results

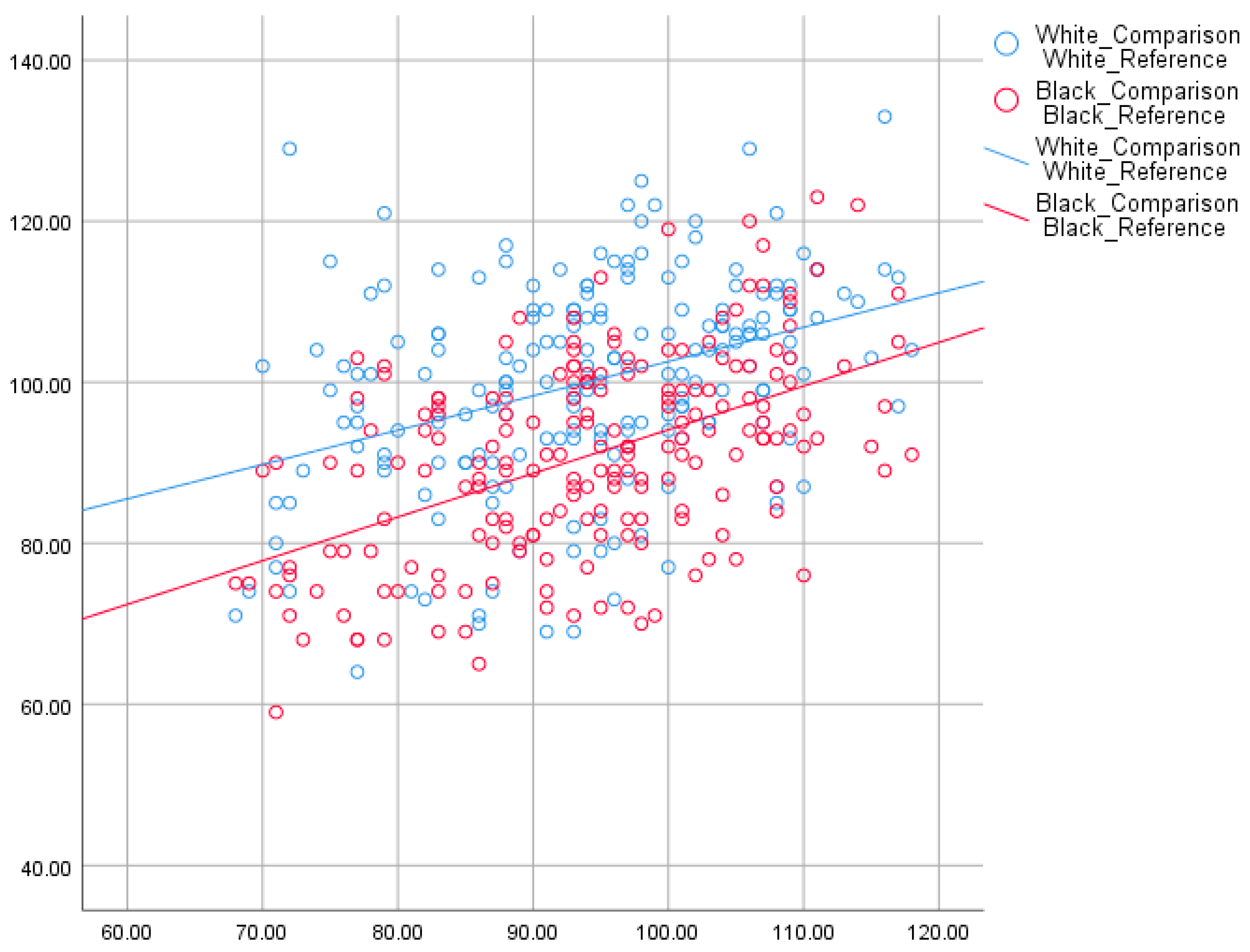
4.1. Mean Differences

Table 1. IQ-Metric Armed Forces Qualification Test (AFQT) scores (with Untransformed Means and Standard Deviations in Parentheses) and g-Scores by Race, Ancestry, and Color.

Race	N	IQ-metric Score (AFQT Mean; SD)	N	White g	N	Black g	N	Color Mean
White, no Afr. Ancestry	3634	100.0 (56.61; 27.60)	3584	0.00 (0.97)			3155	1.74 (0.97)
White w/ Afr. Ancestry	20	91.5 (41.75; 25.88)	19	−0.51 (1.10)			16	2.44 (1.63)
Black w/ Eur. Ancestry	90	92.3 (43.14; 26.10)			88	0.62 (0.98)	80	5.13 (2.07)
Black, no Afr. Ancestry	1717	83.7 (27.92; 23.43)			1700	−0.03 (0.96)	1776	6.25 (1.90)
Among Blacks:
Skin Color_1	6	95.2 (48.13; 15.35)			6	0.79 (0.58)
Skin Color_2	43	87.8 (35.28; 29.04)			42	0.23 (1.08)
Skin Color_3	95	85.2 (30.70; 24.39)			94	0.11 (0.95)
Skin Color_4	153	87.8 (35.18; 25.45)			152	0.27 (0.93)
Skin Color_5	214	84.3 (29.03; 24.81)			210	−0.02 (1.04)
Skin Color_6	258	84.5 (29.37; 25.07)			255	−0.01 (1.03)
Skin Color_7	297	82.4 (25.70; 21.86)			296	−0.09 (0.88)
Skin Color_8	257	83.0 (26.77; 23.07)			253	−0.08 (0.98)
Skin Color_9	122	81.5 (24.08; 21.27)			120	−0.15 (0.92)
Skin Color_10	27	84.7 (29.80; 29.81)			27	−0.08 (1.16)

Note: Skin Color 1 to 10 represents individuals with a score of 1 to 10, respectively, on the NLSY version of Massey and Martin’s skin color scale, which is an 11-point scale with 0 being the lightest classification and 10 being the darkest.

shows AFQT and g-score means, with standard deviations in parentheses, for the racial and color groups. Color means and standard deviations are additionally shown for the racial groups. As can be seen, Whites with African ancestry and Blacks with White ancestry score intermediate in both cognitive ability and color to Whites with no African ancestry and Blacks with no European ancestry. Furthermore, among Blacks, lighter skin color (lower numbers) is generally associated with higher AFQT and g-scores.

4.2. Multivariate Analysis for Color among Black Americans

To determine if the association between color and g-scores resulted from confounding due to age, sex, region of residence in adolescence, and interviewer race/ethnicity (White, Black, or Hispanic), we ran two multivariate regression models. In Model 1, we include color in addition to the just-mentioned covariates. In Model 2, we added a dummy-coded variable for parent-reported White ancestry to gauge to what extent the association between color and ability was independent of that between parent-reported ancestry and ability. The descriptive statistics are shown in

Table 2. Descriptive Statistics for Regression Analysis I.

Variable	Mean	SD	N
g	0.00	0.98	1455
Color	6.19	1.90	1455
Age (in years and months)	15.45	1.43	1455
Sex (Male = 1)	0.45	0.50	1455
Region (South = 1)	0.63	0.48	1455
Interviewer (White = 1)	0.72	0.45	1455
Interviewer (Black = 1)	0.37	0.48	1455
Interviewer (non-Hispanic = 1)	0.92	0.26	1455
European Ancestry (Yes = 1)	0.05	0.21	1455

.

The regression results are shown in

Table 3. Regression Analysis I: The Relation between Darker Skin Color and g, Controlling for Age, Sex, Region, Interviewer Race (Model 1), and Parent-Reported Ancestry (Model II).

Variable	Model 1		Model 2
	B (SE B)	β	B (SE B)	β
(Constant)	1.099 (0.300)		1.056 (0.298)
Color	−0.061 (0.014)	−0.118 *	−0.053 (0.014)	−0.104 *
Age (in years and months)	−0.040 (0.018)	−0.059 *	−0.044 (0.018)	0.064 *
Sex (Male = 1)	−0.174 (0.051)	−0.088 *	−0.176 (0.051)	−0.090 *
Region (South = 1)	−0.062 (0.054)	−0.031	−0.044 (0.053)	−0.022
Interviewer (White = 1)	0.266 (0.078)	0.121 *	0.253 (0.078)	0.115*
Interviewer (Black = 1)	−0.015 (0.066)	−0.007	−0.004 (0.066)	−0.002
Interviewer (non-Hispanic = 1)	−0.187 (0.126)	−0.050	−0.162 (0.125)	−0.044
White Ancestry			0.552 (0.122)	0.118 *
Observations	1455		1455

Note: N = 1455; B = unstandardized regression coefficient with the standard error in parentheses; β = standardized regression coefficient. * Significant at the 0.05 level (2-tailed). Color scores are based on the NLSY’s version of Massey and Martin’s skin color scale; the NLSY scale is an 11-point scale with 0 being the lightest and 10 being the darkest.

. As Model 1 shows, darker color, measured in adulthood, was significantly negatively associated with g-scores, measured in adolescence (β = −0.118). As model 2 shows, this association remained significant when parent-reported ancestry was added as a covariate (β = −0.104). Curiously, interviewer race (White) also predicted g-scores. It is not clear what to make of this, given that the interviewer race variable was from a survey wave a decade after cognitive ability was measured.

As shown in Model 2 of Table 3, ancestry was independently associated with g-scores (β = 0.118). In this sample, the bivariate association between European ancestry and color scores was r = -0.137, N = 1856). This weak association is expected since parent-reported ancestry indexes admixture only within the last couple of generations, yet most admixture within the African American population occurred half a dozen generations ago [36]. Additionally, the dichotomized ancestry variable was strongly imbalanced. Such imbalances attenuate point-biserial correlations [25].

It is arguably inappropriate to correct for sample imbalances, when these reflect imbalances in the population [37]. However, were one interested in doing so, the formula is:

$$r_c=r/\sqrt{r^2+ \left(4P1 P2\right) {(1-r)}^2}$$

(1)

where r_c is the corrected correlation, r is the point-biserial correlation, P1 is the proportion of cases coded 1, P2 is the proportion of the cases coded 0 [37]. Since, of the 1856 cases, 88 had some European ancestry, the corrected correlation would come to:

$$r_c=-0.137/\sqrt{{(-0.137)}^2 + 4(0.0474\times 0.9526){\left(1--0.137\right)}^2 } = -0.35$$

(2)

This is similar to results reported in the literature [38]. Similar transformations could be made for the correlations between ancestry and cognitive ability given in

Table 4. Armed Services Vocational Aptitude Battery (ASVAB) Reliability (Rel.), Black g-loadings, White g-loadings, Black-White Subtest Differences, Correlations between African Ancestry and Subtest Scores among Whites, Correlations between European Ancestry and Subtest Scores among Blacks, Correlations between Color and Subtest Scores among Blacks, and Beta Scores for Color and Subtest Scores among Blacks.

ASVAB Subtests	Rel.	Black g	White g	BW D	Afr. Ancestry (Whites)	Eu. Ancestry (Blacks)	Color r	Color β
General Science	0.86	0.817	0.837	1.123	−0.019	0.145	−0.128	−0.133
Arithmetic Reasoning	0.89	0.815	0.847	1.010	−0.030	0.099	−0.106	−0.116
Word Knowledge	0.86	0.827	0.810	1.016	−0.31	0.119	−0.103	−0.102
Paragraph Comprehension	0.67	0.839	0.834	0.871	−0.035	0.119	−0.094	−0.103
Numerical Operations	0.79	0.681	0.603	0.405	−0.027	0.056	−0.047	−0.061
Coding Speed	0.81	0.530	0.580	0.488	−0.036	0.051	−0.039	−0.060
Auto Information	0.89	0.513	0.483	0.900	0.000	0.091	−0.056	−0.047
Shop Information	0.89	0.555	0.544	1.201	−0.024	0.098	−0.091	−0.076
Mathematics Knowledge	0.92	0.843	0.831	0.861	−0.033	0.117	−0.075	−0.087
Mechanical Comprehension	0.80	0.739	0.793	1.169	−0.025	0.122	−0.104	−0.107
Electronics Information	0.74	0.778	0.742	0.928	−0.031	0.104	−0.115	−0.105
Assembling Objects	0.82	0.623	0.673	0.865	−0.039	0.116	−0.056	−0.065
White g-Scores					−0.038
Black g-Scores						0.137	−0.112	−0.118
N		1788	3603		3603 to 3667	1788 to 1856	1455 to 1479	1455 to 1479

Note: The correlations between ability scores and ancestry are attenuated by the unbalanced dichotomization. These scores can be corrected using Formula (1).

.

4.3. Method of Correlated Vectors

Table 4 shows the ASVAB subtest reliabilities, the Black and White g-loadings, the Black-White subtest differences, the subtest point-biserial correlations with African ancestry among Whites, the subtest point-biserial correlations with European ancestry among Blacks, the subtest correlation with color among Blacks, and the Beta scores, based on regression model 1, for color and subtest scores among Blacks. The correlation with g-scores is also shown for the last four columns. Among Blacks, g-scores were significantly correlated with darker color (r = −0.112; N = 1455, p < 0.001) and with European ancestry (r = 0.137; N = 1788, p < 0.001). Using formula (1), the correlation between European ancestry and g-scores corrected for attenuation owing to unbalanced dichotomization would be rc = 0.344. Among Whites, g-scores were significantly correlated with African ancestry (r = −0.038; N = 3603, p < 0.05). Again, using formula (1), the correlation between African ancestry and g-scores corrected for attenuation owing to unbalanced dichotomization would be r_c = −0.245.

Table 5. Correlation Matrix for the Vectors of g-loadings and the Vectors of Group Differences.

	BW d	Afr. Ancestry (among Whites)	Eur. Ancestry (among Blacks)	Color r (among Blacks)	Color β (among Blacks)
BW g	0.405	−0.572	0.717 *	−0.737 *	−0.877 *
White g		−0.593 *
Black g			0.679 *	−0.728 *	−0.850 *

Note: * Significant at the 0.05 level (2-tailed). The negative correlations for African Ancestry among Whites and for Darker color (r and β) among Blacks indicate a positive Jensen Effect, in the sense of a positive association between the magnitude of group differences and the magnitude of g-loadings, since the association between subtest scores and ancestry index is negative (N = 12).

shows the Pearson correlations between the vectors of g-loadings and the vectors of group differences. For the Black-White difference, this correlation is modest at r = 0.405. This relatively low correlation is consistent with previously reported results based on the ASVAB battery (e.g.; r = 0.31 for 10 subtests from the Profile of American Youth (NLSY79) sample [39]). In the case of European ancestry among Blacks, the association is strong and positive at r = 0.679. For both the color correlation (r = −0.728) and the color Beta (r = −0.850) among Blacks, it is strong and negative. In this case, this negative association indicates a positive Jensen effect in that the (negative) correlations with indices of African ancestry are more pronounced on the more g-loaded subtests. For African ancestry among Whites, the association is moderate to strong and negative r = −0.679. This also indicates a positive Jensen effect, given the signs of the correlations between African ancestry and subtest scores.

4.4. Regression Analyses

The association between darker color and g-scores was negative in the full African American sample. The relation is shown in Figure 2. The lightest colored African Americans are nearly one half of a standard deviation higher in g-scores than the darkest colored individuals of the same group. Represented in IQ-metrics, with the White score as a reference (M = 100) and using the full Black-White sample standard deviation, the lightest two groups (1−2) of African Americans scored 88.2 (N = 48), while the darkest two groups scored 81.6 (N = 147).

We decompose the association between color and g-scores between and within families.

Table 6. Descriptive Statistics for Regression Analyses II and III.

Model 1	Variable	Mean	SD
Between Family, Singleton	g	0.12	0.98
	Color	6.08	1.94
	Age	15.46	1.44
	Sex (Male = 1)	0.43	0.50
	Interviewer Race (White = 1)	0.72	0.45
Model 2	Variable	Mean	SD
Between Family, Full Sibling	g (Average)	−0.16	0.89
	Color (Average)	6.24	1.63
	Age (Average in years and months)	15.45	0.88
	Sex (Both Male = 1)	0.26	0.44
	Sex (Both Female = 1)	0.30	0.46
	Interviewer (Both White = 1)	0.65	0.48
	Interviewer (Both non-White = 1)	0.21	0.41
Model 3 Within Family, Full Sibling	g (Difference)	0.17	0.98
	Color (Difference)	−0.16	1.97
	Age (Difference in years and months)	1.76	1.26
	Sex (Same Sex = 1)	0.56	0.50
	Interviewer (Same race = 1)	0.86	0.35

shows the descriptive statistics for the multivariate analyses. In Model 1, we look at the association between families with singletons, in Model 2, we look at the association between families using full sibling averages, and in Model 3, we look at the association within families between full siblings.

Table 7. Regression Analysis II: The Relation between Darker Skin Color and g among Singletons, Controlling for Age, Sex, and Interviewer Race.

Variable	Model 1 (Between)
	B (SE B)	β
(Constant)	0.592 (0.387)
Color	−0.077 (0.018)	−0.153 *
Age (in years and months)	−0.014 (0.024)	−0.020
Sex (Male = 1)	0.034 (0.069)	0.017
Interviewer Race (White = 1)	0.265 (0.077)	0.121 *
Observations	814

shows the results for the analysis of singleton families. Color was significantly associated with g-scores between singleton families β = −0.153 (N = 814, p < 0.001).

Table 8. Regression Analysis III: The Relation between Darker Skin Color and g among Sibling Pairs, Controlling for Age, Sex, and Interviewer Race between Families (Model 2) and within Families (Model 3).

Variable	Model 2 (Between, Full Sibling)		Model 3 (Within, Full Sibling)
	B (SE B)	β	B (SE B)	β
(Constant)	0.673 (1.072)
Color (average)	−0.097 (0.037)	−0.176 *
Age (average)	−0.018 (0.067)	−0.018
Sex (Both Male = 1)	0.083 (0.147)	0.041
Sex (Both Female = 1)	0.153 (0.142)	0.079
Interviewer Race (Both White = 1)	0.029 (0.175)	0.016
Interviewer Race (Both non-White = 1)	−0.202 (0.206)	−0.092
(Constant)			0.015 (0.213)
Color (difference)			0.013 (0.033)	0.027
Age (difference)			0.009 (0.053)	0.011
Sex (Same Sex = 1)			0.114 (0.134)	0.058
Interviewer Race (Same Race = 1)			0.088 (0.190)	0.032
Observations	225		225

Note: * Significant at the p < 0.05 level.

shows the results for the analysis of sibling pairs. Color was significantly associated with g-scores between families with sibling pairs (β = −0.176 (N = 225, p < 0.010). This association was practically of the same magnitude as that between singleton families. In contrast, there was only a miniscule association between siblings within families (β = 0.027, N = 225).

4.5. Analysis of Full-Sibling Differential Regression to the Mean

For this analysis we imputed ASVAB subtest scores and conducted a factor analysis as above but did this for the Black and White combined sample. The combined sample was used so we could examine differential regression to the mean for which we needed subgroup scores on the same scale. There were 694 White and 301 Black full sibling pairs with one pair selected per household. (There were more sibling pairs with cognitive scores than with both cognitive scores and color scores.) When matched to the same IQ (according to the method discussed in Section 3.5), there were 194 pairs for each group. We ran the analysis several times and the results were generally stable. However, the sample size varies depending on the randomization of the sibling pairs.

As seen in

Table 9. Comparison of Mean to Which the Comparison Siblings Regress.

Sample	N	Reference Sibling			Comparison Sibling
		White	Black	Difference	White	Black	Difference
Total Sibling Sample	694 (w)	105.6	88.2	17.3	105.6	88.1	17.5
	301 (b)
Sample Matched for g	194	94.0	94.0	0	100.0	90.9	9.2

, the White reference sibling sample mean is 94.0. The White comparison siblings, with a mean of 100.0 regress up towards the total White sibling sample mean of 105.6. Similarly, the Black reference sibling sample mean is 94.0. However, the Black comparison siblings, with a mean of 90.9 regress down towards the total Black sibling sample mean of 88.1.

Figure 3 shows the plot for the White and Black full siblings. The differential regression results are more or less consistent with those found by Murray (1999) [31] in his analysis of both the NLSY79 and CNLSY79 datasets. In contrast to Murray’s (1999) [31] results, though, the difference between the regression lines seem to narrow somewhat, instead of widening with increasing IQ. However, this could simply be a sampling issue.

We examined if the slopes of the two regression lines were significantly different. To do this, we combined the Black and White sibling data. Next, we created a variable to denote the race of the sibling pairs (1 = White, 0 = Black). Then, we created a term for the interaction between sibling race and the reference sibling’s score. We then entered these variables into a model with the comparison sibling’s score as the dependent. The results, shown in Table 9 and

Table 10. Regression Analysis to Test for Significant Difference in Slope between Differential Regression lines.

Variable	Model 1 (Between)
	B (SE B)	β	P-value
(Constant)	39.855 (6.799)		0.000
Reference_Sibling	0.542 (0.072)	0.460	0.000
Race	20.067 (9.615)	0.745	0.038
Reference_Sibling* Race	−0.116 (0.102)	−0.411	0.254

Note: The dependent variable is the comparison sibling’s g score (N = 388).

, indicate no significant interaction, which indicates no statistically significant difference in slope.

4.6. Assessment of Measurement Invariance

We examined whether the ASVAB was MI using MGCFA. This technique has been amply described elsewhere [35,40,41], as have tests of multivariate normality, an assumption underlying MGCFA models [42,43]. For this analysis, we used the R package lavaan (Rosseel, 2012; Version 0.6−3 [44]). Based on Monte Carlo simulation findings by Fan and Sivo (2009) [45], we elected to use the χ2 test—noting that our initial values of χ2/df are high because of our large sample size (N = 6739). We also used CFI, TLI, RMSEA, Mc, and Gamma, which are common model selection fit indexes (i.e., CFI > 0.95; Hu and Bentler, 1998 [46]). Moreover, we adopted goodness of fit criteria for nested models noted by Chen (2007) [47], with ΔCFI $\ge$ −0.10, ΔGamma $\ge$ −0.08, ΔRMSEA $\ge$ 0.015, ΔMc $\ge$ −0.03 signal model rejection (Cf. Khojasteh and Lo (2012; Table 17; [48]) for alternative recommendations by different authors).

Our MGCFA was performed on the Black and White groups using all 12 available subtests (General Science, Arithmetic Reasoning, Word Knowledge, Paragraph Comprehension, Numerical Operations, Coding Speed, Auto Information, Mathematics Knowledge, Mechanical Comprehension, Electronics Information, Assembling Objects, and Shop Information). In creating the model, we used the results of an EFA, since a model based off of a theoretical Vernon-like structure didn’t fit the data well and also since previous published models only used the 10 subtest ASVAB from the NLSY79. The best fitting model included four factors we labeled Technical, Verbal, Mathematics, and Spatial, which we subsequently topped with a bifactor g.

All subtests had univariate skewness and kurtosis values below 1 and were thus acceptable [49]. Our values of Mardia’s coefficients were high (b1p = 3.606; b2p = 185.568; p = 12) and our Henze-Zirkler coefficient was 1.118. However, there did not appear to be any deviation from multivariate normality assessed graphically with the MVN R package (Korkmaz, Goksuluk and Zararsiz, 2019; [50]). As such, we believe the data are at least approximately multivariate normal and, consequently, that fitting an MGCFA model is justified. The results are given in

Table 11. Measurement Invariance Model Results.

Model	Description	χ2/df	CFI	TLI	RMSEA	Mc	Gamma
B	Baseline, 4 Stratum II factors	15.493	0.969	0.947	0.046	0.908	0.969
M1	Configural	15.687	0.977	0.954	0.043	0.929	0.976
M2	Metric	11.355	0.977	0.964	0.038	0.930	0.976
M3	Scalar	12.271	0.973	0.961	0.040	0.919	0.972
M4	Strict	12.138	0.970	0.961	0.040	0.910	0.970
M5	Latent Variances	12.841	0.966	0.963	0.047	0.880	0.966
M6	All Latent Means	35.881	0.896	0.890	0.080	0.669	0.903
M6A	Latent Means Group Factors	18.305	0.949	0.943	0.056	0.833	0.950
M6B	Latent Mean Spatial	12.803	0.966	0.963	0.047	0.879	0.966
M6C	Latent Mean Spatial and g	22.039	0.939	0.929	0.061	0.806	0.941

Note: Baseline is the model without g and all models after this stage include a bifactor g. CFI: comparative fit index; TLI: Tucker–Lewis Index; RMSEA: root mean square error of approximation; Mc: McDonald's noncentrality index; Gamma: Gamma hat. N_Black = 2333, N_White = 4406. M6 = all latent means are fixed to zero. M6A = only the latent means of the group’s factors are fixed to zero, g is left to vary between groups; M6B = only the latent mean in the spatial factor is fixed to zero; all other factors are left to vary; M6C = latent means in both g and spatial are fixed to zero.

.

As seen, imposing configural invariance (M1) leads to improved fit over baseline (B). Likewise, metric invariance (M2) leads to no decrement in fit compared to the configural phase. Imposing both scalar (M3) and strict (M4) invariance led to small decrements in fit, but these are within recommended limits. Based on our MGCFA results, we believe the ASVAB is an unbiased assessment tool in the U.S. Black and White populations.

Furthermore, neither the strong nor the contra forms of Spearman’s hypothesis adequately represent the data. We tested this in models M6A through M6C, which correspond to the strong, weak, and contra forms of Spearman’s hypothesis in the nested format used by Frisby and Beaujean (2015) [35]. To do this, we first fitted a model (M5) in which latent variances were constrained. This acts as the baseline for comparing subsequent Spearman hypothesis models. As seen, fit for M5 is acceptable, except that $\Delta$Mc is at the cutoff point. However, given the other $\Delta$fit indexes, we deem M5 to have acceptable fit overall. As expected, when we next constrain all means between groups to equality (M6), the fit drops substantially and the model is untenable. The fit improves somewhat but remains untenable, relative to M5, when we free groups to differ in g alone (M6A). This corresponds to the strong version of Spearman’s hypothesis. When we allow groups to vary in all factors but spatial, the fit recovers and shows no significant detriment relative to model M5. This model corresponds to the weak Spearman’s hypothesis. However, when we additionally constrain g to zero, leaving the technical, mathematical, and verbal factors free to vary, the fit drops substantially and the model is no longer tenable. This latter model corresponds to the contra Spearman's hypothesis. Thus, we are able to affirm the weak Spearman’s hypothesis over the strong and contra versions.

It is important to note that we designated the weak Spearman’s hypothesis as a model with the spatial factor constrained to zero. This was done for two reasons. First, compared to possible alternatives, this was a well-fitting Spearman’s hypothesis model. Second, following Frisby and Beaujean (2015) [35], we constrained the factor exhibiting the smallest group differences; in this case, the spatial factor nearly overlapped with zero at the lower 95% confidence interval. That said, we compared alternative weak and contra Spearman’s hypothesis models individually restricting all other group factors (results not shown). The weak models fit acceptably and all contra models were rejected in terms of model fit. Restricting both spatial and mathematics or spatial and verbal, but not spatial and technical, also led to acceptable fit, so more sophisticated weak models were also viable, but no contra models were, including ones in which only g was constrained (without constraining any group factor).

Table 12. Black-White Mean Differences on Latent Factors.

Factor	Estimate	SE	95% CI
			Lower	Upper
G	1.13	0.03	1.06	1.19
Technical	1.03	0.07	0.9	1.17
Mathematical	−0.46	0.05	−0.35	−0.58
Verbal	0.21	0.06	0.11	0.3
Spatial	0	--	--	--

Note: Estimates came from model M6B. The latent mean difference for spatial was constrained to zero. The means for blacks were fixed at 0.0, with variances for both groups fixed to 1. Positive values indicate higher scores for whites and vice-versa. All values are rounded.

shows the factor mean differences for M6B. As can be seen, Whites had an advantage in g of 1.13 d.

4.7. Full Sibling Differences in Intraclass Correlations and Absolute Differences

Next, we computed intraclass correlations for full siblings. The intraclass correlations (ICC) for g are 0.472 [95% CI: 0.412, 0.527] for Whites (N = 694) and 0.516 [95% CI: 0.428, 0.595] for Blacks (N = 301). Twice, the sibling ICC gives the variance component due to genes, shared environment, and assortative mating, which in this case is close to unity. Next, we examined the absolute differences between full siblings. They were 10.10 IQ-metric points (N = 694) for Whites and 9.97 IQ-metric points (N = 301) for Blacks. These results indicate that the non-shared environmental variance components are approximately the same for Blacks and Whites.

5. Conclusions

We set out to test six predictions of the racial-cognitive model and found support for each. Among African American adolescents and young adults, darker color, an index of African ancestry, was negatively related to cognitive ability (r = −0.112). In contrast, parent-reported European ancestry was positively related to cognitive ability (r = 0.137). These results held controlling for age, sex, region of residence, and interviewer race. Further, while parent-reported ancestry was a predictor of color (β = −0.113, N = 1856), the association between the two indices was weak and both had independent effects on cognitive ability. This low correlation is expected given the imbalanced ancestry variable, as imbalance in a dichotomized variable attenuates point-biserial correlations. The corrected correlation would be r_c = 0.35. This is still low, perhaps because parent-reported ancestry and skin color are indexing recent and distal admixture, respectively.

In both cases, the relationships with cognitive ability were more pronounced on the more g-loaded subtests (r_{Dark_color}$\times$ _g-loading = −0.728; r_{Eur_ancestry}$\times$_g-loading = 0.679). A Jensen effect was also found in regard to the relation between African ancestry and cognitive ability among Whites (r_{Afr_ancestry}$\times$_g-loading = −0.593) and in relation to the mean difference between Blacks and Whites (r_BW$\times$_g-loading = 0.405), too. These findings have practical importance when it comes to research on cognitive ability in relation to social outcomes and ancestry indices such as color. The results suggest that highly g-loaded measures of cognitive ability are needed to capture the full mediating effect of cognitive ability. Similar results have been found in relation to social outcomes and self-identified race (e.g., Nyborg and Jensen, 2001) [51].

While some argue that Jensen effects are readily accountable in terms of cultural factors [52], it so happens that known environmental effects generally do not produce these. This includes adoption gains [53], gains from educational programs like Head Start [54], gains from learning potential programs [55], practice and retest gains [55], secular gains [56], the effects of lead exposure [57], iodine deficiency [58], prenatal toxins like cocaine and alcohol [58], or the effect of traumatic brain injury [58], and environmentality in general [59]. The reason seems to be that environmental effects tend to have larger effects on specific and broad abilities (i.e., Stratum I and II in the conventional three-stratum model of intelligence) than on general mental ability, as indicated by the negative correlation between vectors [60]. Of course, it is always possible that some unidentified set of environmental factors, which happen to induce g-loaded differences whilst also preserving MI, cause the ancestry related differences.

Further, to investigate the association between color and g among African-descent individuals, we conducted an analysis within and between families. We found a robust association among families. This showed up both among singleton families (β = −0.153; N = 814) and among full sibling pair families (β = −0.176; N = 225). However, we found no association within families, between full siblings (β = 0.027, N = 225). This latter finding is inconsistent with a color-based discrimination explanation of the association between color and g-scores. It is consistent, however, with a vertical transmission model.

We looked at differential sibling regression to see if the factors causing the observed group differences acted similarly across the whole range of cognitive ability. This turned out to be the case and the results replicated those of Murray (1999) [31]. This suggests that African Americans who are apt by White standards are no less affected by the factors inducing the mean difference than their less-acute co-racials. For differing interpretations of this effect, with respect to the nature vs. nurture question, see Scarr (1981) [22] vs. Flynn (2019) [52].

As for the mean group differences between Blacks and Whites, we found that strict factorial invariance/MI was tenable. Moreover, we found MGCFA confirmation of the weak version of Spearman’s hypothesis. From a theoretical point of view, MI suggests that group differences are due to the same factors that cause differences within both groups and are thus not due to factors unique to one or the other groups [61,62]. Furthermore, MGCFA verification of Spearman’s hypothesis implies that the Jensen effect between groups is not a result of confounding non-g factors. There are substantial g differences and an explanation of these is needed. The results suggest that the same holds in the case of color and ancestry within the African American group; however, confirmation of this will require a separate analysis of MI with the continuous variable skin color or ancestry as the group.

Regarding the full sibling differences, the ICCs and absolute differences between full siblings were substantially the same for Blacks and Whites. This indicates that non-shared environmental factors account for the same proportion of variance for both Blacks and Whites.

In sum, both color and reported ancestry are associated with cognitive ability within the African American population, the associations are present in adolescence, they are largest on the most g-loaded subtests and they do not show up to a substantial degree between full siblings within families, which differ little in ancestry and not at all in shared environments (by definition). These results strongly suggest that the ancestry-associated differences are due to either to genetic factors or to intergenerationally transmitted shared environmental factors. The psychometric and biometric nature of the racial group differences (the pattern of differential regression to the mean, the finding of MI, the finding of support for the weak Spearman’s hypothesis, the comparable full sibling ICCs, and absolute average differences) reinforce this conclusion.

Given our results, which are consistent with a cognitive capital model, we argue that the cognitive capital model should be tested against the colorism model using genetic-ancestry data from a large sample. Prediction 7 is that genetic ancestry will be associated with cognitive ability independent of color and that race-related phenotypes, including color, will show little independent relation with cognitive ability. If this holds, it will indicate that color is just or largely just a proxy for genetic ancestry. If this turns out to be the case, we propose that the next step will be admixture mapping, specifically looking at the regions of the genome where the association between g and genetic ancestry is pronounced. For logic, see for example, Zou et al. (2015) and Norris et al. (2017) in the context of assortative mating and ancestry [63,64].

Given the polygenicity of g, it may be difficult to discriminate between a shared environmental model and a genetic one without a very large sample size. Generally, in the latter case, the association between g and ancestry will be pronounced on neurologically related regions, while in the former it will follow neutral variation. With a sample size of several thousand, one should be able to determine if the association between g and ancestry is pronounced on genomic regions that code for conspicuous race-related phenotypes as predicted by the colorism model. Additionally, if colorism accurately explains cognitive ability differences between groups, GWAS-identified SNPs related to intelligence should cause lighter skin and showcase substantially elevated expression in the integumentary system in Blacks, although how they would do this with MI being tenable is uncertain.