Abstract
In this article, we present experimental and theoretical studies of pyridine derivatives (pyDs) inspired by natural systems to investigate the electron transfer processes occurring in aqueous media and elaborate a theoretical model that adequately predicts the behavior of new derivatives. Our results might be relevant to scientific and technological applications, including energy storage, redox-active scaffolds for organic synthesis, photoredox catalysis, and new materials. The synthesis of eight pyDs is reported. To improve water solubility, six new compounds are hexafluorophosphate alkylammonium salts. The pyDs exhibit irreversible redox processes, with electron-donating substituents decreasing the cathodic peak potential while electron-withdrawing groups increase it; when both substituents are present, the latter effect prevails. A computational study was performed to investigate the electrochemical behavior of the synthesized compounds and design new electroactive pyDs. DFT calculations provided the predominant species’ redox potentials and acidity constants to elaborate Pourbaix diagrams for each compound. The synthesized molecules exhibit a two-electron-one-proton dismutation process in the water pH window. Beyond this range, stabilized radical species undergo one-electron exchange processes. We correlated experimental and calculated parameters, screening 22 additional derivatives to evaluate their electrochemical behavior, identifying potential candidates capable of performing a one-electron transfer process in the pH window of water, revealing new applications for pyDs.
1. Introduction
The applications and specific devices in daily life drive the search for materials displaying innovative properties [1]. The abundance and sustainability of organic molecules have played a crucial role in this endeavor. In addition, organic compounds can be “engineered” to modulate their chemical or physical properties. Among the different structural motifs investigated, heterocyclic compounds play a predominant role, particularly nitrogen-containing molecules, which are essential in many chemical reactions occurring in all organisms and have considerable pharmacological significance [2,3,4,5,6].
Pyridine derivatives have shown electrochemical properties with a variety of applications spanning from CO2 reduction to diverse catalytic processes. For instance, in recent years, there has been a growing interest in studying molecular metabolism and redox biology to understand the mechanisms of cellular redox balance. In this context, nicotine adenine dinucleotides (NAD) have been called the cell’s “redox currency” [7]. Alkaloids, nitrogen-containing compounds, such as papaverine, strychnine, quinine, and nicotine, have been studied as inhibitors for metal corrosion [8,9]. The use of pyridine (py) and pyridinium ion (pyrH+) has been investigated to evaluate their catalytic role in the reduction of CO2 to methanol or other high-energy chemical feedstocks [10,11,12,13]. Pyridines or 1,4-dihydropyridines (dhpys) substituted at 2,6-, 3,5-, and 1,4-positions, have been synthesized and widely used as hydride donors in organocatalysis, Lewis’s acid catalysis, hydrogen atom donors in radical reactions, and antioxidants [14,15,16]. The electrochemical behavior of N(1)-benzyl and N(1)-propyl-1,4-dihydronicotinamide was also investigated in aqueous solution at pH 7–13, showing a two-electron one-step oxidation process, whose half-wave potential and limiting current are pH-independent [17]. 4-Substituted dhpys have been considered analogs of NADH coenzymes, where the substituent attached to the N1 position of the dhpys derivatives considerably affects their electrochemical behavior [18]. In the search for efficient synthetic organic processes, photoredox catalysis is being widely investigated. Recently, the use of Hantzsch esters as visible-light photoredox catalysts for transition-metal-free coupling of aryl-halides and aryl-sulfinates [19], as well as their use as the emerging versatile class of reagents in photoredox-catalyzed organic synthesis [20], have been reported.
The introduction of pyridine groups into poly(p-phenylenebenzo bisoxazole) (PBO) improved the electronic and optical properties, increasing the oxidation potential from 1.65 to 1.82 V vs. SHE, compared to PBO. The different behavior was attributed to a strong protonation of the pyridine-containing polymer [21]. Similarly, the electronic and steric properties of novel molecular frameworks, such as aza-heteroarenes, can be adjusted by introducing substituents into the heteroaromatic ring. This enables the fine-tuning and expansion of their potential applications [22].
Studying a molecule’s electrochemical behavior for energy storage is an essential prelude to understanding its physicochemical properties. Thus, bipyridinium salts are currently under extensive investigation due to their potential application in redox flow batteries. The electrochemical properties of bipyridinium salts are affected by the number of quaternary nitrogen atoms, the position of the nitrogen atoms (2,2′, 3,3′, and 4,4′), and the presence of bridges between the pyridine rings [16,23]. Besides the above-mentioned investigations, the electrochemical behavior of other nitrogen containing heterocycles has been reported [24,25].
The quest for inexpensive electroactive organic molecules for use in different scientific areas is highly attractive. However, this endeavor requires synthesizing and screening the properties of many molecules. Fortunately, computational methods offer a reliable alternative to time-consuming experimental evaluations for obtaining a priori electrochemical knowledge of many redox-active molecules. For instance, the reduction potential of quinoxaline derivatives with a range of electron-donating and electron-withdrawing groups have been reported. Calculations indicate that adding electron-donating groups, particularly alkyl groups, can significantly lower the reduction potential, albeit with a concomitant decrease in oxidative stability [26]. Also, it has been demonstrated that Artificial Intelligence (AI) assists the design, synthesis, and measurement of functional organic molecules [27].
Several requirements should be considered to use these electroactive molecules for a technical application, such as water solubility, redox potential, and chemical and electrochemical stability. The solubility of organic molecules in water can be increased by functionalizing the moiety with the appropriate groups, particularly charged functionalities. The functional groups affecting solubility can be categorized into negatively charged groups (carboxyl, phosphate and sulfate), positively charged groups (pyridinium, imidazolium, and tetraalkylammonium), and non-charged groups (cyano, mercapto, hydroxyl, morpholino, and polyether). For negatively charged groups, the effect is highly dependent on the pH of the electrolyte [28].
The appealing use of organic molecules to develop new materials, particularly nitrogen-containing heterocyclic compounds, motivated our interest in studying the redox properties of pyridine derivatives (pyDs). Herein, we present experimental and theoretical studies of pyDs inspired by natural systems to investigate the electron transfer processes occurring in aqueous media. Additionally, a theoretical model that adequately predicts the behavior of new derivatives is disclosed. According to the electron transfer process, our findings might be relevant to diverse scientific and technological applications, such as those mentioned above.
Our investigation started with the chemical synthesis of eight pyridine derivatives (structures 1 to 7′ in Figure 1a), six of which are new compounds (1, 2, 3, 4, 5, and 6). For these compounds, electrochemical characterization in aqueous solution and a theoretical study of their Pourbaix diagrams (PDs) were carried out. Furthermore, a theoretical analysis of the PDs for selected pyridine derivatives was performed (Figure 1b, structures 7 to 28).
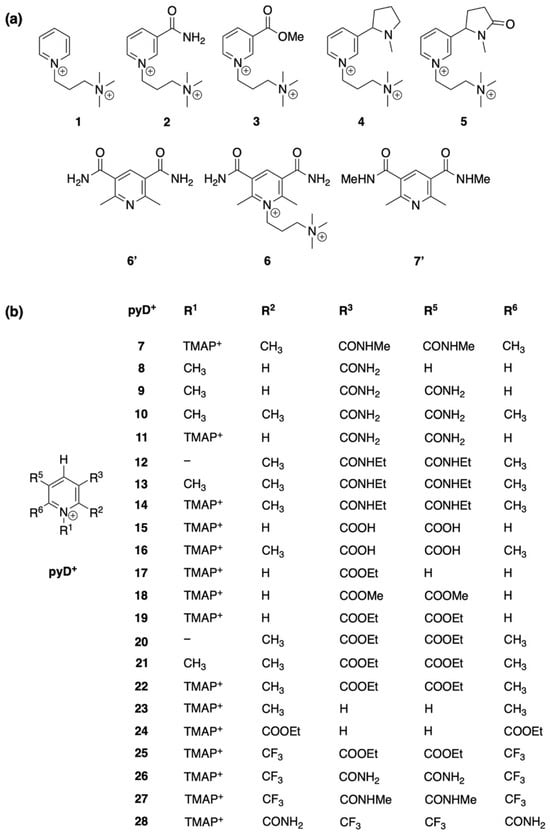
Figure 1.
Structures of pyridine derivatives (pyDs): (a) synthesized compounds as hexafluorophosphate salts and theoretically studied; (b) structures theoretically evaluated.
2. Materials and Methods
2.1. Synthesis
All experiments involving air- and/or moisture-sensitive compounds were conducted in an oven-dried round-bottom flask capped with a rubber septum under a positive pressure of nitrogen. Reaction temperatures refer to that of the bath. Concentration refers to removal of volatiles on a rotary evaporator below 35 °C. Analytical thin-layer chromatography (TLC) was performed using glass plates pre-coated with silica gel (0.25 mm, 60-Å pore size, 230–400 mesh, Merck, Rahway, NJ, USA) impregnated with a fluorescent indicator (254 nm). Materials on TLC plates were visualized under an ultraviolet lamp (254 nm) and/or by submersion of the plate in a solution of phosphomolybdic acid (5%) containing a trace of ceric sulfate in aqueous sulfuric acid (5% v/v) followed by charring on a hot plate. Column chromatography (CC) was performed with silica gel 60 (40–63 µm). All mixed solvent eluents are reported as v/v solutions. All reported compounds were analyzed by thin-layer chromatography (TLC): 1H NMR, 13C NMR, IR, and HRMS.
All the reagents were purchased from Sigma-Aldrich (St. Louis, MO, USA) and were used as received unless other things are stated. Only anhydrous DMF was distilled on CaH2. Acetone, methanol, ether, ethyl acetate, and dichloromethane were distilled prior to use. The solvents used for NMR spectra were purchased from Cambridge Isotope Laboratories, Inc., Tewksbury, MA, USA, and used as received.
Proton nuclear magnetic resonance (1H NMR) spectra and carbon nuclear magnetic resonance (13C NMR) spectra were recorded on Agilent-Inova-300 (Santa Clara, CA, USA), Varian VNMRS-400 NMR spectrometers (Palo Alto, CA, USA), and Magritek-Spinsolve-80 (Malvern, PA, USA). Proton chemical shifts are expressed in parts per million (ppm, δ scale) and are referenced to tetramethylsilane (TMS: 0.0). Carbon chemical shifts are expressed in parts per million (ppm, δ scale) and are referenced to tetramethylsilane (TMS: 0.0). Data are represented as follows: chemical shift, multiplicity (s = singlet; d = doublet; t = triplet; q = quartet; m = multiplet; br = broad; app = apparent), and coupling constant (J) in Hertz (Hz), as required. IR spectra were recorded on a Perkin-Elmer Spectrum 400 FT-IR/FIR spectrometer with ATR (Springfield, IL, USA). Mass spectra assessments were carried out on a JEOL SMX-102a spectrometer (Peabody, MA, USA).
HE and HE-Ox: Diethyl 2,2′-(2,6-dimethyl-1,4-dihydropyridine-3,5-diyl)bis(2-oxoacetate), and diethyl 2,2′-(2,6-dimethylpyridine-3,5-diyl)bis(2-oxoacetate), respectively, were prepared following literature procedures [29,30].
pyD 1: A mixture of pyridine (3 mL) and TMAP-Br (100 mg, 0.38 mmol) was added to a round-bottom flask and the mixture was heated at 70 °C for 18 h. The precipitate that formed, corresponding to the bromide pyridinium salt, was filtered off under vacuum and washed with acetone; this compound has been reported by Gray et al. [31] The white solid was redissolved in methanol (5 mL), followed by the addition of ammonium hexafluorophosphate (160 mg, 0.89 mmol), and the solution was stirred at room temperature for 24 h. The precipitate was filtered under vacuum and washed with methanol to provide 143 mg (80% yield) of a white solid. 1H NMR (500 MHz, DMSO-d6): δ 9.1 (d, J = 5.5 Hz, 2H), 8.7 (tt, J = 7.9, 1.2 Hz, 1H), 8.2–8.2 (m, 2H), 4.6 (t, J = 7.5 Hz, 2H), 3.3 (s, 2H), 3.1 (s, 9H), 2.5–2.4 (m, 2H). 13C NMR (125 MHz, DMSO-d6): δ 146.5, 145.5, 128.7, 62.3, 58.3, 53.0, 24.7. IR ν[cm−1]: 3149.0(w) [ν(C-H, sp2)], 1642.7(m) [ν(C=C)], 1492.8(m) [δ(CH3, CH2)], 1187.8(m) [ν(C-N+)], 824.6(s) [ν(Asym P-F)], 556.0(s) [ν(Sym P-F)]. HRMS (DART+) (m/z) [M-PF6]+ calculated for C11H20F6N2P: 325.1263, found: 325.1312. Spectral data are provided in Figures S1–S3.
pyD 2: Nicotinamide (300 mg, 2.46 mmol) and TMAP-Br (834 mg, 3.19 mmol) were dissolved in anhydrous DMF (6 mL) and the mixture was heated at 70 °C for 18 h. The precipitated dibromide salt was filtered off under vacuum and washed with acetone (the corresponding dichloride salt was reported by Craig et al. [32]). The white solid was redissolved in methanol (4 mL), followed by the addition of ammonium hexafluorophosphate (656.9 mg, 4 mmol), and the solution was stirred at room temperature for 24 h. The precipitate was filtered under vacuum and washed with methanol to afford 837 mg (85% yield) of a white solid. 1H NMR (400 MHz, DMSO-d6): δ 9.7 (s, 1H), 9.4 (d, J = 6.1 Hz, 1H), 9.0 (d, J = 8.2 Hz, 1H), 8.7 (s, 1H), 8.3 (dd, J = 8.0, 6.1 Hz, 1H), 8.2 (s, 1H), 4.8 (t, J = 7.5 Hz, 2H), 3.5–3.4 (m, 2H), 3.1 (s, 9H), 2.6 (q, J = 7.8 Hz, 2H). 13C NMR (100 MHz, D2O): δ 165.7, 146.6, 144.7, 144.7, 134.3, 128.8, 62.4, 58.5, 53.2, 24.5. IR ν[cm−1]: 3382.8(w) [ν(N-H)], 3147.3(m) [ν(C-H, sp2)], 1690.3(s) [ν(C=O)], 1615.9(m) [ν(C=C)], 1478.0(w) and 1400.3(m) [δ(CH3, CH2)], 818.0(s) [ν(Asym P-F)], 554.3(s) [ν(Sym P-F)]. HRMS (DART+) (m/z) [M-PF6]+ calculated for C12H21F6N3OP: 368.1321, found: 368.1377. Spectral data are provided in Figures S4–S6.
pyD 3: 3-(3-(methoxycarbonyl)-1-pyridin-1-yl)-N,N,N-trimthyl-propan-1-amonium hexafluorophosphate. Methylnicotinate (500 mg, 3.65 mmol) and TMAP-Br (1143 mg, 4.38 mmol) were dissolved in anhydrous DMF (6 mL) and the mixture was heated at 70 °C for 18 h. The mixture was cooled at ambient temperature and diluted with ether (6 mL). The precipitate thus formed was filtered off under vacuum and rinsed with ether. The solid was redissolved in methanol (4 mL) and ammonium hexafluorophosphate (1.18 mg, 7.3 mmol) was added and the solution was stirred at room temperature for 16 h. The precipitate was filtered under vacuum and rinsed with methanol to afford 1.25 g (65% yield) of a white solid. 1H NMR (400 MHz, DMSO-d6): δ 9.70 (s, 1H), 9.42 (d, 1H, J = 8.14), 9.03 (d, 1H, J = 6 Hz), 8.36 (d, 1H, J = 6 Hz), 8.33 (d, 1H, J = 6 Hz), 4.8 (app t, 2H, J = 7 Hz), 3.98 (s, 3H), 3.45 (m, 2H), 3.01 (s, 9H), 2.5 (m, 2H). 13C NMR: (76 MHz, DMSO-d6): δ162.8, 148.8, 146.9, 146.1, 130.4, 129.06, 62.2, 58.6, 54.1, 53.0, 52.8, 24.9. IR ν[cm1]: 3321.6(w) [ν(N-H)], 3095.1(w) [ν(C-H, sp2)], 3031.0(w) [ν(C-H, sp3)], 1735.6(m) [ν(C=O)], 1479.2(w) and 1437.3(w) [δ(CH3, CH2)], 1080.0(s) [ν(C-N+)], 829.1(s) [ν(Asym P-F)], 556.3(m) [ν(Sym P-F)]. Spectral data are provided in Figures S7–S9.
pyD 4: (S)-Nicotine (0.19 mL, 1.23 mmol) and TMAP-Br (417.6 mg, 1.60 mmol) were dissolved in anhydrous DMF (5 mL) and the mixture was heated at 70 °C for 18 h. Then, the DMF was concentrated in vacuum and the crude was washed with ethyl acetate. The product was obtained as a slightly red oil. Then, the oil was redissolved in methanol (3.5 mL) and ammonium hexafluorophosphate (411 mg, 2.52 mmol) was added. The solution was stirred at room temperature for 24 h. The precipitate was filtered under vacuum and washed with methanol to provide 490 mg (72% yield) of a beige solid. 1H NMR (500 MHz, DMSO-d6): δ 9.0 (s, 1H), 9.0 (d, J = 6.0 Hz, 1H), 8.6–8.6 (m, 1H), 8.2–8.2 (m, 1H), 4.6 (t, J = 7.7 Hz, 2H), 3.4 (d, J = 8.1 Hz, 2H), 3.3 (d, J = 10.1 Hz, 1H), 3.2 (t, J = 8.6 Hz, 1H), 3.1 (s, 9H), 2.4–2.4 (m, 3H), 2.3–2.3 (m, 1H), 2.2 (s, 3H), 1.9–1.8 (m, 2H), 1.7–1.6 (m, 1H). 13C NMR (125 MHz, DMSO-d6): δ 145.5, 145.2, 144.2, 144.1, 128.5, 67.2, 62.3, 58.3, 56.8, 53.0, 35.3, 24.9, 23.2, 17.1. IR ν[cm−1]: 3105.8(w) [ν(C-H, sp2)], 2975.9(w) [ν(C-H, sp3)], 2810.4(w) [ν(Sym cyclic-CH2)], 1637.8(w) [ν(C=C)], 1492.9 and 1480.5(m) [δ(CH3, CH2)], 824.9(s) [ν(Asym P-F)], 555.3(s) [ν(Sym P-F)]. HRMS (DART+) (m/z) [M-PF6]+ calculated for C16H29F6N3P: 408.1998, found: 408.2026. Spectral data are provided in Figures S10–S12.
pyD 5: (S)-Cotinine (300 mg, 1.7 mmol) and TMAP-Br (578 mg, 2.21 mmol) were dissolved in anhydrous DMF (6.1 mL) and the mixture was heated at 70 °C for 18 h. Then, the DMF was concentrated in vacuum and the crude was washed with ethyl acetate. The product was obtained as a slightly yellow oil. The oil was redissolved in methanol (3.5 mL) and ammonium hexafluorophosphate (583 mg, 3.5 mmol) was added. The solution was stirred at room temperature for 24 h. The precipitate was filtered under vacuum and washed with methanol to provide 752 mg (78% yield) of a white solid. 1H NMR (400 MHz, DMSO-d6): δ 9.0 (d, J = 4.9 Hz, 2H), 8.6–8.5 (m, 1H), 8.2–8.2 (m, 1H), 4.8 (dd, J = 8.4, 5.6 Hz, 1H), 4.6 (dt, J = 7.1, 3.6 Hz, 2H), 3.3–3.3 (m, 2H), 3.0 (s, 9H), 2.6 (s, 3H), 2.5–2.3 (m, 5H), 1.8–1.7 (m, 1H). 13C NMR (100 MHz, DMSO-d6): δ 175.2, 144.9, 144.7, 143.9, 143.2, 128.9, 62.3, 60.9, 58.4, 52.9, 29.7, 28.5, 27.5, 24.8. IR ν[cm−1]: 3105.8(w) and 3068.6(w) [ν(C-H, sp2)], 2979.7(w) [ν(C-H, sp3)], 1682.3(s) [ν(C=O)], 1482.2() [δ(CH3, CH2)], 821.6(s) [ν(Asym P-F)], 555.2(s) [ν(Sym P-F)]. HRMS (DART+) (m/z) [M-PF6]+ calculated for C16H27F6N3OP: 422.1790, found: 422.1850. Spectral data are provided in Figures S13–S15.
pyD 6′ was prepared according to the procedure reported by Blank et al. [33] The product was purified by column chromatography (CH2Cl2/MeOH 5%) to afford 41.4 mg (65% yield) of desired product as a white solid. All the spectroscopic data match the reported values. 1H NMR (500 MHz, DMSO-d6): δ 8.3 (s, 1H), 2.7 (s, 6H). 13C NMR (125 MHz, DMSO-d6): δ 169.4, 158.4, 139.8, 128.1, 24.6. Spectral data are provided in Figures S16 and S17.
pyD 6: 2,6-Dimethylpyridine-3,5-dicarboxamide (200 mg, 1.03 mmol) and TMAP-Br (405 mg, 1.55 mmol) were dissolved in anhydrous DMF (2.6 mL) and the mixture was heated at 70 °C for 18 h. The precipitate formed was vacuum-filtered and washed with cold methanol. The white solid was redissolved in methanol/water (4 mL, 3:1 v/v) mixture and ammonium hexafluorophosphate (583 mg, 3.5 mmol) was added. The solution was stirred at room temperature for 24 h. The precipitate was filtered under vacuum and washed with methanol to provide a beige solid 330 mg (55% yield) of a beige solid. 1H NMR (400 MHz, DMSO-d6): δ 8.5 (s, 1H), 4.3 (t, J = 6.1 Hz, 2H), 3.4 (dd, J = 9.9, 6.4 Hz, 2H), 3.1 (s, 9H), 2.7 (s, 3H), 2.2–2.1 (m, 2H). 13C NMR (100 MHz, DMSO-d6): δ 165.8, 161.9, 141.0, 123.1, 62.9, 52.8, 34.7, 25.2, 22.7. IR ν[cm−1]: 3105.2(w) [ν(C-H, sp2)], 2977.1(w) [ν(C-H, sp3)], 1722.0(s) [ν(C=O)], 1283.1(m) [ν(C-N)], 1112.1(m) [ν(C-N+)], 827.2(s) [ν(Asym P-F)], 556.1(m) [ν(Sym P-F)]. Spectral data are provided in Figures S18–S20.
pyD 7′: N3,N5,2,6-tetramethylpyridine-3,5-dicarboxamide. The preparation of this compound is mentioned in the literature [34], however no details on its structural characterization are provided. A solution of diethyl 2,6-dimethylpyridine-3,5-dicarboxylate (200 mg, 0.79 mmol) in 2 mol L−1 CH3NH2/MeOH (8 mL) was heated in a Schlenk storage tube at 70 °C overnight. The mixture was cooled to ambient temperature and concentrated in vacuum. The residue was taken up in ethyl acetate (20 mL), washed with water (2 × 5 mL), and sat. NaCl (5 mL) was added, and it was dried (Na2SO4). The solvent was removed, and the residue of the product was purified by column chromatography (silica gel, CH2Cl2/MeOH 5%) to afford 141 mg (35% yield) of a white solid. 1H NMR (400 MHz, DMSO-d6): δ 8.4 (s, 2H), 7.7 (s, 1H), 2.8 (d, J = 4.6 Hz, 6H), 2.5 (s, 6H). 13C NMR (100 MHz, DMSO-d6) δ 168.0, 155.7, 134.5, 128.4, 26.0, 22.7. IR ν[cm−1]: 3299.0(m) [ν(N-H)], 3077.3(w) [ν(C-H sp2)], 2960.8(w) [ν(C-H sp3)], 1618.9(s) [ν(C=O)], 1545.7(m) [ν(C=C)], 1296.5(m) [ν(C-Namide)], 1156.3(m) [ν(C-N)]. HRMS (DART+) (m/z) [M + H]+ calculated for C11H16N3O2: 222.1243, found: 222.1250. Spectral data are provided in Figures S21–S23.
2.2. Electrochemistry
Cyclic voltamperometry tests were carried out with a potentiostat–galvanostat model PGSTAT 100N. All electrochemical experiments used a glassy carbon microelectrode (GCM) as the working electrode (WE), after polishing with diamond suspension (1 µm) and clear with deionized water. Platinum (Pt) wire was used as a counter electrode, and AgCl-Ag as a reference electrode (0.27 V vs. SHE). A scan rate of 0.1 V s−1 was applied for cyclic voltamperograms (CVs). All CVs were referred to the SHE. The compounds (2 × 10−3 mol L−1) were prepared in NaCl (1 mol L−1, pH = 7). CVs were performed in positive and negative directions, starting from the zero current potential (Ei=0), after deoxygenation with N2. Also, pyDs were studied in DMSO (99.7%, extra dry, over molecular sieves) using Bu4NPF6 (0.1 mol L−1) as an electrolyte.
2.3. Computational Details
We performed redox potential and pKa calculations using a workflow for the geometry optimization of species shown in Figure 1, with the following specifications. We generated the molecules by making substitutions with the different functional groups on the pyridine ring using SMILES strings. The first module in the workflow performs molecular mechanics (MM) calculations. The structures were converted from smiles to xyz coordinates using the Obabel 2.4.0. software [35], followed by a conformer search and an energy minimization with the MMFF94 force field [36,37,38,39,40]. The second module corresponds to the quantum mechanics (QM) module, which executes density functional theory (DFT) calculations through the Gaussian16 package [41].The QM module takes the MM-optimized coordinates as input for further geometry relaxation using the B3LYP functional [42], a 6-311+G(d,p) basis set [43,44], and an SMD solvation model in water [45]. A frequency analysis is specified to confirm a minimum and to compute the Gibbs free energy.
Redox Potential and pKa Calculations
The estimation of redox potentials and pKa values usually involves methodologies based on thermodynamic cycles [46,47,48]. In general, for a reduction equilibrium in solution (Equation (1)), the standard redox potential (E°calc) is calculated through Equation (2), where ΔGs0, redox is the Gibbs free energy difference between the oxidized and reduced species (Equation (3)), n is the number of electrons, and F is the Faraday’s constant. An absolute value of 4.44 V for the standard hydrogen electrode (SHE) in water was considered as the reference potential value required for the calculations [49].
The calculation of pKa follows a similar procedure. For an acid-base equilibrium (Equation (4)), the standard Gibbs free energy change (ΔGs0,a) is related to the acid dissociation constant (Ka) in its negative logarithmic form (pKa), as described by Equation (5), where R is the gas constant and T is the temperature. An approximation to calculate the ΔGs0,a requires the Gibbs free energy values for the species HA and A− and the solvated proton in water (−269 kcal mol−1) [50,51], as shown in Equation (6).
3. Results and Discussion
The pyridine ring is a π-deficient aromatic system due to the presence of an electronegative nitrogen atom. This characteristic is responsible for the typical chemical reactivity of this heterocyclic compound, i.e., pyridine reacts preferably with nucleophiles. Additionally, the lone pair of electrons on the nitrogen atom confers basic and nucleophilic characteristics to the molecule, forming quaternary ammonium salts readily. The possibility of modulating the electronic distribution on the heteroaromatic ring and its redox properties stimulated our interest in synthesizing nature-inspired pyridines to investigate their electrochemical behavior. For this purpose, we selected Hantzsch ester-derived pyridines and commercially available 3-substituted pyridines such as nicotine and its oxidized metabolite cotinine. Furthermore, computational studies were performed to study the Pourbaix diagram of the synthesized molecules and additional derivatives to find candidates which might have some application.
3.1. Chemical Synthesis
The structures shown in Figure 1 were proposed for chemical synthesis and structure relationship studies in silico. Compounds 1 to 7′ (Figure 1a) were synthesized and characterized to investigate their electrochemical behavior, while structures 7 to 28 (Figure 1b) are derivatives selected for computational studies.
PyDs 1 and 2 were obtained as the di-(hexafluorophosphate) salts; similar procedures have been reported to prepare the dibromide and dichloride salts, respectively [31,32]. PyD 6′ required for our synthetic and electrochemical studies was prepared according to literature procedures [33]. PyD 7′ was also synthesized and characterized; although the preparation of this compound is mentioned in the literature [34], no details on its structural characterization are provided.
The synthesis of the above-mentioned compounds was achieved either by N-alkylation of the corresponding commercially available pyridine ring (py, Scheme 1a), or by constructing the corresponding aromatic ring using literature procedures, followed by the previously described alkylation (Scheme 1b) [29,30].
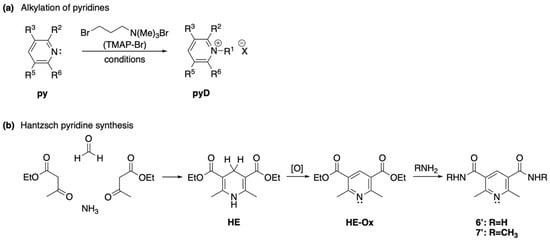
Scheme 1.
General strategies for the synthesis of the selected molecules 1 to 7′. (a) Alkylation of pyridines. (b) Hantzsch pyridine synthesis.
For the alkylation reaction, a solution of the corresponding starting material of 1 to 5 in anhydrous DMF was treated with TMAP-Br to provide the corresponding pyridinium salts. The treatment of an alcoholic solution of the previously obtained bromide salts with an aqueous solution of NH4PF6 afforded the analogous hexafluorophosphate salts. All attempts to N-alkylate the oxidized Hantzsch ester (diethyl 2,6-dimethylpyridine-3,5-dicarboxylate) using TMAP-Br or methyl iodide were unsuccessful, as well as the N-alkylation of amide 7′. While this alkylation reaction might seem trivial, no reports in the literature describe this transformation, and the only reported method for its preparation involves the oxidation of diethyl 1,2,6-trimethyl-1,2,3,4-tetrahydropyridine-3,5-dicarboxylate [52]. Likewise, attempts to convert the oxidized Hantzsch ester into diethylamide derivative via an aminolysis reaction with a 70% aqueous solution of EtNH2 failed. Two additional experiments were also performed, the first one included the hydrolysis of the ethyl ester, acid chloride formation, and subsequent reaction with a 70% solution of EtNH2. In the second attempt, the carboxylic acid was reacted with a 70% aqueous solution of EtNH2 in the presence of dicyclohexylcarbodiimide (DCC) and 1-hydroxybenzotriazole (HOBt). However, both experiments were unsuccessful and only trace amounts of desired product were observed in the 1H NMR of the crude mixture, along with a mixture of several unidentified compounds.
Nevertheless, alkylation of amide 6′ (prepared by aminolysis of the oxidized Hantzsch ester, Scheme 1b) with TMAP-Br proceeded smoothly to provide a single product. Since all the attempts to obtain the diethylamide were unsuccessful, we prepared amide 7′ via aminolysis of the corresponding ethyl dicarboxylate (Scheme 2). However, treatment of 7′ with TMAP-Br to obtain derivative 7, following the general alkylation procedure, resulted in unreacted starting material. The above results show that changing the nature of the substituent on the heterocyclic moiety can dramatically affect the reactivity of the pyridine derivative.

Scheme 2.
Synthetic procedure to obtain compounds 7′ and attempts to obtain 7.
3.2. Electrochemical Characterization
As demonstrated by the cyclic voltamperometry test, the reduction in pyD+ molecules involves the transfer of two electrons and one hydrogen ion at the C-4 position of the pyridine ring (Equation (7)) [53].
The results obtained by cyclic voltamperometry show that the reduction processes of pyDs depend on the type of substituent and counterion [54]. Figure 2a shows the CV performed in a negative scan direction for pyD 1; the cathodic peak potential (Ecp) appears at −1.23 V vs. SHE, its corresponding oxidation signal at −0.03 V vs. SHE, and the peak-to-peak separation (ΔEp) was 1.20 V. When the CV was recorded in a positive direction (Figure 2b), the absence of the oxidative signal at the start of the scan, from 0.10 to 1.00 V vs. SHE, confirms that the oxidative signal at −0.03 V vs. SHE is formed until the reduction in the compound takes place at −1.23 V vs. SHE.
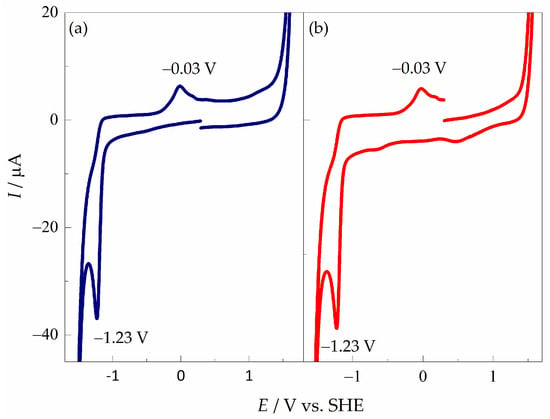
Figure 2.
Cyclic voltamperograms of pyD 1 (2.00 × 10−3 mol L−1) in NaCl (1 mol L−1) using a GCM as working electrode. υ = 0.1 V s−1: (a) cathodic scan and (b) anodic scan.
To obtain more information about the electrochemical activity of pyD 1, inversion potential studies were performed (Figure 3). The results show that the intensity between the cathodic peak current (icpred) and the anodic peak current (iapox) was disproportionate. According to this observation, pyD 1 presents an irreversible electrochemical profile.
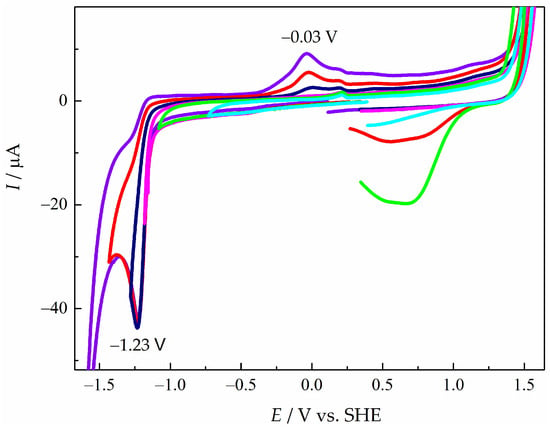
Figure 3.
CVs of pyD 1 (2.00 × 10−3 mol L−1) in NaCl (1.00 mol L−1), obtained from several cathodic inversion potentials (E−l): cian E−l = −0.75 V, green E−l = −1.10 V, magenta E−l = −1.20 V, dark blue E−l = −1.30 V, red E−l = −1.40 V and violet E−l l= −1.60 V vs. SHE. WE: GCM, υ = 0.10 V s−1.
Similar experiments were carried out for the other synthesized compounds under the same conditions as above. The studied derivatives displayed a low solubility (2.00 × 10−3 mol L−1) at neutral medium. Table 1 summarizes the experimental data, including half-wave potentials (E1/2) and peak-to-peak separation (ΔEp). The electrochemical evaluation of the synthesized compounds exhibits a similar behavior among them, showing a single reduction signal from −0.98 to −1.26 V vs. SHE under neutral conditions (Figure 3 and Figures S24–S30), which is characteristic of the pyridines and its derivatives [55,56,57,58]. The associated oxidative signals appear from −0.03 to 0.68 V vs. SHE.

Table 1.
Electrochemical parameters, V vs. SHE, of pyridine derivatives 1 to 7′ in water.
In all cases, ΔEp suggests an irreversible electrochemical process. The presence of electron donor/acceptor groups slightly modifies the reduction peak potential (Ecp) for pyD derivatives. The difference in Ecp would be related to the nature of the synthesized compound’s charge and the substituent’s energy density. The reduction potentials become more negative, depending on the nature of the functional group, observing the following trend: 3, 6, 2, 5, 6′, 1, 7′, and 4 (Table 1). Moreover, in aqueous solutions, the presence of protons facilitates the reduction in the pyDs. These results demonstrate that the substituent and the molecular structure influence the electrochemical properties.
Compound 1 (Figure 1a) was the simplest molecule studied without substituents and is used for comparison purposes. When the pyridine is mono-substituted at the C-3 position with an electron-withdrawing group, the reduction potential increases due to a lower electron density on the pyridine ring. For instance, Ecp V vs. SHE changes from −1.23 to −0.98 (3, R3 = CO2Me), to −1.13 (2, R3 = CONH2), and to −1.17 (5, R3 = pyrrolidone). In contrast, if R3 is an electron-donating group, such as a pyrrolidine in compound 4, the reduction reaction is slightly more challenging due to the increased electron density. Therefore, Ecp for compound 4 appears at a lower potential value, −1.27 V vs. SHE, compared to pyD 1.
When pyD is tetra-substituted with R3 = R5 = CONH2 and R2 = R6 = CH3 (pyD 6), the effect of the electron-withdrawing group dominates over the electron-donating inductive effect of the methyl groups. As a result, the potential shifts to more positive values, with an Ecp = −1.08 V vs. SHE, Figure S29. To evaluate the effect of the alkyl chain attached to the nitrogen atom of the pyridine ring on Ecp, we compared pyD 6′ (Figure S28) with pyD 6. In this comparison, pyD 6′ showed an Ecp = −1.18 V vs. SHE, whereas the potential for pyD 6 was Ecp = −1.08 V vs. SHE. The shift to more positive values is due to a positive charge on the pyridine nitrogen atom. The possibility of resonance structures (Scheme 3) delocalizes the positive charge on a larger surface, facilitating the reduction process. In the case of pyD 6′ and 7′, the Ecp value is more negative for pyD 7′ −1.26 V vs. SHE (Figure S30). Although both compounds contain a carbonyl moiety at C-3 and C-5, for pyD 7′ R3 and R5 are secondary amides; additionally, this compound has two methyl groups at C-2 and C-6 whose inductive effect might be responsible for lowering the reduction potential value.
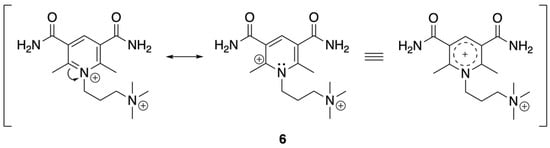
Scheme 3.
Resonance structures for pyD 6.
Due to the amphoteric properties of water, several organic compounds often undergo acid/base reactions when they are oxidized or reduced at the electrode surface. In order to modulate these effects, electrochemical measurements were conducted in the aprotic polar solvent DMSO (99.7%, extra dry, stored over molecular sieves).
The voltamperograms obtained for the compounds in DMSO show a reduction process and its corresponding oxidation process in all cases (Figures S31–S37). The values for each compound are presented in Table 2. For compounds 1, 2, 3, 4, and 5, the reduction potential in DMSO has a ~0.4 V anodic shift with respect to those observed in NaCl (aq). These effects are related to the electron pair donation ability of the solvent playing an important role in the redox potential of an ionic compound, which can be estimated by the parameter known as the donor number, DN [59]. Therefore, less energy is required to carry out the reduction in ionic species in a solvent with high electron donor capacity, resulting in a shift toward anodic potential. For instance, in DMSO (DN = 124.7 kJ mol−1), the cathodic process occurs before than the observed in aqueous solution (DN = 75.312 kJ mol−1).

Table 2.
Electrochemical parameters, V vs. SHE, of pyDs in DMSO.
Additionally, important differences are observed in the Ecp values (Table 2) for the first five compounds with respect to pyDs 6′, 6, and 7′ in DMSO (Figures S31–S37). To understand the difference in redox behavior, a series of experiments consisting in the addition of known amounts of KOH/D2O (0.04 mol L−1) to a DMSO solution of pyDs 1, 2, and 7′, followed by acquisition of the corresponding 1H NMR spectra. The results allowed us to conclude that a nucleophilic attack by the HO− ion occurs at the free positions of the pyD ring (C-2, C-4, C-5, and C-6) in compounds 1 and 2, leading to the formation of a new electroactive species (see Figures S38 and S39). The hydroxylated products undergo an easier oxidation process; however, since compound 7′ has substituents at C-2, C-3, C-5, and C-6 positions, the nucleophilic attack does not occur. In the electrochemical process, the reduced species are more reactive toward the nucleophilic attack. As a consequence, a lower reduction potential can be observed for pyDs 1, 2, 3, 4, and 5 compared to 6, 6′, and 7′.
3.3. Computational Studies
3.3.1. Proton-Coupled Electron Transfer Reactions
For the pyDs, the main redox equilibria in solution were established through a pH predominance zone diagram (PZD), using the pKa values of the oxidized and reduced species involved in Equation (1). Scheme 4 shows the processes for the species considered, where we identify electron transfer reactions (E01, E02, and E03), proton-coupled electron transfer (PCET) reactions (E01A and E02B), and proton transfer reactions (pKaA and pKaB).
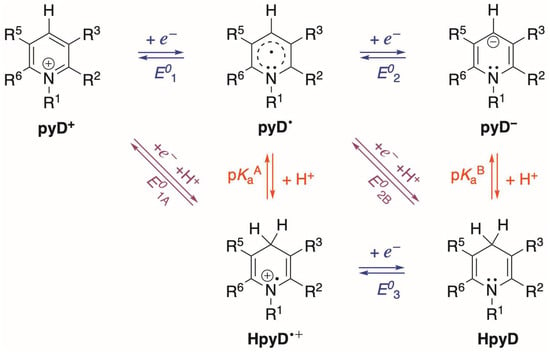
Scheme 4.
Species and reactions considered for theoretical evaluation of pyridine derivatives (pyDs). Electron transfer reactions (horizontal), proton transfer reactions (vertical), and proton-coupled electron transfer reactions (diagonal) are shown.
For these equilibria, the redox potential and pKa were calculated at a B3LYP/6-311+G(d,p) level of theory in water, following the methodology described in computational details. The results obtained for derivatives 1 to 7′ are presented in Table 3, where we can note that the values are consistent through all the derivatives. Notably, the pKaB has an extremely high value, exceeding the pH water scale, which can be attributed to the high basicity of the pyD−.

Table 3.
Calculated standard redox potentials, E0/V vs. SHE, and pKa values for pyridine derivatives 1–7′ in water.
Based on the pKaA and pKaB values, we can plot the PZD of the pyDs (see example in Figure S40 for pyD 1) and establish the predominant equilibria (Equations (8)–(12)), where we identified the following general behavior. At pH < pKaA, the two-electron transfer process is given by Equations (8) and (9), where the redox potential of the first reduction (E01A) is lower than the second reduction (E03), leading to a dismutation process of the HpyD•+ radical species. A similar behavior is observed for the region where pKaA < pH < pKaB (Equations (10) and (11)) since the redox potential E01 is lower than E02B, now producing the dismutation of the pyD• species. Finally, the region where pH > pKaB has a redox potential E01, higher than E02 (the equilibria involve Equations (10) and (12)), indicating that a two-step electron transfer occurs, resulting in the stabilization of the pyD• radical species.
The previous analysis allowed us to establish the general behavior on the pyDs based on the standard redox potential. A further calculation of the pH-dependent redox potential (conditional potential) to construct the Pourbaix diagram could confirm this trend. In the following section, we present the theoretical study of the Pourbaix diagrams for the synthesized (1–7′) and proposed (7–28) pyridine derivatives shown in Figure 1. Although the PDs are applicable only within the stability limits of water (considering pH and redox potential), an extended theoretical PD can help to identify how to direct the processes occurring on a molecule towards a desired region.
3.3.2. Pourbaix Diagrams
To compute the Pourbaix diagram (PD), the conditional potential (E′) was calculated for each pH zone through the Nernst equation (Equation (13)), where E0 is the standard reduction potential, Q is the reaction quotient, and n is the number of electrons transferred. The pH dependence is obtained by considering equal concentrations of oxidized and reduced species.
Four main zones were established from the Pourbaix diagram for pyD 1, shown in Figure 4a. The first one, at pH < 3.35, is characterized by a dismutation of the radical species HpyD•+ (obtained by subtracting Equation (8) from Equation (9)). The dismutation occurs since the conditional potential of the first reduction (dotted green line) is lower than the second (dotted blue line). Consequently, a single-proton two-electron transfer reaction takes place (red line). A similar reaction takes place in the second zone, at 3.35 < pH < 29.91, where the pyD• species undergoes a dismutation process (subtracting Equation (10) from Equation (11)). The third zone is defined at 29.91 < pH < 49.23, where a crossing between the first and second reduction lines is observed (pHcross = 29.91) and the reduction process occurs in two steps: a single-electron transfer (Equation (10)) and a proton-coupled electron transfer reaction (Equation (11)). This zone is characterized by stabilizing the radical species (pyD•). The last zone, at pH > 49.23, is pH-independent and a two-step electron transfer takes place (Equations (10) and (12)).
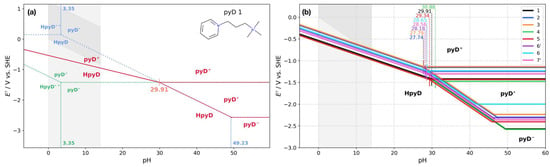
Figure 4.
Pourbaix diagrams (PDs) for pyridine derivatives. (a) PD for compound 1; the overall processes are shown in red lines with dismutation processes at 3.35 < pH < 29.91 and a radical stability window at pH > 29.91. The green and blue dotted lines represent the equilibria with the reactions obtained from the DZP. (b) PDs calculated for pyridine derivatives 1–7′. The pHcross value is shown for each derivative. The shaded area indicates the water stability window in each plot.
The PDs for pyridine derivatives 2 to 7′ were calculated following the same strategy used for derivative 1. Figure 4b illustrates the global process for these derivatives, compared to pyD 1 (black line), showing similar behavior among them. The crossing of pH from the dismutation zone to the radical stability window is in the range of 27−31 pH units. Below this value, the reaction is a single-proton two-electron transfer, which spans the water pH window (0–14) and close to the redox potential lower boundary of the water stability window (gray shaded area). Beyond pHcross occurs the stabilization of the radical species, producing a two-step electron transfer process.
We correlate the experimental and calculated parameters to select the parameters that allow estimating peak potential values from a theoretical parameter or from the peak potentials to predict the undergoing electrochemical transfer processes associated with a molecule. Among the parameters evaluated are the cathodic and anodic peak potentials in water and DMSO (Ecp and Eap) and different calculated parameters from the PDs, such as the conditional potential at pH = 0 (E′pH=0), the crossing pH between the dismutation zone and the radical stability window (pHcross), and the pKaA and pKaB.
In general, the Ecp in water (Figure 5) shows higher correlation with the computed parameters than in DMSO (Figure S41). However, the Eap in water and DMSO have low correlation (Figure S42); this poor correlation could be related to the origin of the oxidation signal and the species generated at the surface electrode. Notably, the peak values for compounds 1, 2, 3, 4, and 5 are different from those values for compounds 6, 6′, and 7′, because the former values exhibited coupled chemical hydroxylation reactions via a nucleophilic attack. Experimentally, the peak-to-peak separation (ΔEp) is an indicator of the system reversibility. The electrochemically characterized compounds (1–7′) have a high ΔEp value that can be considered irreversible (see above discussion of Figure 3). For a reversible system, a low peak-to-peak separation is desired (associated with the oxidation and reduction processes). Since only a good correlation was observed for the Ecp, it would be hard to predict reversibility for these systems from the calculated parameters. However, we can identify other relevant parameters such as the dismutation and radical stability zones.
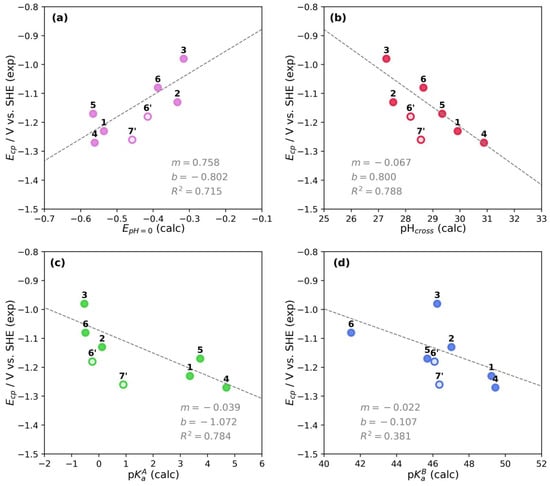
Figure 5.
Correlation plots between experimental Ecp and calculated parameters for pyridine derivatives 1–7′. (a) Ecp vs. E′pH=0. (b) Ecp vs. pHcross. (c) Ecp vs. pKaA. (d) Ecp vs. pKaA. Filled markers are for N-alkylated derivatives 1–6, unfilled markers are for derivatives 6′ and 7′. The linear fitting parameters are shown in each plot considering only N-alkylated derivatives.
From Figure 5, a direct correlation is observed between Ecp and E′pH=0 (Figure 5a); that is, higher peak potentials are obtained at higher E′pH=0. However, the trend is inverse for pHcross (Figure 5b) or a pKa value (Figure 5c,d), which results in lower peak potentials at higher calculated values. The correlation between Ecp and pHcross has the higher R2 = 0.788, when considering only the N-alkylated pyridine derivatives (1–6). We noted that pHcross is a parameter that depends on the calculated standard redox potential and the pKaA and pKaB values. Modifying any of these parameters would result in a different conditional potential and pHcross. Therefore, we can establish that the correlation for Ecp is low when a single parameter is evaluated (E′pH=0, pKaA, or pKaB) but increases by using pHcross since it depends intrinsically on several parameters.
The correlation plot of Ecp and pHcross in Figure 5b also shows the influence of the electron-withdrawing or electron-donating functional groups on the redox potential and pH values compared to pyD 1. The electron-withdrawing groups at C-3 position of the pyridine ring, such as pyD 2 (R3 = CONH2), 3 (R3 = COOMe), and 5 (R3 = pyrrolidone) shift the potential toward higher values, while the pHcross toward lower values. The opposite effect is observed for an electron-donating group such as pyD 4 (R3 = pyrrolidine), displacing the Ecp to lower values and pHcross to higher values. Compound 6 has both types of functional groups, where the effect of the electron-withdrawing substituent at C-3 and C-5 positions (R3 = R5 = CONH2) prevails over the effect of the electron-donating group at C-2 and C-6 positions (R2 = R6 = CH3), resulting in an increase in the redox potential and a decrease in the pHcross. Nevertheless, this effect is not stronger than the observed for compounds 2 and 3. Finally, for derivatives 6′ and 7′, the main structural difference is the lack of the alkyl chain on the pyridine nitrogen atom, which results in a lower redox potential (as can be seen between compounds 6 and 6′), making the reduction process more difficult to conduct, as previously established.
From the previous analysis, we can establish the following remarks: in the PD, pHcross allows the identification of the radical stability window. The shifting of this parameter toward the water pH window would lead to the stabilization of the radical species in solution. Furthermore, from the correlation between Ecp and pHcross, the reduction potential peak can be used to estimate the pH for the radical stabilization and vice versa. Electron-withdrawing groups on the pyridine ring shift the peak potential and pHcross toward the potential and pH water stability window, favoring the stabilization of the radical species.
Given the trends established, different pyridine derivatives were proposed (compounds 7 to 28 in Figure 1b), and their PDs calculated (Figure S43) to modify the electron transfer processes occurring toward the water stability window. Most derivatives exhibit a similar behavior compared to derivative 1, where the radical stability window is at high pH values (pHcross > 25). However, compounds with electron-withdrawing groups such as 25 (R2 = R6 = CF3 and R3 = R5 = COOEt), 26 (R2 = R6 = CF3 and R3 = R5 = CONH2), and 27 (R2 = R6 = CF3 and R3 = R5 = CONHMe) have low pHcross values of 4.77, 4.54, and 7.01, respectively. These derivatives also show a shift toward positive redox potentials due to a higher electron-withdrawing effect on the pyridine ring, which makes them potential candidates for a single-electron transfer process in the water stability window.
The general trend is represented in Figure 6 for pyDs 2, 6, and 26 compared to 1. When the electron-withdrawing effect is weak on the pyridine ring such as in 2 or 6, the process observed in the water stability window corresponds to a 1H+, 2e− transfer process. This process may change by attaching strong electron-withdrawing groups as CF3 in pyD 26, which increases the redox potential and shifts the pHcross toward the water stability window, leading to the stabilization of the radical species and a two-step one-electron transfer process. According to the linear fitting performed previously, compound 26 would have an Ecp of about 0.50 V vs. SHE.
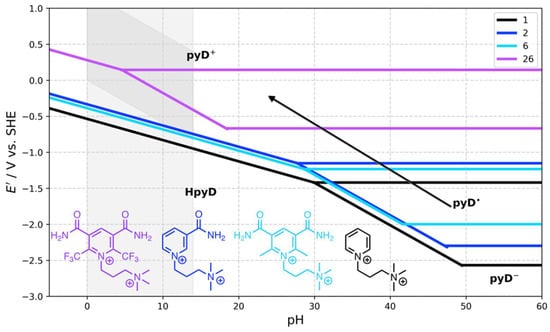
Figure 6.
Comparison of Pourbaix diagrams calculated for pyridine derivatives 1, 2, 6, and 26. The shaded area indicates the water stability window.
4. Conclusions
Eight pyridine derivatives with various substituents attached to the ring were synthesized. To increase the water solubility, six of these compounds were alkylated at the pyridine ring using TMAP-Br, followed by an ion exchange with ammonium hexafluorophosphate (NH4PF6), obtaining new compounds. All efforts to N-alkylate diethyl 2,6-dimethylpyridine-3,5-dicarboxylate (HE-Ox), and 7′ with TMAP-Br or methyl iodide were unsuccessful. These observations, combined with the scarcity of experimental procedures for N-alkylation of 2,6-dimethyl-3,5-dicarbonyl pyridine derivatives, underscore the importance of the nature of substituents attached to the pyridine ring on their physicochemical properties.
Electrochemical studies of synthesized pyDs indicate an irreversible reduction along with its corresponding oxidation processes. The substituents on the pyridine ring influence the cathodic and anodic peak potentials. In water solution, electron-donating groups at C-3 position shift the reduction potential toward more negative values (Ecp = −1.27 V vs. SHE, compound 4), whereas electron-withdrawing groups displace it to less negative values (Ecp = −0.98 V vs. SHE, compound 3). When both groups coexist in the same structure (pyDs 6′, 6, and 7′), the effect of the electron-withdrawing groups predominates, resulting in a less negative redox potential. On the other hand, the alkyl chain attached to N-1 of the pyridine ring facilitates the reduction process due to a delocalization of the positive charge by resonance.
The stability of the reduced species was determined using the Eap value and the difference in peak potentials (ΔEp). This difference increases with the number of substituents on the pyridine ring. Among the derivatives studied, the smallest value was obtained for compound 3 (ΔEp = 1.13 V vs. SHE). Thus, the reversibility of the redox process could be improved by selecting suitable functional groups and substitution positions, leaving the possibility for exploring derivatives that have small ΔEp values, closer to the expected value of 30 mV, for a use in a two-electron or 60 mV for a one-electron exchange process.
The standard reduction potentials and acidity constants were calculated for the synthesized derivatives (1–7′). The predominant equilibria were identified from these values, and the theoretical Pourbaix diagram was constructed for each derivative. We established different correlations between experimental (Ecp and Eap) and theoretical parameters of the PD (E′pH=0, pHcross, pKaA, and pKaB), where a high correlation between Ecp and pHcross was obtained (R2 = 0.788), noting that the latter is a parameter that depends on the calculated standard redox potentials and pKa values. We confirmed the increase of the redox potential caused by the electron-withdrawing groups on the pyridine ring. From this analysis, derivatives with different substitutions were proposed to obtain their PD according to the methodology established. We found three derivatives that modify the processes observed in the pH water stability window. In particular, pyDs 25 (R2 = R6 = CF3 and R3 = R5 = COOEt), 26 (R2 = R6 = CF3 and R3 = R5 = CONH2), and 27 (R2 = R6 = CF3 and R3 = R5 = CONHMe) have pHcross values of 4.77, 4.54, and 7.01, respectively. Therefore, these compounds would exhibit both two- and one-electron transfer processes in the water stability window.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/chemistry7030100/s1, Figure S1: 1H NMR (500 MHz, DMSO-d6) for compound 1; Figure S2: 13C NMR (125 MHz, DMSO-d6) for compound 1; Figure S3: IR spectrum (cm−1) for compound 1; Figure S4: 1H NMR (400 MHz, DMSO-d6) for compound 2; Figure S5: 13C NMR (100 MHz, D2O) for compound 2; Figure S6: IR spectrum (cm−1) for compound 2; Figure S7: 1H NMR (400 MHz, DMSO-d6) for compound 3; Figure S8: 13C NMR (76 MHz, DMSO-d6) for compound 3; Figure S9: IR spectrum (cm−1) for compound 3; Figure S10: 1H NMR (500 MHz, DMSO-d6) for compound 4; Figure S11: 13C NMR (125 MHz, DMSO-d6) for compound 4; Figure S12: IR spectrum (cm−1) for compound 4; Figure S13: 1H NMR (400 MHz, DMSO-d6) for compound 5; Figure S14: 13C NMR (100 MHz, DMSO-d6) for compound 5; Figure S15: IR spectrum (cm−1) for compound 5; Figure S16: 1H NMR (500 MHz, DMSO-d6) for compound 6′; Figure SI-17: 13C NMR (125 MHz DMSO-d6) for compound 6′; Figure S18: 1H NMR (400 MHz, DMSO-d6) for compound 6; Figure S19: 13C NMR (100 MHz, DMSO-d6) for compound 6; Figure S20: IR spectrum (cm−1) for compound 6; Figure S21: 1H NMR (400 MHz, DMSO-d6) for compound 7′; Figure S22: 13C NMR (100 MHz, DMSO-d6) for compound 7′, Figure S23: IR spectrum (cm−1) for compound 7′; Figure S24: CVs of pyD 2 (2.00 × 10−3 mol L–1) in NaCl (1.00 mol L−1), obtained from several cathodic inversion potentials. WE: GCM, υ = 0.10 V s−1; Figure S25: CVs of pyD 3 (2.00 × 10−3 mol L−1) in NaCl (1.00 mol L−1), obtained from several cathodic inversion potentials. WE: GCM, υ = 0.10 V s−1; Figure S26: CVs of pyD 4 (2.00 × 10−3 mol L−1) in NaCl (1.00 mol L−1), obtained from several cathodic inversion potentials. WE: GCM, υ = 0.10 V s−1; Figure S27: CVs of pyD 5 (2.00 × 10−3 mol L−1) in NaCl (1.00 mol L−1), obtained from several cathodic inversion potentials. WE: GCM, υ = 0.10 V s−1; Figure S28: CVs of pyD 6′ (2.00 × 10−3 mol L−1) in NaCl (1.00 mol L−1), obtained from several cathodic inversion potentials. WE: GCM, υ = 0.10 V s−1; Figure S29: CVs of pyD 6 (2.00 × 10−3 mol L−1) in NaCl (1.00 mol L−1), obtained from several cathodic inversion potentials. WE: GCM, υ = 0.10 V s−1; Figure S30: CVs of pyD 7′ (2.00 × 10−3 mol L−1) in NaCl (1.00 mol L−1), obtained from several cathodic inversion potentials. WE: GCM, υ = 0.10 V s−1; Figure S31: CVs of pyD 1 (2.00 × 10−3 mol L−1) in Bu4NPF6 (0.1 mol L−1)/DMSO, obtained from several cathodic inversion potentials. WE: GCM, υ = 0.10 V s−1; Figure S32: CVs of pyD 2 (2.00 × 10−3 mol L−1) in Bu4NPF6 (0.1 mol L−1)/DMSO, obtained from several cathodic inversion potentials. WE: GCM, υ = 0.10 V s−1; Figure S33: CVs of pyD 3 (2.00 × 10−3 mol L−1) in Bu4NPF6 (0.1 mol L−1)/DMSO, obtained from several cathodic inversion potentials. WE: GCM, υ = 0.10 V s−1; Figure S34: CVs of pyD 4 (2.00 × 10−3 mol L−1) in Bu4NPF6 (0.1 mol L−1)/DMSO, obtained from several cathodic inversion potentials. WE: GCM, υ = 0.10 V s−1; Figure S35: CVs of pyD 5 (2.00 × 10−1 mol L−1) in Bu4NPF6 (0.1 mol L−1)/DMSO, obtained from several cathodic inversion potentials. WE: GCM, υ = 0.10 V s−1; Figure S36: CVs of pyD 6 (2.00 × 10−3 mol L−1) in Bu4NPF6 (0.1 mol L−1)/DMSO, obtained from several cathodic inversion potentials. WE: GCM, υ = 0.10 V s−1; Figure S37: CVs of pyD 7′ (2.00 × 10−3 mol L−1) in Bu4NPF6 (0.1 mol L−1)/DMSO, obtained from several cathodic inversion potentials. WE: GCM, υ = 0.10 V s−1; Figure S38: 1H NMR spectra recorded for pyD 1 in DMSO-d6 (red line), and after adding KOH/D2O (0.04 mol L−1) (blue line); Figure S39: 1H NMR spectra recorded for pyD 2 in DMSO-d6 (red line), and after adding KOH/D2O (0.04 mol L−1) (blue line); Figure S40: Predominance zone diagram (PZD) for pyridine derivative 1. At pH < 3.35 a proton-coupled electron transfer reaction occurs for the first reduction (Equation (8)), followed by a single electron transfer (Equation (9)). At 3.35 < pH < 49.23, the first reduction is pH independent (Equation (10)), while the second reduction involves a proton-coupled electron transfer (Equation (11)). Finally, at pH > 49.23 the first and second reductions are pure electron transfer reactions (Equations (9) and (12)); Figure S41: Correlation plots for molecules 1–7′ between the cathodic peak potential (Ecp) and calculated parameters from the PDs: conditional potential at pH = 0 (EpH=0), crossing pH (pHcross), pKaA, and pKaB; Figure S42: Correlation plots for molecules 1–7′ between the anodic peak potential (Eap) and calculated parameters from the PDs: conditional potential at pH = 0 (EpH=0), crossing pH (pHcross), pKaA, and pKaB; Figure S43: Pourbaix diagrams calculated for pyridine derivatives 7–28. The shaded area indicates the water stability window.
Author Contributions
Conceptualization, supervision, and computational studies, M.M.F.-L.; chemical synthesis and structural characterization, J.G.-R. and A.V.; electrochemical experimentation and data collection, G.M.A.-T. and V.M.U.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded (in part) by the UNAM-DGAPA-PAPIIT IA206622 and SECIHTI program under the CBF2023-2024-1229 project.
Data Availability Statement
The data supporting this article have been included as part of the main document and Supplementary Information.
Acknowledgments
The authors thank DGTIC-UNAM for computational resources provided under project LANCAD-UNAM-DGTIC-022 and Chemaxon (https://www.chemaxon.com) for the Marvin software, Marvin 23.10, used for characterizing chemical structures and 1H RMN spectra simulation. G.M.A.-T. gives thanks DGAPA-UNAM for a postdoctoral fellowship award.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wellmann, P.J. The Search for New Materials and the Role of Novel Processing Routes. Discover Mater. 2021, 1, 14. [Google Scholar] [CrossRef] [PubMed]
- Ebenezer, O.; Jordaan, M.A.; Carena, G.; Bono, T.; Shapi, M.; Tuszynski, J.A. An Overview of the Biological Evaluation of Selected Nitrogen-Containing Heterocycle Medicinal Chemistry Compounds. Int. J. Mol. Sci. 2022, 23, 8117. [Google Scholar] [CrossRef] [PubMed]
- Walsh, C.T. Nature Loves Nitrogen Heterocycles. Tetrahedron Lett. 2015, 56, 3075–3081. [Google Scholar] [CrossRef]
- Hohmann−Marriott, M.F.; Blankenship, R.E. Evolution of Photosynthesis. Annu. Rev. Plant Biol. 2011, 62, 515–548. [Google Scholar] [CrossRef]
- Fessel, J.P.; Oldham, W.M. Pyridine Dinucleotides from Molecules to Man. Antioxid. Redox Signal. 2018, 28, 180–212. [Google Scholar] [CrossRef]
- De, S.; Ashok, K.S.K.; Shah, S.K.; Kazi, S.; Sarkar, N.; Banerjee, S.; Dey, S. Pyridine: The Scaffolds with Significant Clinical Diversity. RSC Adv. 2022, 12, 15385–15406. [Google Scholar] [CrossRef]
- Fessel, J.P.; Oldham, W.M. Nicotine Adenine Dinucleotides: The Redox Currency of the Cell. Antioxid. Redox Signal. 2018, 28, 165–166. [Google Scholar] [CrossRef]
- Lecante, A.; Robert, F.; Blandinières, P.A.; Roos, C. Anti-corrosive Properties of S. tinctoria and G. ouregou Alkaloid Extracts on Low Carbon Steel. Curr. Appl Phys. 2011, 11, 714–724. [Google Scholar] [CrossRef]
- Ansari, K.R.; Quraishi, M.A.; Singh, A. Pyridine Derivatives as Corrosion Inhibitors for N80 Steel in 15% HCl: Electrochemical, Surface and Quantum Chemical Studies. Measurement 2015, 76, 136–147. [Google Scholar] [CrossRef]
- Lucio, A.J.; Shaw, S.K. Pyridine and Pyridinium Electrochemistry on Polycrystalline Gold Electrodes and Implications for CO2 Reduction. J. Phys. Chem. C 2015, 119, 12523–12530. [Google Scholar] [CrossRef]
- Seshadri, G.; Lin, C.; Bocarsly, A.B. A New Homogeneous Electrocatalyst for the Reduction of Carbon Dioxide to Methanol at Low Overpotential. J. Electroanal. Chem. 1994, 372, 145–150. [Google Scholar] [CrossRef]
- Gao, W.; Li, Y.; Xiao, D.; Ma, D. Advances in Photothermal Conversion of Carbon Dioxide to Solar Fuels. J. Energy Chem. 2023, 83, 62–78. [Google Scholar] [CrossRef]
- Costentin, C.; Canales, J.C.; Haddou, B.; Savéant, J.M. Electrochemistry of Acids on Platinum. Application to the Reduction of Carbon Dioxide in the Presence of Pyridinium Ion in Water. J. Am. Chem. Soc. 2013, 135, 17671–17674. [Google Scholar] [CrossRef] [PubMed]
- Velena, A.; Zarkovic, N.; Gall Troselj, K.; Bisenieks, E.; Krauze, A.; Poikans, J.; Duburs, G. 1,4-Dihydropyridine Derivatives: Dihydronicotinamide Analogues–Model Compounds Targeting Oxidative Stress. Oxid. Med. Cell. Longev. 2016, 2, 1892412. [Google Scholar] [CrossRef]
- Van Bergen, T.J.; Kellogg, R.M. Photochemistry of 3,5-dicarboalkoxypyridines. Reduction and Rearrangement. J. Am. Chem. Soc. 1972, 94, 8451–8471. [Google Scholar] [CrossRef]
- Khan, E. Pyridine Derivatives as Biologically Active Precursors; Organics and Selected Coordination Complexes. ChemistrySelect 2021, 6, 3041–3064. [Google Scholar] [CrossRef]
- Leduc, P.; Thévenot, D. Electrochemical Properties of Nicotinamide Derivatives in Aqueous Solution: Part IV. Oxidation of N1-alkyl-1,4-dihydronicotinamides. J. Electroanal. Chem. Interfacial Electrochem. 1973, 47, 543–546. [Google Scholar] [CrossRef]
- López-Alarcón, C.; Núñez-Vergara, L.J.; Squella, J.A. Voltammetric Oxidation of Hantzsch 1,4-dihydropyridines in Protic and Aprotic Media: Relevance of the Substitution on N Position. Electrochim. Acta 2003, 48, 2505–2516. [Google Scholar] [CrossRef]
- Zhu, D.-L.; Wu, Q.; Li, H.-Y.; Li, H.-X.; Lang, J.-P. Hantzsch Ester as a VisibleLight Photoredox Catalyst for Transition-Metal-Free Coupling of Arylhalides and Arylsulfinates. Chem. Eur. J. 2020, 26, 3484–3488. [Google Scholar] [CrossRef]
- Wang, P.-Z.; Chen, J.-R.; Xiao, W.-J. Hantzsch Esters: An Emerging Versatile Class of Reagents in Photoredox Catalyzed Organic Synthesis. Org. Biomol. Chem. 2019, 17, 6936–6951. [Google Scholar] [CrossRef]
- Yang, G.; Liu, X.; Xue, Z.; Li, X.; Zhuang, Q.; Han, Z. Electrochemic and Photophysics Properties of Pyridine-Based Electron Transmission Material. J. Macromol. Sci. Part B Phys. 2013, 52, 826–840. [Google Scholar] [CrossRef]
- Calbo, J.; Weston, C.E.; White, A.J.P.; Rzepa, H.S.; Contreras-García, J.; Fuchter, M.J. Tuning Azoheteroarene Photoswitch Performance through Heteroaryl Design. J. Am. Chem. Soc. 2017, 139, 1261–1274. [Google Scholar] [CrossRef] [PubMed]
- Burešová, Z.; Klikar, M.; Mazúr, P.; Mikešová, M.; Kvíčala, J.; Bystron, T.; Bureš, F. Redox Property Tuning in Bipyridinium Salts. Front. Chem. 2021, 8, 631477. [Google Scholar] [CrossRef] [PubMed]
- Maruyama, M.; Murakami, K. Electrochemical Behavior of Nitrogen Heterocycles in N,N-dimethylformamide-water and Aqueous Buffer Solution. J. Electroanal. Chem. Interfacial Electrochem. 1979, 102, 221–235. [Google Scholar] [CrossRef]
- Ballardini, R.; Credi, A.; Gandolfi, M.T.; Giansante, C.; Marconi, G.; Silvi, S.; Venturi, M. Photophysical, Photochemical and Electrochemical Properties of a Series of Aromatic Electron Acceptors Based on N-heterocycles. Inorg. Chim. Acta 2007, 360, 1072–1082. [Google Scholar] [CrossRef]
- Assary, R.S.; Brushett, F.R.; Curtiss, L.A. Reduction Potential Predictions of Some Aromatic Nitrogen-Containing Molecules. RSC Adv. 2014, 4, 57442–57451. [Google Scholar] [CrossRef]
- Sumita, M.; Yang, X.; Ishihara, S.; Tamura, R.; Tsuda, K. Hunting for Organic Molecules with Artificial Intelligence: Molecules Optimized for Desired Excitation Energies. ACS Cent. Sci. 2018, 4, 1126–1133. [Google Scholar] [CrossRef]
- Fischer, P.; Mazúr, P.; Krakowiak, J. Family Tree for Aqueous Organic Redox Couples for Redox Flow Battery Electrolytes: A Conceptual Review. Molecules 2022, 27, 560. [Google Scholar] [CrossRef]
- Kumar, A.; Maurya, R.A. Efficient Synthesis of Hantzsch Esters and Polyhydroquinoline Derivatives in Aqueous Micelles. Synlett 2008, 6, 883–885. [Google Scholar] [CrossRef]
- Zhang, D.; Sha, M. Facile Aromatisation of Hantzsch 1,4-Dihydropyridines by Autoxidation in the Presence of P-toluenesulfonic Acid in Acetic Acid. J. Chem. Res. 2018, 42, 141–144. [Google Scholar] [CrossRef]
- Gray, A.P.; Archer, W.L.; Schlieper, D.C.; Spinner, E.E.; Cavallito, C.J. Bis-ammonium Salts. Unsymmetrical Derivatives of Some Isoquinolines and Related Heterocyclic Bases. J. Am. Chem. Soc. 1955, 77, 3536–3541. [Google Scholar] [CrossRef]
- Craig, H.H.; Huang, P.C.; Gordon Scott, T.; Leonard, N.J. Synthetic Spectroscopic Models Related to Coenzymes and Base Pairs. Quaternized Bisnicotinamides. J. Am. Chem. Soc. 1972, 94, 5872–5879. [Google Scholar] [CrossRef] [PubMed]
- Blank, B.; DiTullio, N.W.; Owings, F.F.; Deviney, L.; Miao, C.K.; Saunders, H.L. Mercapto Heterocyclic Acids, Analogues of 3-Mercaptopicolinic Acid. J. Med. Chem. 1977, 20, 572–576. [Google Scholar] [CrossRef]
- Gelbard, G.; Lin, J.; Roques, N. Reductions with NADH Models. 3. The High Reactivity of Hantzsch Amides. J. Org. Chem. 1992, 57, 1789–1793. [Google Scholar] [CrossRef]
- O’Boyle, N.M.; Banck, M.; James, C.A.; Morley, C.; Vandermeersch, T.; Hutchison, G.R. Open Babel: An Open Chemical Toolbox. J. Cheminform. 2011, 3, 33. [Google Scholar] [CrossRef]
- Halgren, T.A. Merck Molecular Force Field. I. Basis, Form, Scope, Parameterization, and Performance of MMFF94. J. Comput. Chem. 1996, 17, 490–519. [Google Scholar] [CrossRef]
- Halgren, T.A. Merck molecular force field. II. MMFF94 Van der Waals and Electrostatic Parameters for Intermolecular Interactions. J. Comput. Chem. 1996, 17, 520–552. [Google Scholar] [CrossRef]
- Halgren, T.A. Merck Molecular Force Field. III. Molecular Geometries and Vibrational Frequencies for MMFF94. J. Comput. Chem. 1996, 17, 553–586. [Google Scholar] [CrossRef]
- Halgren, T.A.; Nachbar, R.B. Merck Molecular Force Field. IV. Conformational Energies and Geometries for MMFF94. J. Comput. Chem. 1996, 17, 587–615. [Google Scholar] [CrossRef]
- Halgren, T.A. Merck molecular force field. V. Extension of MMFF94 using Experimental Data, Additional Computational Data, and Empirical Rules. J. Comput. Chem. 1996, 17, 616–641. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Becke, A.D. Density-Functional Thermochemistry. III. The role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; People, J.A. Self-Consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian Basis Sets for Molecular Calculations. I. Second Row Atoms, Z = 11–18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Flores-Leonar, M.M.; Moreno-Esparza, R.; Ugalde-Saldívar, V.M.; Amador-Bedolla, C. Further Insights in DFT Calculations of Redox Potential for Iron Complexes: The Ferrocenium/Ferrocene System. Comput. Theor. Chem. 2017, 1099, 167–173. [Google Scholar] [CrossRef]
- Namazian, M.; Zakery, M.; Noorbala, M.R.; Coote, M.L. Accurate Calculation of the pKa of Trifluoroacetic Acid using High-Level AB Initio Calculations. Chem. Phys. Lett. 2008, 451, 163–168. [Google Scholar] [CrossRef]
- Pérez-González, A.; Castañeda-Arriaga, R.; Verastegui, B.; Carreón-González, M.; Alvarez-Idaboy, J.R.; Galano, A. Estimation of Empirically Fitted Parameters for Calculating pKa Values of Thiols in a Fast and Reliable Way. Theor. Chem. Acc. 2018, 137, 5. [Google Scholar] [CrossRef]
- Trasatti, S. The Absolute Electrode Potential: An Explanatory Note (Recommendations 1986). Pure Appl. Chem. 1986, 58, 955–966. [Google Scholar] [CrossRef]
- Donald, W.A.; Leib, R.D.; O’Brien, J.T.; Williams, E.R. Directly Relating Gas-Phase Cluster Measurements to Solution-Phase Hydrolysis, the Absolute Standard Hydrogen Electrode Potential, and the Absolute Proton Solvation Energy. Chem. Eur. J. 2009, 15, 5926–5934. [Google Scholar] [CrossRef]
- Nakai, H.; Ishikawa, A. Quantum Chemical Approach for Condensed-Phase Thermochemistry: Proposal of a Harmonic Solvation Model. J. Chem. Phys. 2014, 141, 174106. [Google Scholar] [CrossRef]
- Webb, J.D.; Laberge, V.S.; Geier, S.J.; Stephan, D.W.; Crudden, C.M. Borohydrides from Organic Hydrides: Reactions of Hantzsch’s Esters with B(C6F5)3. Chem. Eur. J. 2010, 16, 4895–4902. [Google Scholar] [CrossRef] [PubMed]
- Reyes, R.L.; Tanaka, K. The NAD+/NADH Redox Couple-Insights from the Perspective of Electrochemical Energy Transformation and Biomimetic Chemistry. Kimika 2017, 28, 32–43. [Google Scholar] [CrossRef]
- Kim, J.; Ko, S.; Noh, C.; Kim, H.; Lee, S.; Kim, D.; Park, H.; Kwon, G.; Son, G.; Ko, J.W.; et al. Biological Nicotinamide Cofactor as a Redox-Active Motif for Reversible Electrochemical Energy Storage. Angew. Chem. Int. Ed. 2019, 58, 16764. [Google Scholar] [CrossRef]
- Ali, I.; Gill, A.; Omanovic, S. Direct Electrochemical Regeneration of the Enzymatic Cofactor 1,4-NADH Employing Nano-Patterned Glassy Carbon/Pt and Glassy Carbon/Ni Electrodes. Chem. Eng. J. 2012, 188, 173–180. [Google Scholar] [CrossRef]
- Wang, X.; Saba, T.; Yiu, H.H.P.; Howe, R.F.; Anderson, J.A.; Shi, J. Cofactor NAD(P)H Regeneration Inspired by Heterogeneous Pathways. Chem 2017, 2, 621–654. [Google Scholar] [CrossRef]
- Lebègue, E.; Agullo, J.; Morin, M.; Bélanger, D. The Role of Surface Hydrogen Atoms in the Electrochemical Reduction of Pyridine and CO2 in Aqueous Electrolyte. ChemElectroChem 2014, 1, 1013–1017. [Google Scholar] [CrossRef]
- Lebègue, E.; Agullo, J.; Bélanger, D. Electrochemical Behavior of Pyridinium and N-Methyl Pyridinium Cations in Aqueous Electrolytes for CO2 Reduction. ChemSusChem 2018, 11, 219–228. [Google Scholar] [CrossRef]
- Marcus, Y. The Effectivity of Solvents as Electron Pair Donors. J. Solut. Chem. 1984, 13, 599–624. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).