Pentacoordinate Carbon Atoms in a Ferrocene Dication Derivative—[Fe(Si2-η5-C5H2)2]2+
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
3.1. Energetics
3.2. Bonding
3.3. Wiberg Bond Indices
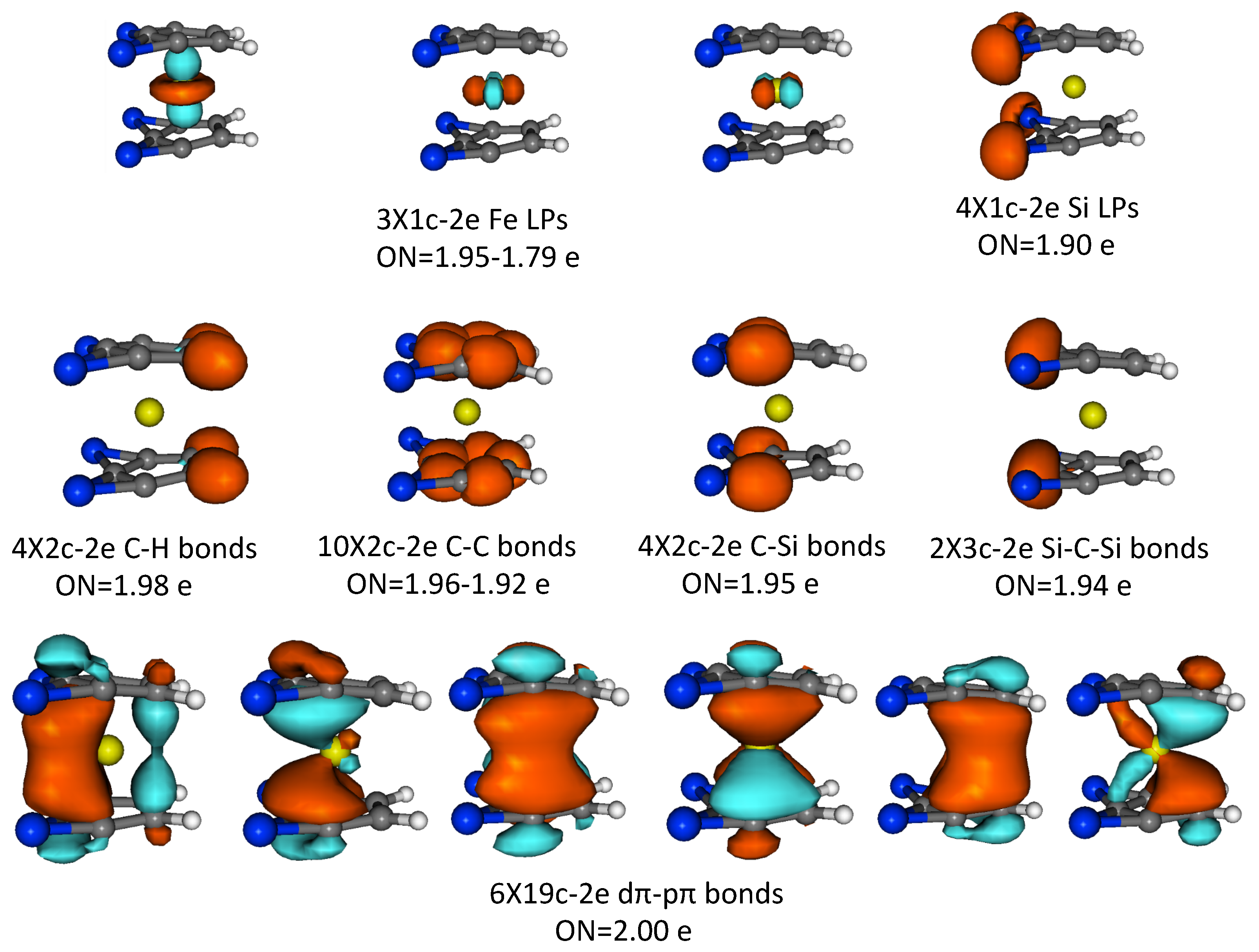
3.4. AdNDP Analysis
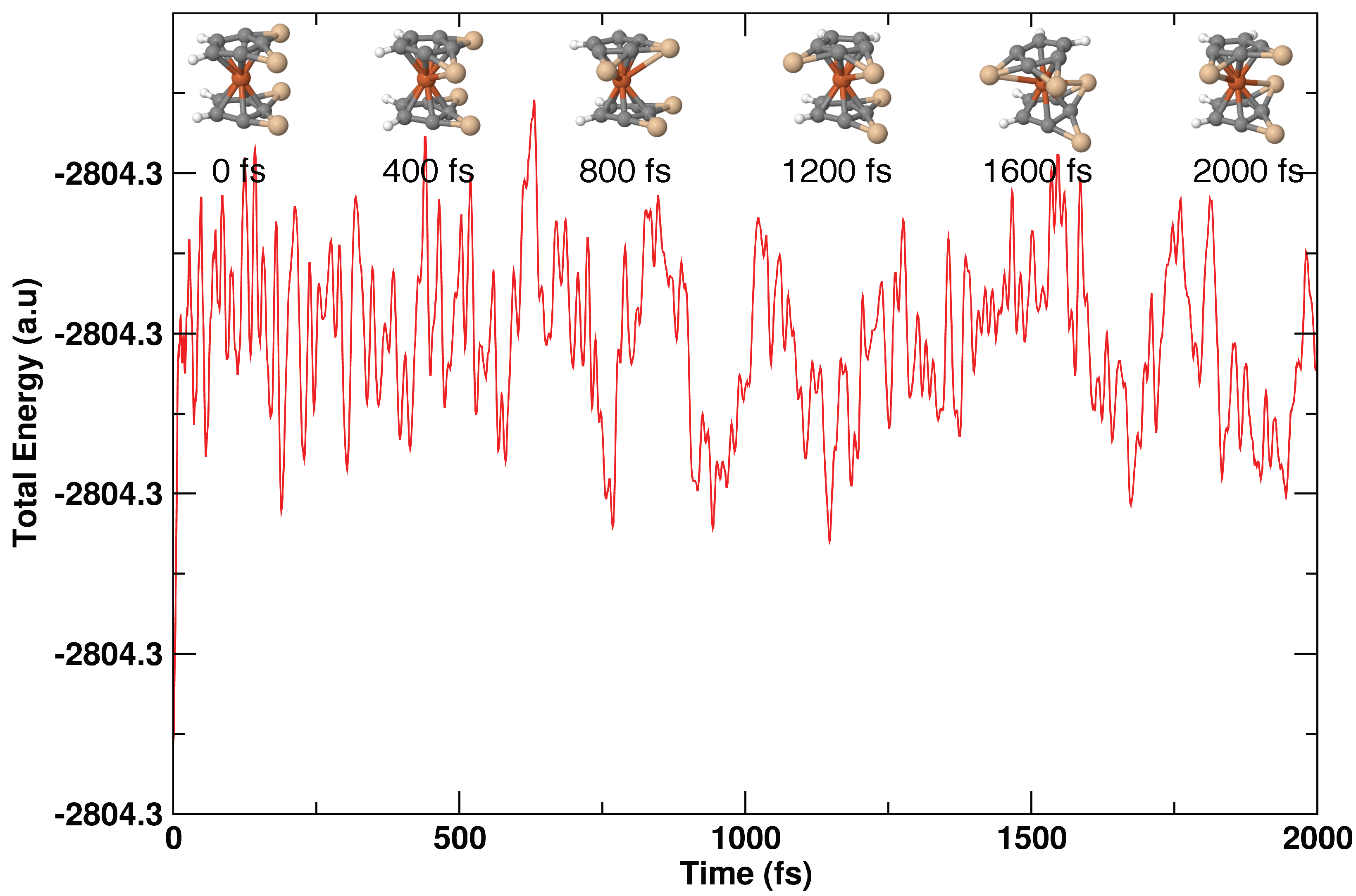
3.5. MD Simulations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADMP | Atom-Centered Density Matrix Propagation |
| AIMD | Ab Initio Molecular Dynamics |
| AdNDP | Adaptive Natural Density Partitioning |
| DFT | Density functional theory |
| EAN | Effective Atomic Number |
| MD | Molecular Dynamics |
| NBO | Natural Bond Order |
| ptC | planar tetracoordinate carbon |
| WBI | Wiberg Bond Index |
References
- Kealy, T.J.; Pauson, P.L. A New Type of Organo-Iron Compound. Nature 1951, 168, 1039–1040. [Google Scholar] [CrossRef]
- Wilkinson, G.; Rosenblum, M.; Whiting, M.C.; Woodward, R.B. The Structure of Iron Bis-Cyclopentadienyl. J. Am. Chem. Soc. 1952, 74, 2125–2126. [Google Scholar] [CrossRef]
- Fischer, E.O.; Pfab, W. Cyclopentadien-Metallkomplexe, Ein Neuer Typ Metallorganischer Verbindungen. Z. Naturforschg B 1952, 7, 377–379. [Google Scholar] [CrossRef]
- Pfab, W.; Fischer, E.O. Zur Kristallstruktur der Di-cyclopentadienyl-Verbindungen des Zweiwertigen Eisens, Kobalts und Nickels. Z. Anorg. Allg. Chem. 1953, 274, 316–322. [Google Scholar] [CrossRef]
- Werner, H. At Least 60 Years of Ferrocene: The Discovery and Rediscovery of the Sandwich Complexes. Angew. Chem. Int. Ed. 2012, 51, 6052–6058. [Google Scholar] [CrossRef]
- Mohammadi, N.; Ganesan, A.; Chantler, C.T.; Wang, F. Differentiation of Ferrocene D5d and D5h Conformers Using IR Spectroscopy. J. Organomet. Chem. 2012, 713, 51–59. [Google Scholar] [CrossRef]
- Walawalkar, M.G.; Pandey, P.; Murugavel, R. The Redox Journey of Iconic Ferrocene: Ferrocenium Dications and Ferrocenate Anions. Angew. Chem. Int. Ed. 2021, 60, 12632–12635. [Google Scholar] [CrossRef]
- Astruc, D. Why is Ferrocene so Exceptional? Eur. J. Inorg. Chem. 2017, 2017, 6–29. [Google Scholar] [CrossRef]
- Malischewski, M.; Adelhardt, M.; Sutter, J.; Meyer, K.; Seppelt, K. Isolation and Structural and Electronic Characterization of Salts of the Decamethylferrocene Dication. Science 2016, 353, 678–682. [Google Scholar] [CrossRef]
- Hoffmann, R.; Alder, R.W.; Wilcox, C.F. Planar Tetracoordinate Carbon. J. Am. Chem. Soc. 1970, 92, 4992–4993. [Google Scholar] [CrossRef]
- Yang, L.M.; Ganz, E.; Chen, Z.; Wang, Z.X.; Schleyer, P.V.R. Four Decades of the Chemistry of Planar Hypercoordinate Compounds. Angew. Chem. Int. Ed. 2015, 54, 9468–9501. [Google Scholar] [CrossRef] [PubMed]
- Yañez, O.; Vásquez-Espinal, A.; Báez-Grez, R.; Rabanal-León, W.A.; Osorio, E.; Ruiz, L.; Tiznado, W. Carbon rings decorated with group 14 elements: New aromatic clusters containing planar tetracoordinate carbon. New J. Chem. 2019, 43, 6781–6785. [Google Scholar]
- Raghunathan, S.; Yadav, K.; Rojisha, V.C.; Jaganade, T.; Prathyusha, V.; Bikkina, S.; Lourderaj, U.; Priyakumar, U.D. Transition between [R]- and [S]-stereoisomers without bond breaking. Phys. Chem. Chem. Phys. 2020, 22, 14983–14991. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.F.; Yu, S.; Hu, T.D.; Xu, J.; Ding, Y.H. CAl3X (X = B/Al/Ga/In/Tl) with 16 valence electrons: Can planar tetracoordinate carbon be stable? Phys. Chem. Chem. Phys. 2018, 20, 26266–26272. [Google Scholar] [CrossRef]
- Job, N.; Khatun, M.; Thirumoorthy, K.; CH, S.S.R.; Chandrasekaran, V.; Anoop, A.; Thimmakondu, V.S. CAl4Mg0/−: Global Minima with a Planar Tetracoordinate Carbon Atom. Atoms 2021, 9, 24. [Google Scholar] [CrossRef]
- Das, P.; Chattaraj, P.K. CSiGa and CGeGa Having Planar Tetracoordinate Carbon Atoms in Their Global Minimum Energy Structures. J. Comput. Chem. 2022, 43, 894–905. [Google Scholar] [CrossRef] [PubMed]
- Merino, G.; Méndez-Rojas, M.A.; Beltrán, H.I.; Corminboeuf, C.; Heine, T.; Vela, A. Theoretical Analysis of the Smallest Carbon Cluster Containing a Planar Tetracoordinate Carbon. J. Am. Chem. Soc. 2004, 126, 16160–16169. [Google Scholar] [CrossRef]
- Wu, Y.B.; Li, Z.X.; Pu, X.H.; Wang, Z.X. Design of Molecular Chains Based on the Planar Tetracoordinate Carbon Unit C2Al4. J. Phys. Chem. C 2011, 115, 13187–13192. [Google Scholar] [CrossRef]
- Suresh, C.H.; Frenking, G. Direct 1-3 Metal-Carbon Bonding and Planar Tetracoordinated Carbon in Group 6 Metallacyclobutadienes. Organometallics 2010, 29, 4766–4769. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, P.; Liang, J.; Jia, W.; Cao, Z. Theoretical study on a family of organic molecules with planar tetracoordinate carbon. J. Mol. Struct. THEOCHEM 2010, 941, 41–46. [Google Scholar] [CrossRef]
- Thirumoorthy, K.; Karton, A.; Thimmakondu, V.S. From High-Energy C7H2 Isomers with A Planar Tetracoordinate Carbon Atom to An Experimentally Known Carbene. J. Phys. Chem. A 2018, 122, 9054–9064. [Google Scholar] [CrossRef]
- Guo, J.; Chai, H.; Duan, Q.; Qin, J.; Shen, X.; Jiang, D.; Hou, J.; Yan, B.; Li, Z.; Gu, F.; et al. Planar Tetracoordinate Carbon Species CLi3E with 12-valence-electrons. Phys. Chem. Chem. Phys. 2016, 18, 4589–4593. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.B.; Jiang, J.L.; Lu, H.G.; Wang, Z.X.; Perez-Peralta, N.; Islas, R.; Contreras, M.; Merino, G.; Wu, J.I.; Schleyer, P.V.R. Starlike Aluminum Carbon Aromatic Species. Chem. Eur. J. 2011, 17, 714–719. [Google Scholar] [CrossRef] [PubMed]
- Thirumoorthy, K.; Thimmakondu, V.S. Flat Crown Ethers with Planar Tetracoordinate Carbon Atoms. Int. J. Quantum Chem. 2021, 121, e26479. [Google Scholar] [CrossRef]
- Guo, J.C.; Wu, H.X.; Ren, G.M.; Miao, C.Q.; Li, Y.X. D3h X3 (X = C, Si and Ge): Superalkali cations containing three planar tetracoordinate X atoms. Comput. Theor. Chem. 2016, 1083, 1–6. [Google Scholar] [CrossRef]
- Thimmakondu, V.S.; Thirumoorthy, K. Si3C2H2 Isomers with A Planar Tetracoordinate Carbon or Silicon Atom(s). Comput. Theor. Chem. 2019, 1157, 40–46. [Google Scholar] [CrossRef]
- Thirumoorthy, K.; Cooksy, A.L.; Thimmakondu, V.S. Si2C5H2 Isomers - Search Algorithms versus Chemical Intuition. Phys. Chem. Chem. Phys. 2020, 22, 5865–5872. [Google Scholar] [CrossRef]
- Das, P.; Chattaraj, P.K. In Silico Studies on Selected Neutral Molecules, CGa2Ge2, CAlGaGe2, and CSiGa2Ge Containing Planar Tetracoordinate Carbon. Atoms 2021, 9, 65. [Google Scholar] [CrossRef]
- Wang, M.H.; Orozco-Ic, M.; Leyva-Parra, L.; Tiznado, W.; Barroso, J.; Ding, Y.H.; Cui, Z.H.; Merino, G. Planar Tetracoordinate Carbons in Allene-Type Structures. J. Phys. Chem. A 2021, 125, 3009–3014. [Google Scholar] [CrossRef]
- Das, P.; Khatun, M.; Anoop, A.; Chattaraj, P.K. CSin (n = 1–3): Prospective Systems Containing Planar Tetracoordinate Carbon (ptC). Phys. Chem. Chem. Phys. 2022, 24, 16701–16711. [Google Scholar] [CrossRef]
- Pancharatna, P.D.; Méndez-Rojas, M.A.; Merino, G.; Vela, A.; Hoffmann, R. Planar Tetracoordinate Carbon in Extended Systems. J. Am. Chem. Soc. 2004, 126, 15309–15315. [Google Scholar] [CrossRef] [PubMed]
- Collins, J.B.; Dill, J.D.; Jemmis, E.D.; Apeloig, Y.; Schleyer, P.V.R.; Seeger, R.; Pople, J.A. Stabilization of Planar Tetracoordinate Carbon. J. Am. Chem. Soc. 1976, 98, 5419–5427. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.F.; Wang, L.S.; Geske, G.; Boldyrev, A. Pentaatomic Tetracoordinate Planar Carbon, [CAl4]2−: A New Structural Unit and Its Salt Complexes. Angew. Chem. Int. Ed. 2000, 39, 3630–3632. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, X.; Yu, S.; Ding, Y.H.; Bowen, K.H. Identifying the Hydrogenated Planar Tetracoordinate Carbon: A Combined Experimental and Theoretical Study of CAl4H and CAl4H−. J. Phys. Chem. Lett. 2017, 8, 2263–2267. [Google Scholar] [CrossRef]
- Röttger, D.; Erker, G. Compounds Containing Planar-Tetracoordinate Carbon. Angew. Chem. Int. Ed. Engl. 1997, 36, 812–827. [Google Scholar] [CrossRef]
- Li, X.; Zhai, H.J.; Wang, L.S. Photoelectron Spectroscopy of Pentaatomic Tetracoordinate Planar Carbon Molecules: CAl3Si− and CAl3Ge−. Chem. Phys. Lett. 2002, 357, 415–419. [Google Scholar] [CrossRef]
- Zhang, C.J.; Wang, P.; Xu, X.L.; Xu, H.G.; Zheng, W.J. Photoelectron Spectroscopy and Theoretical Study of Aln (n = 1–5) Clusters: Structural Evolution, Relative Stability of Star-Like Clusters, and Planar Tetracoordinate Carbon Structures. Phys. Chem. Chem. Phys. 2021, 23, 1967–1975. [Google Scholar] [CrossRef]
- Tal’rose, V.L.; Lyubimova, A.K. Secondary Processes in the Ion Source of the Mass Spectrometer. Dokl. Akad. Nauk SSSR 1952, 86, 909–912. [Google Scholar]
- Yamashita, M.; Yamamoto, Y.; Akiba, K.Y.; Hashizume, D.; Iwasaki, F.; Takagi, N.; Nagase, S. Syntheses and Structures of Hypervalent Pentacoordinate Carbon and Boron Compounds Bearing an Anthracene Skeleton-Elucidation of Hypervalent Interaction Based on X-ray Analysis and DFT Calculation. J. Am. Chem. Soc. 2005, 127, 4354. [Google Scholar] [CrossRef]
- Fernández, I.; Uggerud, E.; Frenking, G. Stable Pentacoordinate Carbocations: Structure and Bonding. Chem. Eur. J. 2007, 13, 8620–8626. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Yamamoto, Y.; Kinoshita, D.; Akiba, K.Y.; Zhang, Y.; Reed, C.A.; Hashizume, D.; Iwasaki, F. Synthesis and Structure of a Hexacoordinate Carbon Compound. J. Am. Chem. Soc. 2008, 130, 6894–6895. [Google Scholar] [CrossRef] [PubMed]
- Vassilev-Galindo, V.; Pan, S.; Donald, J.K.; Merino, G. Planar Pentacoordinate Carbons. Nat. Chem. Rev. 2018, 2, 0114. [Google Scholar] [CrossRef]
- White, E.T.; Tang, J.; Oka, T. CH5+: The Infrared Spectrum Observed. Science 1999, 284, 135–137. [Google Scholar] [CrossRef] [PubMed]
- Schleyer, P.v.R.; Würthwein, E.U.; Kaufmann, E.; Clark, T.; Pople, J.A. Effectively Hypervalent Molecules. 2. Lithium Carbide (CLi5), Lithium Carbide (CLi6), and the Related Effectively Hypervalent First Row Molecules, CLi5-nHn and CLi6-nHn. J. Am. Chem. Soc. 1983, 105, 5930. [Google Scholar] [CrossRef]
- McKee, W.C.; Agarwal, J.; Schaefer, H.F., III; Schleyer, P.V.R. Covalent Hypercoordination: Can Carbon Bind Five Methyl Ligands? Angew. Chem. Int. Ed. 2014, 53, 7875–7878. [Google Scholar] [CrossRef]
- Scherbaum, F.; Grohmann, A.; Müller, G.; Schmidbaur, H. Synthesis, Structure, and Bonding of the Cation [(C6H5)3PAu5C]⊕. Angew. Chem. Int. Ed. 1989, 28, 463–465. [Google Scholar] [CrossRef]
- Dávalos, J.A.; Herrero, R.; Abboud, J.L.M.; Mó, O.; Yáñez, M. How Can a Carbon Atom Be Covalently Bound to Five Ligands? The Case of Si2. Angew. Chem. Int. Ed. 2007, 46, 381. [Google Scholar] [CrossRef]
- Kudo, H. Observation of Hypervalent CLi6 by Knudsen-Effusion Mass Spectrometry. Nature 1992, 355, 432. [Google Scholar] [CrossRef]
- Scherbaum, F.; Grohmann, A.; Huber, B.; Krüger, C.; Schmidbaur, H. Aurophilicity as a Consequence of Relativistic Effects:The Hexakis(triphenylphosphaneaurio)methane Dication [(Ph3PAu)6C]2⊕. Angew. Chem. Int. Ed. 1988, 27, 1544–1546. [Google Scholar] [CrossRef]
- Hogeveen, H.; Kwant, P. Direct Observation of a Remarkably Stable Dication of Unusual Structure: . Tetrahedron Lett. 1973, 14, 1665–1670. [Google Scholar] [CrossRef]
- Malischewski, M.; Seppelt, K. Crystal Structure Determination of the Pentagonal-Pyramidal Hexamethylbenzene Dication C6. Angew. Chem. Int. Ed. 2017, 56, 368–370. [Google Scholar] [CrossRef] [PubMed]
- Olah, G.A.; Rasul, G. Triprotonated Methane, : The Parent Heptacoordinate Carbonium Ion. J. Am. Chem. Soc. 1996, 118, 8503–8504. [Google Scholar] [CrossRef]
- Gao, Y.; Shao, N.; Zhou, R.; Zhang, G.; Zeng, X.C. []: Heptacoordinate Carbon Motif? J. Phys. Chem. Lett. 2012, 3, 2264–2268. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Rahman, A.K.F.; Wang, B. Ab Initio Calculations of Ionic Hydrocarbon Compounds with Heptacoordinate Carbon. J. Mol. Model. 2018, 24, 116. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Huang, Y.; Yin, B.; Yang, B.; Liu, R. Octacoordinate Carbons Encaged Inside Carborane Clusters: A Density Functional Theory Investigation. J. Phys. Chem. A 2008, 112, 7643–7651. [Google Scholar] [CrossRef]
- Guo, J.C.; Feng, L.Y.; Dong, C.; Zhai, H.J. A Designer 32-Electron Superatomic CBe8H12 Cluster: Core-shell Geometry, Octacoordinate Carbon, and Cubic Aromaticity. New J. Chem. 2020, 44, 7286–7292. [Google Scholar] [CrossRef]
- Yang, L.M.; Ding, Y.H.; Sun, C.C. Design of Sandwichlike Complexes Based on the Planar Tetracoordinate Carbon Unit . J. Am. Chem. Soc. 2007, 129, 658–665. [Google Scholar] [CrossRef]
- Yang, L.m.; Ding, Y.h.; Sun, C.c. Assembly and Stabilization of a Planar Tetracoordinated Carbon Radical CAl3Si: A Way To Design Spin-Based Molecular Materials. J. Am. Chem. Soc. 2007, 129, 1900–1901. [Google Scholar] [CrossRef]
- Luo, Q.; Zhang, X.H.; Huang, K.L.; Liu, S.Q.; Yu, Z.H.; Li, Q.S. Theoretical Studies on Novel Main Group Metallocene-like Complexes Involving Planar Hexacoordinate Carbon η6-B6 Ligand. J. Phys. Chem. A 2007, 111, 2930–2934. [Google Scholar] [CrossRef]
- Li, S.D.; Miao, C.Q.; Ren, G.M.; Guo, J.C. Triple-Decker Transition-Metal Complexes (CnHn)M(B6C)M(CnHn) (M = Fe, Ru, Mn, Re; n = 5, 6) Containing Planar Hexacoordinate Carbon Atoms. Eur. J. Inorg. Chem. 2006, 2006, 2567–2571. [Google Scholar] [CrossRef]
- Yañez, O.; Vásquez-Espinal, A.; Pino-Rios, R.; Ferraro, F.; Pan, S.; Osorio, E.; Merino, G.; Tiznado, W. Exploiting Electronic Strategies to Stabilize A Planar Tetracoordinate Carbon in Cyclic Aromatic Hydrocarbons. Chem. Commun. 2017, 53, 12112–12115. [Google Scholar] [CrossRef]
- Thirumoorthy, K.; Chandrasekaran, V.; Cooksy, A.L.; Thimmakondu, V.S. Kinetic Stability of Si2C5H2 Isomer with a Planar Tetracoordinate Carbon Atom. Chemistry 2021, 3, 13–27. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula Into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. A New Local Density Functional for Main-Group Thermochemistry, Transition Metal Bonding, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Phys. 2006, 125, 194101. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.D.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Becke, A.D.; Johnson, E.R. Exchange-Hole Dipole Moment and the Dispersion Interaction. J. Chem. Phys. 2005, 122, 154104. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Glendening, E.D.; Weinhold, F. Natural Resonance Theory: I. General Formalism. J. Comput. Chem. 1998, 19, 593–609. [Google Scholar] [CrossRef]
- Schlegel, H.B.; Millam, J.M.; Iyengar, S.S.; Voth, G.A.; Daniels, A.D.; Scuseria, G.E.; Frisch, M.J. Ab Initio Molecular Dynamics: Propagating the Density Matrix with Gaussian Orbitals. J. Chem. Phys. 2001, 114, 9758–9763. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Coriani, S.; Haaland, A.; Helgaker, T.; Jørgensen, P. The Equilibrium Structure of Ferrocene. ChemPhysChem 2006, 7, 245–249. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Xu, X.; Goddard, W.A. Doubly Hybrid Density Functional for Accurate Descriptions of Nonbond Interactions, Thermochemistry, and Thermochemical Kinetics. Proc. Natl. Acad. Sci. USA 2009, 106, 4963–4968. [Google Scholar] [CrossRef]
- Zhang, I.Y.; Wu, J.; Xu, X. Extending the Reliability and Applicability of B3LYP. Chem. Commun. 2010, 46, 3057–3070. [Google Scholar] [CrossRef]
- Seiler, P.; Dunitz, J.D. Low-Temperature Crystallization of Orthorhombic Ferrocene: Structure Analysis at 98 K. Acta Cryst. B 1982, 38, 1741–1745. [Google Scholar] [CrossRef]
- Zubarev, D.Y.; Boldyrev, A.I. Developing Paradigms of Chemical Bonding: Adaptive Natural Density Partitioning. Phys. Chem. Chem. Phys. 2008, 10, 5207–5217. [Google Scholar] [CrossRef] [PubMed]
- Zubarev, D.Y.; Boldyrev, A.I. Revealing Intuitively Assessable Chemical Bonding Patterns in Organic Aromatic Molecules via Adaptive Natural Density Partitioning. J. Org. Chem. 2008, 73, 9251–9258. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
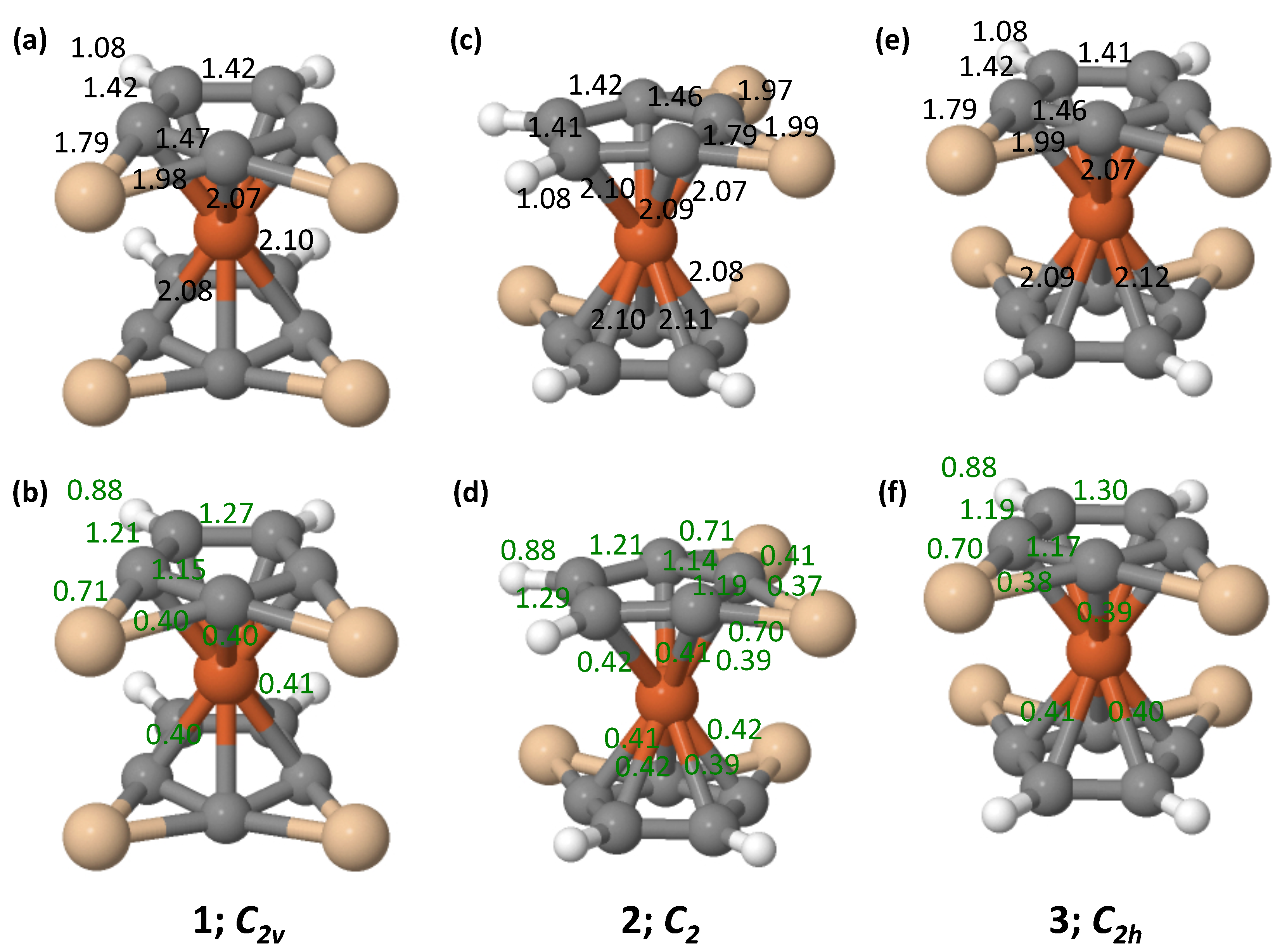
| 1 (Eclipsed) | 2 (Gauche) | 3 (Staggered) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Quintet b | Singlet | Quintet | Singlet | Quintet | ||||||
| Functional | ||||||||||
| B3LYP | −29.14 | −39.04 | −2.34 | −3.16 | −36.36 | −51.01 | −2.47 | −4.59 | −39.25 | −54.01 |
| B3LYP-D3BJ | −7.90 | −19.59 | 2.44 | 1.38 | −13.04 | −30.40 | 8.24 | 5.51 | −2.91 | −22.72 |
| M06-L | 94.58 | 82.77 | 16.74 | 16.75 | 88.72 | 73.84 | 40.34 | 37.89 | 85.93 | 69.80 |
| TPSSh | 95.60 | 82.17 | 13.30 | 12.57 | 89.24 | 72.20 | 30.78 | 28.14 | 86.90 | 69.16 |
| TPSSh-D3BJ | 118.33 | 108.34 | 13.54 | 13.53 | 113.96 | 95.88 | 32.29 | 31.16 | 112.57 | 93.01 |
| B97X-D | 0.31 | −4.17 | −3.06 | 2.04 | −5.11 | −13.61 | −2.78 | −1.21 | −7.82 | −15.63 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shajan, S.; Guo, J.-C.; Sinjari, A.; Thirumoorthy, K.; Thimmakondu, V.S. Pentacoordinate Carbon Atoms in a Ferrocene Dication Derivative—[Fe(Si2-η5-C5H2)2]2+. Chemistry 2022, 4, 1092-1100. https://doi.org/10.3390/chemistry4040074
Shajan S, Guo J-C, Sinjari A, Thirumoorthy K, Thimmakondu VS. Pentacoordinate Carbon Atoms in a Ferrocene Dication Derivative—[Fe(Si2-η5-C5H2)2]2+. Chemistry. 2022; 4(4):1092-1100. https://doi.org/10.3390/chemistry4040074
Chicago/Turabian StyleShajan, Shilpa, Jin-Chang Guo, Aland Sinjari, Krishnan Thirumoorthy, and Venkatesan S. Thimmakondu. 2022. "Pentacoordinate Carbon Atoms in a Ferrocene Dication Derivative—[Fe(Si2-η5-C5H2)2]2+" Chemistry 4, no. 4: 1092-1100. https://doi.org/10.3390/chemistry4040074
APA StyleShajan, S., Guo, J.-C., Sinjari, A., Thirumoorthy, K., & Thimmakondu, V. S. (2022). Pentacoordinate Carbon Atoms in a Ferrocene Dication Derivative—[Fe(Si2-η5-C5H2)2]2+. Chemistry, 4(4), 1092-1100. https://doi.org/10.3390/chemistry4040074








