Orthogonal Space-Time Bluetooth System for IoT Communications

Abstract

There is increasing interest in improving the reliability of short-range wireless links in dense IoT deployments, where BLE is widely used due to its low power consumption and robust GFSK modulation. For this purpose, this work presents a novel Orthogonal Space-Time (OST) scheme for transmission and detection of BLE signals while preserving the BLE GFSK waveform and modulation constraints. The proposed signal processing system integrates advanced OST coding techniques with nonlinear GFSK modulation to achieve high-quality communication while maintaining phase continuity. This implies that the standard BLE GFSK modulator and demodulator blocks can be reused, with additional processing introduced only in the multi-antenna encoder and combiner. A detailed theoretical analysis demonstrates the feasibility of employing the Rayleigh fading channel model in BLE communications and establishes the BER performance bounds for various MIMO configurations. Simulations confirm the advantages of the proposed OST-GFSK signal processing scheme, maintaining a consistent performance when compared with OST linear modulation approaches under Rayleigh fading channels. As a result, the proposed IoT-enabling technology integrates the advantages of widely used OST linear modulation with nonlinear GFSK modulation required for BLE.

1. Introduction

Bluetooth Low Energy (BLE) technology has evolved steadily since its inception, with specifications updated approximately every two years to improve reliability and user experience. These periodic revisions, referred to as BLE inflection points by scholars and members of the Special Interest Group (SIG), address the growing requirements of wireless communication systems and ensure Bluetooth’s continued relevance within personal area networks [1].

Recent iterations of BLE have emphasized improved reliability and robustness to support increasingly dense and interference-prone IoT environments [2]. As IoT deployments scale in size and operate in multipath-rich indoor settings, single-antenna BLE links become vulnerable to deep fading and intermittent packet loss. These limitations motivate the use of multi-antenna techniques in BLE-based IoT systems, since spatial diversity offers a direct mechanism to sustain performance at a low Signal-to-Noise Ratio (SNR) and to improve link robustness without altering the beneficial properties of the BLE waveform.

Multiple-Input Multiple-Output (MIMO) and space-time coding (STC) methods offer a promising solution. The foundational works of Foschini [3], Alamouti [4], and later Tarokh [5] showed how spatial diversity can substantially enhance reliability under fading and interference. Orthogonal STC designs for linear modulations such as PAM, PSK, and QAM achieve full diversity with low decoding complexity, forming the basis for modern multi-antenna systems.

Yet, integrating STC with nonlinear modulations like Continuous-Phase Modulation (CPM) remains challenging. BLE employs a special form of CPM known as Gaussian Frequency Shift Keying (GFSK), chosen for its constant envelope and continuous-phase properties that yield high spectral and power efficiency [6]. Because CPM signals retain phase memory, their receivers are inherently more complex. Several classical works addressed this complexity reduction [7,8,9], and later studies further simplified receivers for nonlinear modulations [10,11,12].

Maintaining orthogonality within CPM frameworks is particularly difficult because phase continuity across antennas conflicts with the independent-symbol assumption used in conventional STC [13,14,15]. Traditional space-time methods therefore break phase continuity and cease to produce genuine CPM signals, as discussed in [16]. Some application domains, such as aeronautical mobile telemetry, have adapted STC concepts to CPM to enhance reliability under stringent conditions [17,18,19,20]. Nevertheless, the performance of these techniques still falls short of that achieved by simpler linear modulations under comparable channel conditions [21]. This motivates further investigation into designs that preserve both the continuous phase and orthogonality—two essential features for BLE compatibility.

1.1. Related Work

Several approaches have extended orthogonal space-time coding to continuous-phase modulations. Classical linear OSTBCs such as [4,5] guarantee exact orthogonality but break phase continuity and therefore cannot be applied to CPM or GFSK. Exact orthogonal CPM schemes were later proposed in [13,14], but these methods rely on CPM-specific phase manipulations that do not exploit the partial response structure of GFSK and therefore do not yield BLE-compliant waveforms. Burst-based CPM OSTBCs such as [19,21] achieve exact orthogonality while preserving the continuous phase through termination tails, but they incur substantial overhead and do not take advantage of the partial-response structure of GFSK. The CPM formats in [18] also provide exact orthogonality but follow the same burst-based architecture with significant overhead and no adaptation to GFSK. The method in [16] achieve only approximate orthogonality through Laurent-domain approximations, while works such as [15] address ST–CPM demodulation but do not construct orthogonal space-time codes. None of these approaches generate a continuous-phase, orthogonal waveform compatible with BLE’s GFSK modulation. As shown in

Table 1. Comparison of space-time coding schemes across modulation family, phase continuity, orthogonality, and GFSK compatibility.

Reference	Mod. Family	Orthogonality	Cont. Phase	Tx × Rx	Tailored to GFSK
[4]	Linear	Exact	No	2 × $n$	No
[5]	Linear	Exact	No	$m\times n$	No
[13]	CPM	Exact	Yes	2 × 1	No
[14]	MSK	Exact	Yes	2 × 1	No
[19]	CPM	Exact	Yes	2 × $n$	No
[21]	CPM	Exact	Yes	2 × $n$	No
[16]	CPM	Approx.	Yes	2 × 1	No
[15]	CPM	No	Yes	2 × $n$	No
[18]	CPM	Exact	Yes	2 × $n$	No
This proposal	GFSK	Exact	Yes	2 × $n$	Yes

, the present work fills this gap by exploiting the partial-response characteristics of GFSK to construct an exact orthogonal space-time design that preserves the continuous phase and remains fully compatible with the BLE GFSK waveform.

1.2. Contributions

The contributions of this work are summarized as follows:

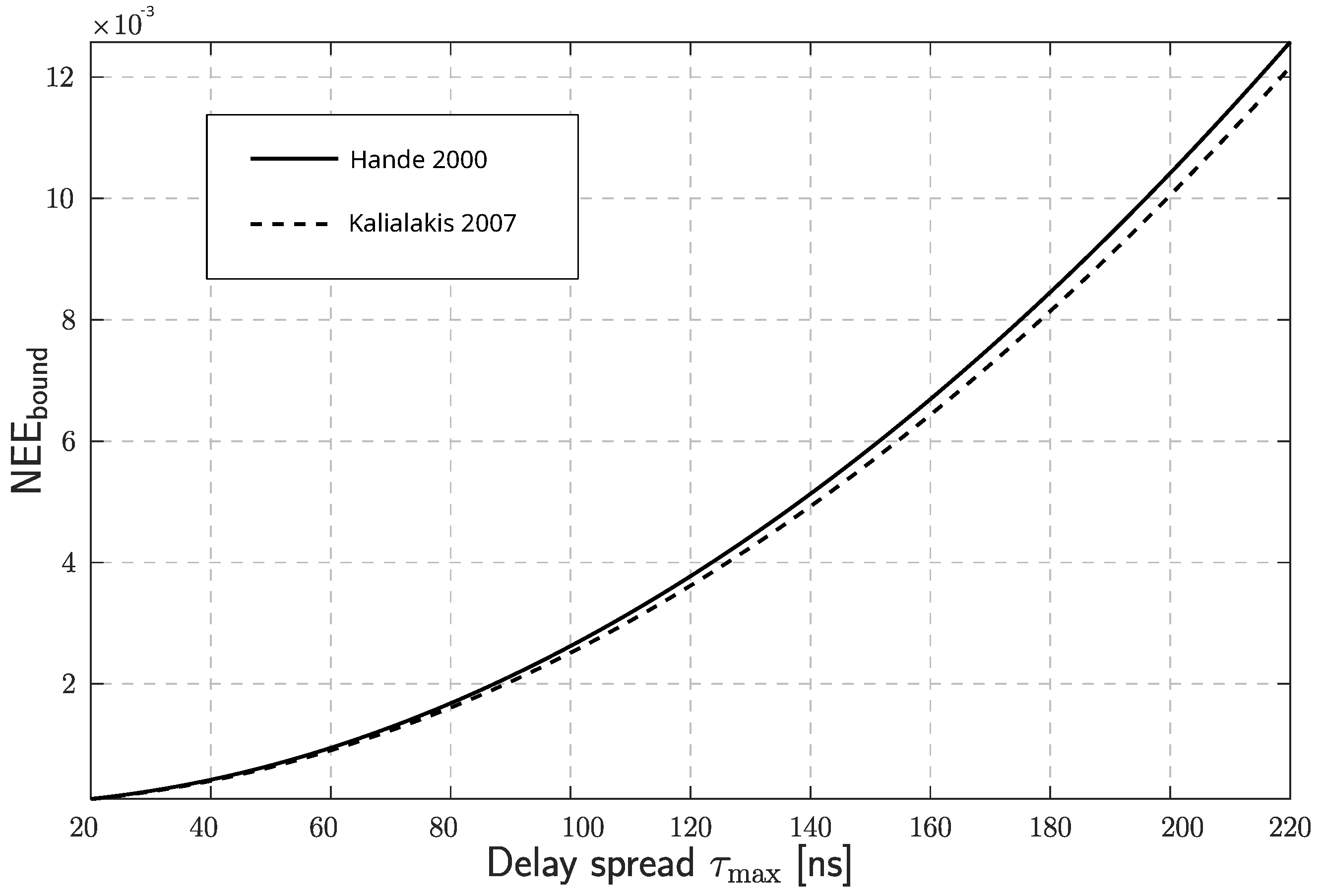
• A formal justification for the flat fading channel assumption in BLE communications is provided.
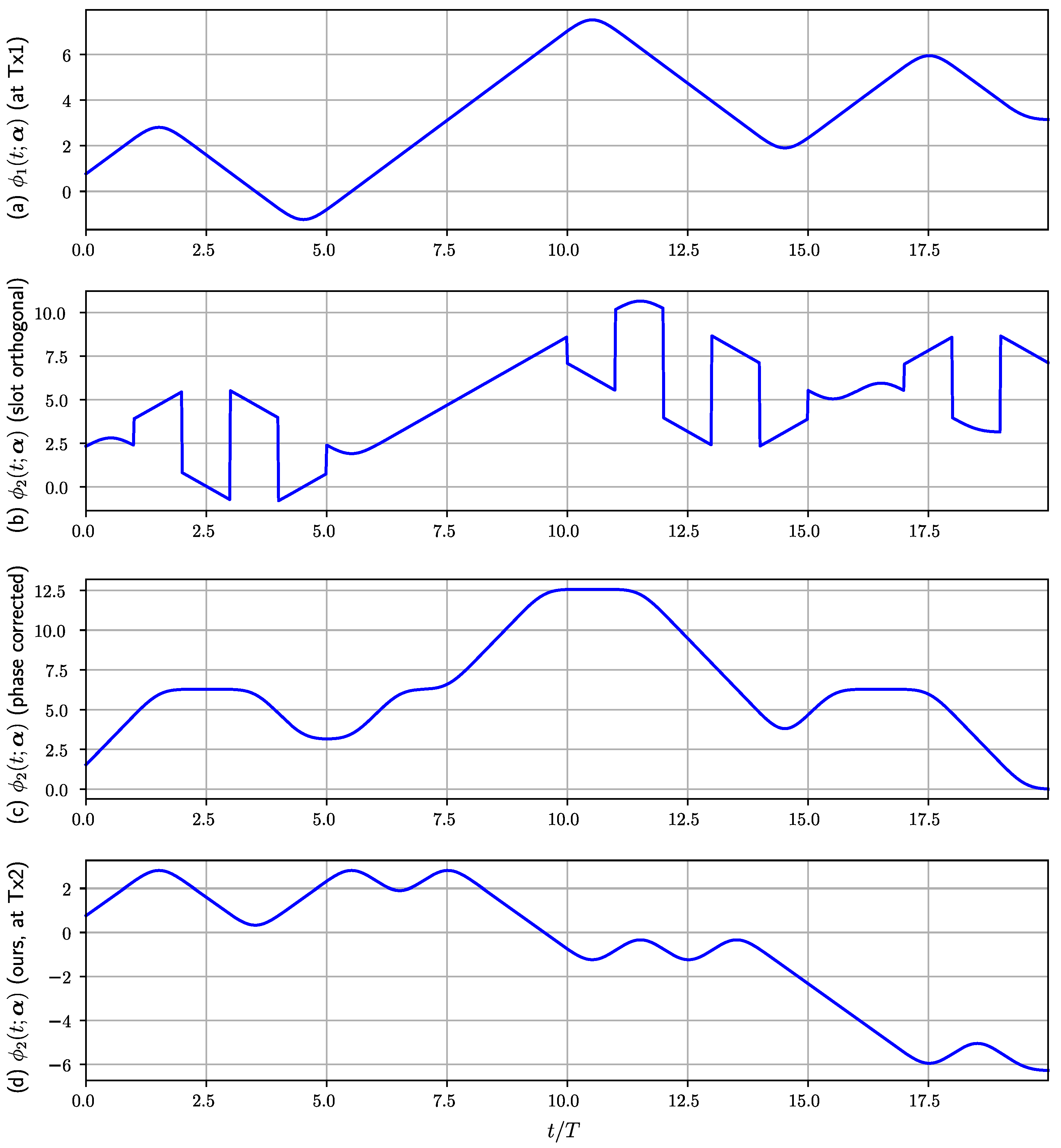
• A new OST-GFSK transmission strategy that maintains phase continuity is proposed.
• A novel data frame format is introduced that achieves orthogonality between transmitted signals, enabling effective use of MIMO techniques.
• The design of a low-complexity signal combiner to optimize receiver performance is proposed.
• Theoretical analysis of the bit error rate (BER) performance under Rayleigh fading channels is provided, supported by simulation results demonstrating comparable performance to linear modulation schemes under similar conditions.

The remainder of this paper is organized as follows. Section 2 presents the BLE signal model and justifies the flat fading channel assumption. Section 3 introduces the single-input multiple-output reference model for receive combining. Section 4 describes the proposed OST-GFSK transmission scheme, including the data frame format, which ensures both phase continuity and orthogonality, and the design of the low-complexity signal combiner for different antenna configurations. Section 5 analyzes the theoretical bit error rate under Rayleigh fading channels, while Section 6 reports the simulation results that support the analytical findings. Finally, Section 7 concludes this paper and outlines future work.

2. BLE Preliminaries

2.1. Signal Model

In BLE specification, the transmitter uses GFSK modulation, which is a nonlinear digital modulation scheme. The input bit stream is mapped to symbols ${\alpha }_i\in \{+1,-1\}$, and the modulator takes N symbols represented by $\mathbf{\alpha }=\{{\alpha }_0,{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_{N-1}\}$ to generate a complex envelope described by

$$s(t;\mathbf{\alpha })=Aexp\left(j\varphi \right(t;\mathbf{\alpha }\left)\right)$$

(1)

where $A=\sqrt{E_s/T}$ and

$$\varphi (t;\mathbf{\alpha })=2\pi \lambda \sum _{i=0}^k{\alpha }_{i}q(t-iT),\hspace{1em}\hspace{1em}kT\le t<(k+1)T$$

(2)

is the phase signal. For BLE, $\lambda \in [0.45,0.55]$ is the modulation index with a nominal value of $\lambda =1/2$, and $T=1/R_b$ is the symbol time interval, with possible bit rates $R_b$ between $1\times {10}^6\mathsf{bits}/\mathsf{s}$ and $2\times {10}^6\mathsf{bits}/\mathsf{s}$. Moreover, $BT=0.5$ is the bandwidth–time product, $E_s$ is the energy of a symbol during an interval of length T, and the phase pulse shaping $q\left(t\right)$ with duration of $L=3$ symbol periods is described as

$$\begin{array}{cc}\hfill q\left(t\right)={\displaystyle \frac{1}{2T}}\underset{0}{\overset{t}{\int }}& Q\left(2\pi BT\left({\displaystyle \frac{\tau -T/2}{\sqrt{\ln \left(2\right)}T}}\right)\right)-Q\left(2\pi BT\left({\displaystyle \frac{\tau +T/2}{\sqrt{\ln \left(2\right)}T}}\right)\right)\mathrm{d}\tau \hfill \end{array}$$

(3)

where

$$Q\left(z\right)={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_z^{\infty }exp\left(-{\displaystyle \frac{{\zeta }^2}{2}}\right)\mathrm{d}\zeta$$

is the complementary error function. Due to the fact that $q\left(t\right)=0,\forall t\le 0$, and $q\left(t\right)=1/2,\forall t\ge LT$, and using the nominal value of the modulation index $h=1/2$, the phase in (2) can be expressed as

$$\begin{array}{cc}\hfill \varphi (t;\mathbf{\alpha })& ={\alpha }_k\pi q(t-kT)+{\alpha }_{k-1}\pi q(t-(k-1)T)+{\alpha }_{k-2}\pi q(t-(k-2)T))+{\theta }_k\hfill \end{array}$$

(4)

with the phase memory term

$${\theta }_k=\left({\displaystyle \frac{\pi }{2}}\sum _{i=0}^{k-L}{\alpha }_i\right)\mathrm{mod}2\pi .$$

(5)

The phase of the GFSK signal in (4) is given by three contributions: the transmitted symbol ${\alpha }_k$, the correlative state vector $({\alpha }_{k-1},{\alpha }_{k-2})$, and the phase memory ${\theta }_k$. Henceforth, during a particular symbol interval $t\in [kT,(k+1\left)T\right]$, the phase signal $\varphi (t;\mathbf{\alpha })$ can be represented by the total memory state vector ${\mathbf{\sigma }}_k={\left[\begin{array}{c}{\theta }_k,{\alpha }_{k-1},{\alpha }_{k-2}\end{array}\right]}^{\top }$ and the symbol ${\alpha }_k$. According to (5), ${\theta }_{k+1}={\theta }_k+(\pi /2){\alpha }_{k-2}$, so that ${\mathbf{\sigma }}_{k+1}={\left[\begin{array}{c}{\theta }_k+(\pi /2){\alpha }_{k-2},{\alpha }_k,{\alpha }_{k-1}\end{array}\right]}^{\top }$. This relation can be represented in matrix notation as

$${\mathbf{\sigma }}_{k+1}=\left[\begin{array}{ccc}1& 0& \pi /2\\ 0& 0& 0\\ 0& 1& 0\end{array}\right]{\mathbf{\sigma }}_k+\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]{\alpha }_k.$$

(6)

Note that since ${\theta }_k$ can only take values in $\{0,\pi /2,\pi ,3\pi /2\}$, then there are 16 possible combinations for ${\mathbf{\sigma }}_{\mathit{k}}$.

2.2. Channel Model

While general communication systems are often subject to time-varying effects such as the ones described in [22], in this work, we provide a formal justification for the flat fading channel assumption in BLE communications. As discussed in [23,24], a received signal for a fading channel is given by

$$r(t;\mathbf{\alpha })=\sum _{i=1}^P{h}_{i}s(t-{\tau }_i;\mathbf{\alpha })$$

for appropriate $h_i\in \mathbb{C}$, where ${\tau }_i\ge 0$ is the path delay spread and P is the number of significant paths. A flat fading channel neglects the delay spread so that $s(t-{\tau }_i;\mathbf{\alpha })\approx s(t;\mathbf{\alpha })$. In this case, the received signal can be written as

$$r_{\mathsf{flat}}(t;\mathbf{\alpha })=hs(t;\mathbf{\alpha })$$

with $h={\sum }_{i=1}^P{h}_i\in \mathbb{C}$. In [23], a criterion to decide if this approximation is valid is proposed. In the following, we apply this criterion for BLE. The criterion is based on studying the average normalized approximation error energy computed as

$$\mathsf{NEE}={\displaystyle \frac{{\displaystyle {\int }_{\mathcal{I}}{\mathbb{E}\left\{\right|e(t;\mathbf{\alpha })|}^2\}\mathrm{d}t}}{{\displaystyle {\int }_{\mathcal{I}}{\mathbb{E}\left\{\right|r(t;\mathbf{\alpha })|}^2\}\mathrm{d}t}}}$$

over an appropriate time interval $\mathcal{I}\subset \mathbb{R}$ covering the transmission signal of bandwidth B. The $\mathsf{NEE}$ corresponds to the ratio between the energy of the approximation error $e(t;\mathbf{\alpha })=r(t;\mathbf{\alpha })-r_{\mathsf{flat}}(t;\mathbf{\alpha })$ and that of the received signal $r(t;\mathbf{\alpha })$. Moreover, the expectation operator $\mathbb{E}\{•\}$ is used under the assumption that ${\tau }_i\in [0,{\tau }_{max}]$ is uniformly distributed and h has independent identically distributed Gaussian real and imaginary parts. While in [23], a bound for the $\mathsf{NEE}$ is provided, it was improved in [25] as

$$\mathsf{NEE}\le {\mathsf{NEE}}_{\mathsf{bound}}:={\displaystyle \frac{B^2}{3.8B_C^2+B^2}}$$

where $B_C=1/{\tau }_{max}$ is the channel coherence bandwidth. For BLE, $B=0.5/T=R_b/2\in [1\times {10}^6,2\times {10}^6]/2$ according to the specification. Moreover, [26] reports experimental measurements for the maximum delay spread ${\tau }_{max}$ for transmission in the BLE band in indoor and outdoor channels. Using this data, a worst-case value can be taken as ${\tau }_{max}=200$ ns. Henceforth, the resulting bound can be computed as ${\mathsf{NEE}}_{\mathsf{bound}}=0.0104$, or equivalently, the approximation error energy is just $1.04\%$ of the energy of the transmitted signal. Henceforth, the flat fading channel assumption is justified for BLE communication systems. It can be noted from Figure 1 that for usual values of ${\tau }_{max}$ between 75 ns and 90 ns, the bound ${\mathsf{NEE}}_{\mathsf{bound}}$ is found to be around $2\times {10}^{-3}$, or $0.2\%$ of the energy of the transmitted signal, which represents a much lower value than the worst case.

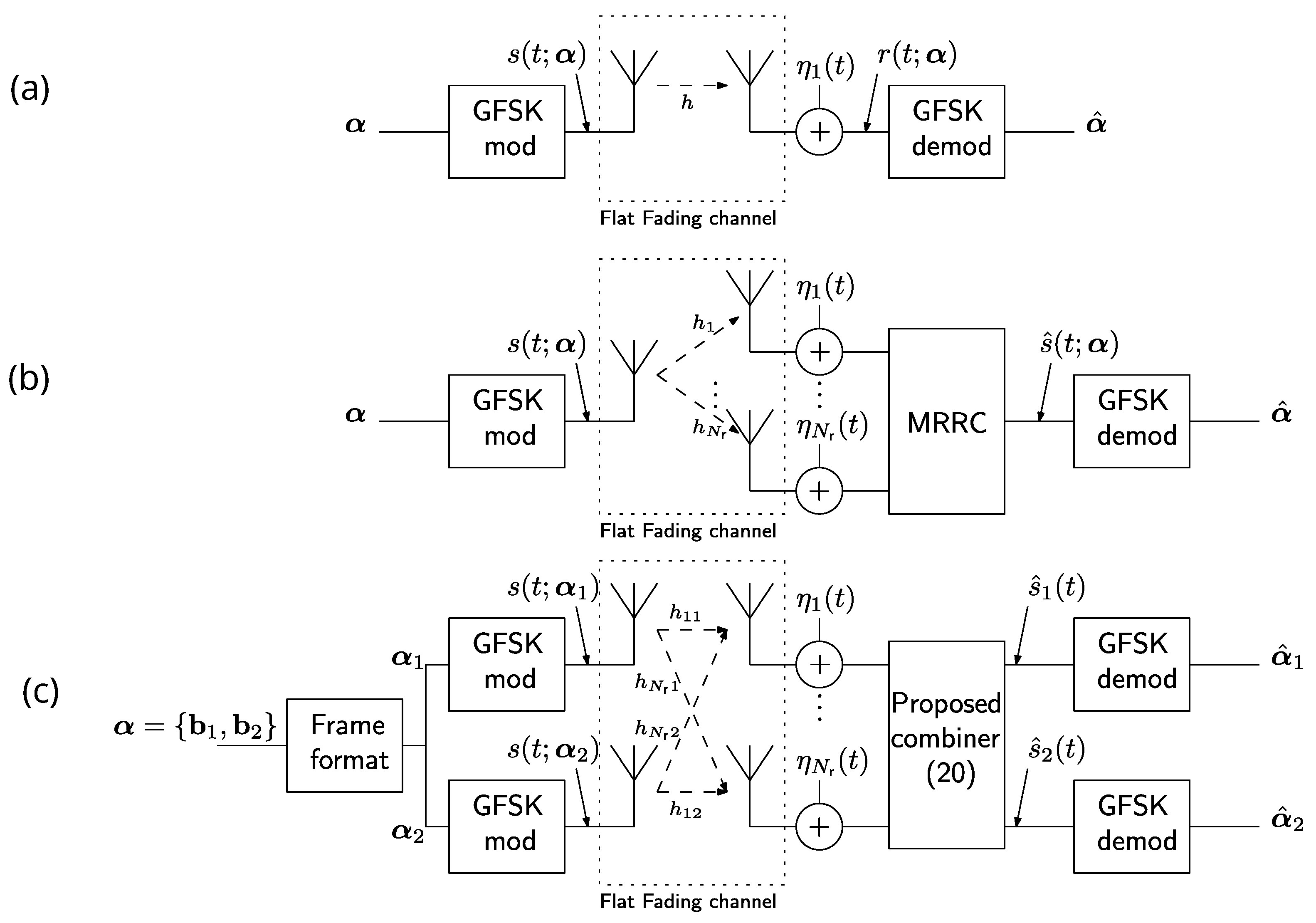
2.3. SISO System Model

A GFSK system model for BLE taking into account a flat fading channel is depicted in Figure 2a). Under this model, for the rest of this work we assume that a received signal always has the form

$$r(t;\mathbf{\alpha })=hs(t;\mathbf{\alpha })+\eta \left(t\right)$$

where $\eta \left(t\right)\in \mathbb{C}$ represents an Additive White Gaussian Noise (AWGN). We assume perfect Channel State Information (CSI), meaning that the coefficient h is known at the receiver. This assumption is reasonable since standard channel estimation techniques can be used for each block. Hence, we assume that h is maintained as constant during the whole block of N transmitted symbols, with independent realizations per block, according to [27].

In this context, on the receiver side, an estimate $\widehat{s}(t;\mathbf{\alpha })$ for $s(t;\mathbf{\alpha })$ can be obtained as

$$\widehat{s}(t;\mathbf{\alpha })={\displaystyle \frac{h^{*}}{{\left|h\right|}^2}}r(t;\mathbf{\alpha }).$$

(7)

Afterwards, a GFSK demodulator is used to extract ${\widehat{\alpha }}_i$ as estimates of the transmitted symbols ${\alpha }_i$ from $\widehat{s}(t;\mathbf{\alpha })$ by means of, e.g., a Viterbi demodulator.

3. GFSK SIMO Maximal-Ratio Receive Combining

In this section, we assume that there is a single $N_{\mathsf{t}}=1$ antenna in the transmitter and $N_{\mathsf{r}}>1$ receiving antennas as depicted in Figure 2b. As a result, under the flat fading channel scenario described in the previous section, $\mathbf{r}(t;\mathbf{\alpha })$ is the $N_{\mathsf{r}}\times 1$ received signal vector:

$$\mathbf{r}(t;\mathbf{\alpha })=\mathbf{H}s(t;\mathbf{\alpha })+\mathbf{\eta }\left(t\right)$$

where $\mathbf{H}={[h_1,\dots ,h_{N_{\mathsf{r}}}]}^{\top }\in {\mathbb{C}}^{N_{\mathsf{r}}\times 1}$ contain the channel coefficients for each antenna in the SIMO case, and $\mathbf{\eta }\left(t\right)\in {\mathbb{C}}^{N_{\mathsf{r}}\times 1}$ is the vector of additive noise terms.

Hence, the analogous of (7) is

$$\widehat{s}(t;\mathbf{\alpha })={\left({\mathbf{H}}^{†}\mathbf{H}\right)}^{-1}{\mathbf{H}}^{†}\mathbf{r}(t;\mathbf{\alpha })$$

where ${(•)}^{†}$ represents the transpose and complex conjugate operator. In a similar fashion as in the SISO case, this can be used as input to a standard GFSK demodulator in order to extract estimated symbols ${\widehat{\alpha }}_i$ for ${\alpha }_i$.

4. Orthogonal Space-Time GFSK MIMO Communications

MIMO communications are known to obtain their best performance when OST schemes are used [5,28]. However, as mentioned in the literature, extending OST to GFSK modulation schemes may compromise the phase continuity of the transmitted signal [13,14], and as a result, they may be incompatible for BLE. Henceforth, this section describes a scheme for OST-GFSK transmission capable of maintaining the phase continuity, taking advantage of BLE-compliant modulation blocks. As a reference, the system described in this section is depicted in Figure 2c).

4.1. OST-GFSK Transmitter

Following from maximum-likelihood approaches for OST [4], consider $N_{\mathsf{t}}=2$ antennas in the transmitter. The proposal is based on taking the original symbol sequence $\mathbf{\alpha }$ and transforming it into two different symbol sequences ${\mathbf{\alpha }}_1,{\mathbf{\alpha }}_2$, carefully arranged in the frame format depicted in Figure 3, described subsequently. Moreover, each antenna at the receiver $\ell =1,2$ transmits

$$s_{\ell }\left(t\right):=s(t;{\mathbf{\alpha }}_{\ell })$$

(8)

using the standard GFSK modulation technique, allowing for phase continuity and BLE compliance.

The frame format for the block-coding scheme is designed to maintain a particular orthogonality property between the two transmitted signals $s_1\left(t\right),s_2\left(t\right)$. The frame format is shaped as follows: firstly, we assume that the symbol sequence can be decomposed in two symbol blocks as $\{{\mathbf{b}}_1,{\mathbf{b}}_2\}=\mathbf{\alpha }$ with ${\mathbf{b}}_1,{\mathbf{b}}_2$ of the same even symbol length $N/2$. Secondly, the transmitted symbol sequences per antenna are formed by

$$\begin{array}{c}\hfill {\mathbf{\alpha }}_1=\{\mathbf{a},{\mathbf{b}}_1,{\mathbf{c}}_1,\mathbf{a},-{\mathbf{b}}_2\},\hspace{1em}\hspace{1em}{\mathbf{\alpha }}_2=\{\mathbf{a},{\mathbf{b}}_2,{\mathbf{c}}_2,\mathbf{a},-{\mathbf{b}}_1\}\end{array}$$

where additional symbol blocks $\mathbf{a},{\mathbf{c}}_1,{\mathbf{c}}_2$ of symbol length 2 are introduced to maintain the orthogonality property between $s_1\left(t\right)$ and $s_2\left(t\right)$. Thus, we consider the time partitions

$$[0,p_{1}T],[p_{1}T,p_{2}T],[p_{2}T,p_{3}T],[p_{3}T,p_{4}T],[p_{4}T,p_{5}T]$$

in which each symbol block of ${\mathbf{\alpha }}_{\ell }$ is sent, with

$$\begin{array}{cc}& p_1=2,p_2=N/2+p_1,p_3=2+p_2\hfill \\ & p_4=2+p_3,p_5=N/2+p_4.\hfill \end{array}$$

In the subsequent analysis, we denote with ${\mathbf{\sigma }}_{\ell ,k}$ the state vector in (6) for each antenna $\ell =1,2$.

Transmission during $\mathit{t}\in [\mathbf{0}\mathbf{,}{\mathit{p}}_{\mathbf{1}}\mathit{T}]$: The initial block is formed as $\mathbf{a}=\{-1,-1\}$. Assuming an initial accumulated phase of ${\theta }_0=0$, the memory state vector is ${\mathbf{\sigma }}_{\ell ,p_1}={[0,-1,-1]}^{\top }$ at $k=p_1=2$, i.e., after transmitting the symbol block $\mathbf{a}$.

Transmission during $\mathit{t}\in [{\mathit{p}}_{\mathbf{1}}\mathit{T},{\mathit{p}}_{\mathbf{2}}\mathit{T}]$: In the curse of the transmission of ${\mathbf{b}}_1$ and ${\mathbf{b}}_2$ in each antenna, respectively, for $t\in [p_{1}T,p_{2}T]$, the transmitted signals can be represented as

$$s_{\ell }\left(t\right)=Aexp\left(j({\varphi }_{{\mathbf{b}}_{\ell }}\left(t\right)+{\theta }_{\ell ,p_1})\right)$$

for antennas $\ell =1,2$, where

$$\begin{array}{cc}\hfill {\varphi }_{{\mathbf{b}}_1}\left(t\right)& =2\pi \lambda \sum _{i=0}^{k-p_1}{\left[{\mathbf{b}}_1\right]}_{i}q(t-iT)\hfill \\ \hfill {\varphi }_{{\mathbf{b}}_2}\left(t\right)& =2\pi \lambda \sum _{i=0}^{k-p_1}{\left[{\mathbf{b}}_2\right]}_{i}q(t-iT)\hfill \end{array}$$

(9)

where for $t\in [kT,(k+1)T),k\in \{p_1,\dots ,p_2\}$ is the phase contribution due the symbols in ${\mathbf{b}}_1$ and ${\mathbf{b}}_2$ only, and

$${\theta }_{\ell ,p_1}={\displaystyle \frac{\pi }{2}}(-1-1)+0=-\pi$$

is the accumulated phase contribution due to the state ${\mathbf{\sigma }}_{\ell ,p_1}={[0,-1,-1]}^{\top }$. Henceforth,

$$\begin{array}{c}\hfill s_1\left(t\right)=A{s}_{1,1}\left(t\right),\hspace{1em}{s}_2\left(t\right)=A{s}_{2,1}\left(t\right)\end{array}$$

with the definitions

$$\begin{array}{cc}\hfill s_{1,1}\left(t\right)& =-exp\left(j{\varphi }_{{\mathbf{b}}_1}\left(t\right)\right)\hfill \\ \hfill s_{2,1}\left(t\right)& =-exp\left(j{\varphi }_{{\mathbf{b}}_2}\left(t\right)\right)\hfill \end{array}$$

(10)

During the transmission of the symbols in ${\mathbf{b}}_1$ and ${\mathbf{b}}_2$ at each antenna $\ell =1,2$, the state ${\mathbf{\sigma }}_{\ell ,k}$ is tracked according to (6) for $k\in \{p_1,\dots ,p_2\}$ with the purpose of computing the resulting memory state vector ${\mathbf{\sigma }}_{\ell ,p_2}$. Hence, due to $p_2-p_1=N/2$ being even, it guarantees that

$${\mathbf{\sigma }}_{\ell ,p_2}={[{\theta }_{\ell ,p_2},{\left[{\mathbf{b}}_{\ell }\right]}_{(N/2-1)},{\left[{\mathbf{b}}_{\ell }\right]}_{(N/2-2)}]}^{\top }$$

complies with

$${\theta }_{\ell ,p_2}=\left(\left({\displaystyle \frac{\pi }{2}}\sum _{i=0}^{(N/2-2)-1}{\left[{\mathbf{b}}_{\ell }\right]}_i\right)\mathrm{mod}2\pi \right)\in \{0,\pi \}$$

(11)

since the summation involves even $(N/2-2)$ term multiples of $\pi /2$, resulting in a multiple of $\pi$ in (11).

Transmission during $\mathit{t}\in [{\mathit{p}}_{\mathbf{2}}\mathit{T},{\mathit{p}}_{\mathbf{3}}\mathit{T}]$: Given the accumulated phase ${\theta }_{\ell ,p_2}\in \{0,\pi \}$, the symbol block ${\mathbf{c}}_{\ell }$, transmitted in this interval, is chosen to obtain ${\theta }_{1,p_3}=0$ and ${\theta }_{2,p_3}=\pi$. This is performed by considering two cases per antenna.

For antenna $\ell =1$, the following hold:

• ${\theta }_{1,p_2}=0$: in this case, ${\mathbf{c}}_1=[1,-1]$ such that ${\mathbf{\sigma }}_{1,p_3}={[0,1,-1]}^{\top }$ leading to ${\theta }_{1,p_3}={\displaystyle \frac{\pi }{2}}(1-1)+0=0$.
• ${\theta }_{1,p_2}=\pi$: in this case, ${\mathbf{c}}_1=[-1,-1]$ such that ${\mathbf{\sigma }}_{1,p_3}={[\pi ,-1,-1]}^{\top }$ leading to ${\theta }_{1,p_3}={\displaystyle \frac{\pi }{2}}(-1-1)+\pi =0$.

For antenna $\ell =2$, the following hold:

• ${\theta }_{2,p_2}=0$: in this case, ${\mathbf{c}}_2=[1,1]$ such that ${\mathbf{\sigma }}_{2,p_3}={[0,1,1]}^{\top }$ leading to ${\theta }_{2,p_3}={\displaystyle \frac{\pi }{2}}(1+1)+0=\pi$.
• ${\theta }_{2,p_2}=\pi$: in this case, ${\mathbf{c}}_2=[1,-1]$ such that ${\mathbf{\sigma }}_{2,p_3}={[\pi ,1,-1]}^{\top }$ leading to ${\theta }_{2,p_3}={\displaystyle \frac{\pi }{2}}(1-1)+\pi =\pi$.

Transmission during $\mathit{t}\in [{\mathit{p}}_{\mathbf{3}}\mathit{T},{\mathit{p}}_{\mathbf{4}}\mathit{T}]$: Both antennas transmit $\mathbf{a}$ in this interval. As a result,

$${\mathbf{\sigma }}_{1,p_4}={[{\theta }_{1,p_3},-1,-1]}^{\top }={[0,-1,-1]}^{\top }$$

and

$${\mathbf{\sigma }}_{2,p_4}={[{\theta }_{2,p_3},-1,-1]}^{\top }={[\pi ,-1,-1]}^{\top }.$$

Henceforth,

$${\theta }_{1,p_4}={\displaystyle \frac{\pi }{2}}(-1-1)+0=\pi$$

and

$${\theta }_{2,p_4}={\displaystyle \frac{\pi }{2}}(-1-1)+\pi =0.$$

Transmission during $\mathit{t}\in [{\mathit{p}}_{\mathbf{4}}\mathit{T},{\mathit{p}}_{\mathbf{5}}\mathit{T}]$: In this interval, antenna $\ell =1$ transmits $-{\mathbf{b}}_2$ and antenna $\ell =2$ transmits $-{\mathbf{b}}_1$. As a result, the transmitted signals comply with

$$\begin{array}{cc}\hfill s_1\left(t\right)& =Aexp\left(j(-{\varphi }_{{\mathbf{b}}_2}(t-T_{\mathsf{off}})+{\theta }_{1,p_4})\right)\hfill \\ \hfill s_2\left(t\right)& =Aexp\left(j(-{\varphi }_{{\mathbf{b}}_1}(t-T_{\mathsf{off}})+{\theta }_{2,p_4})\right)\hfill \end{array}$$

with $T_{\mathsf{off}}=(p_4-p_1)T$, and by noting that ${\varphi }_{-{\mathbf{b}}_{\ell }}\left(t\right)=-{\varphi }_{{\mathbf{b}}_{\ell }}\left(t\right)$ according to (9). Henceforth,

$$\begin{array}{c}\hfill s_1\left(t\right)=A{s}_{1,2}\left(t\right),s_2\left(t\right)=A{s}_{2,2}\left(t\right)\end{array}$$

with the definitions

$$\begin{array}{cc}\hfill s_{1,2}\left(t\right)& =-exp(-j{\varphi }_{{\mathbf{b}}_2}(t-T_{\mathsf{off}}))\hfill \\ \hfill s_{2,2}\left(t\right)& =+exp(-j{\varphi }_{{\mathbf{b}}_1}(t-T_{\mathsf{off}}))\hfill \end{array}$$

(12)

due to ${\theta }_{1,p_4}=\pi$ and ${\theta }_{2,p_4}=0$. Using the definitions of (10) in (12) leads to

$$\begin{array}{cc}\hfill s_{1,2}\left(t\right)& =s_{2,1}{(t-T_{\mathsf{off}})}^{*}\hfill \\ \hfill s_{2,2}\left(t\right)& =-s_{1,1}{(t-T_{\mathsf{off}})}^{*}\hfill \end{array}$$

(13)

From this transmission strategy, an orthogonality property between the transmitted signals is achieved in the intervals $t\in [p_{1}T,p_{2}T]$ and $t\in [p_{4}T,p_{5}T]$. This property implies independent transmission sources, which are very useful to improve the transmit diversity for combating the impairments of fading channels.

Using (13) for $t\in [p_{1}T,p_{2}T]$, the orthogonality property refers to the fact that the following matrix has orthogonal columns:

$$\left[\begin{array}{cc}{s}_{1,1}\left(t\right)& s_{1,2}(t+T_{\mathsf{off}})\\ s_{2,1}\left(t\right)& s_{2,2}(t+T_{\mathsf{off}})\end{array}\right]=\left[\begin{array}{cc}-exp\left(j{\varphi }_{{\mathbf{b}}_1}\left(t\right)\right)& -exp(-j{\varphi }_{{\mathbf{b}}_2}\left(t\right))\\ -exp\left(j{\varphi }_{{\mathbf{b}}_2}\left(t\right)\right)& +exp(-j{\varphi }_{{\mathbf{b}}_1}\left(t\right))\end{array}\right]=\left[\begin{array}{cc}{s}_{1,1}\left(t\right)& s_{2,1}{\left(t\right)}^{*}\\ s_{2,1}\left(t\right)& -s_{1,1}{\left(t\right)}^{*}\end{array}\right]$$

which can be verified as

$$\begin{array}{c}{\left[\genfrac{}{}{0ex}{}{s_{1,1}\left(t\right)}{s_{2,1}\left(t\right)}\right]}^{†}\left[\genfrac{}{}{0ex}{}{s_{2,1}{\left(t\right)}^{*}}{-s_{1,1}{\left(t\right)}^{*}}\right]=\left[s_{1,1}{\left(t\right)}^{*}{s}_{2,1}{\left(t\right)}^{*}\right]\left[\genfrac{}{}{0ex}{}{s_{2,1}{\left(t\right)}^{*}}{-s_{1,1}{\left(t\right)}^{*}}\right]\hfill \\ =s_{1,1}{\left(t\right)}^{*}{s}_{2,1}{\left(t\right)}^{*}-s_{2,1}{\left(t\right)}^{*}{s}_{1,1}{\left(t\right)}^{*}=0\hfill \end{array}$$

This property will be exploited in the receiver design described subsequently.

4.2. OST-GFSK $2\times 1$ Receiver

Assuming the same channel assumptions referred in Section 2.3 and $N_{\mathsf{t}}=2$ and $N_{\mathsf{r}}=1$ antennas at the transmitter and the receiver, respectively, the received signal can be described as

$$\begin{array}{c}\hfill r(t;\mathbf{\alpha })=h_{1}s(t;{\mathbf{\alpha }}_1)+h_{2}s(t;{\mathbf{\alpha }}_2)+\eta \left(t\right)\end{array}$$

(14)

recalling the definition of the transmitted signals from (8), where $h_1,h_2\in \mathbb{C}$ are the channel coefficients that represent the communication flat fading channels assumed to be constant during the transmitted frame, and $\eta \left(t\right)\in \mathbb{C}$ corresponds to the AWGN.

For $t\in [p_{1}T,p_{2}T]$, the proposed signal combiner is

$$\begin{array}{cc}\hfill {\widehat{s}}_1\left(t\right)& ={\displaystyle \frac{1}{{\parallel \mathbf{h}\parallel }^2}}\left(h_1^{*}r(t;\mathbf{\alpha })-h_{2}r{(t+T_{\mathsf{off}};\mathbf{\alpha })}^{*}\right)\hfill \\ \hfill {\widehat{s}}_2\left(t\right)& ={\displaystyle \frac{1}{{\parallel \mathbf{h}\parallel }^2}}\left(h_2^{*}r(t;\mathbf{\alpha })+h_{1}r{(t+T_{\mathsf{off}};\mathbf{\alpha })}^{*}\right)\hfill \end{array}$$

(15)

with $\mathbf{h}={[h_1,h_2]}^{\top }{and\parallel \mathbf{h}\parallel }^2=|h_1{|}^2+{\left|h_2\right|}^2.$ Combining (14) with (15) and expressing in matrix form leads to

$$\begin{array}{c}{\parallel \mathbf{h}\parallel }^2\left[\genfrac{}{}{0ex}{}{{\widehat{s}}_1\left(t\right)}{{\widehat{s}}_2\left(t\right)}\right]=\left[\genfrac{}{}{0ex}{}{h_1^{*}}{h_2^{*}}\genfrac{}{}{0ex}{}{-h_2}{h_1}\right]\left[\genfrac{}{}{0ex}{}{r(t;\mathbf{\alpha })}{r{(t+T_{\mathsf{off}};\mathbf{\alpha })}^{*}}\right]\hfill \\ ={\mathbf{H}}^{†}\left[\genfrac{}{}{0ex}{}{h_{1}s(t;{\mathbf{\alpha }}_1)+h_{2}s(t;{\mathbf{\alpha }}_2)}{h_1^{*}s{(t+T_{\mathsf{off}};{\mathbf{\alpha }}_1)}^{*}+h_2^{*}s{(t+T_{\mathsf{off}};{\mathbf{\alpha }}_2)}^{*}}\right]+{\mathbf{H}}^{†}\mathbf{\eta }\left(t\right)\hfill \end{array}$$

(16)

where

$$\mathbf{H}=\left[\begin{array}{cc}{h}_1& h_2\\ -h_2^{*}& h_1^{*}\end{array}\right],\hspace{1em}{\mathbf{H}}^{†}=\left[\begin{array}{cc}{h}_1^{*}& -h_2\\ h_2^{*}& h_1\end{array}\right],\hspace{1em}\mathbf{\eta }\left(t\right)=\left[\begin{array}{c}\eta \left(t\right)\\ \eta (t+T_{\mathsf{off}})\end{array}\right].$$

Moreover, using (13) to simplify the first term of (16),

$$\begin{array}{c}\left[\genfrac{}{}{0ex}{}{h_{1}s(t;{\mathbf{\alpha }}_1)+h_{2}s(t;{\mathbf{\alpha }}_2)}{h_1^{*}s{(t+T_{\mathsf{off}};{\mathbf{\alpha }}_1)}^{*}+h_2^{*}s{(t+T_{\mathsf{off}};{\mathbf{\alpha }}_2)}^{*}}\right]=A\left[\genfrac{}{}{0ex}{}{h_1{s}_{1,1}\left(t\right)+h_2{s}_{2,1}\left(t\right)}{h_1^{*}{s}_{1,2}{(t+T_{\mathsf{off}})}^{*}+h_2^{*}{s}_{2,2}{(t+T_{\mathsf{off}})}^{*}}\right]\hfill \\ =A\left[\genfrac{}{}{0ex}{}{h_1{s}_{1,1}\left(t\right)+h_2{s}_{2,1}\left(t\right)}{h_1^{*}{s}_{2,1}\left(t\right)-h_2^{*}{s}_{1,1}\left(t\right)}\right]=A\left[\genfrac{}{}{0ex}{}{h_1}{-h_2^{*}}\genfrac{}{}{0ex}{}{h_2}{h_1^{*}}\right]\left[\genfrac{}{}{0ex}{}{s_{1,1}\left(t\right)}{s_{2,1}\left(t\right)}\right]=A\mathbf{H}\left[\genfrac{}{}{0ex}{}{s_{1,1}\left(t\right)}{s_{2,1}\left(t\right)}\right].\hfill \end{array}$$

(17)

Hence, using (16) and (17) on the signal combiner (15) satisfies

$$\begin{array}{cc}& \left[\genfrac{}{}{0ex}{}{{\widehat{s}}_1\left(t\right)}{{\widehat{s}}_2\left(t\right)}\right]={\displaystyle \frac{{\mathbf{H}}^{†}}{{\parallel \mathbf{h}\parallel }^2}}\left(A\mathbf{H}\left[\genfrac{}{}{0ex}{}{s_{1,1}\left(t\right)}{s_{2,1}\left(t\right)}\right]\right)+{\displaystyle \frac{{\mathbf{H}}^{†}}{{\parallel \mathbf{h}\parallel }^2}}\mathbf{\eta }\left(t\right)\hfill \\ & =A{\displaystyle \frac{\left(\right|h_1{|}^2+\left|h_2{|}^2\right)}{{\parallel \mathbf{h}\parallel }^2}}\left[\genfrac{}{}{0ex}{}{s_{1,1}\left(t\right)}{s_{2,1}\left(t\right)}\right]+{\displaystyle \frac{{\mathbf{H}}^{†}}{{\parallel \mathbf{h}\parallel }^2}}\mathbf{\eta }\left(t\right)\hfill \\ & =A\left[\genfrac{}{}{0ex}{}{s_{1,1}\left(t\right)}{s_{2,1}\left(t\right)}\right]+{\displaystyle \frac{{\mathbf{H}}^{†}}{{\parallel \mathbf{h}\parallel }^2}}\mathbf{\eta }\left(t\right).\hfill \end{array}$$

Therefore, using the definitions in (10),

$$\begin{array}{c}\hfill {\widehat{s}}_1\left(t\right)=-Aexp\left(j{\varphi }_{{\mathbf{b}}_1}\left(t\right)\right)+{\overline{\eta }}_1\left(t\right)\\ \hfill {\widehat{s}}_2\left(t\right)=-Aexp\left(j{\varphi }_{{\mathbf{b}}_2}\left(t\right)\right)+{\overline{\eta }}_2\left(t\right)\end{array}$$

(18)

for $t\in [p_{1}T,p_{2}T]$, where ${\overline{\eta }}_1\left(t\right),{\overline{\eta }}_2\left(t\right)$ are the components of the vector $\overline{\mathbf{\eta }}\left(t\right)=({\mathbf{H}}^{†}/{\parallel \mathbf{h}\parallel }^2)\mathbf{\eta }\left(t\right)$. The minus sign in (18) is a consequence of a phase of $-\pi$ at $t=p_{1}T$ introduced due to the transmission of the symbol block $\mathbf{a}=\{-1,-1\}$ during $t\in [0,p_{1}T]$.

Note that ${\widehat{s}}_1\left(t\right)$ and ${\widehat{s}}_2\left(t\right)$ in (18) have the form of a GFSK envelope as in the case of (1). Consequently, ${\widehat{s}}_1\left(t\right)$ and ${\widehat{s}}_2\left(t\right)$ can be introduced directly into a GFSK demodulator to estimate the symbol sequences ${\mathbf{b}}_1$ and ${\mathbf{b}}_2$, respectively, estimating the transmitted input symbol stream $\mathbf{\alpha }=\{{\mathbf{b}}_1,{\mathbf{b}}_2\}$ as a result.

4.3. OST-GFSK $2\times N_{\mathsf{r}}$ Receiver

Assuming the same channel considerations as in Section 4.2, let $N_{\mathsf{t}}=2$ and arbitrary $N_{\mathsf{r}}$ antennas be at the transmitter and the receiver, respectively. Henceforth, the received signals in each antenna can be described as

$$\begin{array}{cc}\hfill r_i(t;\mathbf{\alpha })& =h_{i1}s(t;{\mathbf{\alpha }}_1)+h_{i2}s(t;{\mathbf{\alpha }}_2)+{\eta }_i\left(t\right),i=1,\dots ,N_{\mathsf{r}}\hfill \end{array}$$

(19)

where $h_{ij}$ is the channel coefficient representing the communication flat fading channel between transmitting antenna $j=1,2$ and receiving antenna $i=1,2$; $r_1(t;\mathbf{\alpha }),r_2(t;\mathbf{\alpha })$ are the received signals at receiving antennas 1 and 2, respectively; and ${\eta }_1\left(t\right),{\eta }_2\left(t\right)$ correspond to the AWGN.

For $t\in [p_{1}T,p_{2}T]$, the proposed signal combiner is

$$\begin{array}{cc}\hfill {\widehat{s}}_1\left(t\right)& ={\displaystyle \frac{1}{{\parallel \mathbf{h}\parallel }^2}}\sum _{i=1}^{N_{\mathsf{r}}}\left(h_{i1}^{*}{r}_i(t;\alpha )-h_{i2}{r}_i{(t+T_{\mathsf{off}};\alpha )}^{*}\right)\hfill \\ \hfill {\widehat{s}}_2\left(t\right)& ={\displaystyle \frac{1}{{\parallel \mathbf{h}\parallel }^2}}\sum _{i=1}^{N_{\mathsf{r}}}\left(h_{i2}^{*}{r}_i(t;\alpha )+h_{i1}{r}_i{(t+T_{\mathsf{off}};\alpha )}^{*}\right)\hfill \end{array}$$

(20)

with

$$\begin{array}{cccc}\hfill {\mathbf{h}}_i& ={[h_{i1},h_{i2}]}^{\top },\hfill & \hfill \parallel {\mathbf{h}}_i{\parallel }^2& =|h_{i1}{|}^2+{\left|h_{i2}\right|}^2,\hfill \\ \hfill \mathbf{h}& ={[{\mathbf{h}}_1^{\top },\dots ,{\mathbf{h}}_{N_{\mathsf{r}}}^{\top }]}^{\top },\hfill & \hfill {\parallel \mathbf{h}\parallel }^2& =\sum _{i=1}^{N_{\mathsf{r}}}{\parallel {\mathbf{h}}_i\parallel }^2,\hfill \end{array}$$

or more compactly,

$$\begin{array}{c}\left[\genfrac{}{}{0ex}{}{{\widehat{s}}_1\left(t\right)}{{\widehat{s}}_2\left(t\right)}\right]={\displaystyle \frac{1}{{\parallel \mathbf{h}\parallel }^2}}\sum _{i=1}^{N_{\mathsf{r}}}{\mathbf{H}}_i^{†}\left[\genfrac{}{}{0ex}{}{r_i(t;\mathbf{\alpha })}{r_i{(t+T_{\mathsf{off}};\mathbf{\alpha })}^{*}}\right]\hfill \end{array}$$

(21)

with

$${\mathbf{H}}_i=\left[\begin{array}{cc}{h}_{i1}& h_{i2}\\ -h_{i2}^{*}& h_{i1}^{*}\end{array}\right],\hspace{1em}{\mathbf{H}}_i^{†}=\left[\begin{array}{cc}{h}_{i1}^{*}& -h_{i2}\\ h_{i2}^{*}& h_{i1}\end{array}\right].$$

To simplify (21), note that

$$\begin{array}{c}\left[\genfrac{}{}{0ex}{}{r_i(t;\mathbf{\alpha })}{r_i{(t+T_{\mathsf{off}};\mathbf{\alpha })}^{*}}\right]=\hfill \\ \left[\genfrac{}{}{0ex}{}{h_{i1}s(t;{\mathbf{\alpha }}_1)+h_{i2}s(t;{\mathbf{\alpha }}_2)}{h_{i1}^{*}s{(t+T_{\mathsf{off}};{\mathbf{\alpha }}_1)}^{*}+h_{i2}^{*}s{(t+T_{\mathsf{off}};{\mathbf{\alpha }}_2)}^{*}}\right]+{\mathbf{\eta }}_i\left(t\right)\hfill \end{array}$$

(22)

with ${\mathbf{\eta }}_i\left(t\right)={[{\eta }_i\left(t\right),{\eta }_i(t+T_{\mathsf{off}})]}^{\top }$. Moreover, following a similar reasoning as in (17),

$$\begin{array}{c}\left[\genfrac{}{}{0ex}{}{h_{i1}s(t;{\mathbf{\alpha }}_1)+h_{i2}s(t;{\mathbf{\alpha }}_2)}{h_{i1}^{*}s{(t+T_{\mathsf{off}};{\mathbf{\alpha }}_1)}^{*}+h_{i2}^{*}s{(t+T_{\mathsf{off}};{\mathbf{\alpha }}_2)}^{*}}\right]=A\left[\genfrac{}{}{0ex}{}{h_{i1}{s}_{1,1}\left(t\right)+h_{i2}{s}_{2,1}\left(t\right)}{h_{i1}^{*}{s}_{1,2}{(t+T_{\mathsf{off}})}^{*}+h_{i2}^{*}{s}_{2,2}{(t+T_{\mathsf{off}})}^{*}}\right]\hfill \\ =A\left[\genfrac{}{}{0ex}{}{h_{i1}{s}_{1,1}\left(t\right)+h_{i2}{s}_{2,1}\left(t\right)}{h_{i1}^{*}{s}_{2,1}\left(t\right)-h_{i2}^{*}{s}_{1,1}\left(t\right)}\right]=A\left[\genfrac{}{}{0ex}{}{h_{i1}}{-h_{i2}^{*}}\genfrac{}{}{0ex}{}{h_{i2}}{h_{i1}^{*}}\right]\left[\genfrac{}{}{0ex}{}{s_{1,1}\left(t\right)}{s_{2,1}\left(t\right)}\right]=A{\mathbf{H}}_i\genfrac{}{}{0ex}{}{s_{1,1}\left(t\right)}{s_{2,1}\left(t\right)}.\hfill \end{array}$$

(23)

Using (22) and (23) in (21) leads to

$$\begin{array}{c}\left[\genfrac{}{}{0ex}{}{{\widehat{s}}_1\left(t\right)}{{\widehat{s}}_2\left(t\right)}\right]={\displaystyle \frac{1}{{\parallel \mathbf{h}\parallel }^2}}\sum _{i=1}^{N_{\mathsf{r}}}{\mathbf{H}}_i^{†}\left(A{\mathbf{H}}_i\left[\genfrac{}{}{0ex}{}{s_{1,1}\left(t\right)}{s_{2,1}\left(t\right)}\right]+{\mathbf{\eta }}_i\left(t\right)\right)\hfill \\ ={\displaystyle \frac{1}{{\parallel \mathbf{h}\parallel }^2}}\sum _{i=1}^{N_{\mathsf{r}}}\left(A\left(\right|h_{i1}{|}^2+\left|h_{i2}{|}^2\right)\left[\genfrac{}{}{0ex}{}{s_{1,1}\left(t\right)}{s_{2,1}\left(t\right)}\right]+{\mathbf{H}}_i^{†}{\mathbf{\eta }}_i\left(t\right)\right)\hfill \\ ={\displaystyle \frac{A}{{\parallel \mathbf{h}\parallel }^2}}\left(\sum _{i=1}^{N_{\mathsf{r}}}{\parallel {\mathbf{h}}_i\parallel }^2\right)\left[\genfrac{}{}{0ex}{}{s_{1,1}\left(t\right)}{s_{2,1}\left(t\right)}\right]+{\displaystyle \frac{1}{{\parallel \mathbf{h}\parallel }^2}}\sum _{i=1}^{N_{\mathsf{r}}}{\mathbf{H}}_i^{†}{\mathbf{\eta }}_i\left(t\right)\hfill \\ =A\left[\genfrac{}{}{0ex}{}{s_{1,1}\left(t\right)}{s_{2,1}\left(t\right)}\right]+{\displaystyle \frac{1}{{\parallel \mathbf{h}\parallel }^2}}\sum _{i=1}^{N_{\mathsf{r}}}{\mathbf{H}}_i^{†}{\mathbf{\eta }}_i\left(t\right)\hfill \end{array}$$

(24)

Therefore, using the definitions in (10),

$$\begin{array}{c}\hfill {\widehat{s}}_1\left(t\right)=-Aexp\left(j{\varphi }_{{\mathbf{b}}_1}\left(t\right)\right)+{\overline{\eta }}_1\left(t\right)\\ \hfill {\widehat{s}}_2\left(t\right)=-Aexp\left(j{\varphi }_{{\mathbf{b}}_2}\left(t\right)\right)+{\overline{\eta }}_2\left(t\right)\end{array}$$

(25)

for $t\in [p_{1}T,p_{2}T]$, where ${\overline{\eta }}_1\left(t\right),{\overline{\eta }}_2\left(t\right)$ are the components of the vector

$$\overline{\mathbf{\eta }}\left(t\right)=\left[\begin{array}{c}{\overline{\eta }}_1\left(t\right)\\ {\overline{\eta }}_2\left(t\right)\end{array}\right]={\displaystyle \frac{1}{{\parallel \mathbf{h}\parallel }^2}}\sum _{i=1}^{N_{\mathsf{r}}}{\mathbf{H}}_i^{†}{\mathbf{\eta }}_i\left(t\right)$$

(26)

which reduces to (18) when $N_{\mathsf{r}}=1$. Similar to the case with $2\times 1$, the result in (25), i.e., ${\widehat{s}}_1\left(t\right),{\widehat{s}}_2\left(t\right)$, is introduced into a GFSK demodulator to estimate the symbol sequence $\mathbf{\alpha }=\{{\mathbf{b}}_1,{\mathbf{b}}_2\}$.

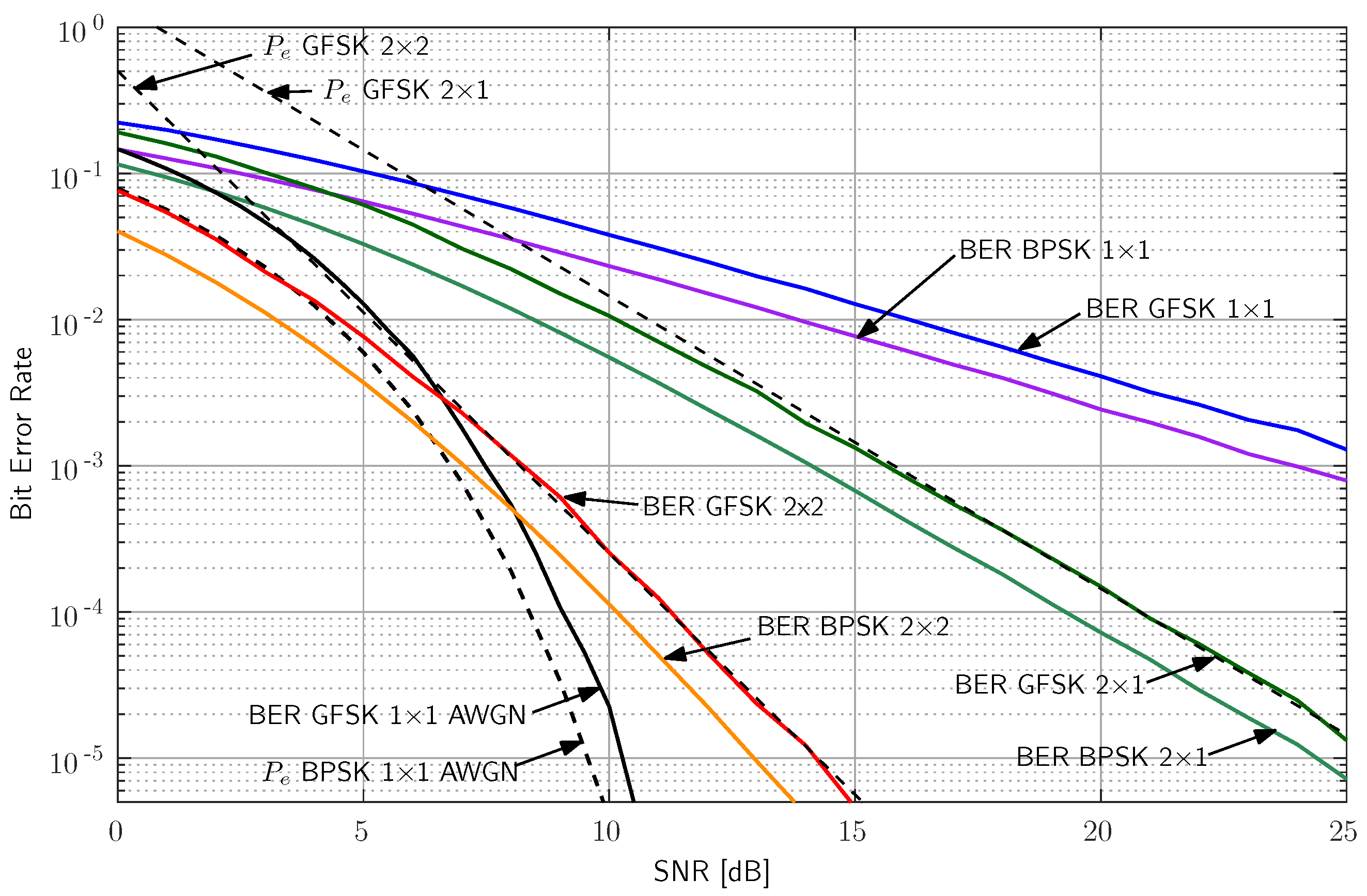
5. Theoretical BER Performance

In this section, we analyze the theoretical error probability for the $2\times N_{\mathsf{r}}$ scheme with $N_{\mathsf{r}}\ge 1$. For this purpose, we borrow the expression of the error probability $P_e$ of the SISO GFSK scheme in the AWGN channel, which is known to be bounded by [29]

$$P_e\le 2\mathcal{Q}\left(d_{min}\sqrt{\mathsf{SNR}}\right)$$

(27)

where $\mathsf{SNR}=E_s/N_0$ and $d_{min}=2.038$ [30] (Chapter 3),

$$\mathcal{Q}\left(z\right)={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_z^{\infty }exp\left(-{\displaystyle \frac{{\zeta }^2}{2}}\right)\mathrm{d}\zeta .$$

and assuming that ${\eta }_i\left(t\right)$ in (19) has variance ${\sigma }^2=N_0/2$ per real and imaginary components and power spectral density of $N_0/2$.

Note that both ${\widehat{s}}_1\left(t\right)$ and ${\widehat{s}}_2\left(t\right)$ in (25) correspond to independent SISO GFSK streaming symbols. Hence, without loss of generality, we consider ${\widehat{s}}_1\left(t\right)$, which is impregnated with noise ${\overline{\eta }}_1\left(t\right)$ with variance, conditioned to a realization of the vector $\mathbf{h}$:

$$\begin{array}{cc}& \mathrm{var}\left({\overline{\eta }}_1\left(t\right)\right|\mathbf{h})=\mathbb{E}\left\{{\overline{\eta }}_1\left(t\right){\overline{\eta }}_1{\left(t\right)}^{*}\right|\mathbf{h}\}=\mathbb{E}\left\{[1\hspace{1em}0]\overline{\mathbf{\eta }}\left(t\right)\overline{\mathbf{\eta }}{\left(t\right)}^{†}\left[\genfrac{}{}{0ex}{}{1}{0}\right]|\mathbf{h}\right\}\hfill \\ & =\mathbb{E}\left\{{\left[\genfrac{}{}{0ex}{}{1}{0}\right]}^{\top }\left({\displaystyle \frac{1}{{\parallel \mathbf{h}\parallel }^2}}\sum _{i=1}^{N_{\mathsf{r}}}{\mathbf{H}}_i^{†}{\mathbf{\eta }}_i\left(t\right)\right){\left({\displaystyle \frac{1}{{\parallel \mathbf{h}\parallel }^2}}\sum _{i=1}^{N_{\mathsf{r}}}{\mathbf{H}}_i^{†}{\mathbf{\eta }}_i\left(t\right)\right)}^{†}\left[\begin{array}{c}1\\ 0\end{array}\right]|\mathbf{h}\right\}\hfill \\ & ={\displaystyle \frac{1}{{\parallel \mathbf{h}\parallel }^4}}{\left[\genfrac{}{}{0ex}{}{1}{0}\right]}^{\top }\left(\sum _{i=1}^{N_{\mathsf{r}}}{\mathbf{H}}_i^{†}\mathbb{E}\left\{{\mathbf{\eta }}_i\left(t\right){\mathbf{\eta }}_i{\left(t\right)}^{†}\right\}{\mathbf{H}}_i\right)\left[\begin{array}{c}1\\ 0\end{array}\right]\hfill \\ & ={\displaystyle \frac{1}{{\parallel \mathbf{h}\parallel }^4}}{\left[\genfrac{}{}{0ex}{}{1}{0}\right]}^{\top }\left(\sum _{i=1}^{N_{\mathsf{r}}}{\mathbf{H}}_i^{†}(N_0/2){\mathbf{H}}_i\right)\left[\genfrac{}{}{0ex}{}{1}{0}\right]={\displaystyle \frac{N_0}{{2\parallel \mathbf{h}\parallel }^4}}{\left[\genfrac{}{}{0ex}{}{1}{0}\right]}^{\top }\left(\sum _{i=1}^{N_{\mathsf{r}}}{\parallel {\mathbf{h}}_i\parallel }^2\right)\left[\genfrac{}{}{0ex}{}{1}{0}\right]={\displaystyle \frac{N_0}{{2\parallel \mathbf{h}\parallel }^2}}\hfill \end{array}$$

where (26) is used as well as ${\mathbf{H}}_i^{†}{\mathbf{H}}_i={\parallel {\mathbf{h}}_i\parallel }^2\mathbf{I}$ and recalling ${\parallel \mathbf{h}\parallel }^2={\sum }_{i=1}^{N_{\mathsf{r}}}{\parallel {\mathbf{h}}_i\parallel }^2$. Henceforth, it can be observed that ${\overline{\eta }}_1\left(t\right)$ (similarly ${\overline{\eta }}_2\left(t\right)$) has an effective power of $N_{\mathbf{h}}=N_0/{\parallel \mathbf{h}\parallel }^2$ conditioned to a realization of $\mathbf{h}$. Therefore, based on (27) and denoting with $P_{e|\mathbf{h}}$ that the error probability for a SISO GFSK demodulator used in (25) conditioned to $\mathbf{h}$ is bounded by

$$P_{e|\mathbf{h}}\le 2\mathcal{Q}\left(d_{min}\sqrt{{\mathsf{SNR}}_{\mathsf{h}}}\right)=2\mathcal{Q}\left(d_{min}\sqrt{{\parallel \mathbf{h}\parallel }^2\mathsf{SNR}}\right)$$

(28)

where ${\mathsf{SNR}}_{\mathsf{h}}$ represents the effective SNR of ${\mathbf{\eta }}_i\left(t\right),i=1,2$ given by

$${\mathsf{SNR}}_{\mathsf{h}}={\displaystyle \frac{E_s}{N_{\mathbf{h}}}}={\displaystyle \frac{{\parallel \mathbf{h}\parallel }^2{E}_s}{N_0}}={\parallel \mathbf{h}\parallel }^2\mathsf{SNR}$$

Finally, denoting $P_e$ as the error probability regardless of $\mathbf{h}$, the total probability theorem is used to obtain

$$P_e={\int }_0^{\infty }{P}_{e|\mathbf{h}}{f}_X\left(x\right)\mathrm{d}x$$

defining the random variable $X={\parallel \mathbf{h}\parallel }^2$ which is a ${\chi }^2$ random variable of $2N_{\mathsf{r}}$ degrees of freedom. Consequently, its probability density function of X is given by

$$f_X\left(x\right)={\displaystyle \frac{1}{N_{\mathsf{r}}-1}}{x}^{N_{\mathsf{r}}-1}exp(-x).$$

Therefore, using the integral from [31] (Equation (3.37)),

$$\begin{array}{cc}\hfill P_e& \le 2{\int }_0^{\infty }\mathcal{Q}\left(d_{min}\sqrt{x\mathsf{SNR}}\right)f_X\left(x\right)\mathrm{d}x\hfill \\ & =2{\int }_0^{\infty }\mathcal{Q}\left(\sqrt{2x\left({\displaystyle \frac{1}{2}}{d}_{min}^2\mathsf{SNR}\right)}\right)f_X\left(x\right)\mathrm{d}x\hfill \\ & =2{\left({\displaystyle \frac{1-\mu }{2}}\right)}^{N_{\mathsf{r}}}\sum _{\ell =0}^{N_{\mathsf{r}}-1}\left(\begin{array}{c}{N}_{\mathsf{r}}-1+\ell \\ \ell \end{array}\right){\left({\displaystyle \frac{1+\mu }{2}}\right)}^{\ell }\hfill \end{array}$$

with $S=d_{min}^2\mathsf{SNR}/2$ and

$$\mu :=\sqrt{{\displaystyle \frac{S}{1+S}}}=d_{min}\sqrt{{\displaystyle \frac{\mathsf{SNR}}{2+d_{min}^2\mathsf{SNR}}}}.$$

Similar to the point discussed in [31] (Chapter 3), at high $\mathsf{SNR}$, if follows that

$${\displaystyle \frac{1+\mu }{2}}\approx 1,{\displaystyle \frac{1-\mu }{2}}\approx {\displaystyle \frac{1}{4S}}$$

and therefore,

$$\begin{array}{cc}\hfill P_e& \le 2{\left({\displaystyle \frac{1-\mu }{2}}\right)}^{N_{\mathsf{r}}}\sum _{\ell =0}^{N_{\mathsf{r}}-1}\left(\genfrac{}{}{0ex}{}{N_{\mathsf{r}}-1+\ell }{\ell }\right){\left({\displaystyle \frac{1+\mu }{2}}\right)}^{\ell }\hfill \\ & \approx 2\left(\genfrac{}{}{0ex}{}{2N_{\mathsf{r}}-1}{N_{\mathsf{r}}}\right){\displaystyle \frac{1}{{\left(4S\right)}^{N_{\mathsf{r}}}}}=2\left(\genfrac{}{}{0ex}{}{2N_{\mathsf{r}}-1}{N_{\mathsf{r}}}\right){\displaystyle \frac{1}{{\left(2d_{min}^2\mathsf{SNR}\right)}^{N_{\mathsf{r}}}}}\hfill \end{array}$$

(29)

6. Simulation Results

In this section, we provide numerical experiments to verify the advantages of the proposal. All simulations were conducted in MATLAB using the standard CPM and GFSK modulation utilities configured to match the BLE parameters described in Section 2.1: the transmitted waveform was generated with a symbol rate of 1 MHz, $BT=0.5$, modulation index $\lambda =0.5$, and 16 samples per symbol, ensuring consistency with the BLE GFSK specification. The receiver employed a Viterbi-based GFSK detector available in the MATLAB CPM routines.

To illustrate the structural differences among existing approaches and the proposed design, Figure 4 compares the phase trajectories generated at both antennas under several representative schemes. Consider two transmitting antennas. Panel (a) shows the standard GFSK signal transmitted on the first antenna, which serves as the baseline for continuity. Panel (b) depicts the result of directly applying an Alamouti-like mapping to the baseband GFSK signal on a slot-by-slot basis, that is, imposing the classical orthogonal structure independently on each time slot without accounting for CPM memory. While baseband signals in panels (a) and (b) are orthogonal, this strategy breaks phase continuity at slot boundaries and produces abrupt transitions. Panel (c) shows the phase-corrected CPM construction of [13], where additional correction terms are introduced to partially restore continuity. Likewise, baseband signals for panels (a) and (c) are orthogonal as well. Moreover, this approach removes the discontinuities. However, the resulting waveform no longer corresponds to a standard GFSK signal and inherits additional structural distortions stemming from the correction mechanism. Panel (d) displays the proposed scheme, where the second antenna transmits a standard GFSK waveform with the proposed frame format for the second antenna, so that orthogonality is achieved frame-wise without modifying the underlying CPM structure. As the figure shows, the proposed design preserves full phase continuity while maintaining strict GFSK compatibility, and it avoids the artificial transitions or shaped corrections that appear in other approaches.

Furthermore, we study the performance of the proposal. Consider as a reference the performance of BPSK in the following conditions: (i) SISO in AWGN channel, (ii) SISO in Rayleigh channel, (iii) OSTC $2\times 1$ in Rayleigh channel, and (iv) OSTC $2\times 2$ in Rayleigh channel. Henceforth, we aim to compare our proposal for OSTC-GFSK in similar conditions. These benchmark BPSK cases correspond to the previously proposed standard space-time codes commonly used in the physical-layer literature, and including them explicitly allows a direct comparison between our OSTC-GFSK scheme and standard OSTC methods.

These four baselines, together with the corresponding GFSK versions, yield eight complete test cases covering both linear and nonlinear modulations under AWGN and fading, and under both SISO and multi-antenna configurations. This set of scenarios is representative of the operating regimes for which BLE and GFSK-based systems are typically evaluated and therefore provides a sufficiently broad basis for assessing the proposed scheme. Moreover, in BLE systems, BER performance is commonly specified directly in terms of received SNR rather than $E_b/N_0$. For example, a 1 MHz BLE signal requires 15 dB SNR to reach a BER of 0.1%, which is the standard reference point used in receiver design. Since BLE employs a fixed-rate binary modulation and our simulations use a fixed symbol duration with normalized transmit power, SNR and $E_b/N_0$ differ only by a constant factor that does not affect the comparative behavior of the BER curves. For these reasons, and to remain aligned with BLE performance practice, our results are reported in terms of SNR.

Simulations were carried out as follows: random sequences of symbols were generated to be modulated with the nonlinear GFSK signal envelope in (1). Then, the AWGN channel noise was added with variance ${\sigma }^2$ computed for the particular value of the SNR. For SISO GFSK in AWGN, we used a standard GFSK Viterbi demodulator. The bit error rate is computed as the ratio between the number of errors for a value of SNR and the total number of symbols. In total, for each value of the SNR, the simulation ended when ${10}^6$ symbol sequences of even $N=800>L=3$ symbols were processed, ensuring statistically stable BER estimates. For the Rayleigh channel, the real and imaginary components of the channel coefficients $h_i$ were sampled from a Gaussian distribution of zero mean and variance 1 and remained fixed per transmitted frame. Simulations were performed for our OSTC-GFSK proposal in both $2\times 1$ and $2\times 2$ schemes.

The performance results are consolidated in Figure 5. The notation $P_e$ corresponds to theoretical bounds for the error probability derived in Section 5, whereas BER denotes the numerically computed bit error rate. As a baseline, the BER of SISO GFSK in the AWGN channel remains separated from BPSK for less than 1 $\mathsf{dB}$. It is important to note that this separation remains consistent between BPSK and GFSK in the rest of the schemes for the Rayleigh channel. Moreover, while the performance of both SISO BPSK and GFSK is degraded in the Rayleigh channel, the performance improves consistently for both by introducing the OSTC scheme due to the diversity gain. The error probability bounds in (29) are shown as well for the $2\times 1$ and $2\times 2$ cases, which are shown to coincide with the numerical BER for medium and high SNR as expected from the theoretical analysis. The figure thus provides, in a compact form, an extensive and representative evaluation across all relevant modulation families, channel conditions, and antenna configurations.

7. Conclusions

This work introduces a novel OST-GFSK communication scheme tailored for BLE systems in IoT applications. By addressing the challenges of integrating OST coding with GFSK modulation, the proposed signal processing scheme achieves substantial improvements in data rate and resilience to fading channels while preserving the BLE GFSK waveform characteristics. Even when the proposal requires an additional antenna, the proposed physical layer may remain interoperable with BLE devices through fallback to standard BLE modes. The proposal uses standard modulation and demodulation pairs, well known for GFSK schemes, along with a novel data frame format to organize the transmitted information such that an orthogonality property is achieved between pairs of frames. This orthogonality property is used to design a novel signal combiner to achieve high performance at the receiver in terms of BER. A detailed theoretical analysis for the error probability under a Rayleigh fading channel is provided for the general $2\times N_{\mathsf{r}}$ case, which is consistent with the experimental results in simulation. Simulations show that the proposed OST-GFSK scheme achieves comparable performance to OST linear modulation (Alamouti BPSK) approaches under Rayleigh fading channels. Consequently, the proposed method combines the benefits of widely adopted OST linear modulation with the nonlinear GFSK modulation essential in BLE. Future work will focus on implementing and validating the proposed OST-GFSK scheme on a Software-Defined Radio (SDR) platform to confirm the theoretical and simulation results in real hardware conditions.