Abstract
Pervasive computing applications deal with the intelligence surrounding users that can facilitate their activities. This intelligence is provided in the form of software components incorporated in embedded systems or devices in close distance with end users. One example of infrastructure that can host intelligent pervasive services is the Edge Computing (EC) ecosystem. EC nodes can execute a number of tasks for data collected by devices present in the Internet of Things (IoT). In this paper, we propose an intelligent, proactive tasks management model based on demand. Demand depicts the number of users or applications interested in using the available tasks in EC nodes, thus characterizing their popularity. We rely on a Deep Machine Learning (DML) model and more specifically on a Long Short Term Memory (LSTM) network to learn the distribution of demand indicators for each task and estimate the future interest in them. This information is combined with historical observations of and support for a decision making scheme to conclude which tasks that are offloaded due to limited interest in them. We have to recognise that, in our decision making, we also take into consideration the load that every task may add to the processing node where it will be allocated. The description of our model is accompanied by a large set of experimental simulations for evaluating the proposed mechanism. We provide numerical results and reveal that the proposed scheme is capable of deciding on the fly, while concluding the most efficient decisions.
1. Introduction
The advent of the Internet of Things (IoT) offers many opportunities in the development of novel applications over a huge infrastructure of numerous devices. These devices are directly connected with the Edge Computing (EC) ecosystem to report the collected data and consume the provided services. At the EC, one can meet nodes with processing capabilities that assist in the provision of services with the minimum possible latency to end users. The main reason for this is that processing activities are kept close to end users. In addition, the processing at the edge can reduce the network traffic [] driving data analytics towards geo-distributed processing, known as edge analytics [,,,]. The discussed activities take the form of a set of tasks that should be executed by EC nodes. EC nodes are characterized by heterogeneity in their computational resources and, more importantly, by a different load. The dynamic environment of the IoT makes the load for EC nodes, fluctuating not only in terms of numbers but also in terms of the computational burden that a task may add to them. Past efforts in the field deal with models that can be adopted to deliver the computational complexity of tasks [], thus we can have an estimate on the burden that tasks may have on processing nodes.
Due to the dynamic nature in which the EC ecosystem and IoT devices act, the requirements of tasks, their number and the demand for them are continuously changing. For alleviating EC nodes from an increased load towards delivering the final response in the minimum possible time, EC nodes may decide to offload a sub-set of tasks to their peers or Cloud. Additional efficient models should be provided that will allocate the offloaded tasks to the available processing nodes towards the conclusion of the desired processing (e.g., the provision of analytics) []. Tasks offloading first appeared in Mobile Cloud Computing (MCC) [,]. MCC targets tasks to offload from mobile nodes to the Cloud where centralized computing and storage take place. Some obstacles for this model are related to the delay in sending tasks and getting responses, especially when communications are realized over a Wide Area Network (WAN). Moreover, the variability in the contextual information of EC nodes, tasks and the collected data define strict requirements for the effective conclusion of the offloading decision. Another significant obstacle is related to the heterogeneity of the EC nodes. Any offloading action should be realized upon the dynamic nodes’ contextual information, thus, any proposed scheme should meet all the imposed requirements. In any case, the decision for offloading tasks and the finalization of the specific allocations should be the result of a monitoring process and a reasoning action executed locally at EC nodes. The challenge is to select the appropriate tasks to be offloaded to peers or the Cloud. In our model, any decision is taken under the following targets: (i) maximize the performance and (ii) minimize the consumption of resources. Finally, decisions should be realized in a distributed manner—i.e., EC nodes independently decide their lines of action. Multiple research efforts deal with centralized approaches; however, these allocation and scheduling models suffer from the drawbacks reported in the literature for Cloud computing [].
In this paper, we focus on the problem of “which” tasks should be offloaded and not on “where” tasks will be offloaded. The “where” question has already been answered by the research community (e.g., in []). For responding to the former (“which”) question, we go beyond the state of the art compared to our previous effort in the domain []. Instead of using an uncertainty management methodology (in [], we propose a model built upon the principles of Fuzzy Logic), we investigate the adoption of Deep Machine Learning (DML) technologies []. More specifically, we build upon a Long Short Term Memory (LSTM) Recurrent Neural Network (RNN) and expose a decision making mechanism for selecting the appropriate tasks to be offloaded by an EC node. We combine the outcome of processing upon past demand observations and future estimates as delivered by the LSTM model with a scheme based on the multi-criteria decision making theory []. Our “reasoning” is motivated by the demand that end users exhibit for every task. It is a strategic decision for our model to incorporate the “popularity” of tasks in the selection process towards supporting popular tasks to be kept locally instead of being offloaded to other nodes. The intuition behind this is two fold: first, nodes save resources through the re-use of the tasks execution framework; secondly, the latency experienced by users is minimized as highly demanded tasks are initiated and executed immediately. We have to notice that EC nodes record the demand for each task as being affected by the mobility of end users/IoT devices. Obviously, the discussed mobility opens up the road for imposing spatio-temporal requirements in our model. The mobility of end users also increases the complexity of the reasoning mechanism when trying to find out if a task will be kept locally and adds uncertainty in node behaviour. The proposed approach is also characterized by the necessary scalability as it can efficiently support an increased number of users—i.e., EC nodes adopt a pre-trained DML model, thus, they can easily apply the envision reasoning no matter the number of end users. We also notice that an EC node may decide to keep the execution of a task locally no matter its popularity when the added load is very low. This aspect is incorporated into our rewarding mechanism that affects the ranking of each task before an offloading action is decided. The following list depicts the contributions of our paper:
- We propose a task management scheme where computation offloading is decided based on task demand;
- We adopt a DML—i.e., LSTM—model to estimate the future demand for each task present in an EC node;
- We provide an “aggregation” mechanism that combines past demand observations and future estimates to feed our reasoning mechanism and decide the tasks that should be offloaded to peers/Cloud;
- We support the “reasoning” mechanism of EC nodes adopting the principles of the multi-criteria theory;
- We provide an extensive experimental evaluation that reveals the pros and cons of the proposed approach. Our evaluation is performed for a set of metrics adopting real traces.
The results indicate that our model is capable of supporting real time applications while exhibiting an increased performance for a large set of experimental scenarios.
The rest of the paper is organized as follows: Section 2 reports on the related work and presents important research efforts in the field. In Section 3, we discuss preliminary information and describe our problem while in Section 4, we present the proposed mechanism. Section 5 is devoted to the description of our experimental evaluation adopting a set of performance metrics. Finally, in Section 6, we conclude our paper giving our future research plans.
2. Related Work
The advent of the EC comes into scene to offer a “cover” of the IoT infrastructure, giving the opportunity of adopting an additional processing layer before the collected data can be transferred to the Cloud. Numerous EC nodes can create an ecosystem of autonomous entities capable of interacting with IoT devices and themselves to execute a set of tasks. Tasks are processing activities requested by applications or end users and can be of any form. For instance, tasks can request for the delivery of Machine Learning (ML) models (e.g., regression, clustering) or ask for the execution of “typical” SQL-like queries upon the available data. The advantage of EC is that these processing activities can be realized close to end users, thus limiting the latency they enjoy []. One can say that it is the best way to keep the processing at the EC ecosystem as long as it is possible before relying on the Cloud. We have to create a cooperative ecosystem that makes EC nodes capable of interacting to execute the requested tasks. This cooperation may involve the offloading of tasks to peers. The most significant reasons for that are the high load that an EC node may face, the absence of the necessary computational capabilities or the lack of the appropriate data.
The research community is very active in the field of task management in a large set of applications domains. Recent studies deal with task offloading solutions—i.e., partitioning, allocation, resource management and distributed execution []. The offloading action belongs to one of the following modes: (i) full offloading and (ii) partial offloading []. In the former mode, tasks will be executed as a whole no matter the location avoiding the partitioning of each task. For instance, we could adopt a model that delivers the appropriate place to offload the desired tasks based on various characteristics (tasks and nodes) []. The latter mode builds on the parallel execution of a set of sub-tasks (a partitioning process is adopted for that) possibly offloaded in different processing nodes. Additional efforts deal with joint tasks allocation—i.e., the allocation of tasks requested by different users/devices/applications []. The target is to minimize the trade off between the performance when executing tasks and meeting the constraints of nodes (e.g., energy resources []). This means that we try to gain from executing tasks requested by multiple users/applications, which can be considered as a type of resource sharing []. An example of a resource sharing model is presented in [] where a polynomial-time task assignment scheme is proposed for allocating tasks with inter-dependency towards achieving guaranteed latency-energy trade-offs.
ML is also adopted in a set efforts dealing with task offloading. Reinforcement learning is a candidate solution that can lead to the best possible action upon a rewarding mechanism []. Tasks allocation can be also studied as an optimization problem [] where constraints can depict the monetary or time costs for solving the problem []. The discussed problem can be formulated as a maximization (maximize the reward) or a minimization (minimize the cost for every allocation) process. In any case, a high number of constraints make the optimization approach an NP-hard problem “dictating” the adoption of an approximate solution or the use of a set of assumptions.
Various schemes have been proposed for supporting the efficient tasks allocation. In [], a dynamic, decentralized resource-allocation strategy based on evolutionary game theory is presented. The matching theory is adopted in []—i.e., the model does not take into consideration the central Cloud in the Mobile Edge Computing (MEC) platform considering the autonomous nature of edge nodes [,]. A coalition-game-based cooperative method to optimize the problem of task offloading is the subject of [] while in [], the authors present game-based strategies for the discussed problem to achieve the Nash equilibrium among mobile users. In [], the authors discuss a model for computational offloading under a scenario of multi-user and multi-mobile edge servers that considers the performance of intelligent devices and server resources. The task scheduling part of the model is based on an auction scheme by considering the time requirements of the computing tasks and the performance of the mobile edge server. In [], the authors propose a device-to-device (D2D)- enabled multi-helper MEC system, in which a local user offloads its tasks to multiple helpers for cooperative computation. The model tries to minimize the latency by optimizing the local user’s task assignment jointly with the time and rate for task offloading and results downloading, as well as the computation frequency for task execution. In any case, the proposed approaches should take into consideration the characteristics of the dynamic environment where EC nodes and IoT devices act. In [], the authors focus on an access control management architecture for a 5G heterogeneous network. Two algorithms are considered—i.e., an optimal static algorithm based on dynamic programming and a two-stage online algorithm to adaptively obtain the current optimal solution in real time. Dynamic programming is also adopted in [] while the integer linear programming is proposed in []. A randomized version of the dynamic programming approach is proposed in [].
Additional research efforts deal with the “cooperation” of EC, IoT and Cloud []. In such a setting, the offloading action can be performed, taking into consideration multiple layers, as we can meet multiple points where processing activities can be realized. Some example technologies adopted to solve the problems focusing on multiple “entities” are the branch and bound algorithm for delivering approximate solutions, the Mixed Integer Linear Programming (MILP), the Iterative Heuristic MEC Resource Allocation (IHRA) algorithm and so on and so forth. All of them result in dynamic decisions based on the realization of every parameter. In [], the authors consider the estimation of the total processing time of each task and for each candidate processing node using linear regression. The same approach is adopted in the effort presented in []. It is critical to estimate the time requirements of tasks (e.g., the round trip time—RTT), taking into consideration all the necessary node and network parameters. If we have in our hands the estimated time, we can easily deliver the burden that every task will cause to a processing node; thus, we can ensure it is fully aligned with the real needs.
Recent developments deal with the advent of Software Defined Networking (SDN) and the need of coordinating virtualized resources []. The optimality of the decision is related to the local or remote task computation, the selection of the appropriate node and the selection of the appropriate path for the offloading action. In [], the authors study the flexible compute-intensive task offloading to a local Cloud, trying to optimize energy consumption, operation speed, and cost. In [], a model based on the Optimal Stopping Theory (OST) is adopted to deliver the appropriate time to offload data and tasks to an edge server. The challenge is to to determine the best offloading strategy that minimizes the expected total delay. Finally, in [], the authors consider unmanned vehicles (i.e., Unmanned Aerial Vehicles—UAVs) and propose a framework enabling optimal offloading decisions as a function of network and computation load, as well as the current state. The optimization is formulated as an optimal stopping time problem over a Markov process.
As exposed by the above provided literature review, past efforts deal with multiple technologies adopted to perform tasks allocation to a set of processing nodes. ML, optimization techniques, approximate models and distributed schemes are some of the adopted schemes. In this paper, we intend to provide the basis for executing such mechanisms. We focus on the initial step before the allocation action—i.e., we propose a mechanism for selecting the tasks that will be offloaded to peer nodes. We incorporate into the decision making model two novel aspects: (i) the adoption of a DML model and (ii) the focus on, not only the current characteristics of tasks (e.g., load, demand), but also on historical demand data and future estimates. It is our strategic decision to have insights into historical task requirements and estimates of the future before we select the tasks to be offloaded. Past requirements and future estimates are smoothly aggregated to be part of the proposed decision-making process while a multi-criteria rewarding mechanism is adopted to support the final ranking of tasks.
3. Preliminaries and Problem Formulation
For the description of the problem under consideration, we borrow the notation provided in [], that deals with the same problem; however, it proposes a different solution compared to the current effort. We consider a set of N EC nodes, , connected with a number of IoT devices being responsible for collecting and storing data while performing the requested tasks. EC nodes stand in the middle between the IoT devices and the Cloud, undertaking the responsibility of receiving the reported data, transferring them upwards to the Cloud for further processing. EC nodes become the host of geo-distributed datasets giving the opportunity of performing the execution of processing activities close to end users. Such processing activities may be requested by users or applications and deal with the execution of tasks either simple or complex. For instance, an application may ask for analytics related to the collected data on a spatio-temporal basis to realize additional services for users. We have to notice that EC nodes, compared to the Cloud, are characterized by limited computational resources; thus, the execution of tasks should be carefully decided. Concerning the collected data, EC nodes should also host the necessary software for storing, processing and retrieving them. It becomes obvious that every EC node can be transformed to an “intelligent” entity, taking decisions related to the management of data and tasks on the fly. In this paper, EC nodes have a clear role to collect the reported data, formulate the local datasets and perform any requested processing. They act as “sinks” for the collected data and tasks demanded by users or applications. When tasks arrive, they are placed in a queue present at each EC node. Then, nodes, if they see that they are overloaded, apply the proposed model and select tasks that should be offloaded to peers. This is affected by the demand of users/applications for each task; thus, EC nodes should maintain a data structure for recording the statistics of requests for each task.
Task execution aims at generating knowledge locally. As tasks may belong to different types (e.g., simple SQL-like queries, ML models generation), they impose different processing requirements for EC nodes. In our past research efforts [], we provide a specific methodology for exposing the computational burden that a task may impose to EC nodes. Without loss of generality, we consider that nodes may support the same number of tasks—i.e., E. At a time instance t, an EC node may have to execute a subset of the aforementioned tasks. For their management, we consider that EC nodes adopt a queue where tasks are placed just after their arrival. A node retrieves the first task from the queue and proceeds with its execution. The number of tasks executed in a time unit defines the throughput of nodes and depends on their computational capabilities; thus, it consequently affects the size of the queue. Tasks present in the queue define the future load of each node being adopted (as we will see later) to estimate if it is feasible to service all the waiting tasks in a reasonable time interval. A task may be requested by a high number of users/applications, indicating the need for repeated executions of it. When a task is popular, EC nodes may re-use the pre-executed instances and limit the time for delivering a response while they save resources. This is significant when tasks share the same parameters (e.g., multiple tasks request the same regression analysis over the hosted data) and the same requests. Additionally, tasks may be characterized by a specific priority (e.g., the same approach as adopted in real time operating systems for serving processes) especially in the case when real time applications should receive the final response as soon as possible. However, the management of priorities is a complex issue as some tasks (especially those with a low priority) may suffer from the starvation effect. In this effort we do not take into account a “preemptive” scheme—i.e., a task with a high priority may interrupt the execution of low priority tasks. This approach is considered first in our future research plans.
As mentioned above, EC nodes are capable of estimating the future load based on tasks present in the queue. In case the future load cannot be efficiently served, EC nodes may decide to offload some of the already present tasks. This is a critical decision as it affects their future performance as well as the time for delivering the final response to users/applications. In this paper, we propose to take into consideration the demand for each task before we decide those that will be offloaded to peers/Cloud. The rationale is to keep the processing locally for tasks requested by many users/applications to re-use the pre-executed activities as explained above. Hence, there will be more room to release resources for the execution of the remaining tasks before additional requests arrive. Let us consider that the demand for a task is represented by a value in the unity interval—i.e., a value close to unity depicts a high demand and the opposite stands for a value close to zero. We focus on the behaviour of a single EC node—i.e., (the same approach holds true for every node in the EC infrastructure). At t, observes the demand for each task and stores it in a dedicated data structure (e.g., a vector). Let this vector be the Tasks Demand Vector (TDV), with . We have to note that may not process the entire set of the E available tasks in the network but only a sub-set of it. In any case, this observation does not affect our model. Hence, for every monitoring epoch—i.e., , updates the corresponding TDV and maintains the W latest recordings (see Figure 1). This is a sliding window approach as wants to keep only “fresh” information about the demand of every task. Consider that the estimated future load for tasks present in the queue (the calculation of the future estimated load can be performed as indicated in []) indicates that their execution is beyond the current “capabilities” of . In this case, should decide to “evict” a number of the M available tasks to peers/Cloud. The final allocation of the evicted tasks can be performed as described in our previous efforts [].
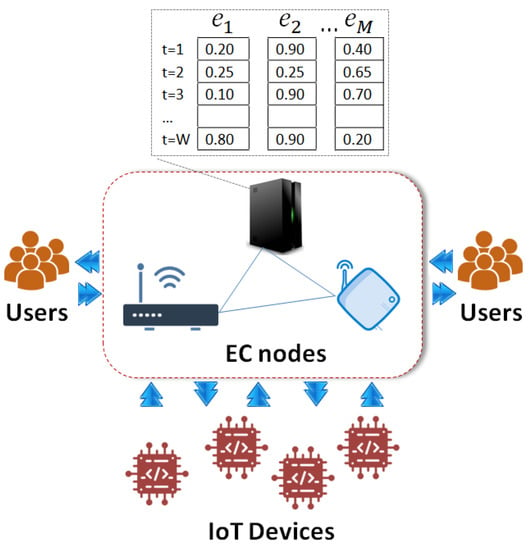
Figure 1.
An example of the proposed architecture.
We provide a solution to the critical research question of which tasks should be selected to be offloaded to peers/Cloud. We aim to keep the execution locally for popular tasks in order to eliminate more time for providing the responses. By offloading non popular tasks, nodes may save resources as they are not benefited from re-using previous outcomes. Additionally, EC nodes may accept a slightly increased latency for non-popular tasks to release more resources for popular tasks. The rationale behind this strategic orientation of our model is simple. A non-popular task may be offloaded to another node that may have increased demand for it (incremental models and caching may be adopted to deliver the final result) paying only the communication cost (for sending the task and getting the response) and the time for waiting for the final outcome. In any case, our model should be accompanied by the appropriate scheme for selecting the right peer for sending the task, as proposed in []. Our focus is to rely on the available TDVs and the load that every task causes in before we perform the final selection. For this, we propose the adoption of historical demand observations and the combination of a DML with the principles of multi-criteria decision making theory—i.e., our final decision is concluded upon the consideration of multiple task characteristics. For characteristics, we assign a penalty/reward in order to produce a ranked list of the available tasks before we select those to be offloaded. Our target is to select the best alternative from a set of available alternatives. Obviously, a unique optimal solution may not present, thus, the adopted rewards incorporate our preference information on the selection process.
We note that decisions made by an EC node affect the decisions and the behaviour of the remaining nodes in the ecosystem. Offloaded tasks should be distributed in peers, thus, they become new tasks for those nodes. The final allocation for each task can be realized based on a model, such as the scheme presented in []. A direct impact of the offloading actions is that tasks could be continuously exchanged in the network till their execution. Evidently, an ageing mechanism is necessary in order to avoid “starvation”—i.e., no node decides to execute some task locally. This means that when a task is being continuously exchanged between EC nodes for a long time, the ageing mechanism will force a node to execute it no matter the reward that the node gains. In that case, the task does not participate in the proposed reasoning process. Nevertheless, the modelling and the implementation of the ageing mechanism are left for future work.
4. Tasks Management at the Edge
4.1. Tasks Demand Indicator
EC nodes rely on TDVs to decide whether a task should be offloaded to peers. applies a monitoring scheme for updating the local TDVs—i.e., with and . At specific epochs, updates the by evicting the oldest observations and storing the most recent ones. Based on , can estimate the future demand for each task and define the Demand Indicator (DI). As we will see later, the DI affects the final ranking of each task, as delivered by a function . realizes the DI of a task as exposed by past observations and future estimates. Formally, the DI could be defined as the number of users/applications requesting a specific task—i.e., . We argue that the DI can be discerned as the DI exposed by past observations and the DI exposed by an estimation process . Both, and are aggregated to deliver the final DI for each task—i.e., . The is delivered by a function that gets the last demand values (e.g., three) for the jth task. can be any function we desire to clearly depict the recent demand observations. The outcome of the discussed function—i.e., is aggregated in a subsequent step with to deliver the . Then, values are adopted in the proposed multi-criteria rewarding mechanism to result in the Offloading Degree (OD) of a task. are fed into the function which is a ranking function to result the final sorted list of the available tasks. In our model, the last-k tasks in the aforementioned list are selected to be offloaded in peer nodes, as proposed in [].
4.2. The Lstm Network for Demand Estimation
Based on the observed TDVs, is able to process a “time series” dataset for the jth task—i.e., . Upon this sequence of demand values, we are able to estimate future values—e.g., . Our aim is to combine what is experienced so far (exposed by TDVs) with the expected realizations of demand. We decided to adopt an LSTM []—i.e., a specific type of RNNs to capture the demand trends for each task. The architecture of the LSTM is presented by Figure 2 (for details about the notation please refer to []).
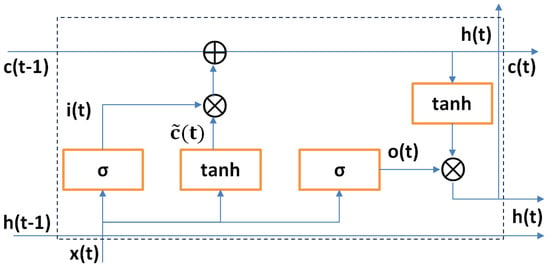
Figure 2.
The architecture of a LSTM neuron.
Our LSTM tries to “understand” every demand value based on previous realizations and efficiently learn the distribution of data. Legacy neural networks cannot perform well in cases where we want to capture the trend of a time series. RNNs and LSTMs are networks with loops inside of them, making the data persist. We note that the LSTM delivers for each task present in the queue of . In our model, we adopt an LSTM for the following reasons: (i) We want to give the opportunity to the proposed model to learn over large sequences of data () and not only over recent data. Typical RNNs suffer from short-term memory and may leave significant information from the beginning of the sequence, making if difficult for the transfer of information from early steps to the later ones; (ii) Typical RNNs also suffer from the vanishing gradient problem—i.e., when a gradient becomes very low during back propagation, the network stops to learn; (iii) LSTMs perform better with the processing of data compared to other architectures as they incorporate multiple “gates” adopted to regulate the flow of the information. Hence, they can learn better than other models upon time series.
Every LSTM cell in the architecture of the network has an internal recurrence (i.e., a self-loop) in addition to the external recurrence of typical RNNs. An LSTM cell also has more parameters than an RNN and the aforementioned gates to control the flow of data. The self-loop weight is controller by the so-called forget gate—i.e., where is the standard deviation of the unit, represents the bias of the unit, represents the input weights, is the vector of inputs (we can get as many inputs as we want out of W recordings), represents the weights of the forget gate and represents the current hidden layer vector. The internal state of an LSTM cell is updated as follows: . Now, b, U and Z represent the bias, input weights and recurrent weights of the cell and depicts the external input gate. We perform similar calculations for the external input and the output gates . The following equations hold true:
The output of the cell is calculated as follows:
We adopt a multiple input, single output LSTM where the final output represents the estimated demand value at —i.e., for the jth task. is, then, combined with the past observations to deliver an efficient decision making mechanism for selecting the tasks that will be offloaded to peers. We have to notice that the LSTM model is trained upon real datasets as we discuss in the experimental evaluation section.
4.3. Aggregating Past Observations and Future Estimates
Having calculated and , the result is the final for each task in the queue. is the outcome of a function that gets and and delivers a value in the unity interval—i.e., . When means that the specific task exhibits a high demand as exposed by past observations and future estimates. The opposite stands for the scenario where . The aggregation of and is performed through the adoption of the Weighted Geometric Mean (WGM) []. The WGM is calculated as follows:
with and, in Equation(4), represents the weight of each demand indicator. is selected to depict the strategy we want to adopt in the delivery of the outcomes. For instance, if , the model pays more attention to the past observations instead of relying on the LSTM result. The opposite stands for .
4.4. The Proposed Rewarding Scheme and Decision Making
We adopt a rewarding mechanism for extracting the reward that gains if it locally executes a task. Tasks with the lowest reward will be offloaded to peer nodes. We rely on multiple rewards—i.e., —one for each parameter affecting the final decision. In our model, we consider two rewards for and for the load that every task will add in the hosting node. For , we consider that, when , we gain a reward ; otherwise we pay a penalty equal to . is a pre-defined threshold for comparing the value. Through the specific approach, we aim at locally keeping the execution of popular tasks as already explained. The same approach also stands for . When , the specific tasks gets a reward equal to ; otherwise, the task gets a penalty equal to . is the pre-defined threshold that indicates when a reward/penalty should be assigned to a task. We have to notice that the reward/penalty for is considered only when the queue size is over a specific percentage, assuming that the maximum queue size is equal to . In general, the proposed methodology is adopted only when faces an increased load and it has to offload some tasks to avoid its overloading that will negatively affect the performance (in a dynamic environment, more tasks will continue to arrive). For both rewards, we apply a sigmoid function for “smoothing” the outcome—i.e., , where and are parameters adopted to “calibrate” its shape. In the above equation, y represents the difference between the aforementioned pairs of parameters with the corresponding thresholds—i.e., . The higher the difference is, the higher the reward becomes. For instance, when , the corresponding reward may quickly approach unity or zero in the scenario where . The same rationale stands for the parameter compared to its threshold . The final reward for the jth task—i.e., the aforementioned OD—is calculated as follows: . Tasks present in the ’s queue are sorted by and the last-k tasks are offloaded to peers.
5. Experimental Evaluation
5.1. Performance Indicators and Setup
We report on the performance of the proposed model as far as the conclusion of correct offloading decision concerns. We also focus on time requirements to result in the final decision for tasks that will be offloaded to peer nodes. We planned to expose the ability of the proposed scheme to get real time decisions to be able to support time-critical applications. We performed a high number of experiments and get the mean value and the standard deviation for a set of performance metrics. For each experimental scenario, we performed 100 experiments, defining specific values for each parameter discussed in the remainder of this section. We evaluated the proposed model upon the simulation of the demand realisations, based on a real trace. For simulating the demand for each task, we relied on the dataset discussed in []. The dataset was generated by an energy analysis of 12 different building shapes—i.e., their glazing area, glazing area distribution and their orientation. From this dataset, we “borrow” the data related to the temperature load of each building to represent the demand for our tasks. We noted that the dataset had an “attitude” to low values.
We adopted a set of performance metrics for evaluating our model, as depicted in Table 1. The following paragraphs are devoted to their description: (i) The average time spent to conclude a decision. was measured for every task as the time spent (CPU time) by the system deciding if a task should be offloaded or not. For this reason, is calculated as the sum of (a) the time spent to get the outcome of the LSTM; (b) the time spent for the rewarding mechanism to deliver the final reward for each task; (c) the time required to deliver the final rankings of tasks and select those that will be offloaded to peers. We note that is measured as the mean required time per task in seconds. (ii) The number of correct decisions . For realizing , we assumeed the cost for executing a task locally compared to the cost for offloading it. The cost for executing a task locally is equal to the waiting time in the queue plus the execution time. The cost for offloading a task involves the migration cost, the waiting time in the “remote” queue, the execution time and the time required for getting the response from the peer node. It becames obvious that, depending on the performance of the network, the “typical” case is to have a higher cost when offloading a task. However, EC nodes can undertake this cost for non popular tasks if it is to release resources for assisting in the execution of popular tasks. Hence, we considered a correct decision as the decision that offloads tasks when their is below the pre-defined threshold —i.e.,
where is the number of experiments. Recall that, at every epoch, we offloaded the last-k tasks of the ranked list. Hence, depicts the percentage of k tasks that were correctly offloaded based on the reasoning of our decision-making mechanism. (iii) We adopted the metric that depicts the percentage of the offloaded tasks that are among the k tasks with the smallest popularity. We try to figure out if the proposed model can detect non popular tasks. We had to remind ourselves that, in our decision-making, the demand/popularity was combined with the load that a task adds to an EC node. We strategically decided to keep the execution of non-popular tasks locally when the load they added was very low.

Table 1.
The adopted performance indicators.
We performed a set of experiments for different W, E, and . We adopt —i.e., different sliding window sizes to measure the effect on , and . The total number of tasks requested by users was set to . Moreover, the weight of past observations was adopted as . The probability of having the demand for a task over a pre-defined threshold was set to . In total, we conducted 100 iterations for each experiment and reported our results for the aforementioned metrics. Our simulator was written in Python adopting the Keras library for building the proposed LSTM. In the LSTM, we adopted the Rectified Linear Unit (ReLU) function to activate the transfer of data in neurons and train the network for 1000 epochs upon data retrieved by the aforementioned dataset. After the training process, the LSTM was fed by values to deliver the final outcomes as described in this paper. The experiments were executed using an Intel i7 CPU with 16gb Ram.
5.2. Performance Assessment
We report on the performance of the proposed model related to the metric. In this set of experiments, we keep —i.e., every EC node should “evict” only a small sub-set of the available tasks and . In Figure 3, we present our outcomes for and for different rewards for the load of each task (). We observe that E (the number of tasks) heavily affects the outcome of . An increased number of tasks leads to an increased mean conclusion time per task. Additionally, the size of the window is inversely proportional to the mean required time—i.e., a low W leads to an increased and vice versa. These results are naturally delivered; an EC node has to process too many tasks; thus, it requires more time to perform the calculations mandated by our model. In Table 2, we provide our results related to the standard deviation of realizations. We observe that, in all the experimental scenarios, the retrieved outcomes are very close to the mean value. This exhibits the “stability” of the approach and proves that the proposed model is capable of minimizing the decision time; thus, being able to support time critical applications. Additionally, a low standard deviation “confirms” the statistical difference between the outcomes retrieved for different experimental scenarios as exposed by mean values. In other words, the mean clearly depicts the performance of our model exhibiting stability and limited fluctuations in the time required to conclude the final decision. To elaborate more on the performance evaluation for the metric, in Figure 4, we present the probability density estimate (pde) of the required time to conclude the final decision. We actually confirm our previous observations. The proposed model requires around 0.8 s (on average) to process 5000 tasks when the sliding window is small. In the case of a large window, our scheme requires 0.4 s (in average) to process 5000 tasks. The remaining evaluation outcomes reveal that when at each EC node, it is possible to manage the requested tasks in times below 0.1 s (on average). This exhibits, again, the ability of the proposed model to react in serving the needs of real time applications requesting the execution of tasks in high rates. This is because we can pre-train the proposed LSTM scheme then upload it at the available EC nodes to be adopted to conclude the offloading decisions. We have to notice that the training process lasts for around 2.5 min (for 1000 epochs). Obviously, the training process can be realized in EC nodes with an increased frequency (if necessary) without jeopardizing their functioning. It should be also noticed that is equal to unity for all the experimental scenarios no matter the values of the adopted parameters. This means that the demand of the selected tasks to be offloaded in peer nodes is below the pre-defined threshold ; thus, no popular tasks are evicted. Recall that the final decision also takes into consideration the load that every task causes into the hosting node and nodes are eager to locally keep tasks with a very low load.
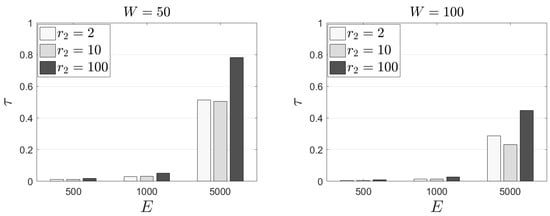
Figure 3.
Performance outcomes for the metric when .

Table 2.
Performance outcomes related to the standard deviation of when .
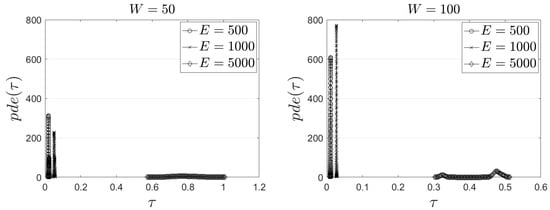
Figure 4.
The pde of for various experimental scenarios.
In Figure 5, we present our results for the metric. We observe that (approximately) half of the selected tasks are between those with the minimum popularity. Our outcomes are similar no matter the size of the sliding window. The same stands true when we focus on the number of tasks. It seems that all the aforementioned parameters are not heavily affecting the final selection. All the retrieved results are in the interval [0.4, 0.6]. We also conclude that the effect of and the corresponding reward does not let get high values. For instance, a task may have a low popularity; however, it may have a very low load as well. This task will get an increased reward and will not be among the last-k tasks that will be offloaded to peers. In Table 3, we present the standard deviation of for the same experimental scenarios. We observe that the retrieved outcomes are in the interval [0.22, 0.33]. These outcomes depict fluctuations in the retrieved mean; thus, the statistical difference between various experimental scenarios is not clear.
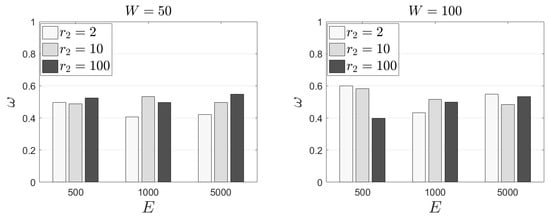
Figure 5.
Performance outcomes for the metric when .

Table 3.
Performance outcomes related to the standard deviation of when .
We performed a set of experiments adopting . Now, the focus of our decision making mechanism is on the demand estimation retrieved by the proposed LSTM model. In Figure 6, we present our results for the and metrics. Again, we observe an increased conclusion time when . decreases as , exhibiting more clearly the effect of paying more attention on the outcome of the LSTM instead of past observations in the decision making model. The best results are achieved for a limited sliding window size—i.e., . As the number of tasks increases, there are multiple tasks with similar evaluation—thus, the model exhibits a slightly reduced (the percentage of the offloaded tasks that are among those with the minimum popularity). We have to also notice that is equal to unity, as in the previous set of experiments.
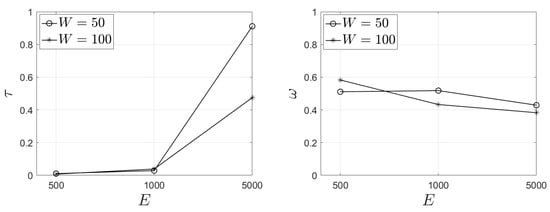
Figure 6.
Performance outcomes for and metrics when and .
In the following experimental scenarios, we adopt different k values—i.e., different number of tasks that should be offloaded to peers. Figure 7 depicts our results. Naturally, increased k and E negatively affect the time requirements of our mechanism. The worst case scenario is met when and . In this case, the proposed mechanism needs around 2 s per task (in average) to extract the final decision. Concerning the metric (Figure 8), we get similar results as in the previous experimental scenarios. Again, around half of the available tasks selected to be offloaded are among those that exhibit the lowest popularity. Finally, realization is equal to unity except in the scenario where and . In this scenario, EC nodes have to evict the 30% (approximately) of the available tasks. In such cases, is equal to 0.70 and 0.89 for , respectively. Now, some tasks with demand over may be offloaded; a decision that is affected by the incorporation of in the rewarding scheme. Evidently, some tasks with low popularity, with a low load as well, may be kept locally. This decision is fully aligned with the above discussed strategic design of the behaviours of EC nodes. In Table 4 and Table 5, we present the performance outcomes for the standard deviation of and when . Both tables exhibit that our results for both performance metrics are very close to their mean. This depicts again the “stability” of the decision making mechanism and a clear view of the increased when k increases as well.
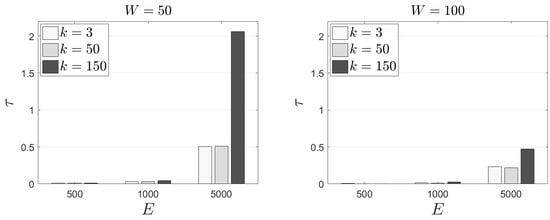
Figure 7.
The time requirements of the proposed model for different k values.
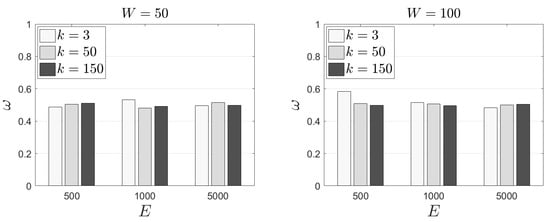
Figure 8.
The performance evaluation of the proposed model for the metric and different k values.

Table 4.
Performance outcomes related to the standard deviation of and when .

Table 5.
Performance outcomes related to the standard deviation of and when .
We compare our LSTM based model with a model that decides upon on only the past demand observations avoiding to pay attention on future estimates—i.e., the Past Behaviour Based Model (PBBM). The PBBM concludes the final decision, taking into consideration only . We try to show the difference in the outcomes when adopting the LSTM. Normally, the use of the LSTM should enhance the performance as it involves decision making for future insights about the demand for each task. In Table 6, we provide our results for the metric. In this set of experiments, we get . We observe that the proposed model outperforms the PBBM, especially when (an exception is observed when and ). The adopted LSTM manages to assist the decision making process when the number of tasks is low, resulting in the appropriate offloading lists. Performing a t-test, we get that the outcomes are significant for a confidence of 90% when and . We have to notice that, in this set of experiments, is retrieved as equal to unity due to the very low number of tasks that should be evicted from EC nodes’ queues. In Table 7 and Table 8, we see the outcomes of another set of experiments for an increased k—i.e., (). Table 7 refers in the metric while Table 8 refers in the metric. We observe that the LSTM model slightly outperforms the PBBM (except one experimental scenario—i.e., , , ) when considering the metric. This means that the LSTM enhances the number of correct offloading decisions when compared to decisions made upon only past observations. Recall that the provided results represent the means of each metric. Concerning the outcomes, we observe a similar performance for both models.

Table 6.
Comparison assessment between the proposed model and the PBBM for the metric ().

Table 7.
Comparison assessment between the proposed model and the PBBM for the metric ().

Table 8.
Comparison assessment between the proposed model and the PBBM for the metric ().
We also compare the performance of our model with the scheme presented in [] where the authors propose a task scheduling algorithm (ETSI) that is based on a heuristic. This heuristic delivers the final outcome based on the remaining energy, the distance from the edge of the network and the number of neighbours calculating the rank of each node. Actually, it consists of a “cost” evaluation mechanism that pays attention to multiple parameters before it concludes the final outcome. Nodes are ranked based on the collected cost, and the node with the lowest ranking is selected for the final allocation. We additionally compare our scheme with the model presented in []. There, a fuzzy logic model is adopted to decide which tasks will be offloaded to peers. The discussed fuzzy logic system tries to manage the uncertainty related with the decision of offloading any incoming task. The authors present the reasoning mechanism upon the requests of every task and define two demand indicators—i.e., the local and the global demand indicators. The fuzzy logic system is fed by the aforementioned indicators and delivers the decision for offloading the available tasks. The comparative assessment between our model and the two aforementioned schemes is performed for the metric and depicted by Figure 9. Specifically, Figure 9 presents the minimum and maximum values of in the entire set of the experimental scenarios. Our scheme outperforms both models. For instance, ETSI manages to result in a limited number of correct decisions related to the offloading of tasks. The highest realization of is 44% (approximately) with the mean and median being around 23–25%. Moreover, the lowest value for in [] is around 84%, depending on the experimental scenario. The proposed model exhibits worse performance than the scheme in [] only when EC nodes should evict too many tasks (like in the scenario when , and ).
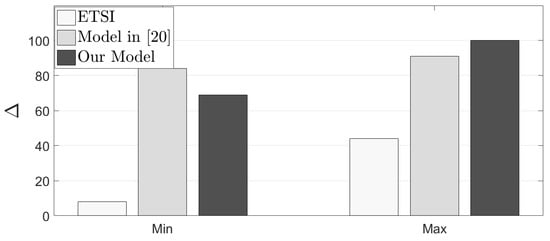
Figure 9.
Comparative assessment of the proposed model for the metric.
Based on the above presented results, we observe that the proposed model manages to have the initially planned impact if adopted in the EC ecosystem. EC nodes can rely on the proposed approach to administrate the incoming tasks requested by users or applications. Initially, we can argue on the limited required time necessary to deliver the offloading decision. As exposed by our experimental evaluation, the proposed scheme can support real time decisions which is very significant when we focus on the dynamic environments of EC and IoT. This gives us the ability to react and manage tasks coming in at high rates. In the majority of our performance evaluation scenarios, the discussed time is below 0.1 s when . In the case of an increased number of tasks—i.e., —the proposed model requires around half of a second for the majority of the adopted scenarios. Additionally, our approach incorporates a “complex” decision making upon multiple parameters/criteria. The complexity deals with the combination of two trends in tasks demand—i.e., the past and the future. Hence, our scheme becomes the “aggregation” point of demand realizations during the time trying to learn from the past and estimate the future. This means that EC nodes try to proactively administrate their available resources devoted for task execution in the most profitable manner. When using the term “profitable”, we mean that EC nodes should offload tasks for which it is judged that they will burden them and exhibit a low demand. If those tasks are kept locally, EC nodes should spend resources for their execution without gaining from the repeated execution (re-using of resources and previous results) of popular tasks. For concluding efficient decisions, our mechanism relies on multiple parameters/criteria and a rewarding scheme for revealing the less “profitable” tasks that should be offloaded to other peer nodes. If this rationale dictates the behaviour of the entire ecosystem, EC nodes will keep for local execution tasks that are profitable for them supporting a cooperative environment where nodes can exchange data and tasks to optimize the use of the available resources and serve end users in the minimum possible time. The first of our future research plans is the definition of an ageing model for avoiding having tasks continuously offloaded in the network. The discussed ageing mechanism will secure that every task will be, finally, executed by a node or on the Cloud.
6. Conclusions and Future Work
Tasks scheduling and offloading actions are significant for a number of application domains. The performance of task execution may be enhanced if we rely on a cooperative model that makes processing nodes interact and exchange tasks. This way, nodes can release resources to serve the remaining tasks reported by users or applications. In this paper, we focus on the discussed problem and take into consideration the dynamic nature of environments, such as the IoT or the EC where nodes interact. We focus on the behaviour of EC nodes related to the management of tasks. We support their behaviour with an intelligent scheme that decides which tasks should be offloaded to peer nodes. We incorporate into the proposed model a deep learning scheme and a rewarding mechanism. Both technologies aim to detect tasks that should be kept locally based on the demand that users/applications exhibit for them. We propose this strategy to benefit from the re-use of the resources and build upon an incremental processing approach towards the minimization of time in the provision of the final responses. We perform an extensive set of simulations and reveal the ability of the proposed scheme to be adopted in real time setups while being aligned with the dynamics of the environment. We present numerical results that exhibit a limited time for training the deep learning model and concluding the final list of tasks that should be offloaded to peer nodes. The first step in our future research agenda is to apply an optimal stopping model for selecting the evicted tasks combined with the outcomes of the deep learning approach. This way, we will be able to create a more robust mechanism that will incorporate the necessary stochastic behaviour in the decision making process.
Author Contributions
Conceptualization, K.K.; methodology, K.K.; software, K.K.; formal analysis, K.K., C.A.; investigation, K.K., C.A.; writing—original draft preparation, K.K., C.A.; writing—review and editing, K.K., C.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shi, C.; Lakafosis, V.; Ammar, M.; Zegura, E. Serendipity: Enabling remote computing among intermittently connected mobile devices. In Proceedings of the ACM International Symposium on Mobile Ad Hoc Networking and Computing, Head Island, SC, USA, 11–14 June 2012. [Google Scholar]
- Pu, Q.; Ananthanarayanan, G.; Bodik, P.K.; Ula, S.; Akella, A.; Bahl, P.; Stoica, I. Low latency geo-distributed data analytics. In Proceedings of the ACM Conference on Special Interest Group Data Commununications, London, UK, 17–21 August 2015; pp. 421–434. [Google Scholar]
- Satyanarayanan, M.; Simoens, P.; Xiao, Y.; Pilai, P.; Chen, Z.; Ha, K.; Hu, W.; Amos, B. Edge analytics in the Internet of Things. IEEE Pervasive Comput. 2015, 14, 24–31. [Google Scholar] [CrossRef]
- Yi, S.; Hao, Z.; Qin, Z.; Li, Q. Fog computing: Platform and applications. In Proceedings of the 3rd IEEE Workshop Hot Topics Web Systems Technologies, Washington, DC, USA, 12–13 November 2015; pp. 73–78. [Google Scholar]
- Zhou, Z.; Chen, X.; Li, E.; Zeng, L.; Luo, K.; Zhang, J. Edge intelligence: Paving the last mile of artificial intelligence with edge computing. Proc. IEEE 2019, 107, 1738–1762. [Google Scholar] [CrossRef]
- Kolomvatsos, K.; Anagnostopoulos, C. An Edge-Centric Ensemble Scheme for Queries Assignment. In Proceedings of the 8th International Workshop on Combinations of Intelligent Methods and Applications in Conjunction with the 30th ICTAI, Volos, Greece, 5–7 November 2018. [Google Scholar]
- Kathidjiotis, I.; Kolomvatsos, K.; Anagnostopoulos, C. Predictive Intelligence of Reliable Analytics in Distributed Computing Environments; Springer: Berlin, Germany, 2020. [Google Scholar]
- Fernando, N.; Loke, S.W.; Rahayu, W. Mobile cloud computing: A survey. Future Gener. Comput. Syst. 2013, 29, 84–106. [Google Scholar] [CrossRef]
- Sanaei, Z.; Abolfazli, S.; Gani, A.; Buyya, R. Heterogeneity in mobile cloud computing: Taxonomy and open challenges. IEEE Commun. Surv. Tutor. 2014, 16, 369–392. [Google Scholar] [CrossRef]
- Islam, M.M.; Morshed, S.; Goswami, P. Cloud computing: A survey on its limitations and potential solutions. Int. J. Comput. Sci. Issues (IJCSI) 2013, 10, 159. [Google Scholar]
- Kolomvatsos, K.; Anagnostopoulos, C. Multi-criteria Optimal Task Allocation at the Edge. Future Gener. Comput. Syst. 2019, 93, 358–372. [Google Scholar] [CrossRef]
- Karanika, A.; Oikonomou, P.; Kolomvatsos, K.; Loukopoulos, T. A Demand-driven, Proactive Tasks Management Model at the Edge. In Proceedings of the IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Glasgow, UK, 19–24 July 2020. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Franco, L.; Montibeller, G. Problem structuring for multicriteria decision analysis interventions. In Wiley Encyclopedia of Operations Research and Management Science; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Lin, L.; Liao, X.; Jin, H.; Li, P. Computation Offloading towards Edge Computing. Proc. IEEE 2019, 107, 1584–1607. [Google Scholar] [CrossRef]
- Wang, Y.; Sheng, M.; Wang, X.; Wang, L.; Li, J. Mobile edge computing: Partial computation offloading using dynamic voltage scaling. IEEE Trans. Commun. 2016, 64, 4268–4282. [Google Scholar] [CrossRef]
- Sardellitti, S.; Scutari, G.; Barbarossa, S. Joint optimization of radio and computational resources for multicell mobile edge computing. IEEE Trans. Signal Inf. Process. Netw. 2015, 1, 89–103. [Google Scholar] [CrossRef]
- Dab, B.; Aitsaadi, N.; Langar, R. Q-Learning Algorithm for Joint Computation Offloading and Resource Allocation in Edge Cloud’. In Proceedings of the IFIP/IEEE Symposium on Integrated Network and Service Management, Arlington, VA, USA, 8–12 April 2019. [Google Scholar]
- Zhou, W.; Fang, W.; Li, Y.; Yuan, B.; Li, Y.; Wang, T. Markov Approximation for Task Offloading and Computation Scaling in Mobile Edge Computing. Mob. Inf. Syst. 2019, 2019, 8172698. [Google Scholar] [CrossRef]
- Shi, W.; Cao, J.; Zhang, Q.; Li, Y.; Xu, L. Edge computing: Vision and challenges. IEEE Internet Things J. 2016, 3, 637–646. [Google Scholar] [CrossRef]
- Kao, Y.; Krishnamachari, B.; Ra, M.; Bai, F. Hermes: Latency optimal task assignment for resource-constrained mobile Computing. IEEE Trans. Mob. Comput. 2017, 16, 3056–3069. [Google Scholar] [CrossRef]
- Du, W.; Lei, T.; He, Q.; Liu, W.; Lei, Q.; Zhao, H.; Wang, W. Service Capacity Enhanced Task Offloading and Resource Allocation in Multi-Server Edge Computing Environment. In Proceedings of the IEEE International Conference on Web Services, Milan, Italy, 8–13 July 2019. [Google Scholar]
- Wang, L.; Jiao, L.; Kliazovich, D.; Bouvry, P. Reconciling Task Assignment and Scheduling in Mobile Edge Clouds. In Proceedings of the IEEE 24th International Conference on Network Protocols, Singapore, 8–11 November 2016. [Google Scholar]
- Dong, C.; Wen, W. Joint Optimization for Task Offloading in Edge Computing: An Evolutionary Game Approach. Sensors 2019, 19, 740. [Google Scholar] [CrossRef]
- Gu, B.; Chen, Y.; Liao, H.; Zhou, Z.; Zhang, D. A Distributed and Context-Aware Task Assignment Mechanism for Collaborative Mobile Edge Computing. Sensors 2018, 18, 2423. [Google Scholar] [CrossRef]
- Anagnostopoulos, C.; Kolomvatsos, K. An Intelligent, Time-Optimized Monitoring Scheme for Edge Nodes. J. Netw. Comput. Appl. 2019, 148, 102458. [Google Scholar] [CrossRef]
- Anagnostopoulos, C.; Hadjiefthymiades, S.; Kolomvatsos, K. Time Optimized User Grouping in Location Based Services. Comput. Netw. 2015, 81, 220–244. [Google Scholar] [CrossRef]
- Zhang, T. Data Offloading in Mobile Edge Computing: A Coalition and Pricing Based Approach. IEEE Access 2018, 6, 2760–2767. [Google Scholar] [CrossRef]
- Jošilo, S.; Dan, G. Selfish Decentralized Computation Offloading for Mobile Cloud Computing in Dense Wireless Networks. IEEE Trans. Mob. Comput. 2019, 18, 207–220. [Google Scholar] [CrossRef]
- Sheng, J.; Hu, J.; Teng, X.; Wang, B.; Pan, X. Computation Offloading Strategy in Mobile Edge Computing. Information 2019, 10, 191. [Google Scholar] [CrossRef]
- Xing, H.; Liu, L.; Xu, J.; Nallanathan, A. Joint Task Assignment and Resource Allocation for D2D-Enabled Mobile-Edge Computing. IEEE Trans. Commun. 2019, 67, 4193–4207. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, J.; Chen, L.; Kiang, G.; Lam, S. Computation Result Reusing for Mobile Edge Computing. Comput. J. 2019, 62, 1450–1462. [Google Scholar] [CrossRef]
- Wu, H.; Wolter, K. Software Aging in Mobile Devices: Partial Computation Offloading as a Solution. In Proceedings of the 2015 IEEE International Symposium of Software Reliability Engineering Workshops, Gaithersburg, MD, USA, 2–5 November 2015; pp. 125–131. [Google Scholar]
- Cuervo, E.; Balasubramanian, A.; Cho, D.K.; Wolman, A.; Saroiu, S.; Chandra, R.; Bahl, P. Maui: Making Smartphones Last Longer with Code Offload. In Proceedings of the 8th International Conference on Mobile Systems, Applications, and Services, San Francisco, CA, USA, 15–18 June 2010; pp. 49–62. [Google Scholar]
- Shahzad, H.; Szymanski, T.H. A Dynamic Programming Offloading Algorithm Using Biased Randomization. In Proceedings of the 9th IEEE International Conference on Cloud Computing, San Francisco, CA, USA, 27 June–2 July 2016; pp. 960–965. [Google Scholar]
- Ning, Z.; Dong, P.; Kong, X.; Xia, F. A Cooperative Partial Computation Offloading Scheme for Mobile Edge Computing Enabled Internet of Things. IEEE Internet Things J. 2019, 6, 4804–4814. [Google Scholar] [CrossRef]
- Kim, K.; Lynskey, J.; Kang, S.; Hong, C. Prediction Based Sub-Task Offloading in Mobile Edge Computing. In Proceedings of the International Conference on Information Networking, Kuala Lumpur, Malaysia, 9–11 January 2019. [Google Scholar]
- Messaoudi, F.; Ksentini, A.; Bertin, P. On Using Edge Computing for Computation Offloading in Mobile Network. In Proceedings of the IEEE Global Communications Conference, Singapore, 4–8 December 2017. [Google Scholar]
- Misra, S.; Saha, N. Detour: Dynamic Task Offloading in Software-Defined Fog for IoT applications. IEEE J. Sel. Areas Commun. 2019, 37, 1159–1166. [Google Scholar] [CrossRef]
- Lin, K.; Pankaj, S.; Wang, D. Task Offloading and Resource Allocation for Edge-of-Things Computing on Smart Healthcare Systems. Comput. Electr. Eng. 2018, 72, 348–360. [Google Scholar] [CrossRef]
- Alghamdi, I.; Anagnostopoulos, C.; Pezaros, D. Time-Optimized Task Offloading Decision Making in Mobile Edge Computing. In Proceedings of the IEEE Wireless Days (WD), Manchester, UK, 24–26 April 2019. [Google Scholar]
- Callegaro, D.; Levorato, M. Optimal Computation Offloading in Edge-Assisted UAV Systems. In Proceedings of the IEEE GLOBECOM, Abu Dhabi, UAE, 9–13 December 2018. [Google Scholar]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Jung, C.; Lee, H.; Lim, Y.; Yamazaki, T. Weighted geometric mean of n-operators with n-parameters. Linear Algebra Appl. 2010, 432, 1515–1530. [Google Scholar] [CrossRef][Green Version]
- Tsanas, A.; Xifara, A. Accurate quantitative estimation of energy performance of residential buildings using statistical machine learning tools. Energy Build. 2012, 49, 560–567. [Google Scholar] [CrossRef]
- Baranidharan, B.; Saravanan, K. ETSI: Efficient Task Allocation in Internet of Things. Int. J. Pure Appl. Math. 2017, 117, 229–233. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).