Abstract
Although Vehicle to Infrastructure (V2I) communications greatly improve the efficiency of early warning systems for car safety, communication privacy is an important concern. Although solutions exist in the literature for privacy preserving VANET communications, they usually require high trust assumptions for a single authority. In this paper we propose a distributed trust model for privacy preserving V2I communications. Trust is distributed among a certification authority that issues the vehicles’ credentials, and a signing authority that anonymously authenticates V2I messages in a zero knowledge manner. Anonymity is based on bilinear pairings and partially blind signatures. In addition, our system supports enhanced conditional privacy since both authorities and the relevant RSU need to collaborate to trace a message back to a vehicle, while efficient certificateless revocation is supported. Moreover, our scheme provides strong unframeability for honest vehicles. Even if all the entities collude, it is not possible to frame a honest vehicle, by tracing a forged message back to an honest vehicle. The proposed scheme concurrently achieves conditional privacy and strong unframeabilty for vehicles, without assuming a fully trusted authority. Our evaluation results show that the system allows RSUs to efficiently handle multiple messages per second, which suffices for real world implementations.
1. Introduction
Governmental organizations, academia and car industry are focusing on the improvement of safety and efficiency of transport systems. Safety systems such as the Antilock Braking System (ABS) and the Electronic Stability Program (ESP) have become mainstream technologies in the car industry for a couple of decades. More recently, Advanced Driver-Assistance Systems (ADAS) can combine car connectivity systems to improve road safety, by taking advantage of the Vehicle to Vechicle (V2V) and Vehicle to Infrastructure (V2I) communications [1].
Vehicular Adhoc Networks (VANET) are a special instance of Mobile Ad hoc Networks (MANET). Nodes in VANET may be mobile or static. The mobile nodes are essentially the vehicles, which are equipped with an on-board unit (OBU). The static nodes include the Road Side Units (RSU), which are network elements installed as roadside infrastructures, that may receive and/or transmit messages to vehicles, such as emergency messages related with accidents, warnings or other safety information, or traffic related data such as congestion avoidance suggestions.
Within a VANET messages are exchanged spontaneously between the nodes that are members of the ad hoc network in that specific time frame. ETSI [2,3] defines the type of messages that are exchanged via the communication channels that are allocated at 5.9 GHz frequency. These types of messages are called Cooperative Awareness Messages (CAM) and are broadcast periodically containing information about the sender, such as position, speed, heading etc. Messages can be exchanged from Vehicle to Vehicle (V2V) or from a Vehicle to Infrastructure (V2I) such as RSU.
As V2V communications are based on beacon messages and have relatively short range, RSUs may act as relays of information gathered by vehicles. For example, in case of an incident causing traffic congestion, the affected vehicles may transfer information related to their current speed to the nearby RSUs. The RSUs will verify the information (e.g., check that similar data are confirmed from various vehicles) and then transmit congestion avoidance suggestions to other vehicles that are nearby.
Finally, another static entity within MANET is the Traffic Management Authority (TMA), which is considered as a trusted authority. The role of the TMA is to manage the network nodes, e.g., adding new nodes in the VANET. In addition, the TMA may assist privacy related functions, such as hiding the identity of vehicles acting as senders of messages. Actually in conditional privacy-preserving authentication schemes, it is required that no one except the TMA, will be able to link a message to a sender.
Although the advances in wireless communication technologies, such as 5G, enable VANETs to contribute on road safety and traffic management, they also increase the exposure of vehicles to security and privacy threats. Furthermore, due to the unique characteristics of a VANET such as mobility, scalability, limited resources and delay constraints, VANETs are vulnerable, not only to highly sophisticated attacks, but also to simpler attacks since traditional countermeasures may not be easy to apply. Therefore typical security controls should be implemented at first to support confidentiality, integrity, availability and non-repudiation. For example, vehicle authentication, and message confidentiality & integrity are necessary to prevent message spoofing or injection attacks [4,5].
In addition to security requirements, privacy requirements are also very important. Anonymity is the most important privacy requirement in VANET communications; the driver’s (or vehicle’s) identity should not be disclosed, not only because an attacker may impersonate honest users to avoid getting traced, but also because anonymity should be preserved in terms of privacy whenever a vehicle becomes an active node of a vehicular network. Data privacy includes driver-related data (e.g., the identity of the driver) and vehicle-related data (e.g., vehicle id, current location, itinerary, trip routes or any other kind of information that may lead to driver/vehicle profiling [5]. Besides anonymity, unlinkability and untraceability are additional privacy concerns. Although it is possible to hide the identity of a node using pseudonyms, if an adversary is able to link different messages with a single pseudonym, then it is relatively easy to trace the itinerary of a unique vehicle and ultimately reveal the actual identity, using other out-of-band information.
Researchers have examined a wide variety of attacks in the past that proved to have an effect both on the vehicle/driver privacy and on road safety [6]. Examples of such attacks are Denial of Service (DoS) [7], sybil attacks [8,9], wormhole attacks [10,11], illusion attacks [12] and purposeful attacks [13]. In the case of sybil attacks, malicious nodes may using fake identities in order to send false information multiple times, thus misleading RSUs on accepting this information as valid. In other cases, malicious nodes may attempt to abuse anonymity in order to mislead RSUs to accept information from forged nodes. Obviously vehicle privacy and VANET security are orthogonal issues, since privacy may be abused to violate VANET communication security and vise versa. Thus, achieving both security and privacy in VANET is still a challenging problem.
Contribution. We propose a distributed model that provides strong privacy and security guarantees for all nodes in V2I communications. Our main contributions involve:
- Trust distribution. To avoid strong trust assumptions for a single TMA authority, our model assumes two independent honest but curious authorities: a Credential Authority (CA) who is responsible for issuing/revoking credentials for vehicles; and a Signing Authority (SA) who is responsible to anonymously authenticating messages of authorized vehicles.
- Enhanced conditional privacy preserving authentication, since all the involved entities (CA, SA and the relevant RSUs) need to collaborate, to trace a message back to a vehicle.
- Vehicle unforgeability and unframeability. Even if all the entities (CA, SA and RSUs) collude, it is not possible to forge messages and/or frame a honest vehicle, by tracing a forged message back to an honest vehicle.
- Efficient Revocation. Revocation will be equivalent to the deletion of an encrypted credential, stored in an anonymous credential list. Revocation management is significantly more efficient in comparison with the use of certificate revocation lists.
Our scheme makes use of crypto building blocks like bilinear pairings, All-or-Nothing Public Key Encryption with Equality Tests (AoN-PKEET), Non-Interative Zero Knowledge Proofs (NIZKP) and partially blind signatures. However, the communication protocol does not require heavy crypto operations for the vehicles. To achieve unframeability and impersonation protection, each vehicle selects a random number upon registration, while for each V2I communication a zero knowledge proof of knowledge is used. The computational intensive operations like pairings are performed by the SA, which can be equipped with advanced computing capabilities. Security is formally analyzed and is based on the security of the underlying primitives used such as bilinear pairings, partially blind signatures and NIZKP.
Paper Structure. The remainder of this paper is organized as follows. In Section 2 we discuss the related work. In Section 3 we describe the proposed model. In Section 4 and Section 5 we thoroughly analyze the security and the efficiency of our model respectively. Finally, in Section 6 we conclude the paper and we discuss the advantages, limitations and possible future extensions.
2. Related Work
Security in vehicular networks was initially discussed in [5,14]. Since then, reducing the confidence level on trusted authorities is an open and challenging problem. Various schemes have been proposed in the literature, attempting to weaken the trust assumption for the authorities, either by distributing the trust among different authorities or by considering semi-trusted authorities. In various schemes vehicles are equipped with Event Data Recorders (EDR) that keep a copy of the communication. Unframeability is assured under the assumption that EDRs are trusted hardware devices. However, impersonating a vehicle is still in question, since VANET schemes offer conditional traceability and only misleading messages are the object of investigation.
In the literature, various group signature schemes have been proposed [15,16], to allow users to anonymously sign messages on behalf of a group. These schemes provide strong unframeability properties, even in the presence of corrupted authorities. Although group signatures have been widely used in VANETs for anonymous authentication (e.g., [17,18]), they require maintaining a Certificate Revocation List (CRL), which leads to long computation delay and consequently high message loss [19]. In addition, re-issuing of keys may be required, when users diverge from honest protocol execution.
Location privacy is the capability of preventing a third party from knowing the present and past location of the vehicle in the network [20]. Thus not only the current location is private (location point privacy protection) but also the trajectory of the vehicle is kept secret (trajectory privacy protection). In the following paragraphs we will briefly review existing privacy preserving communication protocols aiming at location privacy for vehicles, with an emphasis on their security level against vehicle impersonation and framing attacks.
A V2I communication protocol is presented in [21]. Trust is divided in two trusted authorities, the tracing authority (TRA) and the private key generator (PKG). However a collusion of TRA and PKG may impersonate a vehicle.
A scheme based on a semi-trusted authority is presented in [22]. Trust is divided in two authorities; the trusted data center (TDC) who is responsible for managing the real identities of the vehicles and is fully trusted and the semi-trusted management center (STA), who is responsible for managing RSUs and vehicles. To generate a partial key the current and previous location of the vehicle is revealed to the STA. All the IDs and the partial keys of the vehicles are known to the STA. Thus if corrupted, the STA may impersonate a vehicle, create new vehicle identifiers and sign messages on their behalf.
In the scheme of [23], a fully trusted authority TA assigns a real identity RID and a password PWD for each vehicle and pre-loads into its tamper-proof device. TA may impersonate any vehicle by simulating the function of the tamper-proof device.
In [24] a certificateless signature scheme for VANET is presented. The scheme is based on two authorities that are considered as fully trusted: the regional transport authority (RTA) and the key generation center (KGC). An takes as input the of the vehicle and generates a corresponding pseudonym . Although the network is divided in autonomous sub-networks, consecutive RSUs may reveal vehicle’s trajectory. In addition, if the authorities are compromised they may forge and/or frame any vehicle. A compromised KGC may impersonate any vehicle and request from any a pseudonym , while a compromised RTA may impersonate any vehicle and request a partial private key from KGC using vehicle’s .
In [25] a hierarchical privacy preserving pseudonymous authentication protocol for VANET is presented. The scheme is based on two honest-but-curious authorities, the certification authority CA and the revocation authority RA. Authentication of the vehicles is based on long and short term credentials. However the scheme does not address collusion between the authorities. In addition, a collusion of consecutive RSUs may reveal a vehicle’s trajectory since primary pseudonym is always revealed when requesting for short term credentials. Finally, a corrupted CA may refrain from deleting users’ VIDs (vehicle ID) and is able to impersonate any vehicle.
Various protocols in the literature are based on the assumption of a fully trusted authority (TA). In [26] KMC is a trust authority and is fully trusted by all the other entities. Each vehicle is equipped with a tamper proof device. Again the KMC is aware of all sensitive vehicle and driver information and may impersonate any vehicle.
In [27] trust is distributed among a fully trusted authority TA and the RSUs which are considered semi-trusted, lower level authorities. A corrupted TA may impersonate a vehicle and request temporary signing keys from an RSU. Location of the vehicle is periodically revealed to TA.
The ECPP protocol presented in [28] can efficiently deal with the growing revocation list, while achieving conditional traceability. Location of the vehicle is revealed to the RSU when requesting for a short time anonymous key. Obviously, the TA may impersonate any vehicle and acquire a short-time anonymous key. Vehicle impersonation by the TA is also possible in PACP [29], where the TA may impersonate any vehicle in the communication protocol between the OBU and an RSU. Consequently it may also sign messages on behalf of any vehicle. Location of the vehicle is revealed to RSU. SPECS [30] and b-SPECS+ [31] are also vulnerable to impersonation attacks by the TA.
In NECPPA [32] the location and the ID of a vehicle are revealed to the RSUs. In addition, the TA may again impersonate any vehicle in the OBU joining RSU phase. Similarly, in EAAP ([33]) and CL-CPPA [34] the TA may use the relevant information from the registration phase and impersonate any vehicle. In [35] a two-factor lightweight privacy preserving authentication scheme for VANET is presented. It relies on a fully trusted certificate authority CA that distributes trust in tamper-proof devices. The scheme depends on the correct use of tamper-proof devices, while the CA is aware of all sensitive vehicle and driver information and may impersonate any vehicle by simulating the function of the tamper-proof device.
Batch verification schemes like [36,37,38,39,40] either allow authorities to impersonate any vehicle or reveal the current location of the vehicle to the corresponding RSU. Impersonation and framing attacks by dishonest or compromised authorities against vehicles is also possible in the schemes presented in [41,42,43,44,45].
Various recent schemes are subject to impersonation and framing attacks during the registration phase. For example, in [46,47,48] the TA acquires all relevant information of vehicles during registration and can impersonate or frame a vehicle. In [47] it is also assumed that RSUs will not collude with each other. In [49] consecutive RSUs may reveal the driver’s path since a pseudo identity of a vehicle is known to the RSU. Although the real identity of the vehicle is not revealed during registration, impersonation attacks against vehicles are possible if the registration authority colludes with the RSUs.
Very few works, like [50,51] provide security from framing attacks against vehicles. However in both these works the TA may impersonate any vehicle and request pseudo ID from the KGC. Then by creating a pseudo key the TA may sign valid messages using the target vehicle’s credentials.
Paper positioning and comparison with the related work. To the best of our knowledge, the proposed scheme is the first protocol that may protect vehicles from both framing and impersonation attacks by misbehaving authorities, without requiring the maintenance and distribution of revocation lists. Even a collusion of corrupted authorities will not be able to impersonate a vehicle. Thus security from such attacks is assured even for corrupted or compromised authorities. In addition, the location of a vehicle is not revealed. Location privacy however still relies on the assumption of honest-but-curious authorities. In addition to the security and privacy properties, the protocol supports an efficient and privacy-preserving revocation mechanism. Instead of storing and managing large revocation lists, misbehaving drivers are removed by simply deleting their credential from a list of encrypted credentials. The driver is unable to further communicate with other nodes of the VANET. As no essential information is stored in the drivers’ OBUs, relevant attacks will reveal only the encrypted credentials. In the following paragraphs of this paper, a new privacy aware and bulletproof trust model is going to be introduced that aims to solve such issues as the ones described in the previous paragraph.
3. The Proposed Solution
As discussed above, our main design goal is to concurrently achieve security and privacy in V2I communications. In particular the proposed solution will support the following properties:
- Security. Only authenticated nodes (vehicles) will be allowed to communicate with RSUs (unforgeability). In addition, no adversary, even as strong as the collusion of all the authorities, should be able to impersonate a legitimate node (unframeability).
- Privacy. Vehicle anonymity must be assured, meaning that the identity of the vehicle should not be disclosed to RSUs or any external entity. In addition no single entity should not be able to trace the transmitted messages send to one or more RSUs with a particular sender (message-vehicle untraceability). Traceability should only be possible for a collusion of the CA, the SA and the relevant RSUs. Finally, an RSU (or any other external entity) should not be able to link together different messages coming from a single sender, even if the identity of the sender is not revealed (message unlinkability).
- Efficiency. The system must be efficient enough in terms of communication and computation overhead. The RSUs must be able to process multiple messages per second. For example, 100-200 messages/second are sufficient for RSUs to receive informed decisions about the current traffic conditions and unexpected events, even if some messages will be eventually lost in case of bursts. Vehicles must not require to be able to perform crypto operations that are not ‘mainstream’ in terms of computational cost. For example although public key crypto is feasible, bilinear pairings are not within the current state of the art.
- Privacy-preserving and efficient revocation. Finally revocation should be both efficient and privacy preserving. The system should not require CRLs for revocation, as they can become a system bottleneck. At the same time, revocation of a node must not disclose the identity of the node as this would violate the privacy of previous communications.
- Trust Assumptions
We are adopting a scenario involving two trusted authorities. Concerning the privacy properties, we assume that the Credential Authority CA and the Signing Authority SA are honest but curious. An interesting observation might be that although the CA is considered honest, its involvement is reduced in providing an appropriate AoN-PKEET scheme and inspect the behaviour of SA by checking the validity of the NIZKP provided. On the other hand, SA practically has the burden of correct protocol execution without knowing the real identity of the drivers. For the security properties (i.e., vehicle unforgeability and unframeabilty) we assume that all authorities may be compromised. Finally, to protect from outsiders we assume that all the communication is encrypted and integrity protected, using standard security mechanisms such as TLS.
3.1. Building Blocks
The proposed system uses the following primitives as building blocks:
- Bilinear map
Let and be groups of prime order p. A bilinear map is an efficiently computable map which satisfies the following conditions:
- Bilinear: For all and all that .
- Non-degenerate:
- All or Nothing Public Key Encryption with Equality Tests (AoN-PKEET)
AoN-PKEET schemes ([52,53,54,55]) allow entities to perform equality tests between cipher texts without knowing the secret key or the randomness used to encrypt. An additional trapdoor information is provided. While one can tell if two ciphertexts correspond to the same plaintext, no additional information is leaked. Thus, an AoN-PKEET Encryption scheme is an at least IND-CPA secure public key encryption scheme which is compatible with efficient zero-knowledge proofs. In our system we will employ the practical ElGamal based AoN-PKEET of [56], whose security relies on the (S)XDH assumption. Encryption is performed in . The private key is an element and the corresponding public key is . We will describe the AoN encryption () and the additional algorithms and . In both cases appropriate NIZKP can be provided. We refer to [56] for more details.
- On input the public encryption key, a random and a message m, it outputs the encryption .
- On input the secret key, it returns the trapdoor information for , allowing equality tests for ciphertexts.
- On input two ciphertexts and and the trapdoor , it outputs 1, if holds and 0 otherwise. If the output is 1 then .
- Non Interactive Zero Knowldge Proofs (NIZKP)
NIZKP are essentially protocols used by a prover, in order to prove knowledge of some information to a verifier, without revealing anything about the information itself. In our protocol, a custom NIZKP is used by vehicles to prove knowledge of the nonce chosen for credential generation, during registration. In addition, in the communication protocol, the NIZKP of [56] may be used, to force the SA to honest protocol execution. This however will imply an additional computational cost.
- Partially Blind Digital Signature Scheme
Partially blind signatures are a special type of blind signatures consisting of two messages: a message to be blinded and a non-blinded messages having a predefined structure. We utilize the Partially Blind Signature scheme of [57], which is based on Schnorr Signatures. Essentially, the message consists of two parts: . Here m is the actual message that will be blinded using a random b as a blinding factor: . The part is a cleartext, non-blinded message whose form is mutually predefined.
3.2. High Level Description
Let and represent the set of VANET nodes (vehicles) and infrastructures (RSUs) respectively. We assume two independent honest-but-curious authorities. Let CA denote a certification authority for managing the long term credentials for the vehicles and for providing an AoN-PKEET. Let SA denote a Signing Authority, whose main role is to authenticate (by blindly signing) messages of anonymously authenticated vehicles. The RSUs will only accept messages sent by vehicles, only if the messages have been previously authenticated by the SA. Vehicles may send/receive messages from RSUs within range (e.g., traffic information, emergency events etc). The proposed scheme will achieve the security, privacy and efficiency properties described above for V2I communication. The protocol consists of the following four phases/protocols.
Phase 1 (Set Up): During this phase the Credential Authority (CA) will publish all the system parameters, including the public encryption key of an AoN-PKEET scheme. In addition, the CA will securely transfer to the Signing Authority (SA) the trapdoor information , to allow the SA to perform equality tests on messages encrypted with the AoN-PKEET scheme.
It is important to note that although in our set up we assume a single CA, extending the CA to a threshold setting is straightforward. The underlying AoN-PKEET scheme can be easily extended to a threshold scenario, where the role of the CA is distributed to multiple entities and a majority of CAs is needed for decryption.
Phase 2 (Registration): Registration is an ongoing phase and allows new vehicles to dynamically join. For each new vehicle V generates a unique identified , is chosen by the CA and it is AoN-PKEET encrypted by V, using the AoN public key of the CA. The randomness used for the encryption is not revealed to the CA and will be later used by the vehicle, to provide a NIZKP of the assigned . The vehicle also receives from the CA signed proofs on the registration parameters. The CA will forward the encrypted credential to the SA, who will append this to a private list containing the encrypted credentials of all registered users.
The scheme allows SA to perform tests on encrypted messages and determine if they origin from the same original message. Thus SA can determine if a user is indeed a member of the authorized users of the protocol by blindly checking if the users’ encrypted credential belongs to a list of encrypted credentials of all authorized users.
Phase 3 (Secure communication): During the secure communication phase, a registered vehicle V will communicate with the SA in order to authorize the message to be send to the RSU via a partially blind signature.
As described in Section 3.1, messages in partially blind signatures schemes, an input message has two parts: the message to be blinded and an unblinded part with a predefined structure. In our scheme the structure of the unblinded part is defined as , consisting of the current time, concatenated with a randomness that is computed in a predefined way and will serve as the challenge of the NIZKP. Efficiency of the scheme is improved by applying methods presented in [58].
The vehicle will first provide to the SA a fresh AoN-PKEET encryption and an NIZKP of its credential. The SA will use the private list of the encrypted credentials, to check if a match is found with a freshly encrypted credential provided by V. In that case, the SA will blindly sign the message that V wants to send to the RSU.
Phase 4 (Revocation): When needed, the revocation phase will be executed, to anonymously revoke a counterfeit, misused or compromised credential. According to a predefined policy, revocation will be equivalent to the deletion of the encrypted credential stored in the private list maintained by the SA. Therefore, revocation in our scheme is very efficient, as it does not require maintaining and managing revocation lists. Detection of misbehaving vehicles is possible from the timestamps.
3.3. Detailed Protocol Description
We will use the notation shown in Table 1 to describe the cryptographic building blocks employed, which have been briefly described in Section 3.1.

Table 1.
Notation and cryptographic functions used.
3.3.1. Set Up
The protocol is described in Figure 1. On input a security parameter n, the Credential Authority CA generates the bilinear groups , the private/public AoN-PKEET encryption pair and the trapdoor information , as described in Section 3.1. The CA will securely transfer to the SA the trapdoor information. The SA cannot decrypt messages since it has no access to the secret key or the randomness used for message encryption. It may use the trapdoor information to check only for the equality of messages encrypted with the AoN-PKEET scheme of the CA.
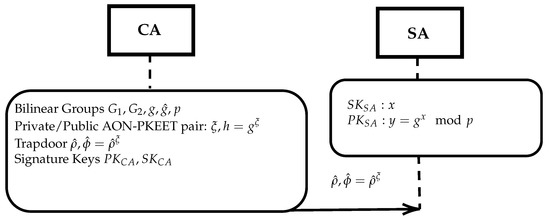
Figure 1.
Set Up.
Finally, each authority possesses a public/private key pair, say (resp. ) to be used for signing and/or communication encryption (In practice each authority may use different key pair for each operation).
For the digital signatures, an algorithm that supports a partially blinded setting can be used. We implement the scheme presented in [57]. Let and denote the private/public key pair of SA, using a typical ElGamal setting, where , for sufficiently long primes .
3.3.2. Registration
We assume that all the communications are encrypted and integrity protected, e.g., using the public keys of the relevant authorities CA and SA. New vehicles can be dynamically added as follows (see Figure 2). Initially V will sent a join-request to the CA. The CA will choose a unique identifier and send this to V along with the current registration time . Then V chooses , computes and also the signature . It will then forward to the CA.
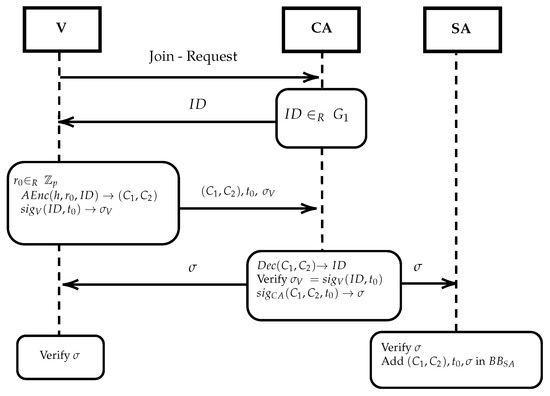
Figure 2.
The Registration protocol.
The CA decrypts to obtain and then verifies . On successful verification, the CA sends to V a signature . In addition, the CA forwards to the SA . Both V and SA will verify and the SA will also publish all information (encrypted credentials, time and signature) in a public bulletin board in increasing order wrt the encrypted credentials, i.e., , so that searching for an encrypted credential can be performed in time.
3.3.3. V2I Communication
Registered vehicles will first authenticate their (partially blinded) messages via the SA and then anonymously send the authenticated messages to RSUs as follows (see Figure 3). Again we assume that all communications are encrypted and integrity protected using the public keys of the SA and/or RSU respectively.
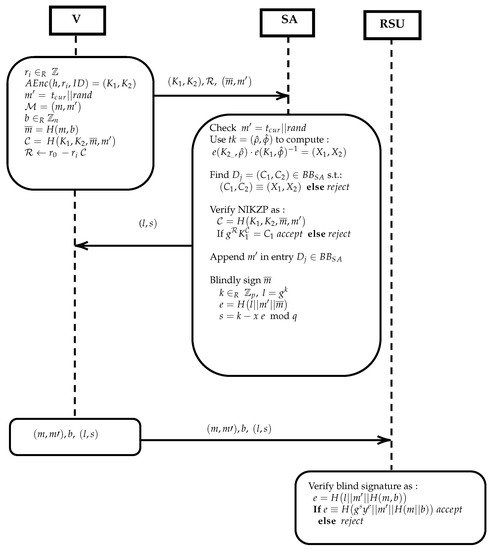
Figure 3.
Secure Communication.
Initially V prepares a fresh encryption of its identifier using a new random value as follows. It chooses and AoN-Encrypts the credential with : . Then V uses the partially blinded signature scheme [57] to blind the message , where m is the actual message to be send blinded. The non-blinded part is predefined as , where is the current time to ensure message freshness and is a randomness that ensures message uniqueness. Then V blinds m using randomness b as: .
In addition, V computes a Non Interactive Zero Knowledge Proof of knowledge for its identifier . This will essentially be a proof that V knows the randomness used to AoN-Encrypt at the registration phase, by using the randomness chosen for the new AoN-Encryption of [59]. V computes a challenge for the NIZKP using the fresh AoN Encryption, the blinded message , and the non-blinded message , i.e.,: .The response is computed as: . Finally, V forwards , and to the SA.
The SA will first check the freshness and uniqueness of the non-blinded message . Then, it uses the trapdoor to compute and to check if there is a match in the , i.e., some entry is identical to . Search is performed in time where N is the number of registered vehicles. This assures the SA that is a re-encryption of a valid credential. If the AoN-PKEET test fails, abort. Else let be the initial encryption of found in .
Now the SA will verify the NIZKP as follows: it computes the challenge (in the same way as V presumably did) and then the checks whether , (i.e., ). If the verification fails, it aborts. If the NIZKP verification succeeds then the SA is assured in zero knowledge that V knows the exponent used in (and therefore a valid ). In addition, notice that also binds the fresh AoN-Encryption of the credential with the blinded message to be signed. If the verification succeeds, then the SA updates by adding the time of request. The non-blinded part is appended in the appropriate line containing . This part of the table is kept private. Multiple requests from the same user can be detected on request. =
Finally, the SA will sign the blinded message , by selecting and computing , and . The signature is send to V. To verify the signature , send by V to an RSU, the receiver must compute again and check if .
V forwards to . The RSU will verify the signature and the current time included in to accept a message.
Notice that even if SA is corrupted it can gain no additional information if the RSU is honest. In addition, a corrupted RSU will learn nothing of a vehicle’s identity since it only checks the validity of SA’s signatures.
3.3.4. Revoking
Revocation is a necessary process of the protocol so as to administer misbehaviour of authorized vehicles. Supposing that a vehicle V is misbehaving, e.g., the message m is false or repeated multiple times etc. The RSU can forward the tuple to the SA which can locate the corresponding line of the misbehaving driver by using the timestamp . Then all information can be forwarded to the CA requesting for further instructions. According to a predefined policy actions can be taken. If necessary the CA can instruct the SA to simply delete the appropriate line from , thus removing V from the list of authorized users. No revocation list is needed for the expired, deleted credentials.
4. Security Analysis
We examine the security and privacy properties of the protocol, based on the relevant requirements set in Section 3. As already stated we assume that CA and SA are honest but curious entities. However, we will show that unframeability holds even if the authorities are corrupted. Adversaries are modeled by probabilistic polynomial time Turing machines (PPT). A negligible function , is a function such that for every positive integer c there exists an integer such that for all we have .
4.1. Unforgeability
Let and be the set up, the registration and the secure communication protocol respectively, as described in Section 3.3. Let be a PPT forging adversary, i.e., an external adversary who monitors the communications between all honest entities and whose goal is to forge the secure communication protocol . In other words, the goal of the adversary is to send a valid looking message to an RSU, without having first issued valid credentials by running , with the authorities that have already run . We assume that is having oracle access to and but has no access to the randomness used to encrypt or the credentials of the users. We will construct an algorithm that attacks the DLOG problem by using an adversary that produces valid .
We will prove that if can successfully forge with non-negligible probability, then can use as a subroutine to successfully attack the DLOG problem with non-negligible probability. We assume that is a challenger for the discrete logarithm problem. We denote as the oracle access of the adversary on a protocol .
- Setup. provides a challenge to , which forwards the challenge to . Then uses its oracle access to with input the challenge , to receive the corresponding output of the set up protocol, i.e., . Thus, an AON-PKEET is set up with and the private and public keys respectively.
- uses its oracle access to , to receive the encryptions of valid credentials . For the encryption of , outputs end sets re randomizing encryptions. Thus, is formed.
- Attack. requests oracle access to for polynomially many executions of . Then, the challenge is given to for forgery. The adversary chooses a message m and computes . It outputs a valid NIZKP such that .
- Guess. receives from the values and outputs its guess . If then wins.
Since, the probability to randomly select a valid equals to . We define the advantage of to break as: . We also define the advantage of to break DLOG as: . Then it holds that:
Since all values are known to , it holds that if an adversary can produce valid with non-negligible advantage, then it can be used by as a subroutine to break the DLOG problem also with non-negligible advantage.
4.2. Unframeability
For unframeability, we assume that, in addition to the previous case, the authorities CA and SA collide with the adversary. Thus the framing adversary , has access to all the secret keys of CA and SA and it is able to decrypt the credentials chosen by valid vehicles upon registration, but has not access to the randomness used by a vehicle during the registration protocol.
The proof is essentially the same as in the previous case, with the difference that now the adversary has full access, and not oracle access, to and during the Setup phase. In addition, in the Attack phase, since the adversary has the ability to decrypt and knows all the credentials, a target is selected (in the previous case a random was chosen for forgery). The adversary encrypts by a randomness r of its choice and computes for a chosen message m. It outputs a valid NIZKP such that .
4.3. Anonymity and Message-Vehicle Untraceability
Let be a PPT tracing adversary, whose goal is to trace the identity related with one or more messages send to one or more RSUs. We allow the adversary to collude with authorities in various scenarios. We denote as the set of authorities colluding with adversary in each scenario. Let be the communication protocol. We formalize the notion of message-vehicle untraceability by an experiment in which has access to an Oracle that on input a security parameter n (which defines the billinear group setting along with an AoN-PKEET) simulates executions of . has access to all public keys used for encrypting, to a history of simulated executions of that includes the transmitted messages. In addition has access to all secret keying material of all entities that belong to the set of all colluding entities. attempts to relate any of the posted messages m with the encryption of the identifier . We say that succeeds if it relates any message with the corresponding encrypted identifier . If succeeds then outputs 1 and zero otherwise.
Suppose there is some statistical noise and k messages are sent for signatures every second. The signature of these messages remain valid for a time frame say . Then is the probability to successfully bind message m submitted on a specific time t with the correct encrypted identifier . The message m remains valid until . Assuming that all messages signed by the SA are forwarded from the vehicles to RSUs at a random time within the valid time frame, then . In the worst case scenario only the k messages submitted on t are published within the time frame.
Definition 1.
provides message-vehicle untraceability if for all PPT adversary there exists a negligible function such that:
Claim 1.
provides vehicle anonymity and message-vehicle untraceability, provided that at least one of system entities ( or RSU) does not belong to the set.
Proof.
Recall that the proposed protocol consist of the following exchanges:
- (a)
- The vehicle requests from the CA an anonymous ID.
- (b)
- The CA sends to the vehicle the anonymous ID and the relevant proofs to the SA.
- (c)
- The vehicle requests a signature from the SA.
- (d)
- The SA responds to the vehicle.
- (e)
- The vehicle sends the blindly signed message to an RSU.
- (f)
- The RSU posts the transmitted message.
To win the game, the adversary should be able to relate the identity of the vehicle with the signature request send by the vehicle to the SA and finally with the blindly signed message send to an RSU . We will show that the adversary will always fail, provided that at least one of the entities is not corrupted.
□
Case 1.
The real identity ID assigned to a vehicle can not be revealed if the Corrupted and the encryption scheme used in is secure.
Proof.
Clearly if the CA is not corrupted the entities belonging to the Corrupted set cannot learn the real identity of the vehicle, since the communication is encrypted using the public key of the CA. □
Case 2.
Messages produced by a vehicle and are authenticated by the SA are untraceable by , provided that the Corrupted.
Proof.
Let . The vehicle computes and sends to the SA. The is revealed since . The adversary has knowledge of all pairs since RSUs collude. The SA will respond using the public key of the vehicle (The public key of the driver can be stored in or can be included in each request). The adversary will attempt to identify which of the is the encryption and relate with the . Assuming the public key cryptosystem of the user and the SA is IND-CPA secure this is not possible. Messages must be shuffled before exported. A linear computation of incoming messages results to linkability. Signatures on random strings can be inserted to further decrease probability. □
Case 3.
Blindly singed messages sent by a vehicle and received by an RSU are untraceable by , provided that the Corrupted.
Proof.
Straightforward since the encryption scheme of the RSUs is IND-CPA secure. □
Lemma 1.
By combining Cases 1, 2 and 3 is is easy to see that the adversary will fail, if at least one of the entities and RSU is honest.
4.4. Message Unlinkability
As defined in Section 3, message unlinkability requires that an RSU, (or any other authority) should not be able to link together different messages that come from a single sender (vehicle), even if the identity of the sender is not known.
Let denote an PPT adversary aiming to break the unlinkability property, who captures the capabilities of honest-but-curious authorities (CA and SA) and RSUs. monitors all the communications of the SA. Let be the communication protocol. We formalize the notion of unlinkability by an experiment in which has Oracle access to . On input a security parameter n (which defines the billinear group setting along with an AoN-PKEET) simulates executions of . has access to the public key used for encrypting and to the history of simulated executions of that includes the transmitted messages. is also allowed to have access to the list of the valid identifiers of all vehicles (although in real life adversary has no knowledge of the list of the identifiers!). attempts to relate any of the messages sent with a valid identified . We say that succeeds if it successfully relates a message with the correct identifier. If succeeds then outputs 1 and zero otherwise.
Definition 2.
provides message unlinkability if for all PPT adversary there exists a negligible function such that:
Where N is the number of different credentials. That is is no better than picking at random. We say that provides unlinkability.
Claim 2.
provides message unlinkability.
Proof.
We assume all communication is encrypted using the public key of SA. The ElGamal scheme, on which the AoN-PKEET is based, provides IND-CPA security under the DDH assumption. After polynomially many executions of the adversary will pick an identifier from the list of identifiers. By simulating the IND-CPA game it will attempt to guess if the next message sent to SA is the encryption of or not. Since ElGamal offers IND-CPA security this is possible only with negligible probability. Thus, there exists a negligible function such that:
□
Traceability:
Only CA can extract the real identity of the vehicle if necessary.
It is obvious that if all three entities collude, traceability is possible. A message is forwarded to RSU, then the encrypted credential can be related to the message sent. The timestamp can be forwarded from the RSU to the SA. This however is a desired protocol function that allows us to address the issue of misbehaving drivers, but only if all the entities collide (e.g., after a legal claim has been issued).
4.5. Scenario-Based Analysis
In addition to the formal security analysis presented above, we informally analyze the security of our protocol for various attack scenarios.
Man-in-The-Middle Attack. In this attack scenario, the adversary intercepts messages and performs data tampering in the communication between a vehicle and an RSU or the SA. However a MiTM attack will not succeed, since it requires from the adversary to forge the actual data sent be the vehicle, which are bind to the certificate of the vehicle via the use of a hash function.
Replay Attack. In this attack scenario, the adversary replays the previously obtained legitimate signature to the receiver. Such attacks will not succeed, since the use of time stamps ensures message freshness.
Identity Revealing Attack. The adversary attempts to reveal the real identity of a target vehicle. Then the adversary can illegally gather the personal data about the vehicle, which will threaten the privacy of the driver. That requires to win the IND-CPA property of the underlying cryptosystem.
Authority Abuse Attack. In this scenario the CA attempts to arbitrarily issue certificates to illegal vehicles or revoke certificates of legal vehicles. Such attacks can be thwarted by employing a threshold CA scenario. In addition, revoking a legal vehicle must be accompanied by a transaction proving misbehaviour. That is equivalent to framing a vehicle which was proven impossible.
In Table 2 we compare our scheme with the related work, in terms of their security and privacy characteristics. Our scheme is one of the few in the literature that provides unframeability and impersonation protection against corrupted authorities. At the same time it does not require maintaining revocation lists or expensive key-re-issuing after each revocation, while it maintains location privacy from honest but curious authorities.

Table 2.
Comparison with existing literature. (MVU = Message Vehicle Untraceability, MU = Message Unlinkability).
5. Efficiency Analysis
All tests were carried out on an Ubuntu 20.04 system with AMD Athlon 5350 APU with Radeon R3 2.05GHz and 8GB of memory. The implementation is based on the Python 3.8.5 programming language. For the simulation we used Simulink from Matlab.
5.1. Efficiency of the Cryptographic Primitives
For our simulation model, we first computed the required time for all the cryptographic primitives utilized in our protocol, summarized in Table 3. For all the experiments, the presented times are the average of 1000 executions.

Table 3.
Cost of the cryptographic primitives (in ms).
5.1.1. Blind Digital Signature Scheme
For our tests, we assumed messages of fixed length (50 characters). For the Partially Blind Digital Signature Scheme we used an implementation of the scheme presented in [57]. Blinding requires a computation of a random integer and a hash function (SHA-256 was used). Signing of a message requires 1 random integer generation, 1 exponentiation, 1 multiplication, 1 modular addition and 1 hash function execution. To verify the signature, 2 hash functions, 2 exponentiations and 1 modular multiplication is required. According to [58] with the help of precomputed values exponentiation can be approximated by 120 modular multiplications.
5.1.2. Encryption Schemes
The following times represent the encryption and decryption of a 50 characters random text with an IND-CPA secure version of RSA and ElGamal. We use RSA for the public key encryption schemes implemented by the SA, the drivers and the RSUs.
5.1.3. Billinear Pairing
Our scheme requires a pairing that can be efficiently computed. During the secure communication protocol we compute the image of a hash function on group elements of . Thus, group elements of are ideally required to have short representations. According to [64], type 3 pairings offer short representation. We implement a type 3 pairing of 256 order in 10.376 ms using the bplib python library. Again the average time of 1000 executions on random elements is used.
5.2. Signing Authority (SA) Performance
We examine the performance for the Signing Authority SA, since SA is involved in each message exchanged via the secure communication protocol. For the simulation Simulink from Matlab was used, were message requests follow a Poisson distribution. A FIFO queue is implemented. For each requested signature, the SA must repeat the following computations.
Computing requires 2 pairings (20.752 ms) , a multiplication ( ms) and computing the inverse of an element (0.151 ms). To verify , the SA must compute an exponent which according to [58] can be approximated with 120 multiplications ( ms), a hash function ( ms) and an exponent (9.036 ms). To verify one subtraction ( ms) to ensure message freshness and a hash function on some information relevant with time to acquire randomness . The overall computation cost for a single message equals to 31.618 ms, as summarized in Table 4.

Table 4.
Processing of incoming messages by the SA.
We assume that the server processes messages at a constant time of 32 ms per message. Since authorities are equipped with sufficient computational power we assume a scenario where 10 servers are available in parallel. In Table 5 we summarize the performance of the SA for 50 up to 250 incoming messages per second. AM stands for Average Messages per second, PDM stands for Poisson Distribution Mean, AQL stands for Average Queue Length, AW for Average Wait time in seconds and MP for the total amount of Messages Processed in 1 h. From our results it is shown that for the examined setup, the SA server can handle 200 messages per second with less than 1 sec delay. Figure 4a,b demonstrate the average wait time and the average queue length for the SA.

Table 5.
SA performance for 50 to 250 messages/s.
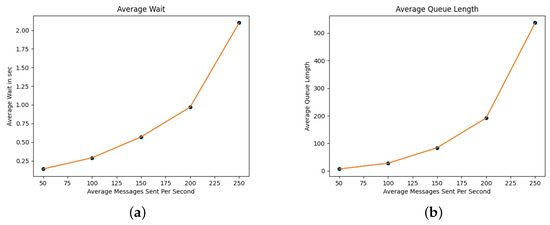
Figure 4.
SA performance. (a) SA: Average Wait time (in sec). (b) SA: Average Queue Length.
5.3. RSU Performance
Again we implement a FIFO waiting queue. For the RSUs we have implemented a single server scenario, were messages are processed at a constant time of 1.6 ms per message (0.615 ms for decrypting and 0.897 ms for signature verification). Again we use the same notation as in the SA analysis. As shown in Table 6 an RSU server can handle up to 400 messages per second with almost 1 s delay time. Figure 5a,b demonstrate the average wait time and the average queue length for the RSU.

Table 6.
RSU performance (100–500 messages/s).
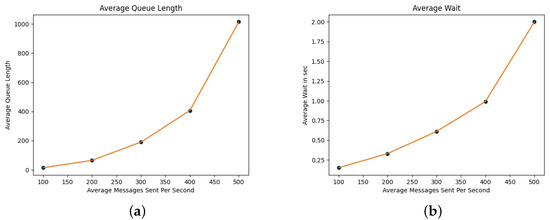
Figure 5.
RSU performance. (a) RSU Average Wait time (in sec). (b) RSU: Average Queue Length.
5.4. End-to-End Cost
In order to assess the overall (computation and communication) end-to-end cost of the secure communication protocol, we simulated 50 RSUs, each equipped with a single CPU, while the SA is equipped with 10 CPUs working in parallel. This is a reasonable assumption since the SA will be equipped in practice with much higher processing power than RSUs. We assume all messages are pending on infinite capacity FIFO queues before they are processed. For the end-to-end cost we add the average wait in queues (for the SA and the RSUs) and the computational cost for each processing step (composition of a message, signature etc)—see Figure 6a,b. We omit the the average waiting time of the RSU FIFO queues since it is zero in all cases. The computational cost of each vehicle is roughly the cost of encryption 1.05 ms.
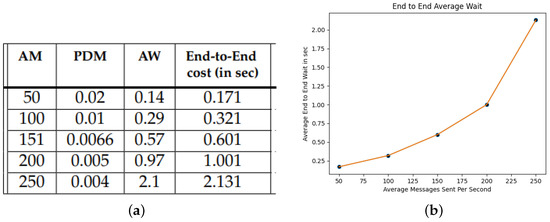
Figure 6.
Overall cost. (a) End-to-end cost for the secure communication protocol. (b) End-to-end average wait time 50–250 messages/s.
As expected, the processing costs related with the SA is the potential bottleneck of our scheme, which however can be easily avoided by assigning proportionally higher parallel processing power to the SA, with respect to the number of covered RSUs.
5.5. Qualitative Efficiency Comparison
In Table 7 we compare the efficiency of our scheme with other similar schemes in the literature. Similarly to [46] let, denote the time required for an exponentiation in , for a multiplication in , for scalar multiplication and point addition in the relevant elliptic curve, for a billinear pairing, for modular exponentiation, multiplication and addition respectively, for exponentiation in billinear pairing, for computing a hash function and for performing binary search.

Table 7.
Qualitative efficiency comparison with existing schemes.
From the vehicle side, our scheme requires 3 modular exponentiations, making it more efficient than [46,63] but less efficient than [60,61] which only require scalar multiplications. The scheme of [62] is the least efficient as it requires pairing functions for the vehicle. From the server side, our scheme requires two pairings and three exponentiations. Although lighter schemes without pairings exist like [60,61], the extra computation cost allows our scheme to provide enhanced security against corrupted colluding authorities and at the same time strong privacy against honest but curious entities. Given that the extra computation burden is at the server and not at the vehicle side, and based on the performance analysis presented above, the proposed scheme can be efficiently implemented in realistic scenarios.
6. Conclusions
We have proposed a secure, privacy-preserving and efficient V2I communication protocol, based on various crypto primitives such as AoN-PKEET, NIZKP and partially blind signatures. Our scheme provides strong security guarantees both from insiders and outsiders, even under the presence of untrusted authorities. Indeed, framing and impersonating trusted vehicles is not possible, even in the case where all authorities are compromised. In addition our scheme provides privacy against honest-but-curious authorities. We formally analyzed the security and privacy properties. Finally, through simulations we measure the efficiency of the proposed scheme for realistic scenarios.
In its current form, our scheme is suitable only for V2I communication. As future work, we intend explore possible extensions of the proposed scheme for V2V communication. We also intend to explore ways to minimize the required trust for the SA, possibly with the use of tamper proof devices.
Author Contributions
Conceptualization , P.K. (Panayiotis Kalogeropoulos) and D.P.; methodology, all; software, P.K. (Panayiotis Kalogeropoulos) and D.P.; validation, P.K.(Panayiotis Kalogeropoulos), and P.K. (Panayiotis Kotzanikolaou); formal analysis, P.K. (Panayiotis Kalogeropoulos) and P.K. (Panayiotis Kotzanikolaou); investigation, P.K. (Panayiotis Kalogeropoulos) and D.P.; resources, P.K. (Panayiotis Kalogeropoulos) and D.P.; data curation, P.K. (Panayiotis Kalogeropoulos) ; writing—original draft preparation, all; writing—review and editing, all; visualization, P.K. (Panayiotis Kalogeropoulos) and D.P; supervision, P.K. (Panayiotis Kotzanikolaou); project administration, P.K. (Panayiotis Kotzanikolaou); funding acquisition, P.K. (Panayiotis Kotzanikolaou). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Plossl, K.; Nowey, T.; Mletzko, C. Towards a security architecture for vehicular ad hoc networks. In Proceedings of the First International Conference on Availability, Reliability and Security (ARES’06), Vienna, Austria, 20–22 April 2006; p. 8. [Google Scholar]
- ITS-ETSI. European profile standard for the physical and medium access control layer of Intelligent Transport Systems operating in the 5 GHz frequency band. ETSI ES 2009, 202, 663. [Google Scholar]
- ITS-ETSI. Volume 102 637-2 V1.2.1 (2011-03), Intelligent Transport Systems (Its); Vehicular Communications; Basic Set of Applications; Part 2: Specification of Co-Operative Awareness Basic Service. ETSI Sophia Antipolis Cedex France. 2010, pp. 14–48. Available online: https://www.etsi.org/deliver/etsi_ts/102600_102699/10263702/01.02.01_60/ts_10263702v010201p.pdf (accessed on 3 May 2022).
- Parno, B.; Perrig, A. Challenges in securing vehicular networks. In Proceedings of the Workshop on Hot Topics in Networks (HotNets-IV), San Diego, CA, USA, 2–4 November 2005; pp. 1–6. [Google Scholar]
- Raya, M.; Papadimitratos, P.; Hubaux, J.P. Securing vehicular communications. IEEE Wirel. Commun. 2006, 13, 8–15. [Google Scholar] [CrossRef]
- Stellios, I.; Kotzanikolaou, P.; Psarakis, M.; Alcaraz, C.; Lopez, J. A survey of iot-enabled cyberattacks: Assessing attack paths to critical infrastructures and services. IEEE Commun. Surv. Tutor. 2018, 20, 3453–3495. [Google Scholar] [CrossRef]
- Raya, M.; Hubaux, J.P. The security of vehicular ad hoc networks. In Proceedings of the 3rd ACM Workshop on Security of ad hoc and Sensor Networks, Alexandria, VA, USA, 7 November 2005; pp. 11–21. [Google Scholar]
- Zhang, C.; Lin, X.; Lu, R.; Ho, P.H. RAISE: An efficient RSU-aided message authentication scheme in vehicular communication networks. In Proceedings of the 2008 IEEE International Conference on Communications, Beijing, China, 19–23 May 2008; pp. 1451–1457. [Google Scholar]
- Guette, G.; Ducourthial, B. On the Sybil attack detection in VANET. In Proceedings of the 2007 IEEE International Conference on Mobile Adhoc and Sensor Systems, Pisa, Italy, 8–11 October 2007; pp. 1–6. [Google Scholar]
- Hu, Y.C.; Perrig, A.; Johnson, D.B. Packet leashes: A defense against wormhole attacks in wireless networks. In Proceedings of the IEEE INFOCOM 2003. Twenty-Second Annual Joint Conference of the IEEE Computer and Communications Societies (IEEE Cat. No. 03CH37428), San Francisco, CA, USA, 30 March–3 April 2003; Volume 3, pp. 1976–1986. [Google Scholar]
- Safi, S.M.; Movaghar, A.; Mohammadizadeh, M. A novel approach for avoiding wormhole attacks in VANET. In Proceedings of the 2009 Second International Workshop on Computer Science and Engineering, Washington, DC, USA, 28–30 October 2009; Volume 2, pp. 160–165. [Google Scholar]
- Lo, N.W.; Tsai, H.C. Illusion attack on vanet applications-a message plausibility problem. In Proceedings of the 2007 IEEE Globecom Workshops, Washington, DC, USA, 26–30 November 2007; pp. 1–8. [Google Scholar]
- Manvi, S.; Kakkasageri, M.; Adiga, D. Message authentication in vehicular ad hoc networks: Ecdsa based approach. In Proceedings of the 2009 International Conference on Future Computer and Communication, Kuala Lumpur, Malaysia, 3–5 April 2009; pp. 16–20. [Google Scholar]
- Raya, M.; Hubaux, J.P. Securing vehicular ad hoc networks. J. Comput. Secur. 2007, 15, 39–68. [Google Scholar] [CrossRef]
- Camenisch, J.; Drijvers, M.; Lehmann, A.; Neven, G.; Towa, P. Short threshold dynamic group signatures. In Proceedings of the International Conference on Security and Cryptography for Networks, Amalfi, Italy, 14–16 September 2020; pp. 401–423. [Google Scholar]
- Gennaro, R.; Goldfeder, S.; Ithurburn, B. Fully Distributed Group Signatures. 2019. Available online: https://www.orbs.com/assets/docs/white-papers/Crypto_Group_signatures-2.pdf (accessed on 3 May 2022).
- Hao, Y.; Cheng, Y.; Ren, K. Distributed key management with protection against RSU compromise in group signature based VANETs. In Proceedings of the IEEE GLOBECOM 2008-2008 IEEE Global Telecommunications Conference, New Orleans, LA, USA, 30 November–4 December 2008; pp. 1–5. [Google Scholar]
- Jiang, Y.; Ge, S.; Shen, X. AAAS: An anonymous authentication scheme based on group signature in VANETs. IEEE Access 2020, 8, 98986–98998. [Google Scholar] [CrossRef]
- Zhu, X.; Jiang, S.; Wang, L.; Li, H.; Zhang, W.; Li, Z. Privacy-preserving authentication based on group signature for VANETs. In Proceedings of the 2013 IEEE Global Communications Conference (GLOBECOM), Atlanta, GA, USA, 9–13 December 2013; pp. 4609–4614. [Google Scholar]
- Dötzer, F. Privacy issues in vehicular ad hoc networks. In International Workshop on Privacy Enhancing Technologies; Springer: Berlin/Heidelberg, Germany, 2005; pp. 197–209. [Google Scholar]
- Ali, I.; Li, F. An efficient conditional privacy-preserving authentication scheme for Vehicle-To-Infrastructure communication in VANETs. Veh. Commun. 2020, 22, 100228. [Google Scholar] [CrossRef]
- Cui, J.; Wu, D.; Zhang, J.; Xu, Y.; Zhong, H. An efficient authentication scheme based on semi-trusted authority in VANETs. IEEE Trans. Veh. Technol. 2019, 68, 2972–2986. [Google Scholar] [CrossRef]
- He, D.; Zeadally, S.; Xu, B.; Huang, X. An efficient identity-based conditional privacy-preserving authentication scheme for vehicular ad hoc networks. IEEE Trans. Inf. Forensics Secur. 2015, 10, 2681–2691. [Google Scholar] [CrossRef]
- Kumar, P.; Kumari, S.; Sharma, V.; Li, X.; Sangaiah, A.K.; Islam, S.H. Secure CLS and CL-AS schemes designed for VANETs. J. Supercomput. 2019, 75, 3076–3098. [Google Scholar] [CrossRef]
- Rajput, U.; Abbas, F.; Oh, H. A hierarchical privacy preserving pseudonymous authentication protocol for VANET. IEEE Access 2016, 4, 7770–7784. [Google Scholar] [CrossRef]
- Wang, M.; Liu, D.; Zhu, L.; Xu, Y.; Wang, F. LESPP: Lightweight and efficient strong privacy preserving authentication scheme for secure VANET communication. Computing 2016, 98, 685–708. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, Q.; Domingo-Ferrer, J.; Qin, B.; Hu, C. Distributed aggregate privacy-preserving authentication in VANETs. IEEE Trans. Intell. Transp. Syst. 2016, 18, 516–526. [Google Scholar] [CrossRef]
- Lu, R.; Lin, X.; Zhu, H.; Ho, P.H.; Shen, X. ECPP: Efficient conditional privacy preservation protocol for secure vehicular communications. In Proceedings of the IEEE INFOCOM 2008-The 27th Conference on Computer Communications, Phoenix, AZ, USA, 13–18 April 2008; pp. 1229–1237. [Google Scholar]
- Huang, D.; Misra, S.; Verma, M.; Xue, G. PACP: An efficient pseudonymous authentication-based conditional privacy protocol for VANETs. IEEE Trans. Intell. Transp. Syst. 2011, 12, 736–746. [Google Scholar] [CrossRef]
- Chim, T.W.; Yiu, S.M.; Hui, L.C.; Li, V.O. SPECS: Secure and privacy enhancing communications schemes for VANETs. Ad Hoc Netw. 2011, 9, 189–203. [Google Scholar] [CrossRef]
- Horng, S.J.; Tzeng, S.F.; Pan, Y.; Fan, P.; Wang, X.; Li, T.; Khan, M.K. b-SPECS+: Batch verification for secure pseudonymous authentication in VANET. IEEE Trans. Inf. Forensics Secur. 2013, 8, 1860–1875. [Google Scholar] [CrossRef]
- Pournaghi, S.M.; Zahednejad, B.; Bayat, M.; Farjami, Y. NECPPA: A novel and efficient conditional privacy-preserving authentication scheme for VANET. Comput. Netw. 2018, 134, 78–92. [Google Scholar] [CrossRef]
- Azees, M.; Vijayakumar, P.; Deboarh, L.J. EAAP: Efficient anonymous authentication with conditional privacy-preserving scheme for vehicular ad hoc networks. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2467–2476. [Google Scholar] [CrossRef]
- Li, J.; Ji, Y.; Choo, K.K.R.; Hogrefe, D. Cl-CPPA: Certificate-less conditional privacy-preserving authentication protocol for the Internet of vehicles. IEEE Internet Things J. 2019, 6, 10332–10343. [Google Scholar] [CrossRef]
- Wang, F.; Xu, Y.; Zhang, H.; Zhang, Y.; Zhu, L. 2FLIP: A two-factor lightweight privacy-preserving authentication scheme for VANET. IEEE Trans. Veh. Technol. 2015, 65, 896–911. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, R.; Lin, X.; Ho, P.H.; Shen, X. An efficient identity-based batch verification scheme for vehicular sensor networks. In Proceedings of the IEEE INFOCOM 2008-The 27th Conference on Computer Communications, Phoenix, AZ, USA, 13–18 April 2008; pp. 246–250. [Google Scholar]
- Zhang, C.; Ho, P.H.; Tapolcai, J. On batch verification with group testing for vehicular communications. Wirel. Netw. 2011, 17, 1851–1865. [Google Scholar] [CrossRef]
- Jiang, S.; Zhu, X.; Wang, L. An efficient anonymous batch authentication scheme based on HMAC for VANETs. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2193–2204. [Google Scholar] [CrossRef]
- Sutrala, A.K.; Bagga, P.; Das, A.K.; Kumar, N.; Rodrigues, J.J.; Lorenz, P. On the design of conditional privacy preserving batch verification-based authentication scheme for Internet of vehicles deployment. IEEE Trans. Veh. Technol. 2020, 69, 5535–5548. [Google Scholar] [CrossRef]
- Shen, J.; Liu, D.; Chen, X.; Li, J.; Kumar, N.; Vijayakumar, P. Secure real-time traffic data aggregation with batch verification for vehicular cloud in VANETs. IEEE Trans. Veh. Technol. 2019, 69, 807–817. [Google Scholar] [CrossRef]
- Horng, S.J.; Tzeng, S.F.; Huang, P.H.; Wang, X.; Li, T.; Khan, M.K. An efficient certificateless aggregate signature with conditional privacy-preserving for vehicular sensor networks. Inf. Sci. 2015, 317, 48–66. [Google Scholar] [CrossRef]
- Mei, Q.; Xiong, H.; Chen, J.; Yang, M.; Kumari, S.; Khan, M.K. Efficient certificateless aggregate signature with conditional privacy preservation in IoV. IEEE Syst. J. 2020, 15, 245–256. [Google Scholar] [CrossRef]
- Wu, L.; Fan, J.; Xie, Y.; Wang, J.; Liu, Q. Efficient location-based conditional privacy-preserving authentication scheme for vehicle ad hoc networks. Int. J. Distrib. Sens. Netw. 2017, 13, 1550147717700899. [Google Scholar] [CrossRef]
- Cui, J.; Wei, L.; Zhang, J.; Xu, Y.; Zhong, H. An efficient message-authentication scheme based on edge computing for vehicular ad hoc networks. IEEE Trans. Intell. Transp. Syst. 2018, 20, 1621–1632. [Google Scholar] [CrossRef]
- Wei, L.; Cui, J.; Xu, Y.; Cheng, J.; Zhong, H. Secure and Lightweight Conditional Privacy-Preserving Authentication for Securing Traffic Emergency Messages in VANETs. IEEE Trans. Inf. Forensics Secur. 2020, 16, 1681–1695. [Google Scholar] [CrossRef]
- Sang, G.; Chen, J.; Liu, Y.; Wu, H.; Zhou, Y.; Jiang, S. PACM: Privacy-Preserving Authentication Scheme with On-Chain Certificate Management for VANETs. IEEE Trans. Netw. Serv. Manag. 2022, 1. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, L.; Xu, C.; Sharif, K.; Ding, K.; Liu, X.; Du, X.; Guizani, M. TPPR: A Trust-Based and Privacy-Preserving Platoon Recommendation Scheme in VANET. IEEE Trans. Serv. Comput. 2022, 15, 806–818. [Google Scholar] [CrossRef]
- Wang, S.; Chen, X.; Tong, F.; Zhang, Y. RSU-Aided Authentication for VANET Based on Consortium Blockchain. In Proceedings of the 2021 IEEE 27th International Conference on Parallel and Distributed Systems (ICPADS), Beijing, China, 14–16 December 2021; pp. 324–331. [Google Scholar]
- Jagriti, J.; Lobiyal, D.K. An Efficient and Anonymous Authentication Key Agreement Protocol for Smart Transportation System. In Proceedings of the 2021 International Conference on Computational Performance Evaluation (ComPE), Online, 1–3 December 2021; pp. 190–194. [Google Scholar]
- Liu, Y.; Wang, L.; Chen, H.H. Message authentication using proxy vehicles in vehicular ad hoc networks. IEEE Trans. Veh. Technol. 2014, 64, 3697–3710. [Google Scholar] [CrossRef]
- Ming, Y.; Cheng, H. Efficient certificateless conditional privacy-preserving authentication scheme in VANETs. Mob. Inf. Syst. 2019, 2019, 7593138. [Google Scholar] [CrossRef]
- Yang, G.; Tan, C.H.; Huang, Q.; Wong, D.S. Probabilistic Public Key Encryption with Equality Test. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; pp. 119–131. [Google Scholar]
- Tang, Q. Public key encryption schemes supporting equality test with authorisation of different granularity. Int. J. Appl. Cryptogr. 2012, 2, 304–321. [Google Scholar] [CrossRef]
- Ma, S.; Huang, Q.; Zhang, M.; Yang, B. Efficient public key encryption with equality test supporting flexible authorization. IEEE Trans. Inf. Forensics Secur. 2014, 10, 458–470. [Google Scholar] [CrossRef]
- Slamanig, D.; Spreitzer, R.; Unterluggauer, T. Adding controllable linkability to pairing-based group signatures for free. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2014; pp. 388–400. [Google Scholar]
- Blazy, O.; Derler, D.; Slamanig, D.; Spreitzer, R. Non-interactive plaintext (in-) equality proofs and group signatures with verifiable controllable linkability. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2016; pp. 127–143. [Google Scholar]
- Liu, J.; Sun, R.; Kou, W. Fair e-payment protocol based on simple partially blind signature scheme. Wuhan Univ. J. Nat. Sci. 2007, 12, 181–184. [Google Scholar] [CrossRef]
- Möller, B. Algorithms for multi-exponentiation. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2001; pp. 165–180. [Google Scholar]
- Hao, F. Schnorr non-interactive zero-knowledge proof. RFC 2017, 8235, 1–13. [Google Scholar]
- Lu, Z.; Wang, Q.; Qu, G.; Zhang, H.; Liu, Z. A blockchain-based privacy-preserving authentication scheme for vanets. IEEE Trans. Very Large Scale Integr. Syst. 2019, 27, 2792–2801. [Google Scholar] [CrossRef]
- Wasef, A.; Shen, X. EMAP: Expedite Message Authentication Protocol for Vehicular Ad Hoc Networks. IEEE Trans. Mob. Comput. 2013, 12, 78–89. [Google Scholar] [CrossRef]
- Sun, Y.; Feng, Z.; Hu, Q.; Su, J. An efficient distributed key management scheme for group-signature based anonymous authentication in VANET. Secur. Commun. Netw. 2012, 5, 79–86. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Jiang, Q.; Obaidat, M.S.; Vijayakumar, P. Bua: A blockchain-based unlinkable authentication in vanets. In Proceedings of the ICC 2020-2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar]
- Galbraith, S.D.; Paterson, K.G.; Smart, N.P. Pairings for cryptographers. Discret. Appl. Math. 2008, 156, 3113–3121. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).