Modelling of Bottom Shear Stresses in Scoured Hole Formed by Nappe Flow During Levee Overtopping
Abstract
1. Introduction
- the existence of a potential core with a constant jet velocity;
- the scour depth is calculated based on the jet velocity, even when the scour depth has sufficiently enlarged to exceed the potential core length.
2. Materials and Methods
2.1. Flow Visualization with Particle Image Velocimetry
2.2. Three-Dimensional Numerical Analysis Using OpenFOAM
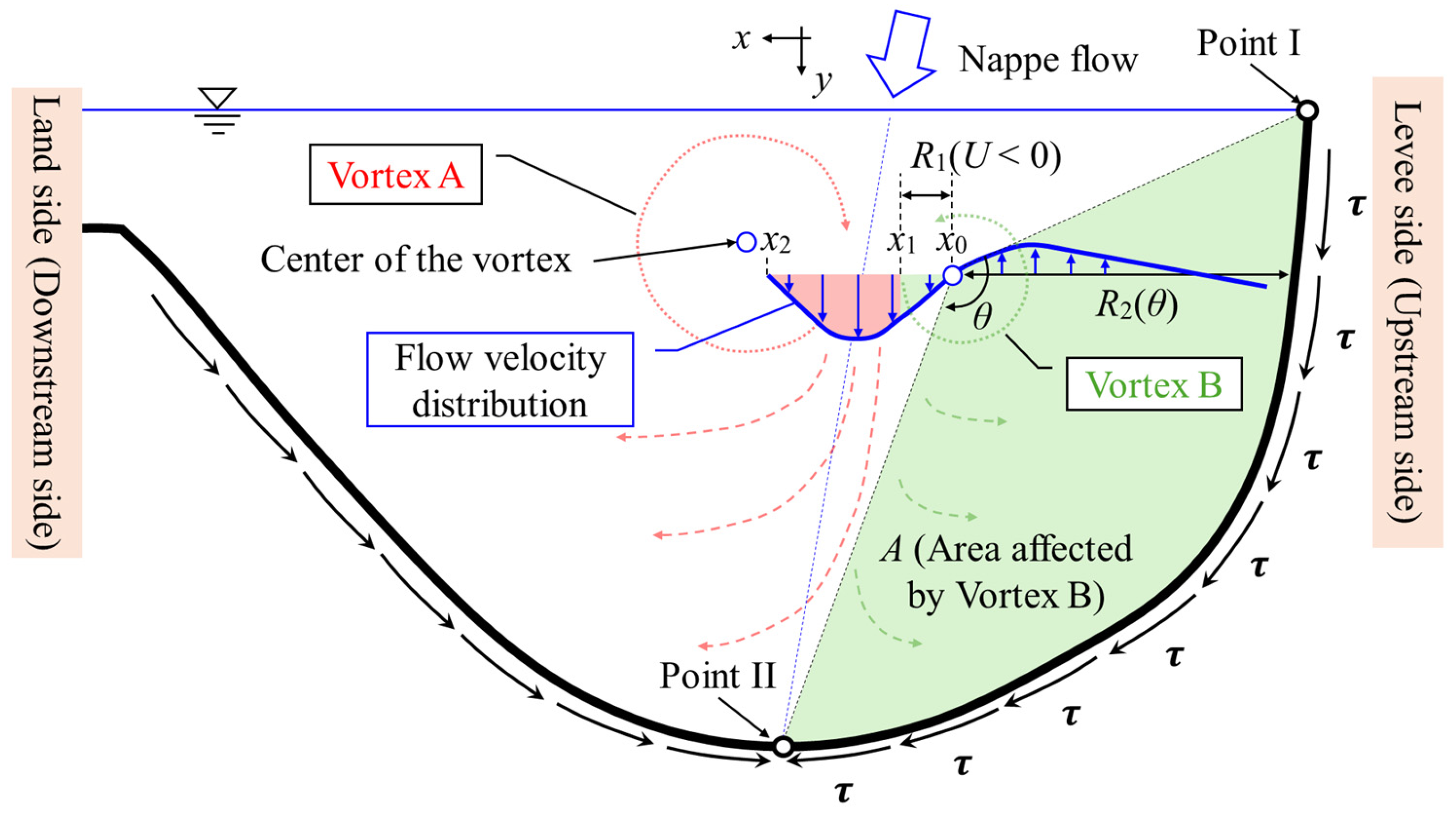
2.3. Modeling of Bottom Shear Stresses in Scour Hole
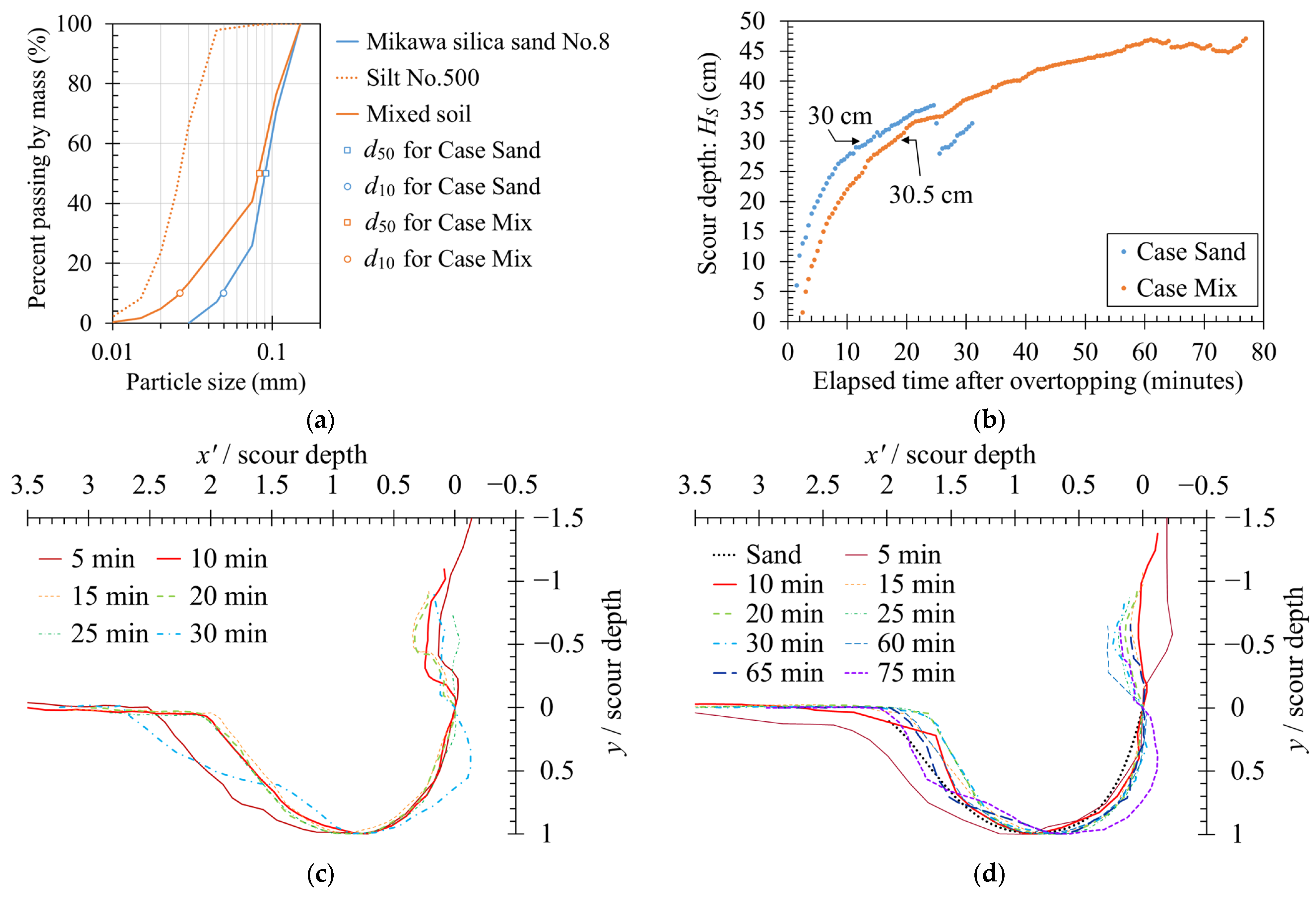
2.4. Previous Experiments on Levee Erosion by Nappe Flow to Compare with the Proposed Method
3. Results
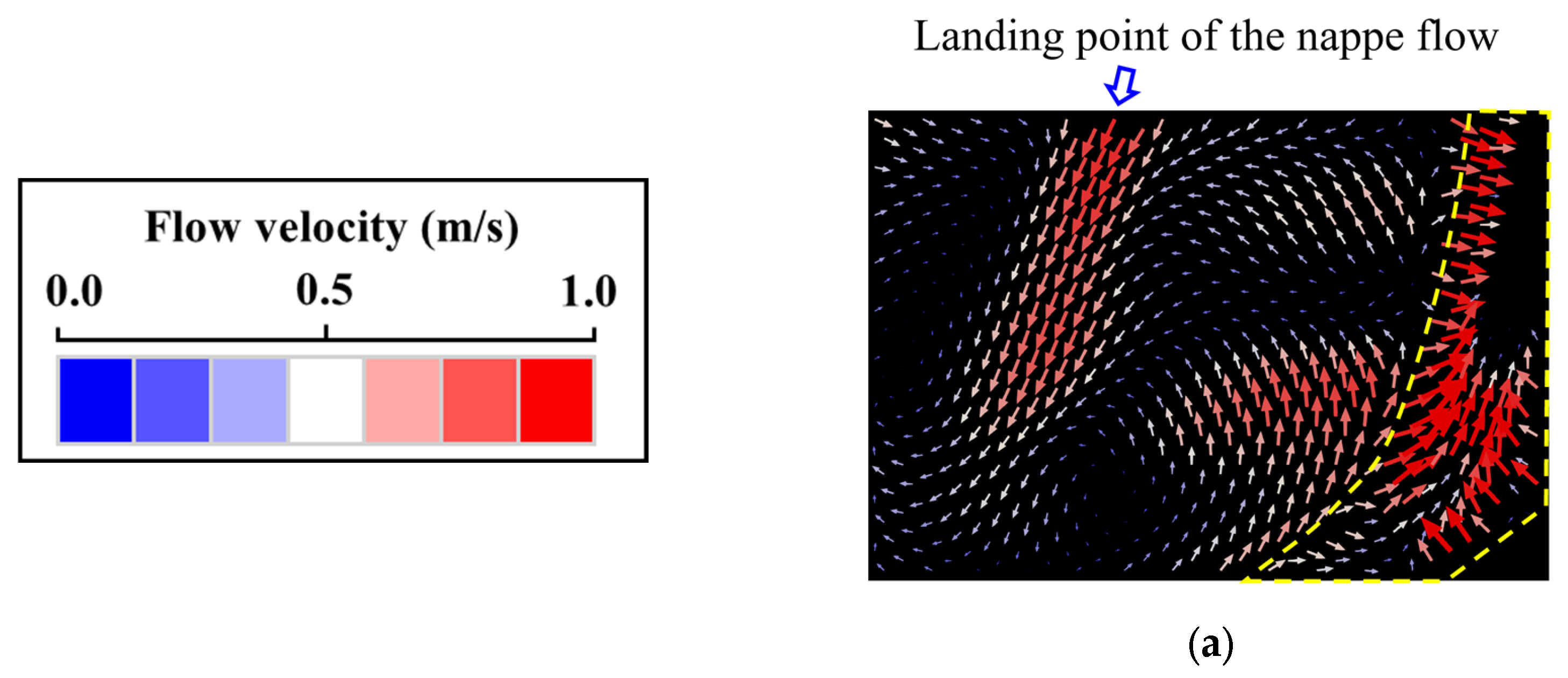
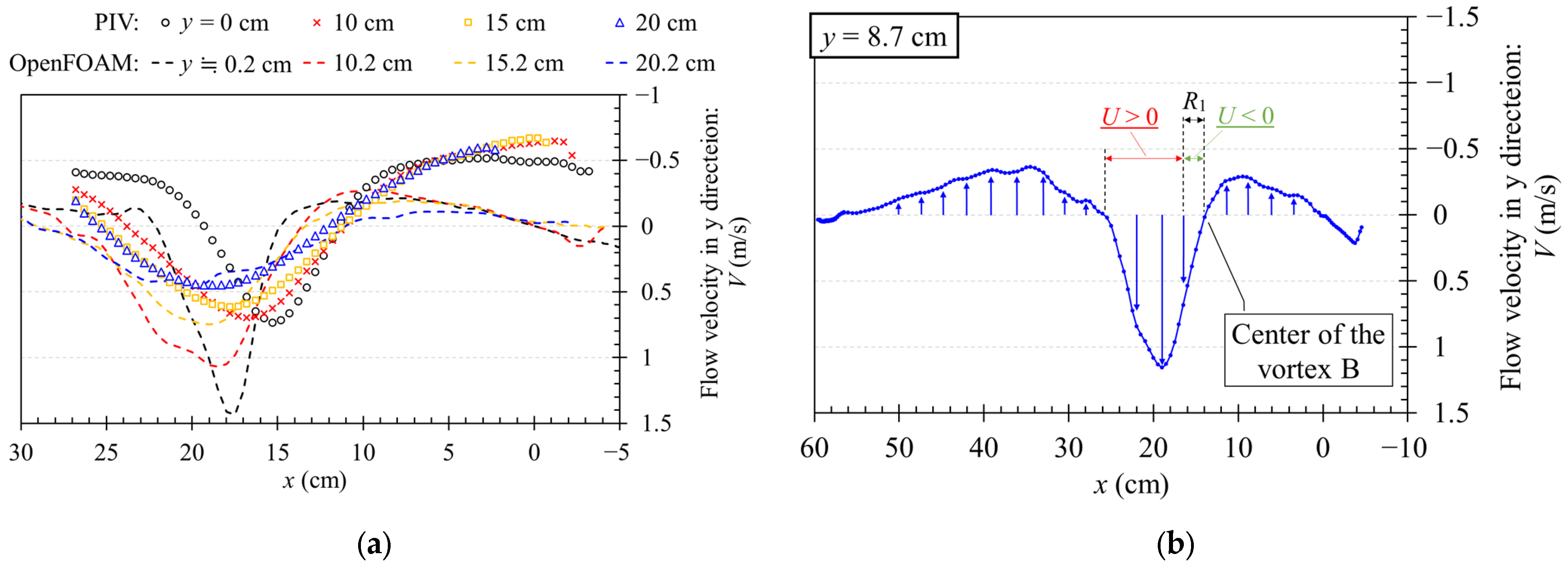
3.1. Results of PIV Experiments
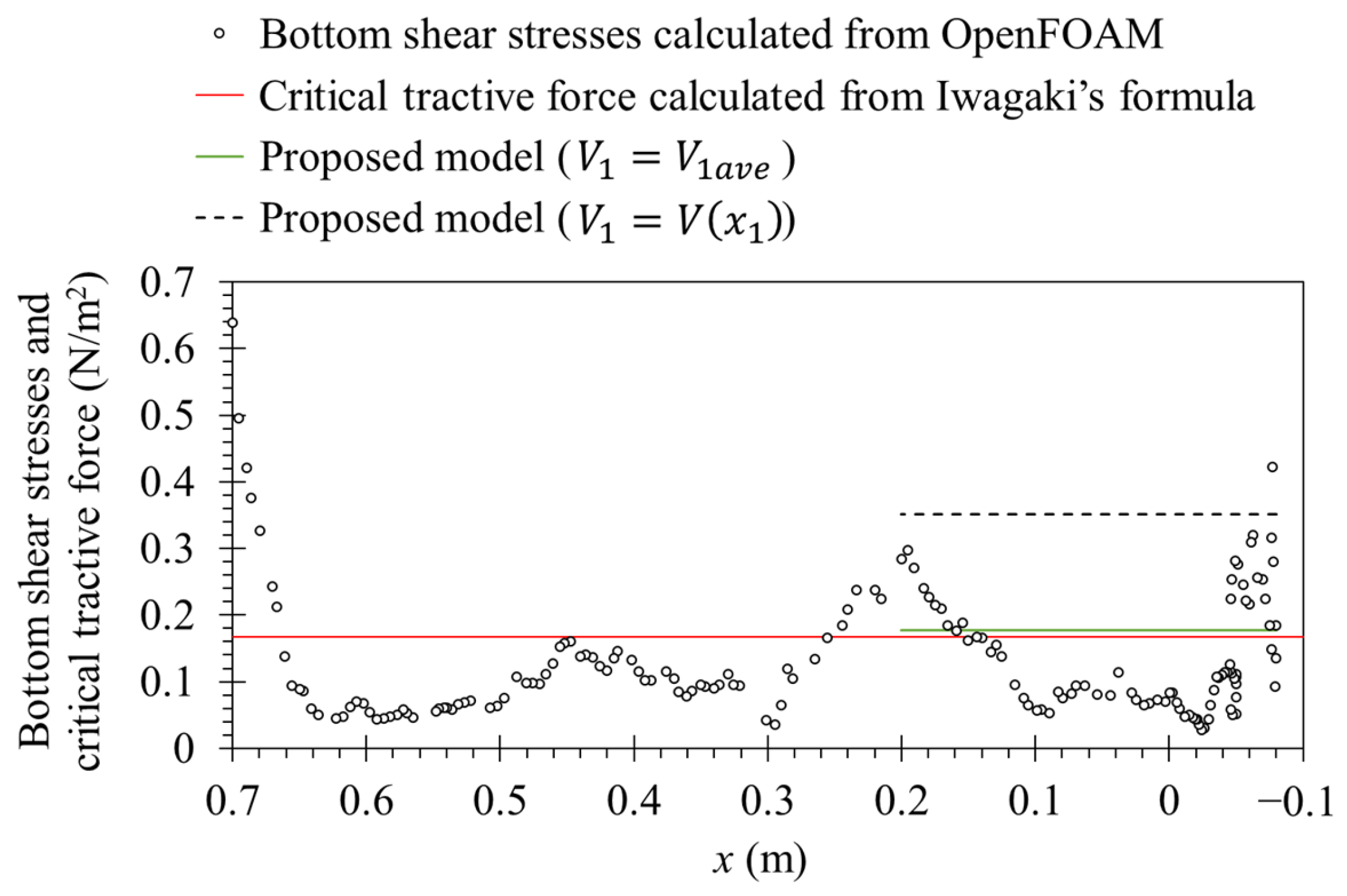
3.2. Results of Three-Dimensional Numerical Analysis with OpenFOAM
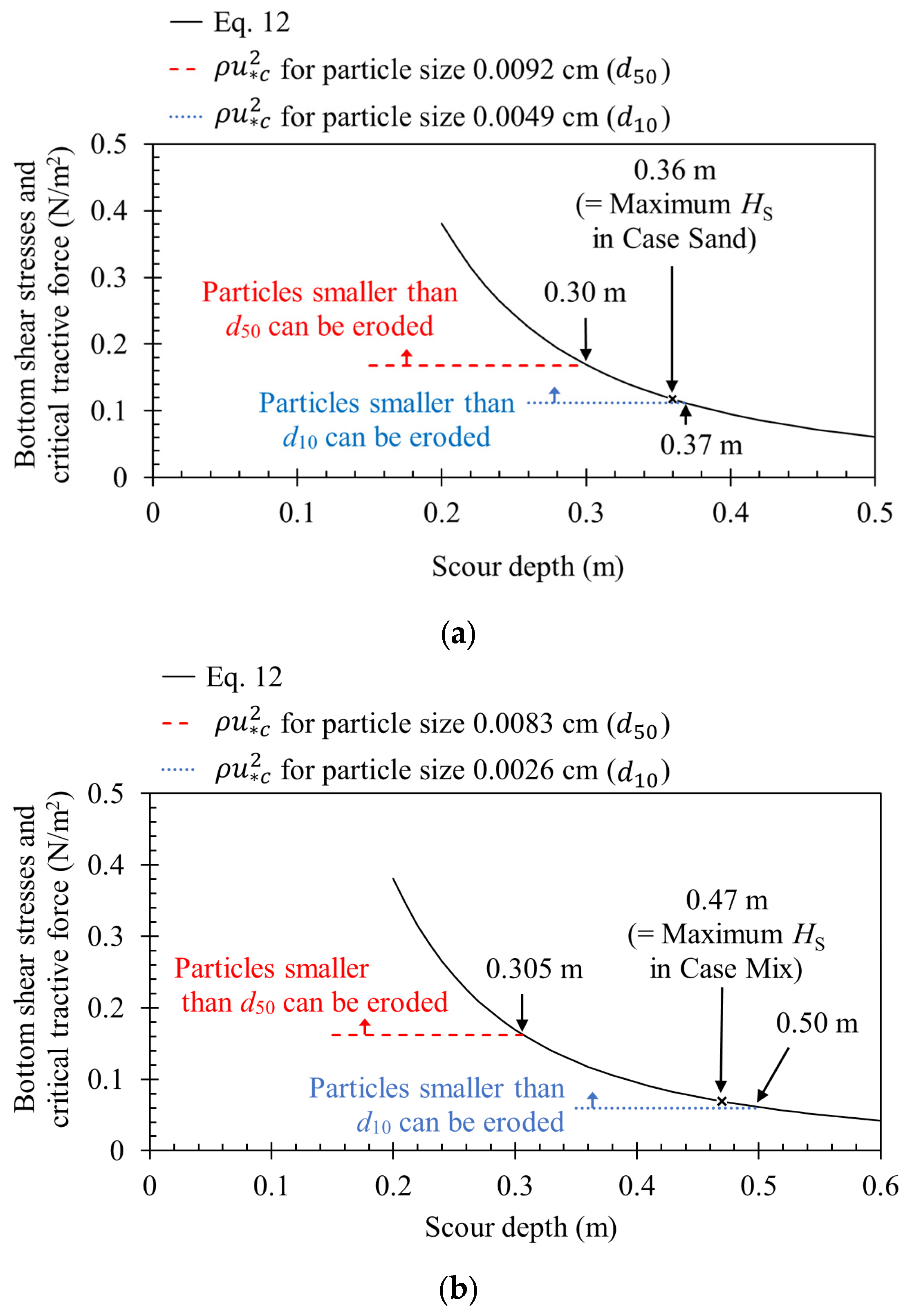
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lavell, A.; Oppenheimer, M.; Diop, C.; Hess, J.; Lempert, R.; Li, J.; Myeong, S. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; Field, C.B., Ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Kundzewicz, Z.W.; Kanae, S.; Seneviratne, S.I.; Handmer, J.; Nicholls, N.; Peduzzi, P.; Mechler, R.; Bouwer, L.M.; Arnell, N.; Mach, K. Flood risk and climate change: Global and regional perspectives. Hydrol. Sci. J. 2014, 59, 1–28. [Google Scholar] [CrossRef]
- Bogárdi, I. Determination of the Degree of Protection Offered by Flood Control Systems on the Basis of Distribution Functions. In Proceedings of the Mathematical Models in Hydrology: Proceedings of the Warsaw Symposium, 1, Illus, Warsaw, Poland, 25–30 March 1974; pp. 246–252. [Google Scholar]
- Chinnarasri, C.; Tingsanchali, T.; Weesakul, S.; Wongwises, S. Flow patterns and damage of dike overtopping. Int. J. Sediment. Res. 2003, 18, 301–309. [Google Scholar]
- ASCE/EWRI Task Committee on Dam/Levee Breaching (ASCE/EWRI-TC). Earthen embankment breaching. J. Hydraul. Eng. 2011, 137, 1549–1564. [Google Scholar] [CrossRef]
- Takahashi, H.; Morikawa, Y.; Mori, N.; Yasuda, T. Collapse of concrete-covered levee under composite effect of overflow and seepage. Soils Found. 2019, 59, 1787–1799. [Google Scholar] [CrossRef]
- Van, M.; Rosenbrand, E.; Tourment, R.; Smith, P.; Zwanenburg, C. Failure Paths for Levees. International Society of Soil Mechanics and Geotechnical Engineering (ISSMGE)—Technical Com-mittee TC201 ‘Geotechnical Aspects of Dikes and Levees’. 2022. Available online: https://issmge.org/files/reports/TC201-Failure-paths-for-levees.pdf (accessed on 20 June 2024).
- Visser, P.J. Breach Growth in Sand-Dikes. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1998. [Google Scholar]
- Zhu, Y.H. Breach Growth in Clay-Dikes. Ph.D. Thesis, University of Technology, Delft, The Netherlands, 2006. [Google Scholar]
- Kanto Regional Development Bureau, Ministry of Land, Infrastructure, Transport and Tourism (KMLIT). The 2nd Kinu River Levee Investigation Committee Document. 2015. Available online: https://www.ktr.mlit.go.jp/ktr_content/content/000633270.pdf (accessed on 31 October 2024). (In Japanese).
- Nakamura, Y.; Miyakawa, T.; Satoh, M. The role of Typhoon Kilo (T1517) in the Kanto-Tohoku heavy rainfall event in Japan in September 2015. J. Meteoro. Soc. Jpn. 2020, 98, 915–926. [Google Scholar] [CrossRef]
- Yasuda, S.; Shimizu, Y.; Deguchi, K. Investigation of the mechanism of the 2015 failure of a dike on Kinu River. Soils Found. 2016, 56, 581–592. [Google Scholar] [CrossRef]
- Zhu, Y.; Visser, P.J.; Vrijling, J.K.; Wang, G. Experimental investigation on breaching of embankments. Sci. China Technol. Sci. 2011, 54, 148–155. [Google Scholar] [CrossRef]
- Ministry of Land, Infrastructure, Transport and Tourism (MLIT). Study on Resilient River Levees Against Overtopping. 2022. Available online: https://www.mlit.go.jp/river/shinngikai_blog/teibou_kentoukai/dai01kai/pdf/kentou.pdf (accessed on 31 October 2024). (In Japanese).
- Pan, Y.; Li, L.; Amini, F.; Kuang, C. Influence of three levee-strengthening systems on overtopping hydraulic parameters and hydraulic equivalency analysis between steady and intermittent overtopping. J. Waterw. Port Coast. Ocean Eng. 2013, 139, 256–266. [Google Scholar] [CrossRef]
- Chanson, H. Embankment overtopping protection systems. Acta Geotech. 2015, 10, 305–318. [Google Scholar] [CrossRef]
- Wahl, T.L. Embankment overtopping protection by riprap considering interstitial flow. In Proceedings of the 2nd International Seminar on Dam Protection against Overtopping, Protections 2016, Ft. Collins, CO, USA, 7–9 September 2016; ISBN 978-1-1889143-27-9. [Google Scholar]
- Onose, R.; Tanaka, N.; Igarashi, Y.; Kou, K. Study on new methods for back slope protection of an embankment considering the overflow erosion and soil-block destruction mechanism. Adv. River Eng. 2022, 28, 91–96. (In Japanese) [Google Scholar]
- Shinohara, A.; Nihei, Y.; Kurakami, Y.; Suzuki, K. Prevention of levee crest overtopping through reinforcement technology. In Proceedings of the 21st Congress of International Association for Hydro-Environment Engineering and Research-Asia Pacific Division: Multi-Perspective Water for Sustainable Development, IAHR-APD 2018, Yogyakarta, Indonesia, 2–5 September 2018; Department of Civil and Environmental Engineering, Faculty of Engineering, Universitas Gadjah Mada: Yogyakarta, Indonesia, 2018; pp. 217–223. [Google Scholar]
- Kainose, A.; Tanaka, N.; Igarashi, Y.; Onose, R.; Kou, K. Evaluation of the effectiveness of strengthening paved embankment top against erosion due to nappe flow through experiments and numerical model analysis. J. Jpn. Soc. Civ. Eng. Ser. B1 2021, 77, I_361–I_366, (In Japanese with English Abstract). [Google Scholar] [CrossRef] [PubMed]
- Abbas, F.M.; Tanaka, N. Utilization of geogrid and water cushion to reduce the impact of nappe flow and scouring on the downstream side of a levee. Fluids 2022, 7, 299. [Google Scholar] [CrossRef]
- Ali, L.; Sekine, K.; Tanaka, N. Evaluating the effectiveness of seepage countermeasures and retrofitting strategies for mitigating nappe flow-induced reverse flow and erosion for overtopping flow from a levee. Geosciences 2024, 14, 233. [Google Scholar] [CrossRef]
- Singh, V.P.; Scarlatos, P.D. Analysis of gradual earth-dam failure. J. Hydraul. Eng. 1988, 114, 21–42. [Google Scholar] [CrossRef]
- Macchione, F. Model for predicting floods due to earthen dam breaching. I: Formulation and evaluation. J. Hydraul. Eng. 2008, 134, 1688–1696. [Google Scholar] [CrossRef]
- Zhu, Y.H.; Visser, P.J.; Vrijling, J.K. A model for headcut erosion during embankment breaching. In Proceedings of the 4th IAHR Symposium on River, Coastal and Estuarine Morphodynamics, Urbana, IL, USA, 4–7 October 2005; pp. 1183–1190. [Google Scholar]
- D’Eliso, C. Breaching of Sea Dikes Initiated by Wave Overtopping: A Tiered and Modular Modelling Approach. Ph.D. Thesis, University of Braunschweig, Braunschweig, Germany, University of Florence, Florence, Italy, 2007. [Google Scholar]
- Stein, O.R.; Julien, P.Y.; Alonso, C.V. Mechanics of jet scour downstream of a headcut. J. Hydraul. Res. 1993, 31, 723–738. [Google Scholar] [CrossRef]
- Palermo, M.; Pagliara, S.; Bombardelli, F.A. Theoretical approach for shear-stress estimation at 2D equilibrium scour holes in granular material due to subvertical plunging jets. J. Hydraul. Eng. 2020, 146, 04020009. [Google Scholar] [CrossRef]
- Dissanayaka, K.D.C.R.; Tanaka, N.; Hasan, M.K. Numerical simulation of flow over a coastal embankment and validation of the nappe flow impinging jet. Model. Earth Syst. Environ. 2024, 10, 777–798. [Google Scholar] [CrossRef]
- Onose, R.; Tanaka, N.; Igarashi, Y. Study on grid material of an embankment considering the overflow erosion and soil-block destruction mechanism. In Proceedings of the10th River Embankment Technology Symposium Proceedings, Tokyo, Japan, 14 December 2022; pp. 29–32. (In Japanese). [Google Scholar]
- Iwagaki, Y. Fundamental study on critical tractive force (I) Hydrodynamical Study on Critical Tractive Force. Trans. J. Jpn. Soc. Civ. Eng. 1956, 41, 1–21, (In Japanese with English Abstract). [Google Scholar]
- Afreen, S.; Yagisawa, J.; Binh, V.D.; Tanaka, N. Investigation of scour pattern downstream of levee toe due to overtopping flow. J. Jpn. Soc. Civ. Eng. Ser. B1 2015, 71, I_175–I_180. [Google Scholar] [CrossRef] [PubMed]




| Stein et al. [27] | Palermo et al. [28] | Our Study | |
|---|---|---|---|
| Method of calculation for the bed shear stress in the scour hole: τ | Using the friction coefficient (Cf) and the impinging flow velocity around the bottom of scour hole (UB). UB is calculated taking into account diffusion within the scour hole. where, Cd is diffusion constant of a jet, U0 is jet velocity at the water surface, TNf is jet thickness at the water surface, J is the scour hole depth (J) along the jet centerline. | Based on the angular-momentum conservation law to rigid bodies. Different point 1: The study focused on a main large vortex (vortex A). is a torque of the moment flux of the jet . R is a moment radius. Different point 2: The study assume the vortex is a cylinder shape. Therefore, same moment radius with the torque of jet was used to calculate a torque of the shear force is the area that shear stress acts on. Different point 3: The velocity before water landing is used as V. | Based on the angular-momentum conservation law to rigid bodies as shown in Equation (3). Different point 1: Our study focused on a secondary levee side vortex (vortex B). Therefore, a coefficient k1 was introduced as shown in Equation (4). Different point 2: The moment radius used to calculate the shear force torque was instead of because vortex B was not cylindrical in shape. Therefore, Equations (5), (8), and (9) are derived. Different point 3: Both the mean velocity (, Equation (7)) and the maximum velocity were considered for . |
| Calculated value of τ (N/m2) | 5.0 | 156.2 | 0.35 (when ) 0.18 (when ) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Igarashi, Y.; Tanaka, N. Modelling of Bottom Shear Stresses in Scoured Hole Formed by Nappe Flow During Levee Overtopping. GeoHazards 2025, 6, 11. https://doi.org/10.3390/geohazards6010011
Igarashi Y, Tanaka N. Modelling of Bottom Shear Stresses in Scoured Hole Formed by Nappe Flow During Levee Overtopping. GeoHazards. 2025; 6(1):11. https://doi.org/10.3390/geohazards6010011
Chicago/Turabian StyleIgarashi, Yoshiya, and Norio Tanaka. 2025. "Modelling of Bottom Shear Stresses in Scoured Hole Formed by Nappe Flow During Levee Overtopping" GeoHazards 6, no. 1: 11. https://doi.org/10.3390/geohazards6010011
APA StyleIgarashi, Y., & Tanaka, N. (2025). Modelling of Bottom Shear Stresses in Scoured Hole Formed by Nappe Flow During Levee Overtopping. GeoHazards, 6(1), 11. https://doi.org/10.3390/geohazards6010011






