Investigation of Tsunami Waves in a Wave Flume: Experiment, Theory, Numerical Modeling
Abstract
:1. Introduction
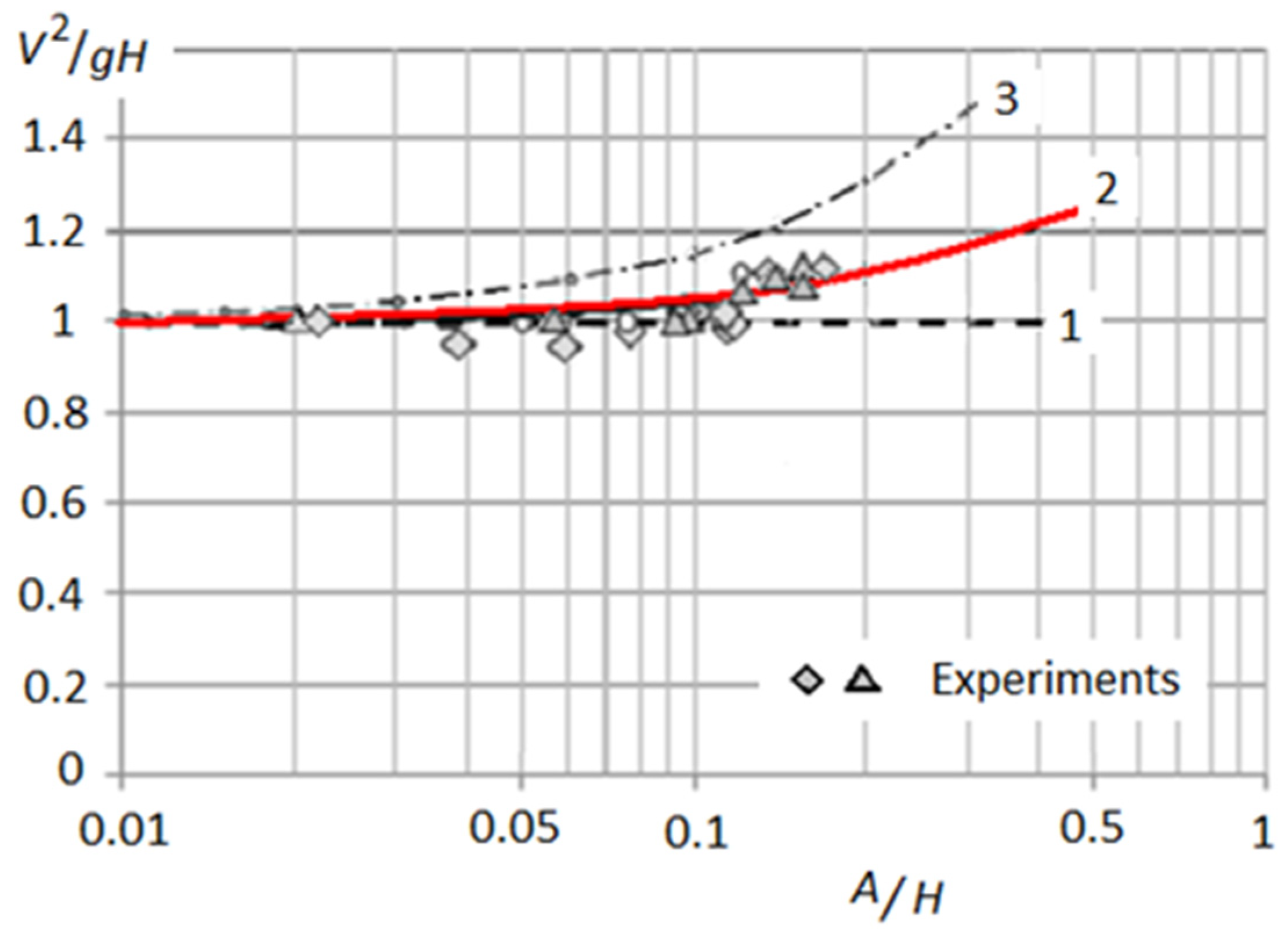
2. Problems of Modeling Tsunami Waves in Experimental Facilities
3. Mathematic Model and Numerical Method
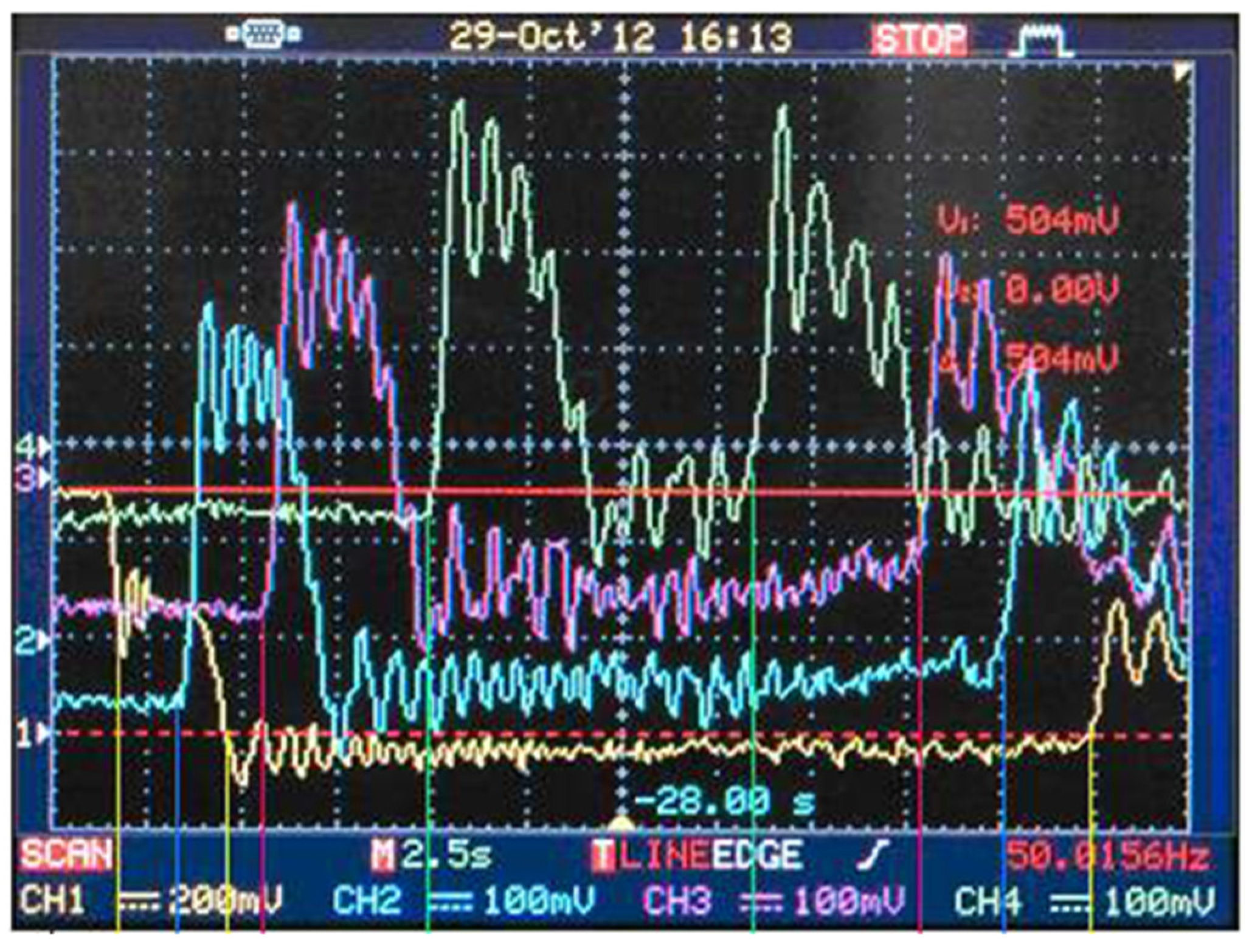
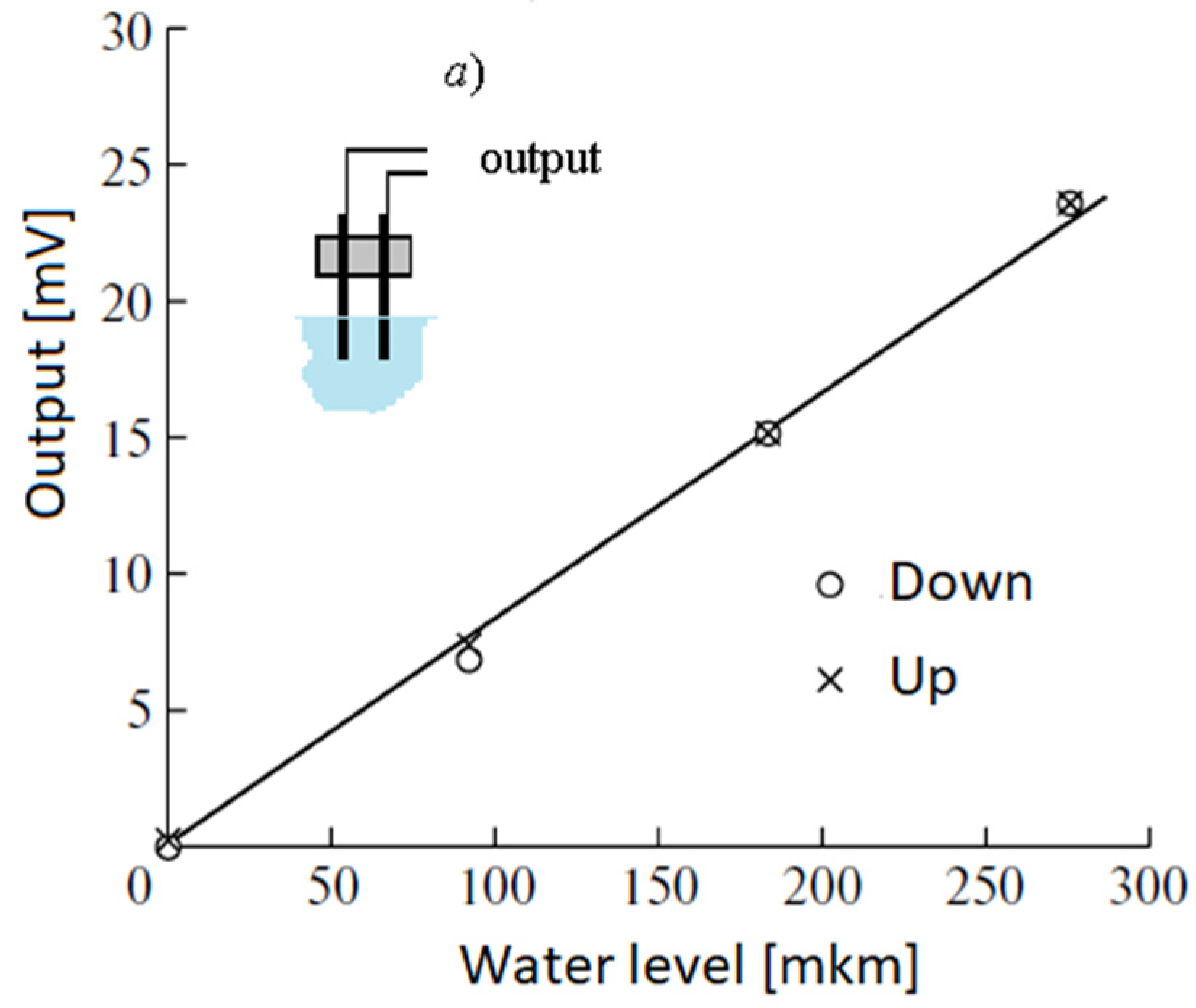
4. Experimental Equipment and Research Methods
- Initial water depth in channel H varied from 100 mm to 103 mm;
- Wave length L ≈ 3 m, averaged incident wave amplitude A in a series of experiments ranged from 0.5 mm to 15 mm.
5. Generation and Propagation of Waves in a Wave Flume
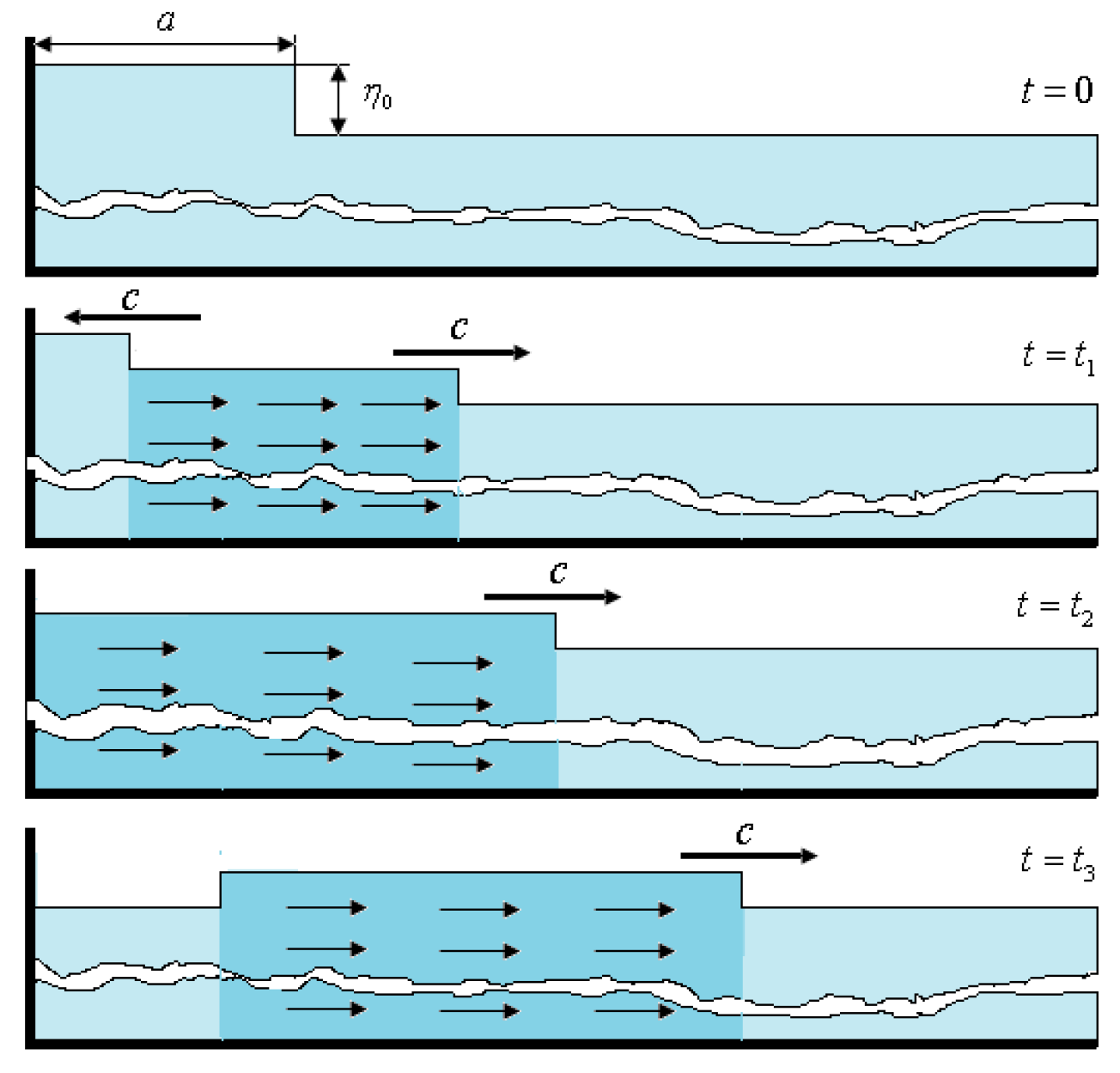
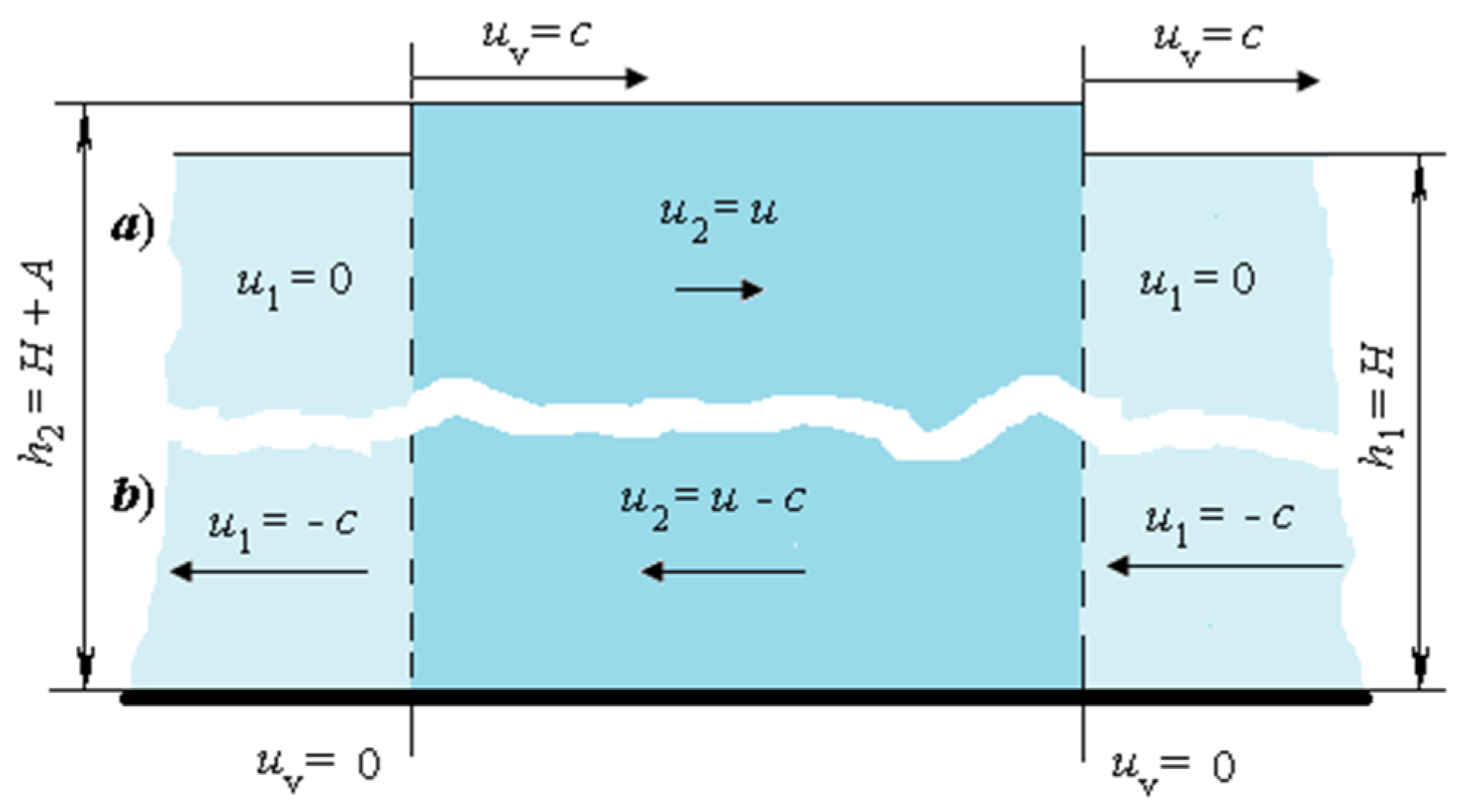
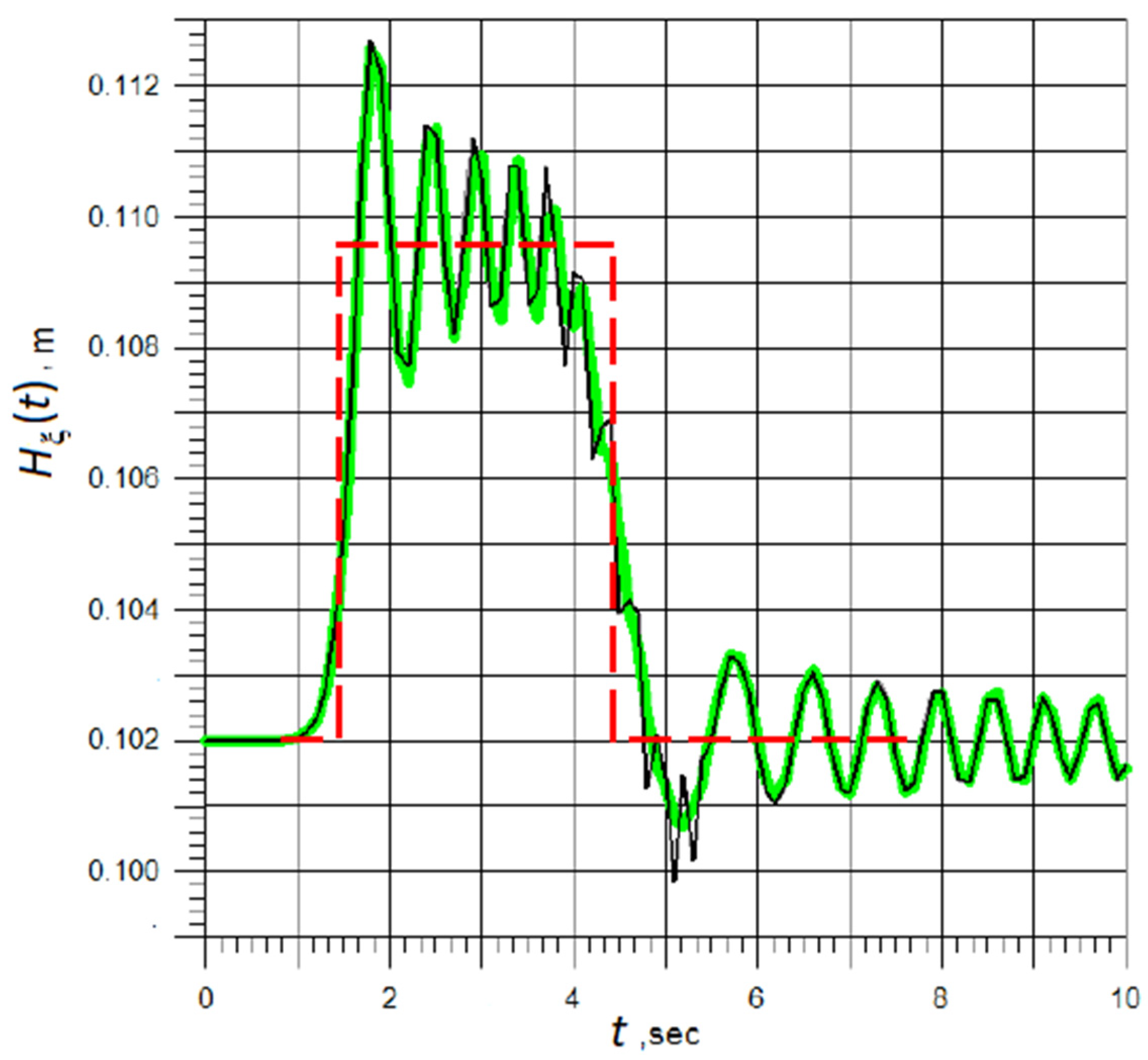
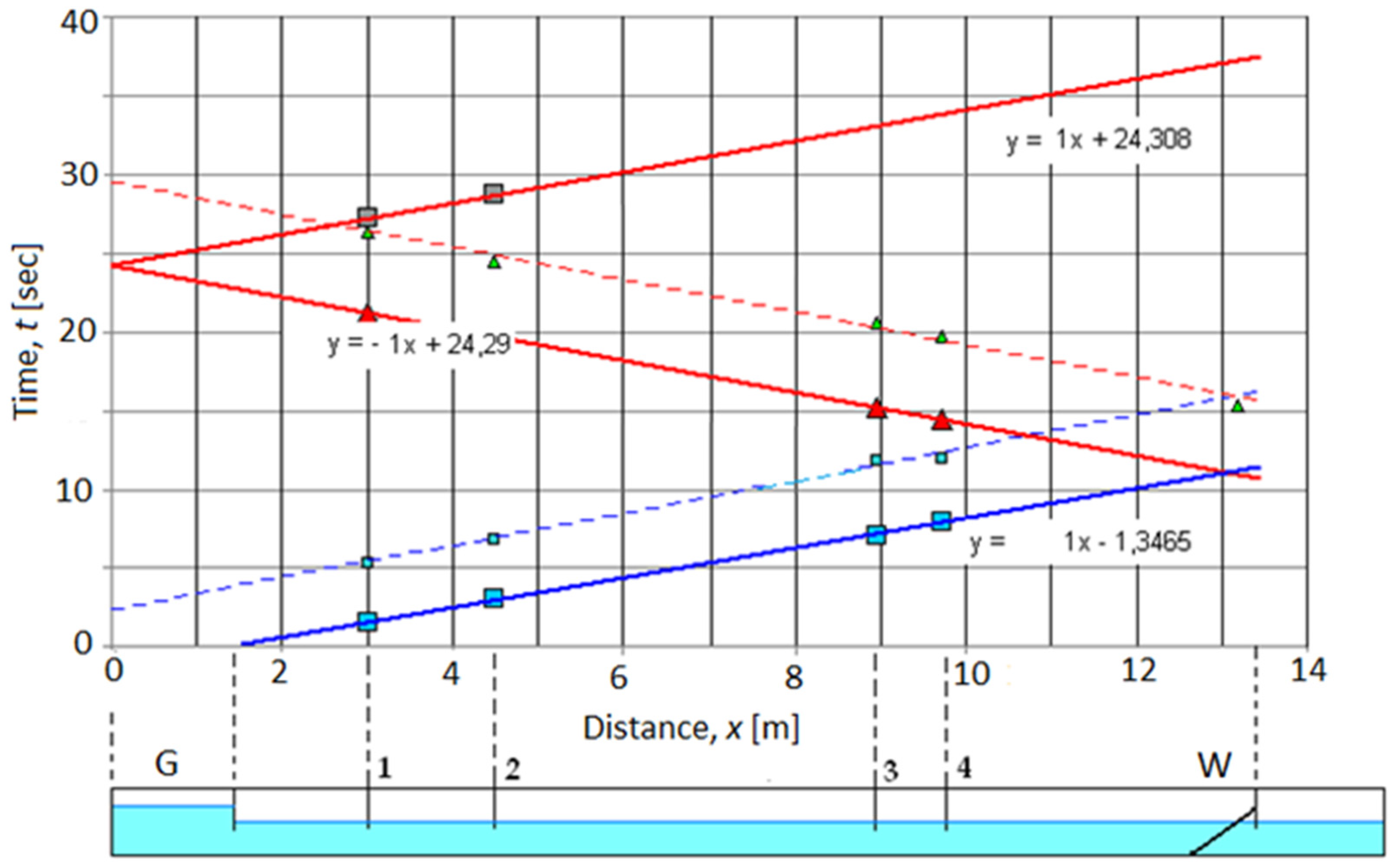
5.1. Wave Initiation
5.2. Wave Propagation
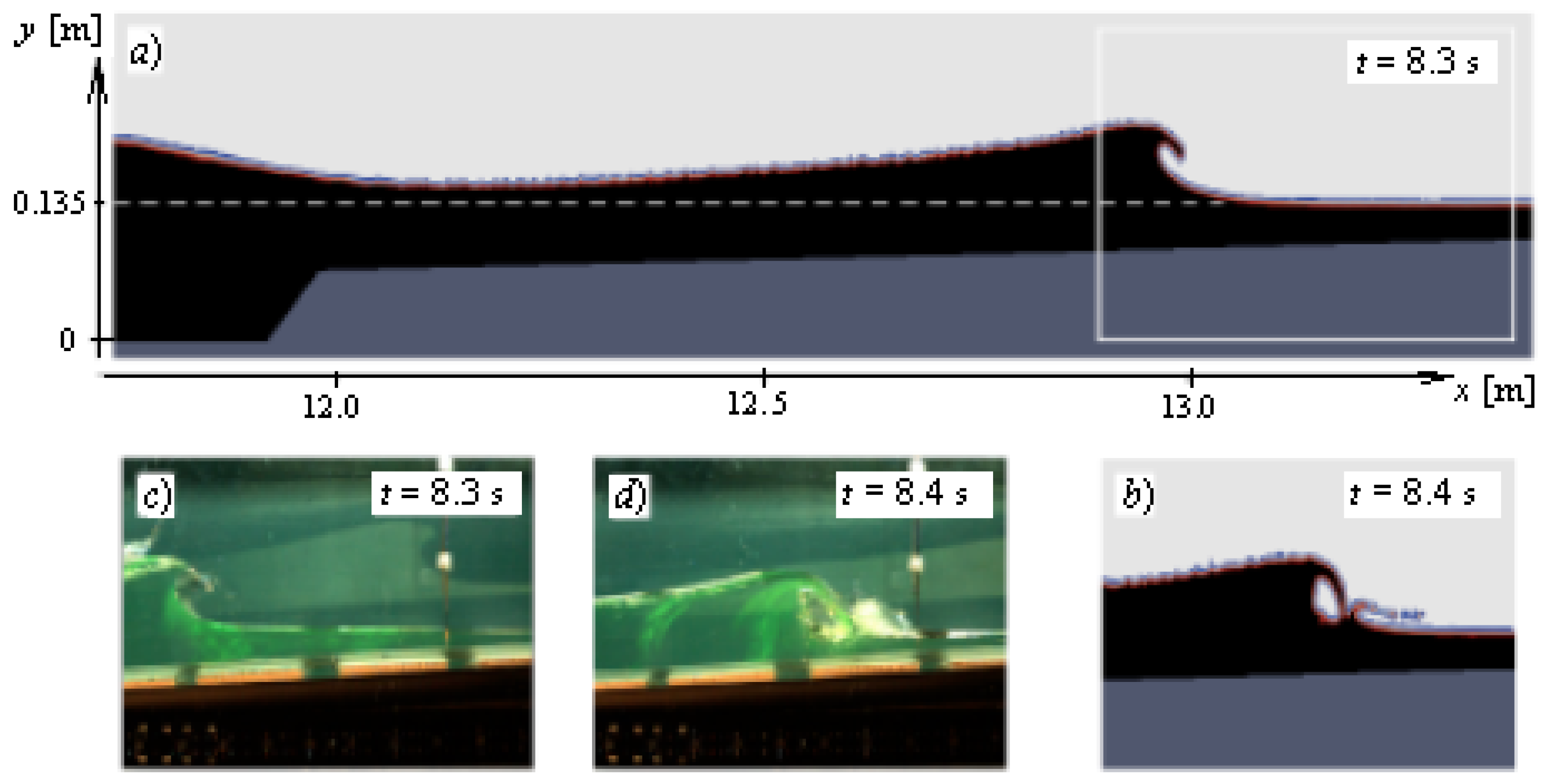
5.3. Transformation of Highly Nonlinear Wave, Which Interacts with Shallow Water
6. Interaction of Tsunami-Like Waves with Impermeable Thin Barriers
6.1. Experimental and Numerical Studies
6.2. Theoretical Studies
7. Conclusions
- Investigation of the features of modeling tsunami waves in a laboratory installation;
- Theoretical, experimental, and numerical studies of the interaction of tsunami waves with underwater obstacles;
- It is shown that at a certain optimal height of a thin impermeable barrier, its effectiveness in suppressing the energy of an incident tsunami wave is 70%, which is explained by the accumulation of energy in large-scale vortex structures near the obstacle.
- The use of precision measuring channels (sensor + equipment) for recording the water level made it possible to simulate the main dimensionless parameters of tsunami waves in a laboratory setup, equivalent to the parameters in large-scale wave flumes;
- The wave generator ensures the creation of gravity waves equivalent to theoretical ones with an instantaneous jump in water level and speed at the leading edge of the wave. In this case, the wavelength does not depend on its height and is determined only by the length of the wave generator;
- In our studies, we studied the interaction of a stationary homogeneous water flow with underwater barriers, since the condition τs < T is always provided, where τs is the time of the establishment of a stationary flow around.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Characteristics of Gravity Waves of the Tsunami Type, Modeled in the Hydrodynamic Channel of the IPRIM RAS
References
- Levin, B.W.; Nosov, M.A. Physics of Tsunamis, 2nd ed.; Springer: Cham, Switzerland, 2016; p. 388. [Google Scholar] [CrossRef]
- Shokin, Y.I.; Chubarov, L.B.; Marchuk, A.G.; Simonov, K.V. Vychislitelnyy Eksperiment v Probleme Tsunami. In Computational Experiment in the Tsunami Problem; Nauka SB: Novosibirsk, Russia, 1989. (In Russia) [Google Scholar]
- Ton van der Plas, T. A Study into the Feasibility of Tsunami Protection Structures for Banda Aceh and a Pre-Liminary Design of an Offshore Rubblemound Tsunami Barrier; Final Thesis Report; Delft University of Technology: Amersfoort, The Netherlands, 2007; pp. 1–24. [Google Scholar]
- Irtem, E.; Seyfioglu, E.; Kabdasli, S. Experimental investigation on the effects of submerged breakwaters on tsunami run-up height. J. Coast. Res. 2011, 64, 516–520. [Google Scholar]
- Fridman, A.M.; Alperovich, L.S.; Pustilnic, L.; Shemer, L.; Marchuk, A.G.; Liberson, D. Tsunami wave suppression using submarine barriers. Physics-Uspekhi 2010, 53, 809–816. [Google Scholar] [CrossRef]
- Boshenyatov, B.V.; Popov, V.V. Eksperimental’nye issledovaniya vzaimodeystviya voln tipa tsunami s podvodnymi pregradami [Experimental studies of the interaction of tsunami-like waves and underwater obstacles]. Izv. Vyss. Uchebnyh Zaved. Phisika 2012, 55, 145–150. (In Russia) [Google Scholar]
- Madsen, P.A.; Fuhrman, D.R.; Schaffer, H.A. On the solitary wave paradigm for tsunamis. J. Geophys. Res. 2008, 113, 1–22. [Google Scholar] [CrossRef]
- Boshenyatov, B.V.; Zhil’tsov, K.N. Matematicheskoye modelirovaniye vzaimodeystviya dlinnykh voln tipa tsunami s kompleksom pregrad [Mathematical simulation of the interaction of long tsunami type waves and complex of barriers]. Mod. High Technol. 2015, 12, 20–23. (In Russia) [Google Scholar]
- Boshenyatov, B.V. The vortex mechanism of suppression of tsunami waves by underwater obstacles. Dokl. Earth Sci. 2017, 447, 1434–1436. [Google Scholar] [CrossRef]
- Qu, К.; Ren, X.Y.; Kraatz, S. Numerical investigation of tsunami-like wave hydrodynamic characteristics and its comparison with solitary wave. Appl. Ocean. Res. 2017, 63, 36–48. [Google Scholar] [CrossRef]
- Shemer, L.; Goulitski, K.; Kit, E. Evolution of wide-spectrum unidirectional wave groups in a tank: An experimental and numerical study. Eur. J. Mech. B/Fluids 2007, 26, 193–219. [Google Scholar] [CrossRef]
- Boshenyatov, B.V.; Levin, Y.K.; Popov, V.V. Ustroystvo izmereniya urovnya vody [Water level measuring device]. RF Patent Application No. 2485452, 10 July 2010. [Google Scholar]
- Kutateladze, S.S.; Mironov, B.P.; Nakoryakov, V.E.; Habahpasheva, E.M. An Experimental Study of Wall Turbulent Flows; Nauka: Novosibirsk, Russia, 1975; pp. 23–30. (In Russia) [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free Boundaries. J. Comp. Phys. 1981, 39, 201. [Google Scholar] [CrossRef]
- OpenFOAM Foundation. OpenFOAM. In User Guide; OpenFOAM Foundation: London, UK, 2016; p. 211. Available online: http://www.openfoam.org (accessed on 15 March 2018).
- Boshenyatov, B.V.; Lisin, D.G. Numerical simulation of tsunami type waves in a hydrodynamic channel. Vestn. Tomsk. Gos. Universiteta. Mat. I Mekhanika [Tomsk. State Univ. J. Math. Mech.] 2013, 6, 45–55. [Google Scholar]
- Zhukovskii, N.E. Theoretical Foundations of Aeronautics; Gostekhizdat: Moscow, Russia, 1925. (In Russian) [Google Scholar]
- Boshenyatov, B.V.; Zhiltsov, K.N. Simulation of the interaction of tsunami waves with underwater barriers. Am. Inst. Phys. Conf. Ser. 2016, 1770, 030088. [Google Scholar] [CrossRef]
- Boshenyatov, B.V.; Zhil’tsov, K.N. Investigation of the interaction of tsunami waves and submerged obstacles of finite thickness in a hydrodynamic wave flume. Vestn. Tomsk. Gos. Universiteta. Mat. I Mekhanika [Tomsk. State Univ. J. Math. Mech.] 2018, 51, 86–103. (In Russia) [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boshenyatov, B.V.; Zhil’tsov, K.N. Vortex suppression of tsunami-like waves by underwater barriers. Ocean. Eng. 2019, 183, 398–408. [Google Scholar] [CrossRef]
- Chierici, F.; Pignagnoli, L.; Embriaco, D. Modeling of the hydroacoustic signal and tsunami wave generated by seafloor motion including a porous seabed. J. Geophys. Res. Ocean. 2010, 115, C0315. [Google Scholar] [CrossRef] [Green Version]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, 2nd ed.; Nauka: Moscow, Rassia; Pergamon Press: Oxford, UK, 1987. [Google Scholar]






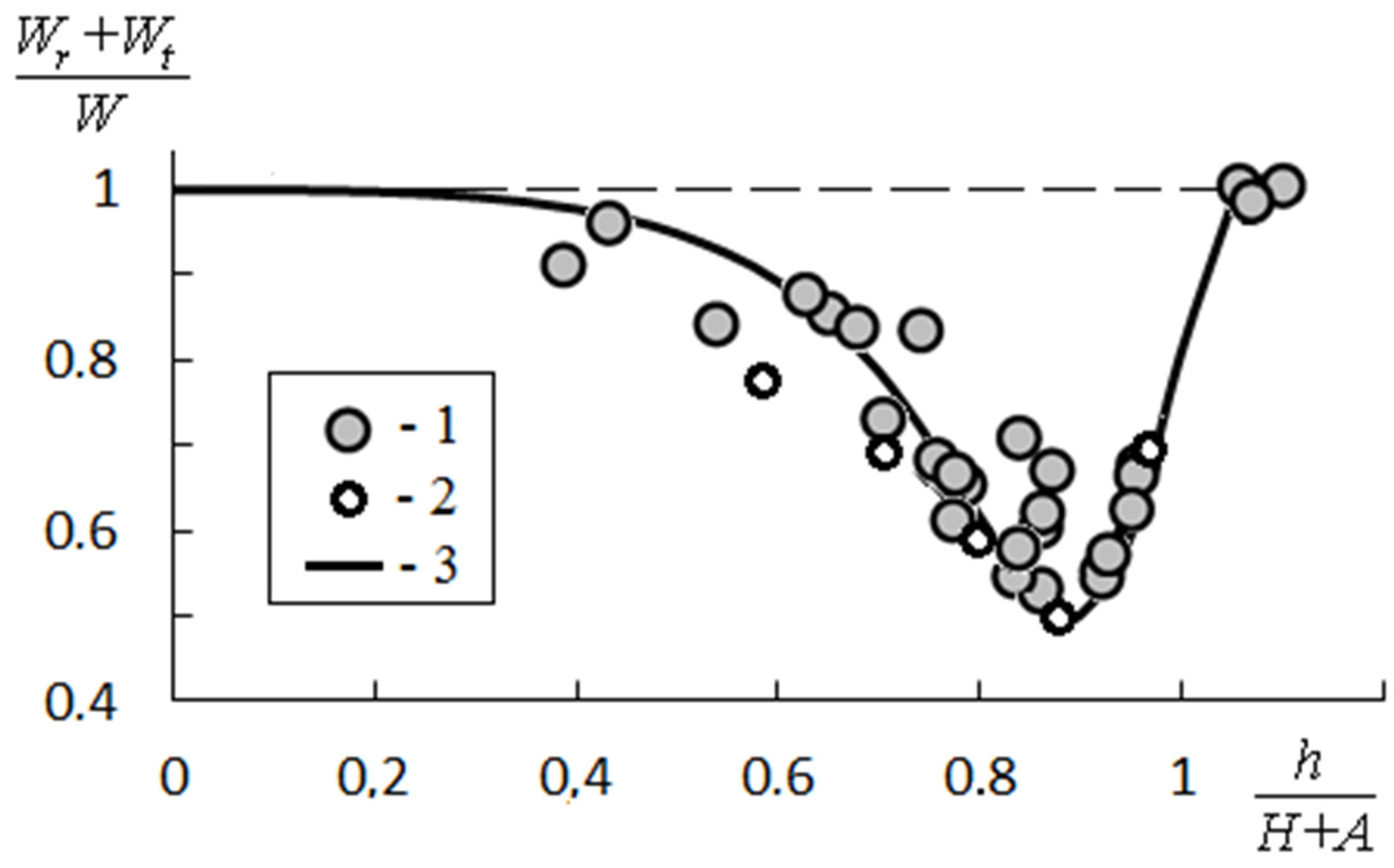
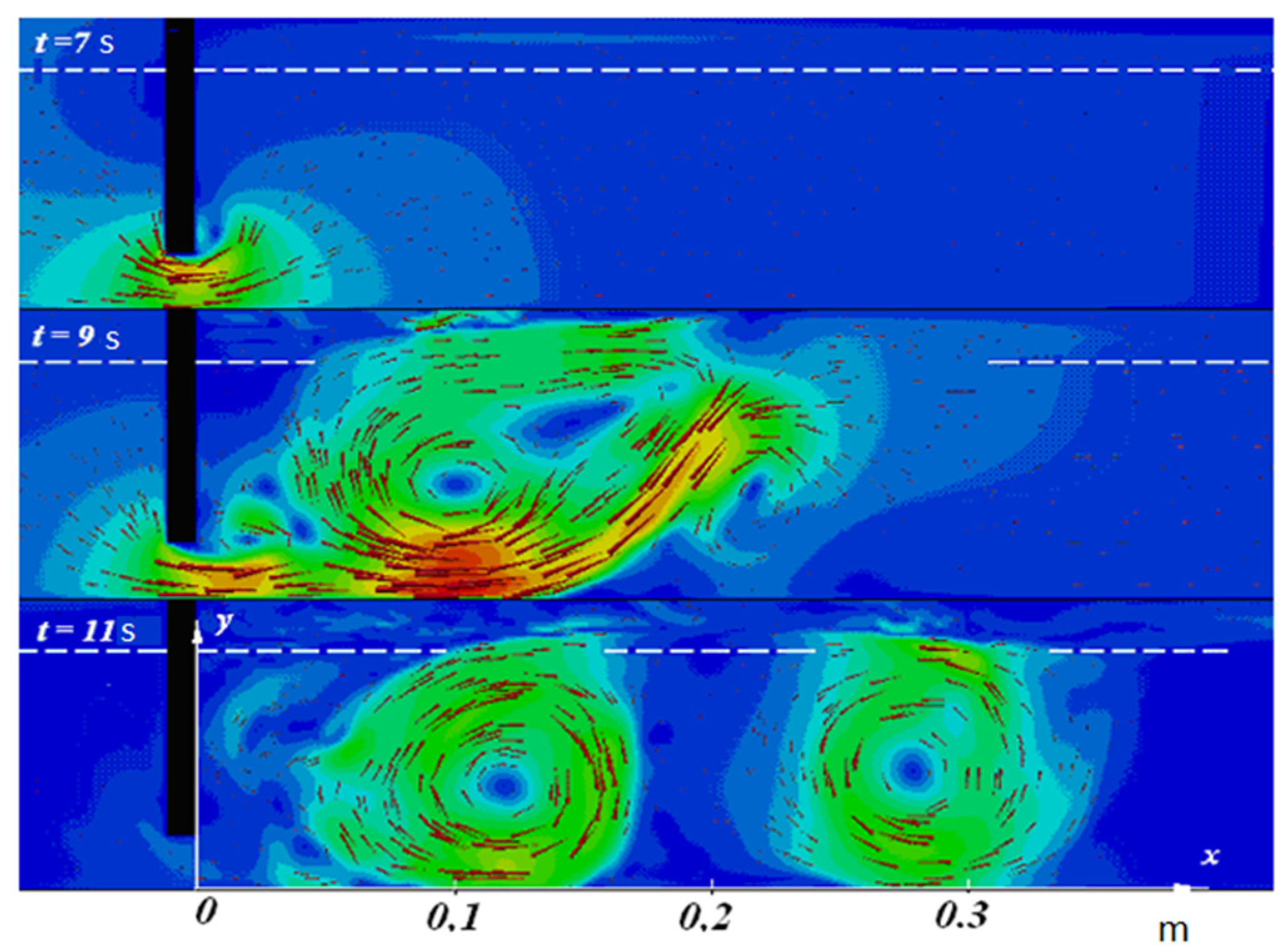
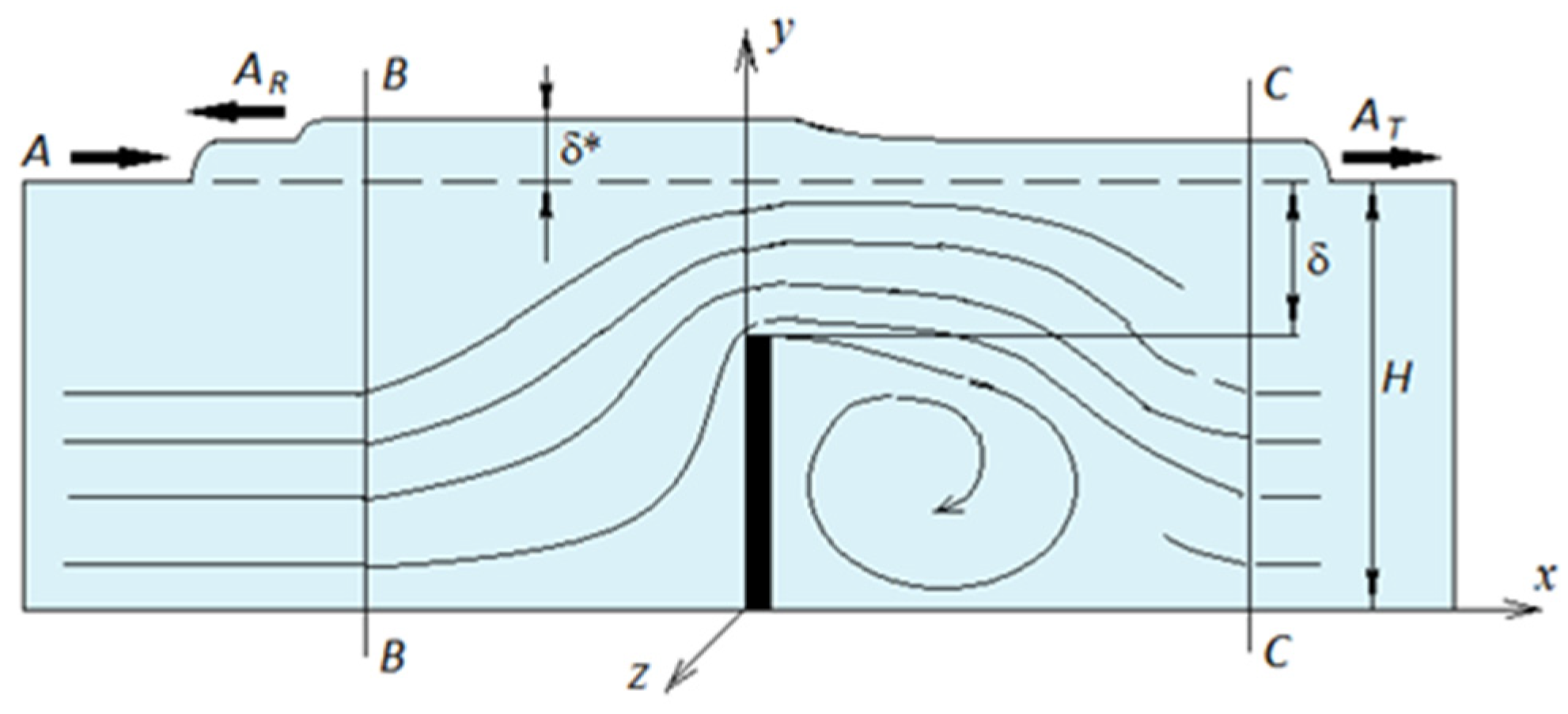
| Zone | Water Depth, H (km) | Wave Height A (m) | Wave Length L (km) | Nonlinearity A/H | Dispersion H/L |
|---|---|---|---|---|---|
| Ocean | 4 | 1 | 400 | 0.00025 | 0.01 |
| Continental shelf | 0.150 | 2.25 | 80 | 0.015 | 0.0019 |
| Shallow | 0.015 | 4 | 30 | 0.27 | 0.0005 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boshenyatov, B.V. Investigation of Tsunami Waves in a Wave Flume: Experiment, Theory, Numerical Modeling. GeoHazards 2022, 3, 125-143. https://doi.org/10.3390/geohazards3010007
Boshenyatov BV. Investigation of Tsunami Waves in a Wave Flume: Experiment, Theory, Numerical Modeling. GeoHazards. 2022; 3(1):125-143. https://doi.org/10.3390/geohazards3010007
Chicago/Turabian StyleBoshenyatov, Boris Vladimirovich. 2022. "Investigation of Tsunami Waves in a Wave Flume: Experiment, Theory, Numerical Modeling" GeoHazards 3, no. 1: 125-143. https://doi.org/10.3390/geohazards3010007
APA StyleBoshenyatov, B. V. (2022). Investigation of Tsunami Waves in a Wave Flume: Experiment, Theory, Numerical Modeling. GeoHazards, 3(1), 125-143. https://doi.org/10.3390/geohazards3010007





