Development of a Robotic Platform with Autonomous Navigation System for Agriculture
Abstract
1. Introduction
2. Materials and Methods
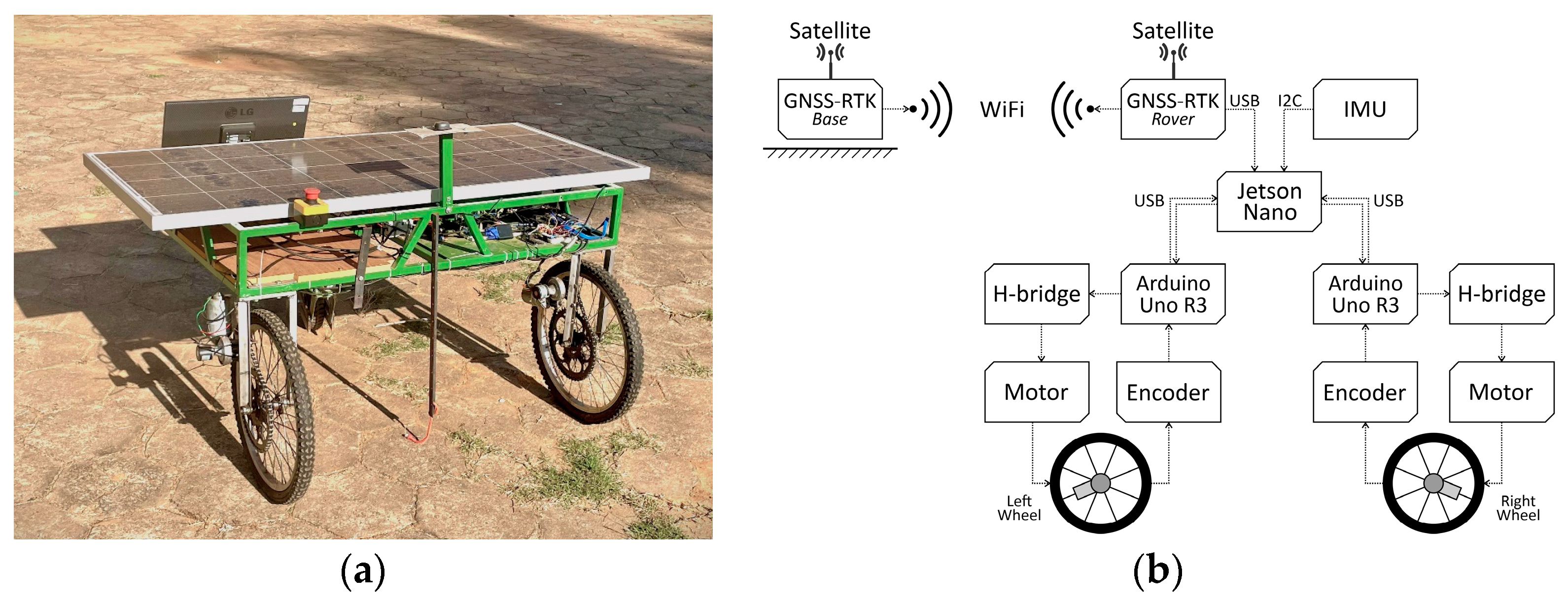
- The robotic platform must have width of 1.2 m to allow movement between rows of tree crops.
- The robotic platform must have a displacement speed of approximately 0.3 m/s.
- The platform must use a differential-drive vehicle model, where the angular velocity of each wheel is independently controlled. The pose of the robotic platform is defined by three independent variables: two for position (x and y) and one for orientation (θ).
- The position and orientation of the robotic platform must be determined using low-cost GNSS-RTK modules with sub-meter accuracy (±0.3 m) and a low-cost IMU sensor.
- The IMU must have a sampling rate of 10 Hz, and the GNSS-RTK must operate at a frequency greater than 5 Hz.
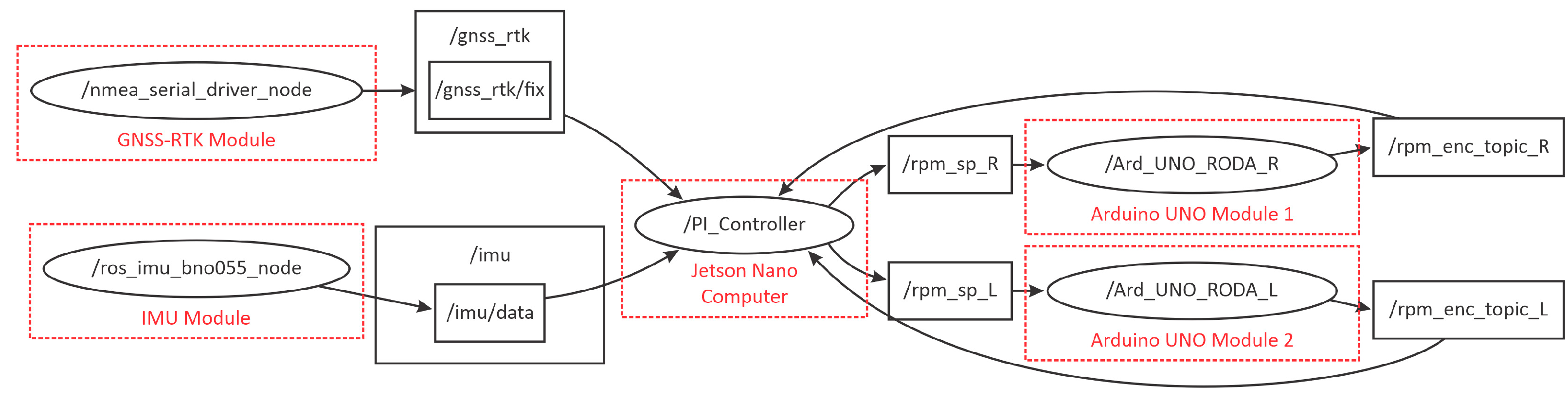
- The navigation algorithm for the robotic platform should be developed based on the Robotic Operating System framework and operate with an execution frequency of 10 Hz.
- The platform must be capable of following predetermined routes defined in a CSV or shapefile format file. This file will contain the sequence of waypoints to be reached, specified in global coordinates using the Universal Transverse Mercator (UTM) coordinate system.
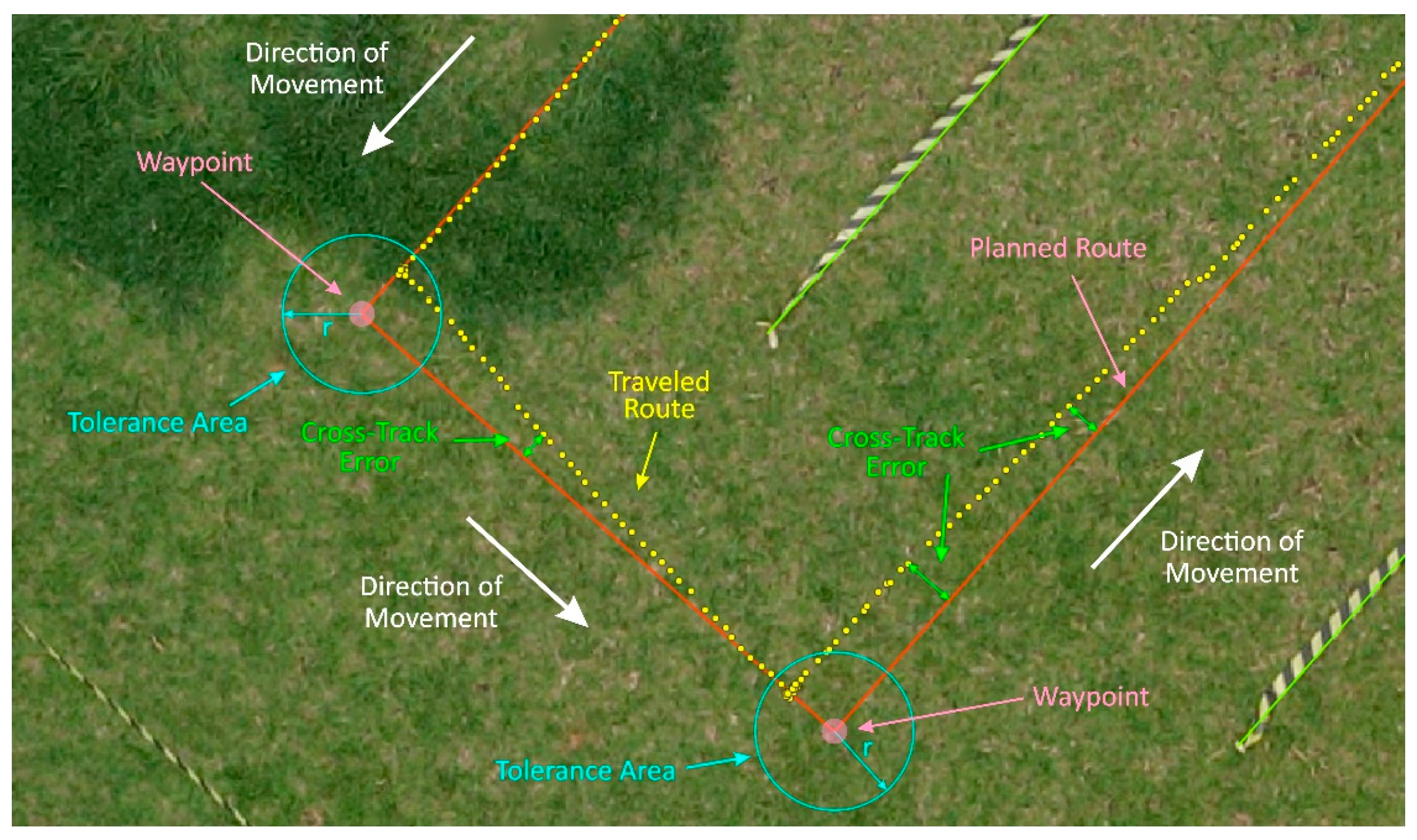
- The platform must follow the route with a maximum lateral error of 0.5 m and a mean absolute error of less than 0.1 m [3].
2.1. Mechanical, Electrical, and Electronic Systems of the Robotic Platform
2.2. Robotic Platform Software
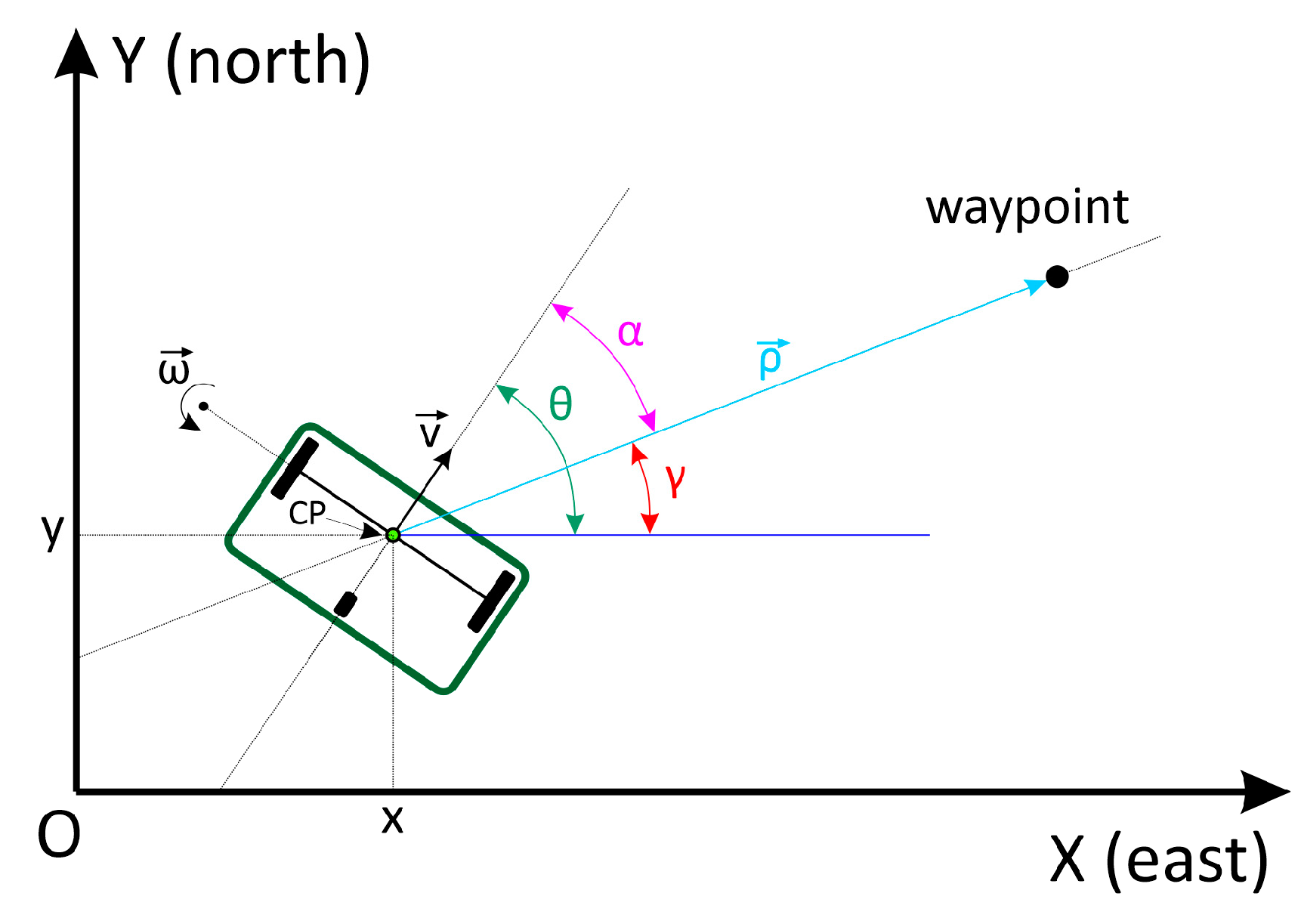
2.2.1. Steering Control Algorithm
- performed the correction of the angle θ provided by the IMU.
- robotic platform rotated around its axis until α approached zero, that is, the wheels rotated in the opposite direction to each other, with the same angular velocity in the module, resulting in zero forward velocity of the platform.
- PI controller was responsible for the steering control of the robotic platform.
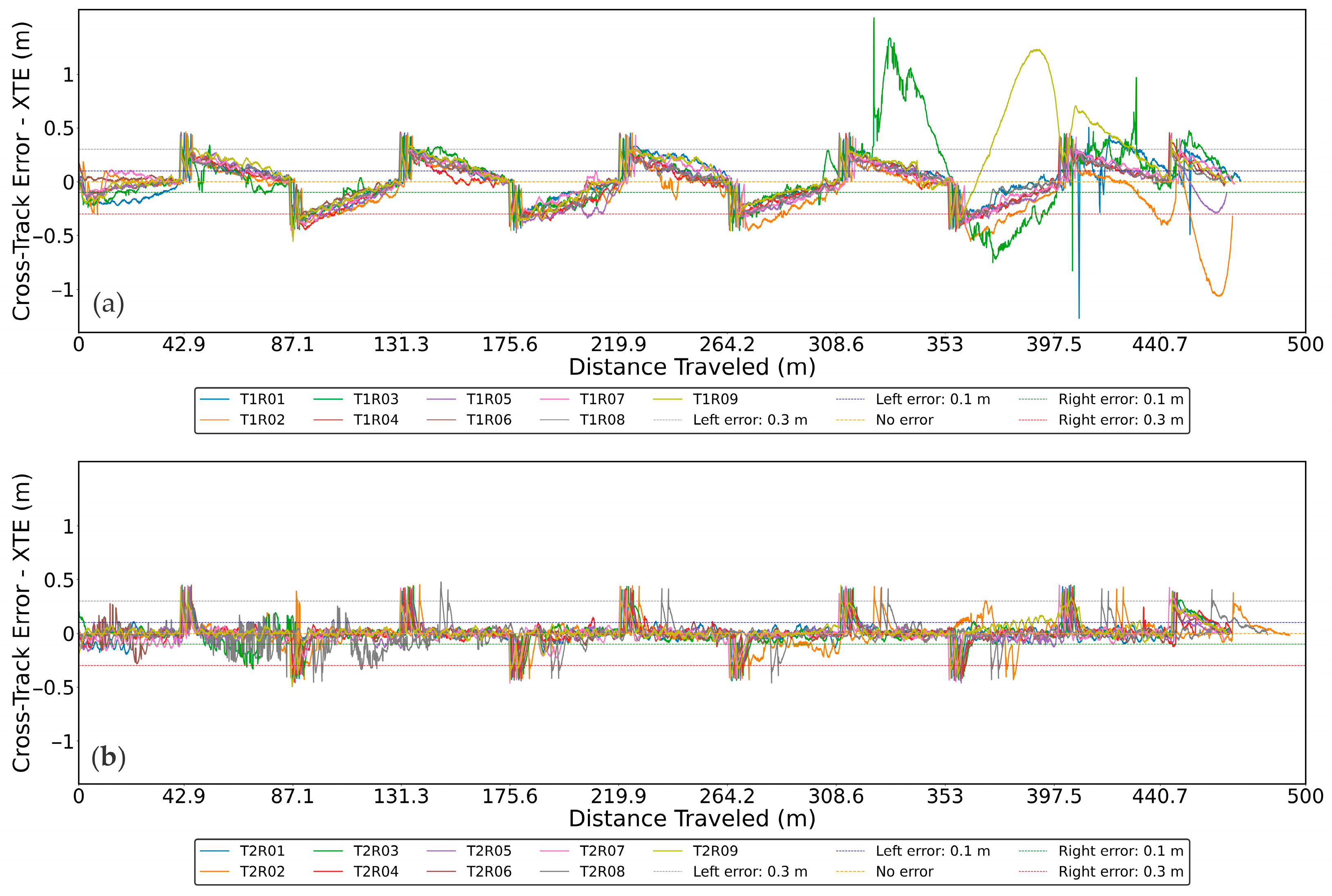
2.3. Navigation Performance Evaluation of the Robotic Platform
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Agnew, J.; Hendery, S. 2023 Global Agricultural Productivity Report: Every Farmer, Every; Virginia Tech College of Agriculture and Life Sciences: Blacksburg, VA, USA, 2023. [Google Scholar]
- Cisternas, I.; Velásquez, I.; Caro, A.; Rodríguez, A. Systematic Literature Review of Implementations of Precision Agriculture. Comput. Electron. Agric. 2020, 176, 105626. [Google Scholar]
- Pini, M.; Marucco, G.; Falco, G.; Nicola, M.; De Wilde, W. Experimental Testbed and Methodology for the Assessment of RTK GNSS Receivers Used in Precision Agriculture. IEEE Access 2020, 8, 14690–14703. [Google Scholar] [CrossRef]
- Gentilini, L.; Rossi, S.; Mengoli, D.; Eusebi, A.; Marconi, L. Trajectory Planning ROS Service for an Autonomous Agricultural Robot. In Proceedings of the 2021 IEEE International Workshop on Metrology for Agriculture and Forestry, MetroAgriFor 2021, Trento-Bolzano, Italy, 3–5 November 2021; pp. 384–389. [Google Scholar]
- Rahmadian, R.; Widyartono, M. Autonomous Robotic in Agriculture: A Review. In Proceedings of the 2020 Third International Conference on Vocational Education and Electrical Engineering (ICVEE), Surabaya, Indonesia, 3–4 October 2020; pp. 1–6. [Google Scholar]
- Zhang, Q.; Chen, Q.; Xu, Z.; Zhang, T.; Niu, X. Evaluating the Navigation Performance of Multi-Information Integration Based on Low-End Inertial Sensors for Precision Agriculture. Precis. Agric. 2021, 22, 627–646. [Google Scholar] [CrossRef]
- Reitbauer, E.; Schmied, C. Bridging Gnss Outages with Imu and Odometry: A Case Study for Agricultural Vehicles. Sensors 2021, 21, 4467. [Google Scholar] [CrossRef] [PubMed]
- Takasu, T.; Yasuda, A. Development of the Low-Cost RTK-GPS Receiver with an Open Source Program Package RTKLIB. In Proceedings of the International Symposium on GPS/GNSS, Jeju International Conference Center. Jeju, Republic of Korea, 4–6 November 2009. [Google Scholar]
- Bechar, A.; Vigneault, C. Agricultural Robots for Field Operations: Concepts and Components. Biosyst. Eng. 2016, 149, 94–111. [Google Scholar]
- Hernanda, T.Y.; Rosa, M.R.; Fuadi, A.Z. Mobile Robot-Ackerman Steering Navigation and Control Using Localization Based on Kalman Filter and PID Controller. In Proceedings of the 2022 5th International Seminar on Research of Information Technology and Intelligent Systems, ISRITI 2022, Yogyakarta, Indonesia, 8–9 December 2022; pp. 154–159. [Google Scholar]
- Levoir, S.J.; Farley, P.A.; Sun, T.; Xu, C. High-Accuracy Adaptive Low-Cost Location Sensing Subsystems for Autonomous Rover in Precision Agriculture. IEEE Open J. Ind. Appl. 2020, 1, 74–94. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, B.; Zhou, J.; Zhang, Y.; Liu, X. Real-Time Localization and Mapping Utilizing Multi-Sensor Fusion and Visual–IMU–Wheel Odometry for Agricultural Robots in Unstructured, Dynamic and GPS-Denied Greenhouse Environments. Agronomy 2022, 12, 1740. [Google Scholar] [CrossRef]
- Abdelhafid, E.F.; Abdelkader, Y.M.; Ahmed, M.; Doha, E.H.; Oumayma, E.K.; Abdellah, E.A. Localization Based on DGPS for Autonomous Robots in Precision Agriculture. In Proceedings of the 2022 2nd International Conference on Innovative Research in Applied Science, Engineering and Technology, IRASET 2022, Meknes, Morocco, 3–4 March 2022. [Google Scholar]







| Quantities | Component | Total Price (USD) * |
|---|---|---|
| 1 | Nvidia Jetson Nano | 224.99 |
| 1 | IMU Adafruit BNO 055 | 34.95 |
| 1 | Router WiFi TP-Link AC1750 | 73.00 |
| 2 | Module GNSS-RTK—EMLID Reach | 1794.00 |
| 2 | Rotary encoder 100 pulses | 37.98 |
| 2 | DC Motor, 24 V, 35 N.m, 55 RPM | 158.00 |
| 2 | 20 × 1.75″ Tire and wheel | 123.98 |
| 1 | 8-inch Swivel Caster Wheels | 20.00 |
| 2 | Sealed Lead Acid Battery 12 V 20 A.h Rechargeable | 205.72 |
| 2 | Arduino Uno R3 Board | 27.60 |
| 1 | Metal Chassi | 100.00 |
| 1 | Cables, screws, chains, pinion and ring gears, etc. | 100.00 |
| Total | 2900.22 | |
| Repetition | Test 1 - Route with Points at Vertices | Test 2 - Route with Points Every 3.0 m | ||||||
|---|---|---|---|---|---|---|---|---|
| Maximum Cross-Track Error (m) | MAE (m) | SD (m) | RMSE (m) | Maximum Cross-Track Error (m) | MAE (m) | SD (m) | RMSE (m) | |
| 1 | 1.269 | 0.157 | 0.104 | 0.188 | 0.443 | 0.060 | 0.084 | 0.103 |
| 2 | 1.064 | 0.178 | 0.181 | 0.254 | 0.453 | 0.067 | 0.084 | 0.107 |
| 3 | 1.525 | 0.224 | 0.212 | 0.309 | 0.449 | 0.062 | 0.084 | 0.105 |
| 4 | 0.464 | 0.146 | 0.111 | 0.183 | 0.452 | 0.054 | 0.079 | 0.096 |
| 5 | 0.458 | 0.165 | 0.107 | 0.197 | 0.461 | 0.053 | 0.074 | 0.091 |
| 6 | 0.462 | 0.134 | 0.099 | 0.167 | 0.451 | 0.056 | 0.082 | 0.099 |
| 7 | 0.512 | 0.141 | 0.098 | 0.172 | 0.462 | 0.062 | 0.085 | 0.105 |
| 8 | 0.477 | 0.137 | 0.098 | 0.168 | 0.478 | 0.068 | 0.089 | 0.112 |
| 9 | 1.230 | 0.220 | 0.225 | 0.314 | 0.497 | 0.061 | 0.087 | 0.107 |
| Average | 0.829 | 0.167 | 0.137 | 0.217 | 0.461 | 0.060 | 0.083 | 0.103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baltazar, J.d.A.; Coelho, A.L.d.F.; Valente, D.S.M.; Queiroz, D.M.d.; Villar, F.M.d.M. Development of a Robotic Platform with Autonomous Navigation System for Agriculture. AgriEngineering 2024, 6, 3362-3374. https://doi.org/10.3390/agriengineering6030192
Baltazar JdA, Coelho ALdF, Valente DSM, Queiroz DMd, Villar FMdM. Development of a Robotic Platform with Autonomous Navigation System for Agriculture. AgriEngineering. 2024; 6(3):3362-3374. https://doi.org/10.3390/agriengineering6030192
Chicago/Turabian StyleBaltazar, Jamil de Almeida, André Luiz de Freitas Coelho, Domingos Sárvio Magalhães Valente, Daniel Marçal de Queiroz, and Flora Maria de Melo Villar. 2024. "Development of a Robotic Platform with Autonomous Navigation System for Agriculture" AgriEngineering 6, no. 3: 3362-3374. https://doi.org/10.3390/agriengineering6030192
APA StyleBaltazar, J. d. A., Coelho, A. L. d. F., Valente, D. S. M., Queiroz, D. M. d., & Villar, F. M. d. M. (2024). Development of a Robotic Platform with Autonomous Navigation System for Agriculture. AgriEngineering, 6(3), 3362-3374. https://doi.org/10.3390/agriengineering6030192







