Construction of a Discrete Elemental Model for Clayey Soil Considering Pressure–Sinkage Nonlinear Relationship to Investigate Stress Transfer

Abstract

The discrete element method (DEM) has been extensively utilized to investigate the mechanical properties of granules, particularly their microscopic behavior, overcoming limitations in field tests such as cost, time consumption, and soil condition restrictions. To ensure the development of reliable DEM simulations, proper contact model selection and parameter calibration are essential. In this research, a DEM parameter calibration method that could represent the nonlinear relationship between clayey soil pressure and sinkage at different moisture contents was proposed. Firstly, the sinking modulus K and the soil deformation exponent n were identified to reflect the nonlinear pressure–sinkage relationship. Then, sensitive DEM parameters on the soli pressure–sinkage relationship were investigated and calibrated, and the effect of moisture content on them was explored. Finally, the transfer of soil internal stress during subsidence was analyzed using the constructed discrete element model. The average error of the sinking modulus K and the soil deformation exponent n between the DEM and the experimental result at four moisture contents were 4.7% and 4.9%, respectively. The relative error of soil internal stress between simulation and experiment was 6.7%, 4.4%, and 9.7% at depths of 50 mm, 100 mm, and 150 mm, respectively. The soil particle trajectory, soil internal stress distribution, and variations during plate pressure–sinkage progress were analyzed by the constructed DEM model. The results demonstrated good agreement with theoretical models and experimental findings. The proposed clayey soil DEM modeling process that considers the pressure–sinkage nonlinear relationship at different moisture contents can be applied in machine-soil research.

1. Introduction

Soil pressure–sinkage characteristic relationships have a significant impact on vehicle passability and vehicle travel resistance in a given geographical area [1]. At the same time, vehicle traffic causes soil compaction, leading to failure of the soil structure and its function [2,3]. Therefore, it is significant to investigate soil pressure modeling for analyzing subsidence and avoiding soil compaction. Several studies have explored the relationship between pressure and subsidence, and the influence factors have been investigated both in the field and in the laboratory by conducting experiments and mathematical modeling in different application environments [4,5,6,7]. However, modeling of the soil–tool interaction has proven to be highly intricate due to the soil structure’s inherent variability and its nonlinear behavior. Additionally, the absence of an instrument capable of true stress measurement adds another layer of complexity to this process.

Computer simulations present significant advantages in conducting such research, such as the finite element method (FEM) and the discrete element method (DEM) [8,9]. The FEM is used to discretize the complex geometrical region of the soil into units with simple geometrical shapes by integrating the units, external loads, and constraints to obtain a system of equations, and then solving the system of equations to obtain an approximate expression of the behavior of the medium [10]. In contrast, the DEM is used to analyze the discrete unit of inter-block contact to determine the contact of the ontological relationship to establish the contact of the physical and mechanical model, according to Newton’s second law of the discontinuous, discrete unit simulation [11]. In recent studies, the application of DEM to investigate stress transfer in soil has been demonstrated [12,13].

In terms of the soil DEM parameter calibration, the most prevalent method involves comparing the results of experiments and simulations using various parameters, such as the repose angle test [14]. This approach is well-suited for soils characterized by low moisture content and high mobility. However, when dealing with cohesive soils featuring high moisture content, the natural accumulation of soil becomes impeded, exerting a notable influence on the calibration outcomes. An alternative effective means for calibrating DEM parameters is through fundamental soil physical property tests. Aikins et al. [15] employed both the direct shear test and cone penetration test to ascertain DEM parameters for black vertosol soil, aiming to explore the effects on disturbance and cutting force measurements for a specifically chosen narrow point opener. They found a relative error of 8% in soil cutting forces when contrasted with field experiments. Wu et al. carried out a uniaxial confined compression test to achieve subsurface soil, and clay soil DEM parameters were calibrated by the unconfined compressive strength test to predict sweep draft force [16].

Therefore, the soil discrete element parameter calibration method should align with the specific application scenario and focus on particular properties to achieve an optimal combination of parameters that accurately represent those properties [17,18]. In investigations involving the pressure-sinking process of cohesive soils, more attention should be paid to the soil’s internal mechanical characteristics. Furthermore, the soil pressure–sinkage relationship is nonlinear. However, most of the existing DEM parameter calibration methods were grounded in static outcomes, such as the pressure at a specific indentation depth [19,20]. Calibrating discrete element parameters based on a particular state without considering the nonlinear nature of the entire pressure-sinking process and moisture content [21] may lead to substantial errors.

This study aimed to develop DEM models that can represent the nonlinear mechanical properties throughout the soil subsidence process, thereby mitigating static calibration errors. The model was subsequently used to investigate variations in soil internal stress during the pressure–sinkage process. The main work includes the following: (1) Plate sinkage tests on soil with moisture contents of 13.2%, 18.1%, 22.7%, and 27.9% and simulation were carried out to analyze the sensitive DEM parameters. The sensitive parameters were then calibrated based on the pressure–sinkage curve characteristics. (2) The variation of soil pressure–sinkage characteristics and DEM parameters with moisture content was analyzed. (3) The transfer of soil internal stress during subsidence was analyzed.

2. Materials and Methods

2.1. Soil Properties

This research utilized soil samples collected from the 0–100 mm layer of a paddy field in Huzhou City, Zhejiang Province, China, characterized as typical clay soil. The soil particle size and its distribution were measured, and the following results were obtained: particles with d < 0.5 mm comprised 9.8%, d = 0.5~0.7mm comprised 29.5%, d = 0.7~0.9 mm comprised 41.9%, and diameter d > 0.9 mm constituted 18.8%. The average moisture content was measured to be 19.68%. The average volumetric weight, compactness, and specific gravity of the soil were 1.355 × 10³ kg/m³, 461.5 Kpa, and 2.44, respectively. Relevant test methods are outlined in

Table 1. Soil property test methods.

Content	Particle Size	Moisture Content	Compactness	Bulk Density	Specific Gravity
Test method	Screening method	LC-DHS-20A electric moisture meter	TYD-2 soil compactness tester	Cutting ring method	Pyknometer

.

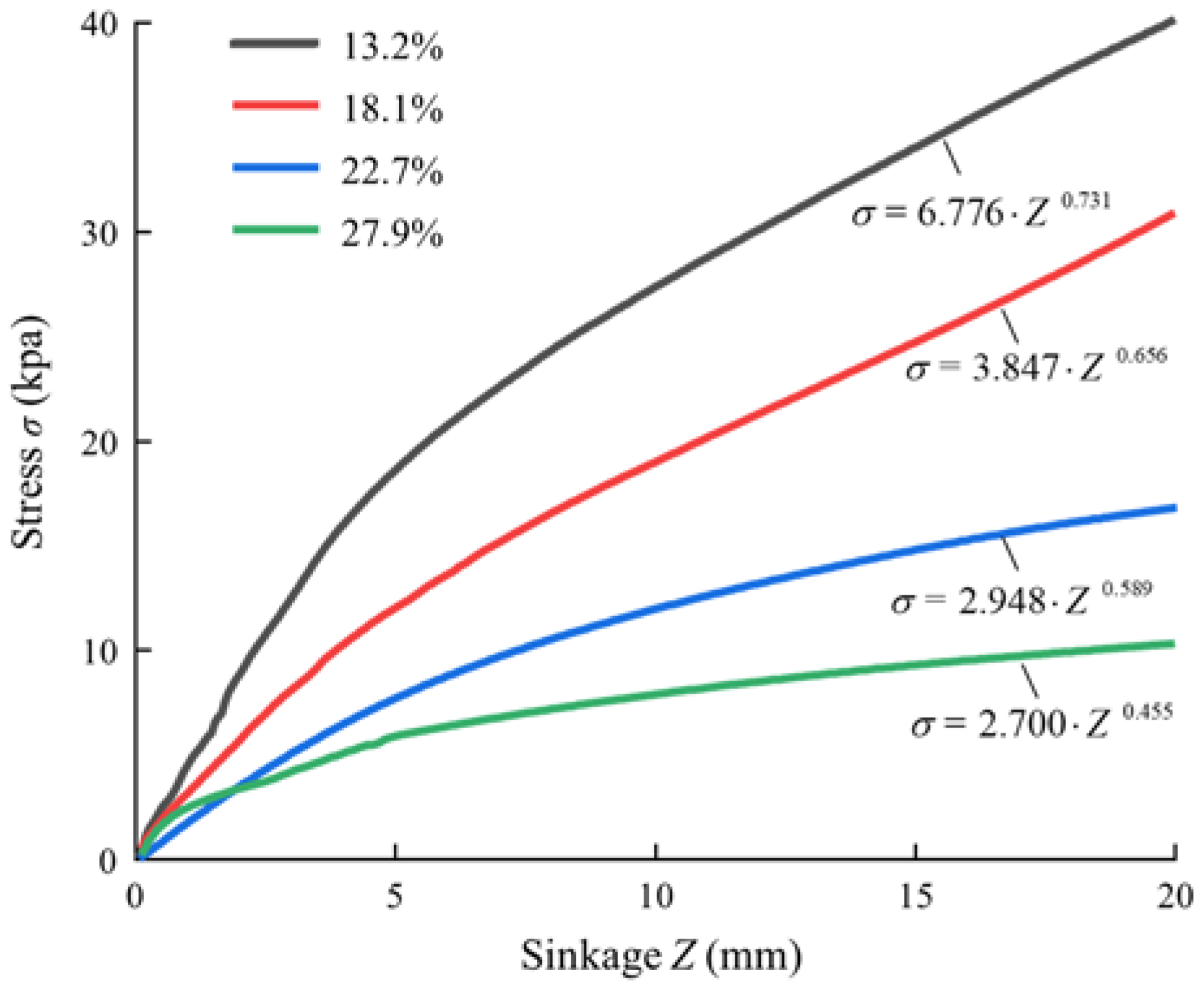
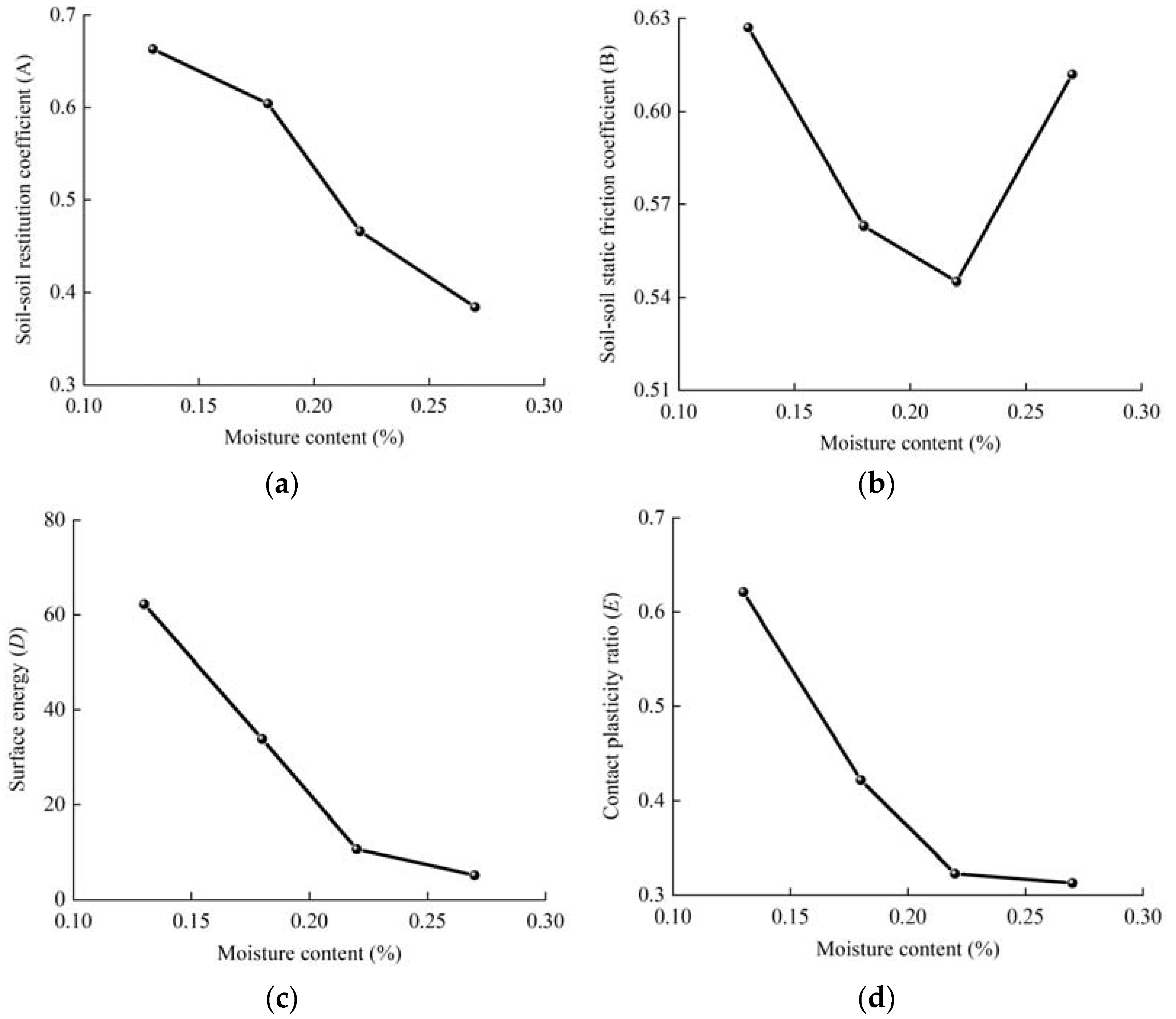
The target moisture content in the experiment was 13%, 18%, 23%, and 28% (with increments of 4%). To obtain different moisture contents, the soil was spread flat in a cool, ventilated area to less than 10% moisture content. A motorized sprayer was used to ensure that the water was evenly mixed with the soil in the preparation of soil with different moisture contents. After spraying the calculated amount of water into the soil, five samples were randomly taken from the soil, and the moisture content was measured. Once the deviation of the actual moisture content from the target moisture content is less than 1 percent, the soil preparation is complete. Otherwise, the process is repeated. The observed moisture content during the experiment was measured at 13.2%, 18.1%, 22.7%, and 27.9%, respectively.

2.2. Plate Sinkage Test (PST) and DEM Parameter Calibration Principle

The plate sinkage test (PST) is able to visualize the soil pressure-sinking characteristics. In this research, the PST was carried out to calibrate and verify the soil DEM parameters. The soil pressure–sinkage relationship can be expressed as an exponential function [4,22].

$$\sigma =K\cdot Z^n$$

(1)

where Z is the subsidence, m; σ is the grounding pressure, KN·m⁻²; K is the sinking modulus; and n is the soil deformation exponent.

Sinking modulus K depends on the soil property and plate geometry. According to Bekker’s theory [23],

$$K={\displaystyle \frac{K_c}{b}}+K_{\phi }$$

(2)

where k_c is the modulus of cohesion deformation; k_φ is the modulus of friction deformation; b is the plate width (radius of a circular plate or width of a rectangular plate), m.

The parameters K and n could characterize the nonlinear soil pressure–sinkage relationship. Their values can be acquired by experiment and curve fitting. Simulation tests with DEM parameters as variables were also carried out. The optimal DEM parameter combinations can be obtained using K and n values as optimization objectives. Compared with the single-point calibration method [24], this calibration method can reflect the nonlinear characteristics of the soil pressure-sinking process, overcome the influence of nonlinear factors on the calibration results, and improve the reliability of parameter calibration.

In this research, four soils with different moisture contents (13.2%, 18.1%, 22.7%, and 27.9%) were used. A steel cylinder with a diameter of 300 mm and a height of 300 mm was used to place the soil, as shown in Figure 1. To achieve the same bulk density in the field, the soil in the cylinder was compacted to predetermined depths marked on the inside wall using a metal plate of the same internal diameter as the cylinder. To avoid the influence of boundary effects on the test results, the ratio of the diameter of the steel cylinder to the pressure plate should be not less than 3 [12], and a 100 mm diameter steel plate was used for the PST. The pressure was loaded and recorded by a universal testing machine (utm6503, Suns, Shenzhen, China) at a loading speed of 0.008 m·s⁻¹. 0.025 m was set as the total sink depth. Three trials with the same parameters were repeated and averaged.

2.3. Contact Model Theory and Parameters to Be Calibrated

The contact model is a description of the behavior of elements in contact with each other. The Edinburgh Elasto-Plastic Adhesion Model (EEPA) includes an adhesion component as a function of plastic contact deformation, as well as a nonlinear hysteresis spring model to account for elastic-plastic contact deformation [25]. The model can reflect the volume of soil particles before and after compaction and the viscosity–plasticity relationship between particles.

In the EEPA, the total normal force (F_n) mainly consists of the hysteretic rebound force (f_hys) and the normal damping force (f_nd):

$$F_n=\left(f_{hys}+f_{nd}\right)u$$

(3)

$$f_{hys}=\left\{\begin{array}{l}{f}_0+k_1{\delta }^n\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{k}_1\left({\delta }^n-{\delta }_p^n\right)\ge k_1{\delta }^n\\ f_0+k_2\left({\delta }^n-{\delta }_p^n\right)\hspace{1em}{\delta }^n>k_2\left({\delta }^n-{\delta }_p^n\right)>-k_{adh}{\delta }^n\\ f_0+k_{adh}{\delta }^n\hspace{1em}\hspace{1em}\hspace{1em}-k_{adh}{\delta }^n\ge k_2\left({\delta }^n-{\delta }_p^n\right)\end{array}\right.$$

(4)

$$f_{nd}={\beta }_n{v}_n$$

(5)

where u is the unit normal vector from the point of contact to the mass center; f₀ is the initial bond strength of the particles, Pa; k₁ is the loading stiffness coefficient; k₂ is the unloading stiffness coefficient; k_adh is the adhesion stiffness coefficient; δ_p is the particle contact overlap; f₀ is the constant pull-off force; β_n is the damping factor; and v_n is the normal velocity, m·s⁻¹.

The key parameters in normal damping force (f_nd) were given by:

$$m^{*}=m_i^{*}{m}_j/\left(m_i+m_j\right)$$

(6)

$${\beta }_n=\sqrt{{\displaystyle \frac{4m^{*}{k}_1}{1+{\left(\frac{\pi }{\ln e}\right)}^2}}}$$

(7)

where m* is the equivalent mass of the particles; e is the coefficient of restitution.

The particle contact tangential force (ft) consists of tangential stiffness (f_ts) and tangential damping (f_td):

$$f_t=f_{ts}+f_{td}$$

(8)

The tangential stiffness (f_ts) is calculated using the iterative theory:

$$f_{ts}=f_{ts\left(n-1\right)}-{\gamma }_t{k}_1{\delta }_t$$

(9)

where f_ts(n−1) is the tangential force at a given moment, N; γ_t is the particle tangential stiffness coefficient; and δ_t is the tangential overlap.

The tangential damping (f_td) is mainly determined by the tangential damping factor β_t and the interparticle tangential velocity v_t:

$$\left\{\begin{array}{l}{f}_{td}={\beta }_t{v}_t\\ {\beta }_t=\sqrt{{\displaystyle \frac{4m^{*}{\gamma }_t{k}_1}{1+{\left(\frac{\pi }{lne}\right)}^2}}}\end{array}\right.$$

(10)

Soil particles slide against each other, and the tangential friction of soil particles conforms to the Coulomb friction criterion. Therefore, the particle shear strength limits under positive stress are as follows:

$$f_{ct}\le \mu \left|f_{hys}+k_{adh}-f_0\right|$$

(11)

where f_ct is the limit of tangential friction between particles, N; μ is the coefficient of rolling friction.

Thus, the parameters that need to be calibrated in EEPA DEM simulations are surface energy, contact plasticity ratio, tensile exp, and the tangential stiff multiplier. In addition, particle interaction parameters that need to be calibrated are the coefficient of restitution, the coefficient of sliding friction, and the coefficient of rolling friction.

2.4. Discrete Element Models for Plate Sinkage Test

The PST DEM simulation was developed in the software EDEM_v2021 (EDEM Academic 2021, DEM Solutions Ltd., Edinburgh, UK). Spherical particles with 5 mm, 4 mm, 3 mm, and 2 mm were created, and their percentages were 18.8%, 41.9%, 29.5%, and 9.8%, respectively, according to the size distribution statistic result. The particles were randomly generated in a cylinder with a height of 400 mm and a diameter of 300 mm (Figure 1b). The total particle number was 99,700, and the average void volume fraction was 40.5%.

To apply compressive stress to the particles, a circular steel plate with a diameter of 100 mm was created. PST were simulated with a sinkage depth of 0.025 m and a loading speed of 0.008 m^−s, which was the same as the experiment. The simulation time step and save interval were set at 3 × 10⁻⁵ s and 0.1 s, respectively. The load on the soil is calculated from the total force of the plate.

Table 2. Parameters used in DEM.

Parameters	Value	Value
Soil	Density (kg/m3)	2600
	Shear’s modulus (Pa)	1.3 × 106
	Poisson’s ratio	0.38
Steel	Density (kg/m3)	7850
	Shear’s modulus (Pa)	7.9 × 1010
	Poisson’s ratio	0.3
Soil–Steel Interaction Coefficient	Restitution	0.55
	Static friction	0.50
	Rolling friction	0.35

lists the DEM parameters utilized in the simulations [10,12]. Soil-metal contact parameters were no longer calibrated due to their insignificant impact on PST simulation [17].

2.5. DEM Parameters Calibration Method

The parameters to be calibrated include three soil–soil contact parameters and four EEPA parameters, as shown in

Table 3. Parameters of the Plackette–Burman test.

Symbol	Simulation Parameters		Low Level	High Level
A	Soil–soil interaction coefficient	Restitution	0.20	0.70
B		Static friction	0.30	0.80
C		Rolling friction	0.10	0.60
D	EEPA	Surface energy	5.00	150.00
E		Contact plasticity ratio	0.30	0.85
F		Tensile Exp	1.50	5.00
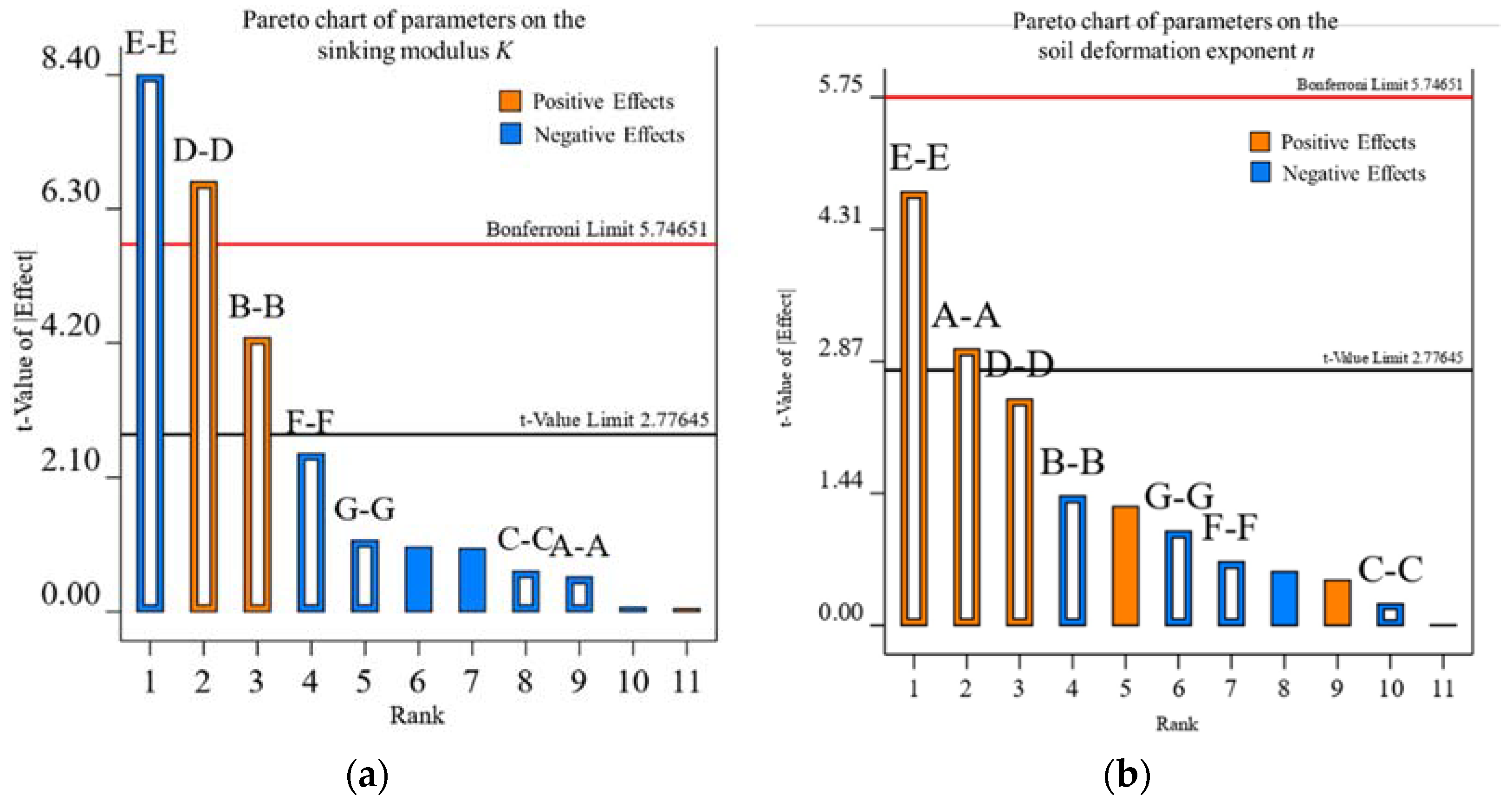
G		Tangential stiff multiplier	0.10	0.60

. Due to the large number of parameters, it is difficult to calibrate them directly. A sensitivity analysis of the above parameters to the pressure–sinkage relationship was first carried out by the Plackette–Burman (PB) test with 11 factors and 1 central point. Four parameters were identified for calibration through sensitivity analysis, as shown in

Table 4. Variable configuration of the Central Composite test.

Level	A	B	D	E
1.682	0.70	0.80	150.00	0.85
1	0.60	0.70	120.60	0.74
0	0.45	0.55	77.50	0.58
−1	0.30	0.40	34.40	0.41
−1.682	0.20	0.30	5.00	0.30

.

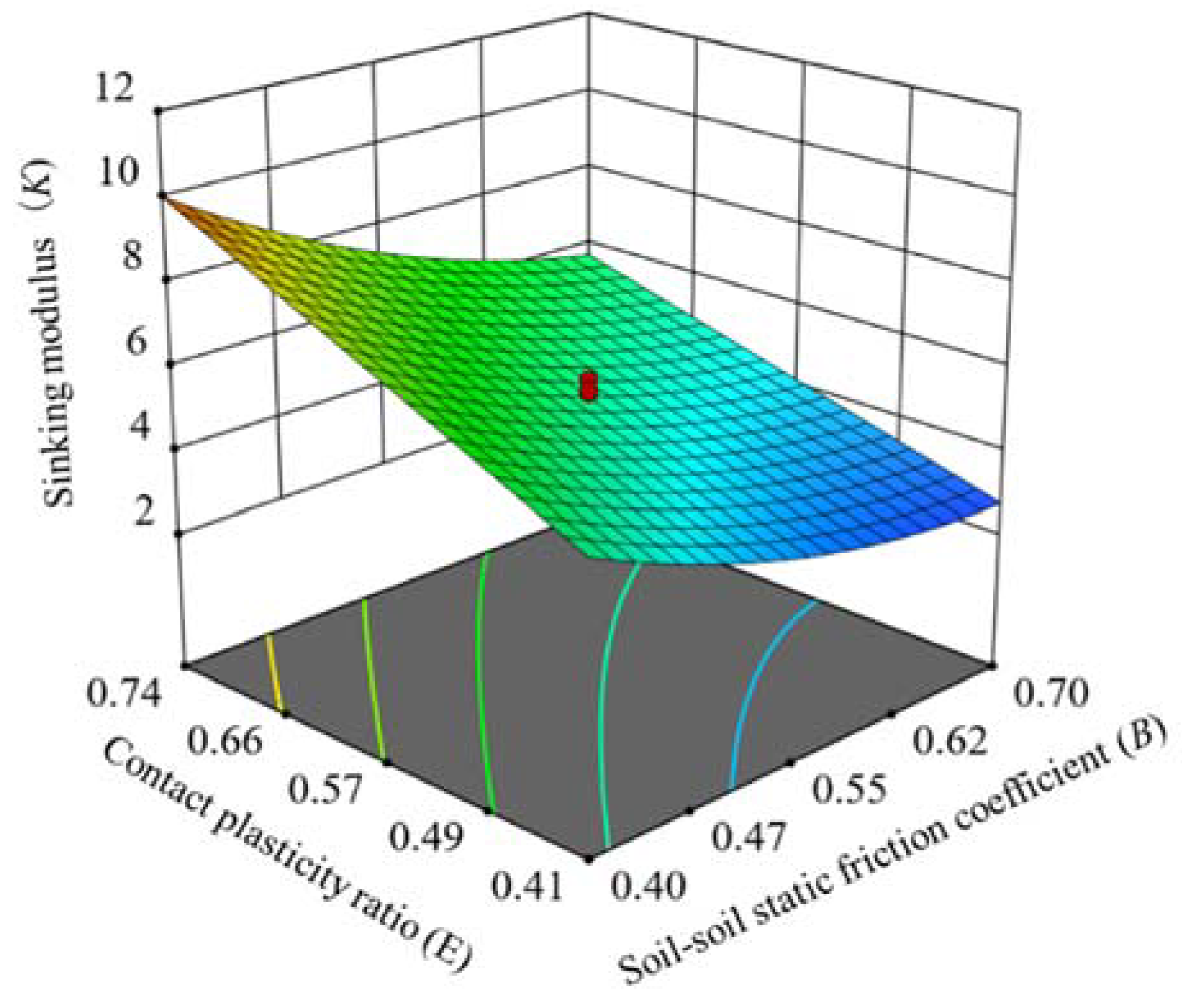
Parameter combinations can be optimized through the Central Composite (CC) test. The relationship between the characteristic parameters (sinking modulus K and soil deformation exponent n) and the sensitive DEM parameters could be analyzed by regression analysis of experiments near the centroid, and mathematical models of the influencing factors and response variables were developed. The test parameter level is shown in Table 4. Other insensitive parameters follow the middle level in the PB test. Considering the randomness of the DEM simulation [13], 10 trials with the same parameters were repeated and averaged.

2.6. Verification Experiment

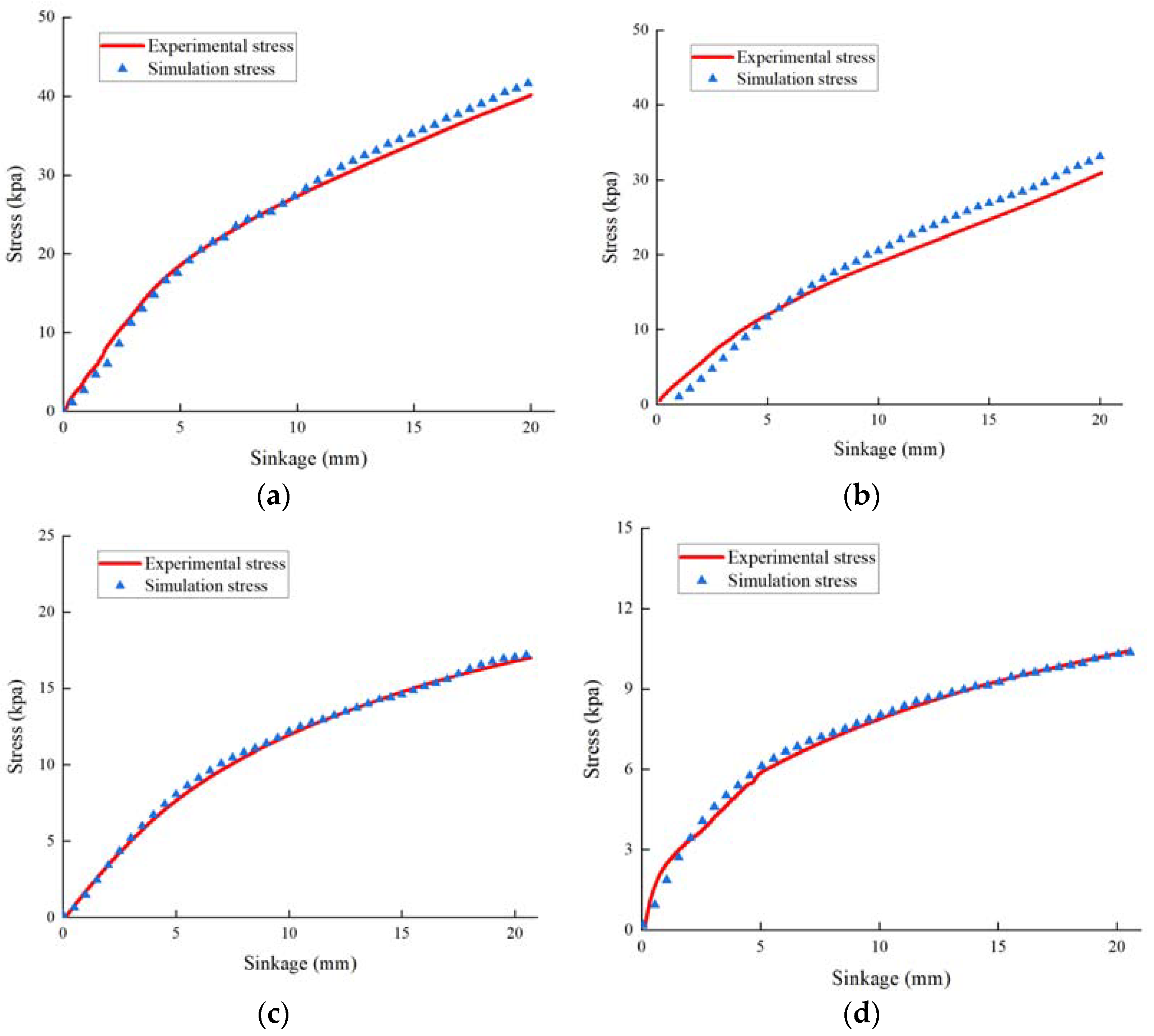
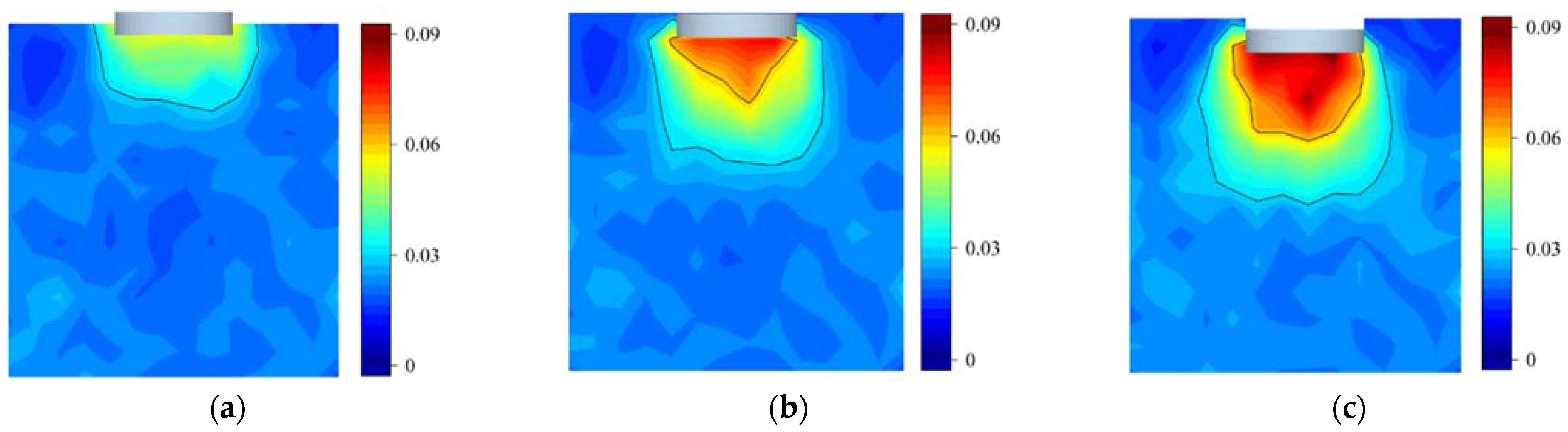
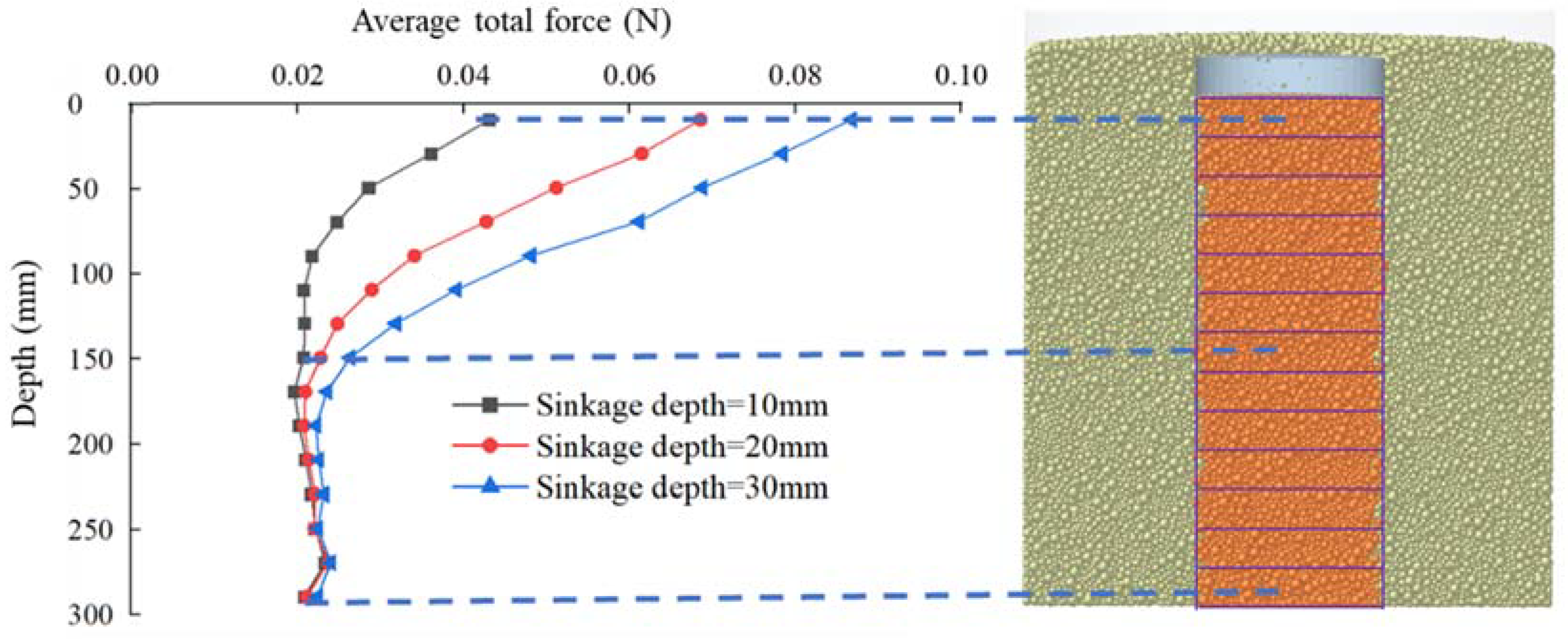
Two methods were used to verify the validity of the simulation model. The first method was the comparison of the pressure-sink curves and characteristic parameters (K and n) between experimental and simulation results using calibration results. The second method was the comparison of soil internal stress at different depths obtained from experiments and simulations. The dynamic signal test system (DH5922N, Donghua, Taizhou, China) and pressure sensors were used to test internal soil stress. The sensors were placed inside the soil below the plate at depths of 50 mm, 100 mm, and 150 mm, respectively, as shown in Figure 2a. In the simulation, three geometric bins were arranged inside the soil at the same position as shown in Figure 2b. The soil moisture content was 22.7% in the verification experiment.

3. Results and Discussion

3.1. Result of PST at Different Soil Moisture Contents

The soil pressure–sinkage relationship fitted based on PST is shown in Figure 3. To assess the performance of the fitting result, the RMSE and R-square were calculated as shown in

Table 5. Fitting result valuation.

Moisture Content (%)	K	n	R-Square	RMSE
13.2	6.776	0.731	0.993	0.860
18.1	3.847	0.656	0.999	0.310
22.7	2.948	0.589	0.988	0.526
27.9	2.700	0.455	0.992	0.220

.

The curve fitting is more accurate, while the RMSE result tends to 0 and the R-square tends to 1. The calculated calculation results indicate that the fitted curve can express the pressure–sinkage relationship at various moisture contents. According to Figure 3, the soil sinking modulus K and deformation exponent n both decreased with the increase in moisture content, indicating that soil compressive capacity decreases with moisture content. The deformation exponent n was less than 1 at all test moisture contents; the load tolerated by continuing to increase the sinkage depth does not change much and exhibits plastic characteristics, indicating that the sample was plastic soil.

3.2. Simulation Model Stability Ansys

In the simulation model, the proportions of particles of size were defined, but the distribution location, etc., is stochastic. To test the stability of the model, 10 repetitions with the same parameters were carried out, as shown in Figure 4. In the case of 10 mm of subsidence, the average pressure of 10 simulation tests was 13.69 Kpa, and the error between each test and the average value was within 4.6%. In the case of 20 mm of subsidence, the average pressure of 10 simulation tests was 17.78 Kpa, and the error between each test and the average value was within 2.6%. Repeated tests showed a relatively small difference, indicating that the simulation model is stable.

3.3. Sensitivity of DEM Parameters to PST

The result of the PB test is shown in

Table 6. Plackette–Burman test result.

No.	A	B	C	D	E	F	G	K	n
1	0.70	0.30	0.60	150.00	0.30	5.00	0.60	8.739	0.671
2	0.70	0.80	0.10	150.00	0.85	5.00	0.01	35.920	0.555
3	0.20	0.80	0.60	150.00	0.30	1.50	0.01	2.007	0.831
4	0.20	0.80	0.10	150.00	0.85	1.50	0.60	6.747	0.422
5	0.20	0.80	0.60	5.00	0.85	5.00	0.60	12.450	0.244
6	0.70	0.30	0.60	150.00	0.85	1.50	0.01	39.520	0.536
7	0.20	0.30	0.10	5.00	0.30	1.50	0.01	1.286	0.657
8	0.70	0.30	0.10	5.00	0.85	1.50	0.60	24.430	0.168
9	0.20	0.30	0.60	5.00	0.85	5.00	0.01	12.790	0.088
10	0.70	0.80	0.60	5.00	0.30	1.50	0.60	3.688	0.560
11	0.70	0.80	0.10	5.00	0.30	5.00	0.01	1.289	0.739
12	0.20	0.30	0.10	150.00	0.30	5.00	0.60	7.764	0.711

. The significance of the DEM parameters on sinking modulus K and soil deformation exponent n were discussed through Pareto charts (Figure 5) and contributions (Table 3).

As shown in Figure 5, the plasticity ratio (E) and surface energy (D) were significant for K because the t-value of the effect exceeded the Bonferroni limit. On the contrary, soil–soil restitution (A), soil–soil rolling friction (C), and tangential stiff multiplier (G) were insignificant for K because the contribution value was lower than the t-value limit. Similarly, soil–soil restitution (A) and plasticity ratio (E) were significant for n. The remaining parameters have little effect. Therefore, the variables used to calibrate the DEM parameters were A, B, D, and E.

3.4. Effect of DEM Parameters on PST

Table 7. Result of the sensitive DEM parameters in the Central Composite test.

No.	A	B	D	E	K	n
1	0.30	0.70	120.60	0.74	5.489	0.762
2	0.45	0.55	77.50	0.58	4.657	0.749
3	0.45	0.55	77.50	0.30	3.408	0.753
4	0.60	0.70	34.40	0.74	7.198	0.616
5	0.60	0.40	120.60	0.74	9.381	0.629
6	0.45	0.80	77.50	0.58	3.847	0.771
7	0.45	0.55	77.50	0.85	9.304	0.721
8	0.30	0.40	120.60	0.74	9.397	0.640
9	0.45	0.55	150.00	0.58	5.153	0.766
10	0.70	0.55	77.50	0.58	5.67	0.687
11	0.60	0.70	120.60	0.41	2.27	0.930
12	0.60	0.40	34.40	0.41	5.613	0.630
13	0.60	0.40	34.40	0.74	10.82	0.541
14	0.45	0.55	5.00	0.58	5.611	0.473
15	0.60	0.70	34.40	0.41	2.985	0.770
16	0.45	0.55	77.50	0.58	5.481	0.711
17	0.30	0.40	120.60	0.41	4.497	0.799
18	0.45	0.55	77.50	0.58	4.644	0.769
19	0.45	0.55	77.50	0.58	5.407	0.712
20	0.30	0.70	34.40	0.74	6.446	0.652
21	0.45	0.55	77.50	0.58	4.037	0.805
22	0.45	0.30	77.50	0.58	10.34	0.577
23	0.60	0.40	120.60	0.41	5.411	0.720
24	0.20	0.55	77.50	0.58	4.784	0.789
25	0.30	0.40	34.40	0.41	5.873	0.628
26	0.60	0.70	120.60	0.74	4.547	0.811
27	0.45	0.55	77.50	0.58	5.74	0.695
28	0.30	0.70	34.40	0.41	3.123	0.738
29	0.30	0.40	34.40	0.74	10.5	0.563
30	0.30	0.70	120.60	0.41	3.028	0.857

shows the results of the Central Composite (CC) test. The results of the ANOVA of the test results are shown in

Table 8. ANOVA for the sensitive DEM parameters in the Central Composite test results.

Source	K			n
	Mean Square	F-Value	p-Value	Mean Square	F-Value	p-Value
Model	11.3400	31.7800	<0.0001 **	0.0181	8.4200	<0.0001 **
A	0.0857	0.2401	0.6312	0.0013	0.5814	0.4576
B	64.3300	180.26	<0.0001 **	0.0794	36.9300	<0.0001 **
D	4.0000	11.2100	0.0044 **	0.1043	48.4800	<0.0001 **
E	77.2200	216.36	<0.0001 **	0.0383	17.7900	0.0007 **
AB	0.2611	0.7316	0.4058	0.0033	1.5300	0.2353
AD	0.1362	0.3815	0.5461	0.0002	0.0911	0.7669
AE	0.0079	0.0222	0.8836	0.0001	0.0658	0.8010
BD	0.0056	0.0156	0.9024	0.0016	0.7289	0.4067
BE	2.5800	7.2400	0.0168 *	0.0002	0.0726	0.7912
DE	0.8845	2.4800	0.1363	0.0003	0.1335	0.7199
A2	0.0064	0.0181	0.8949	0.0010	0.4513	0.5119
B2	6.6900	18.7600	0.0006 **	0.0037	1.7000	0.2116
D2	0.0200	0.0559	0.8163	0.0191	8.9000	0.0093 **
E2	2.3500	6.5900	0.0215 *	0.0009	0.4128	0.5302
Residual	0.3569			0.0022
Lack of Fit	0.3237	0.7649	0.6650	0.0024	1.3400	0.3918
Pure Error	0.4232			0.0018

Note: ** means highly significant (p < 0.01), * means significant (0.01 ≤ p < 0.05).

.

According to Table 8, the regression models p-values of K and n were both less than 0.01, indicating that the models can accurately reflect the relationship among K, n, and A, B, D, E, and F and also correctly predict test results. Among them, B, D, and E were very significant model terms both for K and n. BE, B², and E² were significant for K, and D² was significant for n. The regression models of K and n were given after the insignificant factors were excluded:

K = 9.42 + 0.42A − 34.34B − 0.01D + 20.64E − 16.54BE + 29.32B² + 0.23 × 10⁻⁴D²

(12)

n = 0.44 − 0.05A + 0.41B + 0.44 × 10 − 2D − 0.26E − 0.18 × 10⁻⁴D²

(13)

The soil–soil static friction (B) and contact plasticity ratio (E) interactions on sinking modulus K are shown in Figure 6. As the soil–soil static friction and contact plasticity ratio increase, the modulus of subsidence increases. The effect of soil–soil static friction was more significant according to the curve variation.

3.5. Results and Discussions of DEM Parameter Calibration

Regression models (12) and (13) were used to establish the optimization equation. The optimization objectives were the values of K and n obtained from the PST physical test at different moisture contents. The parameters were limited in the test range.

$$\left\{\begin{array}{l}K=6.776,3.847,2.948,2.700\\ n=0.731,0.656,0.589,0.455\\ s.t.\left\{\begin{array}{l}0.20\le A\le 0.70\\ 0.30\le B\le 0.80\\ 5.00\le C\le 150.00\\ 0.30\le D\le 0.85\end{array}\right.\end{array}\right.$$

(14)

Table 9. Solutions for the optimal combination of DEM parameters at different moisture contents.

Parament	Soil Moisture Content
	13.2%	18.1%	22.7%	27.9%
Soil–soil static friction coefficient (A)	0.663	0.604	0.466	0.384
Soil–soil restitution coefficient (B)	0.627	0.563	0.545	0.612
Surface energy (D)	62.210	33.845	10.658	5.117
Contact plasticity ratio (E)	0.621	0.422	0.323	0.313

and Figure 7 show the solution results and the DEM parameter variation with moisture content. The moisture content is a major determinant of the structural stability of the soil, with a direct effect on the cohesion between soil particles and the strength of the bond. The soil–soil restitution coefficient (B), surface energy (D), and contact plasticity ratio (E) were decreasing with the increasing soil moisture content. It indicates that there is a reduction in soil structural strength as moisture content increases. This is due to the thickening of the bound water film on the particle surface as the moisture content increases. This thickening results in lower adhesion at the soil particle-water-air interface and weaker cohesion between particles. The soil–soil static friction coefficient (A) increased and then decreased with moisture content. This is mainly due to the higher clay particle content of clayey soils. As the moisture content increases, there is more contact and friction between the particles. However, as the moisture content increases, the resistance to relative sliding between particles decreases. This reduction in internal friction angle [4] decreases frictional resistance between particles, making soil particles more prone to returning to their original position and condition.

3.6. Result of the Verification Experiment

The optimized DEM parameters were applied to the PST verification simulation. Pressure and sinkage data were exported and compared to the experimental result, as shown in Figure 8. The pressure–sinkage curve characteristic parameters K and n solved by simulation are shown in

Table 10. Comparison of pressure–sinkage curve characteristic parameters solved by experimental and simulation.

Calibration Target	K				n
Moisture content (%)	13.2	18.1	22.7	27.9	13.2	18.1	22.7	27.9
Experimental result	6.776	3.847	2.948	2.700	0.731	0.656	0.587	0.455
Simulation result	6.288	3.932	2.895	2.495	0.681	0.617	0.592	0.482
Relative error (%)	−7.2	2.2	−1.8	−7.6	−6.9	−5.9	0.9	6.0

. Under different moisture contents, the average relative errors of sinking modulus K and soil deformation exponent n obtained through simulation were 4.7% and 4.9%, respectively, compared to the experimental results. This shows that the nonlinear relationship between pressure and sinking under different moisture contents can be effectively represented by the constructed discrete element model and the calibrated parameters.

The soil internal stress at different depths is shown in Figure 9 (22.7% moisture content). In the case of soil surface stress at 30.20 Kpa, the experimental and simulated values for the internal stress in the soil at a depth of 50 mm, 100 mm, and 150 mm were 27.64 Kpa and 25.77 Kpa, 19.56 Kpa and 20.42 Kpa, and 9.58 Kpa and 10.51 Kpa, respectively. The relative errors were 6.7%, 4.4%, and 9.7%, respectively. The simulated soil internal stress trends were consistent with the experimental results at different depths, indicating the simulation model’s accuracy in replicating soil internal stress transfer.

3.7. Soil Internal Pressure Transfer Analysis Based on DEM

Applying the developed simulation model, the transfer of soil internal stress during plate pressure–sinkage was investigated by analyzing the average total force of soil particles (Figure 10). The soil particle trajectory during plate pressure–sinkage is shown in Figure 11. The soil stress clouds at different plate sinkage depths are shown in Figure 12. The variation curves of soil particle average total force with soil depth are shown in Figure 13. The soil particle trajectories at different depth sections are show in Figure 14. The variation of soil stress clouds with plate sinking depth and section depth is shown in Figure 15.

According to Figure 11 and Figure 12, soil particles underneath the plate move downward due to compression. Soil particles at the edge of the plate move to the surrounding area. This is mainly due to the fact that the soil is a continuous medium, and when the soil is compressed downward, it also generates forces on the surrounding area. For surficial particles, the influence range of lateral exposure to plate compression varies little with sinking depth. For the internal soils, the influence range of lateral exposure to plate compression gradually increases, with an overall envelope shape. At the sinkage depth of 30 mm, the lateral compaction radius was approximately 75 mm, representing about half the radius of the soil cylinder. This indicated that the cylinder diameter was large enough without affecting the result.

According to Figure 12 and Figure 13, the compaction impact depths were approximately 100 mm, 150 mm, and 200 mm at plate sinking depths of 10 mm, 20 mm, and 30 mm, respectively. According to the research of He et al. [6] on pressure transfer coefficients, the relationship between internal soil pressure and subsidence depth can be expressed as

$$\begin{array}{l}{S}_i={\displaystyle \frac{{\sigma }_i}{{\sigma }_{i+1}}}\\ S={\displaystyle {\prod }_{i=1}^n{S}_i}\end{array}$$

(15)

where S_i is the stress transmission coefficient of the ith layer soil, S is the stress transmission coefficient of the whole layer soil, and σ_i is the vertical stress at the soil surface of the ith layer soil.

The stress transfer coefficients of 0–150 mm layer soil were 0.41, 0.44, and 0.43 at the sinkage depths of 10 mm, 20 mm, and 30 mm, respectively, which were basically constant and also verified the stability of the simulation model.

According to Figure 14 and Figure 15, in the vertical direction, the normal stress decreases with depth. In the horizontal direction, the normal stress decreases with an increase in the lateral distance from the center of the plate. However, the influence ranges were not the same. At sinkage depths of 10 mm and 20 mm, the influence range also decreases with depth. But at the sinkage depth of 30 mm, the compaction impact radius at 50 mm, 100 mm, and 150 mm depths was 42 mm, 48 mm, and 34 mm, respectively, which increased and then decreased.

4. Conclusions

This study aimed to simulate clayey soil pressure–sinkage processes, considering nonlinear relationships under different moisture contents. A DEM parameter calibration method, applicable to different moisture contents and capable of representing the nonlinear relationship between soil pressure and sinkage, was proposed. PB tests were carried out to identify the sensitivity of the DEM parameters and calibrated by the CC test. The transfer of soil internal pressure was analyzed by applying the model.

(1)

The sinking modulus K and the soil deformation exponent n could reflect the nonlinear character of the pressure–sinkage relationship and were used as calibration targets. The contact plasticity ratio, surface energy, soil–soil restitution coefficient, and soil–soil static friction coefficient were found to have a significant effect on the sinking modulus K and the soil deformation exponent n by PB tests under different moisture contents.

(2)

The CC test was used to calibrate the parameters. To solve the optimal parameter combination, a multi-objective optimization model of DEM parameters was established. The average errors of the sinking modulus K and the soil deformation exponent n obtained by DEM with the experiment across four moisture contents were 4.7% and 4.9%, respectively. This indicates that the constructed discrete element model, along with the calibrated DEM parameter, can effectively reflect the nonlinear relationship between pressure and sinkage under different moisture contents.

(3)

The soil internal stress transfer during the plate sinkage was investigated using the developed simulation model. The simulation and experimental results are in good agreement with a relative error of 6.7%, 4.4%, and 9.7% for the internal stress in the soil at a depth of 50 mm, 100 mm, and 150 mm, respectively. The soil particle trajectory, soil internal stress distribution, and its variation during plate pressure–sinkage progress could be intuitively investigated by the DEM simulation and are in good agreement with theoretical models and experimental results.

This research mainly discussed the discrete elemental model and its parameter calibration method for clayey soil. However, there is a wide variety of soil types, and the mechanical properties of soils with different properties are very complex. In future research, multiple types of soil pressure–sinkage characteristics will be further investigated. Particle modeling that takes into account the actual shape of the soil will be used for DEM to improve the simulation accuracy.