Prediction of Rice Cultivation in India—Support Vector Regression Approach with Various Kernels for Non-Linear Patterns

Abstract

The prediction of rice yields plays a major role in reducing food security problems in India and also suggests that government agencies manage the over or under situations of production. Advanced machine learning techniques are playing a vital role in the accurate prediction of rice yields in dealing with nonlinear complex situations instead of traditional statistical methods. In the present study, the researchers made an attempt to predict the rice yield through support vector regression (SVR) models with various kernels (linear, polynomial, and radial basis function) for India overall and the top five rice producing states by considering influence parameters, such as the area under cultivation and production, as independent variables for the years 1962–2018. The best-fitted models were chosen based on the cross-validation and hyperparameter optimization of various kernel parameters. The root-mean-square error (RMSE) and mean absolute error (MAE) were calculated for the training and testing datasets. The results revealed that SVR with various kernels fitted to India overall, as well as the major rice producing states, would explore the nonlinear patterns to understand the precise situations of yield prediction. This study will be helpful for farmers as well as the central and state governments for estimating rice yield in advance with optimal resources.

1. Introduction

Never having any disparity in how it is cooked, boiled, or fried, rice is practically an everyday meal in Indian society, with India being the second-largest rice-producing nation in the world after China. Approximately 90% of the world population in Asia has the consumption of rice in its meal planning [1]. Rice is devoured by a major percentage of the population in India. With a high carbohydrate content, it is an instant energy provider, and as the nation’s populace is growing, being in excess of 400 million throughout the subsequent years, interest in the farming of rice is set to soar.

In India, rice is cultivated in a large portion of the states, with West Bengal leading the way in production, followed by Uttar Pradesh, Andhra Pradesh, Punjab, Tamil Nadu, and Bihar. Rice is a major food grain in India, where the yield is emulous with China, with more than 11% of the global production rate. Rice production has increased 3.5 times during the last 55 years, after the Green Revolution was imposed in India. Nowadays, due to industrialization and improper irrigation facilities, the area under cultivation is declining in many regions of India, decreasing the quantity of rice production as well as the yield. Inordinate rain prompting flooding and dry seasons from unusual warmth waves, notwithstanding the ongoing droop in the economy, has prompted testing conditions for farmers. Hence, accurate rice yield prediction is significant for the food security of India and is as concerning as the mushrooming task in agrarian research. Additionally, early forecasting of the rice yield for adequate information will be considerate to the policy planners and farmers, as well for optimal land utilization and designing economic policies.

Various traditional statistical methods were employed to predict the rice yield based on highly influential parameters, such as the area under cultivation and production, that still resulted in a gap in measuring the accurate information. Advanced machine learning techniques make it possible to implement means of predicting the rice yield by overcoming the limitations of traditional techniques and forecasting methods for current needs. The advantage of machine learning algorithms is their ability to analyze the data through different dimensions, and diverse patterns or relationships can be summarized from the data. Rather than the traditional regression methods, machine learning techniques have the ability to train the models and perform better for the nonlinear data patterns. Since machine learning algorithms are entirely data-driven, they can lessen, if not dispose of, forecaster assumptions and bias. This is exceptionally useful for depicting the nonlinear complex patterns in the prediction of rice yield, making these forecasts more robust. Machine learning techniques are playing a prominent role in dealing with such complex situations and making wise decisions in support of farmers as well as decision-makers.

2. Review of the Literature

Most researchers have focused on developing traditional and advanced regression models in linear and nonlinear situations. Starting with the traditional multiple linear regression to predict the crop yield in Andhra Pradesh [2], kernel ridge, lasso, and elastic net regression models considering parameters such as the state, district, season, area, and year have been used to estimate the particular crop yield in India [3].

Applications of machine learning techniques are playing a vital role in handling rice production. Based on accurate predictions by these techniques, farmers can plan how much area to take for particular crop production, as well as the yields of crops. A study intended to forecast the rice yield through support vector regression by including the influencing parameters such as soil nitrogen, rice stem weight, and rice grain weight was performed in [4]. Applications of data mining techniques such as k-means clustering, k-nearest neighbors (KNN), artificial neural networks (ANNs), and support vector machines (SVMs) for predicting the yields of horticultural fields provide incredible innovations in computer science and artificial intelligence [5]. Some researchers employed the polynomial and radial basis function kernels of support vector regression (SVR) to predict the output energy of rice production in Iran [6]. The study investigated the relative importance of climate factors in the yield alteration of paddies in southwestern China. A comparison between an SVM with multiple linear regression (MLR) and an artificial neural network (ANN) have been carried out and validated by various cross-validation techniques such as (those abbreviated as) MAE, mean relative absolute error (MRAE), RMSE, relative root mean square error (RRMSE), and a coefficient of determination. It was further suggested to consider various parameters of soil management practices to increase the precision in the developed models [7]. The researchers proposed the Support vector machine-Based Open Crop Model (SBOCM) to apply support vector machine kernels to optimize different separate examinations of three sorts of rice plantings and a few formative stages after dimensionality reduction by principal component analysis (PCA) and evaluation by fivefold cross validation [8]. SVM, J48, and neural networks are methods in the domain of data mining techniques that infer the most ideal outcomes in augmented harvest output [9]. Using MLR, PCA, and SVM, the researchers measured the relationship between climate variables and rice yield in southwest Nigeria. It provides details on environment rice yield interactions, which can emphatically recognize future variabilities and aid future planting periods [10]. By integrating various classifiers, the authors investigated data mining strategies used for the information collected to predict rice crop yield for the Kharif season of the tropical wet and dry climatic zones of India [11]. Machine learning techniques were used in other studies to predict rice yield. Modeling based on the relationship between previous environmental trends, and crop production rate, which was then compared to a measure of accuracy for obscure climatic conditions. Clustering, Regression Trees, ANN, and Ensemble Learning are the methodologies used, and they are cross-validated using Root Mean Square Error (RMSE) [12]. The researchers proposed a method for determining crop selection based on yield prediction, taking into account factors such as soil type, temperature, water density, and crop category. Since the accuracy of the estimate is dependent on the influenced parameters, a better methodology to improve net crop yield is needed [13]. Another study proposed the use of data mining techniques to accurately estimate the yields of six major crops, including Aus rice, Aman rice, Boro rice, Potato, Jute, and Wheat, which can be economically beneficial for development in a specific area [14].

Another research looked at using different machine learning techniques to predict crop yield data and validating the findings using RMSE values [15]. A study used Modular Artificial Neural Networks (MANN) and SVR to estimate Kharif crop production in Visakhapatnam, with the amount of monsoon rainfall factored in to improve accuracy [16]. Other researchers used SVR with RBF kernel to construct a model of wetland rice production based on climate changes in the Kalimantan province to predict with greater precision [17]. Additionally, some researchers used four machine learning algorithms (SVM, KNN, Linear Regression, and Elastic Net Regression) to predict potato tuber yield with soil and crop properties through proximal sensing on a dataset of six fields across Atlantic Canada with different zones for the year 2017–2018 [18].

3. Materials and Methods

3.1. Data Collection

Rice yield data for the years 1962–2018 were gathered from the Directorate of Economics and Statistics, Ministry of Agriculture, India. The study looked at data from across India as well as the top five rice-producing states, using parameters like Area Under Cultivation (Thousand Hectares), Production (Thousand Tonnes), and Yield (KG/Hectare). Due to the bifurcation in 2014, Andhra Pradesh, one of the top states in rice production, is not included. This study compares rice yields in India and major rice-producing states such as West Bengal, Uttar Pradesh, Punjab, Tamil Nadu, and Bihar to determine the influence of each state.

3.2. Methodology

3.2.1. Support Vector Regression

This study employs the SVR algorithm proposed by Vapnik and Chervonenkis (1963), which incorporates the ε-insensitive loss function. For solving classification and regression analysis, the SVR provides promising features and empirical results. The main idea behind this algorithm is to fit as much data as possible without violating the margin. It tries to find the hyperplane from the given data points and determines the closest relation between the support vectors and the hyperplane’s location, as well as the function that is used to describe them. In certain cases, the SVR tries to suit the best line possible by limiting the number of violation constraints using hypertuning parameters such as ε, γ, and C, the regularization parameter with kernel transformation.

The basics on SVR are recalled below. Let $F=\{(x_1,y_1),(x_2,y_2),\dots ,(x_N,y_N)\}$ be the set of N samples, where $(x_i,y_i)$ are the input vectors corresponding to the output target variables. The regression function where x is augmented by one, b and w are the vectors is given as:

$$y(x)={\displaystyle {\sum }_{i=1}^N{w}_i{x}_i}+b;y,b\in \mathbb{R};x,w\in {\mathbb{R}}^N$$

(1)

$$=w^{T}x+b;x,w\in {\mathbb{R}}^N,$$

(2)

where $x={(x_1,\dots ,x_N)}^T,y={(y_1,\dots ,y_N)}^{T}andw={(w_1,\dots ,w_N)}^T$.

The optimization problem is given by

$$Min\frac{1}{2}{\Vert w\Vert }^2+C{\displaystyle {\sum }_{i=1}^N({\delta }_i+{\delta }_i^{*})}$$

(3)

subject to constraints

$$\left\{\begin{array}{l}{y}_i-w^T{x}_i-b\le \epsilon +{\delta }_i\\ w^T{x}_i+b-y_i\le \epsilon +{\delta }_i^{*}\end{array}\right\};{\delta }_i\ge 0,{\delta }_i^{*}\ge 0,$$

(4)

where C is the regularization parameter; a positive constant penalty coefficient that minimize the flatness or the error of the objection function and ${\delta }_i,{\delta }_i^{*}$ are the slack variables added to shield the error.

The dual formula of non-linear SVR is obtained by using Lagrange Multipliers from the primal function, introducing non-negative multipliers ${\mu }_i$ and ${\mu }_i^{*}$, for each observation $x_i$ given as:

$$L(\gamma )=\min \frac{1}{2}{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j=1}^{N}K({\mu }_i+{\mu }_i^{*})}}({\mu }_i-{\mu }_i^{*})+\epsilon {\displaystyle \sum _{i=1}^N({\mu }_i+{\mu }_i^{*})-}{\displaystyle \sum _{i=1}^N{y}_i({\mu }_i-{\mu }_i^{*})}$$

(5)

where K is the kernel function defined as $K=K(i,j)=\phi {(x_i)}^T\phi (x_j);\phi (x)$ is the transformation that maps $x$ into a high dimensional space subject to constraints.

$$\{{\displaystyle {\sum }_{i=1}^N({\mu }_i-{\mu }_i^{*})}=0;0\le {\mu }_i,{\mu }_i^{*}\le C;i=1,2,\dots ,N\}$$

(6)

The different of kernel functions involved in this study are given below:

1	Linear	$K(i,j)=K(x_i,x_j)$
2	Polynomial	$K(i,j)={(\gamma (x_i,x_j)+r)}^d$
3	Radial Basis Function	$K(i,j)=e^{\left(-\gamma {\left|x_i-x_j\right|}^2\right)}$

where $\gamma$ and r are the structural parameters of the kernel function and d is the degree of the polynomial function.

Hence, the regression estimate of the non-linear kernel is expressed as

$$h(x_i)={\displaystyle {\sum }_{i=1}^N({\mu }_i-{\mu }_i^{*})}K(x_i,x_j)+b$$

(7)

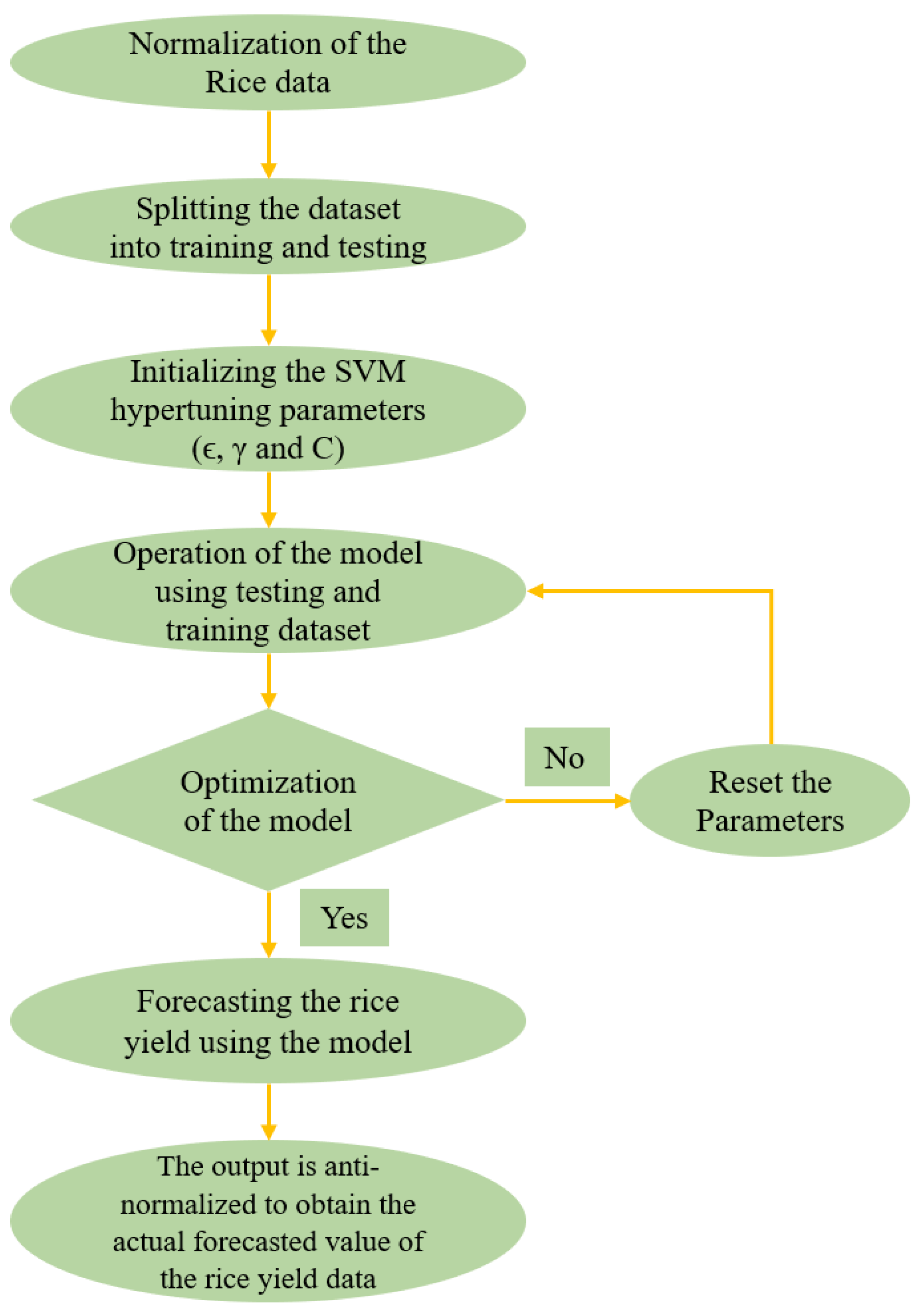
3.2.2. Hyperparameter Optimization

Hyperparameter tuning and cross validation are two activities that are usually performed in data pipelines. Obtaining a suitable configuration for the hyperparameters necessitates precise knowledge and intuition, which is often achieved via the trial-and-error process. As a result, parameter tuning selects values for a model’s parameter that improve the model’s accuracy. For different kernels, the following parameters are used in the analysis.

• Regularization parameter, C: If the hyper-dimensionality plane’s is random, it can be perfectly fitted to the training dataset, resulting in overfitting. As the value of C increases, the hyperplane’s margin shrinks, increasing the number of correctly classified samples.
• Kernel parameter, $\gamma$: This implies the radius of influence, the higher values closer the sample points. This is very sensitive to the model, as when $\gamma$ becomes large, the radii of influence of the support vectors tend to be too small, leading to overfitting.
• Error Parameter, ε: Generally used in regression, it is an additional value of tolerance, when there is no penalty in the errors. The errors are penalized as ε approaches zero, and the higher the values, the greater the model error.
• The non-linear SVR is used in the study to forecast rice yield data. The kernel function is applied to each data set in order to map the nonlinear observations into a higher-dimensional space where they can be separated. The SVR’s efficiency is determined by the hypertuning parameters, which are interdependent [19,20,21,22]

3.2.3. Schematic Diagram of Performing SVR

Figure 1 presents the process of our SVR methodology.

3.3. Cross-Validation Method

The training set is divided into k distinct subsets using k-fold cross validation. Then, during the entire training process, each subset is used for training and the others k-1 are used for validation. This is done to improve the classification and regression tasks’ preparation. The parameter calibration was performed using the training dataset during the training stage, and the trained model was then evaluated by evaluating the testing results using the RMSE and Mean Absolute Error (MAE) metrics. In this analysis, the average values of RMSE and MAE of 10-folds were used for training results.

The RMSE is the measure of the differences between values predicted by a model or an estimator and the values observed. It can be expressed as

$$RMSE=\sqrt{\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{(y_i-\widehat{y})}^2}}$$

(8)

The MAE is the average of absolute difference between the target and predicted values. It is given as

$$MAE=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N\left|y_i-\widehat{y}\right|}$$

(9)

4. Results and Discussion

4.1. Summary Statistics of Rice Parameters

Descriptive statistics such as mean, Standard Deviation (SD), skewness, and kurtosis are evaluated for the Yield (Kg/hectare), Area (Thousand hectares), and Production (Thousand tonnes) for Overall India and major states.

Table 1. Summary statistics of yield (Kg/Hectare) for the years 1962–2018.

States	Mean	Standard Deviation	Skewness	Kurtosis
All India	1653.105	498.9388	0.115	−1.235
Bihar	1187.512	458.9505	1.215	1.243
Punjab	2991.355	923.6729	−0.84	−0.345
Tamil Nadu	2477.671	734.8786	0.033	−1.022
Uttar Pradesh	1519.801	610.1552	−0.217	−1.443
West Bengal	1876.755	629.6552	0.107	−1.521

summarizes the yield for India as a whole and the top five states. The mean values of West Bengal (1876.755 ± 629.6552), Tamil Nadu (2477.355 ± 734.8786), and Punjab (2991.355 ± 923.6729) are more than average of overall India with their standard deviations. The distribution of rice yield for overall India, Tamil Nadu, and West Bengal exhibiting a positively skewed (0.115, 0.033, and 0.107) and platykurtic curve (−1.235, −1.022, and −1.521) as there is a slight drop of yield seen in recent years. For Bihar, there is a positive skewness (1.215) and leptokurtic (1.243) distribution recorded, as a consistent growth of yield is observed in subsequent years. Similarly, for Punjab and Uttar Pradesh, a negative skewed (−0.84 and −0.217) and platykurtic (−0.345 and −1.443) distribution is found, which implies that yield is declining due the influence of many parameters under consideration.

Table 2. Summary statistics of area under cultivation (thousand hectares) for the years 1962–2018.

States	Mean	Standard Deviation	Skewness	Kurtosis
All India	41037.68	2911.21	−0.48	−0.945
Bihar	4576.484	897.5415	−0.644	−1.33
Punjab	1739.461	945.8439	−0.29	−1.464
Tamil Nadu	2198.466	386.5147	−0.033	−0.828
Uttar Pradesh	5278.316	572.2343	−0.404	−1.18
West Bengal	5375.904	432.7927	−0.336	−0.829

shows the summary statistics of rice crop area under cultivation from 1962 to 2018 for India as a whole and the big five rice-producing states. From the table, the mean and SD values of WB (5375.904 ± 432.7927), UP (5278.316 ± 572.2343), and Bihar (4576.484 ± 897.5415) are allocating major land for rice cultivation and least is observed in Punjab (1739.461 ± 945.8439) and Tamil Nadu (2198.316 ± 386.5147). The skewness and kurtosis values are negatively distributed and follow a platykurtic distribution, which implies that there is a drastic decline in areas under cultivation of the major states and overall India.

Table 3. Summary statistics of production (thousand tonnes) for the years 1962–2018.

States	Mean	Standard Deviation	Skewness	Kurtosis
All India	69143.93	24644.12	0.067	−1.316
Bihar	5179.959	1378.052	0.000107	−0.005
Punjab	5999.512	4040.386	−0.033	−1.384
Tamil Nadu	5301.673	1346.065	−0.128	−0.133
Uttar Pradesh	8332.887	3942.218	−0.117	−1.453
West Bengal	10268.23	3896.285	−0.038	−1.659

describes the summary statistics of production of rice for the overall India and major producing states. The mean and SD values of Bihar (5179.959 ± 1378.052), Punjab (5999.959 ± 4040.386), Tamil Nadu (5301.673 ± 1346.065), Uttar Pradesh (8332.887 ± 3942.218), and West Bengal (10268.23 ± 3896.285). Table 3 shows that India and Bihar have positively skewed production and a slight increase, while Punjab, Tamil Nadu, Uttar Pradesh, and West Bengal have negatively skewed production. The kurtosis values for India as a whole are negative, and the major states have a platykurtic distribution. It implies a decline in rice production in the states for the observed years because, as the population grows, the region and production of the states contribute less to the yield earned.

4.2. Rice Yield Prediction of Overall India and Major Producing States Using Various Kernels of SVR with Hypertuning Parameters

Rice yield is primarily affected by the region under cultivation and development, so it was treated as a dependent variable in this analysis, with the other two variables serving as predictors. The best fitted kernels for yield of the overall India and other five states are investigated for both the training and testing data with more accuracy for implementing different user-defined hypertuning parameters such as C, $\epsilon$, γ, and d. A grid search optimization and k-fold cross validation methods are employed to optimize the hyperparameters. In this study, we consider cross validation (k = 10) to evaluate the model performance of training data of rice yield prediction and to reduce error estimates with less bias and variance in the dataset. The set of hyperparameters (C, $\gamma$, and d) is initialized in the given range C $\in$ (0.05, 1.1), $\gamma \in$ (0.05, 0.5) for the polynomial kernel, $\gamma \in$ (0.25, 3) for the RBF kernel, d $\in$ (1, 5) and $\epsilon$ values are set to 0.1 by default. The research focuses on regression models that use SVR and various kernels such as linear, polynomial, and radial basis functions. The findings are summarized in

Table 4. Error analysis and cost values of training and testing datasets by using SVR linear kernel for rice yield prediction.

Dataset	States	RMSE	MAE	Cost
Train	All India	27.52055	23.05118	1.1
	Bihar	80.40918	68.36108	1.1
	Punjab	297.4711	224.2278	0.25
	Tamil Nadu	68.64182	57.58319	0.35
	Uttar Pradesh	43.47316	39.07503	1.1
	West Bengal	41.00673	35.04825	1.05
Test	All India	31.05632	22.72886	1.1
	Bihar	62.60574	50.93586	1.1
	Punjab	493.5309	401.1693	0.25
	Tamil Nadu	84.2756	72.35583	0.35
	Uttar Pradesh	61.46972	52.59493	1.1
	West Bengal	35.11301	30.23646	1.05

,

Table 5. Error analysis and degree, cost, and $\gamma$ values of training and testing datasets by using SVR polynomial kernel for rice yield prediction.

Dataset	States	RMSE	MAE	Degree	Cost	$\mathit{\gamma }$
Train	All India	28.97924	25.07671	2	1	0.35
	Bihar	31.2602	26.9666	3	0.5	0.25
	Punjab	90.38687	74.10524	4	1.1	0.4
	Tamil Nadu	49.27959	42.12796	2	0.85	0.25
	Uttar Pradesh	35.82643	29.72098	4	1	0.25
	West Bengal	37.9135	29.82876	1	1.1	0.4
Test	All India	18.23377	14.55882	2	1	0.35
	Bihar	37.3793	31.71476	3	0.5	0.25
	Punjab	109.3165	89.24507	4	1.1	0.4
	Tamil Nadu	60.88977	58.1863	2	0.85	0.25
	Uttar Pradesh	36.31511	31.64557	4	1	0.25
	West Bengal	35.79188	27.48669	1	1.1	0.4

and

Table 6. Error analysis and Sigma $\left(\gamma \right)$ and cost values of training and testing datasets by using SVR radial basis function kernel for rice yield prediction.

Dataset	States	RMSE	MAE	Sigma $\left(\gamma \right)$	Cost
Train	All India	47.90525	37.5891	0.5	1.1
	Bihar	65.09703	45.87701	0.25	1.1
	Punjab	196.5431	150.9922	2.75	1.1
	Tamil Nadu	131.1512	94.32958	0.25	1.1
	Uttar Pradesh	71.06016	53.27636	0.25	1.1
	West Bengal	69.99749	58.21759	0.25	1
Test	All India	94.60944	55.98602	0.5	1.1
	Bihar	161.7523	85.16538	0.25	1.1
	Punjab	174.8837	140.0258	2.75	1.1
	Tamil Nadu	102.7245	67.17755	0.25	1.1
	Uttar Pradesh	98.70091	69.96868	0.25	1.1
	West Bengal	69.12172	59.52803	0.25	1

.

Table 4 represents the ${\mathit{SVR}}_{\mathit{Linear}}$ kernel for overall India and other five states with RMSE, MAE, and predefined cost function.

It is clearly observed that ${\mathit{SVR}}_{\mathit{Linear}}$ has the best predicted output for the overall India (training and testing datasets) with errors validation such as RMSE (27.52 and 31.056) and MAE (23.0518 and 22.7289) with cost function C = 1.1. For the testing set West Bengal, the ${\mathit{SVR}}_{\mathit{Linear}}$ kernel has the best predicted output with RMSE and MAE as 31.05 and 27.72, respectively, and with C = 1.05.

Table 5 depicts the optimal values of the parameters of error analysis (RMSE and MAE), degree of polynomial, cost, and $\gamma$ values using SVR polynomial kernel. ${\mathit{SVR}}_{\mathit{Polynomial}}$ is the best predicted output for the five major states, i.e., Bihar, Punjab, Tamil Nadu, Uttar Pradesh, and West Bengal in the training dataset by allocating predefined parameters such as degree of polynomial (d $\in$ (1, 5)), Cost (C $\in$ (0.05, 1.1)), and scale parameter ($\gamma \in$ (0.05,0.5)). Similarly, for the testing set, Bihar, Punjab, Tamil Nadu, and Uttar Pradesh have ${\mathit{SVR}}_{\mathit{Polynomial}}$ as the best kernel.

Table 6 depicts the error validation, Sigma ($\gamma \in (0.25,3)$ and cost (C $\in$ (0.05, 1.1) values of the SVR Radial Basis Function on rice yield of overall India and major states. The results revealed that there is no significant performance for the overall India and the major five states by implementing the ${\mathit{SVR}}_{\mathit{RBF}}$ kernel.

4.3. SVR with Different Kernels for Randomly Allocated Testing Data of Rice Yield

Table 7. SVR kernels for testing data of overall India.

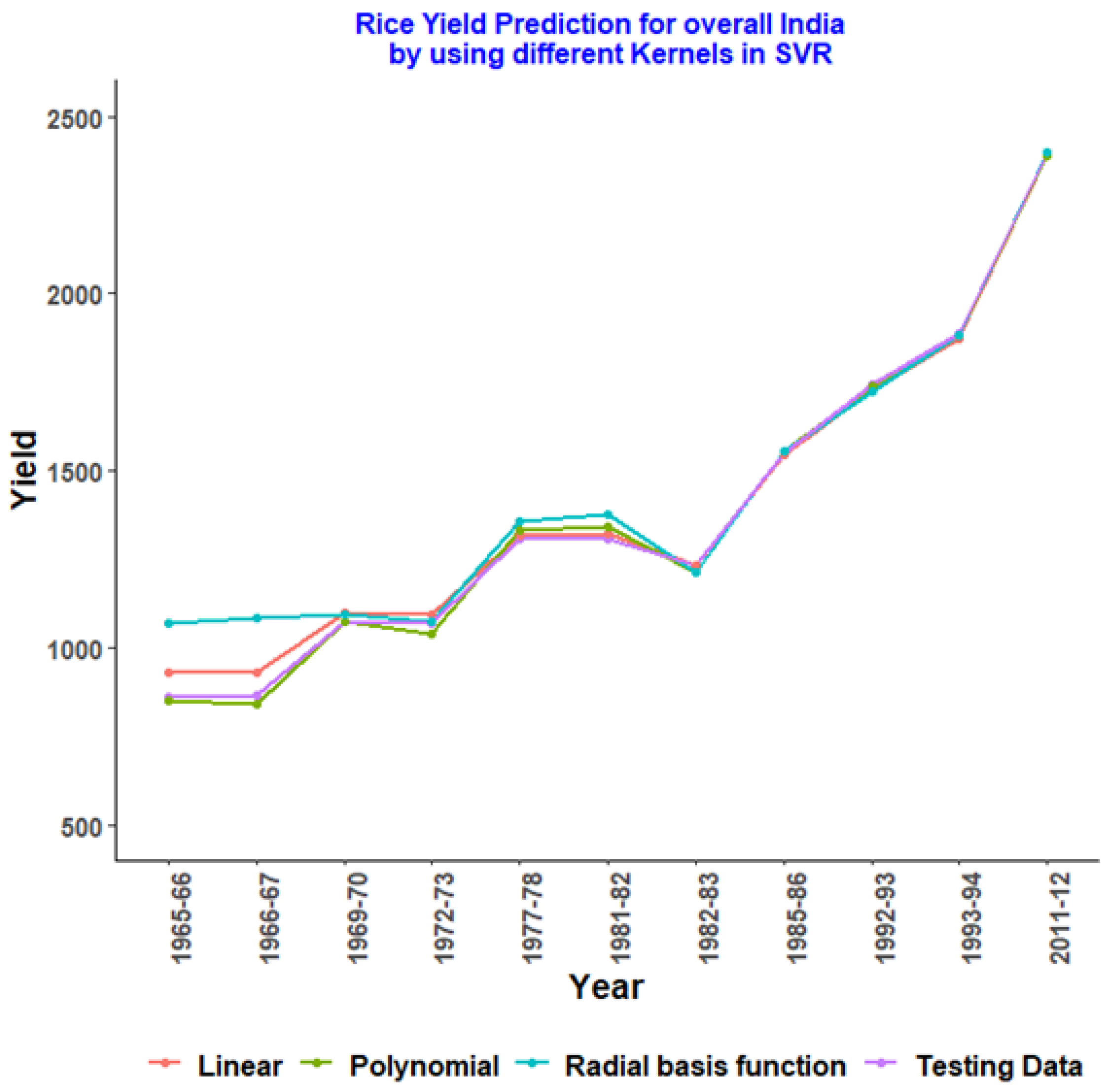
Year	Testing Data	Linear	Polynomial	Radial Basis Function
1965–66	862	927.3773	848.0545	1067.776
1966–67	863	928.2253	841.4404	1082.654
1969–70	1073	1099.57	1074.2819	1095.163
1972–73	1070	1092.218	1040.5272	1071.356
1977–78	1308	1316.539	1331.4916	1354.699
1981–82	1308	1321.101	1342.5861	1374.131
1982–83	1231	1233.836	1214.1736	1211.379
1985–86	1552	1542.52	1555.7508	1556.554
1992–93	1744	1726.412	1737.1086	1725.277
1993–94	1888	1873.587	1883.6489	1883.61
2011–12	2393	2388.328	2389.0101	2399.779

,

Table 8. SVR kernels for testing data of Bihar.

Year	Testing Data	Linear	Polynomial	Radial Basis Function
1965–66	812.06	749.3555	854.4835	820.106
1966–67	365.93	342.1535	342.8664	880.7237
1969–70	729.85	612.1557	761.4629	816.3171
1972–73	946.77	963.1515	995.7426	889.5958
1977–78	983.18	945.5241	997.2016	1029.8179
1981–82	793.07	711.3524	831.4973	826.7751
1982–83	681.44	688.4047	738.9844	739.2374
1985–86	1127.61	1151.086	1128.1617	1142.9612
1992–93	806.16	823.3341	867.6472	778.268
1993–94	1294.78	1364.048	1293.5672	1325.887
2011–12	2154.85	2051.369	2125.3052	2212.6976

,

Table 9. SVR kernels for testing data of Punjab.

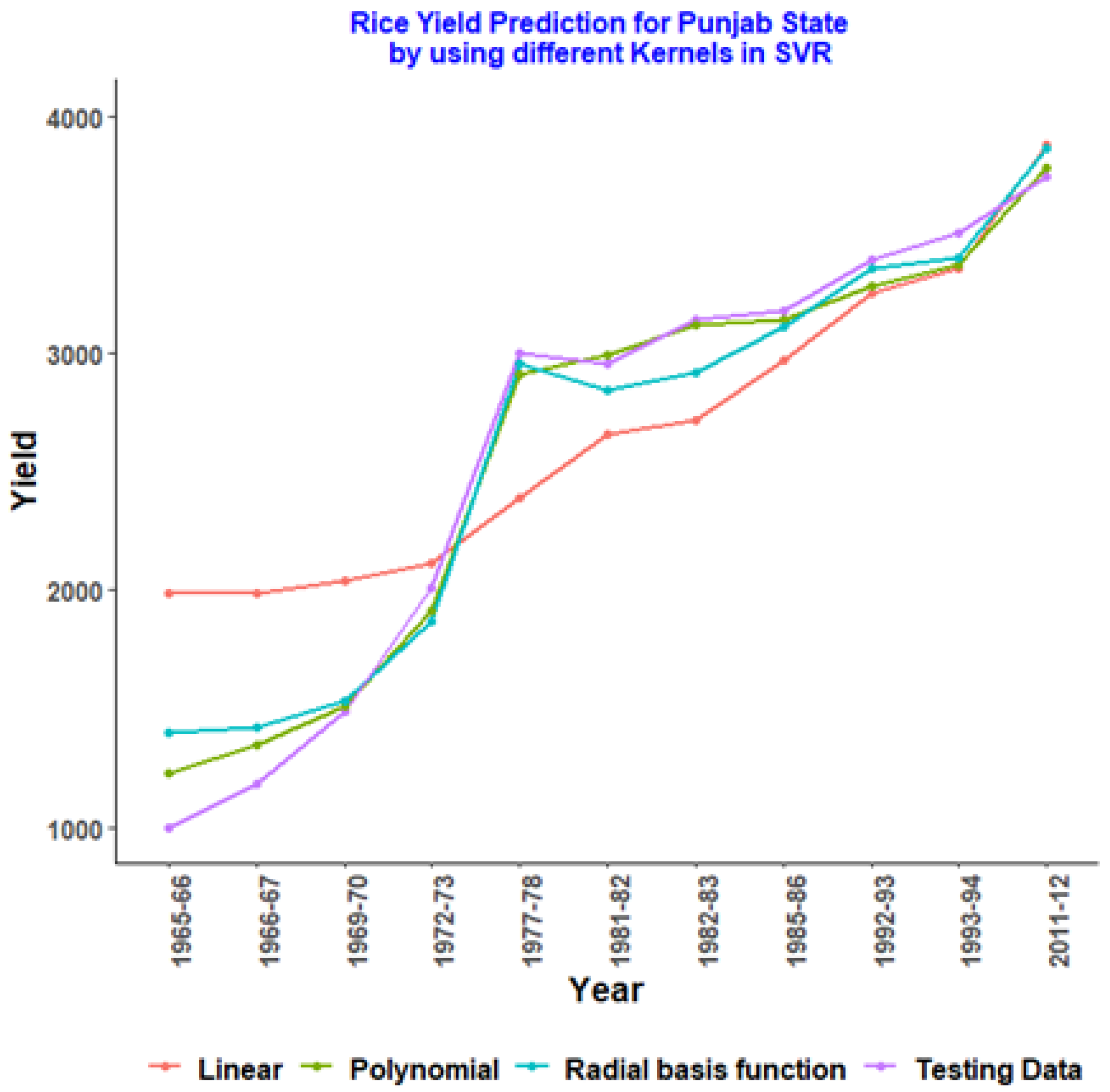
Year	Testing Data	Linear	Polynomial	Radial Basis Function
1965–66	1000	1984.915	1231.086	1400.547
1966–67	1185.96	1987.467	1344.406	1421.784
1969–70	1490.37	2040.976	1510.019	1531.768
1972–73	2008.41	2110.805	1910.526	1869.862
1977–78	3001.2	2389.271	2913.105	2953.451
1981–82	2956.69	2653.454	2994.668	2844.673
1982–83	3144.05	2714.251	3115.535	2918.069
1985–86	3179.05	2972.802	3140.217	3107.372
1992–93	3390.8	3251.927	3282.86	3357.642
1993–94	3507.11	3359.478	3371.527	3397.523
2011–12	3740.95	3876.672	3778.639	3864.746

,

Table 10. SVR kernels for testing data of Tamil Nadu.

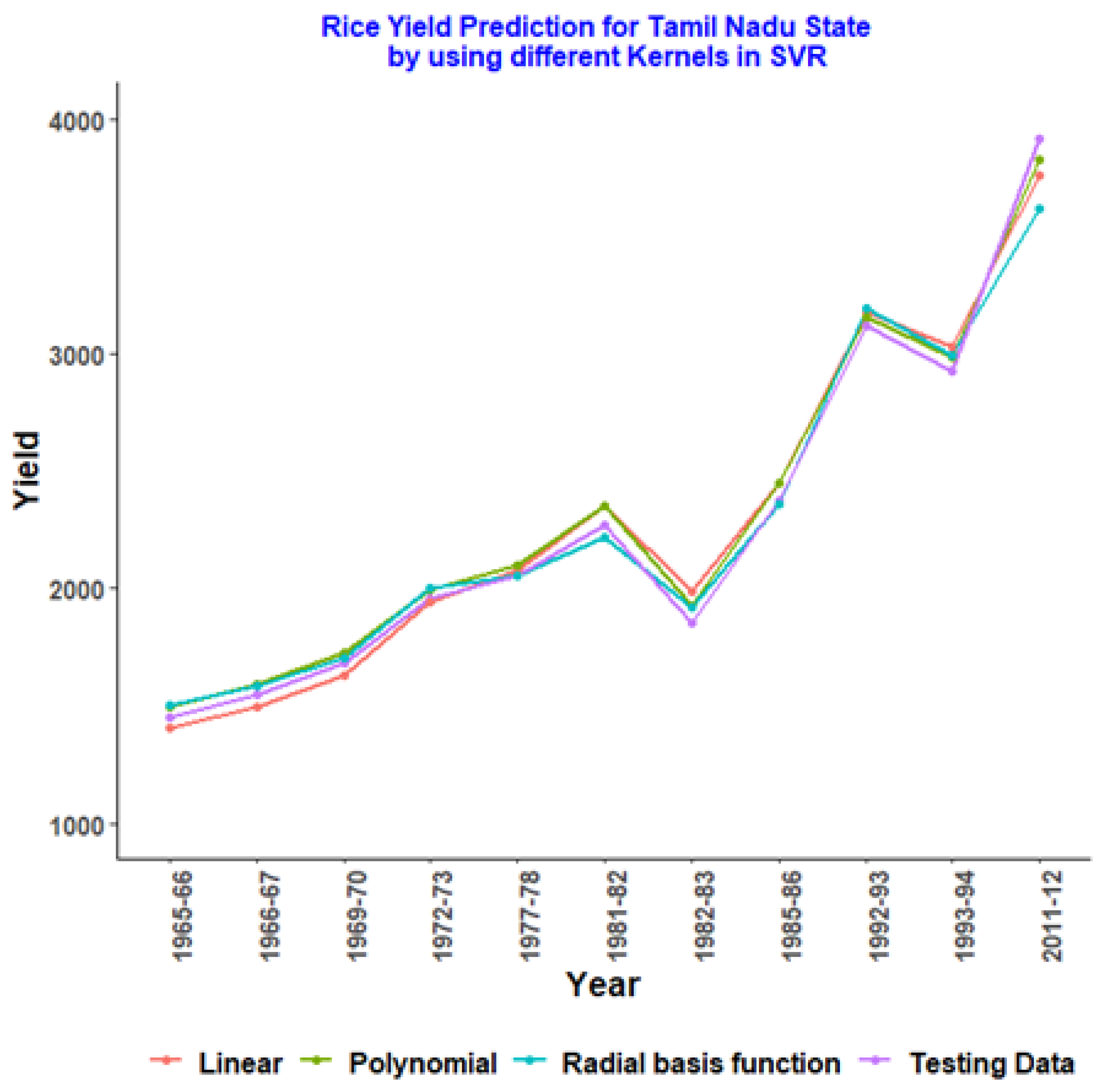
Year	Testing Data	Linear	Polynomial	Radial Basis Function
1965–66	1454.21	1409.09	1493.528	1503.597
1966–67	1551.08	1495.778	1593.943	1586.809
1969–70	1681.58	1632.861	1728.835	1700.689
1972–73	1953.66	1941.907	1996.371	2000.905
1977–78	2050.46	2072.662	2100.432	2052.946
1981–82	2272.8	2349.43	2347.931	2216.156
1982–83	1854.75	1989.945	1925.694	1923.1
1985–86	2371.81	2449.183	2450.186	2355.629
1992–93	3115.59	3177.199	3156.456	3190.227
1993–94	2926.68	3027.936	2984.151	2993.174
2011–12	3917.8	3757.044	3822.656	3615.108

,

Table 11. SVR kernels for testing data of Uttar Pradesh.

Year	Testing Data	Linear	Polynomial	Radial Basis Function
1965–66	556.72	673.1853	540.2164	763.3959
1966–67	452.81	566.0447	423.2931	669.2615
1969–70	779.22	819.2724	799.4894	777.9589
1972–73	748.22	805.2615	759.5732	778.4787
1977–78	1068.93	1049.531	1115.0186	1017.2877
1981–82	1094.45	1067.715	1157.0251	1155.563
1982–83	1114.85	1088.614	1167.6177	1103.6731
1985–86	1488.21	1458.631	1533.773	1548.5288
1992–93	1772.77	1729.739	1777.3107	1820.2415
1993–94	1902.14	1841.217	1881.8026	1923.9034
2011–12	2357.83	2403.677	2319.2443	2296.3077

and

Table 12. SVR kernels for testing data of West Bengal.

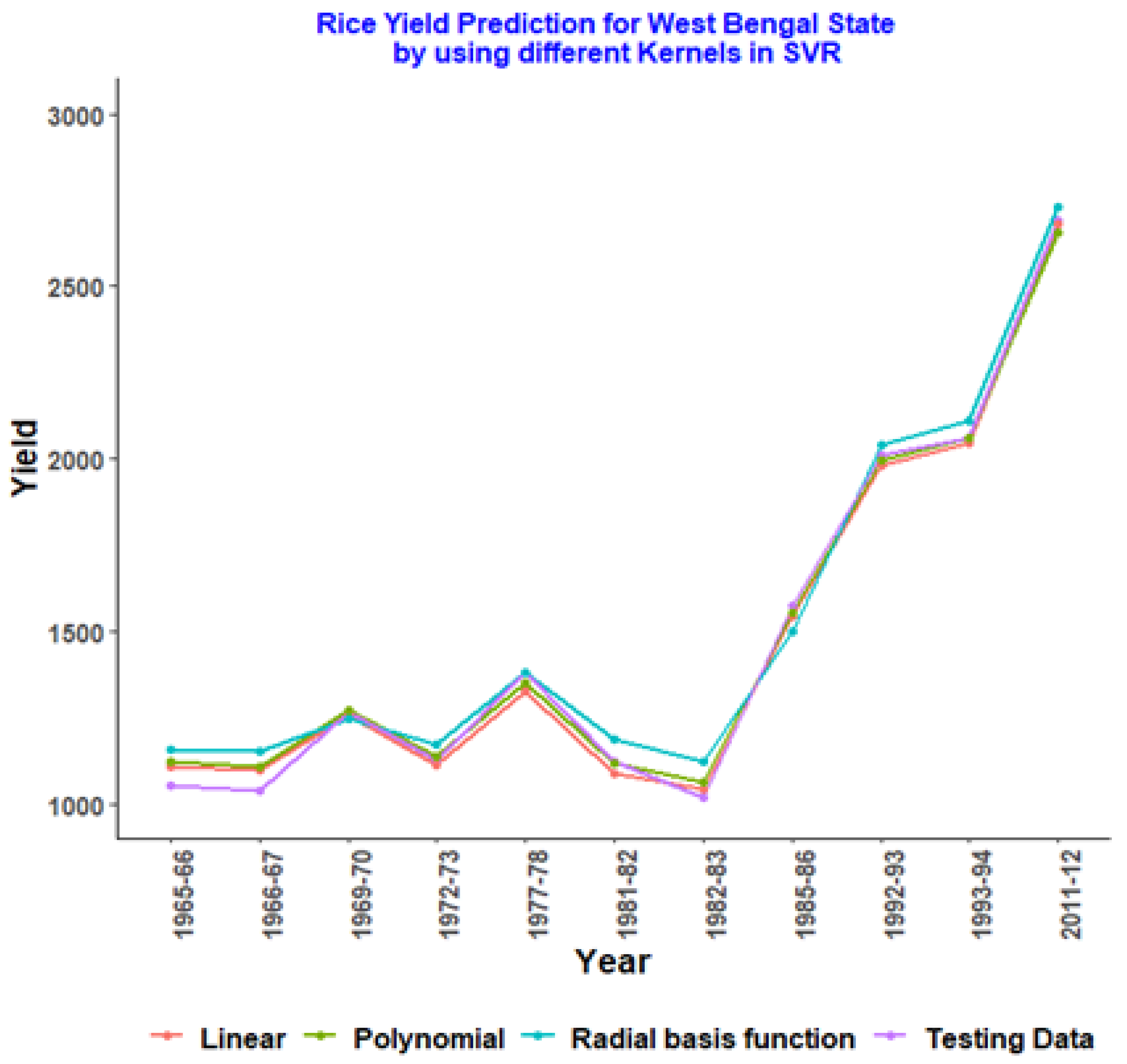
Year	Testing Data	Linear	Polynomial	Radial Basis Function
1965–66	1051.91	1108.185	1119.508	1156.513
1966–67	1037.77	1095.963	1107.669	1152.406
1969–70	1266.08	1254.931	1271.739	1246.331
1972–73	1127.41	1114.321	1137.813	1172.415
1977–78	1381.57	1325.851	1352.202	1377.464
1981–82	1119.5	1086.001	1114.68	1184.133
1982–83	1018.02	1043.034	1062.954	1123.664
1985–86	1573.43	1545.416	1553.579	1499.179
1992–93	2009.9	1982.777	1993.333	2039.329
1993–94	2061.25	2044.542	2058.219	2110.904
2011–12	2688	2680.183	2657.777	2731.098

show the randomly assigned testing data modeled with best fitted SVR kernels such as linear, polynomial, and radial basis function of rice yield training data for India as a whole and the major five rice producing states, as well as graphical representations of the same.

The tables (Table 7, Table 8, Table 9, Table 10, Table 11 and Table 12) and graphical representations (Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7) depict the prediction of testing data (randomly chosen years) of rice yield of the overall India and the major states through various SVR kernels. From the overall summary of

Table 13. Best fitted regression models with SVR kernels.

States	Dataset	RMSE	MAE	Best Fitted SVR Kernels
All India	Training	27.52055	23.05118	Linear
	Testing	31.05632	22.72886
Bihar	Training	31.2602	26.9666	Polynomial
	Testing	37.3793	31.71476
Punjab	Training	90.3869	74.1052	Polynomial
	Testing	109.3165	89.2451
Tamil Nadu	Training	49.2756	42.1280	Polynomial
	Testing	60.8898	58.1863
Uttar Pradesh	Training	35.8264	29.7210	Polynomial
	Testing	36.3151	31.6456
West Bengal	Training	37.9135	29.8288	Polynomial
	Testing	35.11301	30.23646	Linear

, it is observed that ${\mathit{SVR}}_{\mathit{Linear}}$ and ${\mathit{SVR}}_{\mathit{Polynomial}}$ kernels are the best models to predict the rice yield of overall India, and major states show a lower RMSE and MAE as compared to ${\mathit{SVR}}_{\mathit{RBF}}$.

When compared to advanced machine learning techniques, traditional methods for forecasting time series data, such as Autoregressive Integrated Moving Average (ARIMA) models, regression models, and other statistical models [23,24,25], which applied to agricultural production, did not yield good approximation values [4,6,7,8,11,12,17,26,27,28]. One of the drawbacks of conventional approaches is that the time series data must be in chronological order when fitting the models, which can be solved by advanced machine learning techniques that select data points at random and suit well–trained models. In comparison to traditional statistical models, the assumptions of non-parametric techniques like SVR were much more versatile in dealing with such non-linear uncertainty situations in order to train the history of rice productivity more accurately. The exploration of various kernels of SVR for major rice-producing states and India as a whole was described in a much better way in this study, allowing for a much better understanding of the exact patterns of rice yield. Even though the major rice-producing states have non-linear (polynomial) patterns, India’s yield has linear patterns.

Graphical representations of SVR kernels with testing data:

5. Conclusions

The demand for rice in India will continue to rise in the coming decades as the country’s population grows. Predicting agricultural production with advanced machine learning techniques is the need of the hour to deliver high reliability and stability prediction performance, which will help India address food security issues and public health concerns. In place of conventional approaches, the models derived from the SVR with different kernels in this study are very useful in handling both linear and non-linear situations of rice production. As a result, the SVR appears to be a viable alternative to other predictive models. Rice yield is limited in this study since it only considers two influencing factors: Area under cultivation and production; however, it can be expanded by adding other influencing factors such as environmental, climatic, and irrigation, fertilizers, and soil fertility parameters to obtain more accurate results. Farmers and crop planners may use these outbreaking results to predict total yields ahead of time and benefit from land allocation and development of various rice crops. This study will provide researchers and policymakers with information to help them concentrate on developing more accurate prediction models to assist the government in implementing new agricultural policies that favor farmers and agribusiness industries.