Predicting Field Efficiency of Round-Baling Operations in High-Yielding Biomass Crops

1. Introduction

Herbaceous biomass can contribute to the emerging bio-economy as a feedstock for electricity generation, process steam, liquid fuel, commodity chemicals, and other bioproducts. The Southeast USA has unique biomass potential [1] because of: high annual rainfall, considerable land that can be diverted to biomass production without significant competition with food and feed production, and an established woody biomass industry. Grasses, such as switchgrass, are one of the most significant potential sources of biomass. An advantage of switchgrass is that it can be harvested much like hay, which is a well-known operation amongst farmers in the region, and, unlike woody biomass, it provides an annual harvest, and, thus, provides an annual income to the producer.

The two most commonly employed methods of grass harvesting are round and large-square baling. Although large-square balers can achieve a higher field capacity (ha/h), round bales offer several attractive features for the Southeast. Even in a humid environment, round bales can typically be stored under ambient conditions in the field, whereas large-square bales require covered storage. Round balers are less expensive to purchase and operate as they require smaller tractors than large-square balers, an advantage for the smaller farms [2].

Due to high variability of machine capacity within a field, a consistent relationship has not yet been developed for predicting in-field performance of round balers. Such data are needed to define and simulate harvest of biomass for energy applications. Typically, two major issues are poorly represented in these models [3]: available working time during the time window in which the operation is required to be completed and the capacity of forage equipment as impacted by yield. Machinery performance assumptions have a direct bearing on estimates of the number of equipment units needed and the cost to fulfill biorefinery demand during the harvest window. There have been only a few published reports documenting field studies of switchgrass harvest experiments. Plus, most current forage equipment, and emerging technology modifications to this equipment, have limited performance data [4,5,6] for operation in high-yielding conditions.

Simulation of annual yield estimates, which incorporate the weather during the growing season, are often integrated into these models to demonstrate year-to-year effects on biomass feedstock costs. Some simulations show the increased yield potential from genetically modified energy crops. As an example, the modified Integrated Biomass Supply Analysis and Logistics Model (IBSAL) [7] is applied to harvesting stover, straw, and switchgrass with yields ranging from 2 to 7 dry-Mg/ha for straw and stover, and 5 to 50 dry-Mg/ha for switchgrass. While many system effects of crop yield—such as supply radius [7]—have been studied, the impact of yield on round-baler performance has not been modeled.

The mode of operation of round balers, to accumulate grass and then stop to wrap or tie and drop the bale, differentiate it from other agricultural equipment that can be simulated as a continuous operation. Most agricultural field operations—such as planting, mowing and even rectangular baling—can be easily modeled as function of yield. Round baling, however, is not a continuous operation in that the baler must stop for a specified time to package and drop the bale. Whereas increasing yield typically increases field efficiency of continuous field operations, the same is not true for a round baler. In both rectangular and round-baling, the number of bales per field is directly correlated to yield; assuming all bales have approximately equal mass, higher yielding fields produce more bales. As the number of bales increases, so does the number of times that the baler must stop. This time to package and drop bales can significantly decrease field efficiency and is not accounted for in most previous modeling studies of herbaceous biomass harvest operations. The purpose of this study is to develop a mathematical relationship between yield and round-baling field efficiency to predict how the capacity of biomass balers is impacted by high-yielding bioenergy crops. This relationship will be used in modeling a switchgrass harvest operation to more accurately quantify the impact of yield on harvest cost.

2. Materials and Methods

Model simulations for bioenergy planning need to utilize equipment capacity when operating under actual field conditions. Throughput for agricultural machinery is expressed by Srivastava et al. [8] as:

$${\mathrm{C}}_{\mathrm{m}}=\left(\frac{v\cdot \mathrm{W}\cdot \mathrm{Y}\cdot {\mathrm{E}}_{\mathrm{f}}}{{\mathrm{K}}_1}\right)$$

(1)

where:

• C_m = material capacity sometimes referred to as throughput, Mg/h
• v = field speed, km/h
• W = implement working width, m
• E_f = field efficiency, decimal
• Y = unit yield of the field, Mg/ha
• K₁ = 10 km-m/ha.

Some models calculate capacity in their simulation using the typical average speed, field efficiency, and width from the American Society of Agricultural and Biological Engineers (ASABE) Standards [9,10] and assume that these parameters remain constant regardless of yield. Machinery management relationships for these assumptions are shown in Figure 1. The effective speed (green line) is a speed with the field efficiency incorporated, and the field capacity (blue line) is constant over the range of yields. The throughput (red line) is linearly related to yield as given in Equation (1). Srivastava et al. [8] stated that capacity measurements can be on the basis of area covered per unit time (field capacity, C_f, ha/h) or of material processed per unit time (C_m, Mg/h), and these two capacities are related by the following:

$${\mathrm{C}}_{\mathrm{f}}=\left(\frac{{\mathrm{C}}_{\mathrm{m}}}{\mathrm{Y}}\right)$$

(2)

The travel speed of balers, forage choppers, and other machines used to harvest herbaceous biomass are limited by the throughput (C_m) of the machine; these are capacity-limited machines. For a given C_m, W, and Y, Equation (1) can be used to find the allowable or effective travel speed.

Forage machines will jam if a throughput greater than the maximum design throughput (C_mx) is introduced into the machine. The yield (Y_c) at which the maximum throughput is achieved can be expressed as:

$${\mathrm{Y}}_{\mathrm{c}}=\left(\frac{{\mathrm{C}}_{\mathrm{mx}}}{{\mathrm{C}}_{\mathrm{f}}}\right)$$

(3)

This relationship is shown in Figure 2 and compared with the result obtained with the constant assumptions. The field capacity (ha/h) begins to decline, for example, when the maximum throughput (C_mx = 30.8 Mg/h) is reached.

The capacity limit feature is characteristic of all forage equipment. While most forage equipment used in conventional haying operations will never operate with this restriction because the yields are too low, there is good potential that machines will be capacity-limited in high-yielding energy crops [6]. As a result, the relationship used in models must use a lower field capacity than expected based on the ASABE data [9]. The lower field capacity impacts the number of machines required to harvest a given area, which, in turn, impacts the harvest cost calculations.

The area that can be covered in unit time for an operation (planting, cultivation, harvesting) is called field capacity (C_f, ha/h) and is a product of the processing width and effective speed of the machine. Since width and speed are easily measured, field capacity measurements are not complex. For forage machines, such as mowers, rakes, mower-conditioners, or windrowers, the material handling capacity may not be as critical and only the field capacity is measured. The key issue is to better understand the machine’s maximum throughput limits. Maximum throughput has not been advertised by the manufacturers because the value is impacted by crop characteristics and operator skill, however this value is a critical parameter to properly assess machine performance in high-yield conditions [6].

Most machines will not reach maximum throughput in convention forage harvesting. Occasionally, if a baler is used to bale a windrow that has been created by raking multiple rows into a single windrow, it can be operated near or exceed its maximum throughput. In this case, the machine’s performance will be altered as shown in Figure 2.

The material handling capacity is very important for both forage harvesters and balers (and equipment in higher throughput situations). Material handling capacity is the maximum feed rate (maximum throughput, C_mx) that can be accommodated on a sustained basis. This typically is a design limitation of the machine. For example, the feed mechanism of a chopper is adjusted so that it is sequenced with the forward speed. Forage harvester throughput is the product of mass processed per unit travel distance (for example, kg/m) times the forward speed of the harvester (km/h). The product of these two parameters then gives capacity in kg/h. The mass per unit distance can be measured before the material enters the harvester or as it leaves. One method uses the crop yield and effective machine width to obtain an estimate of the feed rate into the machine per unit of forward travel. With the second method, the processed material is caught in a container for a given travel distance and then weighed. Feed rate can be determined for a baler by measuring the average time required to produce a bale and weighing to determine the mass in an average bale [11]. When the machine operates in a field with a high yield, the field capacity (ha/h) decreases because of a reduction in field efficiency (more bales dropped per unit area), and because the operator is reducing the forward speed to limit the amount of material flowing through the machine. If the equipment is operating at maximum throughput (C_mx) in a field with yield (Y), the effective travel speed with an operating width (W), is given by:

$$v_e=\frac{{\mathrm{K}}_1\cdot {\mathrm{C}}_{\mathrm{mx}}}{\mathrm{W}\cdot \mathrm{Y}}$$

(4)

where: v_e = the effective field speed, including a consideration of field efficiency, km/h.

Impact of Higher Yield on Round Balers

Since the round baler stops to wrap and eject a bale, field capacity (ha/h) is directly impacted when there are more bales per unit area harvested. The mass of a single bale (B_m) is impacted by how the baler is operated. This factor is not addressed here. The time to form a bale and the time to wrap/eject the bale can be easily measured. The achieved field capacity (C_fa) is given by:

$${\mathrm{C}}_{\mathrm{fa}}=\frac{\left(\frac{{\mathrm{B}}_{\mathrm{m}}}{{\mathrm{C}}_{\mathrm{m}}}\right)}{\left(\frac{{\mathrm{B}}_{\mathrm{m}}}{{\mathrm{C}}_{\mathrm{m}}}+\frac{{\mathrm{t}}_{\mathrm{w}}}{{\mathrm{K}}_2}\right) }$$

(5)

where:

• B_m/C_m = the time to form a bale, h
• t_w = time to wrap/eject a bale, s
• K₂ = 3600 s/h.

Throughput (C_m), with wrap/eject time, can be used to calculate an “achieved” capacity:

$${\mathrm{C}}_{\mathrm{fa}}=\frac{{\mathrm{C}}_{\mathrm{m}}}{\left(1+\frac{{\mathrm{C}}_{\mathrm{m} }\cdot { \mathrm{t}}_{\mathrm{w}}}{{\mathrm{B}}_{\mathrm{m}}\cdot { \mathrm{K}}_2}\right)}$$

(6)

In this form of the achieved capacity equation, it is easier to see the impact of the wrap/eject time has on the constant capacity assumption (Figure 3). The impact of cumulative wrap/eject time on achieved field capacity as yield increases is large and does impact the capacity parameter used in most models.

Since the system efficiency (E_s = E_f × E_e) can be represented by 2 terms, E_f dealing with the productivity issues and E_e representing the wrap/eject process, Equation (6) can be rewritten as:

$${\mathrm{C}}_{\mathrm{fa}}={\mathrm{C}}_{\mathrm{f}}\cdot {\mathrm{E}}_{\mathrm{f}}\cdot {\mathrm{E}}_{\mathrm{e}}$$

(7)

where: E_e, the wrap/eject efficiency, is given by:

$${\mathrm{E}}_{\mathrm{e}}=\frac{1}{\left(1+\frac{{\mathrm{t}}_{\mathrm{w}} \cdot { \mathrm{C}}_{\mathrm{m}}}{{\mathrm{B}}_{\mathrm{m} }·{ \mathrm{K}}_2}\right)}$$

(8)

This shows that the wrap/eject efficiency is a function of the input variables (C_m, with v, W, and E_f) that are typically used in machinery management and cost models. The new functions that are required for round bales is the time to wrap/eject per bale (t_w), the mass of an average bale (B_m), and the yield (Y). The yield can be an average for a given field or the annual average for all fields harvested, thus it is a known input to the model. While the two efficiencies could remain together, one component is a function of yield and may reinforce that additional modelling consideration is warrantied especially when yields are high.

3. Results

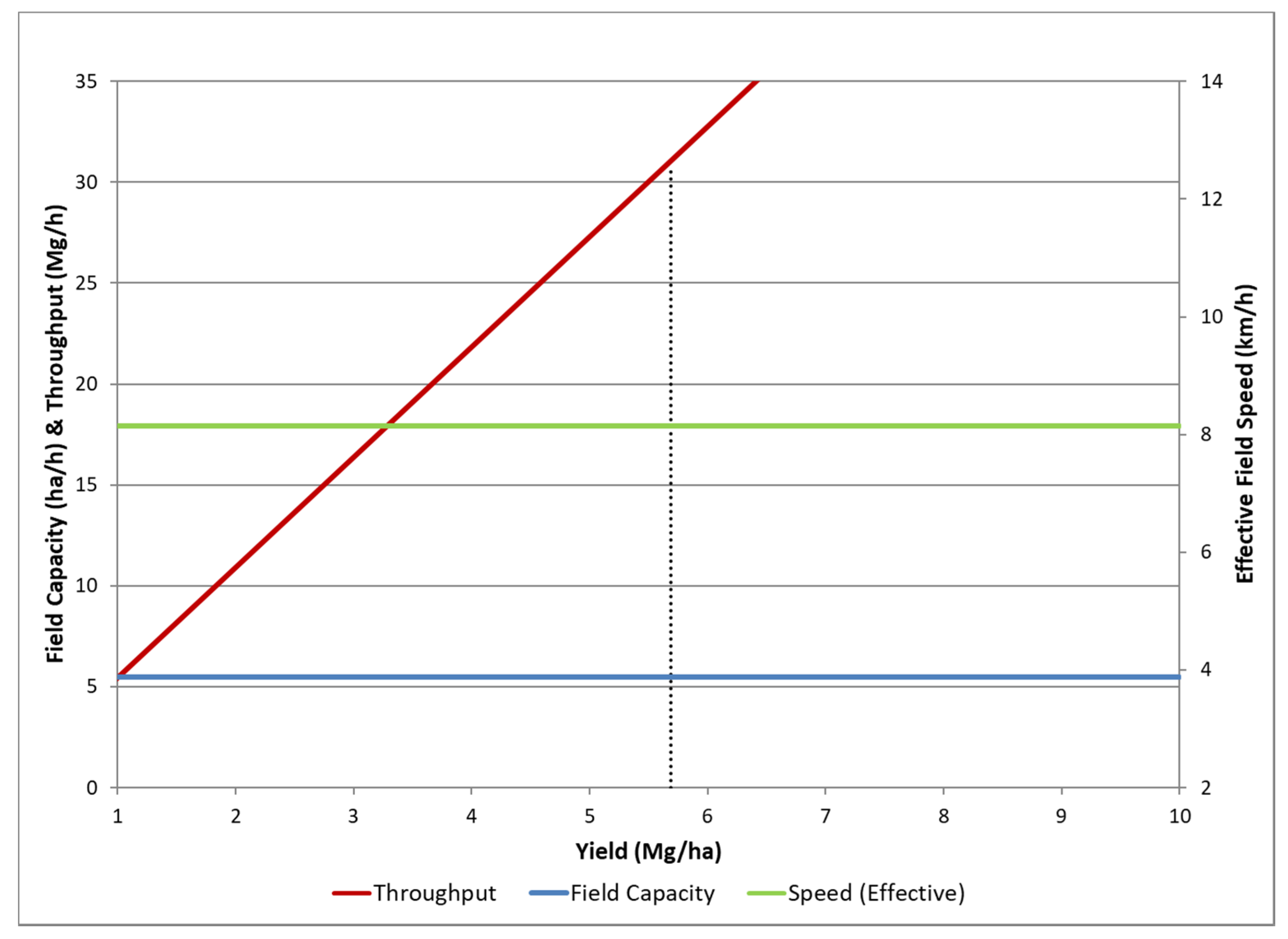
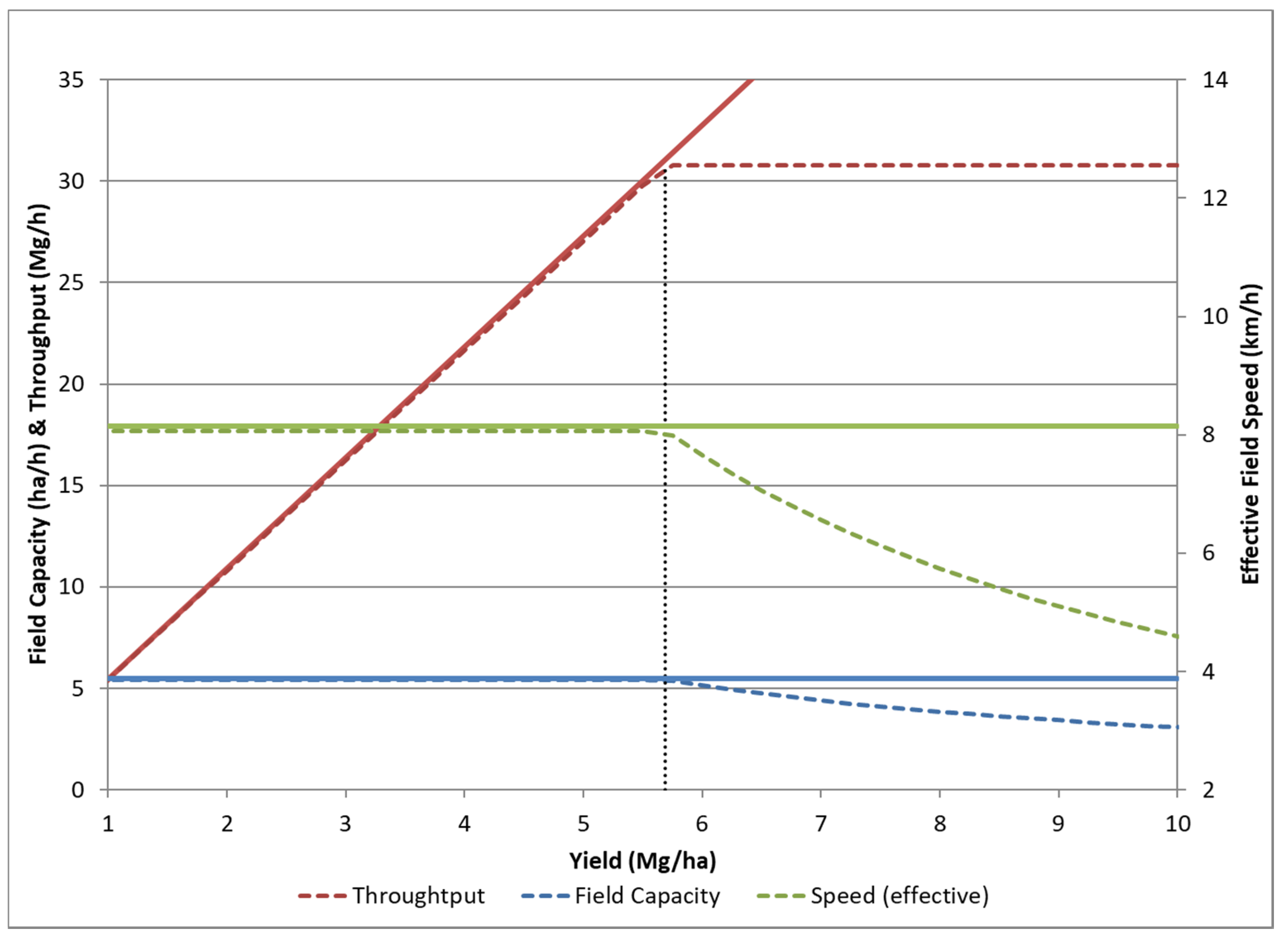
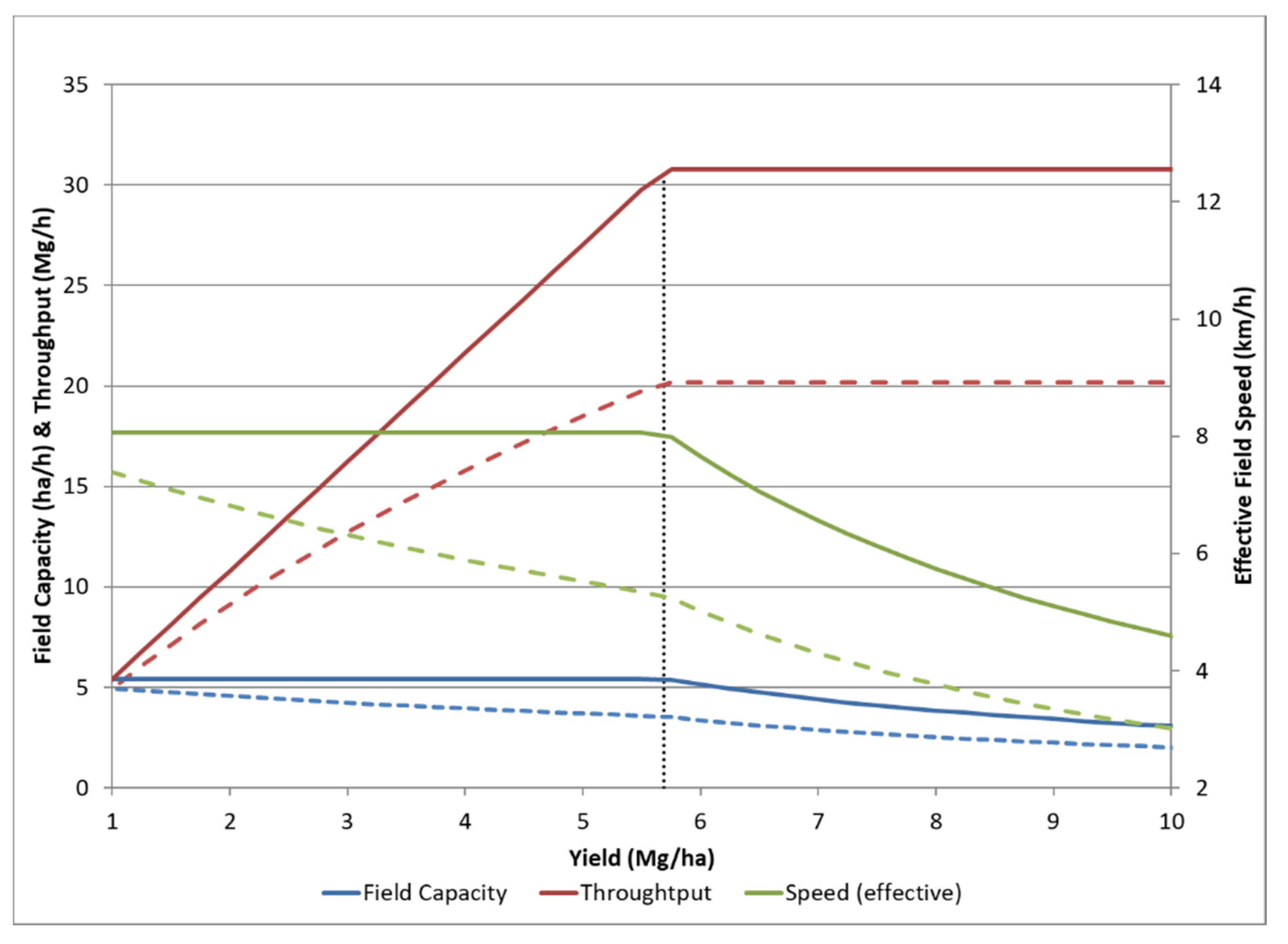
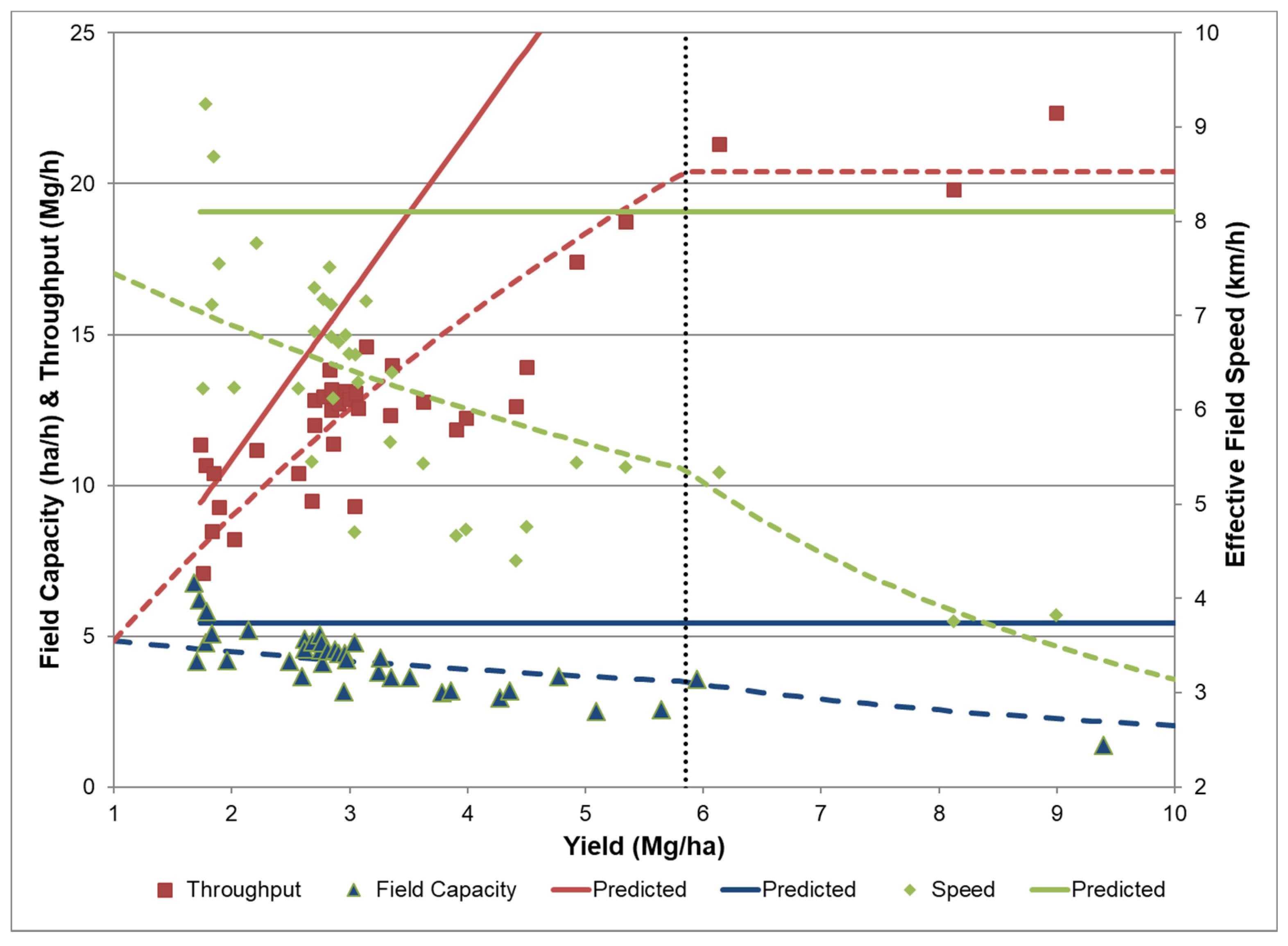
3.1. Example Use of Relationships

As an example, suppose a round baler with a working width (W) of 6.7 m, theoretical field speed (v) of 0.9 km/h, and effective field efficiency (E_f) of 74%. The baler has a maximum throughput of 30.8 Mg/h, thus the critical yield at the transition (Y_c) is 5.6 Mg/ha. The baler creates bales with a mass (B_m) of 0.51 Mg and the time (t_w) to wrap/eject a bale is 32 s. When field data is added in Figure 3, the curves show the impact of both the maximum throughput restriction and bale warp/eject time (Figure 4). Grisso et al. [3] provide measured field performance data, and this is shown in Figure 4 for comparison.

Similar findings were shown in Martelli et al. [12]. While operating in giant reed and switchgrass, they observed that throughput capacities in switchgrass were 11.9 and 12.1 Mg/h for a round and large-square baler, respectively. They also observed that the actual field capacity of the large-square baler was 35% (giant reed) and 18% (switchgrass) higher than the round baler. While the field efficiency was more impacted in the giant reed (0.55) for the round baler compared to 0.74 for the large-square baler. They assumed the increase of biomass flowing through the balers was the reason for these differences. They also noted the highest values of field efficiency were measured with the large-square baler because this machine ties and ejects the bale without stopping, while the round baler stops to wrap/eject the bale, thus reducing the field efficiency and, consequently, the actual field capacity.

The values of capacity reported in the literature are highly variable and only in a few cases measured during field trials. Kemmerer and Liu [13] reported a field capacity of 13 Mg/h for switchgrass baling. Shinners et al. [5] reported productivity values, based on field trails, ranging from 17.7 to 20.3 Mg/h for switchgrass round-baling with net wrap and 25.2 Mg/h for large-square-baling, values in the range compared in our study. Womac et al. [6] reported productivity in round-baling switchgrass in the range 16.1 to 26.8 Mg/h but with an effective field speed ranging from 7.9 to 14.0 km/h.

3.2. Impact on Cost Calculations

In the cost analysis, both round and square balers were used to show the impact of the throughput and yield on the cost to own and operate the machines. The cost factors and assumptions are shown in

Table 1. Machinery cost factors for the balers using the notation and definitions given in ASABE Standard [10].

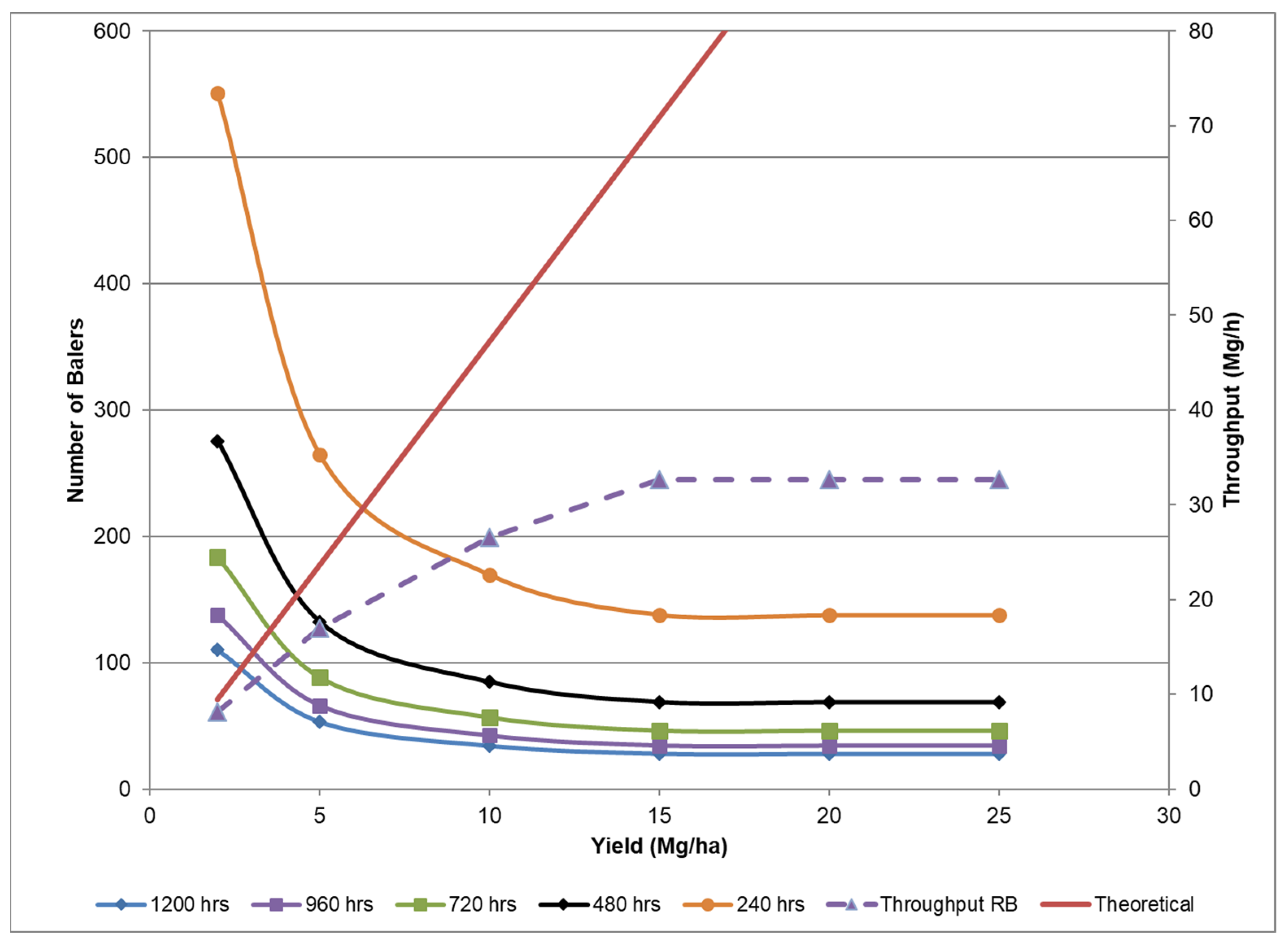
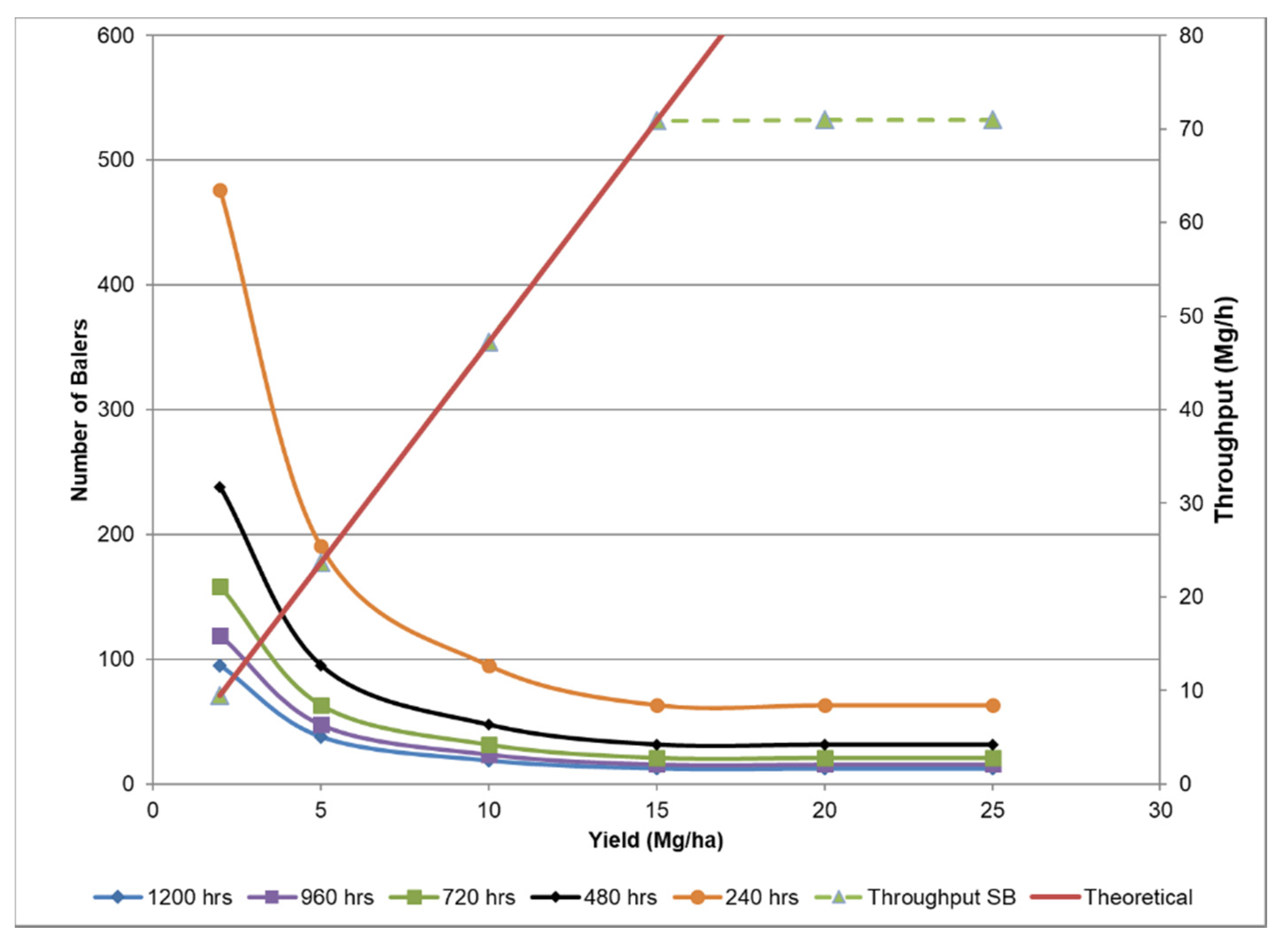
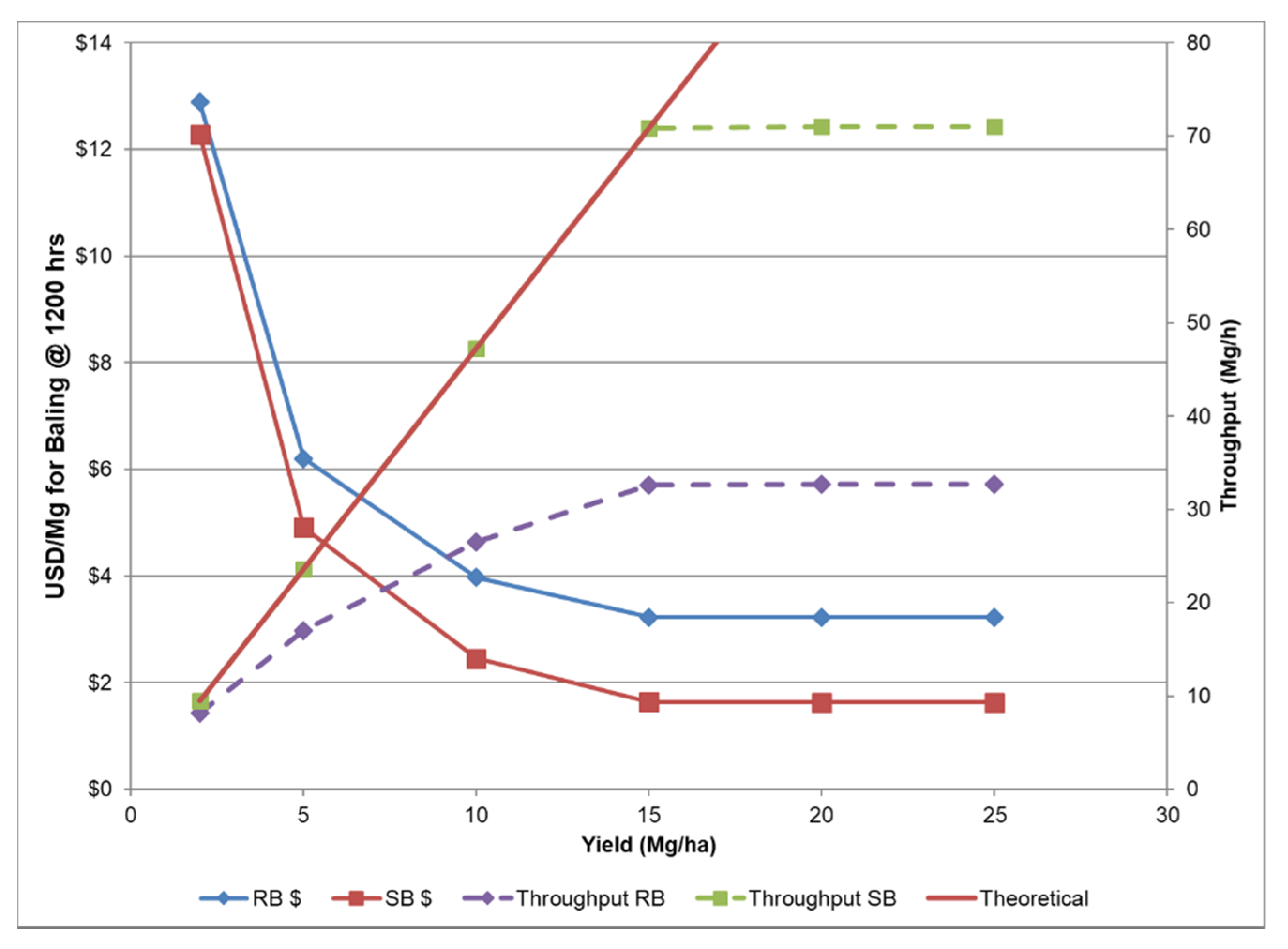
Cost Factors	Round	Large-Square
Purchase price (USD)	45,000	112,000
Design life (h)	1500	3000
Interest rate (%)	8%	8%
Tax rate:	1.00%	1.00%
Housing:	0.75%	0.75%
RF1	0.43	0.1
RF2	1.8	1.8
Labor cost (including benefits) (USD/h)	15	15
Salvage value	10%	10%

. The square baler has a higher purchase price and has higher maintenance costs when compared to the round baler. The balers were operated at 9 km/h, 7 m width, with a C_mx at 71 Mg/h, and 75% effective field efficiency. The round bales weighed 0.52 Mg and took (t_w) 31 s to wrap/eject.

These balers were used to harvest switchgrass for a biorefinery that requires 3000 Mg/day. The results presented here are similar in focus to the analysis completed by Shastri et al. [14]. The analysis is based on having the annual potential of 1200, 960, 720, 480, and 240 h to perform the baling operation. The annual hours define the ability of a set of machines to complete the harvest in a scheduled time-frame. The results in

Table 2. Cost factors for balers as a function of annual use. (n = number of useful yrs of design life).

	Round Baler			Large-Square Baler
h	n	USD/h	USD Annual	n	USD/h	USD Annual
1200	1.3	105.37	126,445	2.5	116.06	139,271
960	1.6	106.02	101,781	3.1	117.68	112,973
720	2.1	107.11	77,118	4.2	120.38	86,676
480	3.1	109.28	52,454	6.3	125.79	60,379
240	6.3	115.80	27,791	12.5	142.01	34,081

were calculated using the procedures given in ASABE Standard [10]. If a 10-h work day is assumed, then the annual hours can be completed in 120, 96, 72, 48, and 24 workdays, respectively. The hourly cost (operating plus ownership) over the chosen range of annual operating hours for the round baler ranged from 105 USD/h to 116 USD/h, while the large-square baler ranged from 116 USD/h to 142 USD/h.

Figure 5 and Figure 6 show the increase in the number of round and large-square balers, respectively, that will be required as annual use and yield increases. As the number of available hours increases, it is obvious that fewer bale units will be required. After the maximum throughput is reached by the baler, no additional balers are required as the yield increases. There is a dramatic impact on the effect of the wrap/eject time of the round baler, as observed in Figure 5. The round baler will need 10–25% more balers due to loss in achieved field capacity. This will increase the need for additional labor (drivers) and power units.

Figure 7 shows the cost per Mg to bale the switchgrass with round and large-square balers. At low yields, the capacities of the two balers are about the same, as well as their costs. However, as the yield increases—and the impact of the wrap/eject time greatly increases—the cost of the operation of the round baler increases, because the baler is moving material through the machine at a lower rate. After the maximum throughput is reached, the cost of the round bale operation (3.23 USD/Mg) is double that of the large-square baler operation (1.63 USD/Mg). The round baler achieved throughput capacity is more than 50% less (32.7 Mg/h compared to 71.0 Mg/h) than the large-square baler. This demonstrates that no matter which baler is used, the best operating conditions for minimal cost (USD/Mg) occurs at maximum throughput (C_mx).

The literature has several cost comparison studies with conflicting results. For example, in Martelli et al. [12] field trials, the baling costs with the round baler were less than the large-square baler for giant reed and switchgrass. They acknowledged that their analysis was optimized by excluding an inefficient annual underutilization of the machinery. Thorsell et al. [15] estimated a lower cost for harvesting switchgrass while using a large rectangular baler than with a large-round bale system. Cundiff et al. [16] found values 2.5 times higher for a large-square baler than a round baler: 4.06 USD/Mg and 1.59 USD/Mg, respectively, in their analysis. Both of these simulated studies did not compensate for the reduction of field capacity of the round baler experienced during biomass baling. We believe that adjusting according to Equation (8) will make these simulations more realistic to field conditions.

4. Summary and Conclusions

A key relationship of round baler field performance was developed to show the impact of maximum throughput (C_mx) on baler field efficiency and field capacity (ha/h). The assumption used in most prior biomass harvest modeling studies that capacity is negligibly impacted by yield is incorrect. Subsequently the number of machines required and the cost of round baler operations has often been underestimated. Impacts are shown for the round baler since a wrap/eject time is required for this baler. Relationships for the bale wrap/eject times were developed. In the round baler example, the impact of wrap/eject time was a 50% reduction in capacity. After the maximum throughput is reached, the cost of the round-baler operation (3.23 USD/Mg) is double that of the large-square-baler operation (1.63 USD/Mg). The round baler achieved throughput capacity is 50% less (32.7 Mg/h compared to 71.0 Mg/h) than the large-square baler.

The function developed in this study to better account for the time required for round balers to package and drop bales in field efficiency and field capacity calculations (Equation (8)) has application beyond studying the impact of yield on biomass harvest costs. It can also be applied to better predict the cost impacts of round baler design parameters, such as wrap or tie time and bale density. Multiple manufacturers have developed prototypes of continuous round balers. Assessing potential cost improvements of these more expensive continuous baler designs will require the more accurate assessment of conventional round-baler field performance provided in this study.