Can Proxy-Based Geospatial and Machine Learning Approaches Map Sewer Network Exposure to Groundwater Infiltration?
Abstract
Highlights
- A geospatial–machine learning framework was developed to screen sewer network exposure to groundwater infiltration (GWI) at high spatial resolution.
- The integration of fuzzy-AHP and K-means clustering yielded robust classification of GWI risk zones (high, intermediate, low), validated by storm overflow discharge data.
- Sensitivity analysis identified five key influencing factors among sixteen: groundwater depth, river proximity, flood potential, rock type, and alluvium.
- The proposed approach supports proactive sewer infrastructure management and planning, contributing to long-term sustainability and resilience under climate and urbanisation pressures.
Abstract
1. Introduction
2. Materials and Methods
2.1. Methodology
2.1.1. Data and Thematic Layers
2.1.2. Classification
2.1.3. Reclassification
2.1.4. Weights of Layers
2.1.5. Combination of Layers
2.1.6. K-Means Clustering
2.1.7. Verification and Comparison of Models
2.1.8. Sensitivity Analysis and Key Influencing Factors
- -
- A combination of all layers assigned equal weights.
- -
- A combination of only high-weighted layers.
2.2. Location Description
3. Results
3.1. Thematic Layers
3.2. Geospatial Technology
3.3. Machine Learning to Classify Risk Regions
3.4. Evaluating Agreement Between Machine Learning and Geospatial Approaches Using Cohen’s Kappa
4. Discussion
4.1. Integrating F-AHP-Based Geospatial Approach with ML to Efficiently Identify High-Risk Areas
4.2. Model Validation and Sensitivity Analysis for Robust Variable Selection in F-AHP GIS and ML Approaches
4.3. K-Means Clustering and Alternative Methods as Pathways for Future Groundwater and Sewer Network Research
4.4. Limitations of the F-AHP-Based Geospatial and ML Approach
4.4.1. How to Move Research from GWD to GWI Probability
4.4.2. Expanding Thematic Layers to Better Capture GWI
4.4.3. Limitations and Consistency Considerations in AHP-GIS Approach
4.4.4. Critical Challenges in Using ML and K-Means Clustering for GWI Risk Assessment
General Considerations
Sewer-Related Considerations
4.4.5. Assessment of Model Agreement and the Influence of Clustering Methods
4.4.6. Hydrological Impacts of Urbanisation on Groundwater–Sewer Interactions
5. Conclusions
- -
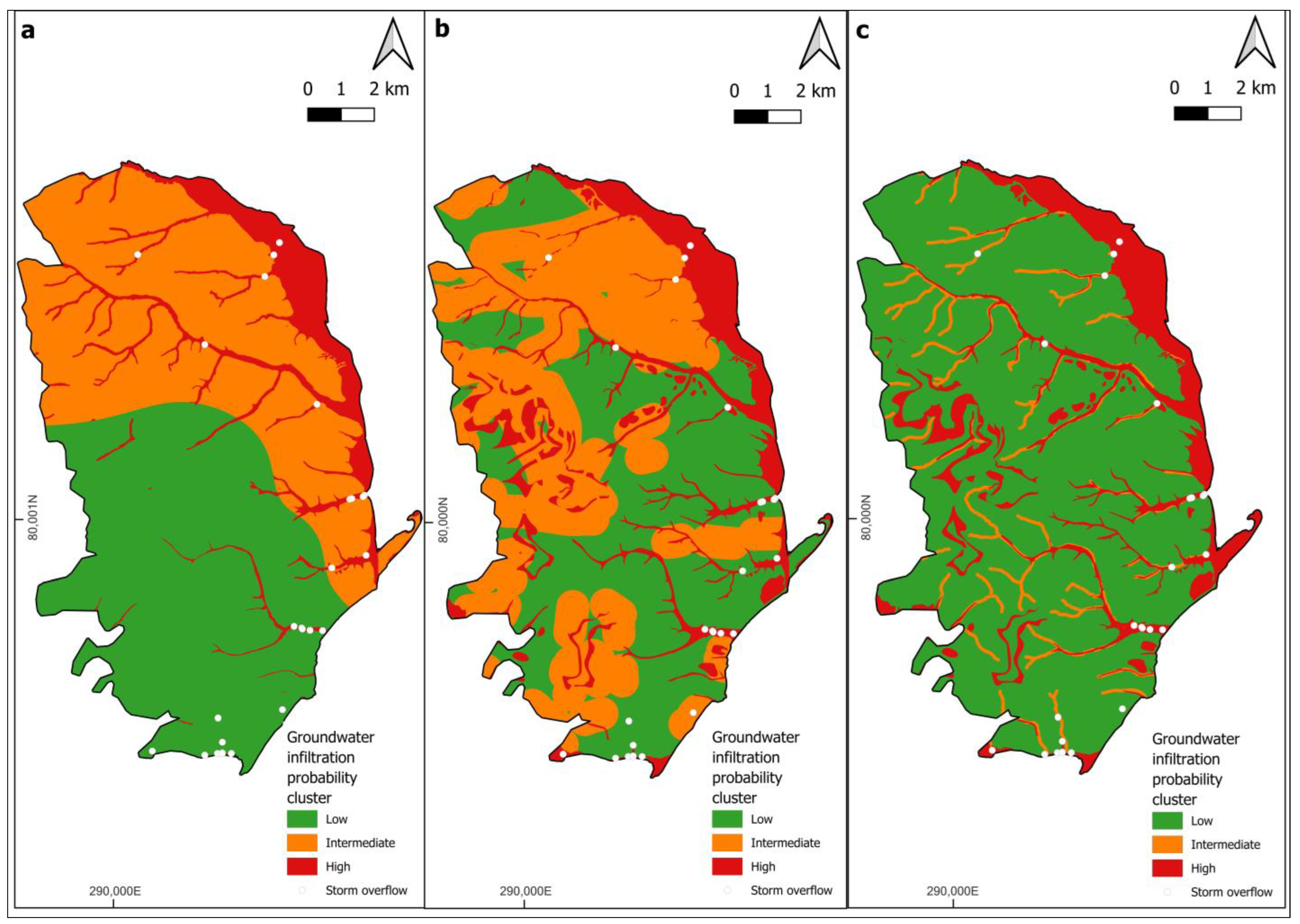
- The CR of 0.02 confirmed the reliability of the pairwise comparisons. Additionally, locations of storm overflow discharges generally aligned with areas of elevated GWI probability, indicating consistency between observed overflows and modelled infiltration probabilities.
- -
- The AHP identified five major contributors to GWI in sewers: GWD, proximity to rivers, flood potential, rock type, and alluvial deposits. However, sensitivity analysis revealed the importance of incorporating all 16 thematic layers, as excluding some led to greater discrepancies between individual-layer outputs and the final map generated through the AHP method.
- -
- The final results derived from the AHP-based GIS model indicated minimal seasonal variation in GWI probability scores, with winter exhibiting the highest values. Overall, a spatial trend was observed, with GWI probabilities gradually increasing from the southwest to the northeast across the study area.
- -
- By combining fuzzified thematic layers weighted through AHP with K-means clustering, we generated a spatial representation of the study area categorised into three GWI risk levels: high, medium, and low. Compared to maps produced using either equal weighting for all layers or only the five dominant factors, this approach yielded more cohesive cluster boundaries.
- -
- A comparison between the F-AHP-based K-means clustering results and the F-AHP-based GIS-derived outputs that incorporated all thematic layers revealed strong consistency between the two approaches, as evidenced by a Kappa coefficient of 0.70 and an 81.44% match in classification outcomes.
6. Recommendations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hughes, J.; Cowper-Heays, K.; Olesson, E.; Bell, R.; Stroombergen, A. Impacts and Implications of Climate Change on Wastewater Systems: A New Zealand Perspective. Clim. Risk Manag. 2021, 31, 100262. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, C.; Zhang, Y.; Zhao, R.; Yan, K.; Wang, W. Data-Driven Method Based on Deep Learning Algorithm for Detecting Fat, Oil, and Grease (FOG) of Sewer Networks in Urban Commercial Areas. Water Res. 2021, 207, 117797. [Google Scholar] [CrossRef] [PubMed]
- Anand, U.; Li, X.; Sunita, K.; Lokhandwala, S.; Gautam, P.; Suresh, S.; Sarma, H.; Vellingiri, B.; Dey, A.; Bontempi, E.; et al. SARS-CoV-2 and Other Pathogens in Municipal Wastewater, Landfill Leachate, and Solid Waste: A Review about Virus Surveillance, Infectivity, and Inactivation. Environ. Res. 2022, 203, 111839. [Google Scholar] [CrossRef]
- Liu, J.; Xiong, J.; Chen, Y.; Sun, H.; Zhao, X.; Tu, F.; Gu, Y. An Integrated Model Chain for Future Flood Risk Prediction under Land-Use Changes. J. Environ. Manag. 2023, 342, 118125. [Google Scholar] [CrossRef]
- Mondal, K.; Bandyopadhyay, S.; Karmakar, S. Framework for Global Sensitivity Analysis in a Complex 1D-2D Coupled Hydrodynamic Model: Highlighting Its Importance on Flood Management over Large Data-Scarce Regions. J. Environ. Manag. 2023, 332, 117312. [Google Scholar] [CrossRef] [PubMed]
- Hoseingholi, P.; Moeini, R. Pipe Failure Prediction of Wastewater Network Using Genetic Programming: Proposing Three Approaches. Ain Shams Eng. J. 2023, 14, 101958. [Google Scholar] [CrossRef]
- Zeydalinejad, N.; Javadi, A.A.; Webber, J.L. Global Perspectives on Groundwater Infiltration to Sewer Networks: A Threat to Urban Sustainability. Water Res. 2024, 262, 122098. [Google Scholar] [CrossRef]
- Ohlin Saletti, A.; Lindhe, A.; Söderqvist, T.; Rosén, L. Cost to Society from Infiltration and Inflow to Wastewater Systems. Water Res. 2023, 229, 119505. [Google Scholar] [CrossRef]
- Saurav, K.C.; Shrestha, S.; Ninsawat, S.; Chonwattana, S. Predicting Flood Events in Kathmandu Metropolitan City under Climate Change and Urbanisation. J. Environ. Manag. 2021, 281, 111894. [Google Scholar] [CrossRef]
- Nguyen, L.V. Integrating Machine Learning and GIS for Sewer Condition Assessment and Visualization. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2024. Available online: https://ntnuopen.ntnu.no/ntnu-xmlui/handle/11250/3150381 (accessed on 20 July 2025).
- Saddiqi, M.M.; Zhao, W.; Cotterill, S.; Dereli, R.K. Smart Management of Combined Sewer Overflows: From an Ancient Technology to Artificial Intelligence. Wiley Interdiscip. Rev. Water 2023, 10, e1635. [Google Scholar] [CrossRef]
- Fu, G.; Jin, Y.; Sun, S.; Yuan, Z.; Butler, D. The Role of Deep Learning in Urban Water Management: A Critical Review. Water Res. 2022, 223, 118973. [Google Scholar] [CrossRef]
- Royal Society Working Group. Machine Learning: The Power and Promise of Computers That Learn by Example. In Technical Report; The Royal Society: London, UK, 2017. [Google Scholar] [CrossRef]
- Cheng, J.C.P.; Wang, M. Automated Detection of Sewer Pipe Defects in Closed-Circuit Television Images Using Deep Learning Techniques. Autom. Constr. 2018, 95, 155–171. [Google Scholar] [CrossRef]
- Ma, S.; Elshaboury, N.; Ali, E.; Zayed, T. Proactive Exfiltration Severity Management in Sewer Networks: A Hyperparameter Optimization for Two-Tiered Machine Learning Prediction. Tunn. Undergr. Space Technol. 2024, 144, 105532. [Google Scholar] [CrossRef]
- Wang, M.; Luo, H.; Cheng, J.C.P. Towards an Automated Condition Assessment Framework of Underground Sewer Pipes Based on Closed-Circuit Television (CCTV) Images. Tunn. Undergr. Space Technol. 2021, 110, 103840. [Google Scholar] [CrossRef]
- Mohammadi, M.M.; Najafi, M.; Kaushal, V.; Serajiantehrani, R.; Salehabadi, N.; Ashoori, T. Sewer Pipes Condition Prediction Models: A State-of-the-Art Review. Infrastructures 2019, 4, 64. [Google Scholar] [CrossRef]
- Kwon, S.H.; Kim, J.H. Machine Learning and Urban Drainage Systems: State-of-the-Art Review. Water 2021, 13, 3545. [Google Scholar] [CrossRef]
- Längkvist, M.; Karlsson, L.; Loutfi, A. A Review of Unsupervised Feature Learning and Deep Learning for Time-Series Modeling. Pattern Recognit. Lett. 2014, 42, 11–24. [Google Scholar] [CrossRef]
- Abdideh, M.; Ameri, A. Cluster Analysis of Petrophysical and Geological Parameters for Separating the Electrofacies of a Gas Carbonate Reservoir Sequence. Nat. Resour. Res. 2020, 29, 1843–1856. [Google Scholar] [CrossRef]
- Szabó, N.P.; Braun, B.A.; Abdelrahman, M.M.G.; Dobróka, M. Improved Well Logs Clustering Algorithm for Shale Gas Identification and Formation Evaluation. Acta Geod. Geophys. 2021, 56, 711–729. [Google Scholar] [CrossRef]
- Mohammed, M.A.A.; Szabó, N.P.; Flores, Y.G.; Szűcs, P. Multi-Well Clustering and Inverse Modeling-Based Approaches for Exploring Geometry, Petrophysical, and Hydrogeological Parameters of the Quaternary Aquifer System around Debrecen Area, Hungary. Groundw. Sustain. Dev. 2024, 24, 101086. [Google Scholar] [CrossRef]
- Jain, A.K. Data Clustering: 50 Years beyond K-Means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Eid, M.H.; Eissa, M.; Mohamed, E.A.; Ramadan, H.S.; Czuppon, G.; Kovács, A.; Szűcs, P. Application of Stable Isotopes, Mixing Models, and K-Means Cluster Analysis to Detect Recharge and Salinity Origins in Siwa Oasis, Egypt. Groundw. Sustain. Dev. 2024, 25, 101124. [Google Scholar] [CrossRef]
- Subbarayan, S.; Thiyagarajan, S.; Gangolu, S.; Devanantham, A.; Nagireddy Masthan, R. Assessment of Groundwater Vulnerable Zones Using Conventional and Fuzzy-AHP DRASTIC for Visakhapatnam District, India. Groundw. Sustain. Dev. 2024, 24, 101054. [Google Scholar] [CrossRef]
- Das, B.; Pal, S.C.; Malik, S.; Chakrabortty, R. Modeling Groundwater Potential Zones of Puruliya District, West Bengal, India Using Remote Sensing and GIS Techniques. Geol. Ecol. Landsc. 2019, 3, 223–237. [Google Scholar] [CrossRef]
- Soyaslan, İ.İ. Assessment of Groundwater Vulnerability Using Modified DRASTIC-Analytical Hierarchy Process Model in Bucak Basin, Turkey. Arab. J. Geosci. 2020, 13, 1127. [Google Scholar] [CrossRef]
- Saaty, T.L. How to Make a Decision: The Analytic Hierarchy Process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Coffey, L.; Claudio, D. In Defense of Group Fuzzy AHP: A Comparison of Group Fuzzy AHP and Group AHP with Confidence Intervals. Expert. Syst. Appl. 2021, 178, 114970. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Marra, M. The State of the Art Development of AHP (1979–2017): A Literature Review with a Social Network Analysis. Int. J. Prod. Res. 2017, 55, 6653–6675. [Google Scholar] [CrossRef]
- Lagogiannis, S.; Papadopoulos, A.; Dimitriou, E. Development of an Automatic Water Monitoring Network by Using Multi-Criteria Analysis and a GIS-Based Fuzzy Process. Environ. Process. 2024, 11, 36. [Google Scholar] [CrossRef]
- Liu, Y.; Eckert, C.M.; Earl, C. A Review of Fuzzy AHP Methods for Decision-Making with Subjective Judgements. Expert. Syst. Appl. 2020, 161, 113738. [Google Scholar] [CrossRef]
- Saltelli, A. Sensitivity Analysis for Importance Assessment. Risk Anal. 2002, 22, 579–590. [Google Scholar] [CrossRef]
- Goodarzi, M.R.; Vazirian, M. A Machine Learning Approach for Predicting and Localizing the Failure and Damage Point in Sewer Networks Due to Pipe Properties. J. Water Health 2024, 22, 487–509. [Google Scholar] [CrossRef]
- Kizilöz, B. Prediction of Failures in Sewer Networks Using Various Machine Learning Classifiers. Urban Water J. 2024, 21, 877–893. [Google Scholar] [CrossRef]
- Pokharel, A. Application of Supervised Machine Learning Algorithms for Developing Service Life Prediction Model of Sewer Pipes. Ph.D. Thesis, The University of Texas at Arlington, Arlington, TX, USA, 2021. [Google Scholar]
- Seng, V. Enhancing Sewer Asset Management Using Machine Learning Algorithms. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2024. [Google Scholar] [CrossRef]
- Sousa, V.; Matos, J.P.; Matias, N. Evaluation of Artificial Intelligence Tool Performance and Uncertainty for Predicting Sewer Structural Condition. Autom. Constr. 2014, 44, 84–91. [Google Scholar] [CrossRef]
- Zhang, D.; Martinez, N.; Lindholm, G.; Ratnaweera, H. Manage Sewer In-Line Storage Control Using Hydraulic Model and Recurrent Neural Network. Water Resour. Manag. 2018, 32, 2079–2098. [Google Scholar] [CrossRef]
- Zhang, D.; Hølland, E.S.; Lindholm, G.; Ratnaweera, H. Hydraulic Modeling and Deep Learning Based Flow Forecasting for Optimizing Inter Catchment Wastewater Transfer. J. Hydrol. 2018, 567, 792–802. [Google Scholar] [CrossRef]
- Ki, S.J.; Lee, C.S.; Jung, W.H.; Park, H.G. Comparison of Classification and Supervised Learning Algorithms in Assessing the Hydraulic Conditions of Sewer Collection Systems: A Case Study of Local Sewer Networks in Jinju City, Korea. Desalination Water Treat. 2018, 124, 202–210. [Google Scholar] [CrossRef]
- Wong, L.S.; Marani, A.; Nehdi, M.L. Gradient Boosting Coupled with Oversampling Model for Prediction of Concrete Pipe-Joint Infiltration Using Designwise Data Set. J. Pipeline Syst. Eng. Pract. 2021, 12, 04021015. [Google Scholar] [CrossRef]
- Qiu, C.; Shao, G.; Zhang, Z.; Zhou, C.; Hou, Y.; Zhao, E.; Guo, X.; Guan, X. Unsupervised Real Time and Early Anomalies Detection Method for Sewer Networks Systems. IEEE Access 2024, 12, 21698–21709. [Google Scholar] [CrossRef]
- Jato-Espino, D.; Sillanpää, N.; Pathak, S. Flood Modelling in Sewer Networks Using Dependence Measures and Learning Classifier Systems. J. Hydrol. 2019, 578, 124013. [Google Scholar] [CrossRef]
- Zhang, Z.; Laakso, T.; Wang, Z.; Pulkkinen, S.; Ahopelto, S.; Virrantaus, K.; Li, Y.; Cai, X.; Zhang, C.; Vahala, R.; et al. Comparative Study of AI-Based Methods—Application of Analyzing Inflow and Infiltration in Sanitary Sewer Subcatchments. Sustainability 2020, 12, 6254. [Google Scholar] [CrossRef]
- Liu, T.; Ramirez-Marquez, J.E.; Jagupilla, S.C.; Prigiobbe, V. Combining a Statistical Model with Machine Learning to Predict Groundwater Flooding (or Infiltration) into Sewer Networks. J. Hydrol. 2021, 603, 126916. [Google Scholar] [CrossRef]
- Abebe, Y.; Tesfamariam, S. Underground Sewer Networks Renewal Complexity Assessment and Trenchless Technology: A Bayesian Belief Network and GIS Framework. J. Pipeline Syst. Eng. Pract. 2020, 11, 04019058. [Google Scholar] [CrossRef]
- Ghavami, S.M.; Borzooei, Z.; Maleki, J. An Effective Approach for Assessing Risk of Failure in Urban Sewer Pipelines Using a Combination of GIS and AHP-DEA. Process Saf. Environ. Prot. 2020, 133, 275–285. [Google Scholar] [CrossRef]
- Van Nguyen, L.; Seidu, R. Application of Regression-Based Machine Learning Algorithms in Sewer Condition Assessment for Ålesund City, Norway. Water 2022, 14, 3993. [Google Scholar] [CrossRef]
- Van Nguyen, L.; Bui, D.T.; Seidu, R. Comparison of Machine Learning Techniques for Condition Assessment of Sewer Network. IEEE Access 2022, 10, 124238–124258. [Google Scholar] [CrossRef]
- Roghani, B.; Tabesh, M.; Cherqui, F. A Fuzzy Multidimensional Risk Assessment Method for Sewer Asset Management. Int. J. Civ. Eng. 2024, 22, 1–17. [Google Scholar] [CrossRef]
- Kazuva, E.; Zhang, J.; Tong, Z.; Liu, X.P.; Memon, S.; Mhache, E. GIS- and MCD-Based Suitability Assessment for Optimized Location of Solid Waste Landfills in Dar Es Salaam, Tanzania. Environ. Sci. Pollut. Res. 2021, 28, 11259–11278. [Google Scholar] [CrossRef]
- Martin, C.; Kamara, O.; Berzosa, I.; Badiola, J.L. Smart GIS Platform That Facilitates the Digitalization of the Integrated Urban Drainage System. Environ. Model. Softw. 2020, 123, 104568. [Google Scholar] [CrossRef]
- Nigusse, A.G.M.; Adhaneom, U.G.; Kahsay, G.H.; Abrha, A.M.; Gebre, D.N.; Weldearegay, A.G. GIS Application for Urban Domestic Wastewater Treatment Site Selection in the Northern Ethiopia, Tigray Regional State: A Case Study in Mekelle City. Arab. J. Geosci. 2020, 13, 311. [Google Scholar] [CrossRef]
- de Oliveira Silva, M.C.; Vasconcelos, R.S.; Cirilo, J.A. Risk Mapping of Water Supply and Sanitary Sewage Systems in a City in the Brazilian Semi-Arid Region Using GIS-MCDA. Water 2022, 14, 3251. [Google Scholar] [CrossRef]
- Wu, Z.; Abdul-Nour, G. Comparison of Multi-Criteria Group Decision-Making Methods for Urban Sewer Network Plan Selection. CivilEng 2020, 1, 26–48. [Google Scholar] [CrossRef]
- Lameche, E.K.; Boutaghane, H.; Saber, M.; Abdrabo, K.I.; Bermad, A.M.; Djeddou, M.; Boulmaiz, T.; Kantoush, S.A.; Sumi, T. Urban Flood Numerical Modeling and Hydraulic Performance of a Drainage Network: A Case Study in Algiers, Algeria. Water Sci. Technol. 2023, 88, 1635–1656. [Google Scholar] [CrossRef] [PubMed]
- Abd-Elaty, I.; Negm, A.; Hamdan, A.M.; Nour-Eldeen, A.S.; Zeleňáková, M.; Hossen, H. Assessing the Hazards of Groundwater Logging in Tourism Aswan City, Egypt. Water 2022, 14, 1233. [Google Scholar] [CrossRef]
- Attwa, M.; Zamzam, S. An Integrated Approach of GIS and Geoelectrical Techniques for Wastewater Leakage Investigations: Active Constraint Balancing and Genetic Algorithms Application. J. Appl. Geophys. 2020, 175, 103992. [Google Scholar] [CrossRef]
- Rojas-Gómez, K.L.; Binder, M.; Walther, M.; Engelmann, C. A Parsimonious Approach to Predict Regions Affected by Sewer-Borne Contaminants in Urban Aquifers. Environ. Monit. Assess. 2023, 195, 1517. [Google Scholar] [CrossRef]
- Williams, V.A. Evaluating the Potential of a Geospatial/Geostatistical Methodology for Locating Rain-Derived Infiltration and Inflow into Wastewater Treatment Systems in the Minneapolis/St. Paul Metropolitan Area, Minnesota, USA. Master’s Thesis, Minnesota State University, Mankato, MN, USA, 2017. [Google Scholar]
- Thapa, J.B.; Jung, J.K.; Yovichin, R.D. A Qualitative Approach to Determine the Areas of Highest Inflow and Infiltration in Underground Infrastructure for Urban Area. Adv. Civ. Eng. 2019, 2019, 2620459. [Google Scholar] [CrossRef]
- Rossi, R.J.; Toran, L. Exploring the Potential for Groundwater Inundation in Coastal US Cities Due to Interactions between Sewer Infrastructure and Global Change. Environ. Earth Sci. 2019, 78, 258. [Google Scholar] [CrossRef]
- Zeydalinejad, N.; Javadi, A.A.; Baldock, D.; Webber, J.L. An Integrated Hydrological-Hydrogeological Model for Analysing Spatio-Temporal Probability of Groundwater Infiltration in Urban Infrastructure. Sustain. Cities Soc. 2024, 116, 105891. [Google Scholar] [CrossRef]
- Sangsefidi, Y.; Bagheri, K.; Davani, H.; Merrifield, M. Data Analysis and Integrated Modeling of Compound Flooding Impacts on Coastal Drainage Infrastructure under a Changing Climate. J. Hydrol. 2023, 616, 128823. [Google Scholar] [CrossRef]
- Sangsefidi, Y.; Barnes, A.; Merrifield, M.; Davani, H. Data-Driven Analysis and Integrated Modeling of Climate Change Impacts on Coastal Groundwater and Sanitary Sewer Infrastructure. Sustain. Cities Soc. 2023, 99, 104914. [Google Scholar] [CrossRef]
- Halfawy, M.R.; Dridi, L.; Baker, S. Integrated Decision Support System for Optimal Renewal Planning of Sewer Networks. J. Comput. Civ. Eng. 2008, 22, 360–372. [Google Scholar] [CrossRef]
- Nguyen, L.V.; Razak, S. Predicting Sewer Structural Condition Using Hybrid Machine Learning Algorithms. Urban Water J. 2023, 20, 882–896. [Google Scholar] [CrossRef]
- Abebe, Y.; Tesfamariam, S. Storm Sewer Pipe Renewal Planning Considering Deterioration, Climate Change, and Urbanization: A Dynamic Bayesian Network and GIS Framework. Sustain. Resilient Infrastruct. 2023, 8, 70–85. [Google Scholar] [CrossRef]
- Saranya, A.; Al Mazroa, A.; Maashi, M.; Nithya, T.M.; Priya, V. Remote Sensing and Machine Learning Approach for Zoning of Wastewater Drainage System. Desalination Water Treat. 2024, 319, 100549. [Google Scholar] [CrossRef]
- Nourani, V.; Ghaneei, P.; Kantoush, S.A. Robust Clustering for Assessing the Spatiotemporal Variability of Groundwater Quantity and Quality. J. Hydrol. 2022, 604, 127272. [Google Scholar] [CrossRef]
- Saltelli, A.; Aleksankina, K.; Becker, W.; Fennell, P.; Ferretti, F.; Holst, N.; Li, S.; Wu, Q. Why so Many Published Sensitivity Analyses Are False: A Systematic Review of Sensitivity Analysis Practices. Environ. Model. Softw. 2019, 114, 29–39. [Google Scholar] [CrossRef]
- DEFRA. LIDAR Composite Digital Terrain Model (DTM)—1m. Department for Environment, Food and Rural Affairs. 2022. Available online: https://environment.data.gov.uk/dataset/13787b9a-26a4-4775-8523-806d13af58fc (accessed on 20 July 2025).
- OS Open Rivers. Ordnance Survey. 2025. Available online: https://www.data.gov.uk/dataset/dc29160b-b163-4c6e-8817-f313229bcc23/os-open-rivers1 (accessed on 20 July 2025).
- DEFRA. England|Catchment Data Explorer. Department for Environment, Food and Rural Affairs. 2025. Available online: https://environment.data.gov.uk/catchment-planning/ (accessed on 20 July 2025).
- Booth, K.A.; Linley, K.A. Geological Indicators of Flooding: User Guidance Notes; British Geological Survey: Nottingham, UK, 2010. [Google Scholar]
- Morton, R.D.; Marston, C.G.; O’Neil, A.W.; Rowland, C.S. Land Cover Map 2023 (land parcels, GB). NERC EDS Environmental Information Data Centre. 2024. Available online: https://catalogue.ceh.ac.uk/documents/50b344eb-8343-423b-8b2f-0e9800e34bbd (accessed on 20 July 2025).
- Lawley, R. User Guide: Soil Parent Material Dataset. In British Geological Survey Open Report; British Geological Survey: Nottingham, UK, 2021. [Google Scholar]
- Smith, A. Digital geological map of Great Britain, information notes, 2013. In British Geological Survey Open Report; British Geological Survey: Nottingham, UK, 2013. [Google Scholar]
- DEFRA. Hydrology Data Explorer—Explore. Department for Environment, Food and Rural Affairs. 2025. Available online: https://environment.data.gov.uk/hydrology/explore (accessed on 20 July 2025).
- Hollis, D.; McCarthy, M.; Kendon, M.; Legg, T.; Simpson, I. HadUK-Grid—A New UK Dataset of Gridded Climate Observations. Geosci. Data J. 2019, 6, 151–159. [Google Scholar] [CrossRef]
- Muhammad, A.M.; Zhonghua, T.; Sissou, Z.; Mohamadi, B.; Ehsan, M. Analysis of geological structure and anthropological factors affecting arsenic distribution in the Lahore aquifer, Pakistan. Hydrogeol. J. 2016, 24, 1891–1904. [Google Scholar] [CrossRef]
- Ahmed, R.; Sajjad, H. Analyzing Factors of Groundwater Potential and Its Relation with Population in the Lower Barpani Watershed, Assam, India. Nat. Resour. Res. 2018, 27, 503–515. [Google Scholar] [CrossRef]
- Ahmad, I.; Dar, M.A.; Fenta, A.; Halefom, A.; Nega, H.; Andualem, T.G.; Teshome, A. Spatial Configuration of Groundwater Potential Zones Using OLS Regression Method. J. Afr. Earth Sci. 2021, 177, 104147. [Google Scholar] [CrossRef]
- Doke, A.B.; Zolekar, R.B.; Patel, H.; Das, S. Geospatial Mapping of Groundwater Potential Zones Using Multi-Criteria Decision-Making AHP Approach in a Hardrock Basaltic Terrain in India. Ecol. Indic. 2021, 127, 107685. [Google Scholar] [CrossRef]
- Su, X.; Liu, T.; Beheshti, M.; Prigiobbe, V. Relationship between Infiltration, Sewer Rehabilitation, and Groundwater Flooding in Coastal Urban Areas. Environ. Sci. Pollut. Res. 2020, 27, 14288–14298. [Google Scholar] [CrossRef] [PubMed]
- Ogden, F.L.; Raj Pradhan, N.; Downer, C.W.; Zahner, J.A. Relative Importance of Impervious Area, Drainage Density, Width Function, and Subsurface Storm Drainage on Flood Runoff from an Urbanized Catchment. Water Resour. Res. 2011, 47, 12503. [Google Scholar] [CrossRef]
- Julínek, T.; Duchan, D.; Říha, J. Mapping of Uplift Hazard Due to Rising Groundwater Level during Floods. J. Flood Risk Manag. 2020, 13, e12601. [Google Scholar] [CrossRef]
- Ghorbani Nejad, S.; Falah, F.; Daneshfar, M.; Haghizadeh, A.; Rahmati, O. Delineation of Groundwater Potential Zones Using Remote Sensing and GIS-Based Data-Driven Models. Geocarto Int. 2017, 32, 167–187. [Google Scholar] [CrossRef]
- Thapa, R.; Gupta, S.; Guin, S.; Kaur, H. Assessment of Groundwater Potential Zones Using Multi-Influencing Factor (MIF) and GIS: A Case Study from Birbhum District, West Bengal. Appl. Water Sci. 2017, 7, 4117–4131. [Google Scholar] [CrossRef]
- Oikonomidis, D.; Dimogianni, S.; Kazakis, N.; Voudouris, K. A GIS/Remote Sensing-Based Methodology for Groundwater Potentiality Assessment in Tirnavos Area, Greece. J. Hydrol. 2015, 525, 197–208. [Google Scholar] [CrossRef]
- Hamill, L.; Bell, F.G. Groundwater Resource Development; Butterworths: London, UK, 1986. [Google Scholar]
- Moubark, K.; Abdelkareem, M. Characterization and Assessment of Groundwater Resources Using Hydrogeochemical Analysis, GIS, and Field Data in Southern Wadi Qena, Egypt. Arab. J. Geosci. 2018, 11, 598. [Google Scholar] [CrossRef]
- D’Aniello, A.; Cimorelli, L.; Cozzolino, L.; Pianese, D. The Effect of Geological Heterogeneity and Groundwater Table Depth on the Hydraulic Performance of Stormwater Infiltration Facilities. Water Resour. Manag. 2019, 33, 1147–1166. [Google Scholar] [CrossRef]
- Pophillat, W.; Sage, J.; Rodriguez, F.; Braud, I. Consequences of Interactions between Stormwater Infiltration Systems, Shallow Groundwater and Underground Structures at the Neighborhood Scale. Urban Water J. 2022, 19, 812–823. [Google Scholar] [CrossRef]
- Singh, S.K.; Zeddies, M.; Shankar, U.; Griffiths, G.A. Potential Groundwater Recharge Zones within New Zealand. Geosci. Front. 2019, 10, 1065–1072. [Google Scholar] [CrossRef]
- Nuissl, H.; Haase, D.; Lanzendorf, M.; Wittmer, H. Environmental Impact Assessment of Urban Land Use Transitions—A Context-Sensitive Approach. Land. Use Policy 2009, 26, 414–424. [Google Scholar] [CrossRef]
- Kourgialas, N.N.; Karatzas, G.P. Flood management and a GIS modelling method to assess flood-hazard areas—A case study. Hydrol. Sci. J. 2011, 56, 212–225. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Flood Susceptibility Mapping Using a Novel Ensemble Weights-of-Evidence and Support Vector Machine Models in GIS. J. Hydrol. 2014, 512, 332–343. [Google Scholar] [CrossRef]
- McGreal, W.S.; Craig, D. Mass-movement activity: An illustration of differing responses to groundwater conditions from two sites in northern Ireland. Ir. Geogr. 1977, 10, 28–35. [Google Scholar] [CrossRef]
- Haridas, V.R.; Aravindan, S.; Girish, G. Remote sensing and its applications for groundwater favourable area identification. Q. J. GARC 1998, 6, 18–22. [Google Scholar]
- Pinto, D.; Shrestha, S.; Babel, M.S.; Ninsawat, S. Delineation of Groundwater Potential Zones in the Comoro Watershed, Timor Leste Using GIS, Remote Sensing and Analytic Hierarchy Process (AHP) Technique. Appl. Water Sci. 2017, 7, 503–519. [Google Scholar] [CrossRef]
- Mohammadi, Z.; Alijani, F.; Rangzan, K. Deflogic: A Method for Assessment of Groundwater Potential in Karst Terrains: Gurpi Anticline, Southwest Iran. Arab. J. Geosci. 2014, 7, 3639–3655. [Google Scholar] [CrossRef]
- Nassery, H.R.; Zeydalinejad, N.; Alijani, F. Speculation on the Resilience of Karst Aquifers Using Geophysical and GIS-Based Approaches (a Case Study of Iran). Acta Geophys. 2021, 69, 2393–2415. [Google Scholar] [CrossRef]
- Zhang, K.; Parolari, A.J. Impact of Stormwater Infiltration on Rainfall-Derived Inflow and Infiltration: A Physically Based Surface–Subsurface Urban Hydrologic Model. J. Hydrol. 2022, 610, 127938. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Network Process: Planning, Priority Setting, Resource Allocation; McGraw Hill International Publication: New York, NY, USA, 1980. [Google Scholar]
- Saaty, T.L. The analytic hierarchy process (AHP). J. Oper. Res. Soc. 1980, 41, 1073–1076. [Google Scholar]
- Saaty, T.L. Decision Making—The Analytic Hierarchy and Network Processes (AHP/ANP). J. Syst. Sci. Syst. Eng. 2004, 13, 1–35. [Google Scholar] [CrossRef]
- Saaty, T.L. Some Mathematical Topics in the Analytic Hierarchy Process. Math. Models Decis. Support. 1988, 48, 89–107. [Google Scholar] [CrossRef]
- Shekar, P.R.; Mathew, A. Integrated Assessment of Groundwater Potential Zones and Artificial Recharge Sites Using GIS and Fuzzy-AHP: A Case Study in Peddavagu Watershed, India. Environ. Monit. Assess. 2023, 195, 906. [Google Scholar] [CrossRef] [PubMed]
- Saaty, T.L. About a Hundred Years of Creativity in Decision Making. Int. J. Anal. Hierarchy Process 2015, 7, 138–144. [Google Scholar] [CrossRef]
- Shirzadi, A.; Bui, D.T.; Pham, B.T.; Solaimani, K.; Chapi, K.; Kavian, A.; Shahabi, H.; Revhaug, I. Shallow Landslide Susceptibility Assessment Using a Novel Hybrid Intelligence Approach. Environ. Earth Sci. 2017, 76, 60. [Google Scholar] [CrossRef]
- Shekhar, S.; Pandey, A.C. Delineation of Groundwater Potential Zone in Hard Rock Terrain of India Using Remote Sensing, Geographical Information System (GIS) and Analytic Hierarchy Process (AHP) Techniques. Geocarto Int. 2015, 30, 402–421. [Google Scholar] [CrossRef]
- Farhat, B.; Souissi, D.; Mahfoudhi, R.; Chrigui, R.; Sebei, A.; Ben Mammou, A. GIS-Based Multi-Criteria Decision-Making Techniques and Analytical Hierarchical Process for Delineation of Groundwater Potential. Environ. Monit. Assess. 2023, 195, 285. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Prediction, Projection and Forecasting: Applications of the Analytic Hierarchy Process in Economics, Finance, Politics, Games and Sports; Springer: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Bonham-Carter, G. Geographic Information Systems for Geoscientists: Modelling with GIS; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Likas, A.; Vlassis, N.; Verbeek, J.J. The Global K-Means Clustering Algorithm. Pattern Recognit. 2003, 36, 451–461. [Google Scholar] [CrossRef]
- Žalik, K.R. An Efficient K-Means Clustering Algorithm. Pattern Recognit. Lett. 2008, 29, 1385–1391. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M. Data Mining, Concepts and Techniques; Morgan kaufmann Publishers: San Francisco, CA, USA, 2006. [Google Scholar]
- Ali, A.; Sheng-Chang, C. Characterization of Well Logs Using K-Mean Cluster Analysis. J. Pet. Explor. Prod. Technol. 2020, 10, 2245–2256. [Google Scholar] [CrossRef]
- Gómez, F.; Flores, Y.; Vadászi, M. Comparative Analysis of the K-Nearest-Neighbour Method and K-Means Cluster Analysis for Lithological Interpretation of Well Logs of the Shushufindi Oilfield, Ecuador. Rud.-Geološko-Naft. Zb. 2022, 37, 155–165. [Google Scholar] [CrossRef]
- Kuo, R.J.; Wang, H.S.; Hu, T.L.; Chou, S.H. Application of Ant K-Means on Clustering Analysis. Comput. Math. Appl. 2005, 50, 1709–1724. [Google Scholar] [CrossRef]
- Javadi, S.; Hashemy, S.M.; Mohammadi, K.; Howard, K.W.F.; Neshat, A. Classification of Aquifer Vulnerability Using K-Means Cluster Analysis. J. Hydrol. 2017, 549, 27–37. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-Means Clustering Algorithm. Appl. Stat. 1979, 28, 100. [Google Scholar] [CrossRef]
- MacQueen, J.B. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics; University of California Press: Oakland, CA, USA, 1967; Volume 5, pp. 281–298. [Google Scholar]
- Saaty, T.L. Decision Making with Dependence and Feedback: The Analytic Network Process; RWS Publication: Pittsburgh, PA, USA, 1997; Volume 4922. [Google Scholar]
- Mohandes, S.R.; Kineber, A.F.; Abdelkhalek, S.; Kaddoura, K.; Elsayed, M.; Hosseini, M.R.; Zayed, T. Evaluation of the Critical Factors Causing Sewer Overflows through Modeling of Structural Equations and System Dynamics. J. Clean. Prod. 2022, 375, 134035. [Google Scholar] [CrossRef]
- Owolabi, T.A.; Mohandes, S.R.; Zayed, T. Investigating the Impact of Sewer Overflow on the Environment: A Comprehensive Literature Review Paper. J. Environ. Manag. 2022, 301, 113810. [Google Scholar] [CrossRef]
- Muttil, N.; Nasrin, T.; Sharma, A.K. Impacts of extreme rainfalls on sewer overflows and WSUD-based mitigation strategies: A review. Water 2023, 15, 429. [Google Scholar] [CrossRef]
- Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Bennett, N.D.; Croke, B.F.W.; Guariso, G.; Guillaume, J.H.A.; Hamilton, S.H.; Jakeman, A.J.; Marsili-Libelli, S.; Newham, L.T.H.; Norton, J.P.; Perrin, C.; et al. Characterising Performance of Environmental Models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Rose, K.A.; Roth, B.M.; Smith, E.P. Skill Assessment of Spatial Maps for Oceanographic Modeling. J. Mar. Syst. 2009, 76, 34–48. [Google Scholar] [CrossRef]
- Sciuto, G.; Diekkruüger, B. Influence of Soil Heterogeneity and Spatial Discretization on Catchment Water Balance Modeling. Vadose Zone J. 2010, 9, 955–969. [Google Scholar] [CrossRef]
- van Vliet, J.; Hagen-Zanker, A.; Hurkens, J.; van Delden, H. A Fuzzy Set Approach to Assess the Predictive Accuracy of Land Use Simulations. Ecol. Model. 2013, 261–262, 32–42. [Google Scholar] [CrossRef]
- Hagen-Zanker, A.; Martens, P. Map Comparison Methods for Comprehensive Assessment of Geosimulation Models. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2008; Volume 5072, pp. 194–209. [Google Scholar] [CrossRef]
- Pontius, R.G.; Huffaker, D.; Denman, K. Useful Techniques of Validation for Spatially Explicit Land-Change Models. Ecol. Model. 2004, 179, 445–461. [Google Scholar] [CrossRef]
- Power, C.; Simms, A.; White, R. Hierarchical Fuzzy Pattern Matching for the Regional Comparison of Land Use Maps. Int. J. Geogr. Inf. Sci. 2001, 15, 77–100. [Google Scholar] [CrossRef]
- Sorichetta, A.; Masetti, M.; Ballabio, C.; Sterlacchini, S.; Beretta, G. Pietro Reliability of Groundwater Vulnerability Maps Obtained through Statistical Methods. J. Environ. Manag. 2011, 92, 1215–1224. [Google Scholar] [CrossRef]
- Koch, J.; Jensen, K.H.; Stisen, S. Toward a True Spatial Model Evaluation in Distributed Hydrological Modeling: Kappa Statistics, Fuzzy Theory, and EOF-Analysis Benchmarked by the Human Perception and Evaluated against a Modeling Case Study. Water Resour. Res. 2015, 51, 1225–1246. [Google Scholar] [CrossRef]
- Flight, L.; Julious, S.A. The Disagreeable Behaviour of the Kappa Statistic. Pharm. Stat. 2015, 14, 74–78. [Google Scholar] [CrossRef]
- Razavi, S.; Jakeman, A.; Saltelli, A.; Prieur, C.; Iooss, B.; Borgonovo, E.; Plischke, E.; Lo Piano, S.; Iwanaga, T.; Becker, W.; et al. The Future of Sensitivity Analysis: An Essential Discipline for Systems Modeling and Policy Support. Environ. Model. Softw. 2021, 137, 104954. [Google Scholar] [CrossRef]
- Budamala, V.; Baburao Mahindrakar, A. Integration of Adaptive Emulators and Sensitivity Analysis for Enhancement of Complex Hydrological Models. Environ. Process. 2020, 7, 1235–1253. [Google Scholar] [CrossRef]
- Mohammadi, M.M. Development of Condition Prediction Models for Sanitary Sewer Pipes. In Civil Engineering Dissertations; University of Texas at Arlington: Arlington, TX, USA, 2019. [Google Scholar]
- Abdallah, M.; Abu Talib, M.; Feroz, S.; Nasir, Q.; Abdalla, H.; Mahfood, B. Artificial Intelligence Applications in Solid Waste Management: A Systematic Research Review. Waste Manag. 2020, 109, 231–246. [Google Scholar] [CrossRef] [PubMed]
- Youssef, A.M.; Pradhan, B.; Tarabees, E. Integrated Evaluation of Urban Development Suitability Based on Remote Sensing and GIS Techniques: Contribution from the Analytic Hierarchy Process. Arab. J. Geosci. 2011, 4, 463–473. [Google Scholar] [CrossRef]
- Minh, H.V.T.; Avtar, R.; Kumar, P.; Tran, D.Q.; Van Ty, T.; Behera, H.C.; Kurasaki, M. Groundwater Quality Assessment Using Fuzzy-AHP in An Giang Province of Vietnam. Geosciences 2019, 9, 330. [Google Scholar] [CrossRef]
- Ridwan Makkulawu, A.; Santoso, I.; Asmaul Mustaniroh, S. Exploring the Potential and Benefits of AHP and GIS Integration for Informed Decision-Making: A Literature Review. Ing. Des. Syst. D’information 2023, 28, 1701. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Use of genetic algorithms for the optimal design of flat plate solar collectors. In Proceedings of the ISES Solar World Congress 2003; Solar Energy for a Sustainable Future, Göteborg, Sweden, 14–19 June 2003; International Solar Energy Society: Freiburg, Germany, 2003. [Google Scholar]
- Turner, A.; Retamal, M.; White, S.; Palfreeman, L. Third Party Evaluation of Wide Bay Water Smart Metering and Sustainable Water Pricing Initiative Project; University of Technology Sydney: Ultimo, Australia, 2010. [Google Scholar]
- Drogkoula, M.; Kokkinos, K.; Samaras, N. A Comprehensive Survey of Machine Learning Methodologies with Emphasis in Water Resources Management. Appl. Sci. 2023, 13, 12147. [Google Scholar] [CrossRef]
- Wunsch, A.; Liesch, T.; Broda, S. Feature-Based Groundwater Hydrograph Clustering Using Unsupervised Self-Organizing Map-Ensembles. Water Resour. Manag. 2022, 36, 39–54. [Google Scholar] [CrossRef]
- Chen, Y.; Qin, B.; Liu, T.; Liu, Y.; Li, S. The Comparison of SOM and K-Means for Text Clustering. Comput. Inf. Sci. 2010, 3, 268–274. [Google Scholar] [CrossRef]
- Kiang, M.Y.; Hu, M.Y.; Fisher, D.M. An Extended Self-Organizing Map Network for Market Segmentation—A Telecommunication Example. Decis. Support. Syst. 2006, 42, 36–47. [Google Scholar] [CrossRef]
- Melo Riveros, N.A.; Cardenas Espitia, B.A.; Aparicio Pico, L.E. Comparison between K-Means and Self-Organizing Maps Algorithms Used for Diagnosis Spinal Column Patients. Inf. Med. Unlocked 2019, 16, 100206. [Google Scholar] [CrossRef]
- He, J.; Tan, A.H.; Tan, C.L.; Sung, S.Y. On Quantitative Evaluation of Clustering Systems. In Clustering and Information Retrieval; Springer: Boston, MA, USA, 2004; pp. 105–133. [Google Scholar] [CrossRef]
- Balakrishnan, P.V.; Cooper, M.C.; Jacob, V.S.; Lewis, P.A. A Study of the Classification Capabilities of Neural Networks Using Unsupervised Learning: A Comparison with K-Means Clustering. Psychometrika 1994, 59, 509–525. [Google Scholar] [CrossRef]
- Kumar, U.A.; Dhamija, Y. Comparative Analysis of SOM Neural Network with K-Means Clustering Algorithm. In Proceedings of the 5th IEEE International Conference on Management of Innovation and Technology, Singapore, 2–5 June 2010; pp. 55–59. [Google Scholar] [CrossRef]
- Mingoti, S.A.; Lima, J.O. Comparing SOM Neural Network with Fuzzy C-Means, K-Means and Traditional Hierarchical Clustering Algorithms. Eur. J. Oper. Res. 2006, 174, 1742–1759. [Google Scholar] [CrossRef]
- Nolte, A.; Haaf, E.; Heudorfer, B.; Bender, S.; Hartmann, J. Disentangling Coastal Groundwater Level Dynamics in a Global Dataset. Hydrol. Earth Syst. Sci. 2024, 28, 1215–1249. [Google Scholar] [CrossRef]
- Celebi, M.E.; Kingravi, H.A.; Vela, P.A. A Comparative Study of Efficient Initialization Methods for the K-Means Clustering Algorithm. Expert. Syst. Appl. 2013, 40, 200–210. [Google Scholar] [CrossRef]
- Heil, J.; Häring, V.; Marschner, B.; Stumpe, B. Advantages of Fuzzy K-Means over k-Means Clustering in the Classification of Diffuse Reflectance Soil Spectra: A Case Study with West African Soils. Geoderma 2019, 337, 11–21. [Google Scholar] [CrossRef]
- Kao, Y.T.; Zahara, E.; Kao, I.W. A Hybridized Approach to Data Clustering. Expert. Syst. Appl. 2008, 34, 1754–1762. [Google Scholar] [CrossRef]
- Laszlo, M.; Mukherjee, S. A Genetic Algorithm That Exchanges Neighboring Centers for K-Means Clustering. Pattern Recognit. Lett. 2007, 28, 2359–2366. [Google Scholar] [CrossRef]
- Nayak, J.; Kanungo, D.P.; Naik, B.; Behera, H.S. Evolutionary Improved Swarm-Based Hybrid K-Means Algorithm for Cluster Analysis. Adv. Intell. Syst. Comput. 2016, 379, 343–352. [Google Scholar] [CrossRef]
- Niknam, T.; Amiri, B. An Efficient Hybrid Approach Based on PSO, ACO and k-Means for Cluster Analysis. Appl. Soft Comput. 2010, 10, 183–197. [Google Scholar] [CrossRef]
- Rogiers, B.; Mallants, D.; Batelaan, O.; Gedeon, M.; Huysmans, M.; Dassargues, A. Model-Based Classification of CPT Data and Automated Lithostratigraphic Mapping for High-Resolution Characterization of a Heterogeneous Sedimentary Aquifer. PLoS ONE 2017, 12, e0176656. [Google Scholar] [CrossRef] [PubMed]
- Sung, C.S.; Jin, H.W. A Tabu-Search-Based Heuristic for Clustering. Pattern Recognit. 2000, 33, 849–858. [Google Scholar] [CrossRef]
- Zhang, C.L.; Jing, Z.L.; Pan, H.; Jin, B.; Li, Z.X. Robust Visual Tracking Using Discriminative Stable Regions and K-Means Clustering. Neurocomputing 2013, 111, 131–143. [Google Scholar] [CrossRef]
- Tewari, A.; Singh, P.K.; Gaur, S.; Mishra, S.; Kumar, R. Cluster-Based Delineation of Optimal Sites for Managed Aquifer Recharge: A Case Study of Lower Betwa River Basin, India. Environ. Earth Sci. 2024, 83, 20. [Google Scholar] [CrossRef]
- Li, J.; Hassan, D.; Brewer, S.; Sitzenfrei, R. Is Clustering Time-Series Water Depth Useful? An Exploratory Study for Flooding Detection in Urban Drainage Systems. Water 2020, 12, 2433. [Google Scholar] [CrossRef]
- Mel, R.; Sterl, A.; Lionello, P. High Resolution Climate Projection of Storm Surge at the Venetian Coast. Nat. Hazards Earth Syst. Sci. 2013, 13, 1135–1142. [Google Scholar] [CrossRef]
- Shende, S.; Chau, K.W. Design of Water Distribution Systems Using an Intelligent Simple Benchmarking Algorithm with Respect to Cost Optimization and Computational Efficiency. Water Supply 2019, 19, 1892–1898. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S. Burst Detection by Analyzing Shape Similarity of Time Series Subsequences in District Metering Areas. J. Water Resour. Plan. Manag. 2020, 146, 04019068. [Google Scholar] [CrossRef]
- Naranjo-Fernández, N.; Guardiola-Albert, C.; Aguilera, H.; Serrano-Hidalgo, C.; Montero-González, E. Clustering Groundwater Level Time Series of the Exploited Almonte-Marismas Aquifer in Southwest Spain. Water 2020, 12, 1063. [Google Scholar] [CrossRef]
- Teimoori, S.; Olya, M.H.; Miller, C.J. Groundwater Level Monitoring Network Design with Machine Learning Methods. J. Hydrol. 2023, 625, 130145. [Google Scholar] [CrossRef]
- Rizwan, A.; Iqbal, N.; Khan, A.N.; Ahmad, R.; Kim, D.H. Toward Effective Pattern Recognition Based on Enhanced Weighted K-Mean Clustering Algorithm for Groundwater Resource Planning in Point Cloud. IEEE Access 2021, 9, 130154–130169. [Google Scholar] [CrossRef]
- Salehnia, N.; Salehnia, N.; Ansari, H.; Kolsoumi, S.; Bannayan, M. Climate Data Clustering Effects on Arid and Semi-Arid Rainfed Wheat Yield: A Comparison of Artificial Intelligence and K-Means Approaches. Int. J. Biometeorol. 2019, 63, 861–872. [Google Scholar] [CrossRef]
- Javadi, S.; Saatsaz, M.; Hashemy Shahdany, S.M.; Neshat, A.; Ghordoyee Milan, S.; Akbari, S. A New Hybrid Framework of Site Selection for Groundwater Recharge. Geosci. Front. 2021, 12, 101144. [Google Scholar] [CrossRef]
- Mohammadrezapour, O.; Kisi, O.; Pourahmad, F. Fuzzy C-Means and K-Means Clustering with Genetic Algorithm for Identification of Homogeneous Regions of Groundwater Quality. Neural Comput. Appl. 2020, 32, 3763–3775. [Google Scholar] [CrossRef]
- Kitzig, M.C.; Kepic, A.; Kieu, D.T. Testing Cluster Analysis on Combined Petrophysical and Geochemical Data for Rock Mass Classification. Explor. Geophys. 2017, 48, 344–352. [Google Scholar] [CrossRef]
- Lharti, H.; Sirieix, C.; Riss, J.; Verdet, C.; Salmon, F.; Lacanette, D. Partitioning a Rock Mass Based on Electrical Resistivity Data: The Choice of Clustering Method. Geophys. J. Int. 2023, 234, 439–452. [Google Scholar] [CrossRef]
- Wang, Y.; Ksienzyk, A.K.; Liu, M.; Brönner, M. Multigeophysical Data Integration Using Cluster Analysis: Assisting Geological Mapping in Trøndelag, Mid-Norway. Geophys. J. Int. 2021, 225, 1142–1157. [Google Scholar] [CrossRef]
- Kayhomayoon, Z.; Ghordoyee Milan, S.; Arya Azar, N.; Kardan Moghaddam, H. A New Approach for Regional Groundwater Level Simulation: Clustering, Simulation, and Optimization. Nat. Resour. Res. 2021, 30, 4165–4185. [Google Scholar] [CrossRef]
- Yin, X.; Chen, Y.; Bouferguene, A.; Al-Hussein, M. Data-Driven Bi-Level Sewer Pipe Deterioration Model: Design and Analysis. Autom. Constr. 2020, 116, 103181. [Google Scholar] [CrossRef]
- Atique, F. Analysis of Urban Pipe Deterioration Using Copula Method; University of Delaware: Newark, DE, USA, 2016. [Google Scholar]
- Opila, M.C. Structural Condition Scoring of Buried Sewer Pipes for Risk-based Decision Making; University of Delaware: Newark, DE, USA, 2011. [Google Scholar]
- Lindner, R. Effectively Managing Sewer Pipeline Infrastructure. J. Undergr. Infrastr. Manag. 2008, 23–25. [Google Scholar]
- Atambo, D.O.; Najafi, M.; Kaushal, V. Development and Comparison of Prediction Models for Sanitary Sewer Pipes Condition Assessment Using Multinomial Logistic Regression and Artificial Neural Network. Sustainability 2022, 14, 5549. [Google Scholar] [CrossRef]
- Afonso, M.J.; Freitas, L.; Chaminé, H.I. Groundwater Recharge in Urban Areas (Porto, NW Portugal): The Role of GIS Hydrogeology Mapping. Sustain. Water Resour. Manag. 2019, 5, 203–216. [Google Scholar] [CrossRef]
- Zhang, K.; Chui, T.F.M. A Review on Implementing Infiltration-Based Green Infrastructure in Shallow Groundwater Environments: Challenges, Approaches, and Progress. J. Hydrol. 2019, 579, 124089. [Google Scholar] [CrossRef]
- Malek Mohammadi, M.; Najafi, M.; Kermanshachi, S.; Kaushal, V.; Serajiantehrani, R. Factors Influencing the Condition of Sewer Pipes: State-of-the-Art Review. J. Pipeline Syst. Eng. Pract. 2020, 11, 03120002. [Google Scholar] [CrossRef]
- Akinci, H.; Özalp, A.Y.; Turgut, B. Agricultural Land Use Suitability Analysis Using GIS and AHP Technique. Comput. Electron. Agric. 2013, 97, 71–82. [Google Scholar] [CrossRef]
- Yap, J.Y.L.; Ho, C.C.; Ting, C.Y. A Systematic Review of the Applications of Multi-Criteria Decision-Making Methods in Site Selection Problems. Built Environ. Proj. Asset Manag. 2019, 9, 548–563. [Google Scholar] [CrossRef]
- Seyedmohammadi, J.; Sarmadian, F.; Jafarzadeh, A.A.; McDowell, R.W. Development of a Model Using Matter Element, AHP and GIS Techniques to Assess the Suitability of Land for Agriculture. Geoderma 2019, 352, 80–95. [Google Scholar] [CrossRef]
- Salman, B.; Salem, O. Modeling Failure of Wastewater Collection Lines Using Various Section-Level Regression Models. J. Infrastruct. Syst. 2012, 18, 146–154. [Google Scholar] [CrossRef]
- Theochari, A.P.; Feloni, E.; Bournas, A.; Baltas, E. Hydrometeorological—Hydrometric Station Network Design Using Multicriteria Decision Analysis and GIS Techniques. Environ. Process. 2021, 8, 1099–1119. [Google Scholar] [CrossRef]
- Van Metre, P.C.; Qi, S.; Deacon, J.; Dieter, C.; Driscoll, J.M.; Fienen, M.; Kenney, T.; Lambert, P.; Lesmes, D.; Mason, C.A.; et al. Prioritizing River Basins for Intensive Monitoring and Assessment by the US Geological Survey. Environ. Monit. Assess. 2020, 192, 458. [Google Scholar] [CrossRef]
- Mashford, J.; Marlow, D.; Tran, D.; May, R. Prediction of Sewer Condition Grade Using Support Vector Machines. J. Comput. Civ. Eng. 2011, 25, 283–290. [Google Scholar] [CrossRef]
- Hwangbo, S.; Al, R.; Chen, X.; Sin, G. Integrated Model for Understanding N2O Emissions from Wastewater Treatment Plants: A Deep Learning Approach. Environ. Sci. Technol. 2021, 55, 2143–2151. [Google Scholar] [CrossRef]
- Chen, K.; Chen, H.; Zhou, C.; Huang, Y.; Qi, X.; Shen, R.; Liu, F.; Zuo, M.; Zou, X.; Wang, J.; et al. Comparative Analysis of Surface Water Quality Prediction Performance and Identification of Key Water Parameters Using Different Machine Learning Models Based on Big Data. Water Res. 2020, 171, 115454. [Google Scholar] [CrossRef] [PubMed]
- Fontecha, J.E.; Agarwal, P.; Torres, M.N.; Mukherjee, S.; Walteros, J.L.; Rodríguez, J.P. A Two-Stage Data-Driven Spatiotemporal Analysis to Predict Failure Risk of Urban Sewer Systems Leveraging Machine Learning Algorithms. Risk Anal. 2021, 41, 2356–2391. [Google Scholar] [CrossRef]
- Friedel, M.J. Estimation and Scaling of Hydrostratigraphic Units: Application of Unsupervised Machine Learning and Multivariate Statistical Techniques to Hydrogeophysical Data. Hydrogeol. J. 2016, 24, 2103–2122. [Google Scholar] [CrossRef]
- Braun, B.Á.; Abordán, A.; Szabó, N.P. Lithology determination in a coal exploration drillhole using Steiner weighted cluster analysis. Geosci. Eng. 2016, 5, 51–64. [Google Scholar]
- Kriegel, H.P.; Kröger, P.; Sander, J.; Zimek, A. Density-Based Clustering. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 231–240. [Google Scholar] [CrossRef]
- Locatelli, L.; Mark, O.; Mikkelsen, P.S.; Arnbjerg-Nielsen, K.; Deletic, A.; Roldin, M.; Binning, P.J. Hydrologic Impact of Urbanization with Extensive Stormwater Infiltration. J. Hydrol. 2017, 544, 524–537. [Google Scholar] [CrossRef]
- Prapanchan, V.N.; Subramani, T.; Karunanidhi, D. GIS and Fuzzy Analytical Hierarchy Process to Delineate Groundwater Potential Zones in Southern Parts of India. Groundw. Sustain. Dev. 2024, 25, 101110. [Google Scholar] [CrossRef]
- Sitorus, F.; Brito-Parada, P.R. Equipment Selection in Mineral Processing—A Sensitivity Analysis Approach for a Fuzzy Multiple Criteria Decision Making Model. Min. Eng. 2020, 150, 106261. [Google Scholar] [CrossRef]
- Sharifi, A.; Tarlani Beris, A.; Sharifzadeh Javidi, A.; Nouri, M.; Gholizadeh Lonbar, A.; Ahmadi, M. Application of Artificial Intelligence in Digital Twin Models for Stormwater Infrastructure Systems in Smart Cities. Adv. Eng. Inform. 2024, 61, 102485. [Google Scholar] [CrossRef]
- Sakti, A.D.; Mahdani, J.N.; Santoso, C.; Ihsan, K.T.N.; Nastiti, A.; Shabrina, Z.; Safira, M.; Rohmat, F.; Yulianto, F.; Virtriana, R. Optimizing City-Level Centralized Wastewater Management System Using Machine Learning and Spatial Network Analysis. Environ. Technol. Innov. 2023, 32, 103360. [Google Scholar] [CrossRef]








| Schematic Layer | Classification and Reclassification | Weight |
|---|---|---|
| Topographic elevation | <5 m = 10; 5–10 m = 9; 10–50 m = 7; 50–100 m = 5; 100–200 m = 3; >200 m = 1 | 3.05 |
| Slope | 0–15° = 10; 15–30° = 7; 30–45° = 3; >45° = 1 | 4.40 |
| Topographic wetness index | >20 = 10; 15–20 = 7; 10–15 = 5; 5–10 = 3; <5 = 1 | 6.40 |
| Drainage order | 10–11 = 10; 8–9 = 9; 6–7 = 7; 3–5 = 3; 1–2 = 1 | 3.20 |
| Groundwater depth | <5 m = 10; 5–10 m = 7; 10–15 m = 3; ≥15 m = 1 | 13.45 |
| Precipitation | >200 mm/month = 10; 150–200 = 7; 100–150 = 5; <100 = 3 | 3.00 |
| Fault proximity | <50 m = 10; 50–100 m = 7; 100–500 m = 5; >500 m = 0 | 6.80 |
| Fault length | >3000 m = 10; 2000–3000 m = 9; 1000–2000 m = 7; 500–1000 m = 5; 100–500 m = 4; <100 m = 3 | 6.80 |
| Rock | Gravel = 10; Sandstone and gravel = 9; Sandstone = 8; Sandstone and subordinate breccia/sandstone and basalt = 7; Breccia and sandstone/sandstone along with sandstone and mudstone/gravel, clayey = 6; Sandstone/breccia/mudstone/limestone = 5; Mudstone–sandstone interbedded = 4; Tuff = 3; Slate = 2; Chert/mudstone = 1 | 8.75 |
| Alluvium | Gravel = 10; Sand and gravel = 9; Sand = 8; Sand with clay and gravel = 6; Clay/sand variants = 4; Clay/silt/sand and silt = 3 | 8.30 |
| Made ground | Artificial (infilled) deposits = 10; Non-artificial = 0 | 5.05 |
| Mass movement | Landslide deposits = 10; Non-landslide = 0 | 3.45 |
| River proximity | <25 m = 10; 25–50 m = 7; 50–100 m = 3; >100 m = 0 | 10.80 |
| Flooding potential | High = 10; Low = 7; None = 0 | 8.00 |
| Land cover/land use (LC/LU) | Freshwater = 10; Saltmarsh/woodland = 7; Heather/littoral rock = 6; Improved grassland = 5; Urban/suburban = 4; Arable/horticulture = 3; Inland rock = 2 | 4.00 |
| (Weathered) soil type | Sand = 10; Sand to sandy loam = 9; Sand to loam = 8; Sandy loam = 7; Clayey loam to sandy loam/loam to sandy loam = 6; Clay to sandy loam/silt to silty loam/loam to silty loam/varied (locally peaty) = 5; Clayey loam to silty loam = 4; Clayey loam = 3; Clay to clayey loam = 1 | 4.55 |
| Statistic Value | Level of Agreement |
|---|---|
| ≤0 | No agreement |
| 0.01–0.20 | None to slight |
| 0.21–0.40 | Fair |
| 0.41–0.60 | Moderate |
| 0.61–0.80 | Substantial |
| 0.81–1.00 | Almost perfect |
| Season | Spring | Summer | Autumn | Winter | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Weighting | AHP | AHP | AHP | AHP | Equal | AHP minus equal weights | Equal | AHP minus equal weights | Equal | AHP minus equal weights |
| Layers | All layers 1 | All layers | All layers | All layers | All layers | All layers | Five layers 2 | All layers (AHP-weighted) minus five layers (equally weighted) | Two layers 3 | All layers (AHP-weighted) minus two layers (equally weighted) |
| Minimum | 0.07 | 0.07 | 0.08 | 0.08 | 0.10 | −0.11 | 0.00 | −0.34 | 0.00 | −0.64 |
| Maximum | 0.78 | 0.78 | 0.78 | 0.78 | 0.72 | 0.11 | 0.93 | 0.30 | 1.00 | 0.47 |
| Range | 0.71 | 0.70 | 0.70 | 0.70 | 0.62 | 0.22 | 0.93 | 0.64 | 1.00 | 1.10 |
| Mean | 0.28 | 0.28 | 0.29 | 0.29 | 0.31 | −0.02 | 0.27 | 0.02 | 0.28 | 0.02 |
| Standard deviation | 0.09 | 0.09 | 0.09 | 0.09 | 0.07 | 0.03 | 0.15 | 0.08 | 0.24 | 0.17 |
| Statistic | Value |
|---|---|
| Minimum | 0.17 |
| Maximum | 0.64 |
| Mean | 0.40 |
| Median | 0.44 |
| Standard deviation | 0.12 |
| First quartile (Q1) | 0.31 |
| Third quartile (Q3) | 0.48 |
| Statistics | K-Means Clustering and AHP-Weighted GIS Approach with Equal-Interval Classification | K-Means Clustering and AHP-Weighted GIS Approach with Quantile Classification | K-Means Clustering and AHP-Weighted GIS Approach with K-Means Clustering for Classification | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Error matrix | cluster | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| 1 | 57,752,516 | 30,868,308 | 1794 | 44,986,749 | 1,265,170 | 0 | 50,222,276 | 5,026,305 | 0 | |
| 2 | 5,815,602 | 28,548,327 | 13,435,235 | 14,084,274 | 31,987,004 | 4478 | 13,008,762 | 47,919,767 | 795,014 | |
| 3 | 0 | 17011 | 2,122,980 | 4,497,095 | 26,181,472 | 15,555,531 | 393,951 | 6,514,881 | 14,803,662 | |
| Kappa | 0.35 | 0.50 | 0.70 | |||||||
| Percentage of the same classifications | 63.82 | 66.78 | 81.44 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeydalinejad, N.; Javadi, A.A.; Jacob, M.; Baldock, D.; Webber, J.L. Can Proxy-Based Geospatial and Machine Learning Approaches Map Sewer Network Exposure to Groundwater Infiltration? Smart Cities 2025, 8, 145. https://doi.org/10.3390/smartcities8050145
Zeydalinejad N, Javadi AA, Jacob M, Baldock D, Webber JL. Can Proxy-Based Geospatial and Machine Learning Approaches Map Sewer Network Exposure to Groundwater Infiltration? Smart Cities. 2025; 8(5):145. https://doi.org/10.3390/smartcities8050145
Chicago/Turabian StyleZeydalinejad, Nejat, Akbar A. Javadi, Mark Jacob, David Baldock, and James L. Webber. 2025. "Can Proxy-Based Geospatial and Machine Learning Approaches Map Sewer Network Exposure to Groundwater Infiltration?" Smart Cities 8, no. 5: 145. https://doi.org/10.3390/smartcities8050145
APA StyleZeydalinejad, N., Javadi, A. A., Jacob, M., Baldock, D., & Webber, J. L. (2025). Can Proxy-Based Geospatial and Machine Learning Approaches Map Sewer Network Exposure to Groundwater Infiltration? Smart Cities, 8(5), 145. https://doi.org/10.3390/smartcities8050145







