Centralised Smart EV Charging in PV-Powered Parking Lots: A Techno-Economic Analysis
Abstract
Highlights
- A centralised smart EV charging algorithm for workplace parking lots is proposed. The algorithm is able to perform cost- or emissions-based EV charging, including a PV system in the optimisation.
- An innovative “benefit-splitting algorithm” is also proposed, to make sure EV owners receive fair compensation for participating in smart charging activities.
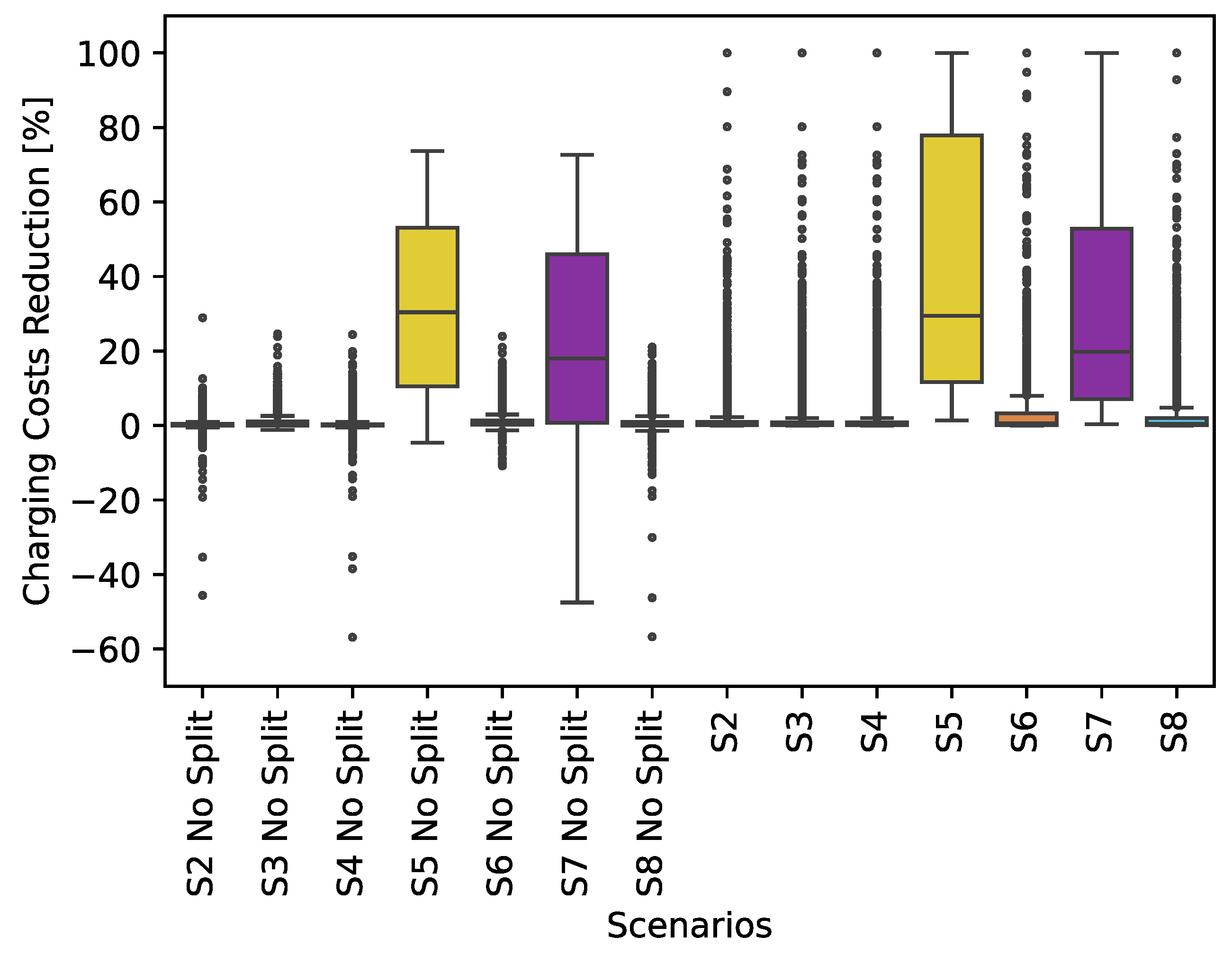
- Our results show possible reductions of up to 11% in EV charging costs, 67% in electricity provision costs for the CPO, and 8% in CO2 emissions if making use of an existing 35 kWp PV system.
- Contracted EV charging capacity for the parking lot can also be reduced, along with EV impact on the power grid.
- Centralised smart EV charging is already implementable in public charging with current technology, and it represents a powerful tool to reduce EV charging costs and their impact on power systems and to deliver grid balancing services as well.
- EV owners’ fair compensation should be addressed when designing advanced smart charging algorithms, especially when delivering services where substantial discomfort can be perceived, e.g., Vehicle-to-Grid (V2G).
Abstract
1. Introduction
2. Related Work
3. Methodology
- Decentralised Smart V1G Charging: there is no central coordinator that schedules all EVs at the same time. Each EV is optimised regardless of the others connected at the same time. It is not possible to limit the total charging power of the location to respond to grid limitations; overloading of the parking lot capacity might happen.
- Centralised Smart V1G Charging: a central coordinator schedules all the EVs for optimal costs or emissions whenever an EV connects to or disconnects from the parking lot. It is possible to limit the total charging power of the location to respond to grid limitations.
3.1. Smart EV Charging Problem Formulation
- is the vector of the power absorbed from the power system for each EV and time instant, i.e., . contains the power absorbed directly from the PV system by each EV at every time instant, i.e., . Finally, contains the power injected into the power grid by the CPO-owned PV system.
- The time-dependent cost of charging the EV from the power system is , and it constitutes the main revenue for the CPO who owns the EV charging stations; is the cost of charging the EVs from the PV system, which can either be equal to or lower if a discount is applied; is the time-dependent energy provision cost for the CPO, including all grid tariffs and taxes. Finally, is the cost of electricity in the day ahead (spot) market price, which is the remuneration the CPO receives when injecting power from the PV system into the grid. These values are used to determine the final cost.
- The net tariffs for the DSO and TSO are and , respectively, out of which the first one is time-dependent only; is the taxation applied to all the other costs.
- The grams of CO2 emitted per kWh of energy consumed from the power grid, or from the PV system, are and . Note that for the latter, a constant value is assumed.
- is the binary variables vector that contains the state of the EVs at each time instant: 0 if the EV is not charging, and 1 if it is.
- is the auxiliary variables vector containing the binary variables ranging from −1 to 1 used to linearise the “charging continuity” constraint from Equation (15).
- The time unit along the whole optimisation horizon is ; n is the EV identifier among the number of EVs considered at the time the algorithm is run. Note that if the decentralised algorithm is considered.
- The simulation timestep in hours is .
- .
- The energy request of the n-th EV at the time when the algorithm is run is , while and are the maximum and minimum charging power allowed by the on-board charger and charging station.
- is the maximum power that can be absorbed for the specific parking installation under study, while is the PV production at time (which is null when no PV is considered in the scenario).
3.2. Centralised vs. Decentralised Smart Charging
- In the decentralised algorithm, the simulation is separately run for each EV once only; hence, the number of EVs connected at time is always equal to one (). In the centralised algorithm, is the number of EVs connected at the time the optimisation is run, , which can be any positive integer number up to the number of available outlets.
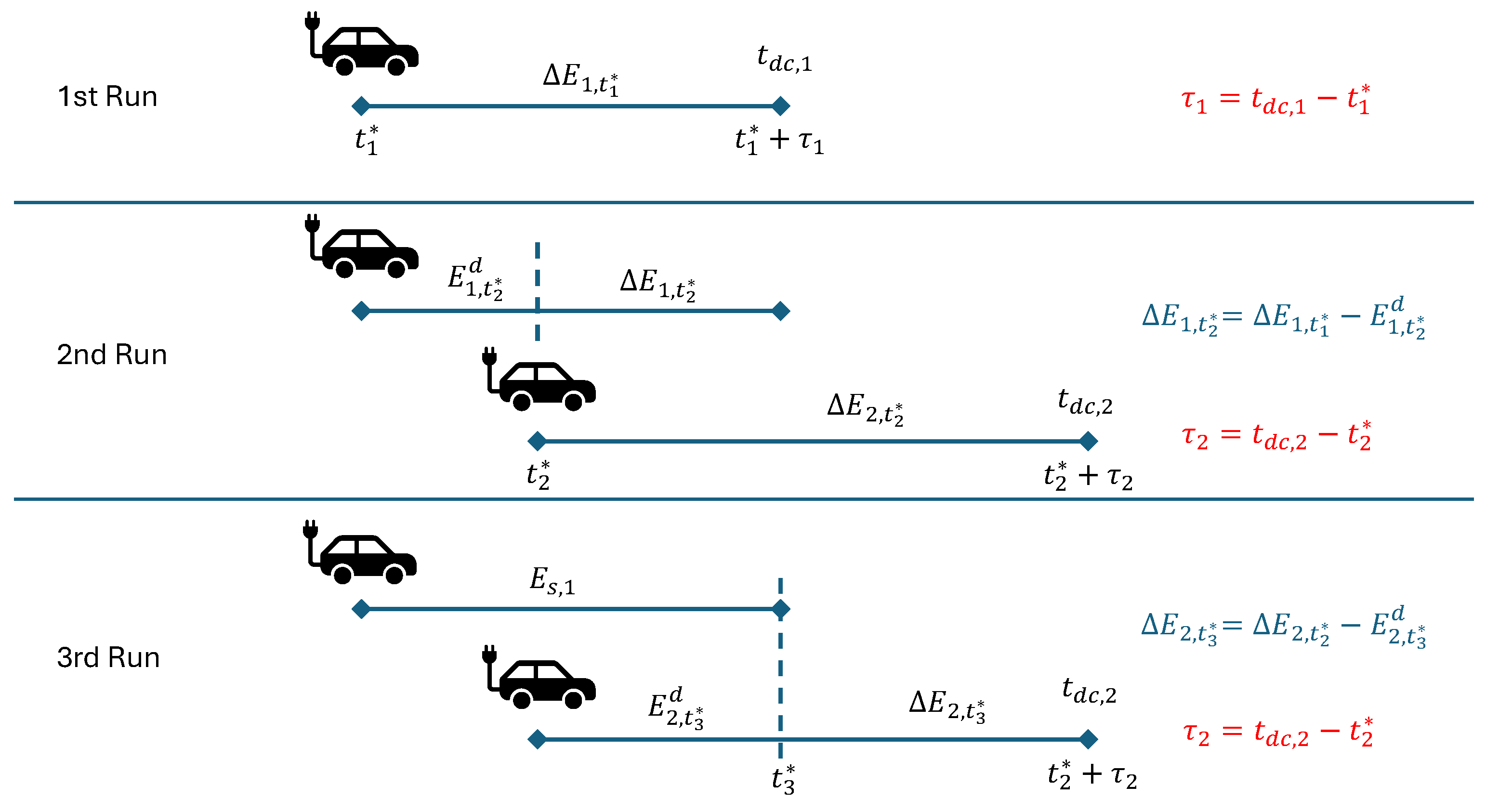
- In the decentralised algorithm, is the number of instants the charging session of the n-th EV lasts. In the centralised one, the formulation changes to Equation (18):where is the number of connected EVs at the time when the optimisation is run. Here, represents one instant in the whole T-long period recorded in the database , while is the disconnection time of the n-th EV. In other words, the optimisation horizon is the time between the instant the optimisation is run and the disconnection instant of the EV that stays connected the longest. In this way, the algorithm can be run whenever an EV is disconnected or connected, and at least one optimal schedule is computed for each EV to follow, independently from the success of the algorithm solving the optimisation problem. It can indeed happen that the total parking lot capacity constraint cannot be respected.
- As a consequence of the previous point, while in the decentralised algorithm the optimisation delivers an amount of energy that is equal to the total energy request from the n-th EV, in the centralised one the optimiser only charges the fraction of energy that has not been charged during the instants before; hence, .
- Finally, since the centralised algorithm runs every time an EV is connected or disconnected in the parking lot, an additional constraint is needed to keep track of whether the n-th EV was charging in the instant before the current one , so
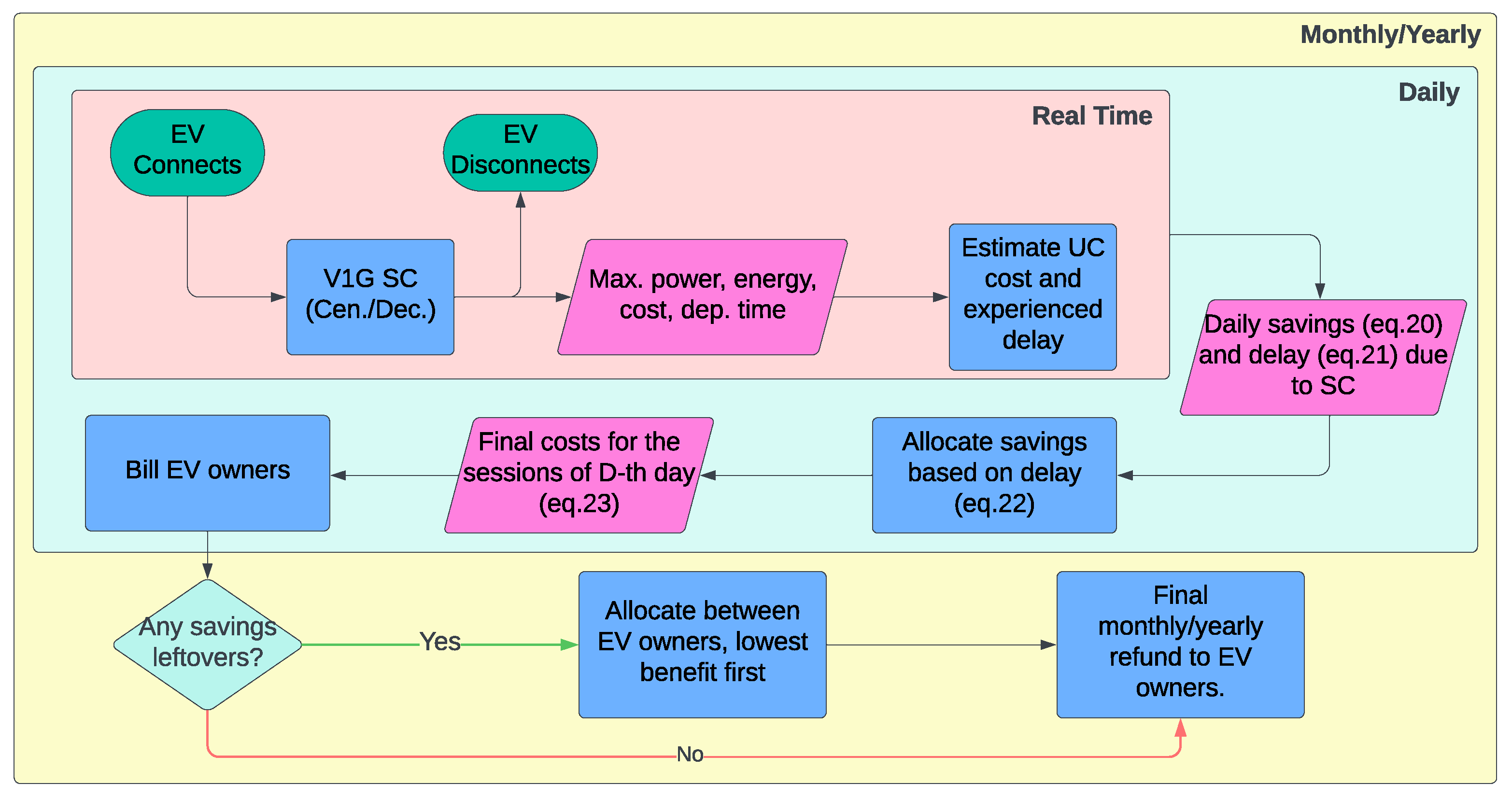
3.3. Benefit-Splitting Algorithm (BSA)
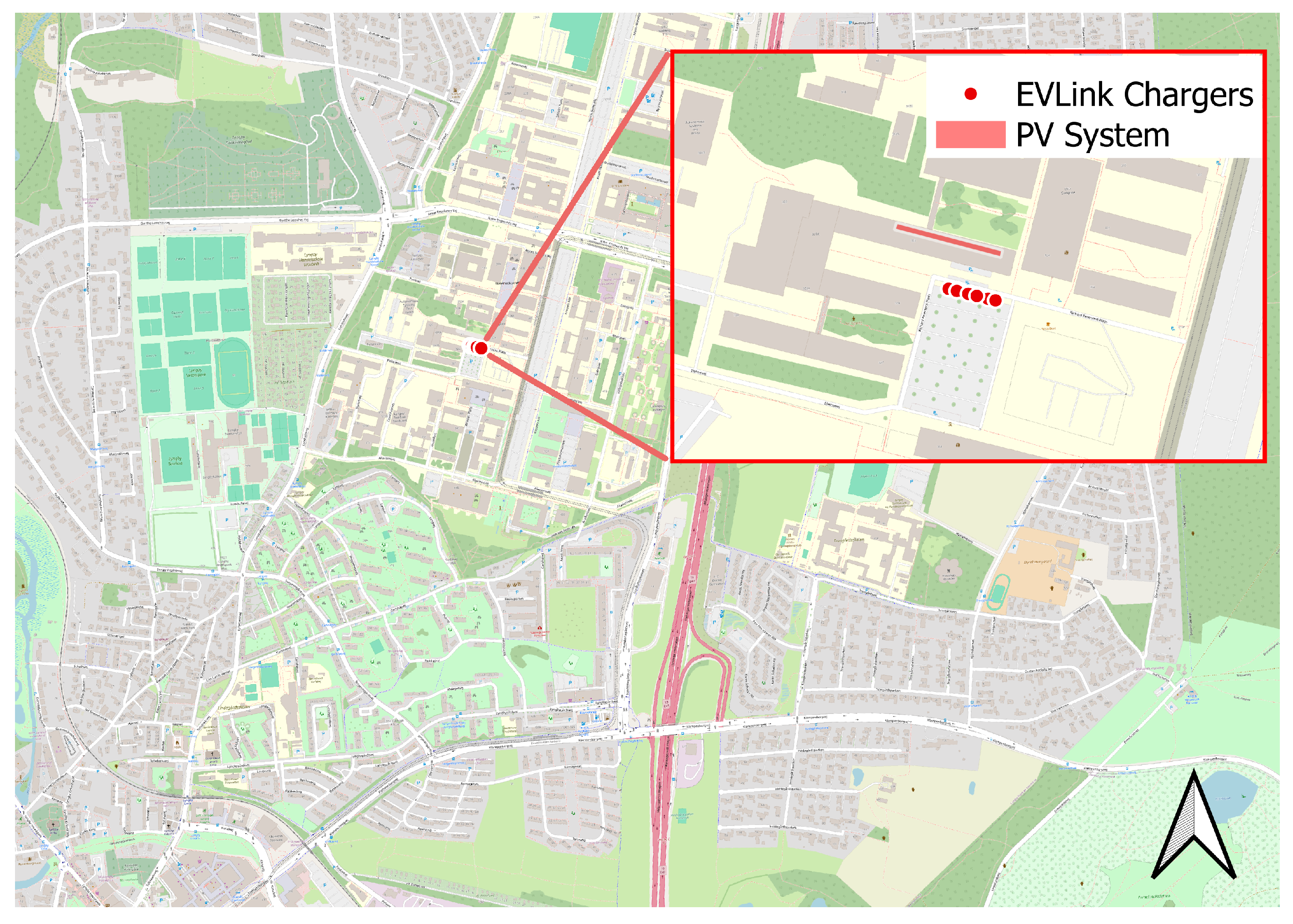
4. Case Study
4.1. EV Charging Dataset
4.2. Costs and Emissions
5. Results
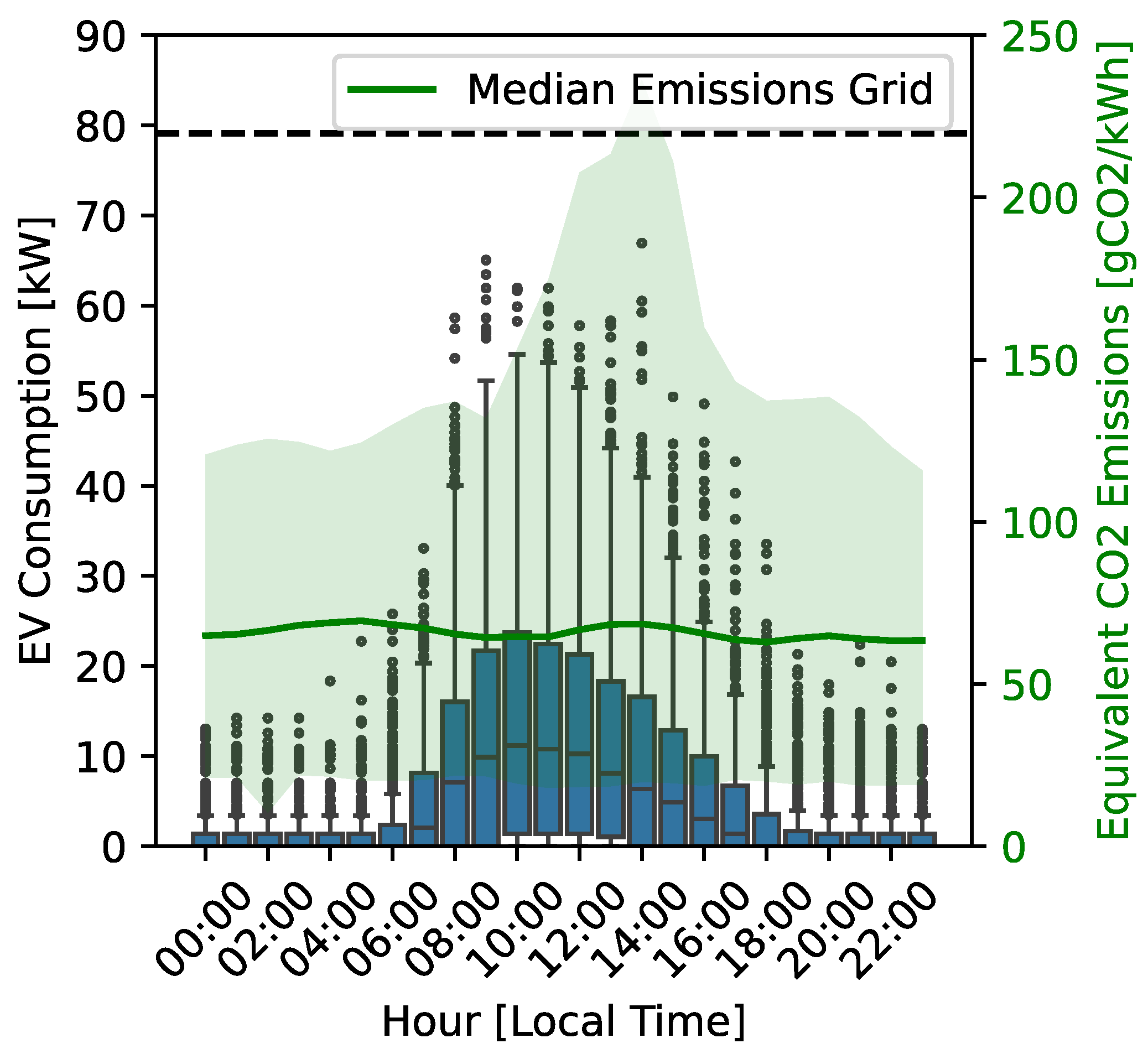
5.1. S1 & S2—Decentralised Optimisation Results
5.2. S3 & S4—Centralised Optimisation Results
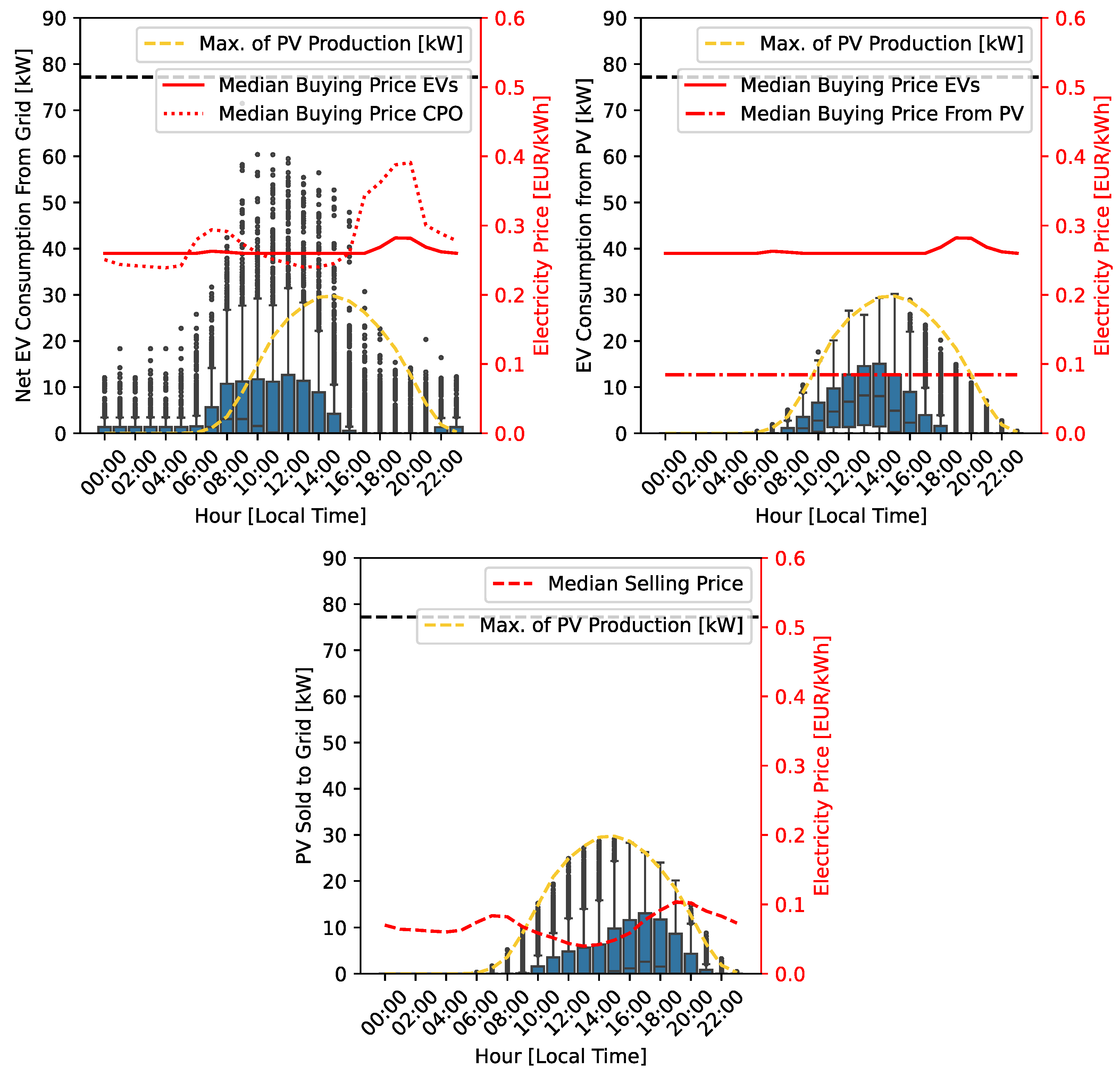
5.3. S5 & S6—PV-Powered Costs-Based Centralised Optimisation Results
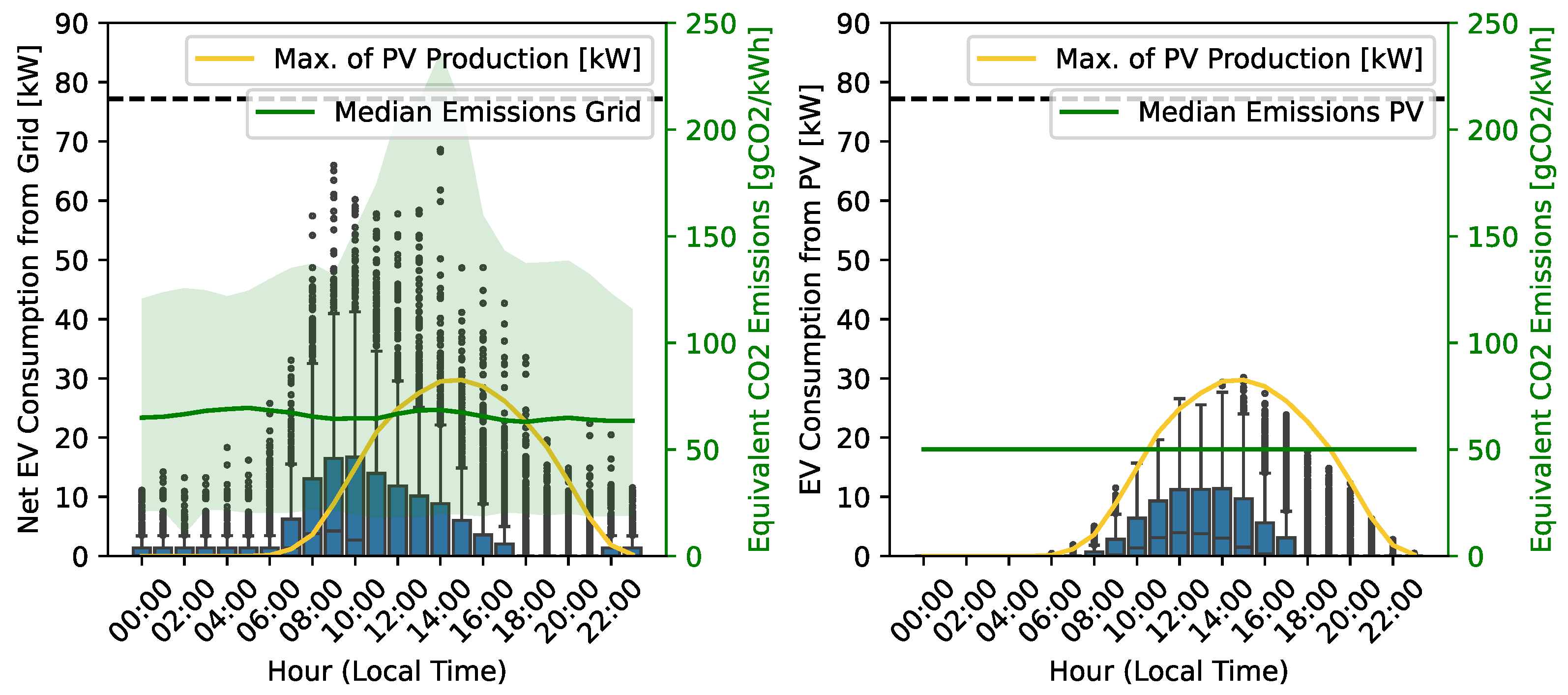
5.4. S7 & S8—PV-Powered Emissions-Based Centralised Optimisation Results
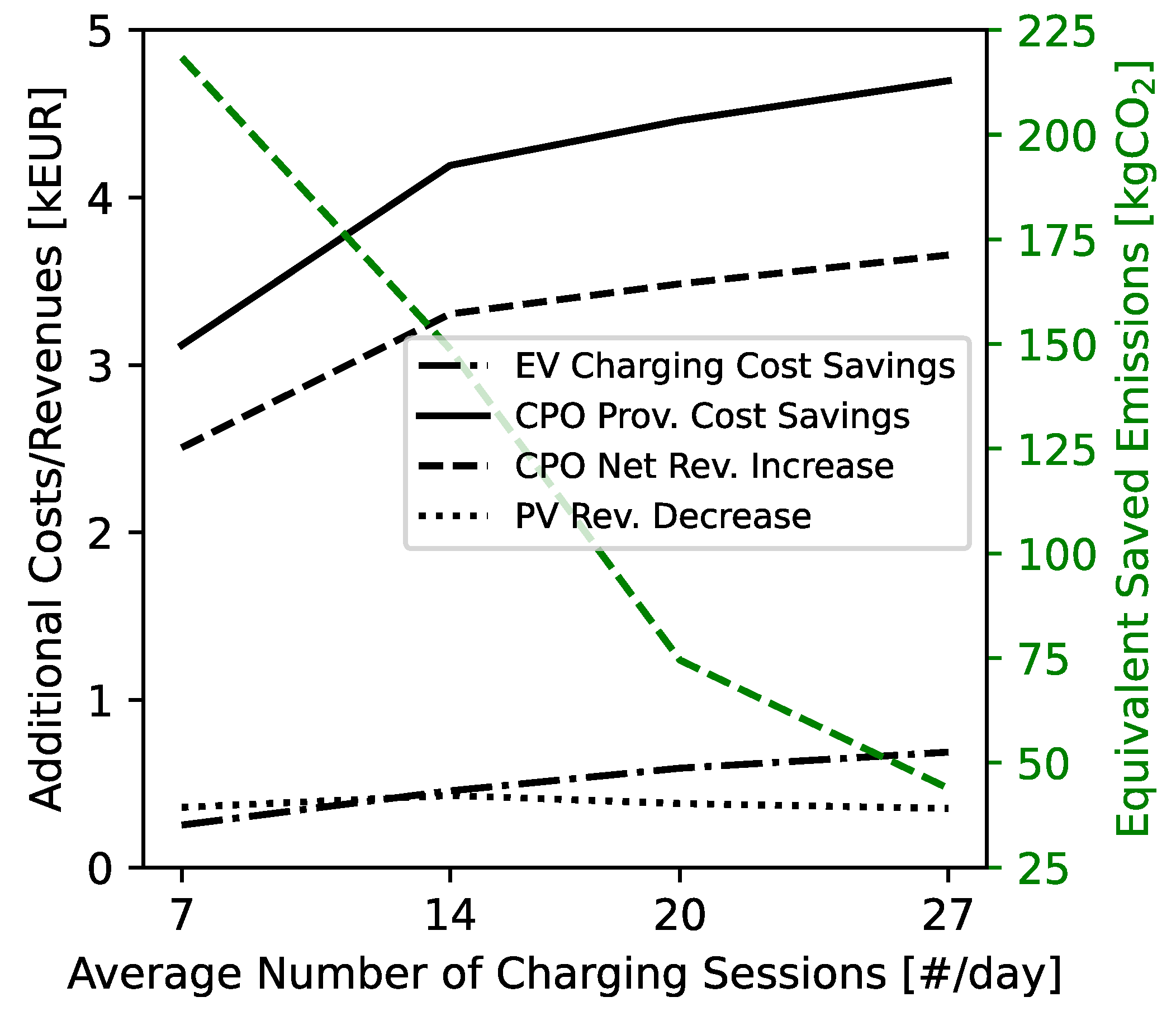
5.5. Benefit-Splitting Algorithm Impact
6. Conclusions
- Due to the minimum charging cost limit and the low price variability during EV connection hours, EV scheduling based on cost without a PV system was not profitable in the analysed parking lot (up to 1.1% cost reduction for the EV owners, and 2.7% for the CPO). It was more efficient to minimise based on the CO2 emissions (5.60% emissions reduction).
- The inclusion of an already-existing PV system led to the highest cost and emission savings (up to 11% for the EV owners and 67% for the CPO). Assuming the most CPO-friendly smart charging scenario, savings of around EUR 1500–2100/year (20–30%) could be realised with 30–80 kWp of installed PV capacity by implementing the proposed smart charging strategy. These values could reach EUR 2500–3500/year (30–35%) if the usage of the parking lot was increased from its current value to an average of two sessions/day per charging station.
- The centralised algorithm was able to quickly and efficiently reduce the peak charging power from the cluster; hence, the parking lot fuse capacity could be reduced from 68.3 to 40 kW with minimal unserved energy issues and a substantial cost reduction for the CPO.
- The SC benefits need to be reallocated to make sure the EV owners do not lose money from centralised SC. The algorithm we propose ensures no economic losses and splits the benefits based on the experienced delay.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Linearisation of the Continuity Constraint
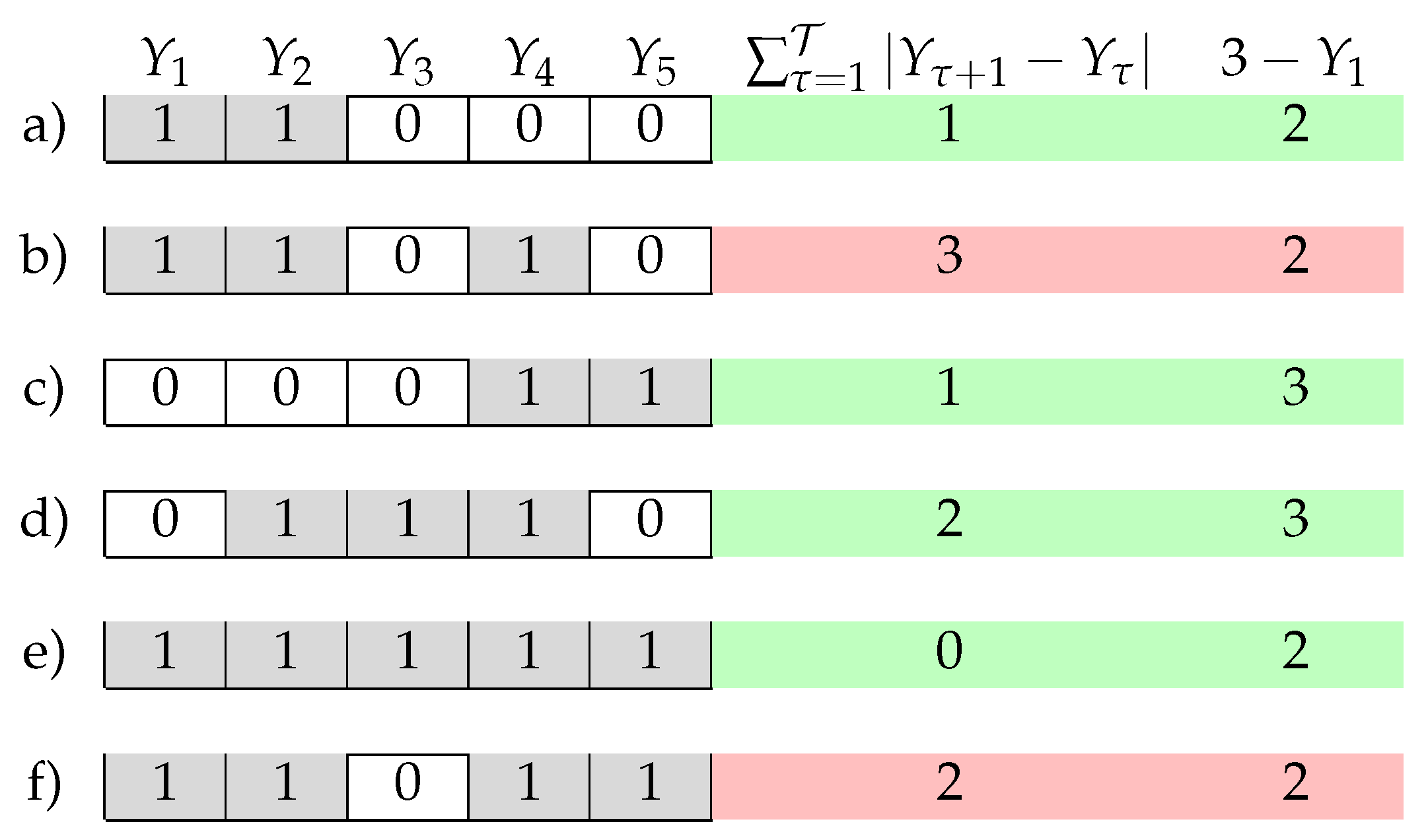
References
- Xia, X.; Li, P. A review of the life cycle assessment of electric vehicles: Considering the influence of batteries. Sci. Total Environ. 2022, 814, 152870. [Google Scholar] [CrossRef]
- IEA. Global EV Outlook 2024; International Energy Agency: Paris, France, 2024. [Google Scholar]
- Secchi, M.; Barchi, G.; Macii, D.; Petri, D. Smart electric vehicles charging with centralised vehicle-to-grid capability for net-load variance minimisation under increasing EV and PV penetration levels. Sustain. Energy Grids Netw. 2023, 35, 101120. [Google Scholar] [CrossRef]
- Engelhardt, J.; Malkova, A.; Cao, X.; Zunino, P.; Zepter, J.M.; Ziras, C.; Marinelli, M. EV4EU D2.3—Optimal Management of V2X in Parking Lots; Technical Report; Technical University of Denmark: Kongens Lyngby, Denmark, 2024. [Google Scholar]
- Qian, K.; Fachrizal, R.; Munkhammar, J.; Ebel, T.; Adam, R. Large-scale EV charging scheduling considering on-site PV generation by combining an aggregated model and sorting-based methods. Sustain. Cities Soc. 2024, 107, 105453. [Google Scholar] [CrossRef]
- Luo, J.; Yuan, Y.; Joybari, M.M.; Cao, X. Development of a prediction-based scheduling control strategy with V2B mode for PV-building-EV integrated systems. Renew. Energy 2024, 224, 120237. [Google Scholar] [CrossRef]
- Luo, J.; Cao, X.; Yuan, Y. Comprehensive techno-economic performance assessment of PV-building-EV integrated energy system concerning V2B impacts on both building energy consumers and EV owners. J. Build. Eng. 2024, 87, 109075. [Google Scholar] [CrossRef]
- Khalid, M.; Thakur, J.; Bhagavathy, S.M.; Topel, M. Impact of public and residential smart EV charging on distribution power grid equipped with storage. Sustain. Cities Soc. 2024, 104, 105272. [Google Scholar] [CrossRef]
- Palmiotto, F.; Zhou, Y.; Forte, G.; Dicorato, M.; Trovato, M.; Cipcigan, L.M. A coordinated optimal programming scheme for an electric vehicle fleet in the residential sector. Sustain. Energy Grids Netw. 2021, 28, 100550. [Google Scholar] [CrossRef]
- Park, K.; Moon, I. Multi-agent deep reinforcement learning approach for EV charging scheduling in a smart grid. Appl. Energy 2022, 328, 120111. [Google Scholar] [CrossRef]
- Tveit, M.H.; Sevdari, K.; Marinelli, M.; Calearo, L. Behind-the-Meter Residential Electric Vehicle Smart Charging Strategies: Danish Cases. In Proceedings of the 2022 International Conference on Renewable Energies and Smart Technologies, REST 2022, Tirana, Albania, 28–29 July 2022. [Google Scholar] [CrossRef]
- Board, A.; Sun, Y.; Huang, P.; Xu, T. Community-to-vehicle-to-community (C2V2C) for inter-community electricity delivery and sharing via electric vehicle: Performance evaluation and robustness analysis. Appl. Energy 2024, 363, 123054. [Google Scholar] [CrossRef]
- Karimi-Arpanahi, S.; Jooshaki, M.; Pourmousavi, S.A.; Lehtonen, M. Leveraging the flexibility of electric vehicle parking lots in distribution networks with high renewable penetration. Int. J. Electr. Power Energy Syst. 2022, 142, 108366. [Google Scholar] [CrossRef]
- Daryabari, M.K.; Keypour, R.; Golmohamadi, H. Robust self-scheduling of parking lot microgrids leveraging responsive electric vehicles. Appl. Energy 2021, 290, 116802. [Google Scholar] [CrossRef]
- Sørensen, L.; Morsund, B.B.; Andresen, I.; Sartori, I.; Lindberg, K.B. Energy profiles and electricity flexibility potential in apartment buildings with electric vehicles—A Norwegian case study. Energy Build. 2024, 305, 113878. [Google Scholar] [CrossRef]
- Srithapon, C.; Månsson, D. Predictive control and coordination for energy community flexibility with electric vehicles, heat pumps and thermal energy storage. Appl. Energy 2023, 347, 121500. [Google Scholar] [CrossRef]
- Amry, Y.; Elbouchikhi, E.; Gall, F.L.; Ghogho, M.; Hani, S.E. Optimal sizing and energy management strategy for EV workplace charging station considering PV and flywheel energy storage system. J. Energy Storage 2023, 62, 106937. [Google Scholar] [CrossRef]
- Jadoun, V.K.; Sharma, N.; Jha, P.; Jayalakshmi, N.S.; Malik, H.; Márquez, F.P.G. Optimal Scheduling of Dynamic Pricing Based V2G and G2V Operation in Microgrid Using Improved Elephant Herding Optimization. Sustainability 2021, 13, 7551. [Google Scholar] [CrossRef]
- Sadati, S.M.B.; Moshtagh, J.; Shafie-khah, M.; Rastgou, A.; Catalão, J.P. Operational scheduling of a smart distribution system considering electric vehicles parking lot: A bi-level approach. Int. J. Electr. Power Energy Syst. 2019, 105, 159–178. [Google Scholar] [CrossRef]
- Cao, X.; Ziras, C.; Engelhardt, J.; Marinelli, M. Distributed control of electric vehicle clusters for user-based power scheduling. In Proceedings of the ITEC Asia-Pacific 2023—2023 IEEE Transportation Electrification Conference and Expo, Asia-Pacific, Chiang Mai, Thailand, 28 November–1 December 2023. [Google Scholar] [CrossRef]
- Abdalla, M.A.A.; Min, W.; Bing, W.; Ishag, A.M.; Saleh, B. Double-layer home energy management strategy for increasing PV self-consumption and cost reduction through appliances scheduling, EV, and storage. Energy Rep. 2023, 10, 3494–3518. [Google Scholar] [CrossRef]
- Dik, A.; Kutlu, C.; Sun, H.; Calautit, J.K.; Boukhanouf, R.; Omer, S. Towards sustainable urban living: A holistic energy strategy for electric vehicle and heat pump adoption in residential communities. Sustain. Cities Soc. 2024, 107, 105412. [Google Scholar] [CrossRef]
- Montes, T.; Batet, F.P.; Igualada, L.; Eichman, J. Degradation-conscious charge management: Comparison of different techniques to include battery degradation in Electric Vehicle Charging Optimization. J. Energy Storage 2024, 88, 111560. [Google Scholar] [CrossRef]
- Bibak, B.; Bai, L. An optimization approach for managing electric vehicle and reused battery charging in a vehicle to grid system under an electricity rate with demand charge. Sustain. Energy Grids Netw. 2023, 36, 101145. [Google Scholar] [CrossRef]
- Li, J.; Wang, G.; Wang, X.; Du, Y. Smart charging strategy for electric vehicles based on marginal carbon emission factors and time-of-use price. Sustain. Cities Soc. 2023, 96, 104708. [Google Scholar] [CrossRef]
- Guo, G.; Gong, Y. Energy management of intelligent solar parking lot with EV charging and FCEV refueling based on deep reinforcement learning. Int. J. Electr. Power Energy Syst. 2022, 140, 108061. [Google Scholar] [CrossRef]
- Heinisch, V.; Göransson, L.; Erlandsson, R.; Hodel, H.; Johnsson, F.; Odenberger, M. Smart electric vehicle charging strategies for sectoral coupling in a city energy system. Appl. Energy 2021, 288, 116640. [Google Scholar] [CrossRef]
- Bartolini, A.; Comodi, G.; Salvi, D.; Østergaard, P.A. Renewables self-consumption potential in districts with high penetration of electric vehicles. Energy 2020, 213, 118653. [Google Scholar] [CrossRef]
- Zhang, L.; Alvarez, E.M.O.; Huang, P. Optimizing coordinated spatio-temporal control of electric vehicles for enhanced energy sharing and performance across building communities. Energy Build. 2024, 312, 114167. [Google Scholar] [CrossRef]
- Gong, J.; Wasylowski, D.; Figgener, J.; Bihn, S.; Rücker, F.; Ringbeck, F.; Sauer, D.U. Quantifying the impact of V2X operation on electric vehicle battery degradation: An experimental evaluation. eTransportation 2024, 20, 100316. [Google Scholar] [CrossRef]
- Shi, J.; Zeng, T.; Moura, S. Electric fleet charging management considering battery degradation and nonlinear charging profile. Energy 2023, 283, 129094. [Google Scholar] [CrossRef]
- Thingvad, A.; Ziras, C.; Marinelli, M. Economic value of electric vehicle reserve provision in the Nordic countries under driving requirements and charger losses. J. Energy Storage 2019, 21, 826–834. [Google Scholar] [CrossRef]
- IEC 60947-2; Low-Voltage Switchgear and Controlgear—Part 2: Circuit-Breakers. International Electrotechnical Committee (IEC): Geneva, Switzerland, 2019.
- Prina, M.G.; Lionetti, M.; Manzolini, G.; Sparber, W.; Moser, D. Transition pathways optimization methodology through EnergyPLAN software for long-term energy planning. Appl. Energy 2019, 235, 356–368. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]

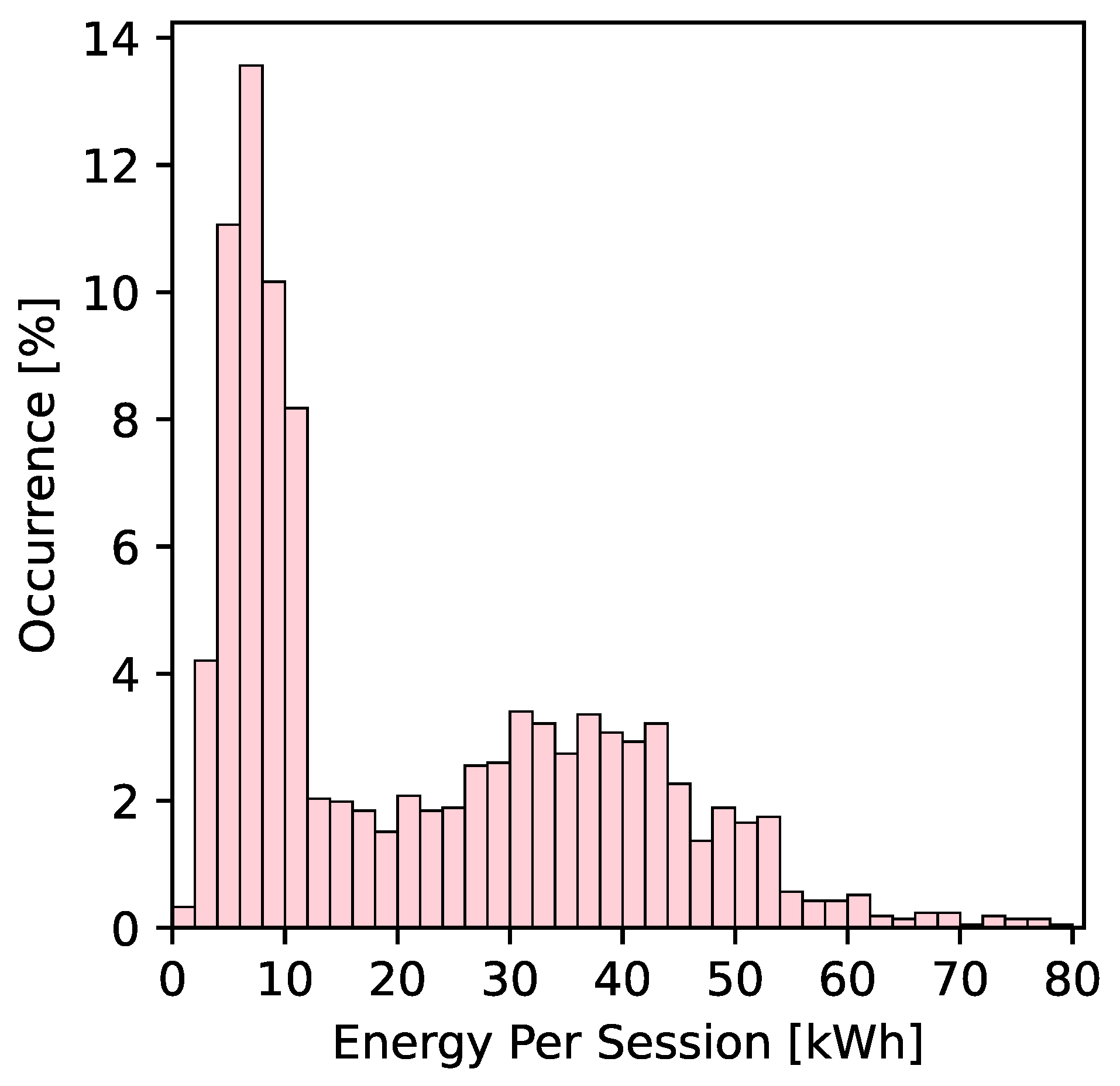


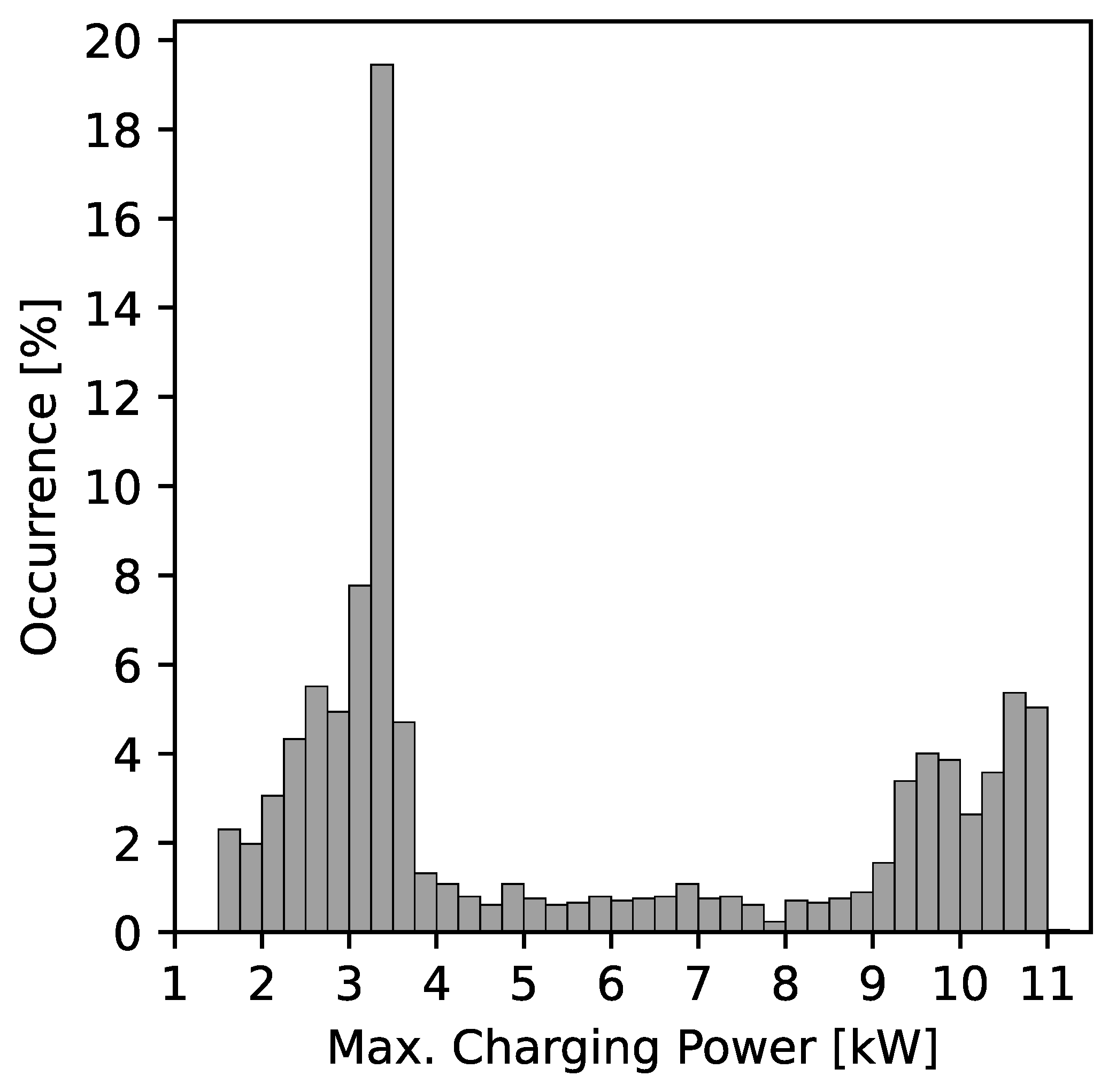

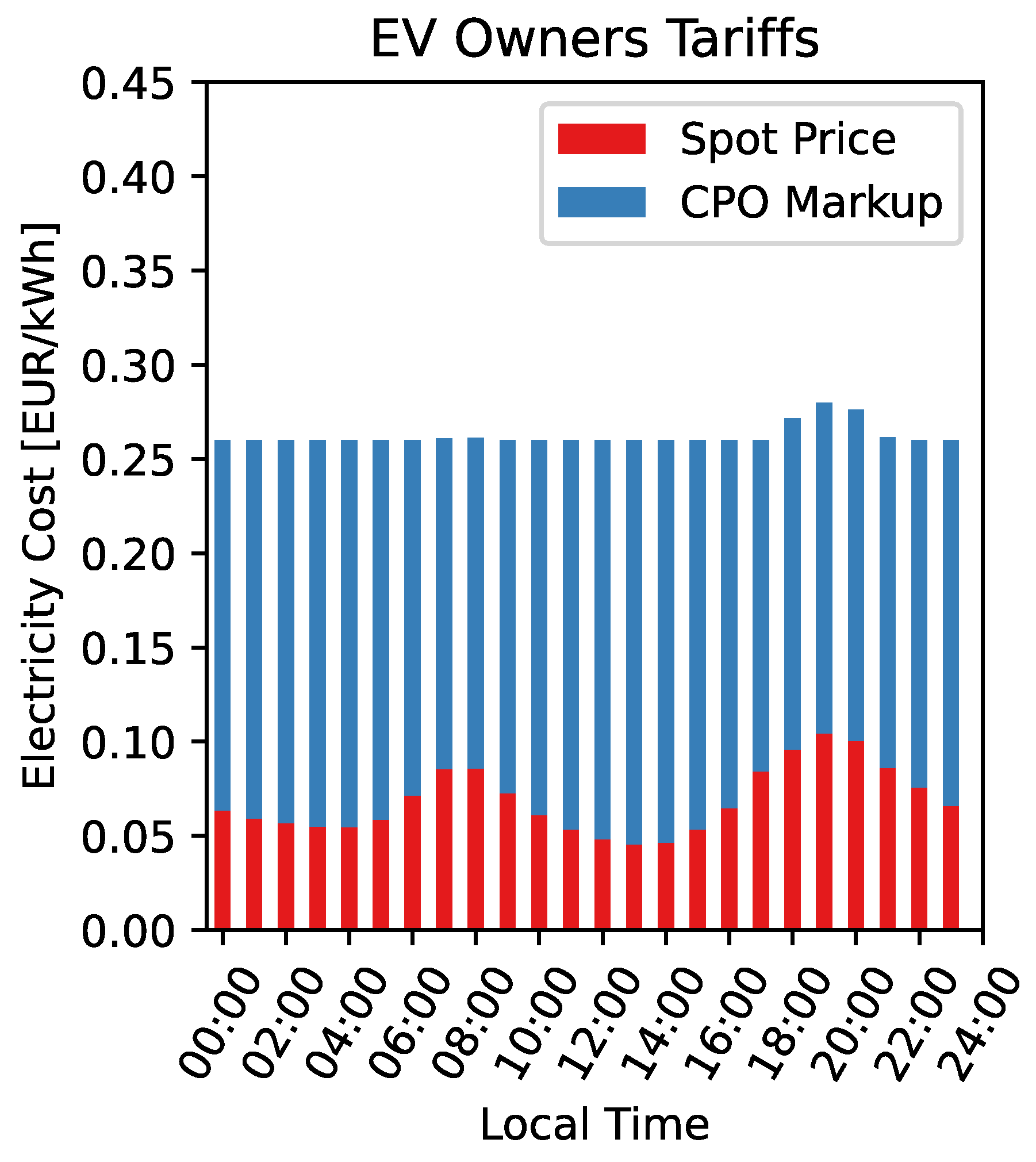
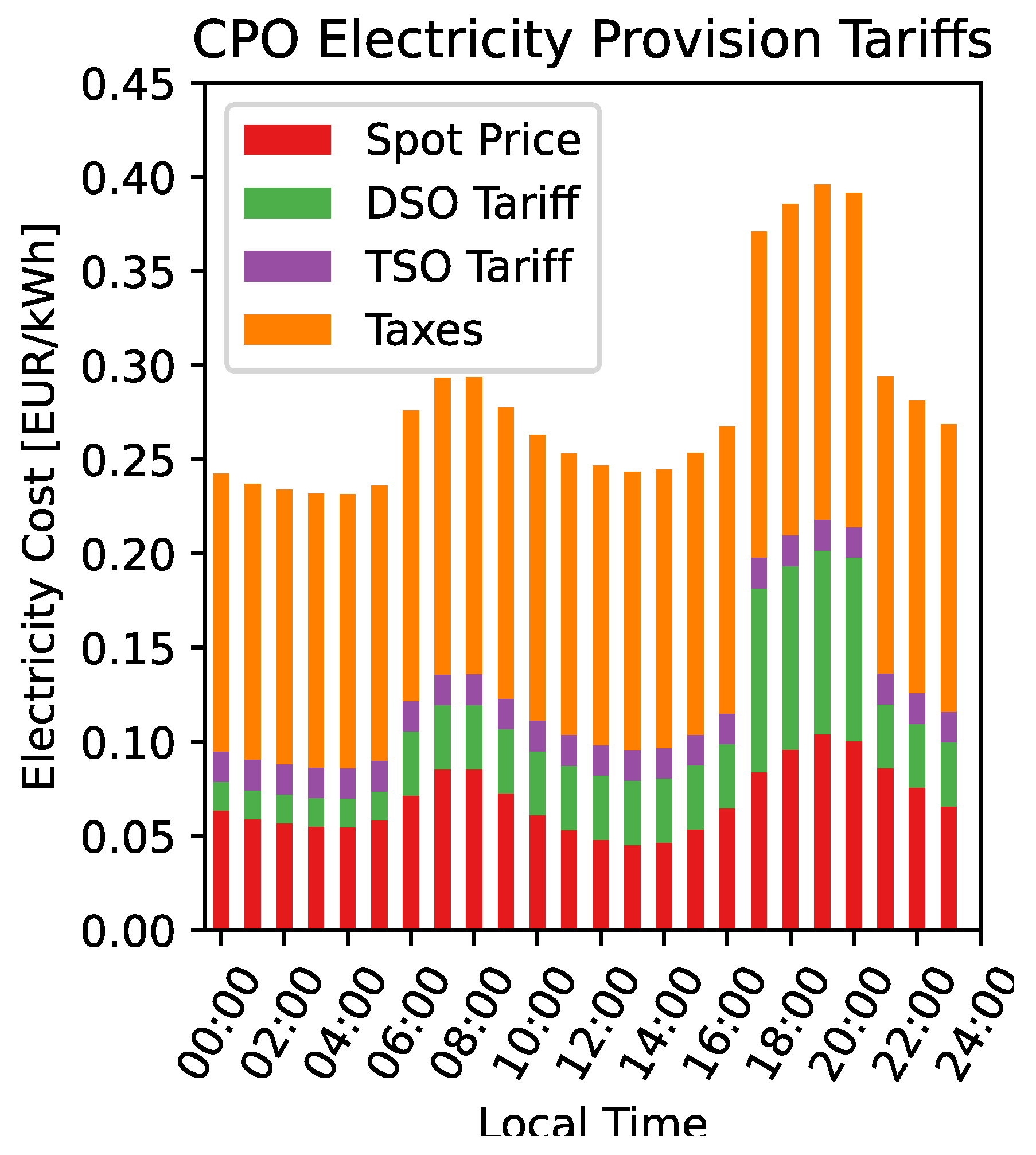




| Primary Objective | Methodology | Algorithm Type | Parking Lot | Metered EV Charging Dataset | Charging Continuity Constraint | SC Benefit Split | Refs. |
|---|---|---|---|---|---|---|---|
| Maximising PV energy usage | HOR | Centralised | YES | YES | NO | NO | [5] |
| MPC | Centralised | YES | NO | NO | NO | [6] | |
| RBC | Centralised | YES | NO | NO | NO | [7] | |
| PSO | Decentralised | NO | YES | NO | NO | [21] | |
| SP | Decentralised | NO | YES | NO | NO | [22] | |
| Minimising EV charging costs | LP | Centralised | YES | NO | NO | NO | [8] |
| QP | Centralised | NO | YES | NO | NO | [9] | |
| RL | Decentralised | YES | NO | NO | NO | [10] | |
| MILP | Decentralised | YES | NO | NO | NO | [23] | |
| MILP | Centralised | YES | YES | NO | NO | [24] | |
| GA | Decentralised | NO | YES | NO | NO | [25] | |
| RT | Decentralised | NO | YES | NO | NO | [11] | |
| MIQCLP | Centralised | YES | YES | YES | YES | This paper. | |
| Minimising system costs | FLC | Centralised | YES | YES | NO | NO | [26] |
| GA | Centralised | YES | NO | NO | NO | [12] | |
| LP | Centralised | NO | NO | NO | NO | [27] | |
| LP | Centralised | NO | NO | NO | NO | [28] | |
| MILP | Centralised | YES | NO | NO | NO | [13] | |
| MILP | Centralised | YES | NO | NO | NO | [14] | |
| MILP | Decentralised | NO | YES | NO | NO | [15] | |
| NLP | Centralised | NO | NO | NO | NO | [16] | |
| NLP | Centralised | YES | NO | NO | NO | [17] | |
| PSO | Centralised | NO | NO | NO | NO | [18] | |
| RBC | Centralised | YES | NO | NO | NO | [29] | |
| Maximising EV charging revenues | NLP | Centralised | YES | NO | NO | NO | [19] |
| RBC | Decentralised | NO | YES | NO | NO | [30] | |
| MILP | Centralised | YES | NO | NO | NO | [31] |
| Scenario | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 |
|---|---|---|---|---|---|---|---|---|
| Centralised | X | X | X | X | X | X | ||
| Decentralised | X | X | ||||||
| Min. Cost | X | X | X | X | ||||
| Min. CO2 | X | X | X | X | ||||
| PV System | X | X | X | X | ||||
| PV Discount | X | X |
| EV Charging Costs | ||||||||
|---|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | |
| UC | 12.90 k€ | 12.90 k€ | 12.90 k€ | 12.90 k€ | 10.17 k€ | 12.86 k€ | 10.17 k€ | 12.86 k€ |
| SC | 12.76 k€ | 12.84 k€ | 12.76 k€ | 12.83 k€ | 9.08 k€ | 12.73 k€ | 9.90 k€ | 12.79 k€ |
| Red. | 1.10% | 0.50% | 1.10% | 0.50% | 10.70% | 1.00% | 2.70% | 0.50% |
| Equivalent CO2 Emissions | ||||||||
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | |
| UC | 3.62 t CO2 | 3.62 t CO2 | 3.62 t CO2 | 3.62 t CO2 | 3.16 t CO2 | 3.16 t CO2 | 3.16 t CO2 | 3.16 t CO2 |
| SC | 3.68 t CO2 | 3.41 t CO2 | 3.60 t CO2 | 3.41 t CO2 | 3.05 CO2 | 3.05 t CO2 | 2.92 t CO2 | 2.92 t CO2 |
| Red. | −1.80% | 5.80% | 0.40% | 5.60% | 3.50% | 3.50% | 7.60% | 7.60% |
| CPO Electricity Provision Costs | ||||||||
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | |
| UC | 13.24 k€ | 13.24 k€ | 13.24 k€ | 13.24 k€ | 7.06 k€ | 4.37 k€ | 7.06 k€ | 4.37 k€ |
| SC | 12.71 k€ | 13.14 k€ | 12.89 k€ | 13.13 k€ | 5.09 k€ | 1.44 k€ | 6.55 k€ | 3.65 k€ |
| Red. | 4.10% | 0.80% | 2.70% | 0.90% | 27.90% | 67.10% | 7.20% | 16.50% |
| Nominal Fuse Limit [kW] | 30 | 40 | 50 | 60 | 70 |
|---|---|---|---|---|---|
| Fuse Limit [A] | 23 | 31 | 39 | 47 | 55 |
| Fuse Overload | 1.4% | 0.2% | 0.0% | 0.0% | 0.0% |
| Energy Demand [MWh] | 47.1 | 47.1 | 47.1 | 47.1 | 47.1 |
| Unserved Energy UC | 3.54% | 0.54% | 0.02% | 0.00% | 0.00% |
| Unserved Energy SC | 1.77% | 0.155% | 0.00% | 0.00% | 0.00% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Secchi, M.; Zepter, J.M.; Marinelli, M. Centralised Smart EV Charging in PV-Powered Parking Lots: A Techno-Economic Analysis. Smart Cities 2025, 8, 112. https://doi.org/10.3390/smartcities8040112
Secchi M, Zepter JM, Marinelli M. Centralised Smart EV Charging in PV-Powered Parking Lots: A Techno-Economic Analysis. Smart Cities. 2025; 8(4):112. https://doi.org/10.3390/smartcities8040112
Chicago/Turabian StyleSecchi, Mattia, Jan Martin Zepter, and Mattia Marinelli. 2025. "Centralised Smart EV Charging in PV-Powered Parking Lots: A Techno-Economic Analysis" Smart Cities 8, no. 4: 112. https://doi.org/10.3390/smartcities8040112
APA StyleSecchi, M., Zepter, J. M., & Marinelli, M. (2025). Centralised Smart EV Charging in PV-Powered Parking Lots: A Techno-Economic Analysis. Smart Cities, 8(4), 112. https://doi.org/10.3390/smartcities8040112





