Highlights
What are the main findings?
- Advanced optimization algorithms ensure high service quality with reduced waiting times and increased reliability, efficiently managing and allocating resources to meet user demands.
- The solutions are robust, adapting to various scenarios and constraints such as different pickup and drop-off locations, time windows, and customer requirements.
- Customized optimization techniques enhance resource use, leading to cost savings and better overall fleet utilization, essential for sustainable urban mobility in smart cities.
What is the implication of the main finding?
- The findings highlight the benefits of implementing customized optimization algorithms in public transportation systems, encouraging investment in technology and infrastructure for smart cities.
- Organizations can use these insights to optimize scheduling, routing, and resource allocation processes, improving performance and service delivery, thus contributing to the overall efficiency of smart city transportation networks.
Abstract
As customers’ expectations continue to rise, advanced on-demand transport services face the challenge of meeting new requirements. This study addresses a specific transportation issue belonging to dial-a-ride problems, including constraints aimed at fulfilling customer needs. In order to provide more efficient on-demand transportation solutions, we propose a new hybrid evolutionary computation method. This method combines customized heuristics including two exchanged mutation operators, a crossover, and a tabu search. These optimization techniques have been empirically proven to support advanced designs and reduce operational costs, while significantly enhancing service quality. A comparative analysis with an evolutionary local search method from the literature has demonstrated the effectiveness of our approach across small-to-large-scale problems. The main results show that service providers can optimize their scheduling operations, reduce travel costs, and ensure a high level of service quality from the customer’s perspective.
1. Introduction
The integration of on-demand transportation within smart cities represents a significant advancement, enhancing the flexibility, efficiency, and responsiveness of urban transport networks. By using advanced algorithms and optimized routing strategies, on-demand services contribute to optimizing resource utilization, reducing operational costs, and improving overall user satisfaction.
In this study, we focus on the dial-a-ride problem (DARP), which is a specific variant of on-demand transportation that focuses on passenger-oriented collective on-demand transportation []. It is classified as an NP-hard problem, as demonstrated by []. The optimization of service quality and cost-efficiency is crucial in this problem. High-quality service, characterized by reduced waiting times, reliable schedules, and customer-centric features, directly impacts user satisfaction and system efficiency. In smart cities, where technological advancements are pivotal in creating responsive and adaptive transportation networks, enhancing service quality can lead to more efficient resource utilization and substantial cost savings. In smart cities, optimizing cost-efficiency leads to reduced operational expenses, such as vehicle total riding time and travel distance, which directly impacts user satisfaction and system reliability. By minimizing costs, we not only ensure financial sustainability but also improve resource utilization and service responsiveness. Thus, prioritizing cost-efficiency alongside service quality supports the development of adaptive, efficient, and user-centric transportation networks, essential for smart city environments. Thus, enhancing service quality in on-demand transportation not only enhances the user experience but also supports the financial sustainability and operational efficiency of smart city transport networks. Therefore, the practical applicability of resolution methods for on-demand transportation problems has gained substantial attention.
In modern transportation systems, customer expectations have evolved to include several specific and nuanced aspects beyond traditional service quality. These new expectations include customers now expecting services tailored to their individual needs and preferences, such as specific pickup and drop-off points, preferred routes, and maximal riding time. To address these evolving expectations, authors [] emphasize the importance of exploring problem variants that incorporate real-life service level criteria. Notable works in this area include studies of [,,,,,,,,]. One specific problem variant that has gained attention is the customer-oriented dial-a-ride problem (CO-DARP), introduced by the authors in []. This problem incorporates constraints from a customer-oriented quality of service perspective and takes into account real-life customer expectations. In this model, customer preferences like preferred pickup and drop-off locations, as well as customer-dependent maximal riding time, are used for providing time windows constraints, and optimizing routes and schedules.
Meeting the individual preferences and needs of passengers contributes to an enhanced service quality. This entails providing choices for route customization, vehicle preferences, and accommodating passengers’ special needs or preferences, such as their desired maximum travel time, preferred time windows, and arrival times. For example, time windows for delivery locations are adjusted based on the preferred maximum travel time and selected time windows for pickups. Regarding the consideration of real constraints on passenger and vehicle waiting times, we highlight the importance of balancing service efficiency with practical constraints. Time window constraints may produce limited passenger waiting times to ensure timely pickups and limited vehicle waiting times to minimize operational costs. Moreover, by incorporating these constraints into our approach, we aim to provide solutions that not only optimize service delivery times but also enhance overall service quality by addressing the diverse needs and preferences of passengers while considering real-world constraints on waiting times for both passengers and vehicles.
Furthermore, the efficiency of tabu search heuristics in solving a large set of dial-a-ride problems has been extensively demonstrated. Studies such as [,,,] have shown that the tabu search yields impressive results when applied to artificial cases of on-demand transportation problems. The ability of the tabu search to effectively explore the solution space and navigate complex constraints makes it a popular choice for tackling DARPs. Moreover, a substantial field of research has focused on the development of hybrid evolutionary methods, combining evolutionary computation with local search (LS) techniques. Contributions in this field include works by [,,,,,]. These hybrid evolutionary methods emphasize the strengths of both evolutionary algorithms and local search heuristics to improve the efficiency and effectiveness of optimization in solving on-demand transportation problems. Authors in [] introduced a hybrid algorithm named the evolutionary local search (ELS) that combines the power of evolutionary computation and local search-based techniques.
In the existing literature, several approaches have been proposed to address the dial-a-ride problem in current transportation systems. These approaches have successfully tackled various aspects of the problem, such as optimizing routing and scheduling, integrating customer preferences, and managing resource allocation. These systems are increasingly incorporating customer exceptions and unique requirements into the design of new transportation problems. Therefore, new methods should focus on not only minimizing transportation costs but also enhancing service quality. These methods should be designed to support the new specifications of transportation systems, which introduce customer exceptions and prioritize customer satisfaction. By addressing both cost and service quality, these methods will provide transportation systems with the ability to meet evolving requirements and deliver an optimal customer experience.
We aim to build upon these advancements by offering an innovative approach that combines advanced optimization algorithms with customized techniques, providing even more efficient and flexible management of the CO-DARP in smart city transportation environments. Therefore, a novel method called the evolutionary tabu search (ETS) is proposed in this paper. This hybrid method combines the strengths of evolutionary algorithms and tabu search techniques, enabling the development of effective routing plans that optimize both the operational efficiency and the quality of service provided. New optimization techniques are proposed supporting advanced designs of service quality supported by the mathematical model. The latter involves the consideration of various factors such as wait times, travel times, and personalized preferences in the routing plans, ensuring a high-quality service that caters to the specific needs of customers.
- A customized insertion heuristic is specifically designed to define an initial feasible vehicle’s plan with good quality. The use of this heuristic is claimed to be suitable for real-life on-demand transportation problems.
- A new tabu search method is introduced, which incorporates a novel customized neighborhood strategy. This neighborhood strategy is specifically designed to enhance both the operational costs and the service quality.
- Specific mutation operators are designed to address the characteristics and requirements of the problem at hand. These operators are dynamically exchanged to contribute to the discovery of high-quality solutions with improved service quality criteria.
- A specific crossover operator is proposed, which is carefully designed to inherit and preserve the advantageous service quality features discovered during the search. This contributes to the generation of new solutions that not only maintain the desired service quality features but also introduce variations that can potentially lead to further improvements.
The results of the comparative study indicate that the ETS method demonstrates a competitive performance when compared with the ELS method. Particularly, when it is applied to small-, medium- and large-scale realistic transport on-demand problems, the ETS method shows notable improvements in the service quality provided to the customers.
The paper is organized as follows: Section 2 presents a literature review of the contributions linked with the present study. Section 3 describes a customer-oriented DARP. Section 4 presents the proposed evolutionary tabu search approach for computing solutions. Section 5 reports the numerical results obtained with the new proposed metaheuristics on benchmark instances, together with a comparative study with another hybrid evolutionary method from the literature. A statistical analysis is conducted in Section 6. A discussion is provided in Section 7. Concluding remarks are set in Section 8.
2. Literature Review
Nowadays, the expectations of customers are increasingly complex, and anterior on-demand transport models should be enhanced []. Therefore, a few years ago, a new research field in DARP resolution emerged towards more realistic models with more rigorous constraints related to customer satisfaction. Authors in [] reviewed various categories of real-life DARP features related to heterogeneity [,], routing properties [,], and quality specifications. In this field of quality specifications, the authors in [] proposed a deeper survey on models being used by advanced research studies involving service quality designs from the customer’s point of view. This research is in relation to maximal riding time (e.g., [,,,]) and time windows (e.g., [,,]).
Authors in [] highlighted the impact of variations in the level of quality of service provided to customers in the operational costs of a DARP. They studied the evolution of the operational costs through the investigation of the permutations of two sets of parameters describing the service level. The maximum deviation from the user preference time and the relative maximum exceedance of the user’s direct journey time is measured according to the variation of certain parameters, such as the size of the transmission network and the diversity of customers. Moreover, the authors validated the potential trade-off between the costs and the quality of service according to variations in the service level parameters being frequently used, such as the size of the time windows and the maximal riding time. These two parameters are also emphasized in the works of [,], which reviewed and defined several measures related to the quality of service. These studies highlighted the maximal riding time and the time windows as the main criteria linked with the level of service that influence the total operational costs, and pointed out the advantage of combining them into the same model.
The quality of service can be expressed differently. In the works of [,,], the maximum ride time is specified for each customer and used to calculate time windows. The need for the time windows redesign was emphasized by [], using the maximal ride time as a parameter.
Other parameters can also be used in designing the service quality with a high level of customer-related criteria and preferences. In this regard, a problem named the customer-oriented DARP was proposed by [], offering a design that provides more flexibility to service providers in producing routing plans closer to customer preferences.
Intelligent transportation problems have been addressed with techniques based on evolutionary computations. Beyond the efficiency of these tools, hybridization approaches combining evolutionary algorithms and local search methods were privileged. The union of these methods provides benefits in diverse settings []. Therefore, their use should be preferred to other methods when seeking better solutions for advanced on-demand transport problems, especially for more realistic DARPs designed from a customer-oriented viewpoint.
Recent advances in the tabu search showed the effectiveness of tabu search techniques in addressing dial-a-ride problems across various contexts and scales (e.g., [,,,,,]). These methods enhance the flexibility, efficiency, and adaptability of transportation systems, addressing the evolving needs of urban populations. Evolutionary computation for transportation problems is highlighted in []. Many works are provided for DARPs using evolutionary algorithms (e.g., [,,,,,,,,,]). These methods effectively handle the high-dimensional search spaces and diverse constraints of DARPs, leading to improved route efficiency and reduced operational costs. By simulating natural selection processes, they offer robust solutions adaptable to demands of on-demand transportation systems.
Authors in [] emphasized the importance of combining genetic and tabu search algorithms. Thus, a large field of research is devoted to hybrid evolutionary methods for customized DARPs, see the existing related works of [,,,,,,,,]. Authors in [] proposed a hybrid evolutionary local search-based algorithm. This method was firstly proposed for solving DARPs of [] with a customer-oriented maximal ride time. To analyze the service providers’ cooperation better, more real-life characteristics are added to the artificial instances. This ELS method is also proposed for solving real-life instances of on-demand transportation []. However, to address real-life cases of on-demand transportation problems better, more advances are required when proposing optimization methods involving optimization techniques that support high-level designs.
Efficient and adaptive transportation solutions are required, driven by increasing urbanization and evolving user expectations. Hybrid evolutionary algorithms offer a promising approach to solving DARPs due to their ability to combine the strengths of multiple optimization techniques. They enhance the search process by the good exploration and exploitation capabilities of local search methods such as the tabu search. This is why we propose to combine the evolutionary schema with a tabu search to tackle customer-oriented DARPs in this present work.
3. The Customer-Oriented DARP
The customer-oriented DARP consists in satisfying on-demand transportation requests including the customer requirements in the decision taken. A passenger request is a transportation demand from a pickup location to a delivery one, which represents, respectively, the original location of the passenger and his/her destination. A set of passengers may be concerned with the same request which is also called a customer in this problem. This set is the same for the pickup and the delivery location. A homogeneous fleet of vehicles starts from the depot and arrives at the location. Note that neither demands nor waiting times are considered at this depot. In this problem, some constraints are aligned with those of the original DARP of [], as follows.
- A request is served exactly once by one vehicle.
- The precedence between pickup and delivery stations is ensured.
- The number of pickups is equal to the number of deliveries in a vehicle tour.
- It is the same vehicle that ensures the pickup and delivery of a request.
- The depot is the departure and arrival station of all the tours.
- The capacity of a vehicle is respected when charging and discharging passengers.
- The maximal total tour duration is a time limit that has to be respected by all the vehicles.
Customer-oriented constraints are designed in the CO-DARP. These constraints are related to maximal riding time and time windows, which are commonly argued as the main attributes for the quality of service in on-demand transportation problems.
3.1. The Problem Formulation
The customer-oriented DARP is defined on a complete weighted digraph, , with the set N of nodes and the set E of connected arcs . The set of nodes, N, includes all . This set includes the depot in two copies denoted by () at the departure, and () at the arrival, the set of pickup nodes {1...n}, and the set of delivery nodes {n + 1...2n}. The notations of the problem are indicated in Table 1. To each request corresponds a pickup node, i, which is its origin, and a delivery node (), which is its destination. Thus, the set of requests can be limited to that of the pickup nodes.

Table 1.
Notations of the problem.
A cost on an arc () is denoted by , where is the transit time on an arc () and is the time spent between the beginning of service and the departure of the vehicle for loading the passengers.
The total travel cost is the sum of all the costs of the visited arcs and the produced penalized waiting times at the visited nodes. A penalty coefficient, , is applied whenever a waiting time, , occurs. Let us consider as the objective function (1) to minimize. It consists of the total travel cost (TTC) related to all the vehicle tours considering waiting time penalties.
The maximal capacity of a vehicle must be checked in the pickups and the deliveries. The number of passengers denoted by is positively incremented in the case of a pickup and negatively otherwise. Thus, the inequality (2) explains that the number of passengers aboard a vehicle must not exceed its maximal capacity, Q.
In this study, particular attention is given to the design of time window constraints. With this concern, the transportation plans are adjusted to the customers’ needs while ensuring adaptability to the existing realistic on-demand transport situations. Time windows at the origin nodes are defined by the inequality (3), and time windows at the destination are obtained by (4) which allow also defining the lower bound and the upper bound for the beginning of service, . In this customer-oriented DARP, the service duration, , is supposed equal to the total number of passengers, . Thus, we have () for all pickup and delivery nodes. However, it is usually considered positive when computing the quantities (3), (4). These time window equations contribute to reducing unnecessary waiting times as well as enhancing the total riding time. More details are provided in [].
The expression (5) limits the maximal riding time, , as a bound linked with each customer . Thus, the riding time, , which is equal to the time spent aboard a vehicle from an origin, i, to a destination () must respect this customer-related bound.
Equation (6) expresses the riding time at node i, being equal to the time between the departure time, , at the origin and the beginning of service, , at the destination. Equation (7) computes the departure time at node i. Note that the departure time at the depot is equal to the beginning of service. Thus () and () since no person enters aboard the vehicle and no service time is assumed.
The quantity in Equation (8) defines potential waiting times. Negative values of waiting times are not allowed since, in DARP, a vehicle can wait but a customer should not; i.e., . The depot is not concerned by any waiting time since we have () and (). The arrival time at node i is the travel time from the depot to it.
For each vehicle tour, we derive a beginning of service time, denoted as , while adhering to a specified time window, i.e., , where i and j represent successive nodes visited within a vehicle tour, v. It is worth noting that the beginning of service at a pickup node is calculated as (). The arrival time at node is calculated as (), where j is a successor node to node . The total tour duration, , for a vehicle is then defined as the time spent from the depot to it (). This is constrained by a maximal common total duration, , as defined in the problem.
3.2. A Time Windows Application on a Realistic Case
To illustrate the concept of time windows, we draw upon a real-life example from problem instance found in the data provided by Chassaing et al. [], as detailed in Section 5. Initially, this problem was tackled using an evolutionary method known as ELS [], as explained in Section 2.
From the solutions obtained, we selected a vehicle tour characterized by a notably high waiting time. Subsequently, we present two scenarios: one before the introduction of customized time window specifications and one after.
Within this tour, we address two specific requests, denoted as () and (), each with respective loads of () and (). These requests are subject to two maximum riding times, namely () and ().
All vehicles are equipped with a maximum capacity constraint of () and are bound by a maximal total tour duration of ().
Figure 1 illustrates an on-demand transport problem involving two requests, denoted as () and (), along with the depot. In the figure, we display the customers’ input parameters, including their loads, maximal riding times, and time windows.
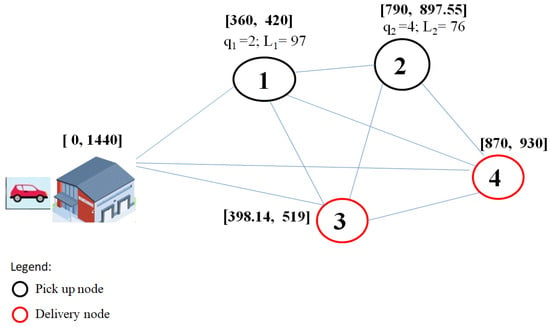
Figure 1.
An on-demand transport network with two requests having time windows, maximal ride times, and loads.
In Table 2, we present the parameters associated with the vehicle’s tour example before the computation of new customized time windows. The first request () assigned to the vehicle involves a pickup node () and a delivery node (). Similarly, the second request comprises a pickup node () and a delivery node (). For each visited node (), the table displays load (), transit time (), arrival time (), beginning of service (), and departure time ().

Table 2.
The vehicle tour specifications.
At the departure node (), we have (), and, at the final arrival node (), we have (), since no waiting time or load considerations are applicable at the depot.
Arrival times are computed at each visited node. For example, the arrival time is calculated as (), resulting in (). Departure times are determined using (7), with computed as (), which equals ().
Riding times for the two requests are calculated as () and () using (6). The waiting time only applies to node (), with (), determined as () using (8). This waiting time, , affects the arrival time at the subsequent node (), as shown in Figure 2.
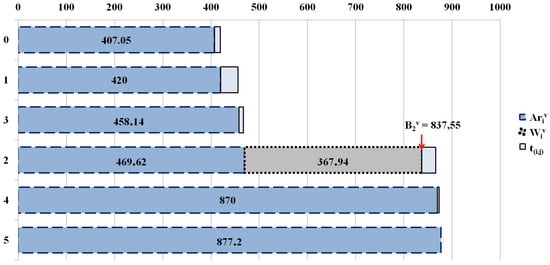
Figure 2.
The vehicle tour schedule before the time windows calculation.
Figure 2 provides a visual representation of the vehicle, v, following the tour of nodes in , as outlined in Table 2.
The total tour duration, , is computed as () at the conclusion of the tour, following the formula . This total duration ensures compliance with the maximum limit ().
In the case of customized time window specifications, new bounds are determined to restrict waiting times. Initially, time windows for delivery nodes are calculated using (4). These resulting bounds are then utilized to establish time windows for origin nodes through (3). Consequently, Table 3 displays new time windows derived from inequalities (3) and (4), resulting in the selection of updated early service times.

Table 3.
The customized design of the time windows related to request 2.
We specifically focus on the time windows associated with request (), as it was the node where waiting times occurred. The new beginning of services, denoted as and , is determined at the pickup and delivery nodes of request 2. Let us note that the initial time windows for these nodes were initially set as [] and [], as indicated in Figure 1.
In Table 3, the new beginning of service [] is selected as the earliest service time at the delivery node (). Consequently, the beginning of service is calculated as (), given that (). Thus, is the new beginning of service at the pickup node (). This earlier beginning of service contributes to the reduction in the waiting time. The new value of is then (). The arrival time, , is also impacted. As (), where 28.45 is the transit time and 207.93 is the reduced waiting time (), then (). This new arrival time will produce a low waiting time (). However, the new total waiting time is equal to (), which is much lower than the initial one equal to ().
As reported in Table 3, with new time windows reduced, as compared with those proposed in Table 2, the quality of the service is enhanced in terms of waiting time. The vehicle tour after the new time windows calculation is illustrated in Figure 3. Only the beginning of service producing a waiting time is indicated in the figure.
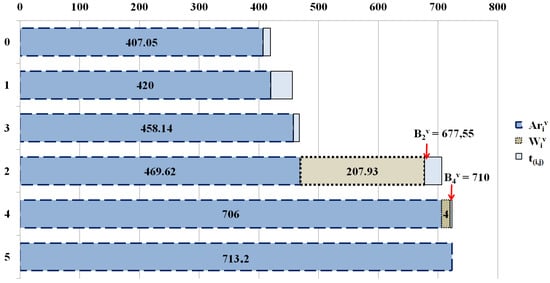
Figure 3.
The vehicle tour schedule after the time windows calculation.
The limitation of the waiting time leads to reducing the total duration, from () in Figure 2 to () in Figure 3. The enhanced is obtained as (), where () and (), see Table 2.
Through the above example, we have analytically demonstrated how the application of customer-oriented constraints in problem resolution can improve service quality, specifically reducing waiting times. Furthermore, this enhancement in service quality contributes to minimizing the total duration, which is advantageous for the service provider. The following sections explain the investigation of time window constraints within the optimization techniques of the ETS.
4. The Evolutionary Tabu Search
This section defines the evolutionary tabu search algorithm with special genetic operators and a tabu search-based method.
4.1. Overview of the Evolutionary Tabu Search Algorithm
The evolutionary tabu search starts by generating an initial solution by the use of an insertion heuristic (see Section 4.2). In order to create individuals composing the first population, a mutation phase is performed where the initial solution is perturbed, producing a set of individuals. Next, each mutated solution in the population is modified by the use of a crossover named self crossover (SXO), provided in Section 4.5. In order to seek improvement in the neighborhoods of each solution, the TS method (see Section 4.6) is applied to each individual. To deal with some constraint violations, a repair procedure (see Section 4.3) is operated on each individual in the TS. Then, the obtained solutions are assessed and the best individual is selected and used for the next iteration in the ETS. This individual is also compared with the potential final solution in the search space. If it improves, it is saved as a potential new solution. In Figure 4, a chart presents the successive steps of the ETS algorithm.
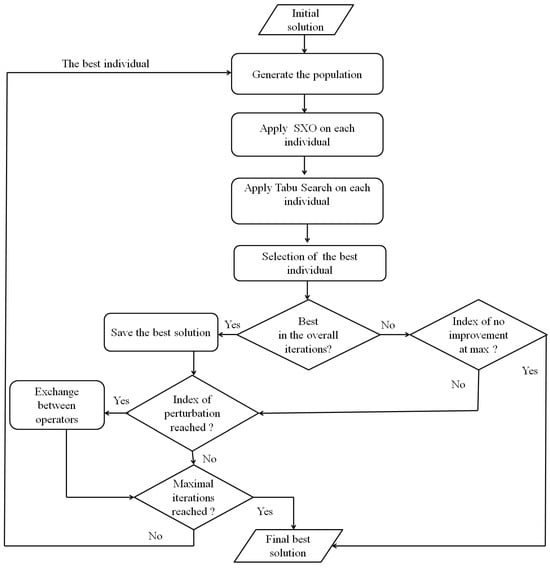
Figure 4.
Flow chart of the ETS algorithm.
Furthermore, in order to increase the perturbation of the search within the ETS, the mutation operators (see Section 4.4) are exchanged after a fixed number of ETS iterations controlled by an index of perturbation. In addition, another index stops the search when no improvement is made during a set of iterations. Otherwise, the overall algorithm stops when the maximal number of iterations is reached.
4.2. The Insertion Heuristic
To construct the initial solution, we propose a new insertion heuristic, see Algorithm 1.
| Algorithm 1 The insertion_heuristic |
|
The heuristic starts by allocating the requests according to the ascending order of their earliest service times. Therefore, it proceeds to the selection of an appropriate vehicle related to its availability capacity and total duration. The requests are inserted in the tour of the vehicles within an available time schedule and when the problem constraints are respected. When a request is allocated (line 7), all the related parameters in relation to vehicles, requests, and time schedules are updated (lines 8–10). In this regard, time windows are computed by the use of Equations (3) and (4) in the problem formulation of Section 3.
In order to release some vehicles’ capacity, deliveries are performed in accordance with their earliest service times and all necessary updates are performed (lines 14–15). This action is also ensured when there are maximum riding time violations (which therefore can be violated during the new request’s insertion) in the tour. Furthermore, a vehicle is set as non-available when its maximal total tour duration is reached. Finally, when all the requests are satisfied, the process comes to an end.
4.3. Repair Operator
Since the metaheuristics are stochastic during the search for better solutions, constraints may be violated. The constraints that may be violated can be linked to the vehicle capacity, the maximal riding time, and the maximal total duration. Therefore, to ensure the feasibility of the solutions, a repair procedure is performed.
To avoid changing the structure of the solution too much, the repair procedure tries to apply a change in the same tour. Thus, in the case of a maximum riding time violation, the delivery schedule is altered by reinserting the destination’s node into another position. With respect to the problem constraints, the same repair action is operated when there is a violation of capacity. Whenever the repaired constraint, the procedure updates the time schedule involving the time windows computation. However, if it is not possible to deal with the feasibility of a tour, the request is reinserted in another route.
In the case of the violation of maximal total duration, lasted requests in the tour are moved to other routes, ensuring the feasibility of the problem constraints in the routes.
4.4. The Mutation Operators
This section introduces both an interruption operator and a swap operator for the mutation phase. Two illustrative examples based on seven requests and two vehicles are provided.
4.4.1. The Interruption Operator
The interruption operator randomly selects a request with waiting time at either the pickup or delivery node. It then cuts the tour before the pickup node of the chosen request and removes that request and the subsequent ones from the route. Subsequently, it attempts to relocate other requests from different routes while adhering to problem constraints and scheduling times.
To facilitate the insertion of requests into another schedule, the operator relies on the customized time windows discussed in Section 3. An illustrative example, based on seven requests and two vehicles, is presented in Figure 5. In this example, the beginning of service for each node is indicated, with node () initially assigned to vehicle .
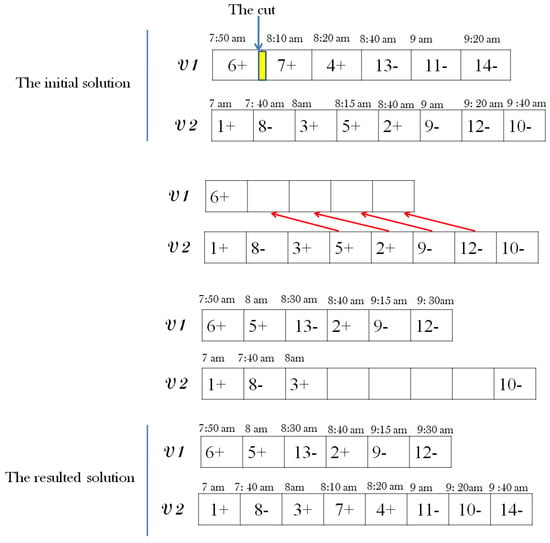
Figure 5.
Construction of a new solution with the interruption operator.
Initially, the tour of vehicle is cut before node (), and the subsequent requests are removed from the tour. The procedure then reallocates requests from the tour of to , respecting constraints related to requests, vehicles, and scheduling.
Next, node 7 is inserted after node () in the tour of . The procedure continues allocating requests in the tour of vehicle until all requests are assigned. Time scheduling is managed through time window equations, ensuring a feasible routing plan with high-quality service in the resulting solution. This enhanced service quality is evident in the elimination of the waiting time previously observed at node 7 in .
4.4.2. The Swap Operator
The swap operator involves exchanging two consecutive delivery locations along the same route, provided that the beginning of service is respected. The procedure manages scheduling time using time window constraints (see Equations (3) and (4) in Section 3) and selects the maximum value between the beginning of service and the new arrival times. This technique enhances service quality when waiting times occur.
Figure 6 illustrates an example of a solution perturbed by the swap operator. The operation involves the two delivery nodes () and () in an illustrative example with seven requests and two vehicles. Beginning of service times are indicated for each node, with node () having a service start time of 8:20 am and node () starting at 8:40 am.
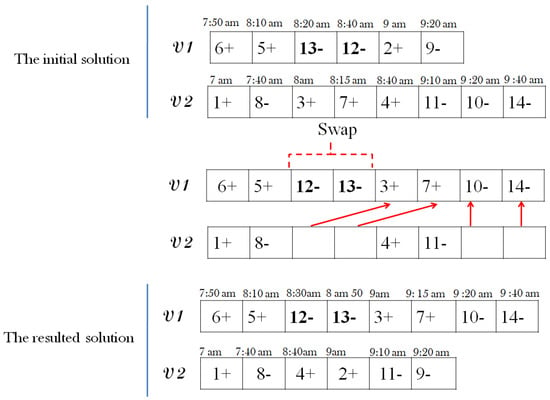
Figure 6.
Construction of a new solution with the swap operator.
As shown in Figure 6, the swap operation is executed while ensuring compliance with problem constraints, including the new time windows computation. Consequently, new beginnings of service are assigned to the two swapped nodes, resulting in nodes () and () having new beginnings of service at 8:30 am and 8:50 am, respectively.
Consequently, requests () and () are transferred to the vehicle tour of . The tour of vehicle is adjusted to accommodate request 2 in its second route, with request 2 having pickup and delivery nodes () and (), respectively. The time schedule is managed and updated using time window equations, considering the maximum values between the beginning of service and the newly provided arrival times at the nodes.
4.5. The Crossover Operator
The crossover operator aims to ensure that the offspring solution inherits positive features from both parents, particularly the good quality of service achieved in the preceding mutation phase.
In our SXO, the parents are not individual solutions, as in classical evolutionary algorithms. Instead, the parents are two selected routes from the same individual. The main steps of the crossover process include:
- Positioning: choose two positions on the two routes, linked to the first pickup nodes in the routes that have similar or close beginnings of service.
- Mapping: temporarily remove the remaining sequences of requests from routes outside the selected cut points in each parent.
- Switching: exchange the two parts between the cut positions between the two routes, respecting the same positions in the time schedule.
- Filling: copy the deleted requests into the child, trying to maintain their initial positions from the parent without introducing redundancy of nodes.
In the example of Figure 7, we consider seven requests and two vehicles. The beginning of service is indicated for each node. The cut is operated on two positions by considering a set of requests with their related pickup and delivery nodes. This criterion aims to ensure the feasibility of the precedence, vehicle capacity, and maximal riding times constraints.
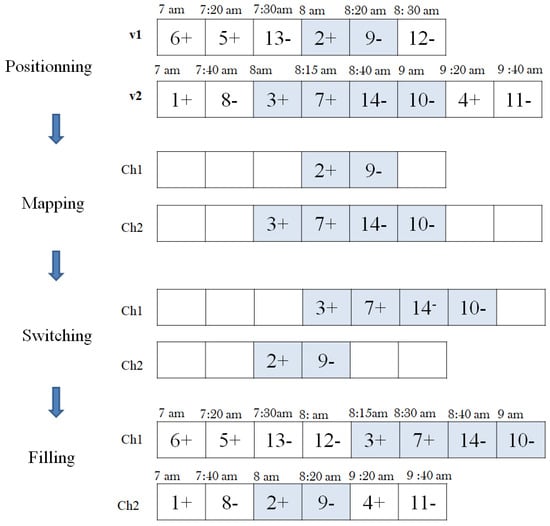
Figure 7.
An illustrative example of the SXO.
In Figure 7, the two blocs of requests {2,9} and {3,7,14,10} are selected from parents and , respectively. The beginning of service in the first pickup, node 2, is 8 am, which is also the case for node 3. In the mapping step, only the two blocs exist in the children and . Next, the blocs are switched between children and the corresponding positions are fulfilled. In the next step, vacant positions are filled by the remaining nodes, ensuring respect for the problem constraints. Whenever a waiting time occurs, the crossover proceeds to the time windows computation seeking its minimization.
4.6. The Tabu Search Method
The tabu search method is a well-known heuristic that was successfully used for DARPs (e.g., [,]). Therefore, we propose to develop a TS especially adapted to the customer-oriented DARP. Thus, a neighborhood strategy supporting the customized design is provided involving service quality enhancement.
In the TS solving method, the move operation involves altering the allocation of requests by changing the position of the request responsible for the largest waiting time within a trip. The request with the highest waiting time value is selected from a trip. Customized time windows for this request are computed using equations provided in Section 3, resulting in a new beginning of service.
Next, the procedure attempts to reinsert the request into another possible position that minimizes the total waiting time. If no waiting time is present in the solution, a random request is selected and moved to a different position. This process involves updates to parameters related to requests, vehicles, and the time schedule.
To maintain solution feasibility after the move operation, the repair procedure (Section 4.3) is applied to restore any violated constraints.
Figure 8 depicts an example of the move operation proposed in our TS. We present a case before and after the move operation. Two vehicles’ routes are considered to satisfy three requests. These latter have origins 1, 2, and 3, with destinations 4, 5, and 6. The beginning of the service is marked on each node. In addition, there are two waiting times that are supposed for nodes 3 and 5, with ( = 20) and ( = 10), respectively.
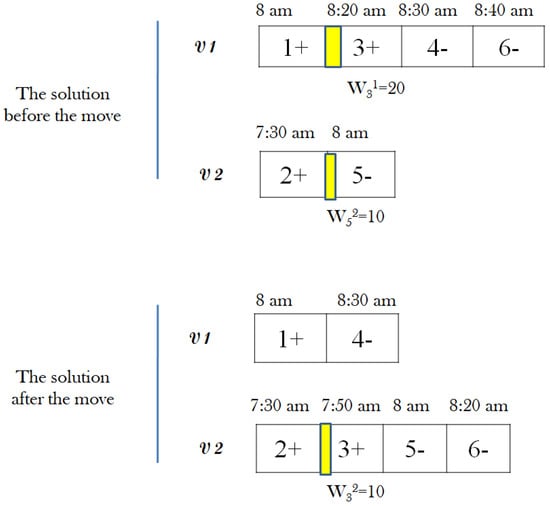
Figure 8.
An illustrative example of the neighborhood strategy of the TS.
The node with the highest waiting time is node 3, corresponding to the pickup node of request 3 in the route of . Initially, this request had a beginning of service at 8:20 am for pickup and 8:40 am for delivery. After computing the time windows, new bounds are determined, which are 7:50 am for pickup and 8:20 am for delivery. To ensure the resulting time schedule, request 3 is inserted in route to minimize waiting times.
This move operation effectively reduces or eliminates unnecessary waiting times, as seen in the case of node 5. Consequently, the total waiting time is reduced to 10 in the resulting solution.
In Figure 8, a new solution is presented, where nodes 1 and 4 are allocated to consecutively, while nodes 2, 3, 5, and 6 are visited in succession by .
5. Computational Experiments
The experiments were conducted on an Intel(R) Core(TM) computer (2.4 GHz) with 4 GB RAM. The evolutionary tabu search algorithm is implemented in C++ and uses a single thread. In this section, a fair comparative study is performed between two hybrid evolutionary methods, which are the ETS and the ELS [] (Section 2) using the same data set. Thus, we first explain the benchmark data set that is used in []. Next, the resolution of one particular instance is detailed to highlight the relevance of the customized design of time windows supported by the ETS. Then, larger experimentation is conducted on small, medium, and large instances of on-demand transportation. Finally, the main outputs are discussed based on a deeper analysis.
5.1. Benchmark Instances
The data set used in all the experimentation is based on the 96 instances of []. These instances represent realistic on-demand transport situations in urban areas. The main data features are reported here.
- The locations are marked by the real distances between them based on the GPS positions of French cities.
- The transportation network density is not the same for all the instances.
- The customers are distributed over a large area, varying according to the instances.
- Time windows are separately defined on both the pickup and destination locations. These time windows are of different sizes according to the customers.
- The maximum riding time for each customer depends on the customer and the distance they have to travel.
- The number of passengers in a location may be greater than 1 up to 4.
- All the vehicles have the same average speed equal to 1.33 km per minute.
- The maximal vehicle tour duration is equal to 480.
- The maximal capacity of the vehicles is equal to 8.
The distances between the origins and the destinations of the customers are distributed so that the majority of the requests (75%) need transportation of between 30 km and 70 km. In addition, the distribution of the maximum riding times is in relation to the travel distances requested by the customers. Thus, the majority of the customers (80%) require a maximal riding time equal to a markup of 100% of their distance. This defines precisely that the maximal riding time is customer-dependent but also depends on the distance of the journey, which reflects realistic situations.
Time windows are supposed to vary between 1 and 4 h. In addition, 50% of the time windows are of 1 h.
5.2. The Relevance of Customer-Oriented Time Windows in the Resolution by ETS
In this part, we analyze the effects of the customer-oriented design of time windows on both the service quality and the travel cost of a solution provided by the ETS. Precisely, we focus on showing the positive impact of the customized time windows formulation provided in Equations (3) and (4) in Section 3 on the waiting times and the total duration. Thus, we compare in-depth two solutions provided by our ETS and the ELS algorithms on the problem instance . As reported later in Table 4, the total number of requests is equal to 10 and the total number of vehicles is equal to 2. The solution obtained with the ELS has a travel cost equal to . However, with the ETS, we obtain a better cost equal to . Note that, for this instance, we have 20 nodes including () and (), the two copies for the depot. Figure 9 presents the solution obtained with the ELS for problem . The travel cost of this solution, which is , is the sum of the cost and 110 of the tours achieved with the two vehicles and , respectively.

Table 4.
Results of the ETS vs. ELS on small-sized problems.

Figure 9.
The solution of the instance obtained with the ELS.
Two cases of waiting times are produced in the solution of the ELS. These waiting times are () in () and () in (). To demonstrate the positive effects of the customized time windows design, we emphasize one vehicle tour having a waiting time (), as it is illustrated by Figure 10. In this figure, we show some of the nodes’ time schedule related to the tour of () of Figure 9. For more clarity, we focus on request 9 with only the depot.
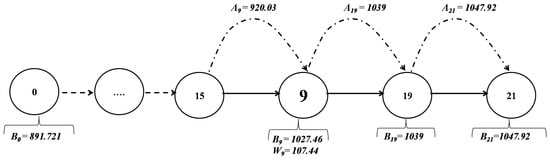
Figure 10.
The schedule time for request 9 in the vehicle () obtained with the ELS.
When we consider the solution provided by the ETS on the same problem instance (see Figure 11), we can note that request 7 is moved from () in the solution of the ELS (Figure 9) to () in the solution of the ETS. This new schedule allows a reduced cost equal to in the solution of the ETS, as compared with for the ELS. Indeed, this request had a high waiting time () at the pickup node in () of the ELS. This waiting time is totally deleted in the solution of the ETS when inserting request 7 in the schedule of (), as reported by Figure 12.

Figure 11.
The solution of the instance obtained with the ETS.
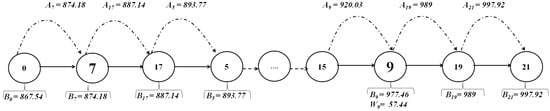
Figure 12.
The details related to requests 7 and 9 in in the solution obtained with the ETS.
Moreover, the waiting time for request 9 is also reduced. This enhancement is due to the time windows design using Equations (3) and (4) and the new bounds [] and [] derived for the pickup node () and the delivery one () of request 9. Consequently, two beginnings of service time are then proposed as () and (). This has also an impact on the overall system performance, producing new values for the vehicle’s arriving times () and () in Figure 12, as compared with () and () in the ELS, see Figure 10.
Consequently, we can argue that the customized design of the service quality term is beneficial for both the customer and the service provider. More precisely, in the solution produced by the ETS method, two levels of enhancement are highlighted: the solution cost in terms of completion time and the service quality in terms of waiting time.
5.3. Results Obtained with the Two Evolutionary Techniques on the Benchmark Problems
In this subsection, we show the ETS performance regarding on-demand transport problems of []. To analyze the behaviour of the ETS better, we propose to divide the instances into three groups, , , and , which, respectively, correspond to small, medium, and large instances. The sets of instances , , and contain 32 instances each. The total number of requests is in {10..60} for , {62..84} for , and {85..128} for .
In all the experimentation, the comparison is based on the deviation or () between the total travel cost and the total waiting time (TWT). The latter is the sum of all waiting times related to all the vehicles’ tours. A negative deviation means a reduction in the values. The computational times are not compared here because those of the ELS [] were not reported.
Table 4, Table 5, and Table 6 are, respectively, related to the benchmark problems from the , , and groups defined previously. In these tables, we successively present the instances’ names, the number of vehicles, and the number of customers, and, for each evolutionary method, we separately present the resulting total travel travel cost and total waiting time. The gaps between the results obtained with the ETS and the ELS techniques are also reported. The gap is set as for computing the level of improvement of the ETS, as compared with the ELS. Improved values are marked with bolt font.

Table 5.
Results of the ETS vs. ELS on medium-sized problems.

Table 6.
Results of the ETS vs. ELS on large-sized problems.
From the observation of Table 4, Table 5 and Table 6, the results obtained with the ETS algorithm compete well with the ones of the ELS algorithm. First, the results show the capability of the ETS algorithm to address real-life and expected on-demand transportation problems with considerable sizes. This is the case of the instances and in Table 5, and and in Table 6.
In Table 4, there is only one instance, , that is not improved by the ETS, as compared with the ELS. However, the gap obtained between the two algorithms in this instance is still low (0,79) in TTC and (5,19) in TWT.
In Figure 13, the diagram shows a comparison of the two evolutionary methods considered. This comparison is based on the number of instances where the TTC or the TWT is improved or not by the ETS, as compared with the ELS.
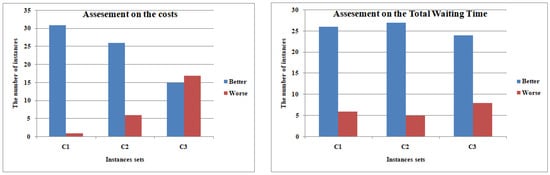
Figure 13.
Number of solutions obtained with the ETS that are better or worse than the solutions of the ELS.
Figure 13 demonstrates the significant improvement in total travel cost (TTC) achieved by the ETS compared with the ELS in the instances, with 31 out of 32 instances showing improvement. For the instances, there is improvement in 26 out of 32 cases. However, in the last group ( instances), the improvement rate is 46.87%, affecting 15 instances. In total, the ETS improves 72 out of 96 on-demand transportation problems tested. This improvement results from the combination of the evolutionary method with TS and the utilization of customized time windows in request scheduling.
In terms of total waiting time, Figure 13 illustrates a substantial enhancement when comparing the ETS with the ELS. The ETS outperforms ELS in 77 out of 96 cases, showcasing the significant contribution of customized time windows in ETS resolution.
Overall, the service quality is well addressed across all instances of TOD. TWT is improved for 26, 27, and 24 instances out of 32 in the , , and classes, respectively.
6. Statistical Analysis of the Results Provided for the Problem
In order to assess well the performance of our new hybridized evolutionary method ETS, a deeper analysis of the results is required. We assess the behavior of the combined methods, which are the TS and the evolutionary algorithm (EA), before their hybridization. In addition, the analysis concerns the hybridized ones, which are the ETS and the ELS. Therefore, statistical significance between the results of the compared algorithms is performed based on the TTC obtained, being the values to not deteriorate when improving the quality of service in the problem.
We follow the work of [], which proposed guidelines to conduct a statistical analysis of experimental studies. To this end, a set of steps is prescribed for statistically comparing the algorithms. However, tests of normality are needed to select the appropriate statistical tests: parametric or non-parametric associated with normal or non-normal data distribution. Many tests are provided in the literature to ensure the distribution of the data used in the experimentation, such as the Shapiro–Wilk test [] or the Kolmogorov–Smirnov [] test.
According to the Shapiro–Wilk test, the results of the algorithms do not follow a normal distribution, as is the case for the majority of the metaheuristics and bio-inspired algorithms []. Therefore, non-parametric tests are selected to derive statistical tests.
6.1. Tests of Differences
In order to detect differences between algorithms, the Friedman’s test is used. It consists in accepting or rejecting the null hypothesis, . This hypothesis considers that the algorithms have a similar performance. Given k is the number of algorithms equal to 4, b the number of instances equal to 96, and the squared sum of the ranks for an algorithm, the Friedman equation is given by (9).
The average ranking of the compared algorithms is provided based on the average of solutions within 10 runs. Next, the sum and the average of the ranking of each algorithm are indicated in Table 7.

Table 7.
Indications of the Friedman test.
Using the values produced in Table 7, the Friedman test (9) produces a value of 151,33. In addition, the critical value () is 7.81 according to the distribution. Thus, if we have , the rejection of the null hypothesis is , and otherwise. In our case, 151.33 > 7.81. Consequently, we deduce that there are differences between the compared algorithms, and the null hypothesis is rejected with a confidence level of 95%.
Moreover, the algorithm is considered to be the best one if it deals with the best average ranking value, as is the case with ETS presenting a less average rank equal to 1.33. However, this indication is not enough to conclude which algorithm has the best performance. Therefore, we proceed by pairwise comparisons to effectively observe the significance of the algorithms’ performance.
6.2. Pairwise Comparisons
In this part, a statistical significance between the compared algorithms is addressed regarding both the obtained solutions values and the distribution of the obtained solutions in the search space. Thus, to analyze the performance of the algorithms in terms of solution values, we compute the absolute difference of the sums of ranks between two algorithms i and j. The difference is significant when it exceeds the critical value equal to 7.81. The winner algorithm is that having the smallest sum of ranks between the two compared ones. In Table 8, the absolute difference between the sums of ranks (previously computed in Table 7) is indicated.

Table 8.
Pairwise comparisons of the ranked solutions value.
Based on the difference of ranking sums in terms of solutions values, all the differences are significant since for each pairwise algorithm. Moreover, these outputs highlight the dominance of the ETS, which occupies the largest number of winner occurrences in Table 8.
Whenever the significance in terms of solution values is analyzed, the one based on the solution value distributions in the search space is mandatory. Therefore, the p-value is calculated for each group of comparisons using the Student t-test distribution in Table 9. Next, the Bonferroni correction method is applied for as . The obtained adjusted p-value is equal to 0.008. A significance is mentioned as Yes when the obtained p-value of a group is less than the adjusted one. Otherwise, it is mentioned as No.

Table 9.
Pairwise comparisons of the solution value distributions.
The cases that indicate the significance of the differences in terms of distribution are TS vs. ELS and TS vs. ETS. Nevertheless, all the other groups indicate no significant result of the solution value distributions in the search space.
6.3. Interpretation of the Statistical Results
According to the results provided in Table 8 and Table 9, we point out that the results’ significance is not the same in terms of solution values and their distribution in the search space. Regarding the guidelines of [], the following interpretations are highlighted.
The TS algorithm indicates no significant results in terms of solution values, as compared with EA, ELS, and ETS (see Table 8). But, the distribution of the values of the solutions provided by this losing method has a statistical significance, as compared with the hybrid evolutionary algorithms, which are the ELS and ETS, see Table 9. Obviously, these advanced methods involve a larger exploration mechanism than the TS as well as the EA, since they present no significant distribution of solution values (Table 9).
As we see in Table 8, the algorithms EA, ELS, and ETS have an increased significance in terms of solution values but not their distribution (Table 9). However, according to the indications of Table 8, the EA is losing against the ELS and ETS regarding the solution values’ significance. Therefore, the EA has a lower performance than the hybridized ones.
Moreover, the two hybridized algorithms ELS and ETS have the same exploration power but with a different exploitation efficiency. Given that the ETS does not provide any losing case in terms of ranking solution values, see Table 8, we can deduce that it dominates the ELS. Thus, we emphasize the effectiveness of the TS when it is used as an exploitation mechanism in the hybrid evolutionary algorithm ETS.
7. Discussion
Our findings highlight the significance of enhancing the service quality in on-demand transportation systems. By reducing waiting times, improving schedule reliability, and implementing customer-centric features, we not only enhance the user satisfaction but also increase the system efficiency. This aligns with the goals of smart cities, where technological innovations are required to create more responsive and adaptive transportation networks. The implications of our findings extend beyond theoretical considerations to practical applications within smart city transportation planning and management. By optimizing the service quality, we can achieve more efficient resource utilization and cost savings.
To tackle DARPs, which are more applicable to real-world scenarios, it is relevant to consider dynamic elements such as variable capacities and real-time transit data.
However, we have started by assuming fixed capacities, which allows us to focus on optimizing the routing and scheduling aspects without the additional complexity of variable capacities. This is a common practice in initial methodological studies, providing a clear framework to demonstrate the core algorithmic innovations. Future works can extend the method to accommodate variable capacities, making it more applicable to real-world scenarios. Similarly, assuming constant transit times simplifies the model, making it more tractable for computational experiments. In real-world applications, transit times can vary due to traffic conditions, roadworks, and other factors. When considering dynamic factors, such as variable transit times and vehicle capacities, the computational complexity of the hybrid evolutionary tabu search method for transport on demand scenarios, like the dial-a-ride problem, increases significantly. Therefore, there are effective strategies to address complexity as efficient dynamic data integration techniques, such as stream processing, to manage real-time transit data effectively. Moreover, a dynamic parameter adjustment would be beneficial to address the complexity. The method should adapt parameters like mutation rates, crossover rates, and neighborhood sizes based on current solution quality and real-time system changes. It would be interesting to use machine learning techniques to predict optimal parameter settings based on historical data and current system states. In addition, we should also integrate heuristics that provide quick, approximate solutions to guide the evolutionary algorithms and tabu search, reducing the search space and improving convergence rates.
Implementing these strategies can significantly improve the scalability of the hybrid evolutionary tabu search method for medium and large networks in transport on-demand scenarios. These enhancements ensure that the method remains robust and efficient, making it suitable for real-world applications in smart cities. Future work will continue to refine these strategies, further improving scalability and practical applicability in diverse urban transport environments.
8. Conclusions
This paper introduces an efficient hybrid algorithm called the evolutionary tabu search that addresses the challenges of solving a specific variant of the dial-a-ride problem with customer-oriented constraints. By combining the evolutionary computation framework with the tabu search, the ETS algorithm offers a powerful approach to optimizing transportation solutions. The primary objective of the ETS method is to provide tailored optimization techniques that support customized designs for the DARP. To this end, the algorithm incorporates specific mutation operators that are designed to address the unique requirements of the problem. These operators are dynamically exchanged during the search process, allowing for the exploration of diverse solution spaces and leading to an improved service quality. To validate the effectiveness of the ETS algorithm, extensive experiments were conducted, comparing its performance with another hybrid evolutionary method from the literature using real-life transportation problems. The results of these experiments demonstrate the superior performance of the ETS algorithm in terms of improvement of the service quality. The introduction of the new tabu search method with its customized neighborhood strategy and tailored evolutionary operators represents a significant contribution to the DARP field. It presents a promising approach for solving the problem at hand by effectively addressing both operational and service quality objectives, thereby providing a valuable tool for decision-making in relevant domains. The findings of the study highlight the strengths and advantages of the ETS method in addressing the challenges and requirements of transport on-demand problems. The method’s ability to deliver competitive results, coupled with the observed improvements in service quality, signifies its potential as an effective solution for optimizing on-demand transportation systems. In future research, it would be valuable to explore the integration of additional criteria, such as waiting time, riding time, and tour cost, within a multi-objective framework. This would further enhance the algorithm’s capability to deliver good solutions that consider multiple aspects of the problem.
Furthermore, future works will extend the model to incorporate dynamic elements such as variable capacities and real-time transit data, making it more relevant for real-world scenarios. Enhancing the method to accommodate real-time data on traffic conditions and vehicle availability should also improve the accuracy and responsiveness of the system. Thus, extending the method to handle variable vehicle capacities and other dynamic constraints is encouraged, making the method more applicable to diverse urban transport scenarios in smart cities.
In conclusion, the presented hybrid optimization method provides a significant advancement in solving DARPs for smart cities. It not only enhances service quality and operational efficiency but also sets the stage for further research and development to adapt the method to the dynamic and complex nature of real-world transportation systems.
Author Contributions
Conceptualization, S.N. and H.B.; methodology, S.N.; software, S.N.; validation, S.N., H.B. and W.A.M.; formal analysis, S.N.; investigation, S.N.; resources, S.N.; data curation, S.N.; writing—original draft preparation, H.B.; writing—review and editing, S.N.; visualization, W.A.M.; supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data required to reproduce the above findings are available to download from Scopus Document Searcher using the keywords specified at the methodology.
Acknowledgments
We would like to express our gratitude to the administrative staff of the Business Higher School of Tunis for their assistance in coordinating logistics and facilitating communication. I express my sincere gratitude to the technical support team of the LARODEC laboratory for their expertise in maintaining equipment and providing troubleshooting assistance. I also thank LARODEC laboratory for generously providing access to their facilities and resources, which significantly contributed to the success of our experiments.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Cordeau, J.F.; Laporte, G. A tabu search heuristic for the static multi-vehicle dial-a-ride problem. Transp. Res. Part Methodol. 2003, 37, 579–594. [Google Scholar] [CrossRef]
- Healy, P.; Moll, R. A new extension of local search applied to the dial-a-ride problem. Eur. J. Oper. Res. 1995, 83, 83–104. [Google Scholar] [CrossRef]
- Molenbruch, Y.; Braekers, K.; Caris, A. Typology and literature review for dial-a-ride problems. Ann. Oper. Res. 2017, 259, 295–325. [Google Scholar] [CrossRef]
- Chassaing, M.; Duhamel, C.; Lacomme, P. An ELS-based approach with dynamic probabilities management in local search for the Dial-A-Ride Problem. Eng. Appl. Artif. Intell. 2016, 48, 119–133. [Google Scholar] [CrossRef]
- Parragh, S.N. Introducing heterogeneous users and vehicles into models and algorithms for the dial-a-ride problem. Transp. Res. Part Emerg. Technol. 2011, 19, 912–930. [Google Scholar] [CrossRef] [PubMed]
- Braekers, K.; Kovacs, A.A. A multi-period dial-a-ride problem with driver consistency. Transp. Res. Part Methodol. 2016, 94, 355–377. [Google Scholar] [CrossRef]
- Masmoudi, M.A.; Braekers, K.; Masmoudi, M.; Dammak, A. A hybrid genetic algorithm for the heterogeneous dial-a-ride problem. Comput. Oper. Res. 2017, 81, 1–13. [Google Scholar] [CrossRef]
- Agrawal, V.; Lightner, C.; Lightner-Laws, C.; Wagner, N. A bi-criteria evolutionary algorithm for a constrained multi-depot vehicle routing problem. Soft Comput. 2017, 21, 5159–5178. [Google Scholar] [CrossRef]
- Bahadori-Chinibelagh, S.; Fathollahi-Fard, A.M.; Hajiaghaei-Keshteli, M. Two constructive algorithms to address a multi-depot home healthcare routing problem. IETE J. Res. 2019, 68, 1108–1114. [Google Scholar] [CrossRef]
- Masson, R.; Lehuédé, F.; Péton, O. The dial-a-ride problem with transfers. Comput. Oper. Res. 2014, 41, 12–23. [Google Scholar] [CrossRef]
- Molenbruch, Y.; Braekers, K.; Caris, A. Benefits of horizontal cooperation in dial-a-ride services. Transp. Res. Part Logist. Transp. Rev. 2017, 107, 97–119. [Google Scholar] [CrossRef]
- Nasri, S.; Bouziri, H.; Aggoune-Mtalaa, W. An evolutionary descent algorithm for customer-oriented mobility-on-demand problems. Sustainability 2022, 14, 3020. [Google Scholar] [CrossRef]
- Melachrinoudis, E.; Min, H. A tabu search heuristic for solving the multi-depot, multi-vehicle, double request dial-a-ride problem faced by a healthcare organisation. Int. J. Oper. Res. 2011, 10, 214–239. [Google Scholar] [CrossRef]
- Paquette, J.; Cordeau, J.F.; Laporte, G.; Pascoal, M.M. Combining multicriteria analysis and tabu search for dial-a-ride problems. Transp. Res. Part Methodol. 2013, 52, 1–16. [Google Scholar] [CrossRef]
- Torgal, M.; Dias, T.G.; Fontes, T. A multi objective approach for DRT service using tabu search. Transp. Res. Procedia 2021, 52, 91–98. [Google Scholar] [CrossRef]
- Carotenuto, P.; Paradisi, L.; Storchi, G. A flexible transport service for passengers. Transp. Res. Procedia 2014, 3, 442–451. [Google Scholar] [CrossRef][Green Version]
- Viana, R.J.; Santos, A.G.; Martins, F.V.; Wanner, E.F. Optimization of a demand responsive transport service using multi-objective evolutionary algorithms. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Prague, Czech Republic, 13–17 July 2019; pp. 2064–2067. [Google Scholar]
- Belhaiza, S. A hybrid adaptive large neighborhood heuristic for a real-life dial-a-ride problem. Algorithms 2019, 12, 39. [Google Scholar] [CrossRef]
- Chu, J.C.Y.; Chen, A.Y.; Shih, H.H. Stochastic programming model for integrating bus network design and dial-a-ride scheduling. Transp. Lett. 2022, 14, 245–257. [Google Scholar] [CrossRef]
- Nguyen, J.; Powers, S.T.; Urquhart, N.; Farrenkopf, T.; Guckert, M. Modelling the impact of individual preferences on traffic policies. Comput. Sci. 2022, 3, 365. [Google Scholar] [CrossRef]
- Detti, P.; Papalini, F.; de Lara, G.Z.M. A multi-depot dial-a-ride problem with heterogeneous vehicles and compatibility constraints in healthcare. Omega 2017, 70, 1–14. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, M.; Lim, A. A memetic algorithm for the patient transportation problem. Omega 2015, 54, 60–71. [Google Scholar] [CrossRef]
- Braekers, K.; Caris, A.; Janssens, G.K. Exact and meta-heuristic approach for a general heterogeneous dial-a-ride problem with multiple depots. Transp. Res. Part Methodol. 2014, 67, 166–186. [Google Scholar] [CrossRef]
- Nasri, S.; Bouziri, H.; Aggoune-Mtalaa, W. Customer-Oriented Dial-A-Ride Problems: A Survey on Relevant Variants, Solution Approaches and Applications. In Emerging Trends in ICT for Sustainable Development; Springer: Berlin/Heidelberg, Germany, 2021; pp. 111–119. [Google Scholar]
- Wong, K.I.; Han, A.; Yuen, C. On dynamic demand responsive transport services with degree of dynamism. Transp. Transp. Sci. 2014, 10, 55–73. [Google Scholar] [CrossRef]
- Carotenuto, P.; Martis, F. A double dynamic fast algorithm to solve multi-vehicle Dial a Ride Problem. Transp. Res. Procedia 2017, 27, 632–639. [Google Scholar] [CrossRef]
- Marković, N.; Nair, R.; Schonfeld, P.; Miller-Hooks, E.; Mohebbi, M. Optimizing dial-a-ride services in Maryland: Benefits of computerized routing and scheduling. Transp. Res. Part Emerg. Technol. 2015, 55, 156–165. [Google Scholar] [CrossRef]
- Hu, T.Y.; Chang, C.P. A revised branch-and-price algorithm for dial-a-ride problems with the consideration of time-dependent travel cost. J. Adv. Transp. 2015, 49, 700–723. [Google Scholar] [CrossRef]
- Ho, S.; Nagavarapu, S.C.; Pandi, R.R.; Dauwels, J. An improved tabu search heuristic for static dial-a-ride problem. arXiv 2018, arXiv:1801.09547. [Google Scholar]
- Molenbruch, Y.; Braekers, K.; Caris, A. Operational effects of service level variations for the dial-a-ride problem. Cent. Eur. J. Oper. Res. 2017, 25, 71–90. [Google Scholar] [CrossRef]
- Paquette, J.; Cordeau, J.F.; Laporte, G. Quality of service in dial-a-ride operations. Comput. Ind. Eng. 2009, 56, 1721–1734. [Google Scholar] [CrossRef]
- Paquette, J.; Bellavance, F.; Cordeau, J.F.; Laporte, G. Measuring quality of service in dial-a-ride operations: The case of a Canadian city. Transportation 2012, 39, 539–564. [Google Scholar] [CrossRef]
- Parragh, S.N.; Pinho de Sousa, J.; Almada-Lobo, B. The dial-a-ride problem with split requests and profits. Transp. Sci. 2015, 49, 311–334. [Google Scholar] [CrossRef]
- Glover, F.; Kelly, J.P.; Laguna, M. Genetic algorithms and tabu search: Hybrids for optimization. Comput. Oper. Res. 1995, 22, 111–134. [Google Scholar] [CrossRef]
- Nasri, S.; Bouziri, H. Improving total transit time in dial-a-ride problem with customers-dependent criteria. In Proceedings of the IEEE/ACS 14th International Conference on Computer Systems and Applications (AICCSA), Hammamet, Tunisia, 30 October–3 November 2017; pp. 1141–1148. [Google Scholar]
- Cheikh-Graiet, S.B.; Dotoli, M.; Hammadi, S. A Tabu Search based metaheuristic for dynamic carpooling optimization. Comput. Ind. Eng. 2020, 140, 106217. [Google Scholar] [CrossRef]
- Gmira, M.; Gendreau, M.; Lodi, A.; Potvin, J.Y. Tabu Search for the Time-Dependent Vehicle Routing Problem with Time Windows on a Road Network. Eur. J. Oper. Res. 2020, 288, 129–140. [Google Scholar] [CrossRef]
- Aziz, H.A.; Garikapati, V.; Rodriguez, T.K.; Zhu, L.; Sun, B.; Young, S.E.; Chen, Y. An optimization-based planning tool for on-demand mobility service operations. Int. J. Sustain. Transp. 2022, 16, 45–56. [Google Scholar] [CrossRef]
- Chen, Z.G.; Zhan, Z.H.; Kwong, S.; Zhang, J. Evolutionary computation for intelligent transportation in smart cities: A survey. IEEE Comput. Intell. Mag. 2022, 17, 83–102. [Google Scholar] [CrossRef]
- Cubillos, C.; Urra, E.; Rodríguez, N. Application of genetic algorithms for the DARPTW problem. Int. J. Comput. Commun. Control. 2009, 4, 127–136. [Google Scholar] [CrossRef]
- Rekiek, B.; Delchambre, A.; Saleh, H.A. Handicapped person transportation: An application of the grouping genetic algorithm. Eng. Appl. Artif. Intell. 2006, 19, 511–520. [Google Scholar] [CrossRef]
- Jorgensen, R.M.; Larsen, J.; Bergvinsdottir, K.B. Solving the dial-a-ride problem using genetic algorithms. J. Oper. Res. Soc. 2007, 58, 1321–1331. [Google Scholar] [CrossRef]
- Sun, B.; Wei, M.; Yang, C.; Xu, Z.; Wang, H. Personalised and coordinated demand-responsive feeder transit service design: A genetic algorithms approach. Future Internet 2018, 10, 61. [Google Scholar] [CrossRef]
- Nasri, S.; Bouziri, H. Towards a fair mobility: An evolutionary algorithm for customers-dependent transport on demand problems. In Proceedings of the 2019 International Conference on Internet of Things, Embedded Systems and Communications (IINTEC), Tunis, Tunisia, 20–22 December 2019; pp. 34–40. [Google Scholar]
- Molenbruch, Y.; Braekers, K.; Hirsch, P.; Oberscheider, M. Analyzing the benefits of an integrated mobility system using a matheuristic routing algorithm. Eur. J. Oper. Res. 2021, 290, 81–98. [Google Scholar] [CrossRef]
- Chevrier, R.; Liefooghe, A.; Jourdan, L.; Dhaenens, C. Solving a dial-a-ride problem with a hybrid evolutionary multi-objective approach: Application to demand responsive transport. Appl. Soft Comput. 2012, 12, 1247–1258. [Google Scholar] [CrossRef]
- Ghoseiri, K.; Ghannadpour, S.F. Multi-objective vehicle routing problem with time windows using goal programming and genetic algorithm. Appl. Soft Comput. 2010, 10, 1096–1107. [Google Scholar] [CrossRef]
- Li, J.; Tomita, K.; Kamimura, A. A Novel Genetic Algorithm for a Multi-Vehicle Dial-a-Ride Problem. In Proceedings of the 2022 International Conference on Advanced Robotics and Mechatronics (ICARM), Guilin, China, 3–5 July 2022; pp. 682–689. [Google Scholar]
- Perera, T.; Prakash, A.; Gamage, C.N.; Srikanthan, T. Hybrid genetic algorithm for an on-demand first mile transit system using electric vehicles. In Proceedings of the International Conference on Computational Science, Las Vegas, NV, USA, 12–14 December 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 98–113. [Google Scholar]
- Godart, A.; Manier, H.; Bloch, C.; Manier, M.A. Hybrid metaheuristic for the Pickup and Delivery Problem designed for passengers and goods transportation. IFAC-PapersOnLine 2019, 52, 2584–2589. [Google Scholar] [CrossRef]
- Chassaing. Instances of Chassaing. 2020. Available online: http://fc.isima.fr/~lacomme/Maxime/ (accessed on 19 July 2020).
- LaTorre, A.; Molina, D.; Osaba, E.; Poyatos, J.; Del Ser, J.; Herrera, F. A prescription of methodological guidelines for comparing bio-inspired optimization algorithms. Swarm Evol. Comput. 2021, 67, 100973. [Google Scholar] [CrossRef]
- Shaphiro, S.; Wilk, M. An analysis of variance test for normality. Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Razali, N.M.; Wah, Y.B. Power comparisons of shapiro-wilk, kolmogorov-smirnov, lilliefors and anderson-darling tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).