Optimal Dispatch Strategy for Electric Vehicles in V2G Applications
Abstract
:1. Introduction
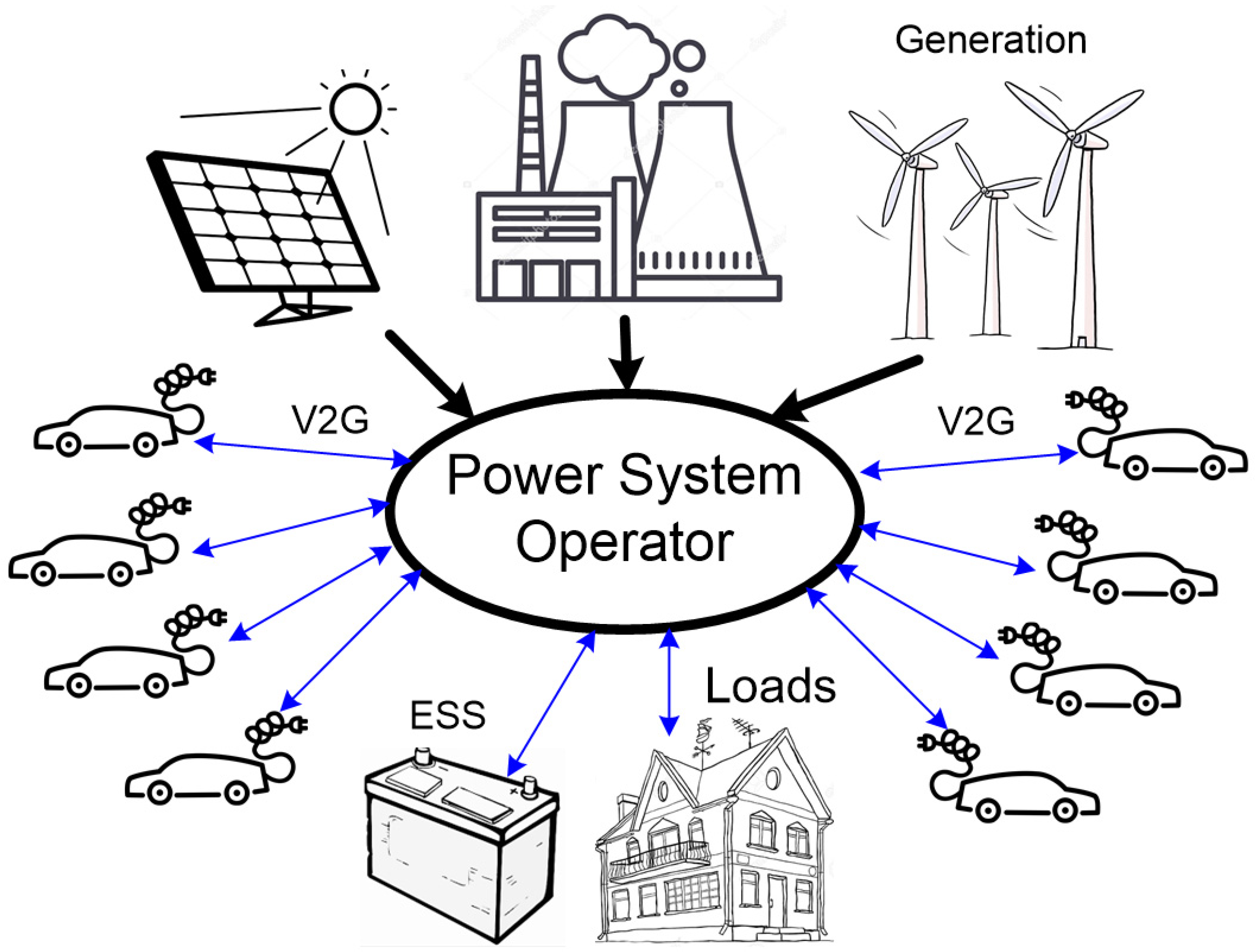
1.1. Dispatch Architectures of V2G Technology
1.2. Motivation
1.3. Innovation and Contribution
- A novel hourly EV battery wear model has been developed to precisely predict the hourly wear cost of EV batteries while considering all of the crucial aspects such as temperature, power level, and the SoC.
- A modified GWO method that uses a contemporary technique known as gradual reduction of the swarm size for GWO (GRSS-GWO), to reduce the convergence time and improve the accuracy of the findings.
- An accurate scheduling model for optimally charging and discharging the electricity of EVs utilizing V2G technology.
- An accurate economic model that may be used to assess the money that EV owners can earn by participating in technological projects that use V2G.
1.4. Paper Outlines
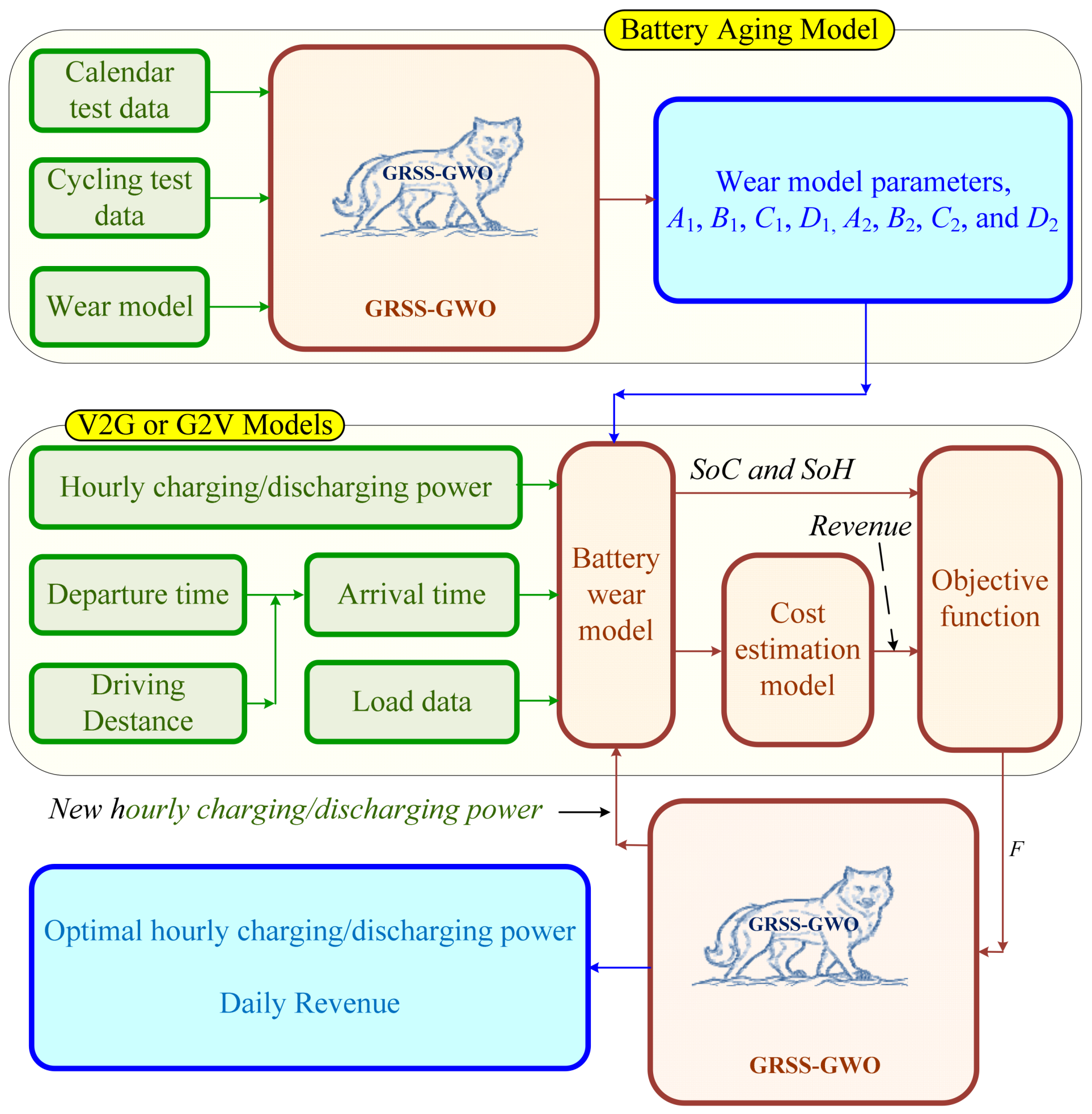
2. Battery Wear Modelling
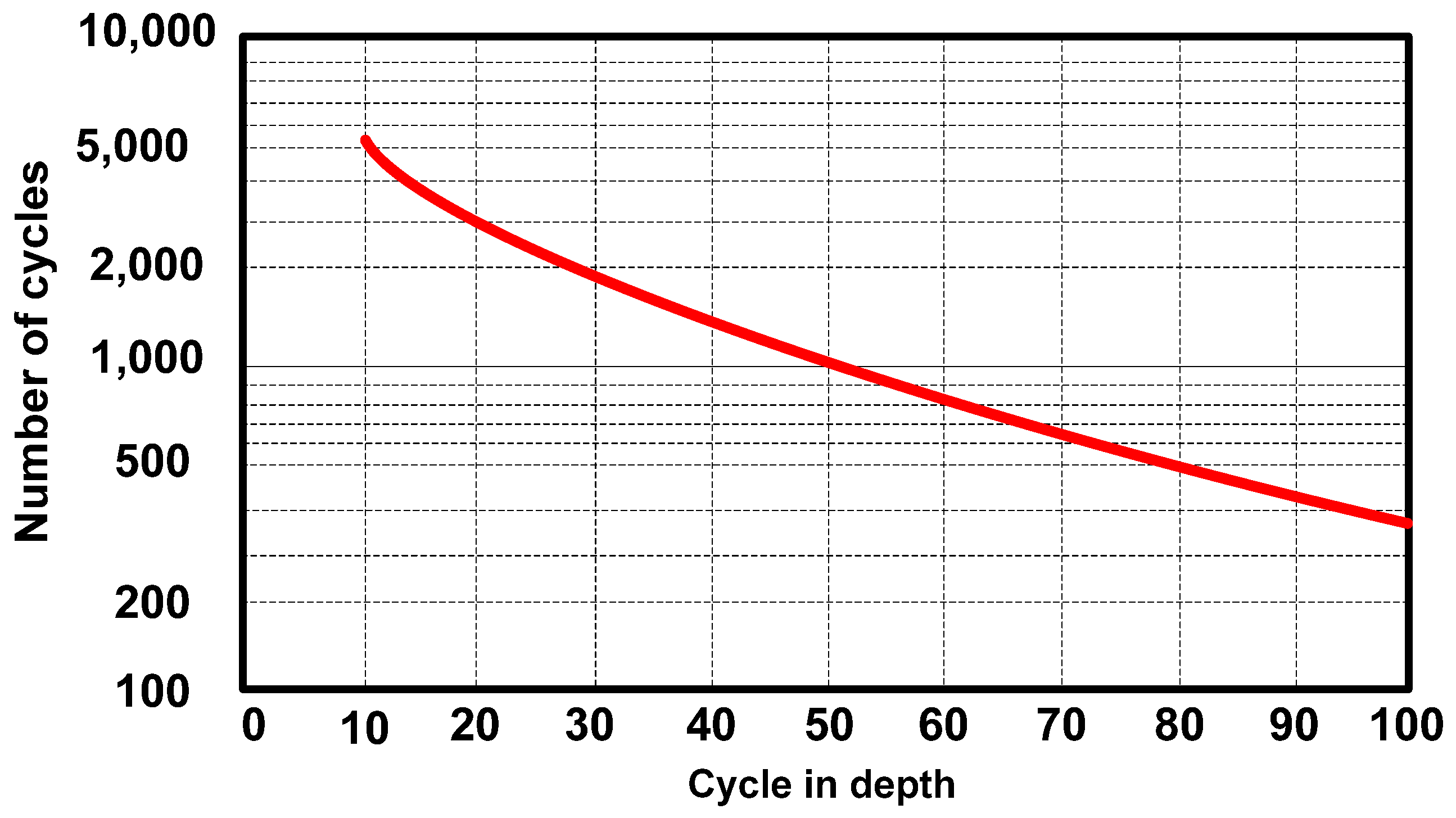
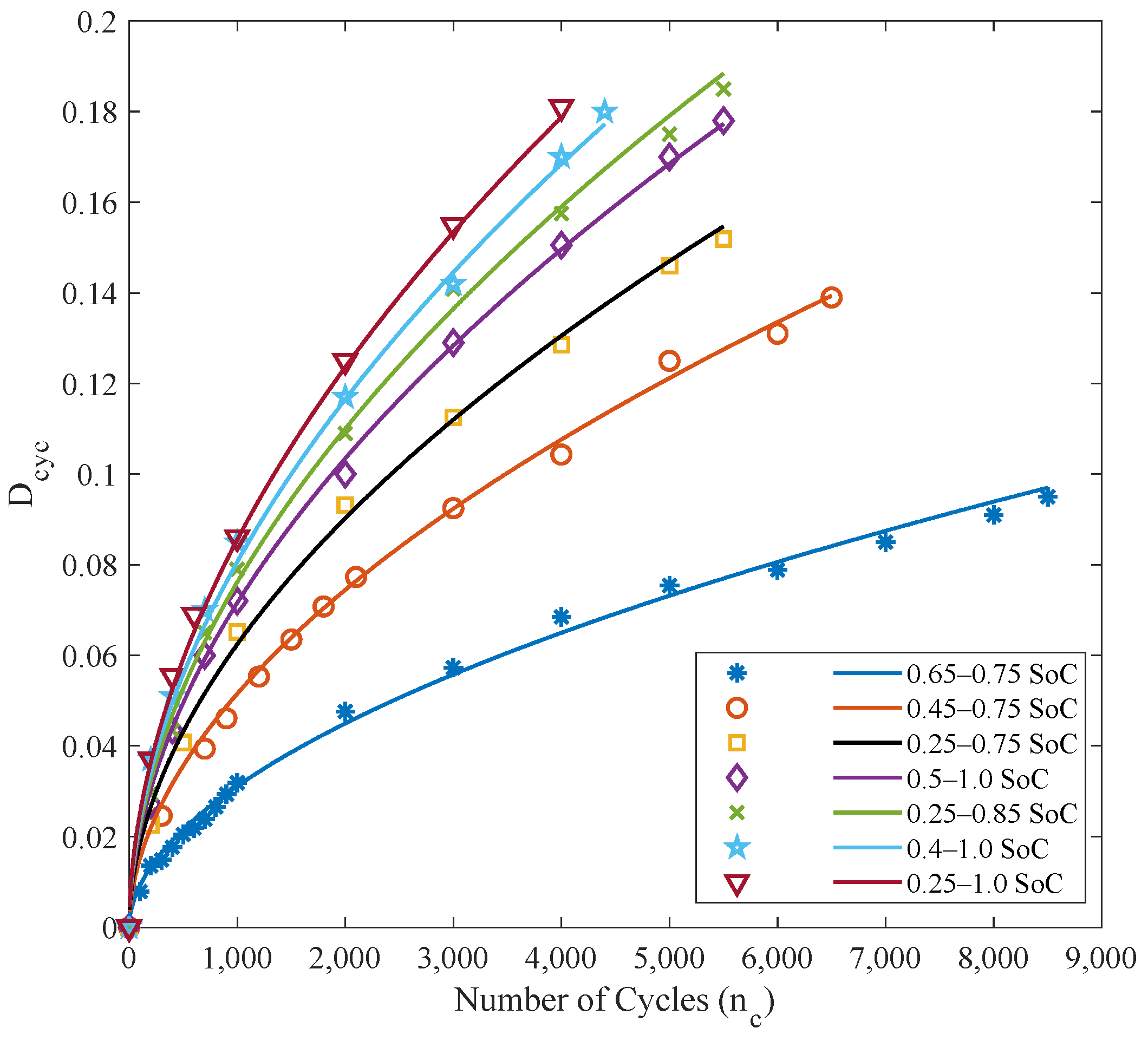
2.1. Wear Modeling Based on Achievable Cycle Count (ACC)
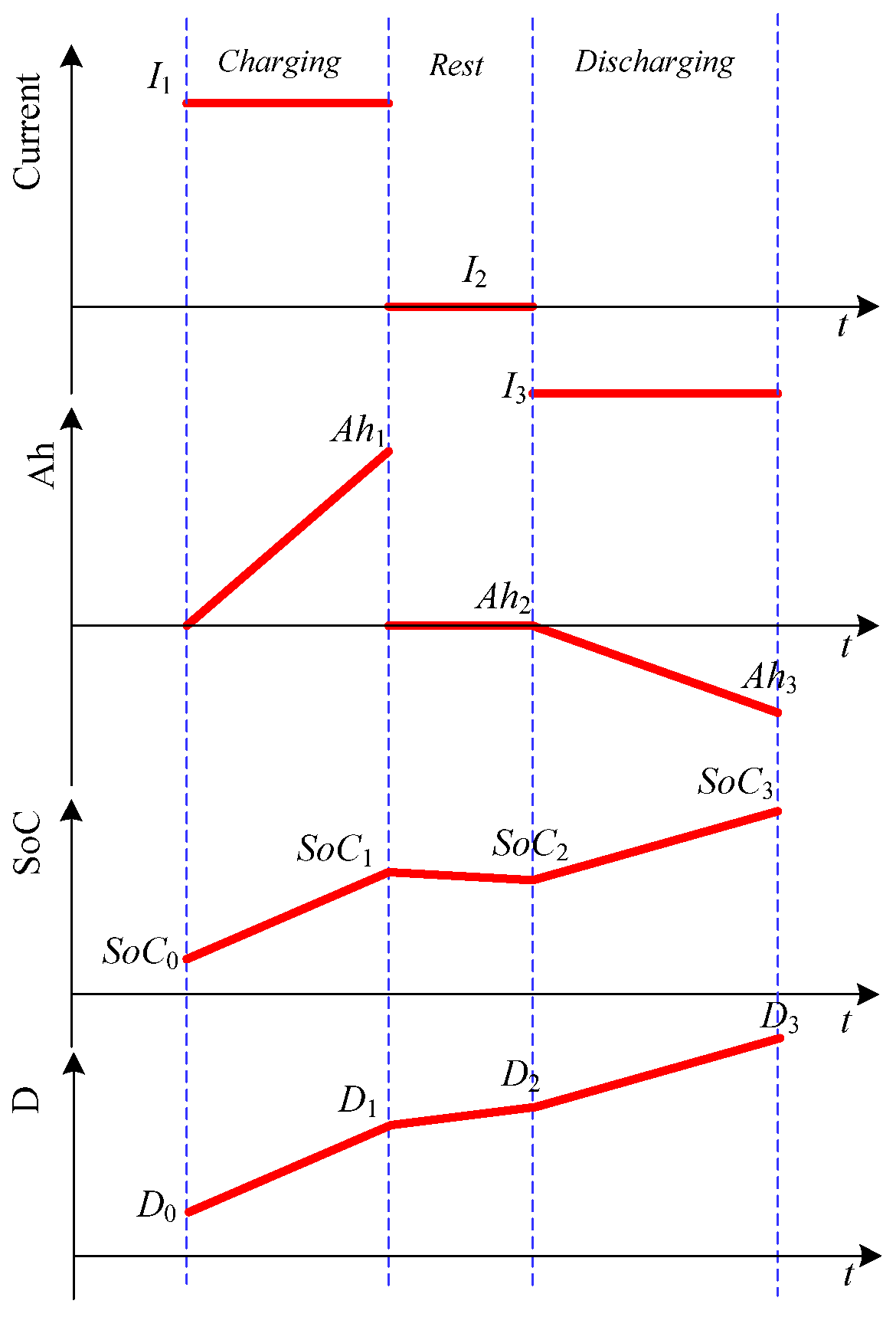
2.2. Novel Battery Wear Model (NBWM)
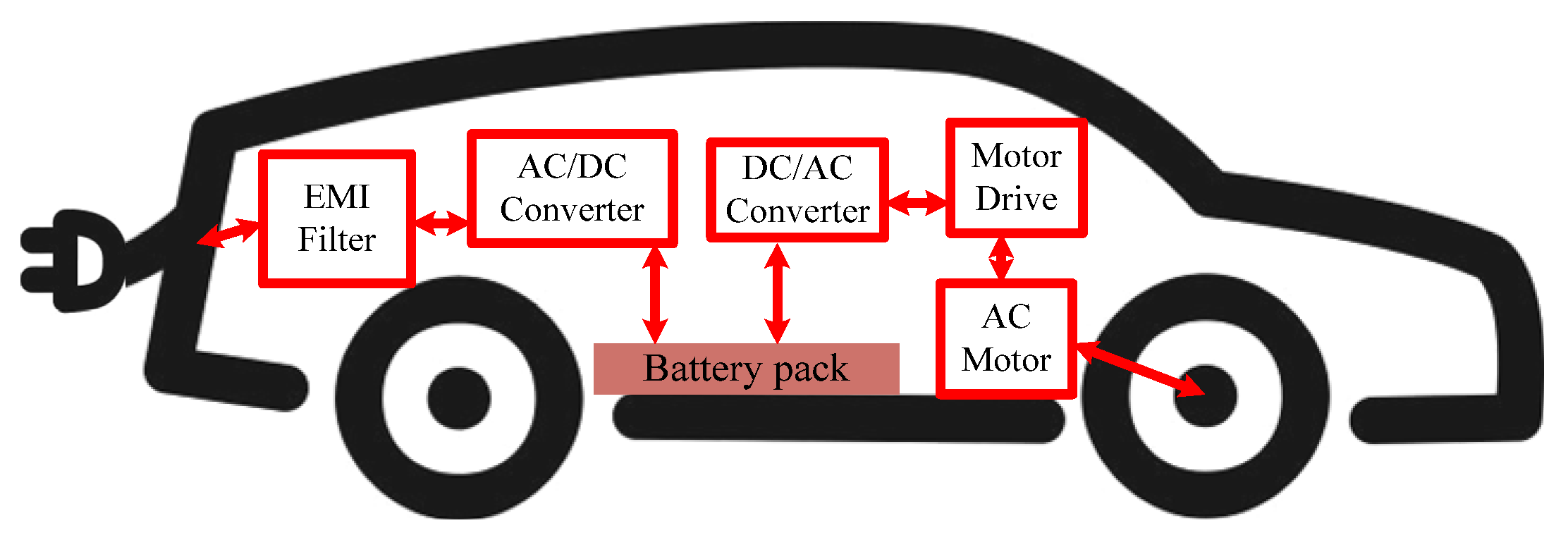
3. Decentralized EV Aggregator
4. Optimization Algorithm
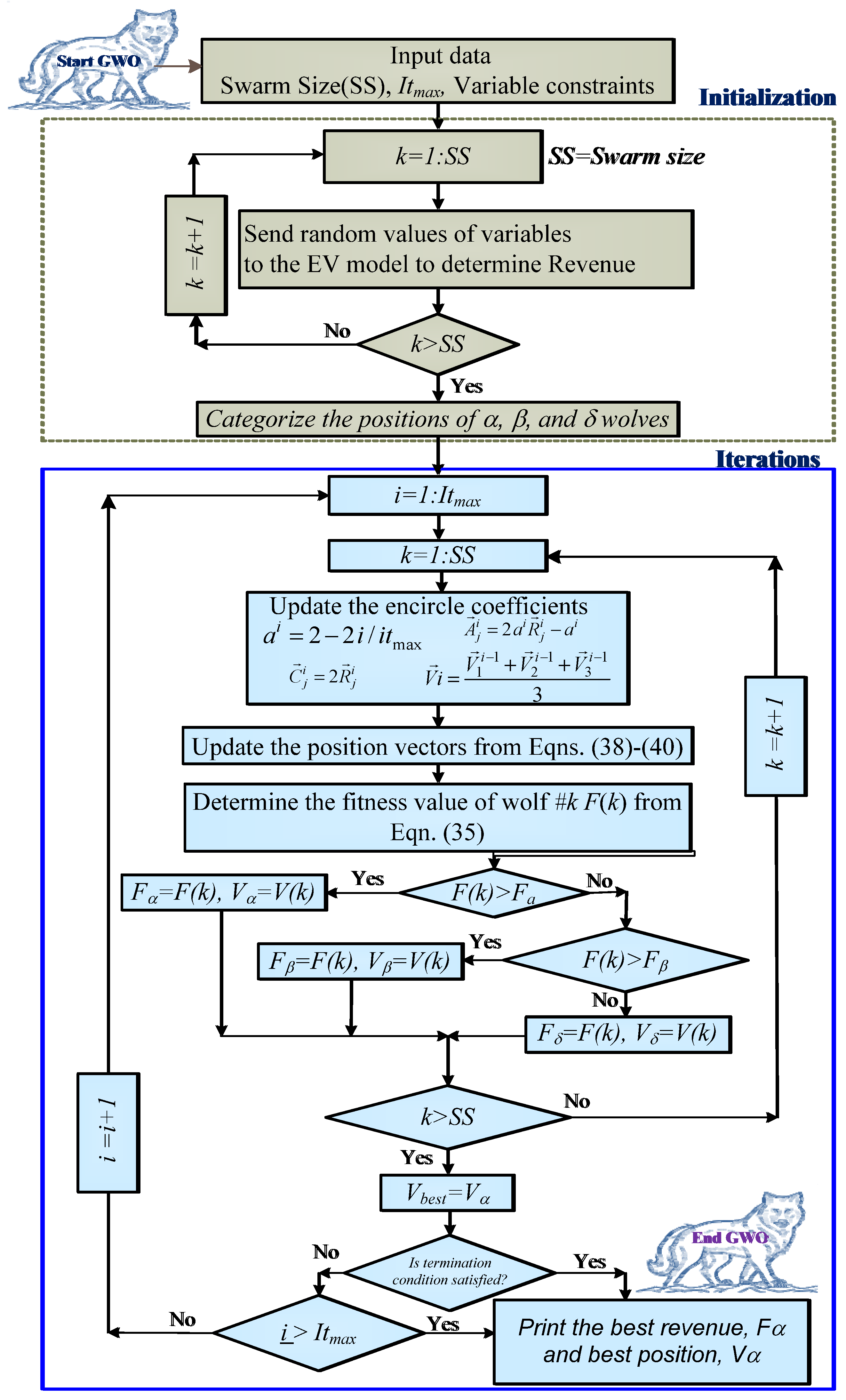
4.1. Standard Grey Wolf Optimization Algorithm
- Initialization: A population of wolves is randomly initialized inside the search space, taking into account the zero value for the trip time. Each wolf symbolizes the cyclic process of charging and discharging energy over 24 h.
- Assessment of fitness: The fitness of each wolf within the population must be evaluated using the objective function as shown in Equation (35). The fitness value corresponds to the total income generated during 24 h.
- Provide a current update on the spatial distribution of wolves: The objective of this analysis is to ascertain the spatial distribution of the alpha, beta, delta, and omega wolves following their respective fitness values. The optimal solution is denoted by the symbol alpha, which is thereafter followed by beta, delta, and omega, as shown by the given equations.
- Apply boundary constraints: several boundary conditions such as the zero charging/discharging power during the driving trip, the charge/discharge power, and the SoC are within the specified limits.
- Update the fitness values: the new position is applied to the objective function, and the fitness values for each wolf is obtained.
- Update the best solution: the alpha wolf position is updated, if a better solution is found than the previous one.
- Repeat steps 2–5: the steps are repeated until a termination criterion is met (e.g., the maximum number of iterations or reaching a satisfactory solution).
4.2. Novel Gradual Reduction of Swarm Size of GWO (GRSS-GWO)
5. Simulation Work
5.1. Simulation Software
5.2. Simulation Results
5.3. Battery Wear Parameters Estimation
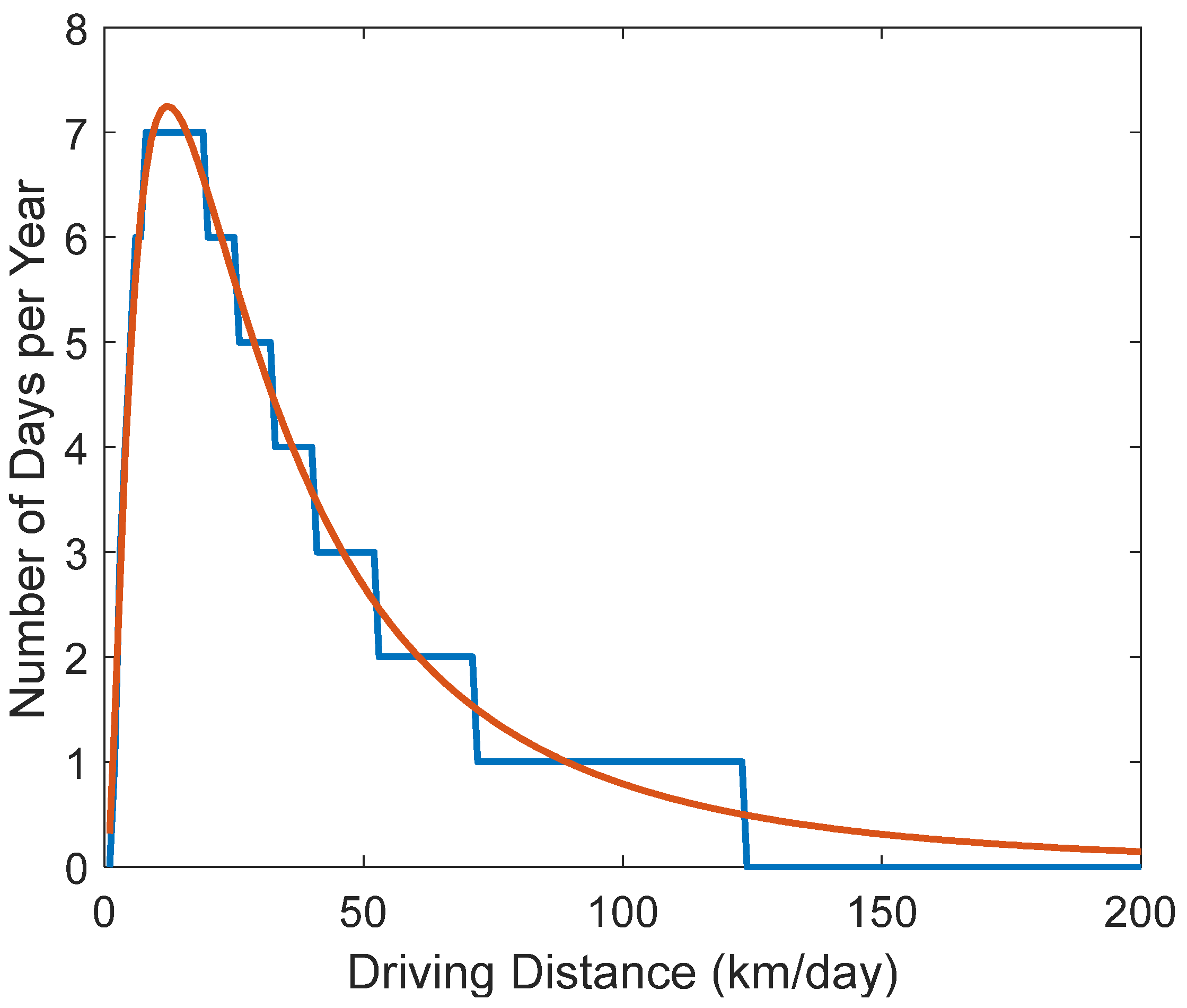
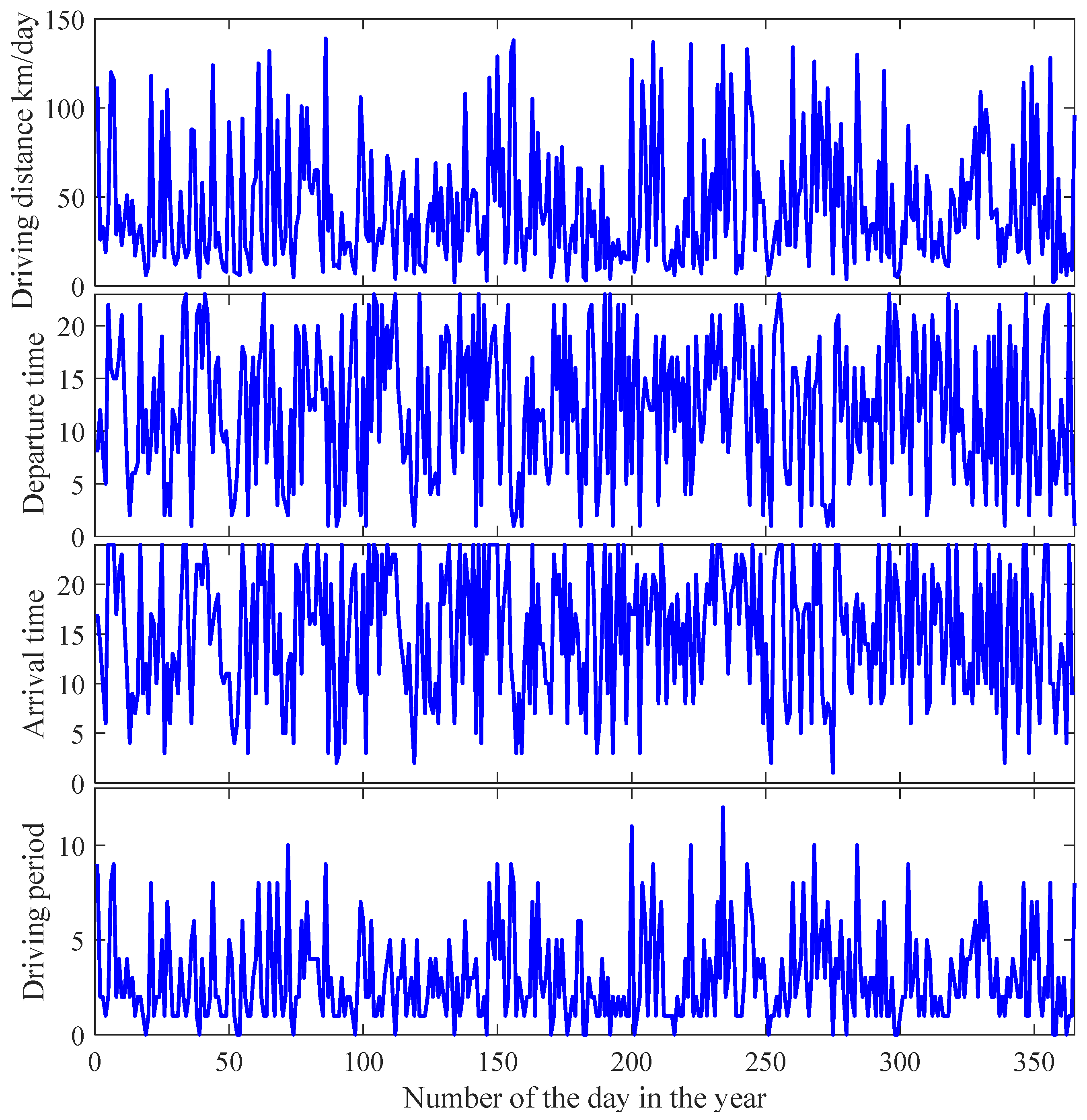
5.4. Scheduling the Random Trip Length and Departure and Arrival Times
- The EV takes only one trip each day.
- The energy consumption per hour is constant during the trip.
- The minimum SoC during the discharging is 0.3.
- The average speed during the trip is selected as constant, equal to 15 km/h.
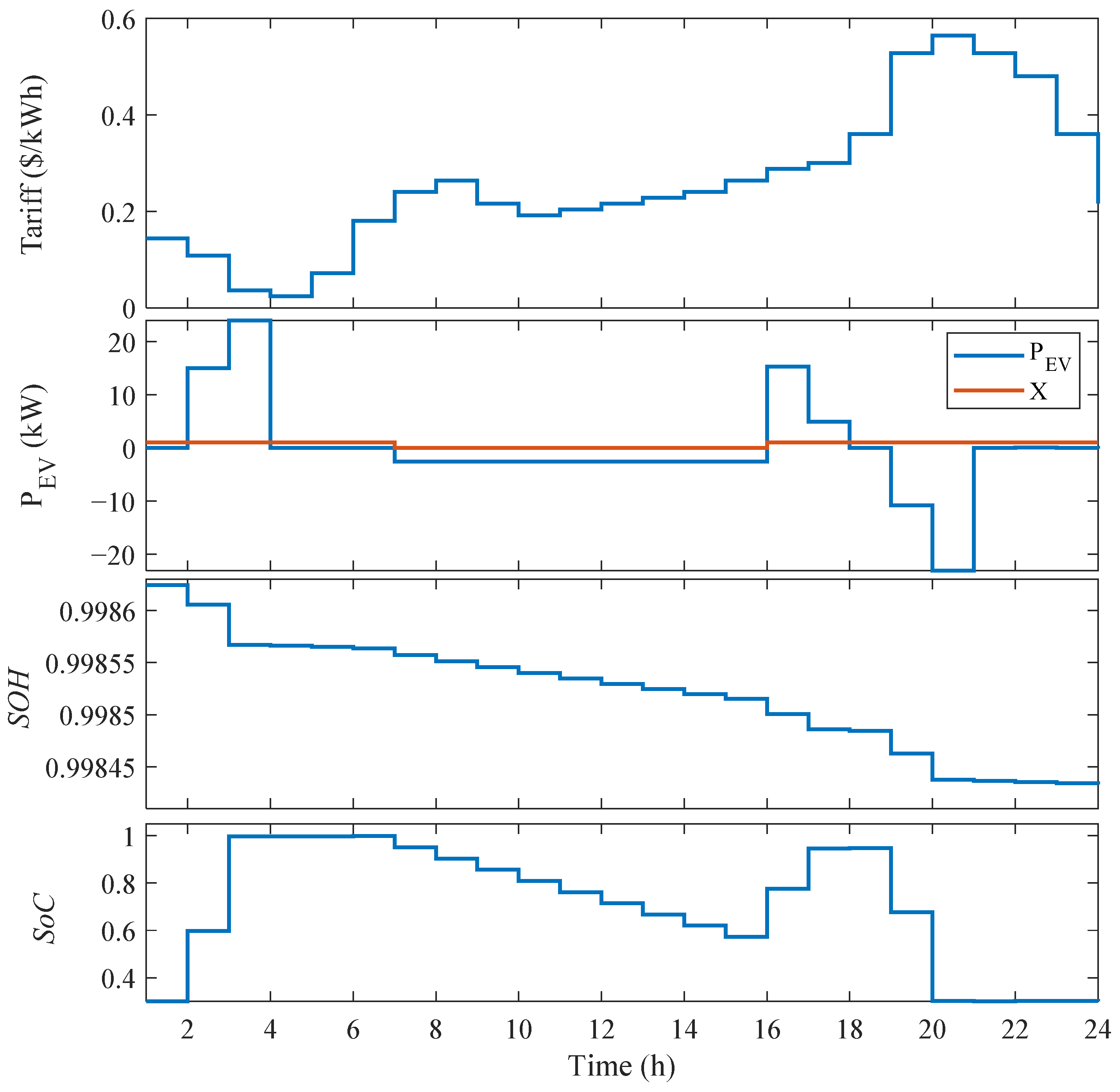
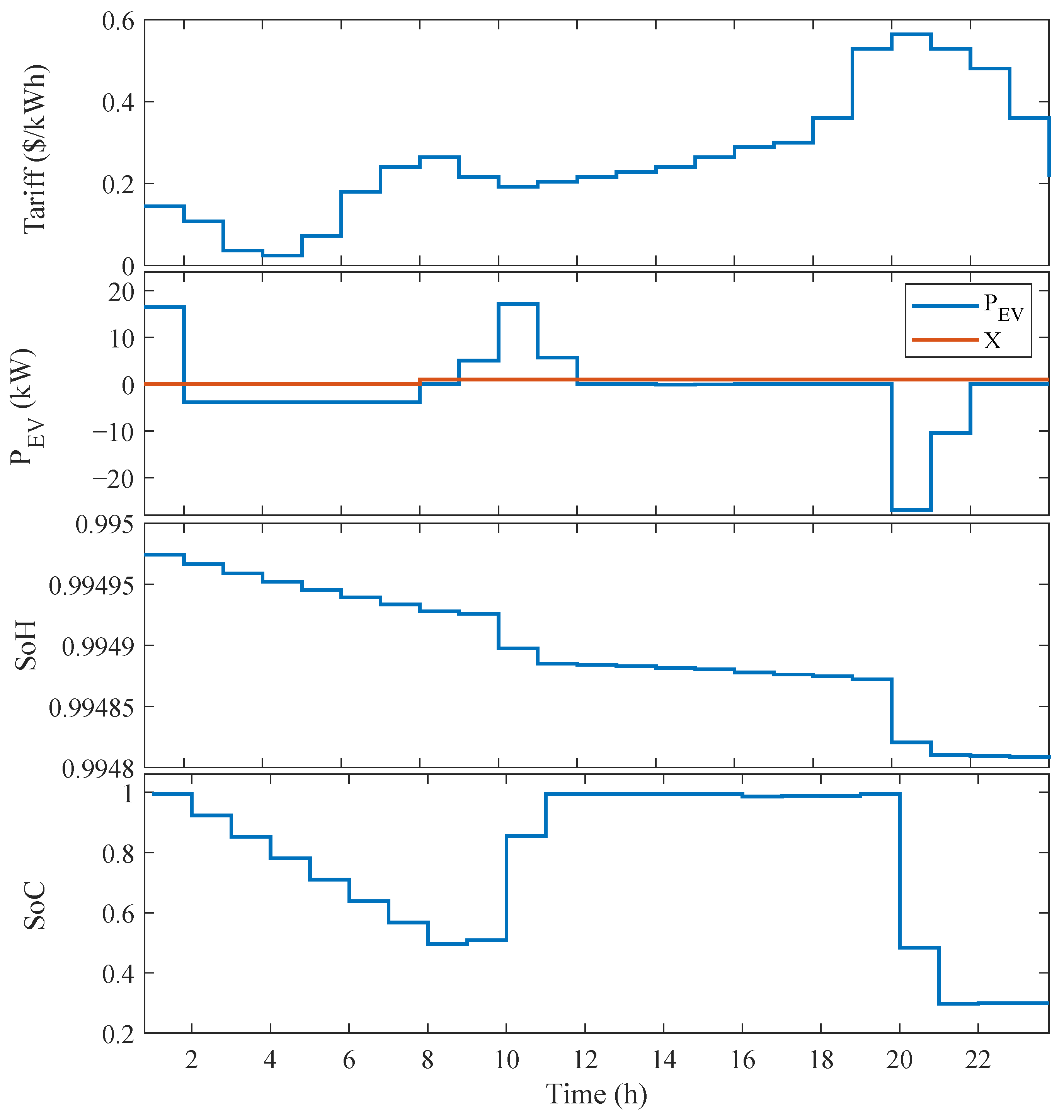
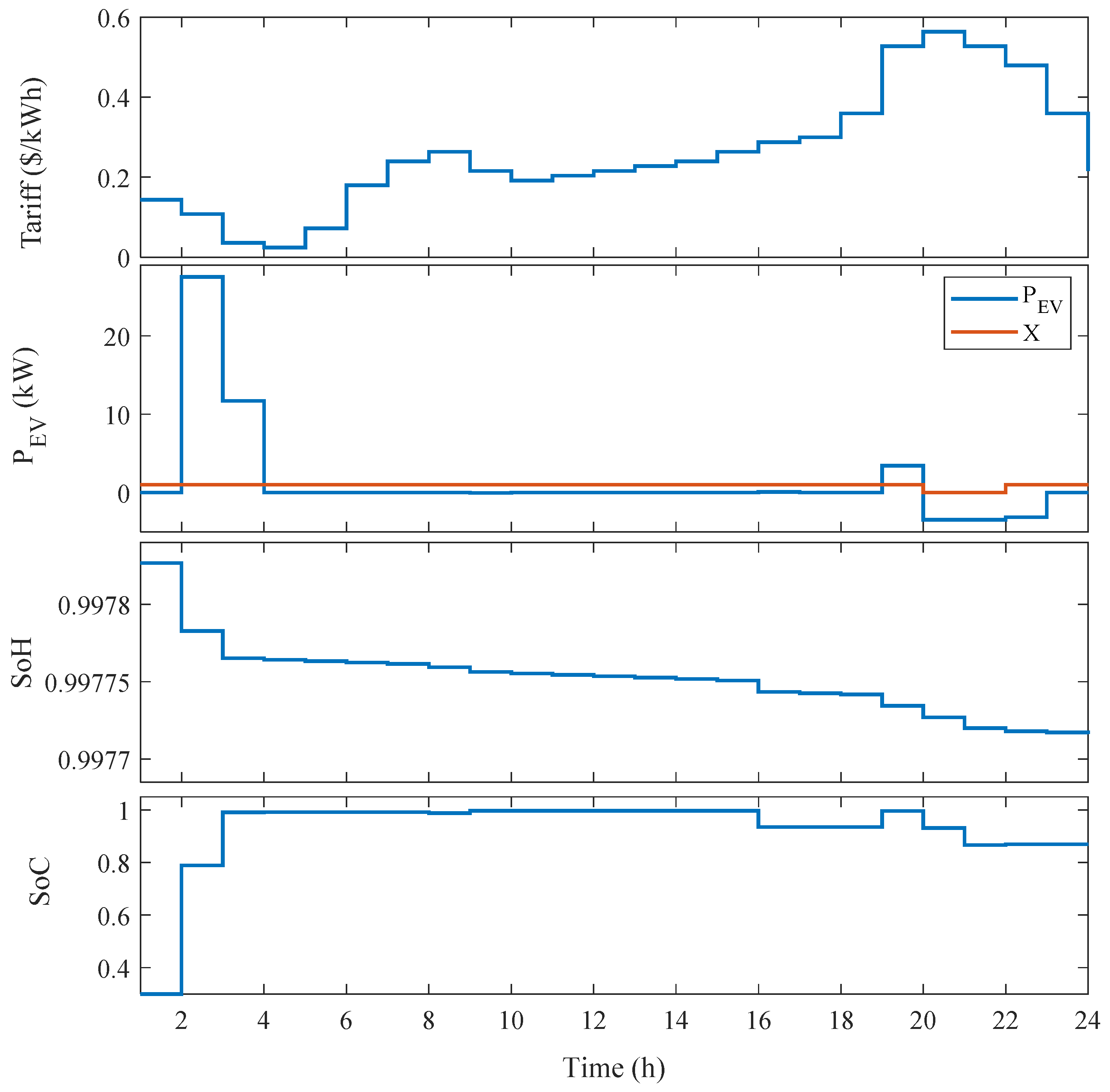
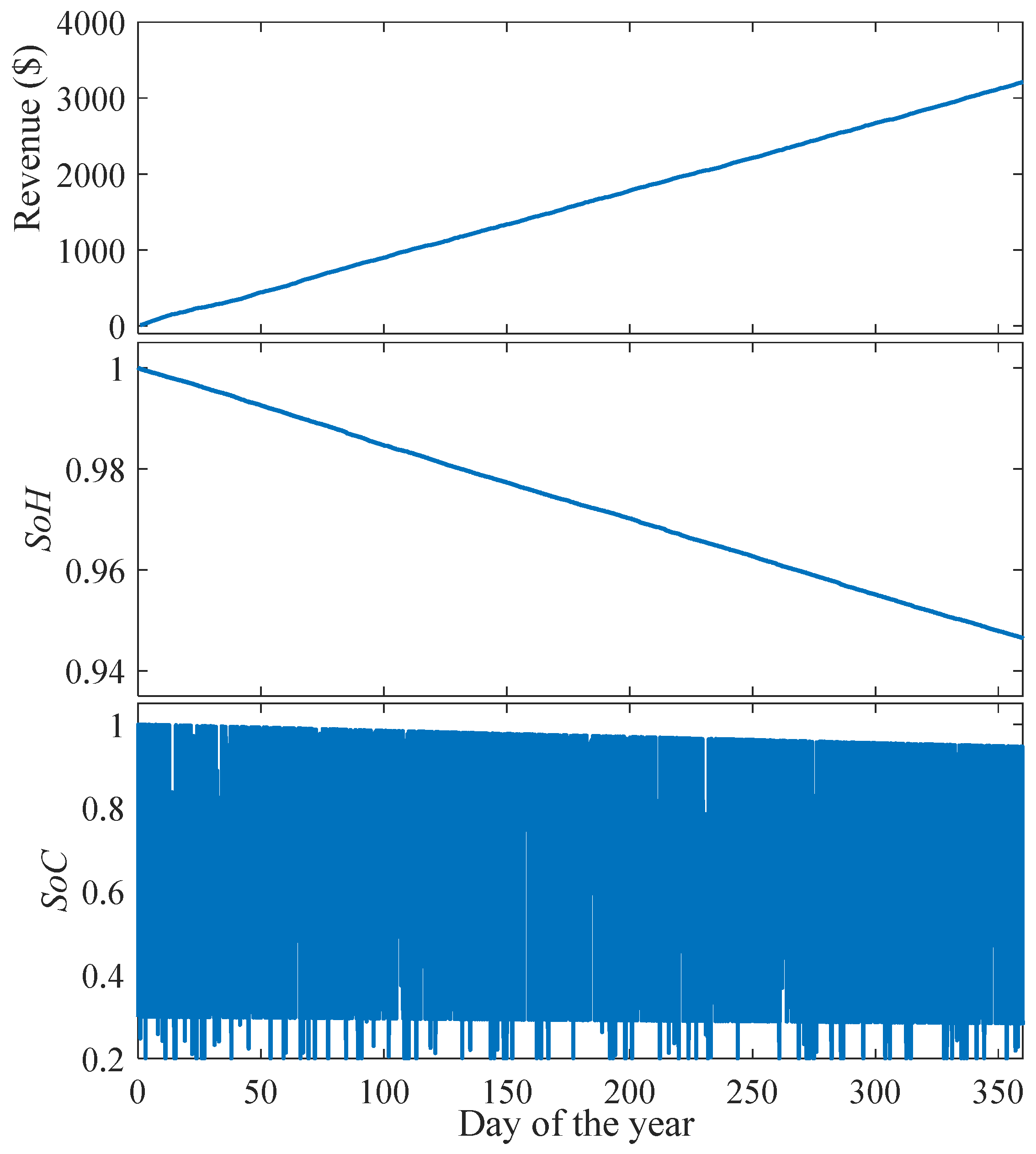
5.5. Results of Optimal Schedule of EV Aggregator
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
List of Symbols and Abbreviations
| Symbol | Definitions | Symbol | Definitions |
| V2G | vehicle-to-grid | Td | departure time |
| G2V | grid-to-vehicle | Tr | arrival time |
| EV | electric vehicle | uav | average EV speed |
| SoC, s | state of charge | PEV | the power of the battery |
| SoH | state of health | EEVD | energy of the driving period |
| DoD, D | depth of discharge | X | dispatch matrix |
| ESS | energy storage system | battery charging efficiency | |
| DSM | demand side management | battery discharging efficiency | |
| REDG | renewable energy distributed generator | σ | daily self-discharge |
| GWO | grey wolf optimization | EoL | end of life |
| GRSS | gradual reduction of swarm size | Cw | daily cost due to battery wear |
| LIB | lithium-ion battery | Cb | price of the new battery |
| Crate | current rate | C2nd | price of the second-life battery |
| ACC | achievable cycle count | daily V2G battery wear cost | |
| WDF | wear density function | daily driving battery wear cost | |
| Nc | number of cycles | daily battery wear charging cost | |
| a and b | battery specification parameters | daily calendar battery wear cost | |
| AWC | average wear cost | CC | daily total charging cost |
| battery efficiency | hourly tariff (USD/kWh) | ||
| Cb | total battery price | charging cost for V2G | |
| Ebr | battery rated capacity | Tch | charging time |
| TWC | total wear cost | daily revenue due to V2G | |
| Pb | battery power | battery SoC at the beginning of the trip | |
| R | ideal gas constant | required SoC at the beginning of the trip | |
| Ea | activation energy parameter | w1 | weight value |
| LAM | loss of active materials | PSO | particle swarm optimization |
| SEI | solid electrolyte interphase | CSA | cuckoo Search Algorithm |
| tu | rise time | BA | bat algorithm |
| W | battery wear | d | number of variables |
| Wcal | calendar battery wear | position of ariable j at iteration i | |
| Wcyc | cycling battery wear | random vector | |
| T | temperature | a | GWO control parameter |
| SoCmin | minimum SoC | itmax | maximum number of iterations |
| SoCmax | maximum SoC | F | objective function |
| SoCa | average SoC | Vbest | the position of the best wolf |
| RMSE | root mean square error | Fbest | fitness value of the best wolf |
| Wm | measured battery wear | Vworst | the position of the worst wolf |
| Wc | calculated battery wear | Fbest | fitness value of the worst wolf |
| nm | number of test points | SS | swarm size |
| fdes | distribution function | OMC | operating and maintenance cost |
| LEV | daily driving distance | μEV | variance of the daily distance of EV |
| σEV | average daily distance | βEV | specific power consumption |
| EEV | EV trip consumed energy |
References
- Ali, M.U.; Zafar, A.; Nengroo, S.H.; Hussain, S.; Junaid Alvi, M.; Kim, H.J. Towards a smarter battery management system for electric vehicle applications: A critical review of lithium-ion battery state of charge estimation. Energies 2019, 12, 446. [Google Scholar] [CrossRef]
- Gonzalez, I.; Calderón, A.J.; Folgado, F.J. IoT real time system for monitoring lithium-ion battery long-term operation in microgrids. J. Energy Storage 2022, 51, 104596. [Google Scholar] [CrossRef]
- Moulik, B.; Söffker, D. Battery Management System for Future Electric Vehicles. Appl. Sci. 2020, 10, 5095. [Google Scholar] [CrossRef]
- Damiano, A.; Gatto, G.; Marongiu, I.; Porru, M.; Serpi, A. Vehicle-to-grid technology—State-of-the-art and future scenarios. J. Energy Power Eng. 2014, 8, 152–165. [Google Scholar]
- Sortomme, E.; El-Sharkawi, M.A. Optimal combined bidding of vehicle-to-grid ancillary services. IEEE Trans. Smart Grid 2011, 3, 70–79. [Google Scholar] [CrossRef]
- Alotaibi, M.A.; Eltamaly, A.M. Upgrading conventional power system for accommodating electric vehicle through demand side management and V2G concepts. Energies 2022, 15, 6541. [Google Scholar] [CrossRef]
- Lopes, J.A.P.; Soares, F.J.; Almeida, P.M.R. Integration of electric vehicles in the electric power system. Proc. IEEE 2010, 99, 168–183. [Google Scholar] [CrossRef]
- Kempton, W.; Tomić, J. Vehicle-to-grid power fundamentals: Calculating capacity and net revenue. J. Power Sources 2005, 144, 268–279. [Google Scholar] [CrossRef]
- Fasugba, M.A.; Krein, P.T. Cost benefits and vehicle-to-grid regulation services of unidirectional charging of electric vehicles. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17 September 2011; pp. 827–834. [Google Scholar]
- Mwasilu, F.; Justo, J.J.; Kim, E.K.; Do, T.D.; Jung, J.W. Electric vehicles and smart grid interaction—A review on vehicle to grid and renewable energy sources integration. Renew. Sust. Energy Rev. 2014, 34, 501–516. [Google Scholar] [CrossRef]
- Mignoni, N.; Carli, R.; Dotoli, M. Distributed Noncooperative MPC for Energy Scheduling of Charging and Trading Electric Vehicles in Energy Communities. IEEE Trans. Control Syst. Technol. 2023, 31, 2159–2172. [Google Scholar] [CrossRef]
- Tushar, M.H.K.; Zeineddine, A.W.; Assi, C. Demand-side management by regulating charging and discharging of the EV, ESS, and utilizing renewable energy. IEEE Trans. Ind. Inform. 2017, 14, 117–126. [Google Scholar] [CrossRef]
- Sortomme, E.; El-Sharkawi, M.A. Optimal charging strategies for unidirectional vehicle-to-grid. IEEE Trans. Smart Grid 2010, 2, 131–138. [Google Scholar] [CrossRef]
- De Los Ríos, A.; Goentzel, J.; Nordstrom, K.E.; Siegert, C.W. Economic analysis of vehicle-to-grid (V2G)-enabled fleets participating in the regulation service market. In Proceedings of the 2012 IEEE PES Innovative Smart Grid Technologies (ISGT), Washington, DC, USA, 16–20 January 2012; pp. 1–8. [Google Scholar]
- Weiller, C. Plug-in hybrid electric vehicle impacts on hourly electricity demand in the united states. Energy Policy 2011, 39, 3766–3778. [Google Scholar] [CrossRef]
- Fernandez, L.P.; San Román, T.G.; Cossent, R.; Domingo, C.M.; Frias, P. Assessment of the impact of plug-in electric vehicles on distribution networks. IEEE Trans. Power Syst. 2010, 26, 206–213. [Google Scholar] [CrossRef]
- Vasirani, M.; Kota, R.; Cavalcante, R.L.G.; Ossowski, S.; Jennings, N.R. An agent-based approach to virtual power plants of wind power generators and electric vehicles. IEEE Trans. Smart Grid 2013, 4, 1314–1322. [Google Scholar] [CrossRef]
- Ma, Z.; Callaway, D.S.; Hiskens, I.A. Decentralized charging control of large populations of plug-in electric vehicles. IEEE Trans. Control Syst. Technol. 2011, 21, 67–78. [Google Scholar] [CrossRef]
- Kumar, K.N.; Sivaneasan, B.; Cheah, P.H.; So, P.L.; Wang, D.Z. V2G capacity estimation using dynamic EV scheduling. IEEE Trans. Smart Grid 2013, 5, 1051–1060. [Google Scholar] [CrossRef]
- Madzharov, D.; Delarue, E.; D’haeseleer, W. Integrating electric vehicles as flexible load in unit commitment modeling. Energy 2014, 65, 285–294. [Google Scholar] [CrossRef]
- Safdarian, F.; Ciftci, O.; Kargarian, A. A Time Decomposition and Coordination Strategy for Power System Multi-Interval Operation. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Tuttle, D.P.; Baldick, R. The evolution of plug-in electric vehicle-grid interactions. IEEE Trans. Smart Grid 2012, 3, 500–505. [Google Scholar] [CrossRef]
- Soares, J.; Morais, H.; Sousa, T.; Vale, Z.; Faria, P. Day-ahead scheduling including demand response for electric vehicles. IEEE Trans. Smart Grid 2013, 4, 596–605. [Google Scholar] [CrossRef]
- Kandpal, B.; Pareek, P.; Verma, A. A robust day-ahead scheduling strategy for EV charging stations in unbalanced distribution grid. Energy 2022, 249, 123737. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Alotaibi, M.A. Novel fuzzy-swarm optimization for sizing of hybrid energy systems applying smart grid concepts. IEEE Access 2021, 9, 93629–93650. [Google Scholar] [CrossRef]
- Safdarian, F.; Lamonte, L.; Kargarian, A.; Farasat, M. Distributed optimization-based hourly coordination for V2G and G2V. In Proceedings of the 2019 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 7–8 February 2019; pp. 1–6. [Google Scholar]
- Faria, A.S.B. A Chance-constrained Approach for Electric Vehicle Aggregator Participation in the Reserve Market. Doctoral Dissertation, Universidade do Porto, Porto, Portugal, 2019. [Google Scholar]
- Soman, S.S.; Zareipour, H.; Malik, O.; Mandal, P. A review of wind power and wind speed forecasting methods with different time horizons. In Proceedings of the North American Power Symposium (NAPS), Arlington, TX, USA, 26–28 September 2010; pp. 1–8. [Google Scholar]
- Shao, S.; Zhang, T.; Pipattanasomporn, M.; Rahman, S. Impact of TOU rates on distribution load shapes in a smart grid with PHEV penetration. In Proceedings of the IEEE PES T&D 2010, New Orleans, LA, USA, 19–22 April 2010; pp. 1–6. [Google Scholar]
- Cao, Y.; Tang, S.; Li, C.; Zhang, P.; Tan, Y.; Zhang, Z.; Li, J. An optimized EV charging model considering TOU price and SOC curve. IEEE Trans Smart Grid 2012, 3, 388–393. [Google Scholar] [CrossRef]
- Darabi, Z.; Ferdowsi, M. Aggregated impact of plug-in hybrid electric vehicles on electricity demand profile. Smart Power Grids 2012, 2011, 319–349. [Google Scholar] [CrossRef]
- Han, S.; Han, S.; Aki, H. A practical battery wear model for electric vehicle charging applications. Appl. Energy 2014, 113, 1100–1108. [Google Scholar] [CrossRef]
- Peterson, S.B.; Apt, J.; Whitacre, J.F. Lithium-ion battery cell degradation resulting from realistic vehicle and vehicle-to-grid utilization. J. Power Sources 2010, 195, 2385–2392. [Google Scholar] [CrossRef]
- Peterson, S.B.; Whitacre, J.F.; Apt, J. The economics of using plug-in hybrid electric vehicle battery packs for grid storage. J. Power Sources 2010, 195, 2377–2384. [Google Scholar] [CrossRef]
- Zhou, C.; Qian, K.; Allan, M.; Zhou, W. Modeling of the cost of EV battery wear due to V2G application in power systems. IEEE Trans. Energy Convers 2011, 26, 1041–1050. [Google Scholar] [CrossRef]
- Lödl, M.; Witzmann, R. Operation strategies of hybrid energy storages in low voltage distribution grids with a high degree of decentralized. In Proceedings of the 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Berlin, Germany, 14–17 October 2012; pp. 1–7. [Google Scholar]
- Bashash, S.; Moura, S.J.; Forman, J.C.; Fathy, H.K. Plug-in hybrid electric vehicle charge pattern optimization for energy cost and battery longevity. J. Power Sources 2011, 196, 541–549. [Google Scholar] [CrossRef]
- Hoke, A.; Brissette, A.; Maksimović, D.; Pratt, A.; Smith, K. Electric vehicle charge optimization including effects of lithium-ion battery degradation. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011; pp. 1–8. [Google Scholar]
- Eltamaly, A. A novel energy storage and demand side management for entire green smart grid system for NEOM city in Saudi Arabia. Energy Storage 2023, e515. [Google Scholar] [CrossRef]
- Almutairi, Z.A.; Eltamaly, A.M.; El Khereiji, A.; Al Nassar, A.; Al Rished, A.; Al Saheel, N.; Al Marqabi, A.; Al Hamad, S.; Al Harbi, M.; Sherif, R.; et al. Modeling and Experimental Determination of Lithium-Ion Battery Degradation in Hot Environment. In Proceedings of the 23rd International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 13–15 December 2022; pp. 1–8. [Google Scholar]
- Wang, J.; Purewal, J.; Liu, P.; Hicks-Garner, J.; Soukazian, S.; Sherman, E.; Sorenson, A.; Vu, L.; Tataria, H.; Verbrugge, M.W. Degradation of lithium ion batteries employing graphite negatives and nickel–cobalt–manganese oxide+ spinel manganese oxide positives: Part 1, aging mechanisms and life estimation. J. Power Sources 2014, 269, 937–948. [Google Scholar] [CrossRef]
- Thompson, A. Economic implications of lithium ion battery degradation for Vehicle-to-Grid (V2X) services. J. Power Sources 2018, 396, 691–709. [Google Scholar] [CrossRef]
- Franke-Lang, R.; Kowal, J. Electrochemical Model-Based Investigation of Thick LiFePO4 Electrode Design Parameters. Modelling 2021, 2, 259–287. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Sources 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- Zhu, L.; He, J.; He, L.; Huang, W.; Wang, Y.; Liu, Z. Optimal Operation Strategy of PV-Charging-Hydrogenation Composite Energy Station Considering Demand Response. Energies 2022, 15, 5915. [Google Scholar] [CrossRef]
- Venkatapathy, K.; Tazelaar, E.; Veenhuizen, B. A systematic identification of first to second life shift-point of lithium-ion batteries. In Proceedings of the 2015 IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19–22 October 2015; pp. 1–4. [Google Scholar]
- Rohr, S.; Wagner, S.; Baumann, M.; Müller, S.; Lienkamp, M. A techno-economic analysis of end of life value chains for lithium-ion batteries from electric vehicles. In Proceedings of the 2017 Twelfth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 11–13 April 2017; pp. 1–14. [Google Scholar]
- Eltamaly, A.M.; Farh, H.M.; Abokhalil, A.G. A novel PSO strategy for improving dynamic change partial shading photovoltaic maximum power point tracker. Energy Sources Part A Recovery Util. Environ. Eff. 2020, 1–15. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer0. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Eltamaly, A.M. An improved cuckoo search algorithm for maximum power point tracking of photovoltaic systems under partial shading conditions. Energies 2021, 14, 953. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Musical chairs algorithm for parameters estimation of PV cells. Sol. Energy 2022, 241, 601–620. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Al-Saud, M.S.; Abokhalil, A.G. A novel scanning bat algorithm strategy for maximum power point tracker of partially shaded photovoltaic energy systems. Ain Shams Eng. J. 2020, 11, 1093–1103. [Google Scholar] [CrossRef]
- Carli, R.; Dotoli, M. A distributed control algorithm for waterfilling of networked control systems via consensus. IEEE Control Syst. Lett. 2017, 1, 334–339. [Google Scholar] [CrossRef]
- Rabie, A.H.; Eltamaly, A.M. A new NEST-IGWO strategy for determining optimal IGWO control parameters. Neural Comput. Appl. 2023, 35, 15143–15165. [Google Scholar] [CrossRef]
- Wen, L. Grey Wolf Optimizer based on Nonlinear Adjustment Control Parameter. In Proceedings of the 4th International Conference on Sensors, Mechatronics and Automation (ICSMA 2016), Zhuhai, China, 12–13 November 2016; Volume 136, pp. 643–648. [Google Scholar]
- Gao, Z.; Zhao, J. An Improved Grey Wolf Optimization Algorithm with Variable Weights. Comput. Intell. Neurosci. 2019, 2019, 2981282. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Oudalov, A.; Ulbig, A.; Andersson, G.; Kirschen, D.S. Modeling of lithium-ion battery degradation for cell life assessment. IEEE Trans. Smart Grid 2018, 9, 1131–1140. [Google Scholar] [CrossRef]





| Item | Value |
|---|---|
| No. of modules | 24 |
| Module capacity | 2.4 kWh |
| Battery price Cb | $140/kWh |
| 2nd life battery price | $60/kWh |
| OMC | $0.1/kWh/year |
| 0.95 | |
| σ | 0.01% |
| Items | GRSS-GWO | GWO | PSO | BA |
|---|---|---|---|---|
| Convergence time (s) | 0.213 441 117 | 0.821 158 456 | 0.978 254 151 | 1.149 123 715 |
| RMSE (%) | 0.001 951 035 | 0.002 113 658 | 0.002 121 756 | 0.002 243 674 |
| A1 | 472.701 163 681 | 470.414 149 675 | 470.405 579 729 | 470.398 767 233 |
| B1 | −2.069 836 312 | −2.060 865 899 | −2.058 069 457 | −2.057 654 982 |
| C1 | −6316.876 455 349 | −6269.356 878 725 | −6270.556 534 254 | −6270.129 739 985 |
| D1 | 0.576 031 765 | 0.576 901 653 | 0.576 713 898 | 0.576 797 138 |
| A2 | 26.055 099 431 | 26.163 873 352 | 25.993 877 910 | 26.106 763 973 |
| B2 | 2.688 801 914 | 2.690 645 631 | 2.687 945 918 | 2.691 875 219 |
| C2 | −2102.375 825 405 | −2101.912 746 436 | −2102.534 674 362 | −2102.439 726 652 |
| D2 | 0.520 987 158 | 0.521 812 028 | 0.521 736 832 | 0.521 052 637 |
| Items | Dumb Charge | V2G |
|---|---|---|
| Yearly wear (%) | 2.55 | 5.34 |
| Battery life time (year) | 7.8431 | 3.7453 |
| Yearly charging cost ($) | 904.6 | 765.4 |
| Yearly wear cost ($) | 587.5 | 1230.3 |
| Total yearly cost ($) | 1492.1 | 1995.7 |
| Income due to V2G ($) | - | 5240.7 |
| Yearly revenue ($) | - | 3245 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eltamaly, A.M. Optimal Dispatch Strategy for Electric Vehicles in V2G Applications. Smart Cities 2023, 6, 3161-3191. https://doi.org/10.3390/smartcities6060141
Eltamaly AM. Optimal Dispatch Strategy for Electric Vehicles in V2G Applications. Smart Cities. 2023; 6(6):3161-3191. https://doi.org/10.3390/smartcities6060141
Chicago/Turabian StyleEltamaly, Ali M. 2023. "Optimal Dispatch Strategy for Electric Vehicles in V2G Applications" Smart Cities 6, no. 6: 3161-3191. https://doi.org/10.3390/smartcities6060141
APA StyleEltamaly, A. M. (2023). Optimal Dispatch Strategy for Electric Vehicles in V2G Applications. Smart Cities, 6(6), 3161-3191. https://doi.org/10.3390/smartcities6060141







