Cumulatively Anticipative Car-Following Model with Enhanced Safety for Autonomous Vehicles in Mixed Driver Environments
Abstract
:1. Introduction
2. Methodology
3. Results Evaluating the CACF Model Using Micro-Simulation
3.1. Model Setup in VISSIM
3.2. Integration of SSAM into VISSIM
4. Results and Discussion
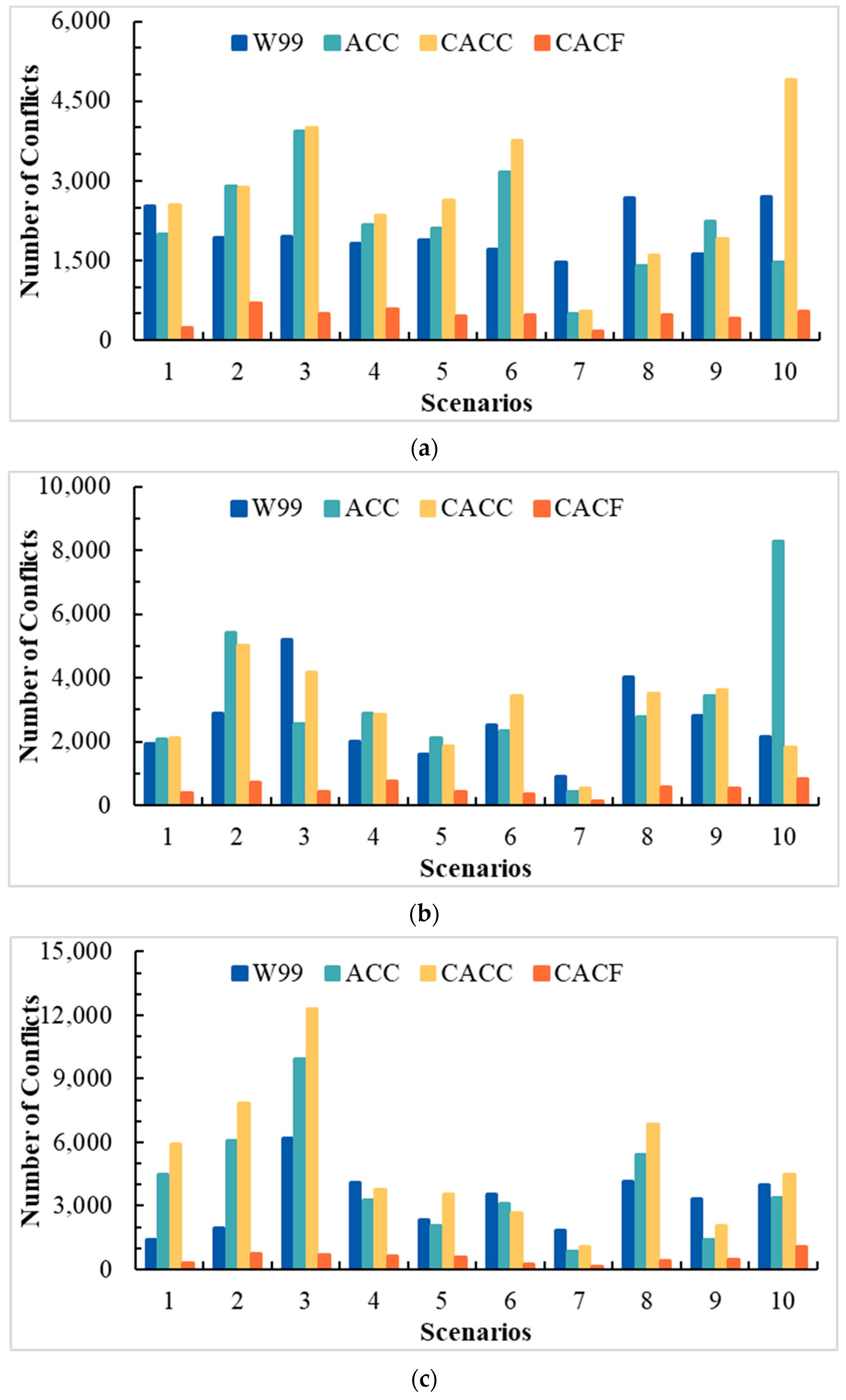
4.1. Evaluating the Safety of the Models in the Case Study
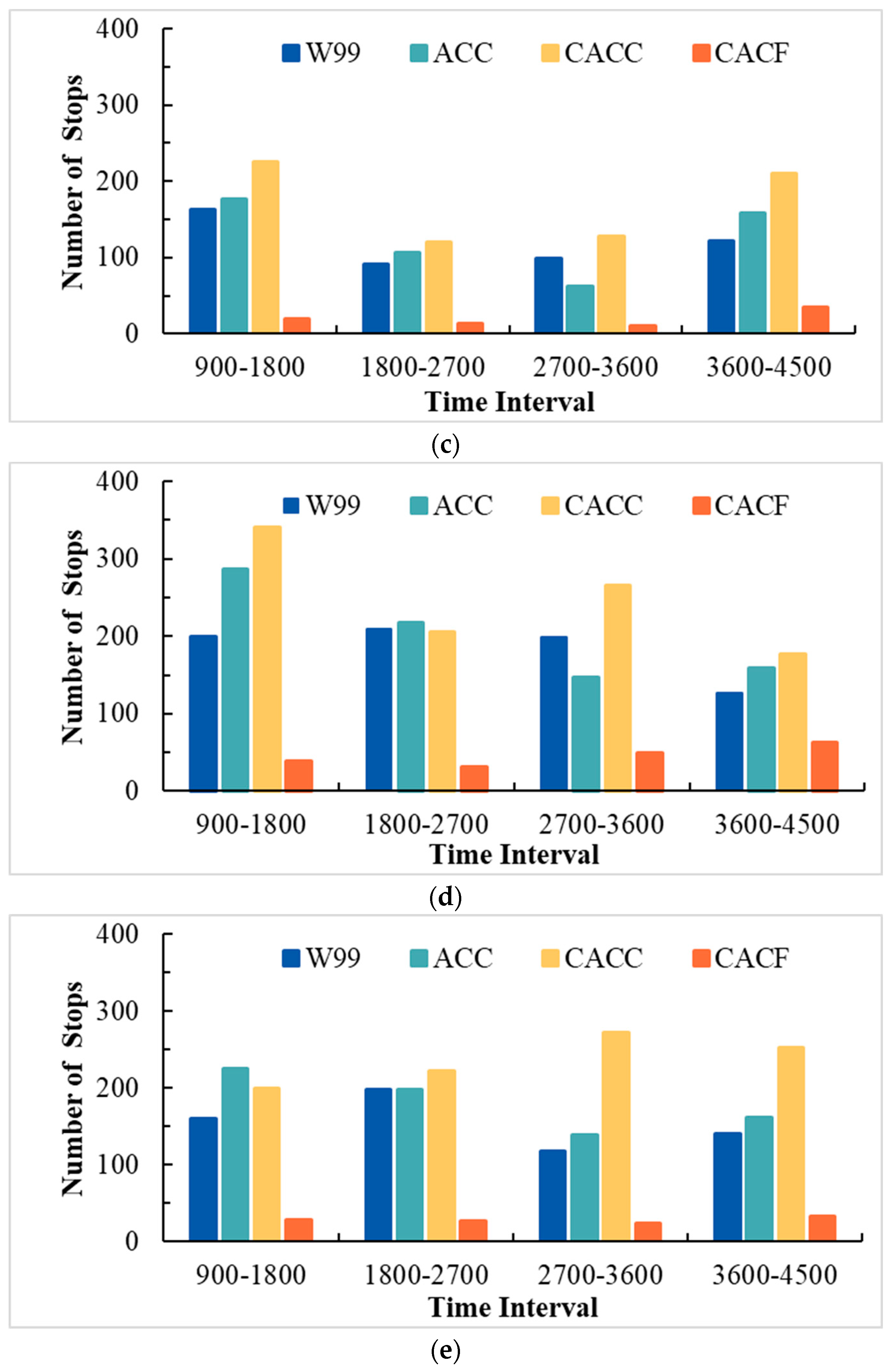
4.2. Evaluating the Mobility of the Models in the Case Study
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Full Name |
| AV | autonomous vehicle |
| ACC | adaptive cruise control |
| CACC | cooperative adaptive cruise control |
| CACF | cumulatively anticipative car-following |
| MACF | multi-anticipative car following |
| OVM | optimal velocity model |
| W99 | Wiedemann 99 |
| V2V | vehicle-to-vehicle |
| V2I | vehicle-to-infrastructure |
| V2X | vehicle-to-everything |
| VISSIM | Verkehr In Städten—SIMulationsmodell |
| PTV | Planung Transport Verkehr |
| SSAM | surrogate safety assessment model |
| COM | component object model |
| DLL | dynamic link library |
| GUI | graphical user interface |
| PET | post encroachment time |
| TTC | time-to-collision |
Appendix A
| Length | |
| length of previous vehicle () | |
| Coordinate | |
| coordinate of the ego vehicle | |
| coordinate of the previous vehicle | |
| Headway | |
| headway of previous vehicle ( and ) | |
| headway of ego vehicle and previous vehicle | |
| headway of ego vehicle and previous vehicle () | |
| headway time of ego vehicle, equal to , because ego vehicle is AV | |
| headway time of previous vehicle () | |
| Distance | |
| predicted desired distance between previous vehicle ( and ) | |
| predicted real distance between previous vehicle ( and ) | |
| safe distance of ego vehicle | |
| safe distance between previous vehicle ( and ) | |
| distance between ego vehicle and its previous vehicle (9th vehicle), | |
| distance between previous vehicle and () | |
| desired distance between ego vehicle and its previous vehicle | |
| Velocity | |
| velocity difference between ego vehicle and previous vehicle () | |
| velocity of ego vehicle | |
| velocity of previous vehicle () | |
| desired velocity of ego vehicle | |
| desired velocity of vehicle () | |
| Acceleration | |
| acceleration of ego vehicle | |
| acceleration of previous vehicle () | |
| desired acceleration of ego vehicle, this value only works when there is no preceding reference vehicle | |
| desired acceleration of previous vehicle () | |
| emergency acceleration of previous vehicle , calculate value for the emergency condition where distance between two vehicles is less than | |
| optimal acceleration of ego vehicle, the final result | |
| Type | |
| type of previous vehicle | |
| Parameter | |
| standstill distance, set as 1.5 | |
| headway time, set as 0.5 | |
| minimum acceleration, set as −3 | |
| maximum acceleration, set as 2 | |
| constant factor set as 1.0, 0.58, 0.1 | |
| Constant factor | |
| sensitivity coefficients of a driver to the difference between the th and the th velocities | |
| Constant factors defining the network uncertainties for predicted distance and desired acceleration, equal to 0 or 1 |
Appendix B
- Input: the information come from PTV VISSIM external driver model DLL and the constant factor of the model {}
- Output: optimal acceleration of ego vehicle ()
References
- Sae International Taxonomy and Definitions for Terms Related to Driving Automation Systems for On-Road Motor Vehicles. SAE Int. 2018, 4970, 1–5. [CrossRef]
- Tang, Q.; Dagley, G.; Ghamsari, A.; Price, M.; Hoover, J. Automatic Vehicle Configuration Based on Sensor Data. U.S. Patent 10,525,850, 7 January 2020. [Google Scholar]
- Harlow, C.; Peng, S. Automatic Vehicle Classification System with Range Sensors. Transp. Res. Part C Emerg. Technol. 2001, 9, 231–247. [Google Scholar] [CrossRef]
- Wu, J.; Xu, H.; Tian, Y.; Zhang, Y.; Zhao, J.; Lv, B. An Automatic Lane Identification Method for the Roadside Light Detection and Ranging Sensor. J. Intell. Transp. Syst. 2020, 24, 467–479. [Google Scholar] [CrossRef]
- Younsi, M.; Diaf, M.; Siarry, P. Automatic Multiple Moving Humans Detection and Tracking in Image Sequences Taken from a Stationary Thermal Infrared Camera. Expert Syst. Appl. 2020, 146, 113171. [Google Scholar] [CrossRef]
- Hollands, R.G. Will the Real Smart City Please Stand up? City 2008, 12, 303–320. [Google Scholar] [CrossRef]
- Maglaras, L.A.; Al-Bayatti, A.H.; He, Y.; Wagner, I.; Janicke, H. Social Internet of Vehicles for Smart Cities. J. Sens. Actuator Netw. 2016, 5, 3. [Google Scholar] [CrossRef]
- Aghabayk, K.; Sarvi, M.; Young, W. A State-of-the-Art Review of Car-Following Models with Particular Considerations of Heavy Vehicles. Transp. Rev. 2015, 35, 82–105. [Google Scholar] [CrossRef]
- Brackstone, M.; McDonald, M. Car-Following: A Historical Review. Transp. Res. Part F Traffic Psychol. Behav. 1999, 2, 181–196. [Google Scholar] [CrossRef]
- Chen, J.; Liu, R.; Ngoduy, D.; Shi, Z. A New Multi-Anticipative Car-Following Model with Consideration of the Desired Following Distance. Nonlinear Dyn. 2016, 85, 2705–2717. [Google Scholar] [CrossRef]
- Jin, S.; Wang, D.-H.; Huang, Z.-Y.; Tao, P.-F. Visual Angle Model for Car-Following Theory. Phys. A Stat. Mech. Its Appl. 2011, 390, 1931–1940. [Google Scholar] [CrossRef]
- Dian-Hai, W.; Sheng, J. Review and Outlook of Modeling of Car Following Behavior. China J. Highw. Transp. 2012, 25, 115. [Google Scholar]
- VanderWerf, J.; Shladover, S.; Kourjanskaia, N.; Miller, M.; Krishnan, H. Modeling Effects of Driver Control Assistance Systems on Traffic. Transp. Res. Rec. 2001, 1748, 167–174. [Google Scholar] [CrossRef]
- Li, S.; Li, K.; Rajamani, R.; Wang, J. Model Predictive Multi-Objective Vehicular Adaptive Cruise Control. IEEE Trans. Control. Syst. Technol. 2010, 19, 556–566. [Google Scholar] [CrossRef]
- Stanton, N.A.; Young, M.S. Driver Behaviour with Adaptive Cruise Control. Ergonomics 2005, 48, 1294–1313. [Google Scholar] [CrossRef] [PubMed]
- Van Arem, B.; Van Driel, C.J.; Visser, R. The Impact of Cooperative Adaptive Cruise Control on Traffic-Flow Characteristics. IEEE Trans. Intell. Transp. Syst. 2006, 7, 429–436. [Google Scholar] [CrossRef]
- Zhao, L.; Sun, J. Simulation Framework for Vehicle Platooning and Car-Following Behaviors under Connected-Vehicle Environment. Procedia-Soc. Behav. Sci. 2013, 96, 914–924. [Google Scholar] [CrossRef]
- Milanés, V.; Shladover, S.E.; Spring, J.; Nowakowski, C.; Kawazoe, H.; Nakamura, M. Cooperative Adaptive Cruise Control in Real Traffic Situations. IEEE Trans. Intell. Transp. Syst. 2013, 15, 296–305. [Google Scholar] [CrossRef]
- Sengupta, R.; Rezaei, S.; Shladover, S.E.; Cody, D.; Dickey, S.; Krishnan, H. Cooperative Collision Warning Systems: Concept Definition and Experimental Implementation. J. Intell. Transp. Syst. 2007, 11, 143–155. [Google Scholar] [CrossRef]
- Shladover, S.E.; Nowakowski, C.; Lu, X.-Y.; Ferlis, R. Cooperative Adaptive Cruise Control: Definitions and Operating Concepts. Transp. Res. Rec. 2015, 2489, 145–152. [Google Scholar] [CrossRef]
- Vander Werf, J.; Shladover, S.E.; Miller, M.A.; Kourjanskaia, N. Effects of Adaptive Cruise Control Systems on Highway Traffic Flow Capacity. Transp. Res. Rec. 2002, 1800, 78–84. [Google Scholar] [CrossRef]
- Xiao, L.; Gao, F. A Comprehensive Review of the Development of Adaptive Cruise Control Systems. Veh. Syst. Dyn. 2010, 48, 1167–1192. [Google Scholar] [CrossRef]
- Bando, M.; Hasebe, K.; Nakayama, A.; Shibata, A.; Sugiyama, Y. Dynamical Model of Traffic Congestion and Numerical Simulation. Phys. Rev. E 1995, 51, 1035. [Google Scholar] [CrossRef] [PubMed]
- Cheng, R.; Ge, H.; Wang, J. An Improved Continuum Model for Traffic Flow Considering Driver’s Memory during a Period of Time and Numerical Tests. Phys. Lett. A 2017, 381, 2792–2800. [Google Scholar] [CrossRef]
- Helbing, D.; Tilch, B. Generalized Force Model of Traffic Dynamics. Phys. Rev. E 1998, 58, 133. [Google Scholar] [CrossRef]
- Lenz, H.; Wagner, C.; Sollacher, R. Multi-Anticipative Car-Following Model. Eur. Phys. J. B-Condens. Matter Complex Syst. 1999, 7, 331–335. [Google Scholar] [CrossRef]
- Chen, S.; Hu, J.; Shi, Y.; Peng, Y.; Fang, J.; Zhao, R.; Zhao, L. Vehicle-to-Everything (V2X) Services Supported by LTE-Based Systems and 5G. IEEE Commun. Stand. Mag. 2017, 1, 70–76. [Google Scholar] [CrossRef]
- Gupta, M.; Benson, J.; Patwa, F.; Sandhu, R. Secure V2V and V2I Communication in Intelligent Transportation Using Cloudlets. IEEE Trans. Serv. Comput. 2020, 15, 1912–1925. [Google Scholar] [CrossRef]
- Milanés, V.; Villagrá, J.; Godoy, J.; Simó, J.; Pérez, J.; Onieva, E. An Intelligent V2I-Based Traffic Management System. IEEE Trans. Intell. Transp. Syst. 2012, 13, 49–58. [Google Scholar] [CrossRef]
- Bagheri, M.; Siekkinen, M.; Nurminen, J.K. Cellular-Based Vehicle to Pedestrian (V2P) Adaptive Communication for Collision Avoidance. In Proceedings of the 2014 International Conference on Connected Vehicles and Expo (ICCVE), Vienna, Austria, 3–7 November 2014; pp. 450–456. [Google Scholar]
- Saeed, U.; Hämäläinen, J.; Mutafungwa, E.; Wichman, R.; González, D.; Garcia-Lozano, M. Route-Based Radio Coverage Analysis of Cellular Network Deployments for V2N Communication. In Proceedings of the 2019 International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Barcelona, Spain, 21–23 October 2019; pp. 1–6. [Google Scholar]
- Broggi, A.; Cappalunga, A.; Caraffi, C.; Cattani, S.; Ghidoni, S.; Grisleri, P.; Porta, P.P.; Posterli, M.; Zani, P.; Beck, J. The Passive Sensing Suite of the TerraMax Autonomous Vehicle. In Proceedings of the 2008 IEEE Intelligent Vehicles Symposium, Eindhoven, Netherlands, 4–6 June 2008; pp. 769–774. [Google Scholar]
- Park, S.; Kim, Y.; Matson, E.T.; Smith, A.H. Accessible Synthetic Aperture Radar System for Autonomous Vehicle Sensing. In Proceedings of the 2016 IEEE Sensors Applications Symposium (SAS), Catania, Italy, 20–22 April 2016; pp. 1–6. [Google Scholar]
- Van Arem, B.; De Vos, A.; Vanderschuren, M.J.W.A. The Microscopic Traffic Simulation Model MIXIC 1.3. 1997. Available online: https://trid.trb.org/view/634929 (accessed on 11 July 2023).
- Abou-Senna, H.; Abdel-Aty, M.; Wu, J.; Darius, B. MRI-2: Integrated Simulation and Safety; Technical Report; University of Central Florida: Orlando, FL, USA, 2015. [Google Scholar]
- Huang, F.; Liu, P.; Yu, H.; Wang, W. Identifying If VISSIM Simulation Model and SSAM Provide Reasonable Estimates for Field Measured Traffic Conflicts at Signalized Intersections. Accid. Anal. Prev. 2013, 50, 1014–1024. [Google Scholar] [CrossRef]
- Tettamanti, T.; Varga, I. Development of Road Traffic Control by Using Integrated VISSIM-MATLAB Simulation Environment. Period. Polytech. Civ. Eng. 2012, 56, 43–49. [Google Scholar] [CrossRef]
- PTV Group. PTV Vissim 2020 User Manual; PTV Group: Karlsruhe, Germany, 2020; p. 1278. [Google Scholar]
- Dowling, R.; Skabardonis, A.; Alexiadis, V. Traffic Analysis Toolbox, Volume III: Guidelines for Applying Traffic Microsimulation Modeling Software; Federal Highway Administration. Office of Operations: Washington, DC, USA, 2004. [Google Scholar]
- Wiegand, J.D.; Yang, C. Traffic Simulation Runs: How Many Needed? Public Roads 2011, 74, 30–35. [Google Scholar]
- Fyfe, M.R. Safety Evaluation of Connected Vehicle Applications Using Micro-Simulation. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, 2016. [Google Scholar]
- Chin, H.-C.; Quek, S.-T. Measurement of Traffic Conflicts. Saf. Sci. 1997, 26, 169–185. [Google Scholar] [CrossRef]
- Pu, L.; Joshi, R.; Energy, S. Surrogate Safety Assessment Model (SSAM)—Software User Manual; Turner-Fairbank Highway Research Center: McLean, VA, USA, 2008. [Google Scholar]
- Das, P. Risk Analysis of Autonomous Vehicle and Its Safety Impact on Mixed Traffic Stream; Rowan University: Glassboro, NJ, UDA, 2018; ISBN 0-355-87574-8. [Google Scholar]
- Hayward, J.C. Near Miss Determination through Use of a Scale of Danger. Transp. Res. Rec. 1972, 384, 24–34. [Google Scholar]
- Lee, D.N. A Theory of Visual Control of Braking Based on Information about Time-to-Collision. Perception 1976, 5, 437–459. [Google Scholar] [CrossRef] [PubMed]
- Manual, H.C. Highway Capacity Manual; Transportation Research Board: Washington, DC, USA, 2000; Volume 2. [Google Scholar]


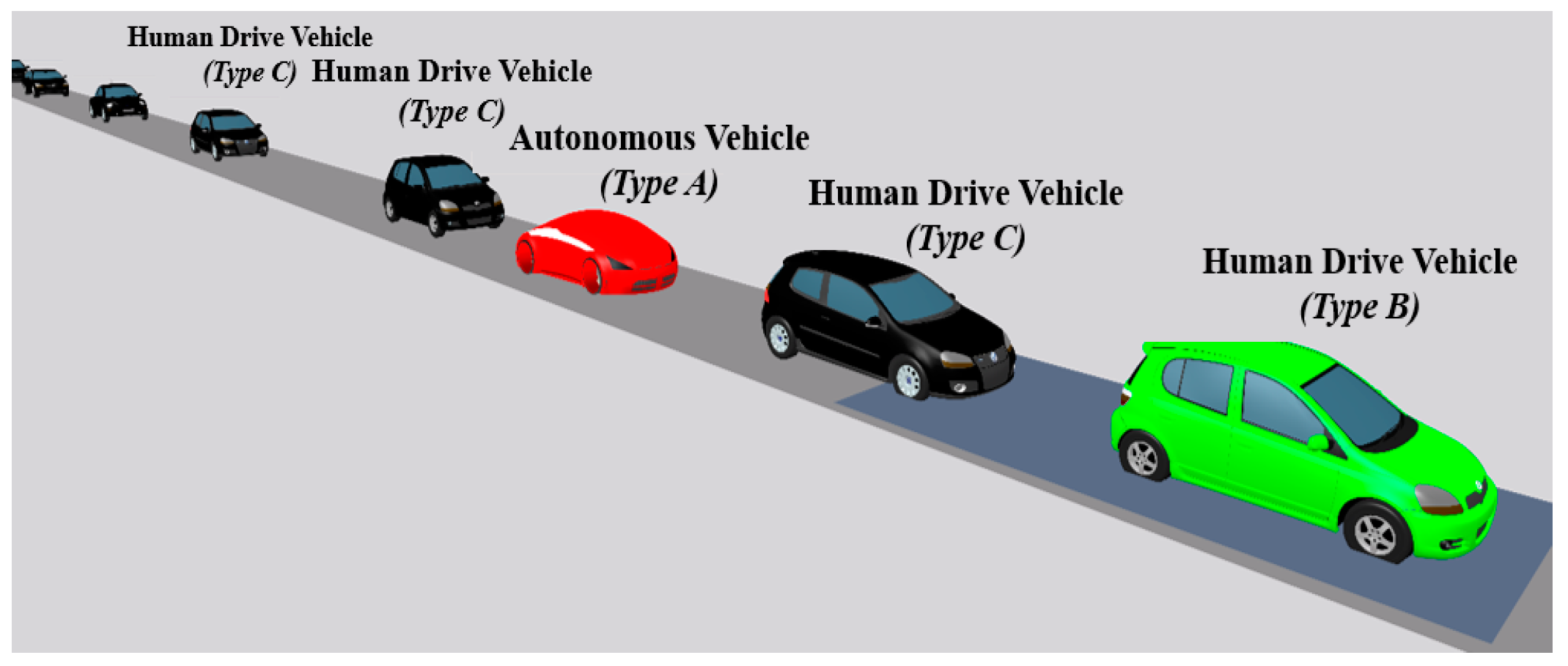




| Parameters | |
|---|---|
| Length of Freeway Road | 5000 m |
| Number of Vehicles | 2250 pc/h/ln |
| (freeway capacity) | 2300 pc/h/ln |
| 2350 pc/h/ln | |
| 2400 pc/h/ln | |
| 2450 pc/h/ln | |
| Types | autonomous vehicle (Type A, 10% of freeway capacity) |
| human driver vehicle (Type B, 1% of freeway capacity, stop in front of a stop sign) | |
| human driver vehicle (Type C, 89% of freeway capacity, no stopping in front of a stop sign) | |
| Time Interval | 0–900 (warmup time, not included) |
| 900–1800 | |
| 1800–2700 | |
| 2700–3600 | |
| 3600–4500 |
| Model | Speed | Seed | Case |
|---|---|---|---|
| W99 | 24.59 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 1–10 |
| 26.82 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 11–20 | |
| 29.06 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 21–30 | |
| 31.29 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 31–40 | |
| 33.53 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 41–50 | |
| ACC | 24.59 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 51–60 |
| 26.82 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 61–70 | |
| 29.06 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 71–80 | |
| 31.29 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 81–90 | |
| 33.53 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 91–100 | |
| CACC | 24.59 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 101–110 |
| 26.82 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 111–120 | |
| 29.06 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 121–130 | |
| 31.29 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 131–140 | |
| 33.53 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 141–150 | |
| CACF | 24.59 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 151–160 |
| 26.82 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 161–170 | |
| 29.06 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 171–180 | |
| 31.29 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 181–190 | |
| 33.53 m/s | 1, 6, 11, 16, 21, 26, 31, 36, 41, 46 | 191–200 |
| W99 | ACC | CACC | CACF |
|---|---|---|---|
| 24.59 m/s | 77.69% | 79.31% | 83.31% |
| 26.82 m/s | 80.20% | 84.07% | 82.16% |
| 29.06 m/s | 83.99% | 86.85% | 89.60% |
| 31.29 m/s | 80.37% | 83.33% | 83.84% |
| 33.53 m/s | 80.93% | 87.03% | 89.20% |
| Speed Limit | W99 | ACC | CACC | |
|---|---|---|---|---|
| 24.59 m/s | Average | 77.69% | 79.31% | 83.31% |
| Maximum | 74.65% | 82.59% | 86.05% | |
| Minimum | 88.81% | 67.00% | 69.17% | |
| 26.82 m/s | Average | 80.20% | 84.07% | 82.16% |
| Maximum | 84.24% | 90.12% | 83.71% | |
| Minimum | 85.76% | 71.11% | 75.43% | |
| 29.06 m/s | Average | 83.99% | 86.85% | 89.60% |
| Maximum | 82.99% | 89.43% | 91.44% | |
| Minimum | 91.97% | 86.75% | 89.58% | |
| 31.29 m/s | Average | 80.37% | 83.33% | 83.84% |
| Maximum | 79.59% | 81.15% | 84.31% | |
| Minimum | 89.49% | 80.75% | 88.12% | |
| 33.53 m/s | Average | 80.93% | 87.03% | 89.20% |
| Maximum | 74.86% | 86.67% | 89.81% | |
| Minimum | 91.37% | 93.94% | 93.25% |
| Speed Limit | Time Interval | W99 | ACC | CACC |
|---|---|---|---|---|
| 24.59 m/s | 900–1800 | 89.96% | 79.84% | 91.66% |
| 1800–2700 | 83.09% | 70.46% | 53.48% | |
| 2700–3600 | 91.32% | 84.70% | 93.54% | |
| 3600–4500 | 64.34% | 89.84% | 89.44% | |
| 26.82 m/s | 900–1800 | 88.10% | 91.74% | 87.32% |
| 1800–2700 | 88.49% | 88.25% | 87.89% | |
| 2700–3600 | 80.86% | 78.81% | 68.67% | |
| 3600–4500 | 65.07% | 72.19% | 70.91% | |
| 29.06 m/s | 900–1800 | 87.63% | 88.58% | 91.02% |
| 1800–2700 | 84.93% | 87.06% | 88.60% | |
| 2700–3600 | 89.76% | 83.63% | 92.04% | |
| 3600–4500 | 71.73% | 78.18% | 83.52% | |
| 31.29 m/s | 900–1800 | 80.51% | 86.40% | 88.60% |
| 1800–2700 | 84.81% | 85.36% | 84.44% | |
| 2700–3600 | 75.34% | 66.69% | 81.59% | |
| 3600–4500 | 50.32% | 60.69% | 64.60% | |
| 33.53 m/s | 900–1800 | 82.49% | 87.60% | 85.92% |
| 1800–2700 | 86.42% | 86.39% | 87.85% | |
| 2700–3600 | 80.00% | 83.03% | 91.35% | |
| 3600–4500 | 76.92% | 79.99% | 87.15% |
| Speed | W99 | ACC | CACC | CACF | |
|---|---|---|---|---|---|
| 24.59 m/s | Mean | 22.60 m/s | 22.41 m/s | 22.12 m/s | 23.94 m/s |
| Minimum | 22.18 m/s | 21.18 m/s | 20.72 m/s | 23.55 m/s | |
| Maximum | 23.17 m/s | 23.68 m/s | 23.67 m/s | 24.27 m/s | |
| Standard Deviation | 0.51 | 1.16 | 1.35 | 0.33 | |
| 26.82 m/s | Mean | 23.04 m/s | 22.33 m/s | 22.72 m/s | 24.85 m/s |
| Minimum | 21.74 m/s | 19.08 m/s | 20.91 m/s | 24.42 m/s | |
| Maximum | 24.50 m/s | 24.62 m/s | 24.61 m/s | 25.31 m/s | |
| Standard Deviation | 1.39 | 2.52 | 1.68 | 0.51 | |
| 29.06 m/s | Mean | 23.76 m/s | 22.58 m/s | 22.46 m/s | 26.73 m/s |
| Minimum | 21.24 m/s | 18.00 m/s | 18.44 m/s | 26.29 m/s | |
| Maximum | 25.50 m/s | 26.01 m/s | 25.91 m/s | 27.43 m/s | |
| Standard Deviation | 2.17 | 3.65 | 3.85 | 0.72 | |
| 31.29 m/s | Mean | 19.89 m/s | 19.08 m/s | 19.47 m/s | 23.28 m/s |
| Minimum | 17.83 m/s | 16.89 m/s | 16.59 m/s | 22.25 m/s | |
| Maximum | 22.00 m/s | 22.10 m/s | 21.92 m/s | 24.05 m/s | |
| Standard Deviation | 2.41 | 2.80 | 3.05 | 0.84 | |
| 33.53 m/s | Mean | 21.96 m/s | 19.91 m/s | 19.80 m/s | 25.33 m/s |
| Minimum | 20.39 m/s | 17.0 m/s | 16.55 m/s | 24.57 m/s | |
| Maximum | 23.35 m/s | 21.90 m/s | 22.74 m/s | 26.12 m/s | |
| Standard Deviation | 1.71 | 2.86 | 3.53 | 1.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Ahemd, H.U.; Huang, Y.; Lu, P. Cumulatively Anticipative Car-Following Model with Enhanced Safety for Autonomous Vehicles in Mixed Driver Environments. Smart Cities 2023, 6, 2260-2281. https://doi.org/10.3390/smartcities6050104
Yang X, Ahemd HU, Huang Y, Lu P. Cumulatively Anticipative Car-Following Model with Enhanced Safety for Autonomous Vehicles in Mixed Driver Environments. Smart Cities. 2023; 6(5):2260-2281. https://doi.org/10.3390/smartcities6050104
Chicago/Turabian StyleYang, Xinyi, Hafiz Usman Ahemd, Ying Huang, and Pan Lu. 2023. "Cumulatively Anticipative Car-Following Model with Enhanced Safety for Autonomous Vehicles in Mixed Driver Environments" Smart Cities 6, no. 5: 2260-2281. https://doi.org/10.3390/smartcities6050104
APA StyleYang, X., Ahemd, H. U., Huang, Y., & Lu, P. (2023). Cumulatively Anticipative Car-Following Model with Enhanced Safety for Autonomous Vehicles in Mixed Driver Environments. Smart Cities, 6(5), 2260-2281. https://doi.org/10.3390/smartcities6050104







