A Spatio-Temporal Task Allocation Model in Mobile Crowdsensing Based on Knowledge Graph
Abstract
1. Introduction
- We propose a novel spatiotemporal knowledge graph (STKG) that can be directly used to learn task graphs reflecting the patterns of task transitions. To our knowledge, this is the first method that learns weighted isomorphic task graphs using heterogeneous knowledge graphs in spatiotemporal crowdsensing.
- We introduce a novel Knowledge Graph-based GTA approach that seamlessly integrates the learned task transition graph with an RNN-based model to effectively capture sequence transition patterns. Furthermore, to enhance the effectiveness of personalized task allocation, we introduce a meticulously designed similarity function to measure the preferences of different users.
- We extensively evaluate our approach on three real datasets and demonstrate that GTA outperforms existing solutions with higher accuracy.
2. Related Works
2.1. Task Allocation
2.2. Mobility Prediction
| Category | Authors | Objective |
|---|---|---|
| Task Allocation | Zhao et al. [9,10] | Formulate the Dynamic Delayed Binary Matching (DDBM) problem and design Value-Based Task Assignment (VBTA) and Policy Gradient-Based Task Assignment (PGTA) frameworks |
| Liu et al. [11] | Propose a task allocation framework based on federated preference learning to ensure data privacy and assign tasks according to worker preferences | |
| Wang et al. [12] | Solve multi-task competition and priority issues, optimize task allocation to maximize spatio-temporal coverage, and consider spatio-temporal constraints | |
| Li et al. [13] | Propose a worker selection problem in heterogeneous perception tasks to minimize costs and maintain worker trajectories | |
| Li et al. [14] | Study the time-constrained task allocation problem, maximize the utility of mobile crowdsourcing platforms, and improve system efficiency and productivity | |
| Wang et al. [15] | Optimize task allocation from the perspective of task organizers and participants, solve problems such as unfair allocation and worker load, and improve work flexibility | |
| Mobility Prediction | Zhang et al. [16] | Multi-task allocation method based on mobility prediction to optimize task completion rate |
| Yang et al. [17] | Use the markov model to predict the probability of workers completing tasks and optimize task allocation | |
| Wang et al. [18] | Multi-objective optimization algorithms using movement prediction models, including task coverage maximization and task cost minimization | |
| Wang et al. [19] | Multi-task allocation algorithm for maximizing spatiotemporal coverage under total budget constraint | |
| Prediction and Task Allocation | Cheng et al. [26] | Consider current and future workers/tasks, improve global task allocation, increase task allocation accuracy |
| Zhang et al. [27] | A task allocation framework based on worker churn prediction, which optimizes the allocation of individual tasks by predicting worker churn | |
| Zhao et al. [28] | Considering current and future workers/tasks (location unknown), maximizing the number of task allocation | |
| Zhai et al. [29] | Use the SeqST-ResNet deep learning model to effectively capture the temporal dependence of historical tasks | |
| Wang et al. [30] | Research on task allocation problem based on worker churn to achieve the highest total task allocation reward | |
| Wei et al. [31] | Joint Predictive Model (JPM), considering worker location and preference category, predicts worker location and preference category | |
| Wang et al. [32] | Use knowledge graph technology to predict task allocation, optimize task allocation, and explore complex spatio-temporal relationships | |
| Quan et al. [33] | Propose Conv-STAN and CT-Voting prediction methods to predict the future distribution of crowdsourced entities |
2.3. Prediction and Task Allocation
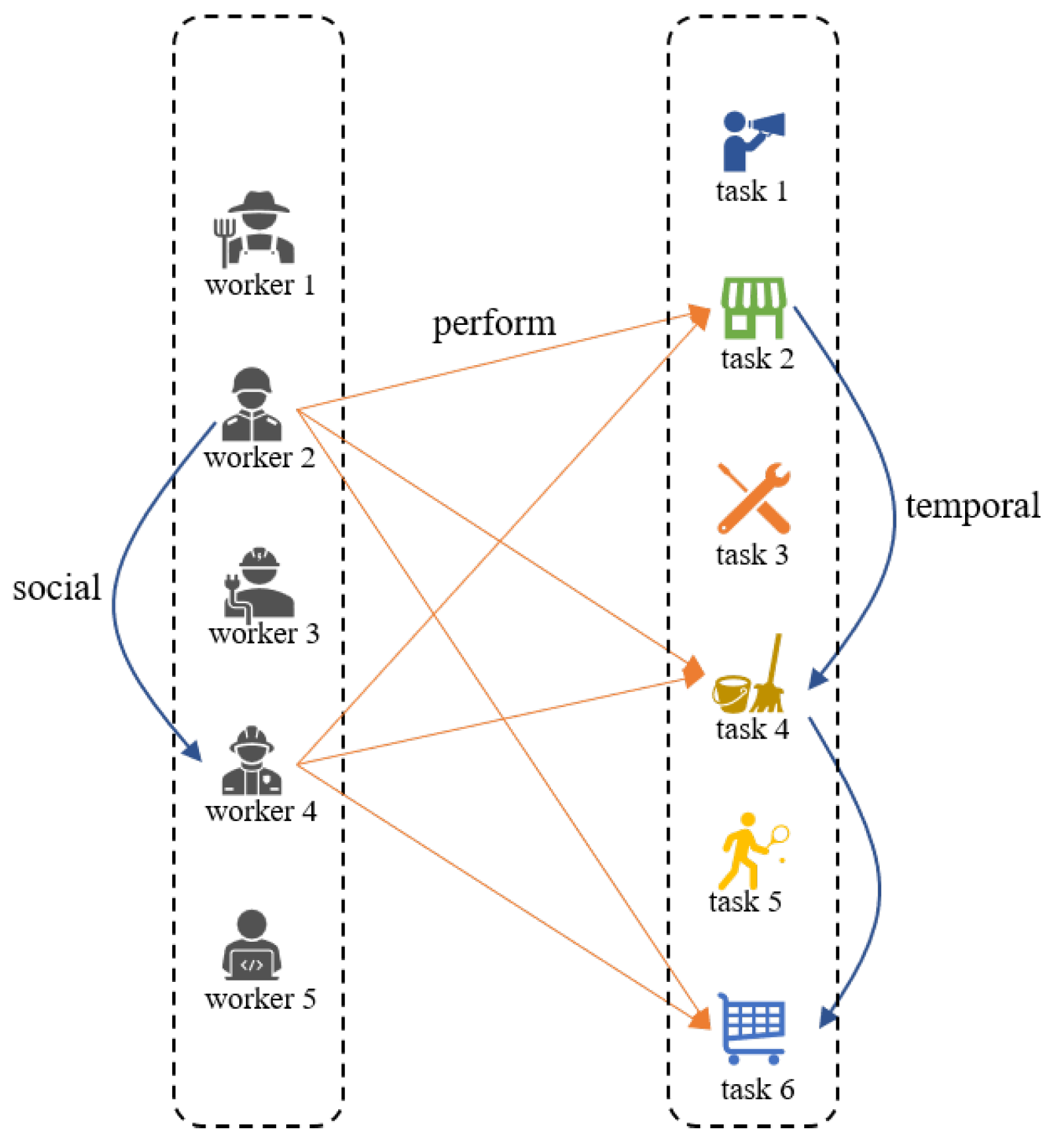
3. Preliminaries
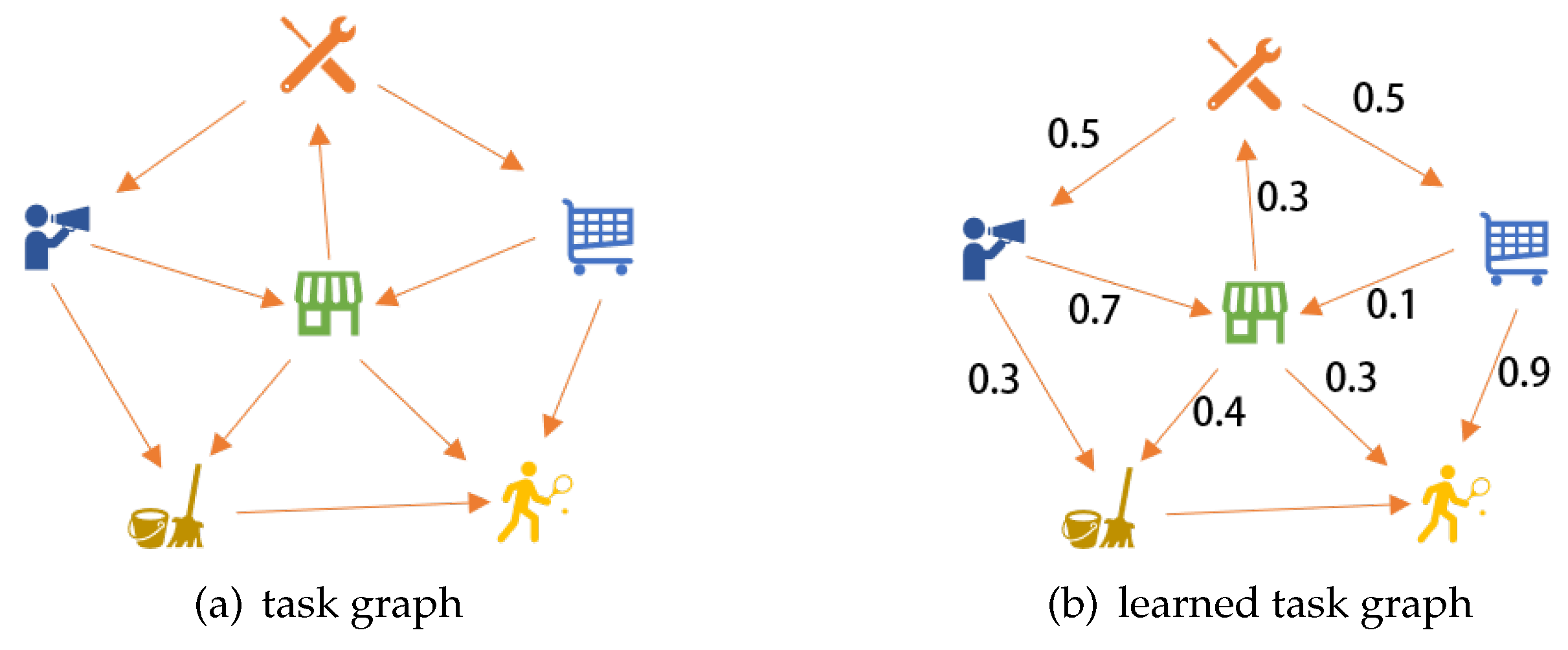
4. Transition Graph Learning
4.1. Spatio-Temporal Knowledge Graph
4.2. Spatio-Temporal Knowledge Graph Embedding
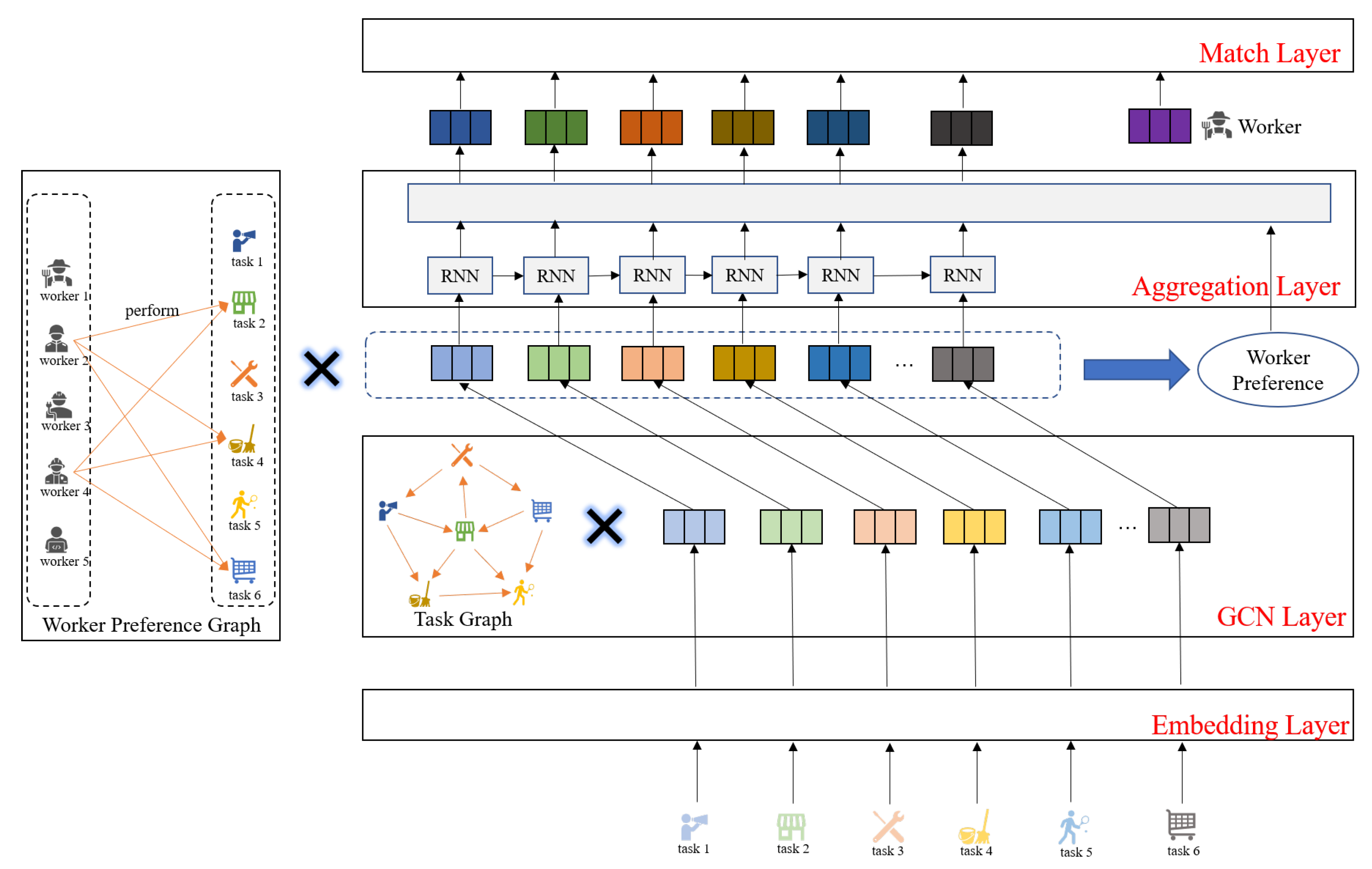
5. Model Framework
5.1. Multimodal Embedding Layer
5.2. GCN Layer
5.3. Aggregation Layer
5.4. Prediction Layer
6. Experimental
6.1. Dataset
6.2. Evaluation Metrics
6.3. Parameter Settings
6.4. Comparative Algorithms
- STRNN [39]: An invariant RNN model that incorporates spatio-temporal features between consecutive visits.
- DeepMove [40]: A state-of-the-art model that utilizes recurrent and attention layers to capture periodicity.
- STGN [41]: Learn the long-term and short-term preferences of users and extend the LSTM model using spatial and temporal gates.
- GeoSAN [42]: A state-of-the-art model that employs hierarchical gridding of GPS locations for spatial discretization and utilizes self-attention layers for matching, without explicit use of spatio-temporal intervals.
6.5. Allocation Performance
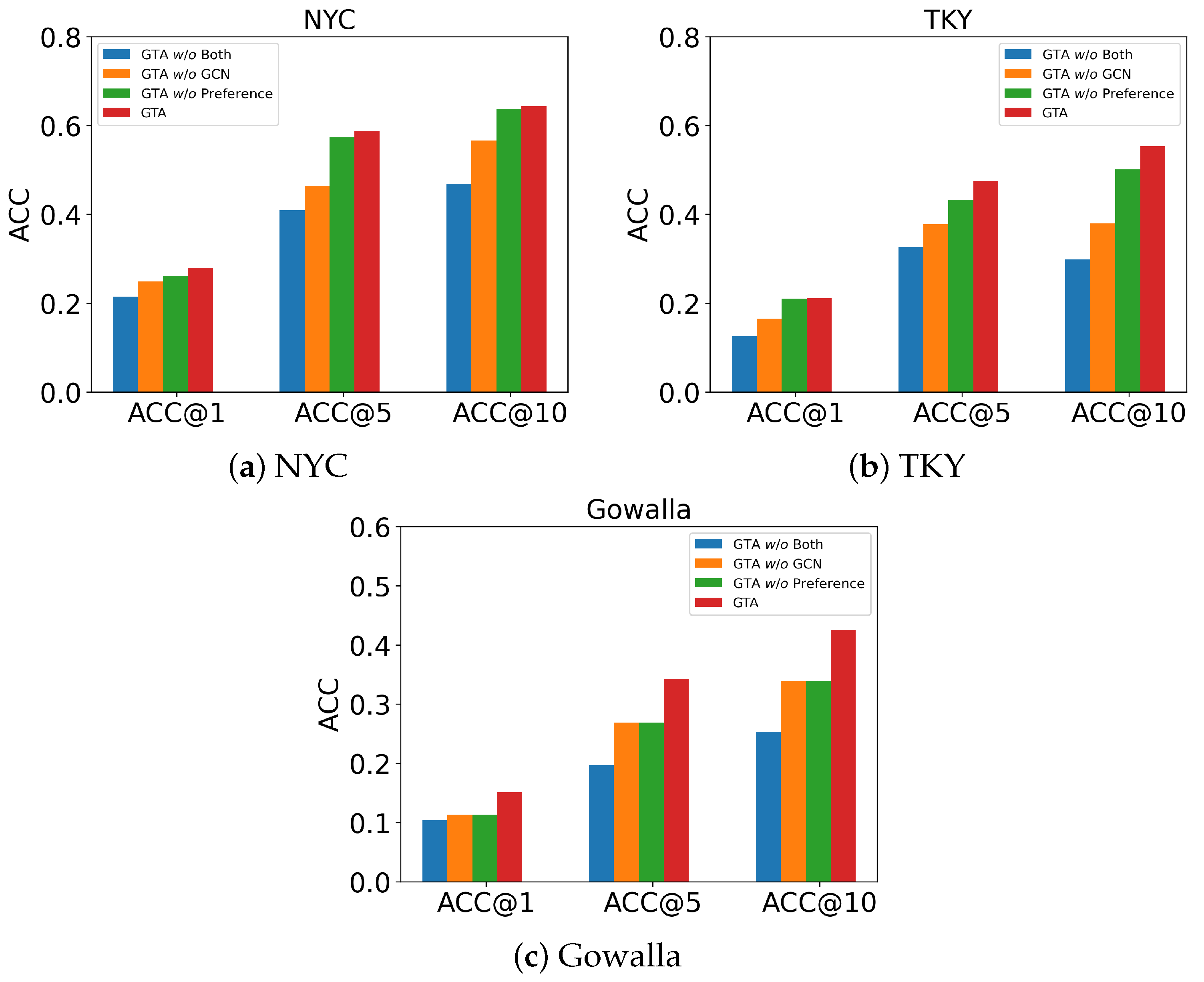
6.6. Ablation Study
6.7. Comparison Experiment on Embedding Layer Dimension
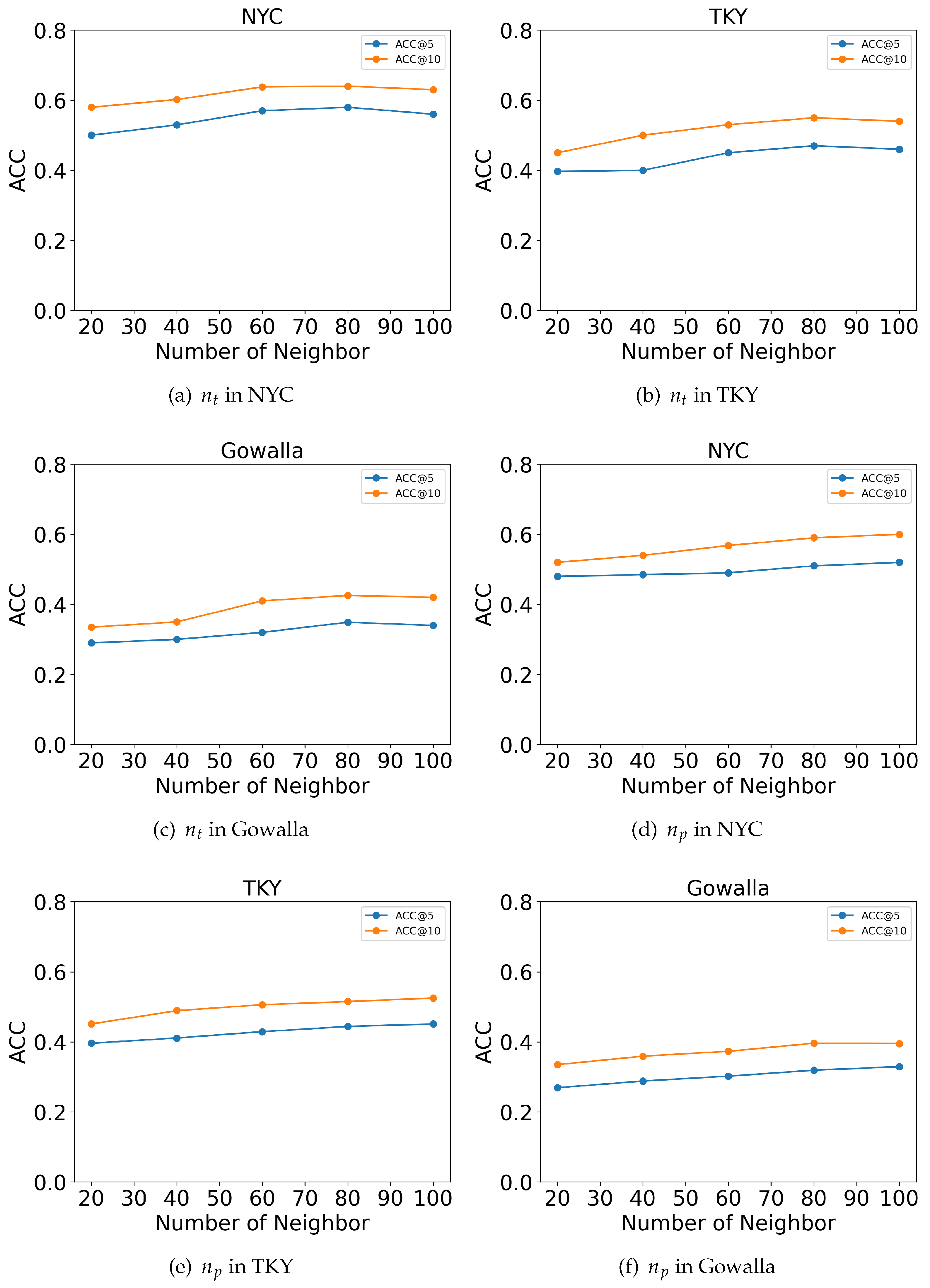
6.8. Comparison Experiment on Graph Neighbor
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, S.; Yu, Y.; Guo, L.; Yeoh, P.L.; Ni, Q.; Vucetic, B.; Li, Y. Truthful online double auctions for mobile crowdsourcing: An on-demand service strategy. IEEE Internet Things J. 2022, 9, 16096–16112. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, L.; Wang, Y.; Fu, Y. Adaptive trajectory prediction via transferable gnn. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 6520–6531. [Google Scholar]
- Ray, A.; Chowdhury, C.; Bhattacharya, S.; Roy, S. A survey of mobile crowdsensing and crowdsourcing strategies for smart mobile device users. CCF Trans. Pervasive Comput. Interact. 2023, 5, 98–123. [Google Scholar] [CrossRef]
- Yang, D.; Fankhauser, B.; Rosso, P.; Cudre-Mauroux, P. Location prediction over sparse user mobility traces using rnns. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, Yokohama, Japan, 7–15 January 2021; pp. 2184–2190. [Google Scholar]
- Rao, X.; Chen, L.; Liu, Y.; Shang, S.; Yao, B.; Han, P. Graph-flashback network for next location recommendation. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 1463–1471. [Google Scholar]
- Han, P.; Wang, J.; Yao, D.; Shang, S.; Zhang, X. A graph-based approach for trajectory similarity computation in spatial networks. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, 14–18 August 2021; pp. 556–564. [Google Scholar]
- Li, Y.; Chen, T.; Luo, Y.; Yin, H.; Huang, Z. Discovering collaborative signals for next POI recommendation with iterative Seq2Graph augmentation. arXiv 2021, arXiv:2106.15814. [Google Scholar]
- He, X.; Deng, K.; Wang, X.; Li, Y.; Zhang, Y.; Wang, M. Lightgcn: Simplifying and powering graph convolution network for recommendation. In Proceedings of the 43rd International ACM SIGIR conference on research and development in Information Retrieval, Xi’an, China, 25–30 July 2020; pp. 639–648. [Google Scholar]
- Zhao, B.; Dong, H.; Wang, Y.; Pan, T. A task allocation algorithm based on reinforcement learning in spatio-temporal crowdsourcing. Appl. Intell. 2022, 53, 13452–13469. [Google Scholar] [CrossRef]
- Zhao, B.; Dong, H.; Wang, Y.; Pan, T. PPO-TA: Adaptive task allocation via Proximal Policy Optimization for spatio-temporal crowdsourcing. Knowl.-Based Syst. 2023, 264, 110330. [Google Scholar] [CrossRef]
- Liu, J.; Deng, L.; Miao, H.; Zhao, Y.; Zheng, K. Task Assignment with Federated Preference Learning in Spatial Crowdsourcing. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; pp. 1279–1288. [Google Scholar]
- Wang, J.; Wang, Y.; Zhang, D.; Wang, F.; Xiong, H.; Chen, C.; Lv, Q.; Qiu, Z. Multi-task allocation in mobile crowd sensing with individual task quality assurance. IEEE Trans. Mob. Comput. 2018, 17, 2101–2113. [Google Scholar] [CrossRef]
- Li, H.; Li, T.; Wang, W.; Wang, Y. Dynamic participant selection for large-scale mobile crowd sensing. IEEE Trans. Mob. Comput. 2018, 18, 2842–2855. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X. Multi-task allocation under time constraints in mobile crowdsensing. IEEE Trans. Mob. Comput. 2019, 20, 1494–1510. [Google Scholar] [CrossRef]
- Wang, J.; Wang, F.; Wang, Y.; Zhang, D.; Lim, B.; Wang, L. Allocating heterogeneous tasks in participatory sensing with diverse participant-side factors. IEEE Trans. Mob. Comput. 2018, 18, 1979–1991. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X. Multi-task allocation in mobile crowd sensing with mobility prediction. IEEE Trans. Mob. Comput. 2021, 22, 1081–1094. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, W.; Wang, E.; Wu, J. A prediction-based user selection framework for heterogeneous mobile crowdsensing. IEEE Trans. Mob. Comput. 2018, 18, 2460–2473. [Google Scholar] [CrossRef]
- Wang, L.; Yu, Z.; Han, Q.; Guo, B.; Xiong, H. Multi-objective optimization based allocation of heterogeneous spatial crowdsourcing tasks. IEEE Trans. Mob. Comput. 2017, 17, 1637–1650. [Google Scholar] [CrossRef]
- Wang, L.; Yu, Z.; Zhang, D.; Guo, B.; Liu, C.H. Heterogeneous multi-task assignment in mobile crowdsensing using spatiotemporal correlation. IEEE Trans. Mob. Comput. 2018, 18, 84–97. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Zhang, D.; Wang, F.; He, Y.; Ma, L. PSAllocator: Multi-task allocation for participatory sensing with sensing capability constraints. In Proceedings of the 2017 ACM Conference on Computer Supported Cooperative Work and Social Computing, Portland, OR, USA, 25 February–1 March 2017; pp. 1139–1151. [Google Scholar]
- Xiao, M.; Wu, J.; Huang, L.; Wang, Y.; Liu, C. Multi-task assignment for crowdsensing in mobile social networks. In Proceedings of the 2015 IEEE Conference on Computer Communications (INFOCOM), Hong Kong, 26 April–1 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 2227–2235. [Google Scholar]
- Guo, B.; Liu, Y.; Wu, W.; Yu, Z.; Han, Q. ActiveCrowd: A framework for optimized multitask allocation in mobile crowdsensing systems. IEEE Trans.-Hum.-Mach. Syst. 2016, 47, 392–403. [Google Scholar] [CrossRef]
- Liu, W.; Yang, Y.; Wang, E.; Han, Z.; Wang, X. Prediction based user selection in time-sensitive mobile crowdsensing. In Proceedings of the 2017 14th Annual IEEE International Conference on Sensing, Communication, and Networking (SECON), San Diego, CA, USA, 12–14 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–9. [Google Scholar]
- Lai, C.; Zhang, X. Duration-sensitive task allocation for mobile crowd sensing. IEEE Syst. J. 2020, 14, 4430–4441. [Google Scholar] [CrossRef]
- Deng, L.; Zhao, Y.; Fu, Z.; Sun, H.; Liu, S.; Zheng, K. Efficient Trajectory Similarity Computation with Contrastive Learning. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; pp. 365–374. [Google Scholar]
- Cheng, P.; Lian, X.; Chen, L.; Shahabi, C. Prediction-based task assignment in spatial crowdsourcing. In Proceedings of the 2017 IEEE 33rd International Conference on Data Engineering (ICDE), San Diego, CA, USA, 19–22 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 997–1008. [Google Scholar]
- Zhang, D.; Xiong, H.; Wang, L.; Chen, G. CrowdRecruiter: Selecting participants for piggyback crowdsensing under probabilistic coverage constraint. In Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Seattle, WA, USA, 13–17 September 2014; pp. 703–714. [Google Scholar]
- Zhao, Y.; Zheng, K.; Cui, Y.; Su, H.; Zhu, F.; Zhou, X. Predictive task assignment in spatial crowdsourcing: A data-driven approach. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 13–24. [Google Scholar]
- Zhai, D.; Liu, A.; Chen, S.; Li, Z.; Zhang, X. SeqST-ResNet: A sequential spatial temporal ResNet for task prediction in spatial crowdsourcing. In Proceedings of the Database Systems for Advanced Applications: 24th International Conference, DASFAA 2019, Chiang Mai, Thailand, 22–25 April 2019; Proceedings, Part I 24. Springer: Berlin/Heidelberg, Germany, 2019; pp. 260–275. [Google Scholar]
- Wang, Z.; Zhao, Y.; Chen, X.; Zheng, K. Task assignment with worker churn prediction in spatial crowdsourcing. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Queensland, Australia, 1–5 November 2021; pp. 2070–2079. [Google Scholar]
- Wei, X.; Sun, B.; Cui, J.; Qiu, M. Location-and-Preference Joint Prediction for Task Assignment in Spatial Crowdsourcing. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. 2022, 42, 928–941. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Zhao, G. Dynamic link prediction method of task and user in Mobile Crowd Sensing. Comput. Commun. 2022, 189, 110–119. [Google Scholar] [CrossRef]
- Quan, J.; Wang, N. An optimized task assignment framework based on crowdsourcing knowledge graph and prediction. Knowl.-Based Syst. 2023, 260, 110096. [Google Scholar] [CrossRef]
- Bordes, A.; Usunier, N.; Garcia-Duran, A.; Weston, J.; Yakhnenko, O. Translating embeddings for modeling multi-relational data. Adv. Neural Inf. Process. Syst. 2013, 2, 2787–2795. [Google Scholar]
- Wang, Z.; Zhang, J.; Feng, J.; Chen, Z. Knowledge graph embedding by translating on hyperplanes. In Proceedings of the AAAI Conference on Artificial Intelligence, Quebec City, QC, Canada, 27–31 July 2014; Volume 28. [Google Scholar]
- Lin, Y.; Liu, Z.; Sun, M.; Liu, Y.; Zhu, X. Learning entity and relation embeddings for knowledge graph completion. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; Volume 29. [Google Scholar]
- Yang, D.; Qu, B.; Yang, J.; Cudre-Mauroux, P. Revisiting user mobility and social relationships in lbsns: A hypergraph embedding approach. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 2147–2157. [Google Scholar]
- Cho, E.; Myers, S.A.; Leskovec, J. Friendship and mobility: Friendship and mobility: User movement in location-based social networks. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 21–24 August 2011; pp. 1082–1090. [Google Scholar]
- Liu, Q.; Wu, S.; Wang, L.; Tan, T. Predicting the next location: A recurrent model with spatial and temporal contexts. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Feng, J.; Li, Y.; Zhang, C.; Sun, F.; Meng, F.; Guo, A.; Jin, D. Deepmove: Predicting human mobility with attentional recurrent networks. In Proceedings of the 2018 World Wide Web Conference, Lyon, France, 23–27 April 2018; pp. 1459–1468. [Google Scholar]
- Zhao, P.; Luo, A.; Liu, Y.; Xu, J.; Li, Z.; Zhuang, F.; Sheng, V.S.; Zhou, X. Where to Go Next: A Spatio-Temporal Gated Network for Next POI Recommendation. IEEE Trans. Knowl. Data Eng. 2022, 34, 2512–2524. [Google Scholar] [CrossRef]
- Lian, D.; Wu, Y.; Ge, Y.; Xie, X.; Chen, E. Geography-aware sequential location recommendation. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual, 6–10 July 2020; pp. 2009–2019. [Google Scholar]


| Parameters | Value |
|---|---|
| Learning rate | 0.001 |
| Embedding dimension | 50 |
| Batch size | 1 |
| Dropout rate | 0.3 |
| Epochs | 80 |
| number of neighbors | 50 |
| NYC | TKY | Gowalla | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ACC@1 | ACC@5 | ACC@10 | ACC@1 | ACC@5 | ACC@10 | ACC@1 | ACC@5 | ACC@10 | |
| STRNN | 0.1487 | 0.1645 | 0.2661 | 0.1153 | 0.1783 | 0.2793 | 0.1037 | 0.1669 | 0.2327 |
| DeepMove | 0.1761 | 0.2235 | 0.2781 | 0.1398 | 0.2893 | 0.3451 | 0.1129 | 0.1931 | 0.2637 |
| STGN | 0.2023 | 0.3566 | 0.5102 | 0.1728 | 0.3203 | 0.3689 | 0.1181 | 0.2118 | 0.3268 |
| GeoSAN | 0.2365 | 0.4775 | 0.5226 | 0.1942 | 0.3925 | 0.4747 | 0.1333 | 0.2942 | 0.3905 |
| GTA | 0.2791 | 0.5871 | 0.6437 | 0.2105 | 0.4757 | 0.5537 | 0.1512 | 0.3425 | 0.4256 |
| NYC | TKY | Gowalla | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ACC@1 | ACC@5 | ACC@10 | ACC@1 | ACC@5 | ACC@10 | ACC@1 | ACC@5 | ACC@10 | |
| GTA Both | 0.2147 | 0.4095 | 0.4687 | 0.1253 | 0.3269 | 0.2983 | 0.1037 | 0.1969 | 0.2529 |
| GTA GCN | 0.2487 | 0.4645 | 0.5661 | 0.1653 | 0.3783 | 0.3792 | 0.1137 | 0.2689 | 0.3394 |
| GTA Preference | 0.2612 | 0.5734 | 0.6378 | 0.2098 | 0.4327 | 0.5013 | 0.1229 | 0.3019 | 0.4037 |
| GTA | 0.2791 | 0.5871 | 0.6437 | 0.2105 | 0.4757 | 0.5537 | 0.1512 | 0.3425 | 0.4256 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, B.; Dong, H.; Yang, D. A Spatio-Temporal Task Allocation Model in Mobile Crowdsensing Based on Knowledge Graph. Smart Cities 2023, 6, 1937-1957. https://doi.org/10.3390/smartcities6040090
Zhao B, Dong H, Yang D. A Spatio-Temporal Task Allocation Model in Mobile Crowdsensing Based on Knowledge Graph. Smart Cities. 2023; 6(4):1937-1957. https://doi.org/10.3390/smartcities6040090
Chicago/Turabian StyleZhao, Bingxu, Hongbin Dong, and Dongmei Yang. 2023. "A Spatio-Temporal Task Allocation Model in Mobile Crowdsensing Based on Knowledge Graph" Smart Cities 6, no. 4: 1937-1957. https://doi.org/10.3390/smartcities6040090
APA StyleZhao, B., Dong, H., & Yang, D. (2023). A Spatio-Temporal Task Allocation Model in Mobile Crowdsensing Based on Knowledge Graph. Smart Cities, 6(4), 1937-1957. https://doi.org/10.3390/smartcities6040090






