Application of Classic and Novel Metaheuristic Algorithms in a BIM-Based Resource Tradeoff in Dam Projects

Abstract

In recent years, dam construction has become more complex, requiring an effective project management method. Building Information Modeling (BIM) affects how construction projects are planned, designed, executed, and operated. Therefore, reducing execution time, cost, and risk and increasing quality are the primary goals of organizations. In this paper, first, the time and cost of the project were obtained via the BIM process. Subsequently, optimization between the components of the survival pyramid (time, cost, quality, and risk) in construction projects was completed in a case study of the Ghocham storage dam in five different modes, including contractor’s offers, BIM, actual, and two other modes based on the expert’s opinions. For this aim, five different meta-heuristic optimization algorithms were utilized, including two classical algorithms (Genetic and Simulated Annealing) and three novel algorithms (Black Widow Optimization, Battle Royale Optimization, and Black Hole Mechanics Optimization). In four cases, once each element of the survival pyramid was optimized separately, all four cases were traded off simultaneously. Moreover, the results were obtained from all the mentioned algorithms in five scenarios based on the number of function evaluation (N_fe), Standard Deviation (SD), Computation Time (CT), and Best Cost (BC). MATLAB software completed the coding related to the objective functions and optimization algorithms. The results indicated the appropriate performance of GA and BHMO algorithms in some scenarios. However, only the GAs should be considered effective algorithms in a dam construction projects’ time–cost–quality–risk (TCQR) tradeoff.

1. Introduction

Infrastructure projects are large, intricate, and typically cost millions. These projects can affect millions of people, possess a long-life cycle, involve complicated management, and have considerable uncertainty. Building Information Modeling (BIM) is an emerging and effective technology and process that has rapidly changed how buildings are conceived, designed, constructed, and operated [1]. The rapid development of BIM provides novel opportunities to ameliorate the efficiency and effectiveness of the construction procedure and improve the employment of emerging technologies throughout the project life cycle, not only in buildings but also in infrastructure [2]. BIM is defined as “the systematic process of managing and disseminating the overall information generated during the development and operation of the project’s design” [3,4], fundamentally describes the exchange, interpretation, and use of metadata around computer-aided design (CAD) models, and supports the multiple roles of various stakeholders in the construction and operation process [5]. Integrating BIM into each project’s early design phase provides an intriguing opportunity for project management [6,7]. Compared with a set of CAD drawings, BIM is a “richer repository”; that is, some multi-disciplinary methods can build construct information and the characteristics of buildings’ BIM models digitally and graphically. By sharing and exporting the data required by the project team, BIM enables the usage of information in the architectural model, reducing the need to recreate the model and accelerating the design whilst allowing for some more repetition [8]. In broad terms, BIM increases design and construction quality, lowers project labor and costs, and is a quicker and more effective method to manage construction [9].

Because of overpopulation and the increasing complexity of construction projects, the project manager should balance the project’s time, cost, quality, and risk at the early stages of the project. Evidence suggests that most project activities can be consummated earlier than scheduled in construction projects by reducing their time or allocating additional resources and equipment, thus increasing project costs exponentially. In addition, shortening the operating time can reduce project quality and increase risk because uncertainty decreases with increasing time. Therefore, optimization problems are prominent topics in scientific and practical engineering research. Based on the number of optimized goal functions, optimization problems can be divided into single-objective and multi-objective.

Regarding multi-objective optimization (MOP) problems, two or more objective functions must be computed simultaneously. In addition, these objective functions are always inconsistent [10]. Time–Cost–Quality–Risk Trade-off Problems (TCQRTP) are one of the significant challenges in project management. In this situation, there are some practical solutions. Various optimization techniques have been proposed for TCQRT problems. The Critical Path Method (CPM) can be used as a basic quantitative technique for project management with no time limit and resource constraints. Assuming an ideal completion time, the CPM sets the minimum time required to complete the project. However, it has been abolished due to limitations such as its arithmetic complexity, especially in large construction projects [11]. Mathematical programming methods transform TCQRTP into mathematical models and use linear programming [12]. As a method for achieving the best results, linear programming (LP) was proposed by Volkerson and Perra, assuming a continuous time–cost relationship represented by linear relationships. However, it can only be used considering a linear relationship between time and cost for any activity on the network. As the number of activities increases, the network becomes too intricate; the LP method requires much computational effort [13,14].

Furthermore, heuristic methods are based on general rules and lack mathematical precision. They provide but do not guarantee optimality. Most innovative methods only consider linear time–cost–quality–risk relationships in a project’s activities [12], thus indicating its inefficiency in TCQRTP. However, over the last few years, researchers have most frequently used meta-heuristic optimization algorithms to solve TCQRTP. Meta-heuristic optimization algorithms are designed by imitating insects, animals, and birds [15]. In general, nature-inspired meta-heuristic algorithms fall into four main groups: (i) evolution-based algorithms, (ii) swarm-based algorithms, physics-based algorithms, and (iii) human behavior-based algorithms.

Chassiakos, Samaras, and Theodorakopoulos [14] presented a time–cost tradeoff model based on the CPM method that can be used for any discrete cost–time relationship for project activities. Feng, Liu, and Burns [12] developed a new algorithm using the GA and Pareto methods for time–cost tradeoff (TCT) problems. In another paper, the authors presented the time–cost tradeoff model under uncertainty using genetic algorithms (GA) with simulation techniques [16]. El-kholy [17] presented a TCT model that considers budget variability and time uncertainty based on a linear programming model. Aziz et al. [18] proposed a new approach called the Smart Critical Path Method System (SCPMS), which combines CPM and GA. The authors aimed to optimize resources to simultaneously reduce project time and cost with maximum quality. Ballesteros-Pérez et al. [19] proposed a non-linear model for TCT problems with three main variables: crashed durations, crashed costs, and the number of resources. The authors concluded that the proposed models allow both discrete and continuous configurations and definite and random ones. Chen and Tsai [20] analyzed time–cost tradeoff problems with fuzzy parameters, a practical method for complex project networks. Since the fuzzy environment in TCT problems includes only membership functions, with uncertainty about projects and their duration, Abdel-Basset et al. [21] used the neutrosophic theory to solve TCT problems. Albayrak [22] proposed a new hybrid algorithm (NHA) developed by combining particle swarm optimization (PSO) and a genetic algorithm to solve TCT problems. However, with the development of countries worldwide, various projects, in addition to time and cost, added other parameters, such as quality, safety, risk, etc., to their contracts. These novels and emerging contracts put more pressure on decision-makers in the construction industry to find optimal/near-optimal models while maximizing quality and minimizing construction costs and time [23].

Regarding the time–cost–quality tradeoff, Babu and Suresh [7] suggested that the quality element should be included in the TCT problems. A linear programming model was created by the authors in order to address time–cost–quality tradeoff (TCQT) problems; Khang and Myint [24] employed the model at a cement factory in Bangkok, Thailand in order to validate the suggested model. El-Rayes and Kandil [23] developed a three-dimensional time–cost–quality tradeoff analysis rather than conventional two-dimensional analysis. The authors used this model to minimize a highway construction project’s time and cost while maximizing its quality. Tareghian and Taheri [25] solved a TCQT problem using an electromagnetic scattering search that can be performed on large projects. In addition, Kannimuthu et al. [26] designed a framework for TCQT problems in a multi-state resource-constrained project planning environment solved by the Relaxed-Restricted Pareto Filtering (RR-PARETO3) algorithm. Tran et al. [27] developed the opposition multiple objective symbiotic organisms search (OMOSOS) approach, an appropriate method to solve time, cost, quality, and work continuity tradeoff problems. Using an opposition-based multiple objective differential evolution algorithms, which employs an opposition-based learning strategy for early population onset and generational leap, Luong et al. [28] solved the TCQT problem. On the other hand, there have not been many studies on tradeoff concerns, including time, cost, and quality. To put it another way, researchers have hardly ever considered the risk component in TCQT issues. Mohammadipour and Sadjadi [29] considered risk in the cost–quality tradeoff. The authors used appropriate linear programming to reduce not just the total extra cost of the project but also the overall risk of the project as well as the overall decline in the quality of the project as a whole. Safaei [30] developed a multi-objective mathematical programming model for the sake of the time–cost–quality–risk tradeoff solved by the Multipurpose Genetic Algorithm (NSGAII). Some other applications of metaheuristic algorithms can be found in [31,32,33,34,35].

However, several papers on integrating BIM and optimization for different purposes in the architect, engineering, and construction (AEC) industry have been published recently. Although various meta-heuristic algorithms can solve optimization problems, genetic algorithms (GAs) have been the most commonly used in previous studies, indicating their appropriate and efficient performance in optimization problems in civil engineering [36,37,38,39,40]. In dam construction projects, there are a wide variety of resources, each of which has its own time and cost, affecting the project’s risk and quality. Hence, the project managers should balance them to achieve the minimum time, cost, and risk and maximum quality. In this study, for the time–cost–quality–risk tradeoff, five meta-heuristic optimization algorithms were used, including Genetic Algorithm (GA), Annealing Simulation (SA), Black Widow Optimization Algorithm (BWO), Battle Royale Optimization Algorithm (BRO), and Black Hole Mechanical Optimization Algorithm (BHMO). The primary purpose of selecting the mentioned algorithms was to compare the performance of traditional and novel meta-heuristic optimization algorithms in a civil construction project. However, being parameter-free and having a fast convergence behavior and the lowest possible objective function evaluation could be deemed the privileges of the meta-heuristic algorithm. For this purpose, the Ghocham storage dam was selected as a case study. Five different modes were implemented for this problem; in four cases, each component of the survival pyramid was optimized separately, and finally, all four cases were traded off simultaneously. Research has rarely focused on the time–cost–quality–risk tradeoff of construction projects based on the BIM process. Hence, the key novelty of this research work is the employment of novel and classic metaheuristic algorithms to resource tradeoffs in dam construction projects based on the Building Information Modeling (BIM) approach. In contrast, previous papers have assessed the capabilities of metaheuristic algorithms in resource tradeoff problems in residential buildings. The core purposes of this research were:

Evaluating the role of the Building Information Modeling (BIM) process in reducing the execution time and cost of infrastructure projects;

Providing a model for optimizing the components of the survival pyramid (time, cost, quality, and risk) of a dam construction project;

Comparing the performance of novel and traditional meta-heuristic optimization algorithms with each other.

2. Design Example

In this paper, time, cost, quality, and risk optimization were implemented on a dam construction project with a case study on the Ghocham storage dam located in Kurdistan province, Iran. Objective functions were analyzed both individually and in combination. Meanwhile, all algorithms were performed in MATLAB on a Core i7-7700 HQ 2.80 processor with 16 GB of RAM.

2.1. Case Study

Ghocham dam (Figure 1), an earth-fill embankment dam with a clay core, was constructed to store, regulate, and exploit the water needed to irrigate agricultural lands in the Qorveh plain, Dehgolan. Ghocham dam is located in Kurdistan province, next to Qucham village and 18 km northwest of Dehgolan city, located on Cham Mirki River. Its height and tank volumes are 42 m and 64 million cubic meters, respectively. Furthermore, its overflow is made of free concrete with a length of 135 m, and the water diversion structure is two metal pipes with a diameter of 2 m and a length of 328 m. The rock material at the Ghocham dam site mainly comprises brown mud, marl, and light tuffs between conglomerate sandstone and black basalts covered by silty clay soils [41].

2.2. BIM-Based Modeling

In the current study, the time (4D) and cost (5D) of the 17 main activities of Ghocham dam were obtained by BIM using Autodesk Revit^® 2020, MS Project, and Navisworks. As a result, some clashes and changes were found. For this aim, the whole plan of the project was divided into 14 sections of equal length. Each section was modelled in the family environment of Revit with swept blend form, and then all of them moved to the project environment. So, the volume of materials and other required information was extracted from the material takeoff of Revit. Based on the information supplied, the project’s schedule was created in MS Project, thereby providing the time and cost of the project based on the BIM process. Finally, an animation of the construction process was developed by Navisworks; as a result, some clashes with the integrated model were detected. Figure 2 shows the 11th section of the Ghocham dam modelled in Revit. In the following, the algorithms used are briefly explained.

2.3. Algorithms

2.3.1. Genetic Algorithms (GAs)

Genetic algorithms are a family of computational models that encode potential solutions or possible hypotheses for a specific problem in a chromosome-like data structure. They are inspired by Charles Darwin’s theory of natural evolution, which adopts the survival of the fittest [42]. GA was introduced by Holland [43]; however, then GAs were developed by Jong [44] and Goldberg [45]. The main idea of this algorithm is the transmission of inherited traits by genes that store information about all organisms in the genes. GAs are a set of decisions (chromosome composition) and a potential solution to a problem. Each string is evaluated following the fitness value of its objective function. Those who perform better (fitness value) survive longer than those who perform worse. In other words, in GAs, a population of practical solutions is trying to survive in assessing fitness in a search space. Genetic information is then exchanged between chromosomes by producing offspring (Crossover) or mutations. As a result, a new generation with a better survival ability is produced. Hence, the five main stages in GAs are (i) generating initial (zero) population, (ii) Fitness Function, (iii) Selection, (iv) Crossover, and (v) Mutation [46].

2.3.2. Simulated Annealing (SA) Algorithm

SA is one of the most preferred algorithms in optimization problems, which was inspired by the annealing process of the metal behavior suggested by Kirkpatrick et al. [47]. The annealing process represents the arrangements of optimal molecular metal particles, where the potential energy of the matter is minimized and seeks to cool the metals slowly following exposure to high heat. Generally, the SA algorithm adopts a continual motion due to the variable temperature parameter mimicking the metal annealing transaction [48]. The energy level and moving to any new stage of design variables can affect the objective function. Although this method was primarily developed for discrete problems, it can be utilized in continuous problems, similarly to GA [49].

2.3.3. Black Widow Optimization (BWO) Algorithm

Being a population-based optimization algorithm, the BWO algorithm is nature-inspired based on Latrodectus Hasselti’s lifestyle and bizarre behaviors. This algorithm was suggested by Hayyolalam and Pourhaji Kazem [50]. Spiders are spread worldwide and in all ecological environments, ranking 7th in total species diversity. The black widow spiders are primarily nocturnal species, and females spin their webs at night. However, when it comes to their sexuality, whenever a female black widow wants to mate, she puts specific points on her web with pheromones to appeal to the man’s attention. During or after mating, males are often cannibalized by females. However, these males appear to be more successful in reproduction than males that can escape. A female black widow may lay between 4 and 10 bags of eggs, each with an average of about 250 eggs. After hatching, the offspring become involved in the eating of siblings [51].

Nonetheless, they remain on their mothers’ web for a moment, which may even swallow the mother. This cycle leads to the survival of the fit and influential individuals, the best of which is the global optimum of the objective function. The population size can be controlled by density-dependent cannibalism and may be imperative in the population of black widow spiders. The BWO algorithm consists of four main stages, namely (i) the initial population of spiders that could be indispensable for creating a candidate widow matrix of size $N_{pop}\times N_{var}$, (ii) breeding to reproduce the novel generation, (iii) cannibalism, and (iv) mutation [50,52].

2.3.4. Battle Royale Optimization (BRO) Algorithm

The BRO algorithm is one of the population-based algorithms inspired by the strategy of the battle royale video games suggested by Rahkar Farshi [53]. The BRO utilizes a population of possible solutions to reach the leading solution. Any solution is considered as a soldier making an effort to conquer their closest soldiers. BRO commences with a random population evenly distributed all over the problem space. Each person (soldier/player) attempts to harm the nearest soldier by firing a gun in the following stage. Thus, soldiers in better situations harm their nearest neighbors. Finally, the best soldier will win at the end of the iteration.

2.3.5. Black Hole Mechanics Optimization (BHMO) Algorithm

BHMO algorithm is one of the physics-based algorithms developed by Kaveh et al. [54]. BHMO uses a vigorous mathematical kernel based on a covariance matrix between each variable and its cost. This covariance matrix causes searching for the optimum orientation for escalating or reducing the extent variable. Using this technique, any variable is quickly guided to its best comparative value. In addition, each variable is assumed to be independent of the others concerning the cost function. This feature escapes the local optimizations that exist in the search space. In addition to the mathematical core, a physical simulation assists in performing the variables in any step. Based on black hole mechanics, this physical simulation updates the variables in the vicinity of the assumption global best in each stage. Moreover, weak variables are eliminated due to the physical simulation after scrolling the whole by the mathematical core. According to Albert Einstein’s general theory of relativity, a black hole has a strong gravitational pull that swallows stars (the number of variables in the problem) and other astronomical objects. BHMO consists of four primary procedures: data generation (star positions), Kerr black hole creation, Schwarzschild black hole creation, and data elimination.

All algorithms were determined and performed with specific parameters in this study, as shown in

Table 1. Specific setting parameters of optimization algorithms.

Algorithms	Number of Population (npop)	Maximum Iterations	Crossover Probability (pc)	Mutation Probability (pm)	Initial Temperature	Temp. Reduction Rate	Rate of Cannibalism	Maximum Fault
GA	50	1000	0.8	0.3	-	-	-	-
SA	50	1000	-	-	0.025	0.99	-	-
BWO	50	1000	0.8	0.4	-	-	0.5	-
BRO	50	1000	-	-	-	-	-	4
BHMO	50	1000	-	-	-	-	-	-

.

2.4. Statement of the Optimization Problem

All 17 activities listed in

Table 2. Technical data of Ghocham Storage Dam.

Number	Activity	IF	Options	Time (day)	Cost ($)	Total Quality	Risk
1	Production and depot of materials	29.7	1	618	2,839,772.29	82.9	0.6
			2	725	2,889,977.86	89.6	0.55
			3	863	3,333,557	90.6	0.45
			4	1180	3,410,322.08	92.2	0.4
			5	1325	3,434,836.80	98.4	0.35
2	Excavation	5.74	1	370	4,423,56.13	70.4	0.5
			2	396	471,813.80	81.6	0.45
			3	405	498,030.90	89.2	0.3
			4	625	614,238.83	90.4	0.25
			5	776	677,675.64	95.8	0.2
3	Water diversion system	0.59	1	108	49,887.70	61.15	0.6
			2	125	5,777,1.12	73.25	0.52
			3	133	60,760.65	86.8	0.4
			4	620	65,808.38	89.8	0.2
			5	981	69,435.89	96.85	0.15
4	Installation of instrument	0.92	1	590	95,000.59	65.2	0.45
			2	650	99,413.75	84.2	0.4
			3	700	104,500.65	87.2	0.36
			4	865	105,943.76	91.8	0.3
			5	1100	108,341.907	99.2	0.25
5	Execution of watertight wall	0.29	1	76	23,294.62	63.7	0.6
			2	92	28,168.29	71.3	0.55
			3	100	30,437.25	81.5	0.45
			4	129	32,310	87	0.3
			5	148	34,482.99	96	0.2
6	Execution of Clay Core	3.49	1	547	280,737.01	63.6	0.55
			2	680	340,196.06	79.4	0.48
			3	745	370,893.38	80.5	0.35
			4	890	402,953.34	86.5	0.3
			5	937.5	412,170.10	99.3	0.25
7	Execution of upstream cofferdam	0.94	1	255	59,861.93	65.2	0.62
			2	300	736,38.78	72.9	0.5
			3	330	79,850.54	85.9	0.45
			4	390	105,705.03	87.2	0.4
			5	411	111,269.17	95.7	0.35
8	Execution of downstream slope	0.27	1	135	17,589.16	78.4	0.5
			2	150	20,253.38	86.6	0.48
			3	179	23,659.39	89.1	0.4
			4	185	29,688.48	91.8	0.3
			5	199	32,267.01	97.1	0.15
9	Execution of shell	28.04	1	584	2,479,199.62	62.5	0.65
			2	700	3,011,527.29	82.7	0.6
			3	749	3,191,887.04	84.4	0.52
			4	995	3,249,155.25	89.6	0.48
			5	1187	3,312,267.10	98.4	0.4
10	Filter	16.21	1	476	1,273,574.88	62	0.5
			2	580	1,578,142.74	80.45	0.45
			3	633	1,699,257.18	82.6	0.35
			4	910	1,782,747.89	87.2	0.3
			5	1131	1,914,451.23	99.1	0.2
11	Drainage	2.67	1	557	210,302.85	65.4	0.65
			2	650	236,849.44	81.2	0.5
			3	701	249,032.16	92.8	0.4
			4	810	305,495.09	94.2	0.3
			5	865.6	316,063.02	99.2	0.15
12	Riprap	1.75	1	402	148,457.60	61	0.45
			2	475	173,985.10	75	0.4
			3	525	191,141.19	84	0.3
			4	605	199,074.95	89	0.25
			5	640	207,777.73	97	0.1
13	Downstream Slope protection	2.51	1	431	183,128.60	61.8	0.6
			2	470	204,852.49	78.45	0.5
			3	533	234,328.72	87.7	0.3
			4	590	245,872.53	91.1	0.25
			5	719	297,138.96	98.05	0.15
14	Stabilized bromine	5.77	1	295	490,744.86	65.4	0.45
			2	325	561,580.62	80.6	0.35
			3	390	642,318.40	83	0.3
			4	542	659,361.98	90.2	0.2
			5	645	682,148.34	95.6	0.15
15	Overflow spillway	1.28	1	90	60,036.43	65.2	0.4
			2	112	85,059.44	81.6	0.35
			3	150	126,640.15	89.8	0.25
			4	252	132,695.37	92.3	0.15
			5	404	152,145.68	99	0.1
16	Crown of the dam	0.16	1	20	16,211.68	64.8	0.65
			2	26	17,340.41	81.8	0.5
			3	30	19,706.53	85.7	0.35
			4	118	20,901.50	90.7	0.25
			5	181	21,762.78	98.2	0.15
17	Installation of hydromechanical equipment	0.22	1	196	100,626.41	65	0.65
			2	210	94,197.85	80.1	0.58
			3	240	80,005	85.3	0.52
			4	736	51,719.71	89.6	0.45
			5	1108.7	26,724.98	98.4	0.4

were imported into the BIM model and analyzed in this research. A construction project’s activities and their interconnections are shown on an activity-on-node (AON) diagram with M nodes. Each activity could be carried out in many different ways, each with its range of possible outcomes in terms of time, cost, quality, and risk. By determining the optimal course of action for each activity, the TCQR tradeoff optimization strategy strives to reduce the project’s time, cost, and risk while simultaneously increasing the quality. Consequently, in Equation (1), the first objective function is to reduce the project’s length of time.

$$T_p=\mathit{IF} [\min \left(\max \left(S{T}_i+D_i\right)\right)\left]=\mathit{IF}\right[\min \left(\max \left(F{T}_i\right)\right)]; i=1,\dots ,M$$

(1)

where $D_i$ is each activity’s duration in the project; $S{T}_i$ and $F{T}_i$ show the start and finish times of activity, respectively; and $M$ elucidates the overall nodes in the project scheduling [55]. Additionally, direct costs (DC), indirect costs (IC), and tardiness costs (TC) make up a project’s overall cost (TC). While there are various methods for determining a project’s total cost, this analysis only considers direct, indirect, and tardiness costs for theory’s sake. Cost minimization is the objective of the following objective function, as shown in Equation (2):

$$\min C=D_{C_i}^j+I_{C_i}^j+TC$$

(2)

$$D_{C_i}^j={\displaystyle \sum }_{i=1}^n{C}_i^j$$

(3)

$$I_{C_i}^j=C_{ic}\times T$$

(4)

$$TC=\left\{\begin{array}{c}{C}_1\left(T_0-T\right) if T\le T_0\\ \left(e^{\frac{T-T_0}{T_0}}-1\right)\left(D_{C_i}^j+I_{C_i}^j\right) if T>T_0\end{array}\right.$$

(5)

where $T{C}_p$ shows the project’s overall cost; $D_{C_i}^j$ and $I_{C_i}^j$ demonstrate the direct and indirect cost associated with ith activity’s jth execution mode, respectively;$C_{ic}$ is the reward for completing the ith activity which is zero in the current study; TC shows the tardiness cost which is considered zero in the current study; $T_0$ is the project’s contractual planned duration;$C_1$ shows the reward for completing the task early; and $T$ is the total project duration [56,57]. The overall project quality is the sum of the quality of each activity, which might vary depending on the resources available for the project. The quality of the activities improves as their duration is extended, but the quality begins to decline at a certain point. Therefore, the quality performance index (QPIi) provided in Equation (6) represents the quality of each activity [57].

$$QP{I}_i=IF [a_i{t}_i^2+b_i{t}_i+c_i]$$

(6)

where $t_i$ is the duration of activity ith; $a_i$, $b_i$, and $c_i$ are the coefficients decided by the quadratic function regarding BD (Figure 3). The longest, best, and shortest durations are LD, BD, and SD, respectively. However, Equation (7) is used to determine BD. Finally, Equation (8) formulates the objective function for quality as follows:

$$BD=SD+0.613\left(LD-SD\right)$$

(7)

$$\max Q={\displaystyle \sum }_{i=1}^M\frac{QP{I}_i}{M}$$

(8)

The project’s conditions, delivery methods, and contract terms all significantly determine the real project risk. A function that combines the two elements—(i) the project’s overall float; and (ii) resource volatility—is referred to as a “risk value.” The float utilization may lead to higher project risk and schedule overruns when non-critical processes have a high level of temporal uncertainty. Therefore, construction managers must make timetable modifications to reduce unanticipated resource consumption changes during the project’s execution. Floating non-critical processes might lead to more efficient resource consumption [58,59,60]. Consequently, the fourth objective function for risk can be formulated as Equation (9):

$$\min R=IF [w_1\times \left(1-\frac{T{F}_c+1}{T{F}_{max}+1}\right)+w_2\times \left(\frac{{{\displaystyle \sum }}_{i=1}^{Pd}{\left(R_t-\overline{R}\right)}^2}{P_d{\left(\overline{R}\right)}^2}\right)+w_3\times \left(1-\frac{\overline{R}}{\max \left(R_t\right)}\right)]$$

(9)

where $T{F}_c$ and $T{F}_{max}$ show the total current float and total flexible scheduling float of the project; $\overline{R}$ elucidates uniform resource level; $R_t$ shows the resource required on day t; and w_i demonstrates the weights.

Finally, to evaluate the capability of the mentioned algorithms to the time–cost–quality–risk (All) tradeoff simultaneously, Equation (10) was used:

$$F\left(x\right)=IF [\frac{T-T_{min}}{T_{max}-T_{min}}+\frac{R-R_{min}}{R_{max}-R_{min}}+\frac{Q_{min}-Q}{Q_{max}-Q_{min}}]+\frac{C-C_{min}}{C_{max}-C_{min}}$$

(10)

The primary operations of the Ghocham Storage Dam each have five executive modes, according to Table 2, the research’s foundation. This table was prepared using the expertise and experiences of some brilliant people. Executive mode’s time and cost NO.1 represent the contractor’s first proposals, NO.3 comes from BIM, and NO.5 represents the project’s real-time and cost as determined by the construction’s current state. Based on the suggestions of industry experts, two more executive modes were also considered. Admittedly, contractors’ first estimates are sometimes unreasonable and idealistic to catch employers’ attention, which is why most projects fail. Because most contractors do not consider rework, conflicts, employer nonpayment, extreme weather, etc., each activity is arbitrarily stated in three quality indicators with different percentages. The proportion of the combined influence of the three quality modes yields the final quality in each line. Finally, a random risk percentage was determined for each activity based on the opinions of top professors and industry professionals.

3. Results and Discussion

Based on

Table 3. Results of different algorithms in optimization for the first scenario (time).

Algorithms	Time (Days)	Percentage Error
ga	521.4379	0
SA	546.7391	4.85
BHMO	526.1435	0.90
BRO	526.9079	1.04
BWO	530.7564	1.78

, the total project time based on the contractor’s offers, BIM, and actual was 790, 906, and 1489 days, respectively. Additionally, the total costs of the project based on offers, BIM, and actual were USD 35,825,939.56, USD 44,670,213.59, and USD 48,244,124.9 according to the project contracts in 2010, respectively. BIM could significantly reduce the time and cost of the Ghocham dam since BIM can detect clashes and provide beneficial communication and cooperation among stakeholders and the project team. Since balancing time, cost, quality, and risk of the project within the project’s scope has become an important criterion for evaluating a project’s success, seeking a time–cost–quality–risk tradeoff is becoming the main concern of stakeholders and project teams.

In this research, the lowest time (T_min) and maximum time (T_max) were equal to 521.4379 and 546.7391 days, respectively; the lowest cost (C_min) and the highest cost (C_max) were equivalent to 35,524,075.6 and 36,266,567.6$, respectively. The lowest quality (Q_min) and the highest quality (Q_max) were equivalent to 73 and 77.967035, respectively, and the lowest risk (R_min) and the highest risk (R_max) were equal to 0.293685 and 0.31941, respectively. The number of optimization variables in each scenario was 17, which corresponded to the 17 rows of the sample of the status of Ghocham dam. Table 3 presents the optimization results for the first scenario (time) using different algorithms. So, the GA had the 1st rank among other meta-heuristic algorithms; subsequently, BHMO achieved the 2nd rank. So, the GA algorithm achieved good results, which means that the genetic algorithm balances between exploration and exploitation processes. On the other hand, SA algorithms gave the largest value for the time of the Ghocham dam, indicating their weak capability in providing the optimum and least times in dam construction projects. Hence, project managers should employ the GA for time optimization purposes in their construction projects.

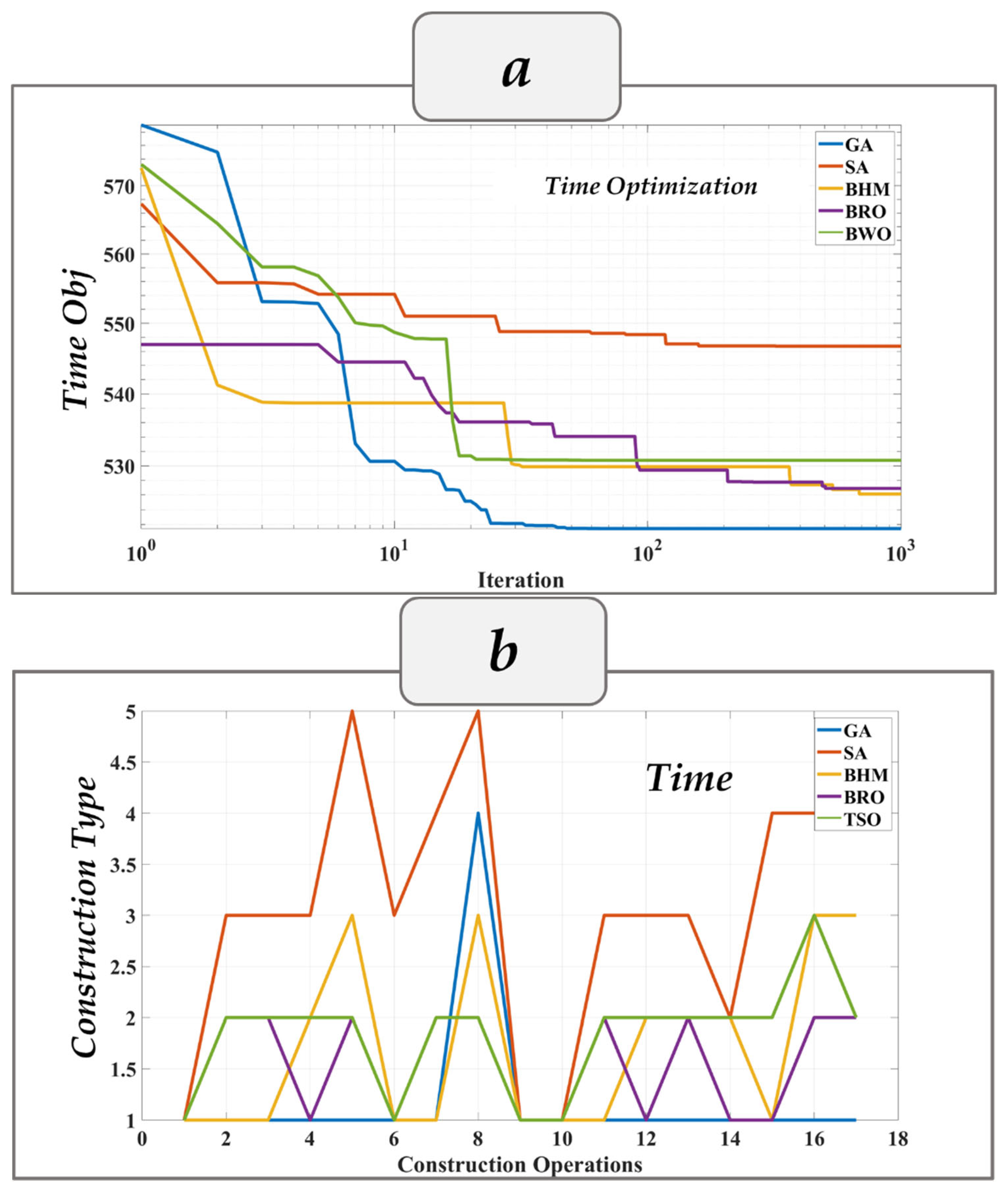
Figure 4a shows the convergence curves for the first scenario (time) using different algorithms. It can be observed that the GA algorithm converged quickly to the optimal value of 521.43 days in the first iterations, while the convergence speed of other algorithms was slower. Therefore, in comparison to the results produced using other methods, the convergence curves validated the GA’s quick convergence tendency. The GA method starts with the initialization of search agents, evaluates them using the cost function, and then updates the search agents in accordance with the function evaluation, which is how the computational complexity of the GA is expressed using big-oh notation. Moreover, the highest error percentage was related to the SA algorithm, with 4.62%, and the lowest was connected to the BHMO algorithm, which had an error of 0.89%. Hence, the GA and BHMO algorithms should be deemed appropriate in the time optimization of the Ghocham dam project. However, Figure 4b indicates the optimization variables’ status or the genotype space during the optimization process for this scenario. As shown through the mentioned figure, the selected algorithms of the stated scenario tended to mode number 1, representing the contractor’s offers. Furthermore, some algorithms selected mode 3 or BIM as the optimum value in some activities.

In contrast, the proportion of other executive modes, including the number 4 and the number 5, included lower values. It is important to note that in some cases, algorithms also leaned towards modes 2 and 3, requiring more attention to the interpolation process. It is apparent from the data that the contractors proposed an ideal close to the optimum time at the project’s initial phase regarding the algorithm’s results. Still, they did not consider risks and uncertainties. The emergence of reworks in the project and lack of cooperation and communication among contractors and owners could cause time overrun, considered a project failure. However, in dam construction projects, utilizing BIM processes from the whole life cycle could decrease the total executing time of the project, of which there was an exponential decrease of 583 days from 1489 to 906 days in the Ghocham dam.

The statistical results of the optimum time for different optimization algorithms based on 30 independent runs are presented in

Table 4. Statistical results for different algorithms based on 30 independent runs in the first scenario (time).

Algorithms	Best	Mean	Worst	Std.	Nfe	CT (s)
GA	521.43	521.50	521.74	0.08	50,000	2.78
SA	546.73	566.60	610.31	19.16	50,000	2.41
BHMO	526.14	529.67	533.67	1.68	50,000	1.80
BRO	526.90	529.35	532.67	1.53	50,000	4.86
BWO	530.75	532.01	535.42	1.08	50,000	13.85

. The value of N_fe (number of function evaluation) was assumed to be a constant value for all algorithms to compare and analyze the algorithms. Overall, it is notable that the GA optimization algorithm gave better results than other algorithms in the time optimization of the Ghocham dam. It can be observed that the computational time (CT) of the BWO optimization algorithms took significantly longer than other optimization algorithms, registered at nearly 14 s. In contrast, the second-lowest CT in any optimization algorithm was seen in the BHMO algorithm, accounting for approximately 1.71 s. Turning to the Standard Deviation (Std.), the lowest value of Std. was seen for the GA algorithms, which was nearly zero, while the SA algorithm gave the highest weight of Std., which means the data were more spread out. The large difference between the “best” and the “worst” values can influence the Std values. The greatest Std number indicates that the algorithm was unable to provide an analytical result that was consistent since the Std value measures how near the results from the 30 distinct trials are to its average value (mean value). This occurred because the algorithms were always trapped in the local results, especially for high-dimensional problems [61]. Regarding the worst cost obtained from algorithms, the SA optimization algorithms calculated the highest worst value, indicating the SA algorithm’s uncertainty in a single run.

Table 5. Results of different algorithms in optimization for the second scenario (cost).

Algorithms	Cost (USD)	Percentage Error
GA	35,524,075.6	0
SA	36,266,567.61	2.09
BHMO	36,119,823.65	1.67
BRO	35,999,010.06	1.33
BWO	35,670,839.86	0.41

illustrates the optimization results for the second scenario (cost) using different algorithms. The current table presents the percentage of changes or rate of the error to the best answer reported by the best algorithms, which were GA and BWO algorithms in this scenario. The BWO algorithm provides a proper balance between the exploration and exploitation stages, one of the most critical features of meta-heuristic algorithms. The mentioned algorithm could obtain outstanding results compared to other experimental algorithms, especially compared to BRO. However, regarding the results, the SA optimization algorithm was ineffective in optimizing the Ghocham dam’s cost, providing the highest cost in the Ghocham dam. Consequently, project managers ought to utilize the GA for cost optimization purposes in their construction projects.

Figure 5a shows the convergence curves for the second scenario (cost) using different algorithms. It can be observed that the GA and BWO algorithms converged quickly to the optimal value of 35,524,075.6 and 35,670,839.86$, respectively, in the first iterations, while the convergence speed of other algorithms was slower. Moreover, the highest error percentage of 2.09%, was related to the SA algorithm, and the lowest error of 0.41% was related to the BWO algorithm. Figure 5b elucidates the genotype space during the optimization process for this scenario. As can be seen, the selected algorithms of this scenario, in most cases, tended to mode number 1, which represents the contractor’s offers, while the proportion of other executive modes, including mode number 3 (BIM) and mode number 5, were lower values.

In some cases, the algorithms also leaned to modes 2 and 4, which required more attention to the interpolation process. Like the first scenario, the contractors had a nearly optimum quantity surveying and estimating at the initial stage of the project; however, increasing clashes and reworks, lack of effective cost and budget management, and squandering materials could trigger a cost overrunning. BIM significantly reduced the project’s cost from USD 48,244,124.9 to USD 44,670,213.59, a 7.40% reduction in cost.

Table 6. Statistical results for different algorithms based on 30 independent runs in the second scenario (cost).

Algorithms	Best	Mean	Worst	Std.	Nfe	CT (s)
GA	35,524,075.6	7.90 × 1010	3.67 × 1011	1.15 × 1011	50,000	3.10
SA	36,266,567.61	1.49 × 1011	4.05 × 1011	1.13 × 1011	50,000	2.45
BHMO	36,119,823.65	2.31 × 1011	3.75 × 1011	9.47 × 1010	50,000	1.81
BRO	35,999,010.06	1.95 × 1011	3.76 × 1011	9.01 × 1010	50,000	4.57
BWO	35,670,839.86	1.47 × 1011	3.74 × 1011	1.03 × 1011	50,000	14.05

shows the statistical results of the optimum cost of the Ghocham dam for different optimization algorithms based on 30 independent runs. Overall, GA and BWO algorithms gave the best objective function value for the second scenario. Like the first scenario, the BRO optimization algorithm took a longer computational time than the other algorithms, followed by the BWO optimization algorithm with nearly 14.05 s. In comparison, the better and lower value of CT in any optimization algorithms was seen in the BHMO algorithm, registered at nearly 1.81 s. Regarding the worst value obtained from algorithms, the SA optimization algorithms calculated the highest worst value, which means the SA algorithm is not an appropriate algorithm for a single run of cost optimization. However, the lowest value of the Std of the BRO optimization algorithm indicates how close the results obtained from the 30 different trials to its mean value, while the GA optimization algorithm could not provide a consistent result in the analysis.

Table 7. Results of different algorithms in optimization for the third scenario (quality).

Algorithms	Quality	Percentage Error
GA	97.89	0
SA	79.03	23.86
BHMO	78.29	25.03
BRO	79.23	23.55
BWO	79.24	23.53

shows the optimization results for the third scenario (quality) using different algorithms. This table presents the percentage of changes or errors to the best answer reported by the best algorithms. However, only the GA algorithm provided high quality rather than other meta-heuristic algorithms, registered at a mere 97.89, followed by the BWO optimization algorithm. In stark contrast, the BHMO gave the least and improper quality value in this project, elucidating its weak performance in providing the highest quality in dam construction projects.

Figure 6a shows the convergence curves for the third scenario (quality) using different algorithms. It can be observed that the GA algorithm converged quickly to the optimal value of approximately 97.89 in the first iterations, while the convergence speed of other algorithms was slower. Moreover, the highest error, with 25.03%, was related to the BHMO algorithm, and the lowest error, with 23.53%, was related to the BWO algorithm. However, the values of quality obtained by the SA and BHMO algorithms were nearly close. Figure 6b demonstrates the genotype space during the third scenario’s optimization process.

In most cases, the selected algorithms of this scenario tended to mode number 3, which BIM obtained, while the proportion of other executive modes, including modes number 1 and number 5, were lower values. It is important to emphasize that the algorithms also tended to modes 2 and 4, requiring more attention to the interpolation process. It can be understood that utilizing BIM in dam construction management can provide an optimum quality value for organizations.

Table 8. Statistical results for different algorithms based on 30 independent runs in the third scenario (quality).

Algorithms	Best	Mean	Worst	Std.	Nfe	CT (s)
GA	97.89	93.19	73	6.88	50,000	3.47
SA	79.03	77.10	76.10	0.78	50,000	2.46
BHMO	78.29	77.60	76.65	0.35	50,000	1.97
BRO	79.23	76.01	73.49	1.40	50,000	4.69
BWO	79.24	75.39	73.78	1.24	50,000	14.35

elucidates the statistical results of the optimum quality of the Ghocham dam for different optimization algorithms based on 30 independent runs. Overall, the GA optimization algorithm gave the best objective function value for the third scenario in the Ghocham dam. The worst value was given by the BHMO algorithm, indicating its insufficiency for a single run of quality optimization. Although the BWO optimization algorithm had a longer computational time than the other algorithms and lasted roughly 14.35 s, it provided the highest quality value compared to all optimization algorithms, not considering the GA. Furthermore, the lowest value of the Std of the BHMO algorithm indicates how close the results obtained from the 30 different trials were to their mean value. The GA optimization algorithm could not provide a consistent result in the analysis. Nonetheless, based on the results obtained, the BHMO algorithm demonstrated an unsatisfactory role in the quality optimization of the Ghocham dam.

Table 9. Results of different algorithms in optimization for the fourth scenario (risk).

Algorithms	Risk	Percentage Error
GA	0.293	0
SA	0.319	8.75
BHMO	0.302	2.96
BRO	0.300	2.33
BWO	0.307	4.58

shows the optimization results for the fourth scenario (risk) utilizing different algorithms. In this table, the percentage of changes or the error to the best answer reported by the best algorithms, GA and BRO algorithms, was also presented. On the other hand, the highest risk value was obtained by the SA algorithm, which could be deemed as an unacceptable algorithm in giving the least risk in dam construction projects.

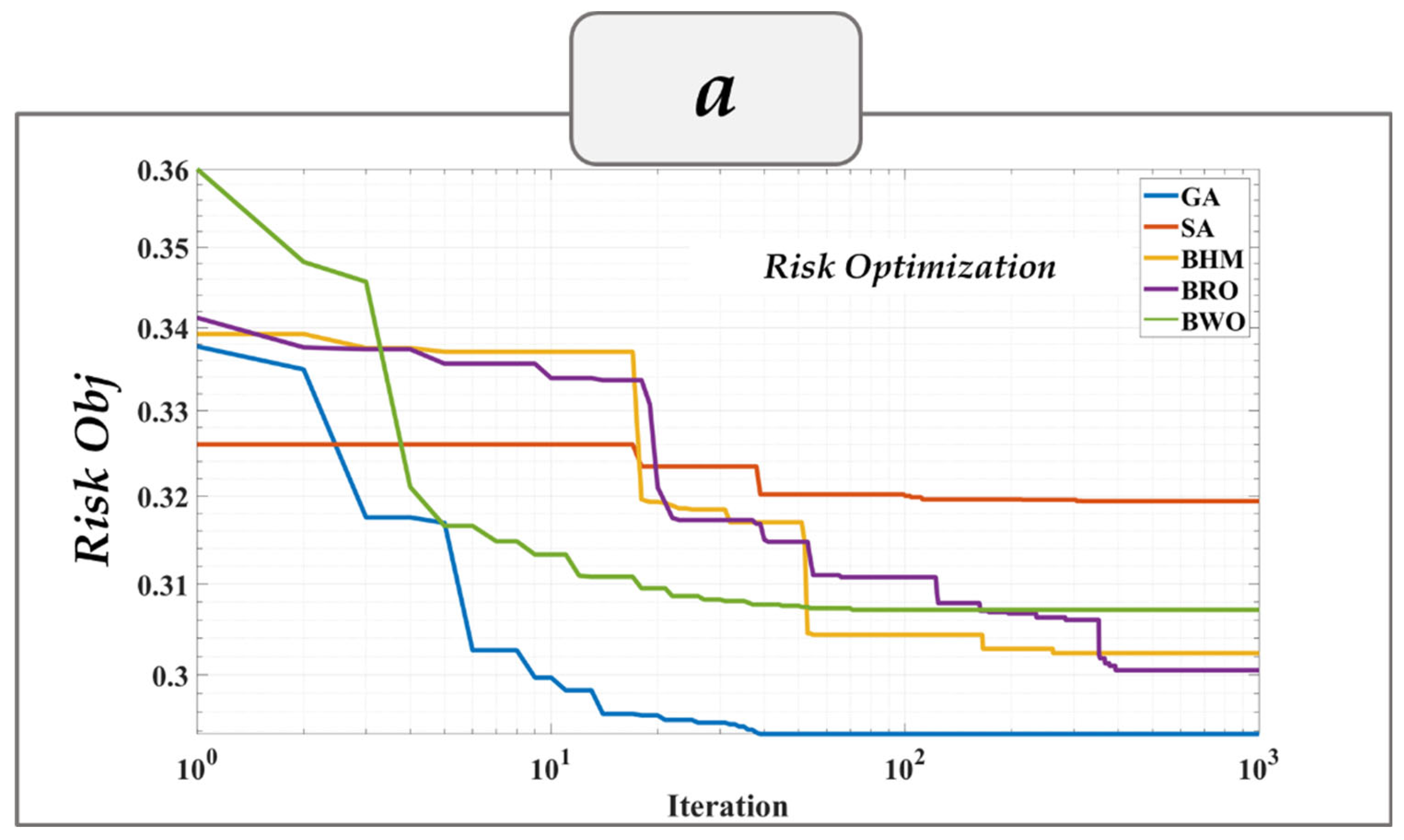
Figure 7a shows the convergence curves for the fourth scenario (risk) using different algorithms. It can be observed that the GA and BRO algorithms converged quickly to the optimal value of 0.293 and 0.300, respectively, in the first iterations. In contrast, the convergence speed of the other algorithms was slower. Moreover, the highest error, with an 8.75 percent error, was related to the SA algorithm, and the lowest error, with 2.33, was related to the BRO algorithm. Figure 7b shows the risk scenario’s genotype space during the optimization process. As can be seen, the selected algorithms of this scenario, in most cases, tended to mode number 5, which was obtained by the contractor’s offers, whereas the proportion of other executive modes, including mode number 1 and number 3 (obtained from BIM), which were lower values. It is worth noting that the algorithms also tended to modes 2 and 4, which require more attention to the interpolation process.

Table 10. Statistical results for different algorithms based on 30 independent runs in the fourth scenario (risk).

Algorithms	Best	Mean	Worst	Std.	Nfe	CT (s)
GA	0.293	0.294	0.295	0.0005	50,000	2.88
SA	0.319	0.343	0.399	0.0221	50,000	2.46
BHMO	0.302	0.305	0.310	0.0019	50,000	1.92
BRO	0.300	0.306	0.311	0.0027	50,000	4.33
BWO	0.307	0.308	0.310	0.0008	50,000	13.04

demonstrates the statistical results of the optimum risk of the Ghocham dam for different optimization algorithms based on 30 independent runs. The GA optimization algorithm gave the best objective function value for the fourth Ghocham dam scenario. While the worst value was given by the SA optimization algorithms, signifying its poor reliability for a single trial run of risk optimization. Although the BWO optimization algorithm took a longer computational time than the other algorithms and lasted nearly 13.04 s, it provided the lowest risk value compared to the SA optimization algorithm. However, the CT for the GA algorithm was 1.81, greater than that of SA.

Furthermore, the BWO optimization algorithm obtained the lowest value of the Std, which shows how close the results obtained from the 30 different trials were to their mean value. In stark contrast, due to the higher value of Std rather than other algorithms, the SA optimization algorithm could not provide a consistent result in the analysis. Nonetheless, based on the results obtained, the GA and BRO optimization algorithms demonstrated an unsatisfactory role in the risk optimization of the Ghocham dam.

Table 11. Results of different algorithms in optimization for the fifth scenario (all).

Algorithms	Total	Percentage Error
GA	1.92	0
SA	3.52	83.14
BHMO	3.08	60.03
BRO	3.12	62.48
BWO	2.53	31.77

shows the optimization results for the fifth scenario (total) using different algorithms. The percentage of changes or rate of the error to the best answer reported by the best algorithms, which in this scenario was the GA algorithm, are presented. Consequently, the GA algorithm can be considered an ideal algorithm for TCQRT problems in hydropower construction projects with a higher level of complexity.

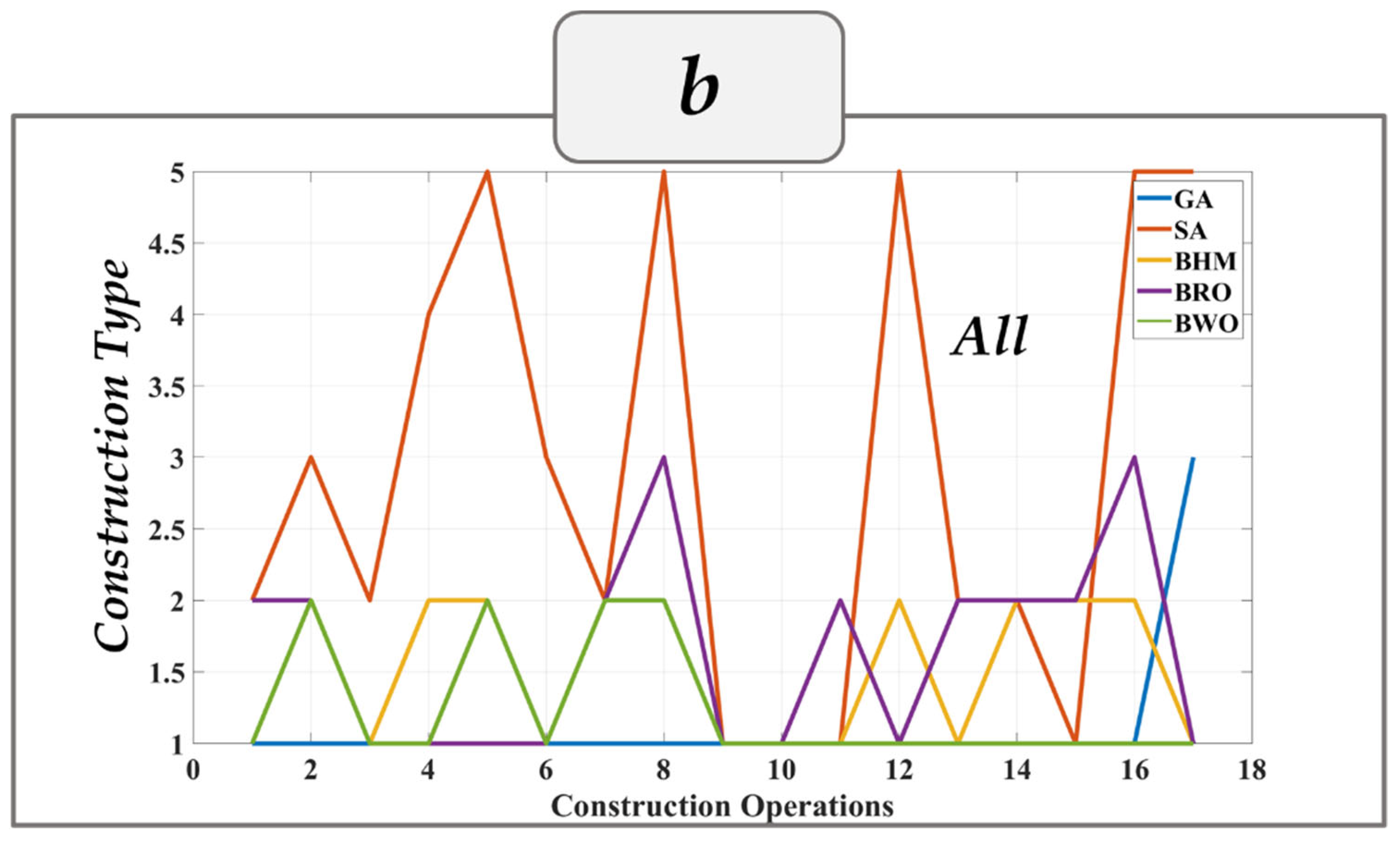
Figure 8a shows the convergence curves for the fifth scenario (total) using different algorithms. It can be observed that the GA and BWO algorithms converged quickly to the optimal value of 1.92 in the first iterations. On the other hand, the convergence speed of other algorithms was slower. Moreover, the highest error percentage was related to the SA algorithm, with an 83.14 percentage error, and the lowest error was connected to the BWO algorithm, which had an error of 31.77. Figure 8b shows the status of the optimization variables or the genotype space during the optimization process for this scenario. As can be seen, the selected algorithms of this scenario, in most cases, tended to mode number 1, which represents the contractor’s offers, while the proportion of other executive modes, including mode number 3 (obtained from BIM) and mode number 5, which were lower values. In some cases, the algorithms also leaned to modes 2 and 4, which required more attention to the interpolation process.

Table 12. Statistical results for different algorithms based on 30 independent runs in the fifth scenario (all).

Algorithms	Best	Mean	Worst	Std.	Nfe	CT (s)
GA	1.92	1.94	2.09	0.0408	50,000	2.96
SA	3.52	4.03	4.48	0.2517	50,000	2.43
BHMO	3.08	3.20	3.27	0.0406	50,000	2.08
BRO	3.12	3.25	3.38	0.0581	50,000	4.56
BWO	2.53	2.64	3.03	0.0910	50,000	12.56

demonstrates the statistical results of the Time–Cost–Quality–Risk Trade-off of the Ghocham dam for different optimization algorithms based on 30 independent runs. Overall, the GA optimization algorithm gave the best value of the objective function for the fifth scenario in the Ghocham dam, which means the GA algorithm provided relevant results for the Time–Cost–Quality–Risk Trade-off of the Ghocham dam, while the worst value was given by the SA optimization algorithms, signifying its poor reliability for a single trial run of risk optimization. Like all previous scenarios, the BWO optimization algorithm took a longer computational time than the other algorithms; its CT lasted nearly 12.57 s. However, the CT for the GA algorithm was 1.88, greater than that of SA.

Furthermore, the BHMO algorithm obtained the lowest value of the Std, which shows how close the results obtained from the 30 different trials were to their mean value. On the other hand, because of the higher value of Std rather than other algorithms, the SA optimization algorithm could not provide a consistent result in the analysis. Nonetheless, based on the results obtained, only the GA optimization algorithm played a satisfactory role in the Time–Cost–Quality–Risk Trade-off in the Ghocham dam.

4. Conclusions

According to the acquired findings, it is feasible to operate on project management by planning, directing, and managing resources to accomplish particular objectives in other development projects while considering time, cost, quality, and risk indicators. This study focused on the role of BIM and miscellaneous meta-heuristic algorithms in dam construction management. Hence, five different meta-heuristic algorithms were implemented in MATLAB to optimize a dam construction project’s time, cost, quality, and risk; for this purpose, the Ghocham dam in Iran was selected as a case study. Finally, a TCQR tradeoff was analyzed. According to the results, it is evident that the implementation BIM process can decrease the time and cost of dam construction projects while not providing optimal time and cost.

Additionally, the project team and contractors can use the BIM process to achieve the desired optimum quality in their dam projects. According to the findings, the suggested objective function and genetic algorithms (GAs) and Black Hole Mechanics Optimization (BHMO) algorithm could be suitable models for other organizations to improve the construction sector’s quantitative and qualitative indicators of other hydropower projects of this research. According to these results, the GA and BHMO optimization algorithms provided better and more appropriate optimal results, and the general results are as follows:

• In the implementation BIM process in the Ghocham dam’s construction management, there was a reduction of 7.4% in cost and 39.1% in time;
• Using the GA optimization algorithm reduces approximately 42.5% and 65% of the project execution time compared to the BIM process and the actual execution time of the Ghocham dam project, respectively. Furthermore, the SA and BHMO algorithms provided the lowest computational time in time optimization compared to other algorithms;
• The best performance in reducing project costs was for the GA and BWO algorithms, while other algorithms charged higher costs, which is not cost-effective. The BHMO optimization algorithm gave the best and lowest computational time (CT), accounting for nearly 1.81 s;
• The GA algorithm was the only algorithm that performed best in the third scenario (quality) by calculating the 97.89% quality index. In contrast, other algorithms did not perform well, while the BHMO algorithm calculated the worst quality;
• Only the GA and BRO optimization algorithms provided the lowest risk index, indicating their appropriate performance in risk optimization in the Ghocham dam;
• The BWO optimization algorithm gave all scenarios the longest computational time (CT);
• In the time–cost–quality–risk tradeoff, only the GA algorithm converged rapidly to the optimal value in the first iterations, while the convergence speed of the other algorithms was slower.

The limitation of this research work is that only a limited number of metaheuristic algorithms were considered for tradeoff problems. Future works should focus on assessing and comparing the efficiency of different novel metaheuristic optimization algorithms with classic algorithms such as GAs. They should also consider other modes in their resource tradeoff problems, such as carbon dioxide (CO₂) emissions by each resource option in their life cycle. Furthermore, they should analyze the efficiency of the metaheuristic algorithms used in this study in other infrastructure projects regarding optimizing the survival pyramid’s components, and they could propose a novel multi-objective version of one of the newly proposed metaheuristics to tradeoff the mentioned modes in two-by-two manners.