Next Article in Journal
Requirements and Architecture of a Cloud Based Insomnia Therapy and Diagnosis Platform: A Smart Cities Approach
Previous Article in Journal
Role of Internet of Things (IoT) and Crowdsourcing in Smart City Projects
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Smart Cities
Volume 4
Issue 4
10.3390/smartcities4040069
smartcities-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Use of Machine Learning for Leak Detection and Localization in Water Distribution Systems

by
Neda Mashhadi
,
Isam Shahrour
*,
Nivine Attoue
,
Jamal El Khattabi
and
Ammar Aljer
Civil and Geo-Environmental Engineering Laboratory (LGCgE), Lille University, 5900 Lille, France
*
Author to whom correspondence should be addressed.
Smart Cities 2021, 4(4), 1293-1315; https://doi.org/10.3390/smartcities4040069
Submission received: 8 August 2021 / Revised: 27 September 2021 / Accepted: 28 September 2021 / Published: 1 October 2021
(This article belongs to the Special Issue Machine Learning and Big Data in Geosciences)
Browse Figures
Versions Notes

Abstract

:
This paper presents an investigation of the capacity of machine learning methods (ML) to localize leakage in water distribution systems (WDS). This issue is critical because water leakage causes economic losses, damages to the surrounding infrastructures, and soil contamination. Progress in real-time monitoring of WDS and ML has created new opportunities to develop data-based methods for water leak localization. However, the managers of WDS need recommendations for the selection of the appropriate ML methods as well their practical use for leakage localization. This paper contributes to this issue through an investigation of the capacity of ML methods to localize leakage in WDS. The campus of Lille University was used as support for this research. The paper is presented as follows: First, flow and pressure data were determined using EPANET software; then, the generated data were used to investigate the capacity of six ML methods to localize water leakage. Finally, the results of the investigations were used for leakage localization from offline water flow data. The results showed excellent performance for leakage localization by the artificial neural network, logistic regression, and random forest, but there were low performances for the unsupervised methods because of overlapping clusters.

1. Introduction

Water leakage constitutes an important issue in managing water distribution systems because it causes economic losses, damages to the surrounding soil and infrastructures, and soil contamination. According to the World Bank [1], the non-revenue water (NRW) level in developing countries ranges from 40% to 50% of the water pumped into the distribution systems. The American Water Works Association Research Foundation (AWWARF) estimated that water utilities in the United States suffered from 250,000 to 300,000 main breaks per year, causing approximately USD 3 billion in annual damages [2]. In [3], it was reported that the water losses from leakage in some countries in the Middle East represented 50% of the water supply. Reference [4] identified leakage as one the most common operational problems in the water distribution system of Athens.
Relevant research has been conducted for the development of methods for water leakage detection. These methods can be classified into hardware- and software-based methods. The first category uses various technologies such as acoustic monitoring [5], gas injection [6], thermography [7], ground-penetrating radar [8], and free-swimming systems [9]. Acoustic monitoring includes technologies for listening sticks, leak noise correlation, and leak noise loggers. These methods have high performances but suffer from the high cost. The gas injection method injects a non-toxic, water-insoluble, and lighter-than-air gas into water pipes. The leak can be detected by scanning the ground surface using gas detectors. This method is characterized by speed tracing, but its high cost reduces its practical use. The ground-penetrating radar method is based on tracking the reflection of electromagnetic waves generated at the ground surface. It provides information about the presence of anomalies in the subsoil. Water leaks can be detected by identifying soil voids created by water leaks or by detecting sections of pipes that appear deeper than they actually are due to the increase in the dielectric properties of the surrounding saturated soils. This method can be used for metallic or plastic pipes, but it is expensive and time-consuming. The free-swimming systems methods are based on introducing the water pipes of capsules with an embedded power source, electronic components, and instrumentation (acoustic sensor, accelerometer, magnetometer, GPS synchronized ultrasonic transmitter, and temperature sensor). These capsules record the internal environment of the pipes and send the recorded data to a server. The analysis of registered data permits detection and localize anomalies related to water leakage. This method is well adapted for pipes with large diameters.
The second category of water leakage detection methods is based on analyzing data related to the water operation system. It includes statistical methods [10,11], the water balance method [12], the minimum night flow method [6], the real-time transient modeling [13], and the negative pressure wave [14]. Leak detection using statistical methods is based on the determination of the statistical characteristics of the water flow and pressure in the water network and the determination of the outliers, which could be related to water leakage. The efficiency of these methods is related to the quality of the recorded data and the regularity of the consumption patterns. The water balance method relies on the principle of mass conservation. A leak is identified if the difference between the amount of water put into the water network and the sum of water consumption and usage exceeds an established tolerance. The efficiency of this method depends on the quality of the monitoring system and the knowledge of the water usage in the water network. The MNF method is based on water flow analysis when the water demand is low and the water pressure is high. A leak alarm is generated when the MNF exceeds a threshold, depending on the water network’s characteristics and usage. This method is widely used; its efficiency depends on the quality of the water network monitoring and the regularity of the water usage. The real-time transient modeling method is based on comparing the hydraulic recorded data with the results of hydraulic models. The efficiency of this method depends on the quality of recorded data and the quality of the hydraulic models and their calibration. The harmful pressure wave method is based on tracking acoustic waves created by the water pressure drop resulting from the water leak. Pressure sensors are installed at the beginning and the end stations of the pipeline. The record of the generated waves allows for the detection and localization of water leakage. This method is efficient but suffers from high operating costs.
The large variety of developed methods highlights the great difficulty of detecting and localizing water leakage in urban water distribution systems because of the complexity.
The recent progress in the real-time monitoring of the water distribution systems has been offering new opportunities to develop data-based methods for water leakage detection and localization. Machine learning-based methods have been widely used to detect and localize water leakage in water distribution systems.
Caputo and Pelagagge [15] used artificial neural networks (ANNs) to detect and localize the water leak in water distribution systems. Data were generated using a hydraulic model of the water network for various operating conditions and cases with different locations and amounts of the water leak. The method detected leaks correctly in small water distribution systems. Salam et al. [16] used the radial basis function neural network method for leak detection. The hydraulic software, EPANET, was used for data generation. The pressure variations in the water network were used as input data for the ANN model, while the leak intensity and locations constituted the output parameters. The authors showed that the method could detect the magnitude and the location of leakage with a 98% accuracy. Mounce et al. [17] used the ANN method to identify anomalies in the water distribution time series data in a pattern matching-based approach. This method was based on the similarity research between new events and profiles established from past events. This research allowed the classification of the new events and consequently to identify abnormal events, which could be related to leak. Recently, Rojek and Studzinski [18] used the ANN method to detect and localize water leakage in the water distribution systems. Tests on real off-line data showed that the ANN method correctly identified the localization of simulated leaks.
Zhang et al. [19] used the multiclass support vector machine method (SVM) for leakage detection in a large-scale water distribution network. First, the method K-means clustering was used to subdivide the water network into leakage zones. Then, data with leakage events were generated using the Monte Carlo method together with the hydraulic model. The authors showed that the multiclass SVM could identify the leakage zone using flow and pressure data. However, Chan et al. [20] reported that this method faced a significant challenge concerning determining the number of clusters and the high impact of the random determination of the first cluster on the clustering process.
Soldevila et al. [21] used the K-nearest neighbors to classify data generated by the hydraulic model EPANET from the simulation of leakage events at the totality of the nodes of the water distribution network. Data were then used to train the K-Nearest Neighbors model to localize the leakage area. The good performance of this method in the localization of one water leak was assessed on three examples.
Ciupke [22] used the regression tree method to detect water leakage. Alerts were established when the water flow exceeded the normal water flow range. The method was tested on real examples and gave very good results, even for detecting small leaks.
Van der Walt et al. [23] analyzed the capacity of Bayesian probabilistic analysis, the support vector machine, and an artificial neural network to detect and localize water leakage from pressure and flow data. These methods were compared to data generated from numerical modeling and laboratory tests. Since analysis showed that the performances of these methods depend on the complexity of the water network and the amount of available data, the authors did not propose general recommendations for the use of the machine learning methods for leak detection.
This literature review shows that intensive research has been conducted to use machine learning methods for leakage localization. However, the literature is still missing a comparison of the different categories of machine learning methods to localize water leakage in the same water distribution system. This paper proposes to fill this gap by comparing the capacities of various categories of machine learning methods to localize leakage in a complex water distribution system based on the water network of the scientific campus of Lille University in France.

2. Materials and Methods

2.1. Research Methodology

This research aimed at investigating the capacity of machine learning methods to localize the position of leakages in water distribution systems using flow and water pressure data. Following the methodology proposed by different scholars [15,16,19,23], the hydraulic software EPANET was used to create data related to different scenarios of leakage in the water distribution system of the scientific campus. For each leakage scenario, EPANT provided the water flow from the supply sections and the pressure in five hydraulic areas of the campus. The generated data were then used for training and testing six machine learning methods. The tests were first conducted with water flow and pressure data.
The performances of the machine learning methods were investigated using the parameters accuracy, precision, recall, and F1-score, which are determined from the confusion matrix (Table 1):
P r e c i s i o n = T r u e p o s i t i v e T r u e p o s i t i v e + F a l s e p o s i t i v e
R e c a l l = T r u e p o s i t i v e T r u e p o s i t i v e + F a l s e n e g a t i v e
F 1 − s c o r e = 2 × P r e c i s i o n × R e c a l l P r e c i s i o n + R e c a l l
A c c u r a c y = T r u e p o s i t i v e + T r u e n e g a t i v e T r u e p o s i t i v e + F a l s e p o s i t i v e + T r u e n e g a t i v e + F a l s e n e g a t i v e
The following sections present the generated data and the machine learning methods used in this research.

2.2. Data Generation

Data were generated using the software EPANET, developed by the Water Supply and Water Resources Division (Formerly the Drinking Water Research Division) of the US Environmental Protection Agency.
The water distribution network of the scientific campus of Lille University was used as support for this research. This campus represents a small town with approximately 150 buildings and 25,000 users including students, faculty members, and technical, and administrative staff [24]. Figure 1 illustrates the water distribution network of the campus [25,26]. The water network is composed of 15 km of strongly meshed pipes. The water company supplies the campus with water in three sections, located in the North, West, and South of the campus (Figure 1).
Figure 2 shows the EPANET hydraulic model of the campus. It includes 45 pipes and 33 junctions. The water network was divided into five hydraulic zones as indicated in Figure 2. Data were generated by modeling the water leakage according to 215 leak scenarios (leak configuration), summarized in Table 2 and Figure 2. Zone 1 was the largest and most complex zone. It included 62 leakage scenarios. Zones 4, 5, 2, and 3 had 47, 41, 35, and 41 leakage scenarios.
For each leak scenario, EPANET was used to determine the water flow from the three supply sections (FL1, FL2, and FL3) and the pressure values at the five observation nodes (Table 3, Figure 2).
Each leak scenario was modeled under two conditions. The first condition concerned a constant pressure at the water supply sections, which were considered tanks with a constant water height (H = 40 m). The second condition concerned the water leak, which was considered by the following condition between the pressure (P) and water:
Q = C × Pa
The parameters C and a characterize the water leakage, which designate the emitter coefficient and emitter exponent, respectively. Simulations were conducted with a = 0.5 and C = 1.
Table 4 provides a statistical analysis of the generated leak data. It shows that tank 1 provided the highest water supply rate (supply flow rate = 0.41), followed by tank 2 (flow rate = 0.35). This means that the water supply of the campus was mainly provided from the north and west of the campus, where the construction density was higher than that in the south of the campus. The highest average pressure is observed in zone 3, located in the South of the campus (average pressure approximately 35 m), followed by zones 5 and 4 (average pressure approximately 30 m). The average pressure in zones 1 and 2 was approximately 28 m.
Figure 3 illustrates the impact of the leakage position on the flow rate ratios FL1, FL2, and FL3. It shows that leakage in zones 1 and 2 caused a high flow rate from tank 1 (FL1), a medium flow rate from tank 2 (FL2), and a low flow rate from tank 3 (FL3). Leakage in zone 3 caused a high flow rate from tank 3 (FL3), medium flow from tank 2 (FL2), and low flow from tank 1 (FL1). Leakage in zone 4 caused a high flow rate from tank 2 (FL2) and low to medium flow from tank 3 (FL3). Finally, leakage in zone 5 caused a high flow rate from tank 1 and tank 2 (FL1 and FL2) and flow from tank 3 (FL3). Table 5 summarizes the impact of the leakage position on the water flow rate from the three supply sections. It can be observed that a high flow rate from tank 2 (FL2) could be attributed to leakage in zone 4, and a high flow rate from tank 3 (FL3) could be attributed to leakage in zone 3. A high flow rate from tank 1 (FL1) could be attributed to leakage in zone 1. The medium flow rate from tanks 1 and 2 could be related to leakage in zones 2 and 5.
Figure 4 illustrates the impact of the leakage position on the pressures from PZ1 to PZ5. It shows that leakage in each zone caused a significant drop in the pressure in the leakage zone. It also shows a significant impact of some leakages in a zone on the pressure in other zones, such as the impact of (i) leakage in zone 1 on the pressure in zone 2 (ii) leakage in zone 2 on the pressure in zone 1, (iii) leakage in zone 3 on the pressure in zone 4, and (iv) leakage in zone 5 on the pressure in zone 2.

2.3. Use of Machine Learning Methods

Analyses were conducted with three supervised machine learning methods (logistic regression, decision tree, and random forest), two unsupervised methods (hierarchical classification and a combination of the principal component analysis (PCA) and the K-means methods, and an artificial neural network (ANN). In addition, simulations were conducted using the Kaggle platform (https://www.kaggle.com, accessed on 20 September 2021). The following sections briefly present the methods used in this research.
The logistic regression is used for binary classification [27]. The method used in this work waws based on the functions:
h_(θ) (x) = g(θ^(T)x)
g(z) = 1/(1 − e^(−z) )
where x is the input data, and θ is the parameter determined by the minimization of the cost function.
The decision tree method is based on applying a series of questions to determine the model response [28,29]. This method classifies a population into branch-like segments that construct a tree with a root node, internal nodes, and leaf nodes. The model generates a flowchart (tree), where each internal node (represented by a question) tests some features and guides down through the branches (the result of the splitting) with a “gini” coefficient, which is defined as follows:
G = ∑ i = 1 c p i x 1 − p i
The parameter c designates the number of total classes; p(i) is the probability of picking a data point with class i.
Random forest methods are used for both classification and regression by combining randomized decision trees [30,31]. Each decision tree gives a vote for a target variable. The random forest algorithm chooses the combination that obtains the highest vote. This method has high predictive accuracy; it is efficient on large data sets and works well with missing data. However, it suffers from interpretation difficulties and overfitting in the case of noisy data.
The hierarchical classification method is used to build a hierarchy of clusters. The results of clustering are usually presented in a dendrogram. Hierarchical classification could be conducted using (i) a “bottom-up” approach, where each observation starts in its cluster, and pairs of clusters are merged as one move up the hierarchy or (ii) a “top-down” approach, where all observations start in one cluster; splits are performed when moving down the hierarchy. The Ward method is used in this analysis [32]. The PCA method is used to reduce the input data dimension by focusing on the principal components [33].
K-means clustering is a type of unsupervised learning. It aims at partitioning n observations into k clusters [34]. Initially, K initial means are randomly generated. Then, K clusters are created by associating each observation with the nearest centroid. Next, the objective function, the sum of the distance, is optimized until the best cluster centers candidates are found. Finally, data points are clustered based on feature similarity.
The ANN is inspired from the human brain functioning [35]. It transforms the input data (input layer) through a series of neural layers (hidden layers) to output data (output layer). The transformation is based on weights, which are adjusted by optimizing the prediction of a training data set. The Sigmoid function is used in data transformation.

2.4. Input and Output Parameters

Machine learning methods were used with the following input and output parameters:
Input parameters: water flow at the three supply sections (FL1, FL2, FL3) and water pressure values at five observation points (Pz1, Pz2, Pz3, Pz4, Pz5)
Output parameter: number of the campus zone (Z1, Z2, Z3, Z4, Z5).

3. Results

3.1. Supervised Methods

The training phase of the supervised methods was conducted with 80% of the data, while 20% was used for the testing phase.
Table 6 summarizes the results obtained with the water supply flow data. It shows that both the logistic regression and random forest methods gave excellent results with an accuracy = 1.0, precision = 1.0, recall = 1.0, and F1-score = 1. The decision tree method gave very good results with an accuracy = 0.95, precision = 0.96; recall = 0.95, and F1-score = 0.95.
Figure 5 shows the confusion matrix of the decision tree method. It indicates excellent performances for zones 1, 2, and 5. For zone 3, the precision was equal to 0.78, and for zone 4, the recall was equal to 0.75.
Table 7 summarizes the results obtained with the pressure data. It can be observed that both the logistic regression and the random forest methods gave excellent results with an accuracy = 1.0, precision = 1.0, and a recall = 1.0. The decision tree method gave good results with an accuracy = 0.88, precision = 0.91, recall = 0.94, and F1-score = 0.91. Figure 6 shows the confusion matrix for the decision tree method. It indicates excellent performances for all the zones, except for zone 1 (recall = 0.70) and the zone 2 (precision = 0.54). The bad results for zones 1 and 2 could be related to the spatial proximity of these zones and their hydraulic interaction (Figure 2 and Figure 4).
Pressure and flow data were used with only the decision tree method. The logistic regression and the random forest methods gave excellent results with either the flow or pressure data. Table 8 summarizes the classifications report for the decision tree. It shows that this method gives excellent results with an accuracy of 0.98, precision of 0.97, recall of 0.97, and F1-score of 0.96. It can be observed that the performance obtained with the flow and pressure data was better than that obtained with the flow data (Table 6) and pressure data (Table 7). Figure 7 shows the confusion matrix for the decision tree method. It indicates excellent performances for all the zones, except for zone 2 (recall = 0.83) and the zone 5 (precision = 0.83).

3.2. Unsupervised Methods

Figure 8 shows the results obtained with the hierarchical classification method with the pressure data. It shows the existence of three groups: the first group, G1, was composed of the pressures in zones 3 and 4; the second group, G2, concerned the pressure in zone 1; the third group, G3, included the pressures in zones 2 and 5.
Figure 9 illustrates the classification with water flow rate and pressure data. It shows the presence of fiive groups: G1 with the pressure in zone 4; G2 with the flow rate FL1 and the pressure in zone 3, G3 with the pressures in zones 2 and 5; G4 with the flow rate FL2, G5 with the flow rate FL3 and the pressure in zone 1.
Figure 10 illustrates the results obtained by applying the PCA and K-means methods on the flow rate data for k = 5 clusters. The component PC1 shows three clusters and two partially overlapping clusters. The component PC2 indicates two clusters and three partially overlapping clusters. Thus, in the (PC1, PC2) plan, the five clusters could be well distinguished.
Figure 11 illustrates the results obtained with the pressure data for k = 5 clusters. Both PC1 and PC2 showed significant overlapping clusters. In the (PC1, PC2) plan, the five clusters were not well distinguished.
Figure 12 illustrates the results obtained with flow rate and pressure data for k = 5 clusters. Both PC1 and PC2 showed clusters overlapping. In the (PC1, PC2) plan; only three clusters could be well distinguished.

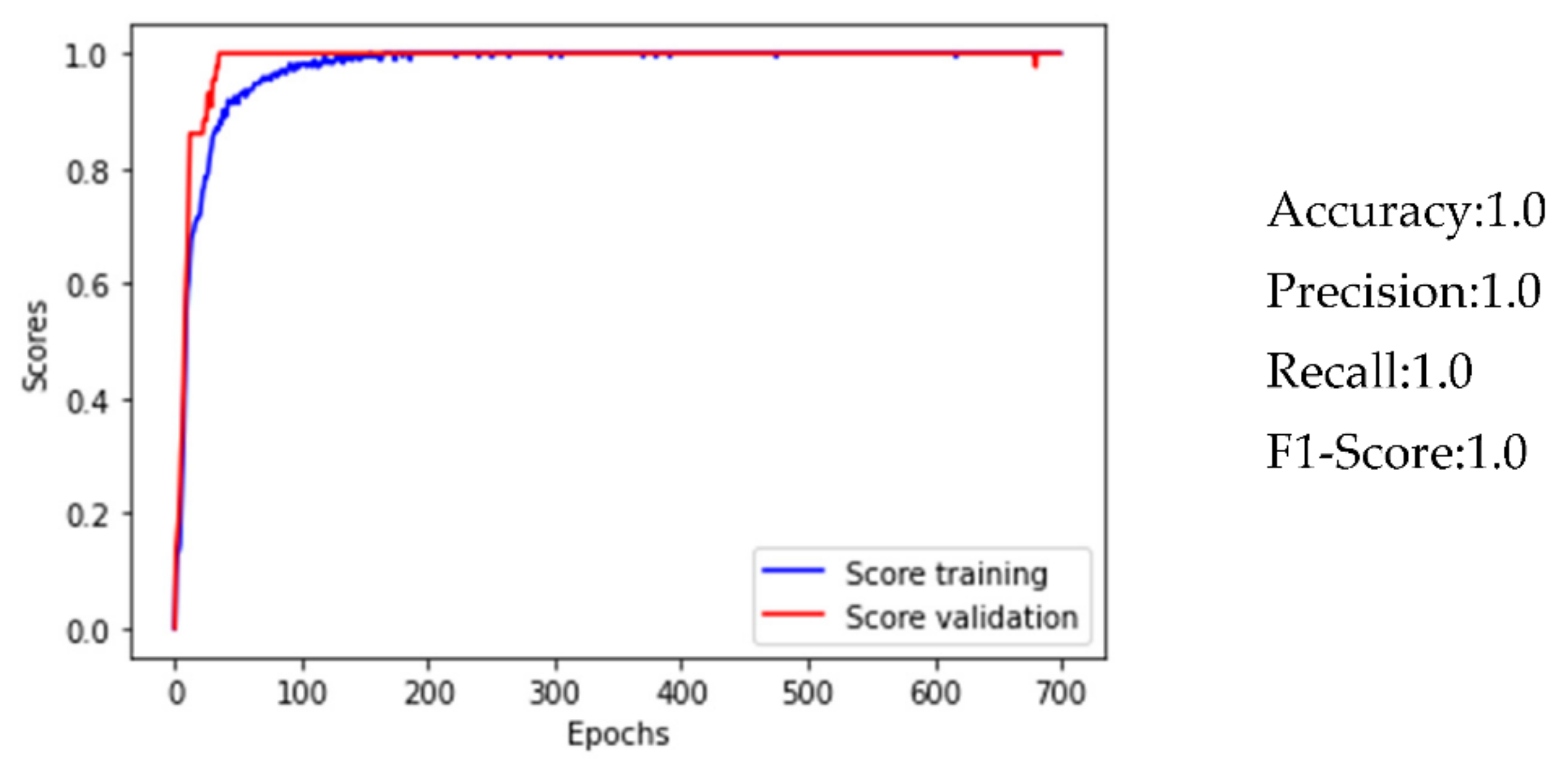
3.3. Artificial Neural Network

Analyses were conducted with a multilayer backpropagation neural network model. Figure 13 shows the results of the application of the ANN method with the water supply data. It indicates a rapid convergence of the ANN model. Indeed, a good convergence was observed with approximately 20 epochs. The ANN model gave excellent results with an accuracy = 1.0, precision = 1.0, recall = 1.0, and F1-Score = 1.0 (Table 9).
Figure 14 illustrates the results obtained with the pressure data. The convergence of the training phase was obtained with approximately 150 epochs, while the convergence of the validation phase was achieved with around 50 epochs. The model gave excellent results with an accuracy = 1.0, precision = 1.0, recall = 1.0, and F1-Score = 1.0 (Table 9).
Figure 15 illustrates the results obtained with flow and pressure data. It indicates a convergence of the training stage with approximately 100 epochs and convergence of the validation stage with approximately 50 epochs. The model gave excellent results with an accuracy = 1.0, precision = 1.0, recall = 1.0, and F1-Score = 1.0 (Table 9).

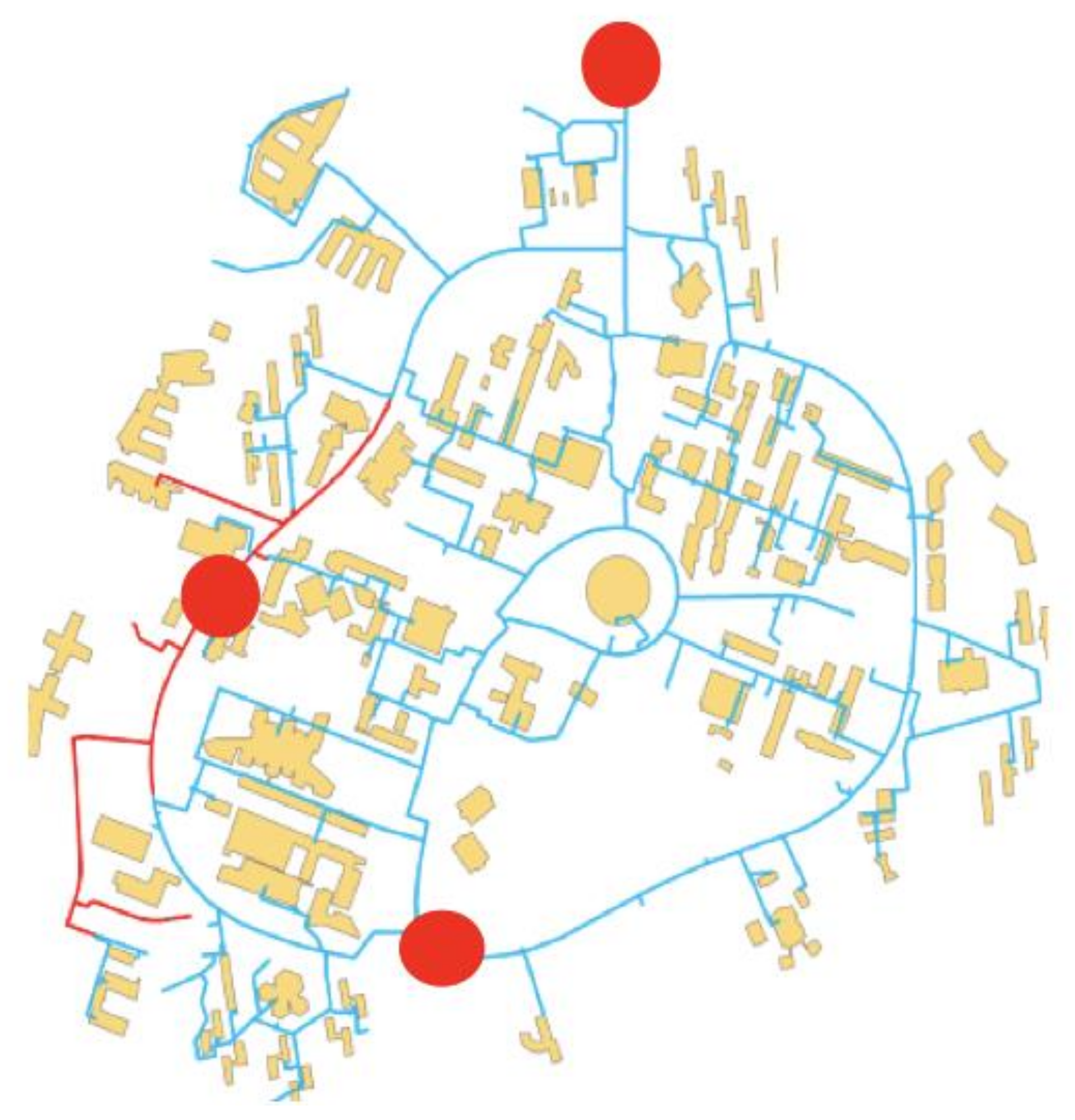
3.4. Analysis of the Water Leak in the Scientific Campus of Lille University

This section presents an analysis of the leak in the scientific campus of Lille University. The analysis was based on daily flow data collected in 2015 at the three supply sections: FL1 in the North, FL2 in the west, and FL3 in the South. The year 2015 was selected because of the availability of data for this year and the observation of several abnormal events in the water consumption, related to water leakage. The water usage in the campus concerns mainly domestic activities in the students’ residences, academic activity, and buildings’ cleaning. Water is not used for irrigation. Since the water usage is related to regular activities, the water consumption at the daily scale is expected to be regular.
The following sections present a successively analysis of the daily water consumption and leakage detection and localization.

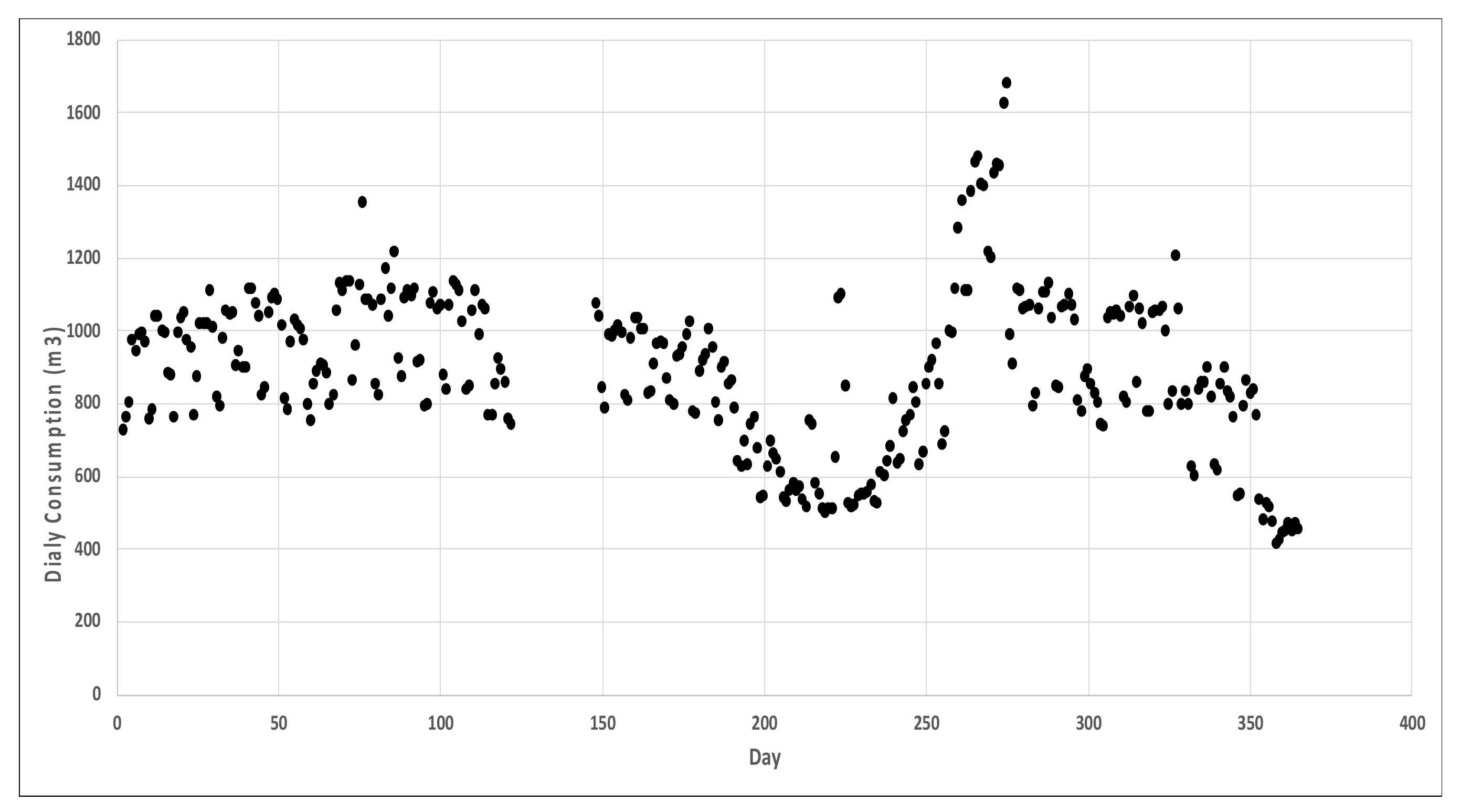
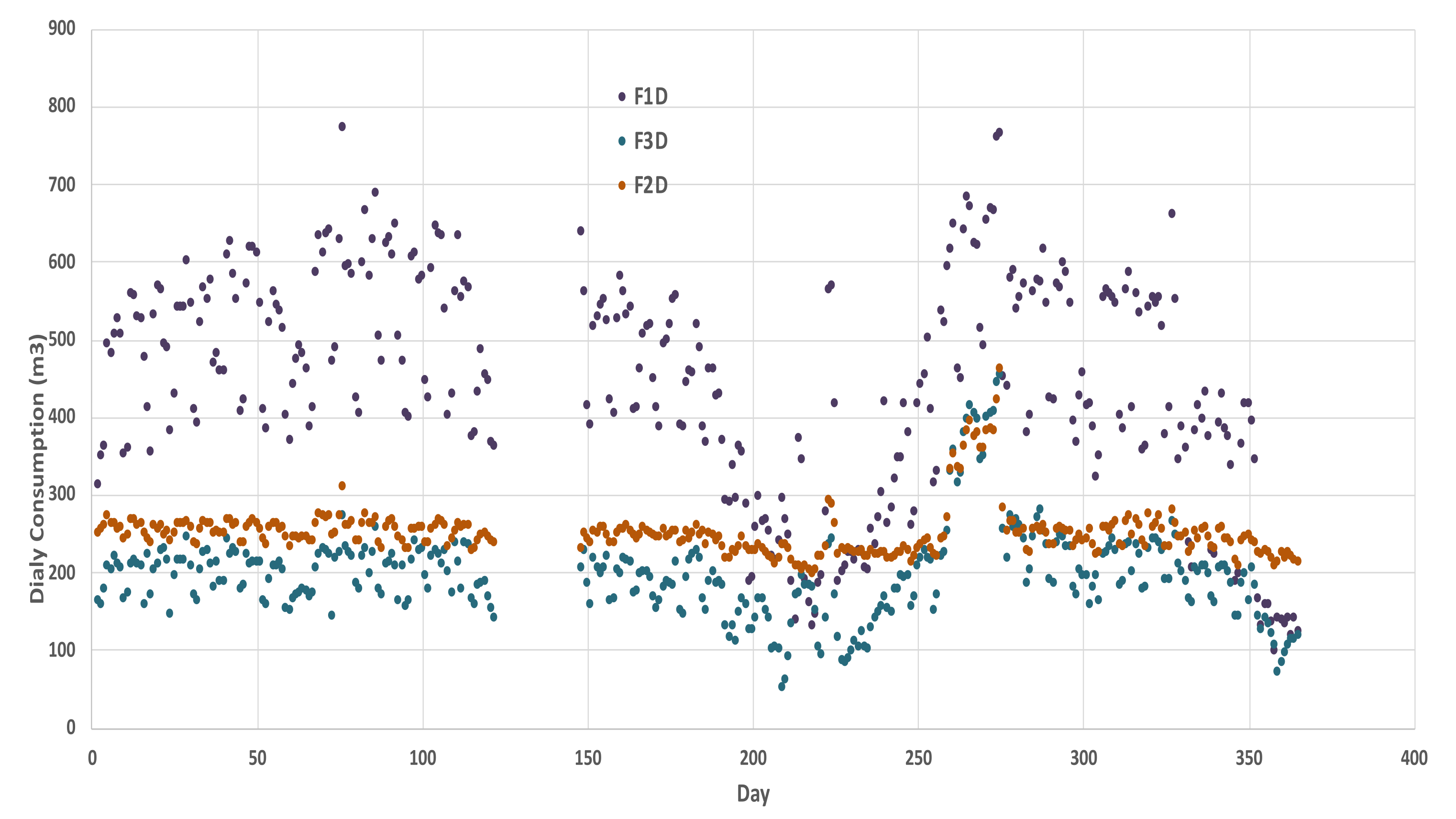
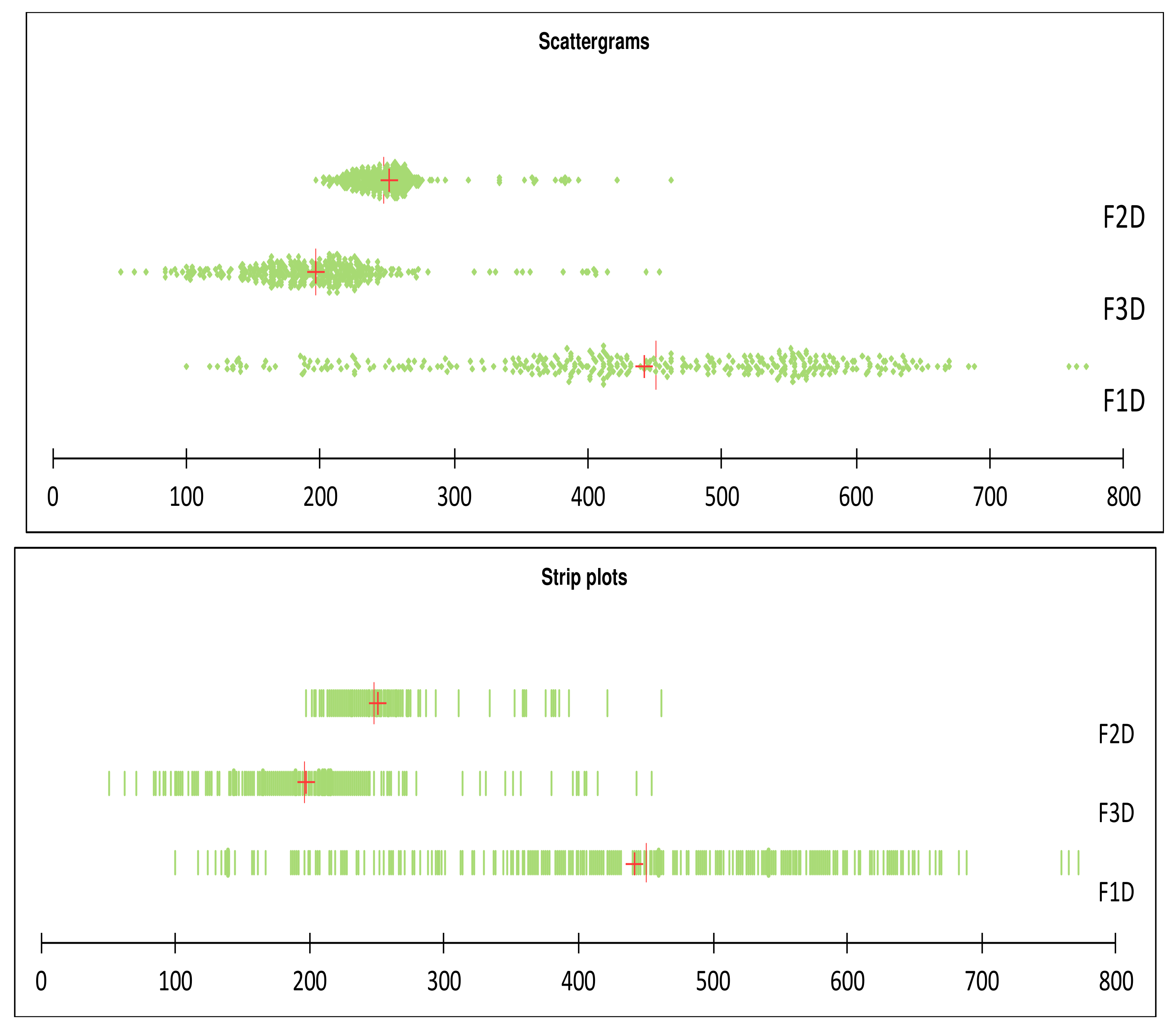
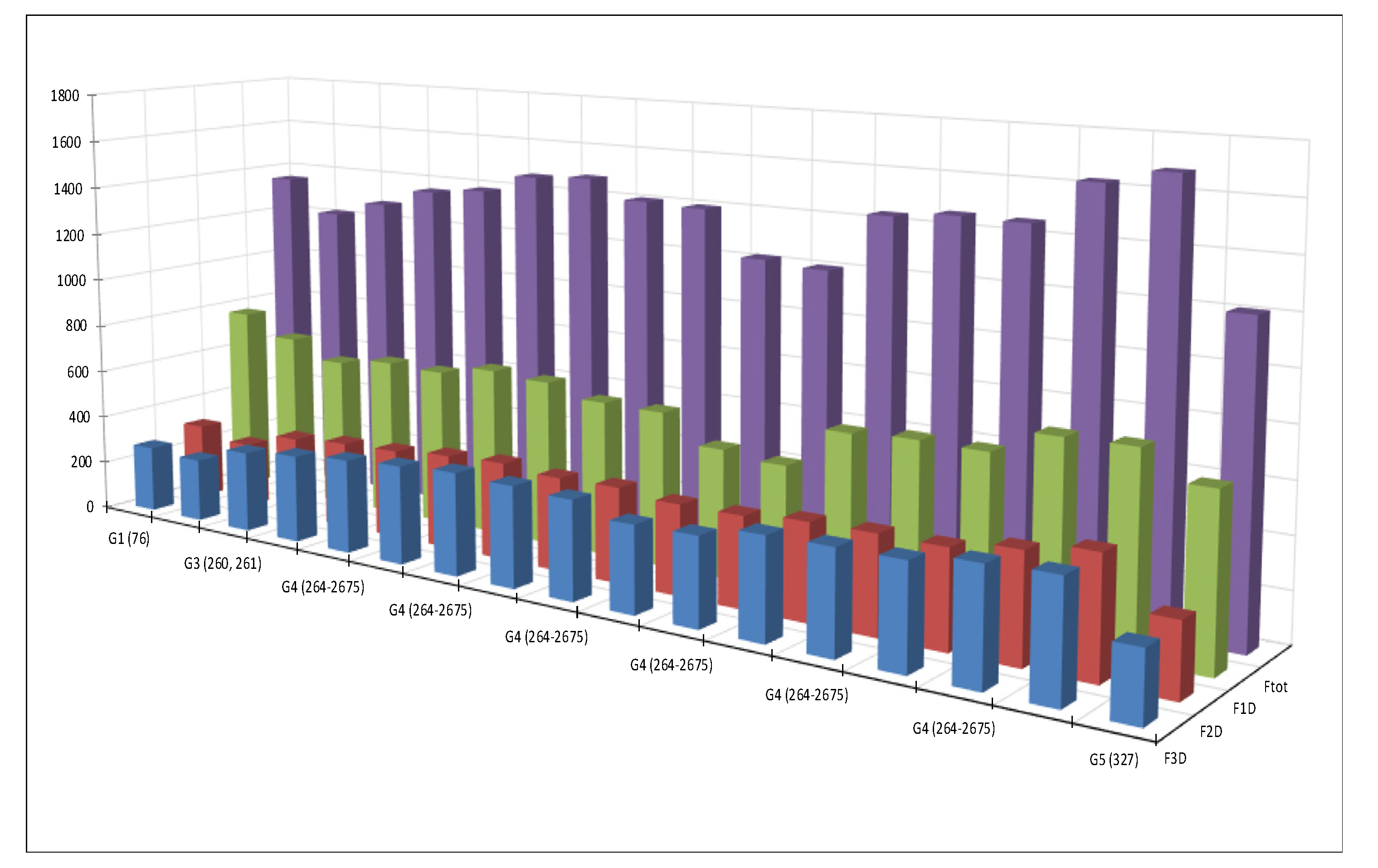
3.5. Analysis of the Daily Water Consumption (Qd)

Figure 16 illustrates the variation of the daily water consumption of the campus (Qd). It indicates missing data in the period from May 3 to May 27. This period is not considered in the analysis. This figure shows a significant variation in Qd. The minimum daily consumption was equal to 414 m3, while the maximum was equal to 1680 m3 and the average consumption was equal to 890 m3. Low daily consumption values could be attributed to the vacation periods, while the high daily consumption values could be associated with water leakage.
Figure 17 and Figure 18 illustrate the repartition of the daily water supply among the three supply sections. They show that the daily water supply from the North (F1D) was higher than those from the west and south campus. It also had the most significant variation (Table 10): the minimum daily supply was equal to 100 m3, while the maximum was equal to 772 m3 and the average was equal to 442 m3; compared with F2D (Resp F3D): minimum = 197 m3 (Resp. 51 m3), maximum = 772 m3 (Resp. 454 m3) and average = 251 m3 (Resp. 197 m3). Thus, the water supply F1D accounted for about 50% of the total water supply, while F2 accounted for 28% and F3 for 22% of the campus water supply.

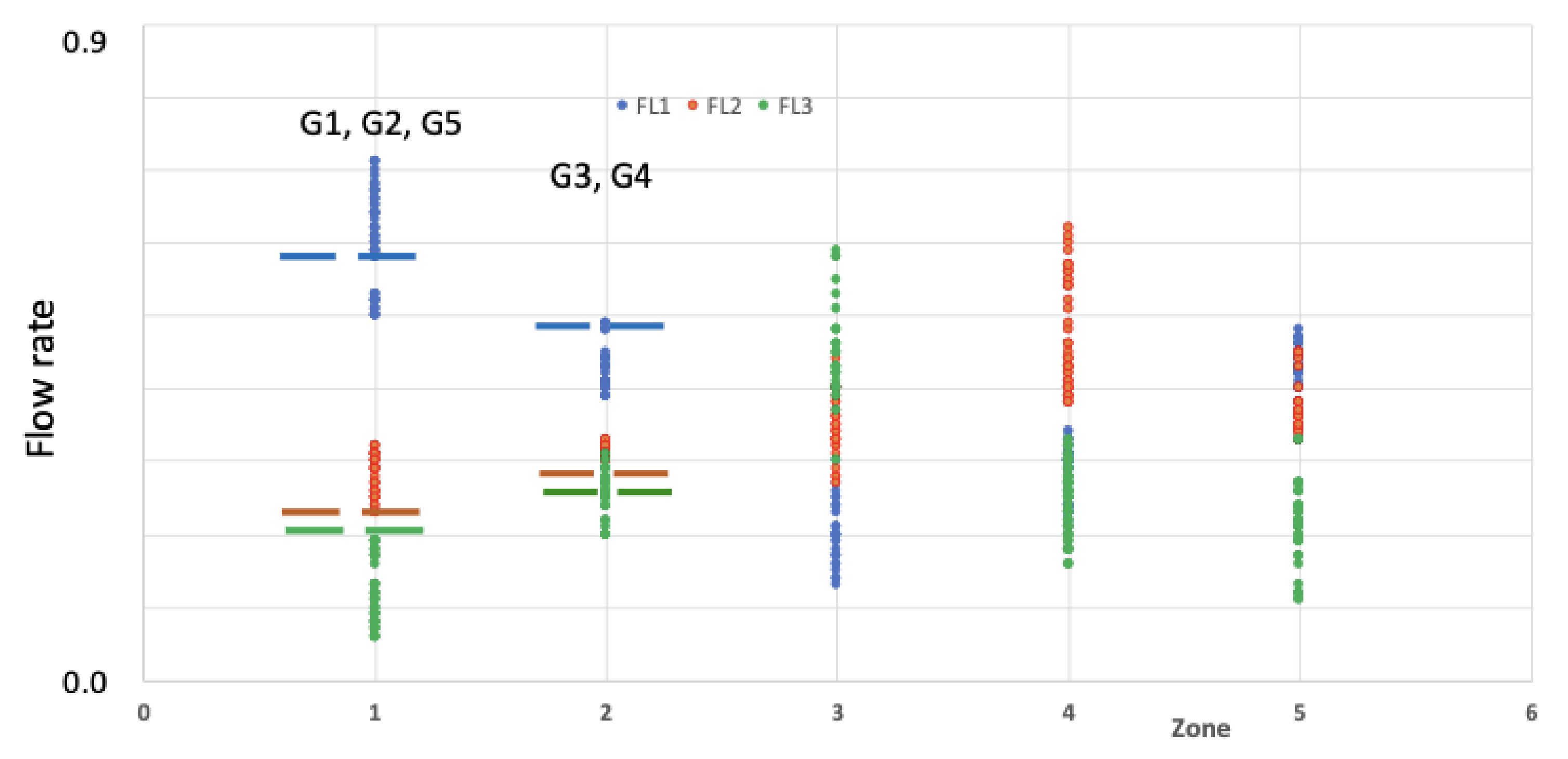
3.6. Leakage Analysis

The identification of leakage events was based on the observation of abnormal water consumption. Figure 19 and Figure 20 show the events with water consumption exceeding 1200 m3/h (average water consumption + 1.5 standard deviation). We observed the presence of five groups of events, which are summarized in Table 11. The first group (G1) corresponds to day 76 with consumption exceeding by approximately 464 m3 of the water consumption average (Qav), followed by day 86 (G2) which exceeded Qav by 326 m3. The third group corresponds to days 260 and 261, with water consumption exceeding Qav by 390 and 467 m3. The fourth group is related to days 264–275, with water consumption exceeding Qav by values included in the interval 311–790 m3. The last leak (G5) occurred on day 327, with consumption exceeding Qav by 318 m3.
Figure 21 and Table 12 show the repartition of the water supply ratios related to leakage events. It shows that the ratio associated with FL1 was higher than those associated with FL2 and FL3. FL1 accounted for 56% of the total water supply for groups G1, G2, and G5, while FL2 and FL3 accounted for approximately 22% each. For groups G3 and G4, FL1 accounted for approximately 46% of the water supply, while FL2 and FL3 accounted for approximately 27% each.

3.7. Leakage Localization

For the localization of leakage events G1 to G5, the water supply ratios corresponding to the leakage events are reported in Figure 22. The ratios of water flow for the events G1, G2 and G5 are indicated by the water flow ratios (FL1, FL2, and FL3) for zone 1, while those related to the events G3 and G4 are reported by the water flow ratios for zone 2. Therefore, it could be observed that leakages G1, G2, and G5 well matched with the water flow repartition for leakages in zone 1, while leakages G3 and G4 well matched with the water flow repartition for leakages in zone 2. This observation indicates that leakages G1, G2, and G5 could be attributed to zone 1, while leakages G3 and G4 could be attributed to zone 2.

4. Discussion

This research concerned the detection and localization of leaks in urban water distribution networks. This issue is of significant concern in the management of the water distribution systems, because leaks in the water distribution system cause substantial economic, social, and environmental impacts and severe damages to the surrounding soils and infrastructures.
Despite the important research on the development and use of hardware- and software-based methods for the detection, localization, and localization of water leaks, professionals still need efficient and cost-effective methods to detect water leaks in complex water distribution systems.
The recent progress in smart monitoring and artificial intelligence provides significant opportunities to develop data-based methods for leak detection and localization. The literature review showed an important concern in the use of these methods. However, on the one hand, the majority of the applications using artificial intelligent methods remain at the research stage. On the other hand, the literature review revealed a lack of comprehensive use of these methods. This research aimed to fill the gap in this area by thoroughly investigating the machine learning methods to detect and localize leaks in the water distribution system.
The water network of the scientific campus of Lille University was used as support for this research. This use was motivated by the campus’ representativity of a small town, the complexity of the water network and the availability of data about the water network asset and water consumption. The water network is monitored by approximately 93 automated meter readings (AMRs) that record the water supply and consumption in the main buildings at an hourly time interval.
The physical water network was completed by constructing a Lab pilot of this network to investigate, under well-controlled conditions, the impact of the position of a leak on the water flow rates. Results of experiments showed an evident influence of the leak position leak on the water supply flow rates when the leak was in the proximity of the water supply. However, the impact is unclear for other locations, which means that the leak position could not be systematically determined from only the supply flow rates. In the future, it could be interested to monitor the pilot with pressure cells to investigate the possibility of improving the leak localization using the water supply flow rates and the pressure variation in the water network.
A large data set was built regarding the impact of leaks on the water network of the scientific campus on the variations in the water supply flow rates and the pressure in five campus zones. This data set was constructed using the hydraulic software EPANET. The data set included the responses of the water network to 215 individual and double leaks.
The data set was used for training and testing the following six machine learning methods:
  • Three supervised methods: logistic regression, decision tree, and random forest;
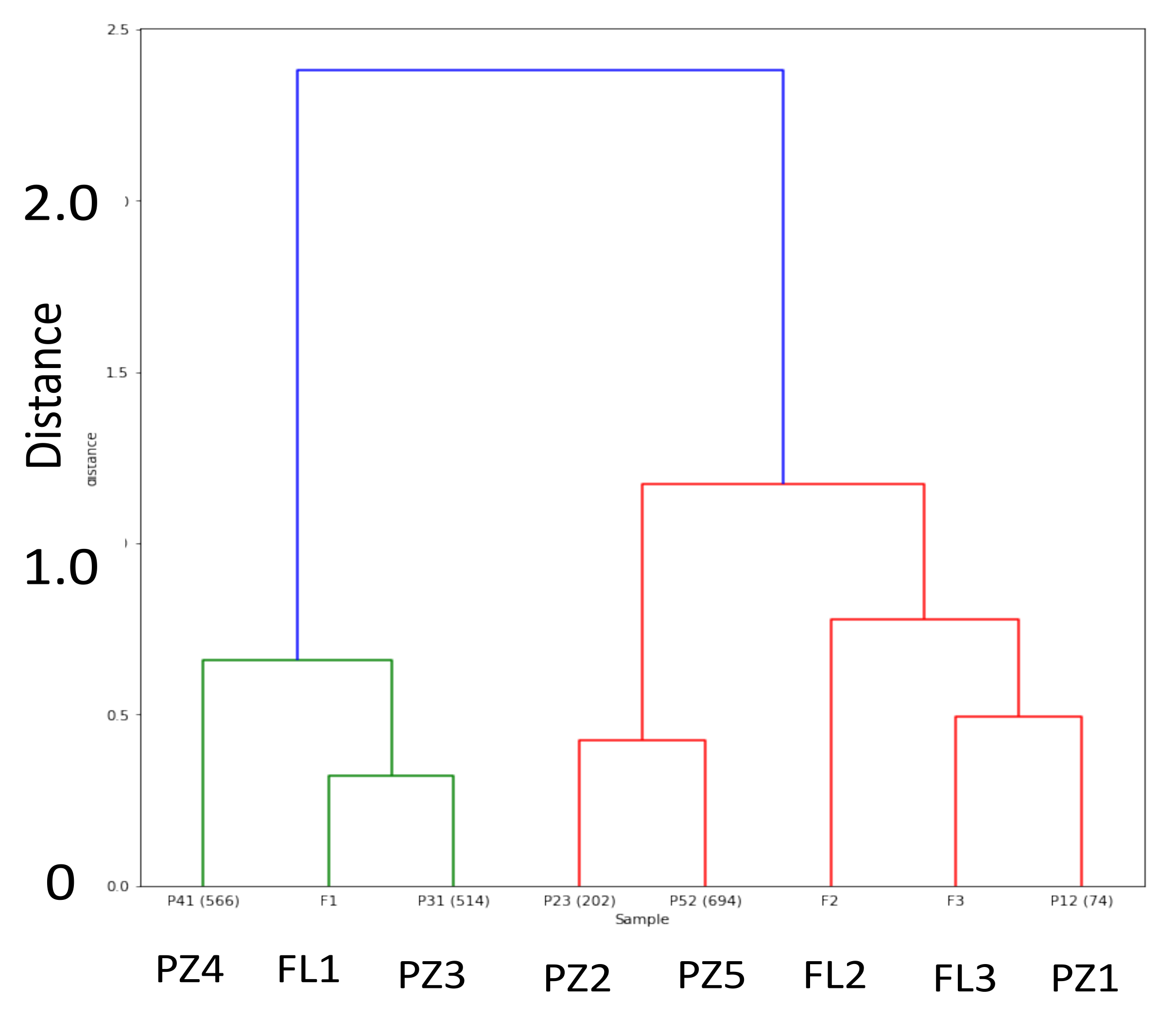
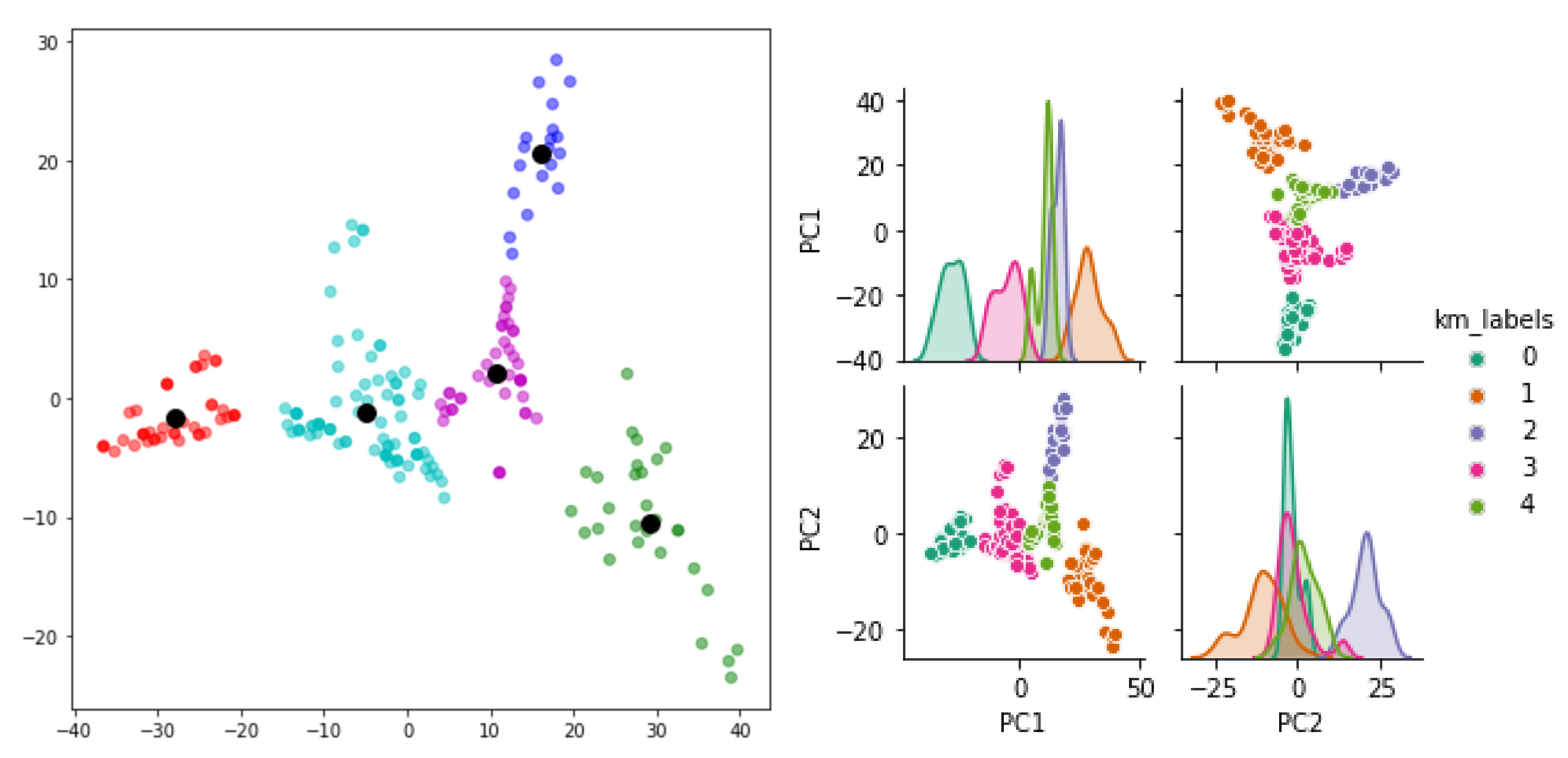
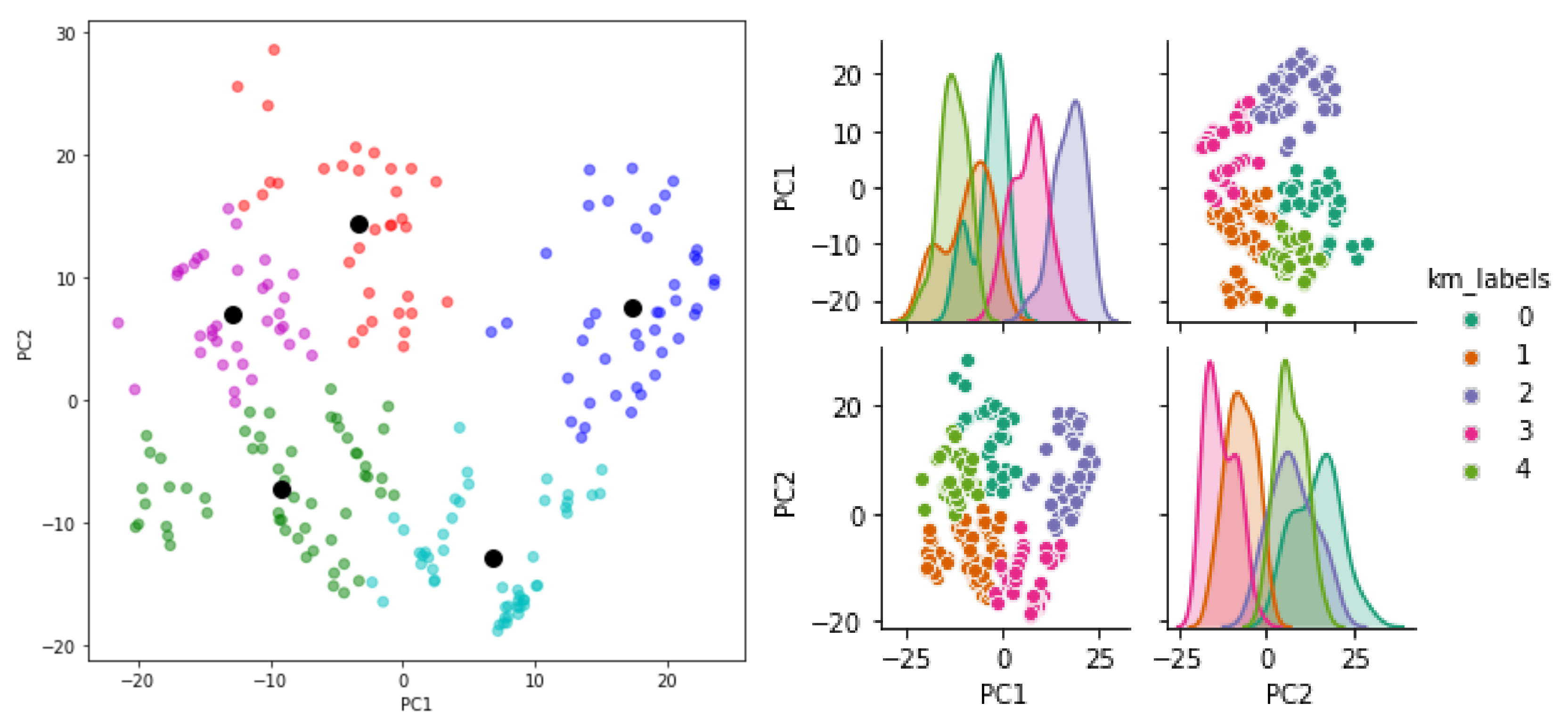
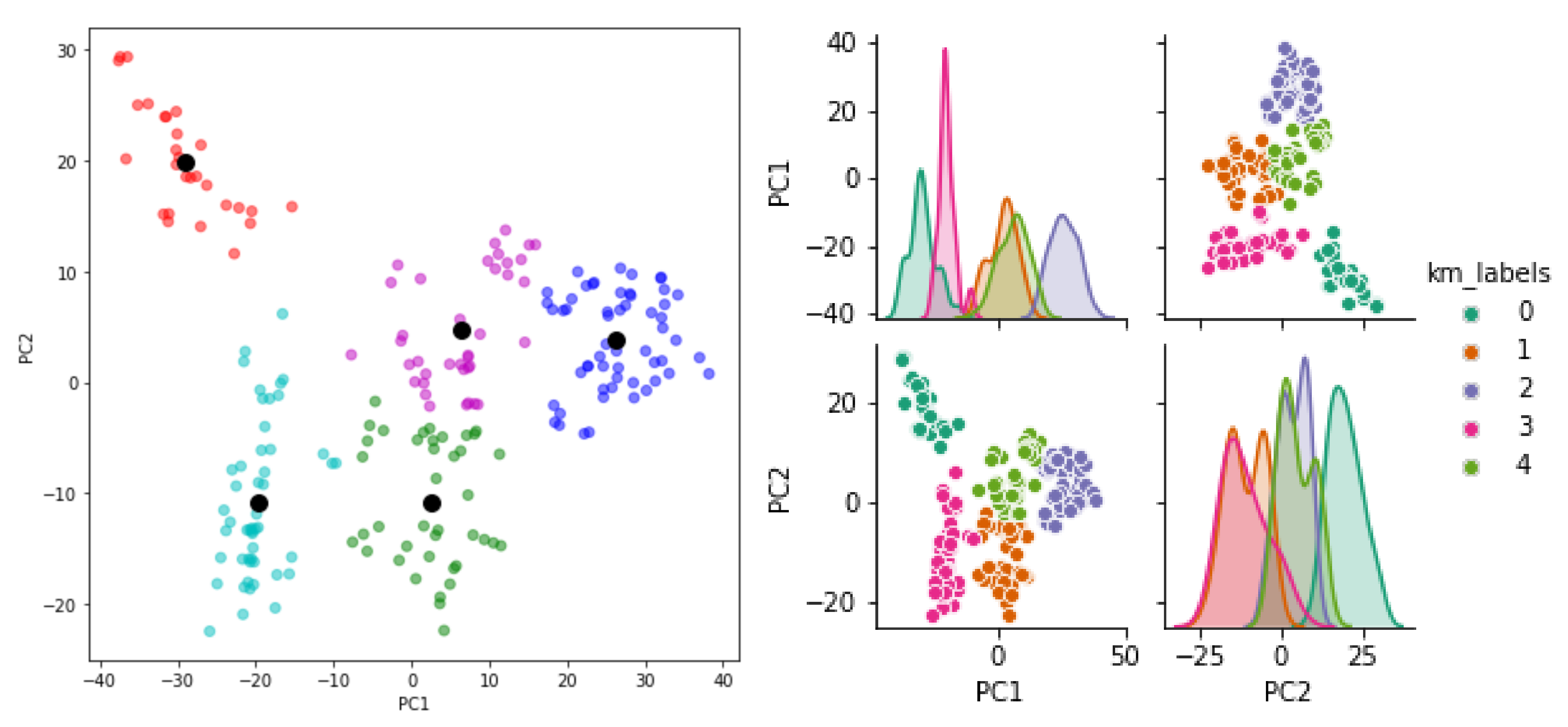
  • Two unsupervised methods: The hierarchical classification method and a combination of the PCA and K-means classification method;
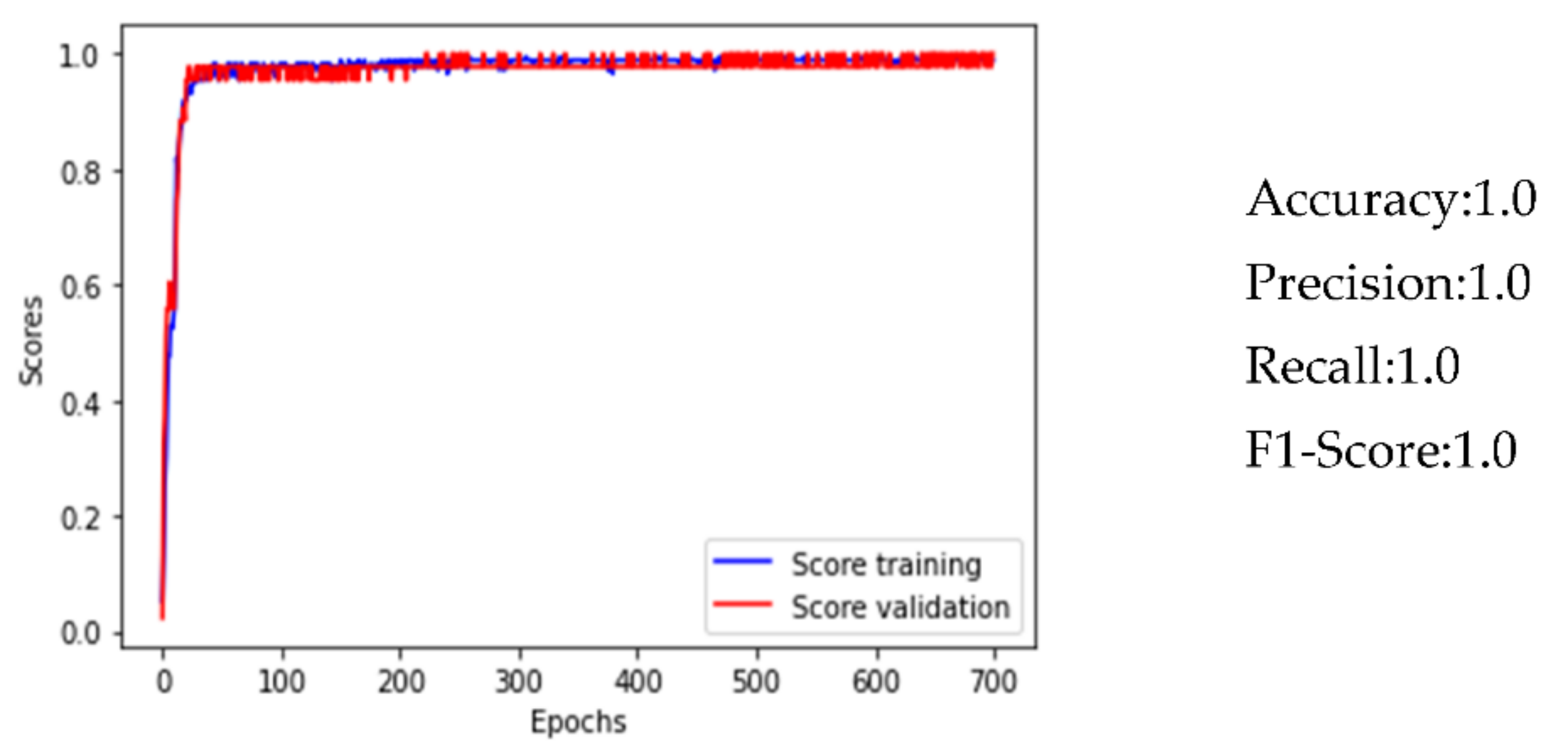
  • The ANN
The results of the tests conducted on these methods showed:
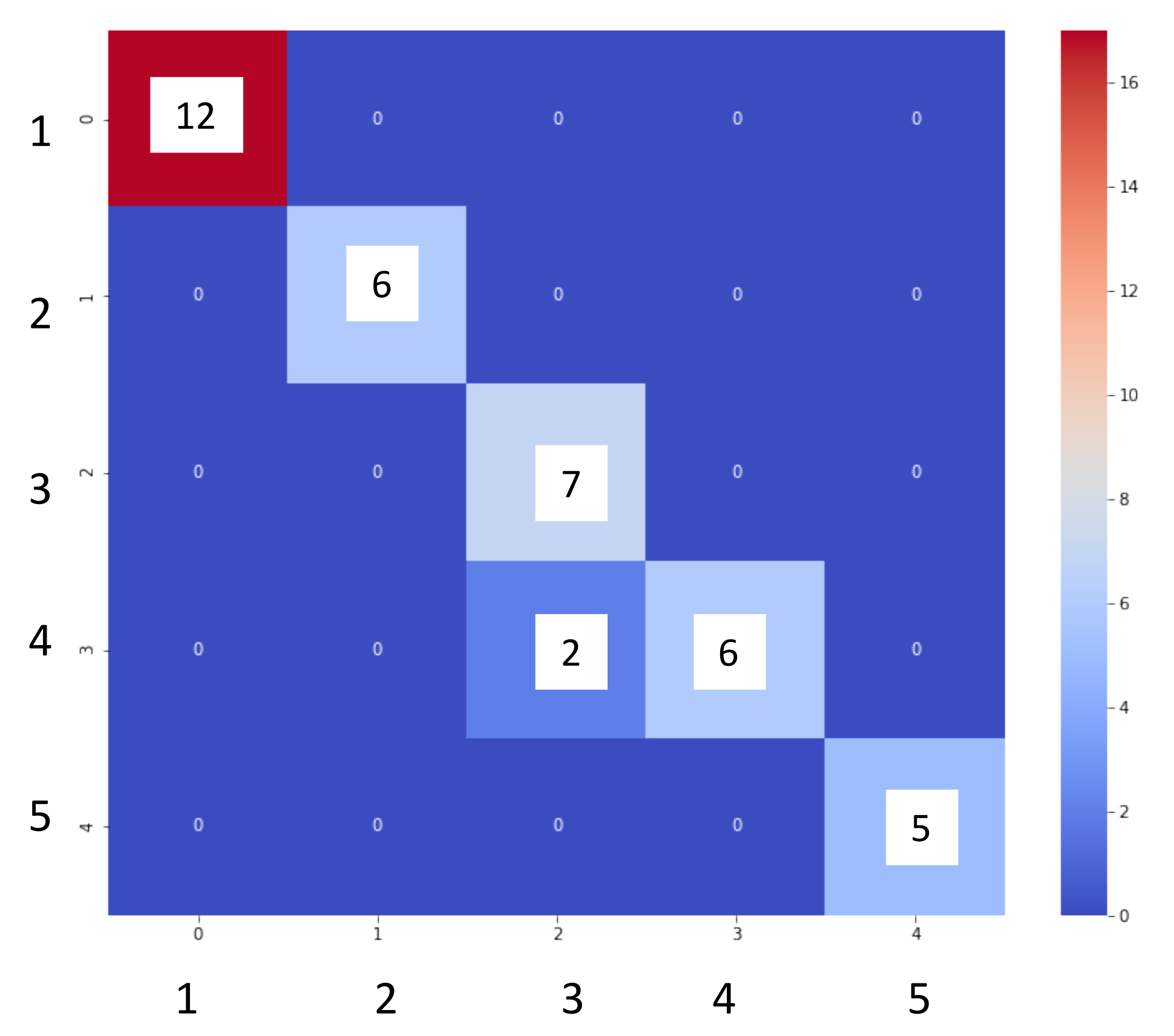
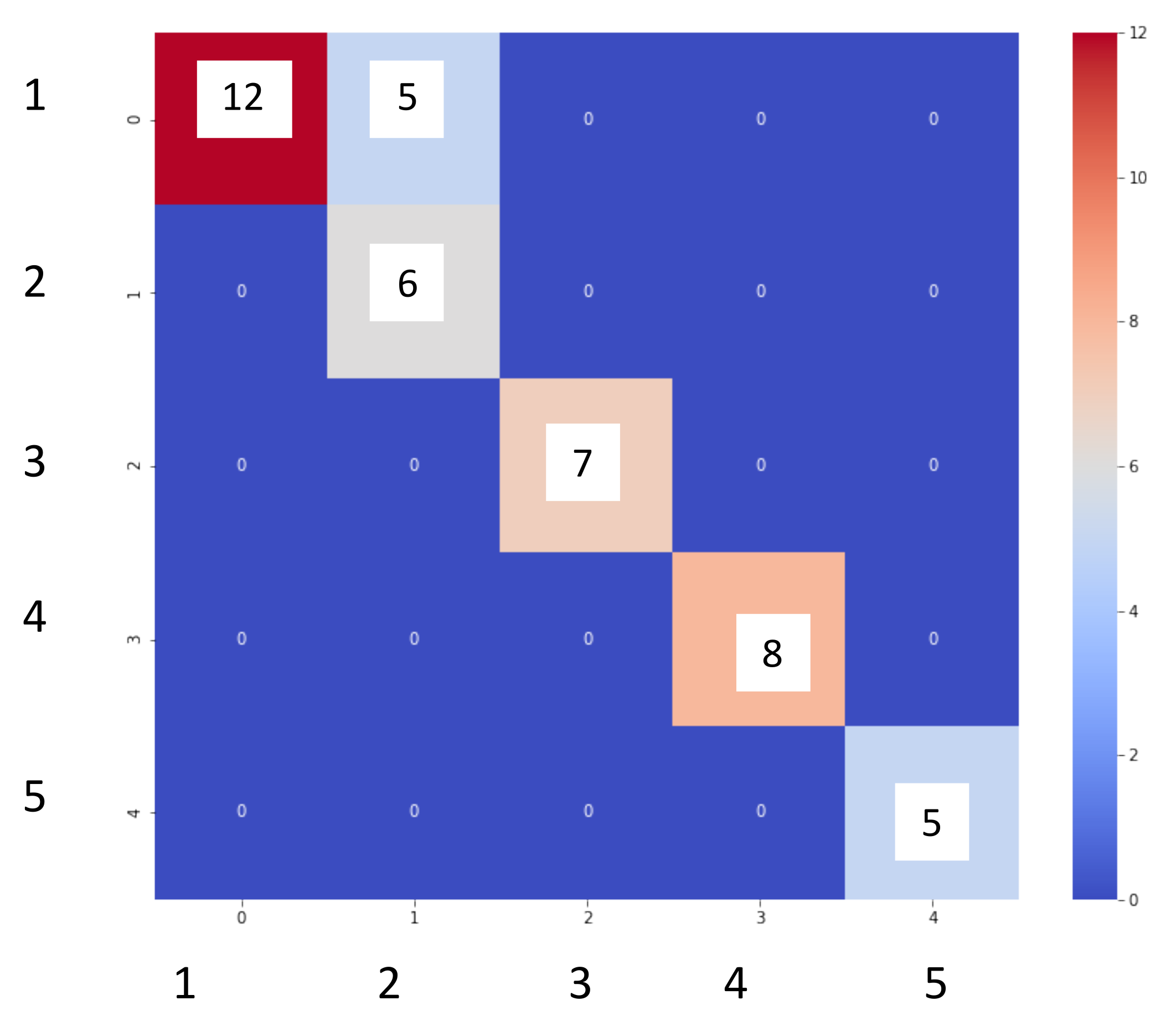
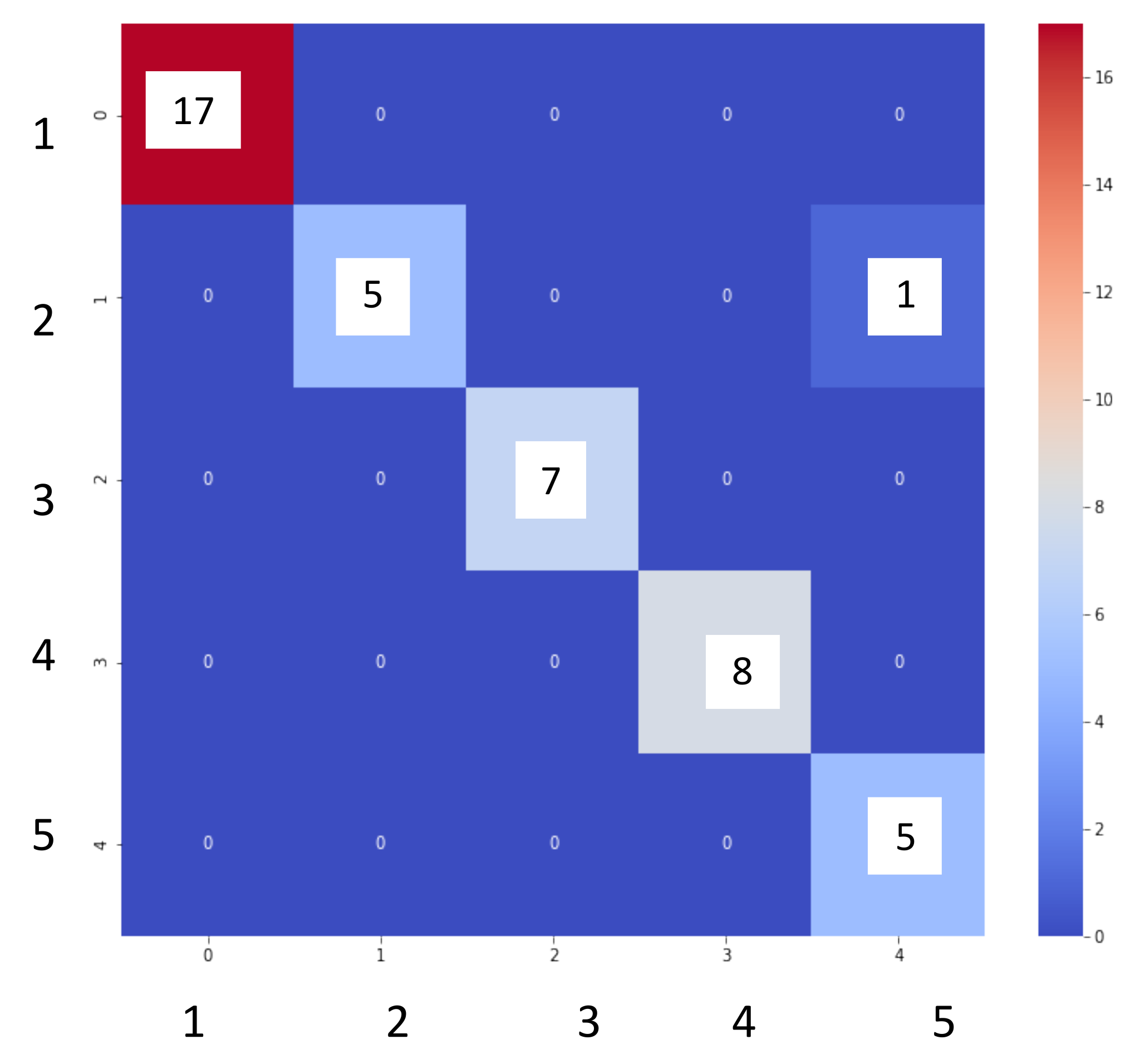
  • Excellent performance of the supervised methods in the localization of leaks in the water network. Both the logistic regression and the random forest predicted the position of the leak with an accuracy = 1.0. In contrast, the decision tree predicted leaks with an accuracy = 0.98 with pressure and flow data;
  • Excellent performances by the ANN for the localization of water leaks in the water network (accuracy = 1.0);
  • Some difficulties in exploiting the clustering capacity of the unsupervised methods in the leak localization because of overlapping clusters.
The results of this research were used to investigate the position of water leaks in the campus using water flow data rates recorded in 2015. Unfortunately, difficulties were encountered in the determination of the position of leaks because of a lack of pressure data. Therefore, in the future, we recommend extending the monitoring of the campus water network by adding cell pressure on the campus and flow rates in critical sections of the water network.

5. Conclusions

This paper presented an investigation of the use of machine learning methods to local leakage in the water distribution network. Leakage localization was based on the creation of hydraulic zones in the water distribution network. For each zone, sensors are used to measure the water supply variations and the water pressure. Collected data were then used for the construction of the machine learning models.
This methodology was used to investigate the capacity of six machine learning methods to localize leaks in the water distribution network of the scientific campus of Lille University. Data were generated using EPANET software. The investigation showed (i) excellent performance from the supervised methods, in particular, the logistic regression and random forest; (ii) excellent performances by the artificial neural network; (iii) difficulties in the exploitation of the clustering capacity of the unsupervised methods in leak localization because of clusters’ overlapping. Offline water supply flow data were then used for the localization of water leakage in the scientific campus. The results gave some indications about the localization of the water leakage.
This paper shows that the ANN and the supervised logistic regression and random forest methods performed well in the localization of the water leakage in the water distribution systems, mainly when using both water flow and pressure data. These results are based on data generated using the software EPANET. Therefore, they should be confirmed on data collected from complex water networks, including water supply flow and pressure data in the subzones of the water network, and the localization of leakage events.

Author Contributions

N.M., I.S. and J.E.K. conceived the research idea; A.A. and I.S. established the research methodology; N.M., N.A. and I.S. conducted the data analysis and discussed the results. All authors have read and agreed to the published version of the manuscript.

Funding

This research did not beneficiate from specific funding support.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data sharing not applicable.

Conflicts of Interest

All other authors have no conflict of interest.

References

  1. Kingdom, B.; Liemberger, R.; Marin, P. The Challenge of Reducing Non-Revenue (NRW) Water in Developing Countries. How the Private Sector Can Help: A Look at Performance-Based Service Contracting; Water Supply and Sanitation (WSS) Sector Board Discussion Paper N. 8; The World Bank: Washington, DC, USA, 2006. [Google Scholar]
  2. Thornton, J.; Sturm, R.; Kunkel, G. Water Loss Control, 2nd ed.; McGraw Hill: New York, NY, USA, 2008; ISBN 9780071499187. [Google Scholar]
  3. Renzetti, S.; Dupont, D. Buried Treasure: The Economics of Leak Detection and Water Loss Prevention in Ontario. Environmental Sustainability Research Centre (ESRC) Working Paper Series. 2013. Available online: http://hdl.handle.net/10464/4279 (accessed on 30 June 2021).
  4. Kanakoudis, V.K. A troubleshooting manual for handling operational problems in water pipe networks. Water Supply Res. Technol.-AQUA 2004, 53, 109–124. [Google Scholar] [CrossRef]
  5. Hunaidi, O.; Wang, A.; Bracken, M.; Gambino, T.; Fricke, C. Acoustic methods for locating leaks in municipal water pipe networks. In Proceedings of the International Conference on Water Demand Management, Dead Sea, Jordan, 30 May–3 June 2004; pp. 1–14. [Google Scholar]
  6. Adegboye, M.A.; Fung, W.-K.; Karnik, A. Recent Advances in Pipeline Monitoring and Oil Leakage Detection Technologies: Principles and Approaches. Sensors 2019, 19, 2548. [Google Scholar] [CrossRef] [Green Version]
  7. Fahmy, M.; Moselhi, O. Detecting and locating leaks in underground water mains using thermography. In Proceedings of the 26th International Symposium on Automation and Robotic in Construction (ISARC), Austin, TX, USA, 24–27 June 2009; pp. 61–67. [Google Scholar]
  8. Ayala–Cabrera, D.; Herrera, M.; Izquierdo, J.; Ocaña–Levario, S.; Pérez–García, R. GPR-Based Water Leak Models in Water Distribution Systems. Sensors 2013, 13, 15912–15936. [Google Scholar] [CrossRef]
  9. Noran, P.; Obenauf, P. Asset Management of a Failing 36" Ductile Iron Sewage Force Main. In Pipelines 2010; American Society of Civil Engineers: Reston, WV, USA, 2010; pp. 566–576. [Google Scholar] [CrossRef]
  10. Zhang, X. Statistical leak detection in gas and liquid pipelines. Pipes Pipelines Int. 1993, 38, 20–26. [Google Scholar]
  11. Buchberger, S.G.; Nadimpalli, G. Leak Estimation in Water Distribution Systems by Statistical Analysis of Flow Readings. J. Water Resour. Plan. Manag. 2004, 130, 321–329. [Google Scholar] [CrossRef]
  12. Lambert, A. International report: Water losses management and techniques. Water Sci. Technol. Water Supply 2002, 2, 1–20. [Google Scholar] [CrossRef] [Green Version]
  13. Billmann, L.; Isermann, R. Leak detection methods for pipelines. Automatica 1987, 23, 381–385. [Google Scholar] [CrossRef]
  14. Silva, R.; Buiatti, C.; Cruz, S.; Pereira, J. Pressure wave behaviour and leak detection in pipelines. Comput. Chem. Eng. 1996, 20, S491–S496. [Google Scholar] [CrossRef]
  15. Caputo, A.C.; Pelagagge, P.M. Using Neural Networks to Monitor Piping Systems. Process Saf. Prog. 2003, 22, 119–127. [Google Scholar] [CrossRef]
  16. Salam, A.E.U.; Tola, M.; Selintung, M.; Maricar, F. On-line monitoring system of water leakage detection in pipe networks with artificial intelligence. ARPN J. Eng. Appl. Sci. 2014, 9, 1817–1822. [Google Scholar]
  17. Mounce Stephen, R.; Mounce, R.B.; Boxall, J.B. Novelty detection for time series data analysis in water distribution systems using support vector machines. J. Hydroinformatics 2011, 13, 672–686. [Google Scholar] [CrossRef]
  18. Rojek, I.; Studzinski, J. Detection and localization of water leaks in water nets supported by an ICT system with artificial intelligence methods as a way forward for smart cities. Sustainability 2019, 11, 518. [Google Scholar] [CrossRef] [Green Version]
  19. Zhang, Q.; Wu, Z.Y.; Zhao, M.; Qi, J.; Huang, Y.; Zhao, H. Leakage Zone Identification in Large-Scale Water Distribution Systems Using Multiclass Support Vector Machines. J. Water Resour. Plan. Manag. 2016, 142, 4016042. [Google Scholar] [CrossRef]
  20. Chan, T.K.; Chin, C.S.; Zhong, X. Review of Current Technologies and Proposed Intelligent Methodologies for Water Distributed Network Leakage Detection. IEEE Access 2018, 6, 78846–78867. [Google Scholar] [CrossRef]
  21. Soldevila, A.; Blesa, J.; Tornil-Sin, S.; Duviella, E.; Fernandez-Canti, R.M.; Puig, V. Leak localization in water distribution networks using a mixed model-based/data-driven approach. Control Eng. Pract. 2016, 55, 162–173. [Google Scholar] [CrossRef] [Green Version]
  22. Ciupke, K. Leak Detection Using Regression Trees. In Advances in Technical Diagnostics. ICDT 2016. Applied Condition Monitoring; Timofiejczuk, A., Łazarz, B., Chaari, F., Burdzik, R., Eds.; Springer: Cham, Switzerland, 2018; Volume 10. [Google Scholar] [CrossRef]
  23. van der Walt, J.C.; Heyns, P.S.; Wilke, D.N. Pipe network leak detection: Comparison between statistical and machine learning techniques. Urban Water J. 2018, 15, 953–960. [Google Scholar] [CrossRef]
  24. Shahrour, I.; Abbas, O.; Abdallah, A.; AbouRjeily, Y.; Afaneh, A.; Aljer, A.; Ayari, B.; Farrah, E.; Sakr, D.; Al Masri, F. Lessons from a Large-Scale Demonstrator of the Smart and Sustainable City BT—Happy City—How to Plan and Create the Best Livable Area for the People; Brdulak, A., Brdulak, H., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 193–206. [Google Scholar] [CrossRef]
  25. Farah, E.; Shahrour, I. Leakage Detection Using Smart Water System: Combination of Water Balance and Automated Minimum Night Flow. Water Resour. Manag. 2017, 31, 4821–4833. [Google Scholar] [CrossRef]
  26. Farah, E.; Abdallah, A.; Shahrour, I. SunRise: Large scale demonstrator of the smart water system. Int. J. Sustain. Dev. Plan. 2017, 12, 112–121. [Google Scholar] [CrossRef]
  27. Harrell, F.E. Regression Modeling Strategies; Springer: Berlin/Heidelberg, Germany, 2001; ISBN 0-387-95232-2. [Google Scholar]
  28. Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Wadsworth, Inc.: Belmont, CA, USA, 1984. [Google Scholar]
  29. Lin, N.; Noe, D.; He, X. Tree-based methods and their applications In Springer Handbook of Engineering Statistics; Pham, H., Ed.; Springer: London, UK, 2006; pp. 551–570. [Google Scholar]
  30. Prinzie, A.; Van den Poel, D. Random Forests for multiclass classification: Random MultiNomial Logit. Expert Syst. Appl. 2008, 34, 1721–1732. [Google Scholar] [CrossRef]
  31. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
  32. Ward, J.H., Jr. Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
  33. Mohamad Asri, M.N.; Mat Desa, W.N.S.; Ismail, D. Combined Principal Component Analysis (PCA) and Hierarchical Cluster Analysis (HCA): An efficient chemometric approach in aged gel inks discrimination. Aust. J. Forensic Sci. 2020, 52, 38–59. [Google Scholar] [CrossRef]
  34. Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-Means Clustering Algorithm. J. R. Stat. Soc. Ser. C 1979, 28, 100–108. [Google Scholar] [CrossRef]
  35. Dave, V.S.; Dutta, K. Neural network-based models for software effort estimation: A review. Artif. Intell. Rev. 2014, 42, 295–307. [Google Scholar] [CrossRef]
Smartcities 04 00069 g001 550
Figure 1. The water distribution system of the scientific campus [25] (the red circles indicate the water supply of the campus).
Figure 1. The water distribution system of the scientific campus [25] (the red circles indicate the water supply of the campus).
Smartcities 04 00069 g001
Smartcities 04 00069 g002 550
Figure 2. EPANET model of the water network ono the scientific campus (45 pipes, 33 junctions). Ln designates the position of leak n, Pzm designates the position of the pressure sensor number m. The black squares indicate the supply section.
Figure 2. EPANET model of the water network ono the scientific campus (45 pipes, 33 junctions). Ln designates the position of leak n, Pzm designates the position of the pressure sensor number m. The black squares indicate the supply section.
Smartcities 04 00069 g002
Smartcities 04 00069 g003 550
Figure 3. Impact of the leak localization on the water supply flow rate.
Figure 3. Impact of the leak localization on the water supply flow rate.
Smartcities 04 00069 g003
Smartcities 04 00069 g004 550
Figure 4. Impact of the leak localization on the pressure values at the observation points.
Figure 4. Impact of the leak localization on the pressure values at the observation points.
Smartcities 04 00069 g004
Smartcities 04 00069 g005 550
Figure 5. Confusion matrix for the decision tree method—flow data.
Figure 5. Confusion matrix for the decision tree method—flow data.
Smartcities 04 00069 g005
Smartcities 04 00069 g006 550
Figure 6. Confusion matrix for the decision tree method—pressure data.
Figure 6. Confusion matrix for the decision tree method—pressure data.
Smartcities 04 00069 g006
Smartcities 04 00069 g007 550
Figure 7. Confusion matrix for the decision tree method—flow and pressure data.
Figure 7. Confusion matrix for the decision tree method—flow and pressure data.
Smartcities 04 00069 g007
Smartcities 04 00069 g008 550
Figure 8. Hierarchical Classification method-results with the pressure data.
Figure 8. Hierarchical Classification method-results with the pressure data.
Smartcities 04 00069 g008
Smartcities 04 00069 g009 550
Figure 9. Hierarchical classification method—results with the flow rate and pressure data.
Figure 9. Hierarchical classification method—results with the flow rate and pressure data.
Smartcities 04 00069 g009
Smartcities 04 00069 g010 550
Figure 10. PCA and K-means clustering—flow rate data.
Figure 10. PCA and K-means clustering—flow rate data.
Smartcities 04 00069 g010
Smartcities 04 00069 g011 550
Figure 11. PCA and K-means clustering-Pressure data.
Figure 11. PCA and K-means clustering-Pressure data.
Smartcities 04 00069 g011
Smartcities 04 00069 g012 550
Figure 12. PCA and K-means clustering—flow rate and pressure data.
Figure 12. PCA and K-means clustering—flow rate and pressure data.
Smartcities 04 00069 g012
Smartcities 04 00069 g013 550
Figure 13. Application of the ANN method with the water supply data.
Figure 13. Application of the ANN method with the water supply data.
Smartcities 04 00069 g013
Smartcities 04 00069 g014 550
Figure 14. Application of the ANN method with pressure data.
Figure 14. Application of the ANN method with pressure data.
Smartcities 04 00069 g014
Smartcities 04 00069 g015 550
Figure 15. Application of the ANN method with flow and pressure data.
Figure 15. Application of the ANN method with flow and pressure data.
Smartcities 04 00069 g015
Smartcities 04 00069 g016 550
Figure 16. Variation of the daily water consumption (Qd) of the Scientific Campus in 2015.
Figure 16. Variation of the daily water consumption (Qd) of the Scientific Campus in 2015.
Smartcities 04 00069 g016
Smartcities 04 00069 g017 550
Figure 17. Variations in the repartition of the daily water supply on the scientific campus in 2015.
Figure 17. Variations in the repartition of the daily water supply on the scientific campus in 2015.
Smartcities 04 00069 g017
Smartcities 04 00069 g018 550
Figure 18. Scatter grams and strip plots of the repartition of the daily water supply on the scientific campus in 2015.
Figure 18. Scatter grams and strip plots of the repartition of the daily water supply on the scientific campus in 2015.
Smartcities 04 00069 g018
Smartcities 04 00069 g019 550
Figure 19. Variation of the daily water consumption of the campus–Events with consumption exceeding 1200 m3 (average water consumption + 1.5 standard deviation) could be related to leakage, (line in the red color).
Figure 19. Variation of the daily water consumption of the campus–Events with consumption exceeding 1200 m3 (average water consumption + 1.5 standard deviation) could be related to leakage, (line in the red color).
Smartcities 04 00069 g019
Smartcities 04 00069 g020 550
Figure 20. Scatter grams and strip plots of the distribution of the daily water consumption of the campus; events with consumption exceeding 1200 m3 (average water consumption + 1.5 standard deviation) could be related to leakage (line in the red color).
Figure 20. Scatter grams and strip plots of the distribution of the daily water consumption of the campus; events with consumption exceeding 1200 m3 (average water consumption + 1.5 standard deviation) could be related to leakage (line in the red color).
Smartcities 04 00069 g020
Smartcities 04 00069 g021 550
Figure 21. Repartition of the water supply ratios related to leak events.
Figure 21. Repartition of the water supply ratios related to leak events.
Smartcities 04 00069 g021
Smartcities 04 00069 g022 550
Figure 22. Localization of the leakage events (G1 to G5) on the campus.
Figure 22. Localization of the leakage events (G1 to G5) on the campus.
Smartcities 04 00069 g022
Table
Table 1. Confusion matrix.
Table 1. Confusion matrix.
ActualPrediction
PositiveNegative
PositiveTrue PositiveFalse Negative
NegativeFalse PositiveTrue Negative
Table
Table 2. Leakage scenarios were used for the generation of data (leak nodes are given in Figure 2).
Table 2. Leakage scenarios were used for the generation of data (leak nodes are given in Figure 2).
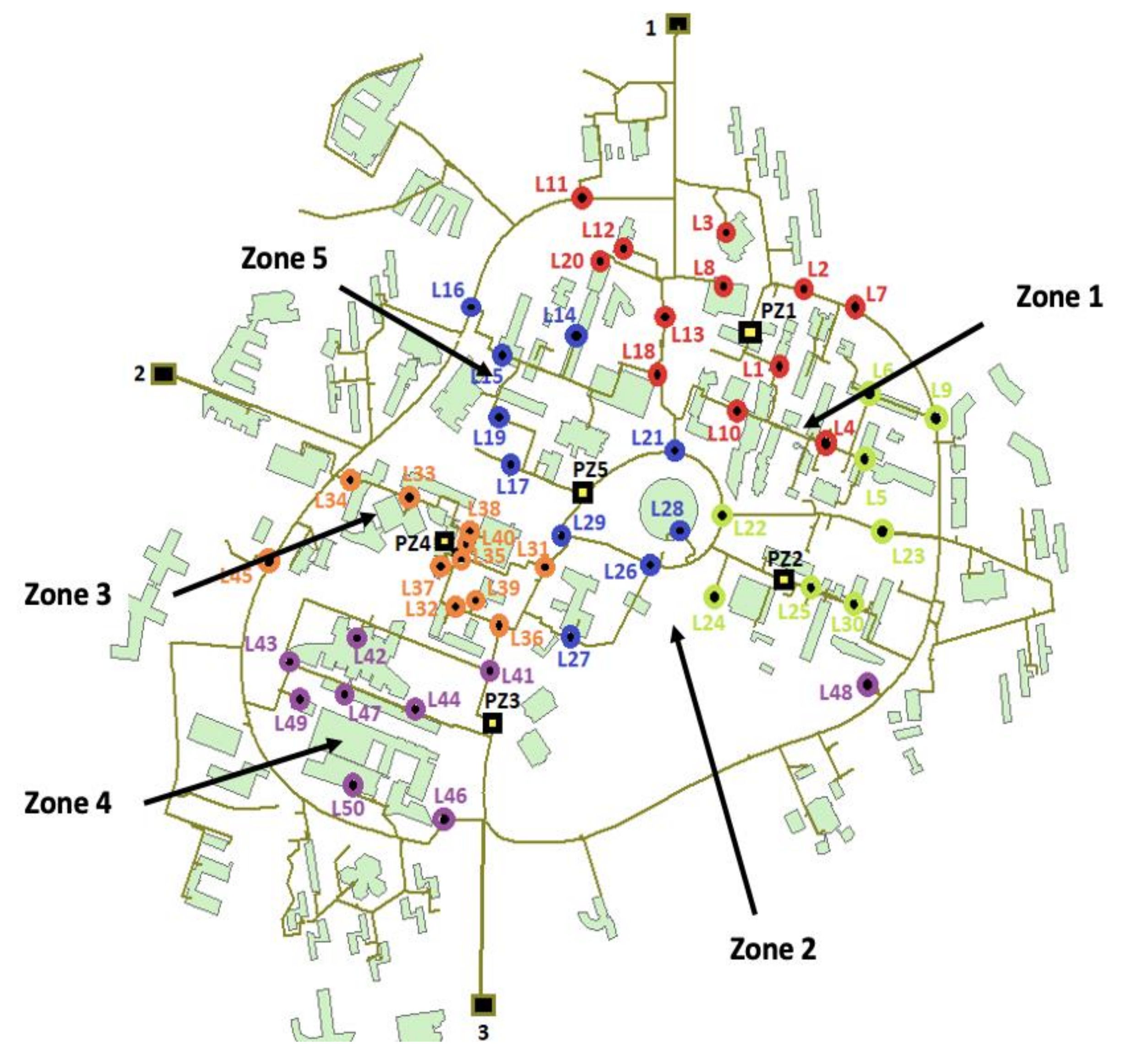
ZonePosition of Water Leak
1
(62 leak scenarios)		L1, L2, L4, L7, L8, L10, L13, L18, L20
L10 + L11; L10 + L12; L10 + L13; L10 + L18; L10 + L2; L10 + L20; L10 + L3; L10 + L4; L10 + L7; L10 + L8; L11 + L12; L11 + L13; L11 + L18; L11 + L2; L11 + L20; L11 + L3: L11 + L4; L11 + L7; L11 + L8; L12 + L13; L12 + L18; L12 + L2; L12 + L20; L12 + L4; L12 + L7; L12 + L8; L13 + L18; L13 + L2; L13 + L20; L13 + L3; L13 + L4; L13 + L7; L13 + L8; L18 + L2; L18 + L20; L18 + L3; L18 + L4; L18 + L7; L18 + L8; L2 + L20; L2 + L4; L2 + L7; L2+ L8; L1 + L10; L1 + L11; L1 + L12; L1 + L13; L1 + L18; L1 + L2; L1 + L20; L1 + L3; L1 + L4; L1 + L7; L1 + L8
2
(35 leak scenarios)		L5, L6, L9, L22, L23, L24, L25, L30
L23 + L22; L24 + L22; L24 + L23; L25 + L22; L25 + L23; L25 + L24; L30 + L22; L30 + L23; L30 + L24; L30 + L25; L5 + L22; L5 + L23; L5 + L24; L5 + L25; L5 + L30; L6 + L22; L6 + L24; L6 + L25; L6 + L30; L6 + L5; L9 + L22; L9 + L23; L9 + L24; L9 + L25; L9 + L30; L9 + L5; L9 + L6:
3
(30 leak scenarios)		L41, L42, L43, L44, L46, L47, L48, L49, L50
L41 + L44; L41 + L46; L41 + L47; L41 + L48; L41 + L50; L42 + L44; L42 + L46; L42 + L47; L42 + L48; L42 + L50; L43 + L44; L43 + L46; L43 + L47; L43 + L48; L43 + L50; L44 + L46; L44 + L47; L44 + L48; L44 + L50; L46 + L47; L47 + L48; L47 + L50; L48 + L49; L50 + L49
4
(47 leak scenarios)		L31, L32, L33, L34, L35, L36, L37, L38, L39, L40, L45
L31 + L36; L31 + L37; L31 + L38; L31 + L39; L31 + L45; L32 + L36; L32 + L37; L32 + L38; L32 + L39; L32 + L45; L33 + L36; L33 + L37; L33 + L38; L33 + L39; L33 + L45; L34 + L36; L34 + L37; L34 + L38; L34 + L39; L34 + L45; L35 + L36; L35 + L37; L35 + L38; L35 + L39; L35 + L45; L36 + L37; L36 + L38; L36 + L39L36 + L45;L37 + L38; L37 + L39; L37 + L45; L38 + L39; L38 + L45; L39 + L45; L40 + L45
5
(41 leak scenarios)		L14, L16, L17, L19, L21, L26, L27, L28, L29
L14 + L21; L14 + L26; L14 + L27; L14 + L28; L14 + L29; L15 + L21; L15 + L26; L15 + L27; L15 + L28; L15 + L29; L16 + L21; L16 + L26; L16 + L27; L16 + L28; L16 + L29; L17 + L21; L17 + L26; L17 + L27; L17 + L28; L17 + L29; L19 + L21; L19 + L26; L19 + L27; L19 + L28; L19 + L29; L21 + L26; L21 + L27; L21 + L28; L21 + L29;L26 + L27; L26 + L28; L26 + L29; L27 + L28; L27 + L29; L28 + L29
Table
Table 3. Pressure observation nodes (positions are given in Figure 2).
Table 3. Pressure observation nodes (positions are given in Figure 2).
Zone12345
Pressure nodePZ1PZ2PZ3PZ4PZ5
Table
Table 4. Statistical descriptive parameters of the pressure and flow rate data.
Table 4. Statistical descriptive parameters of the pressure and flow rate data.
MinimumMaximumAverageStandard Deviation
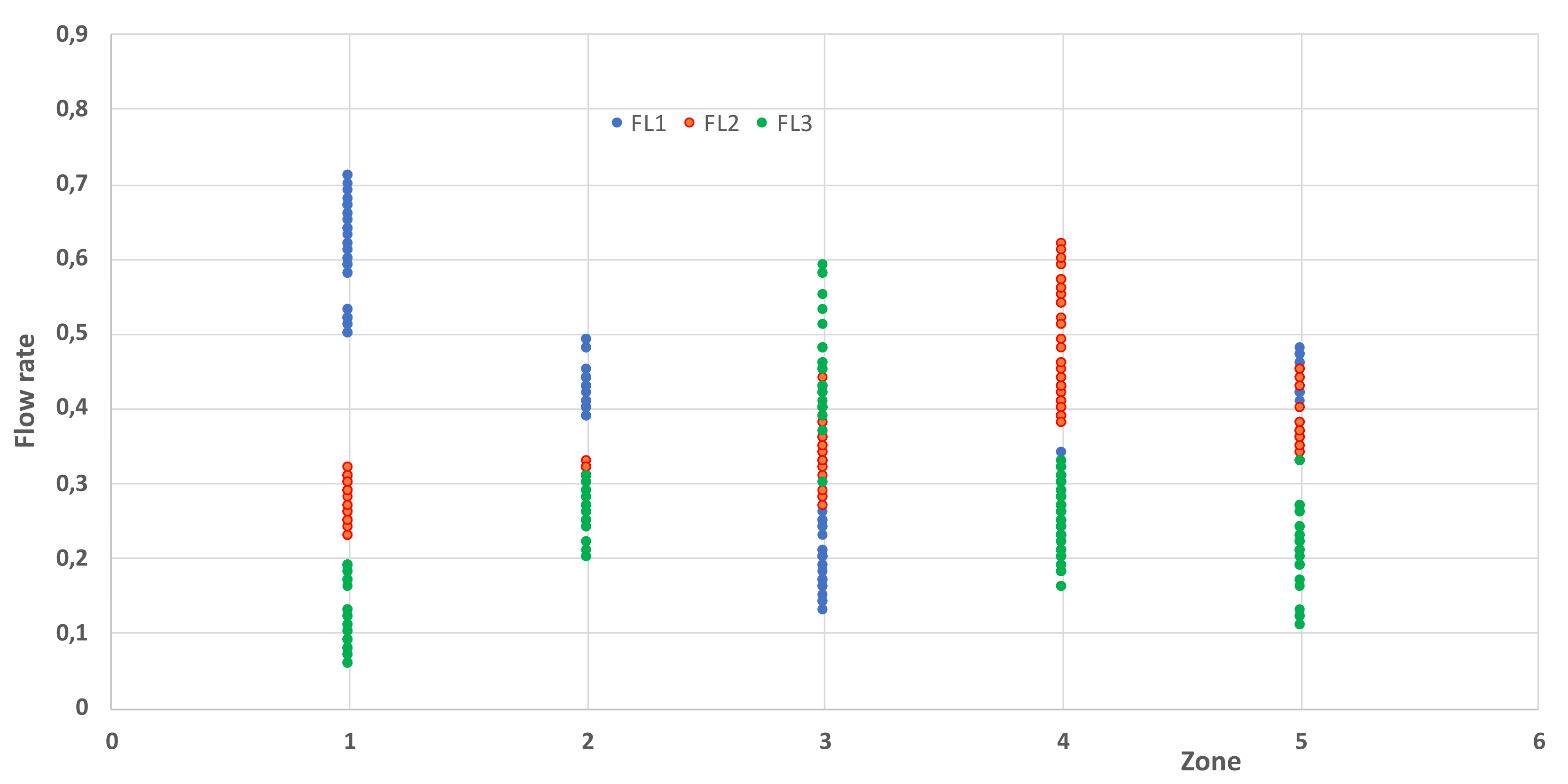
FL1 (%)0.130.710.40.15
FL2 (%)0.230.620.350.82
FL3 (%)0.600.590.230.11
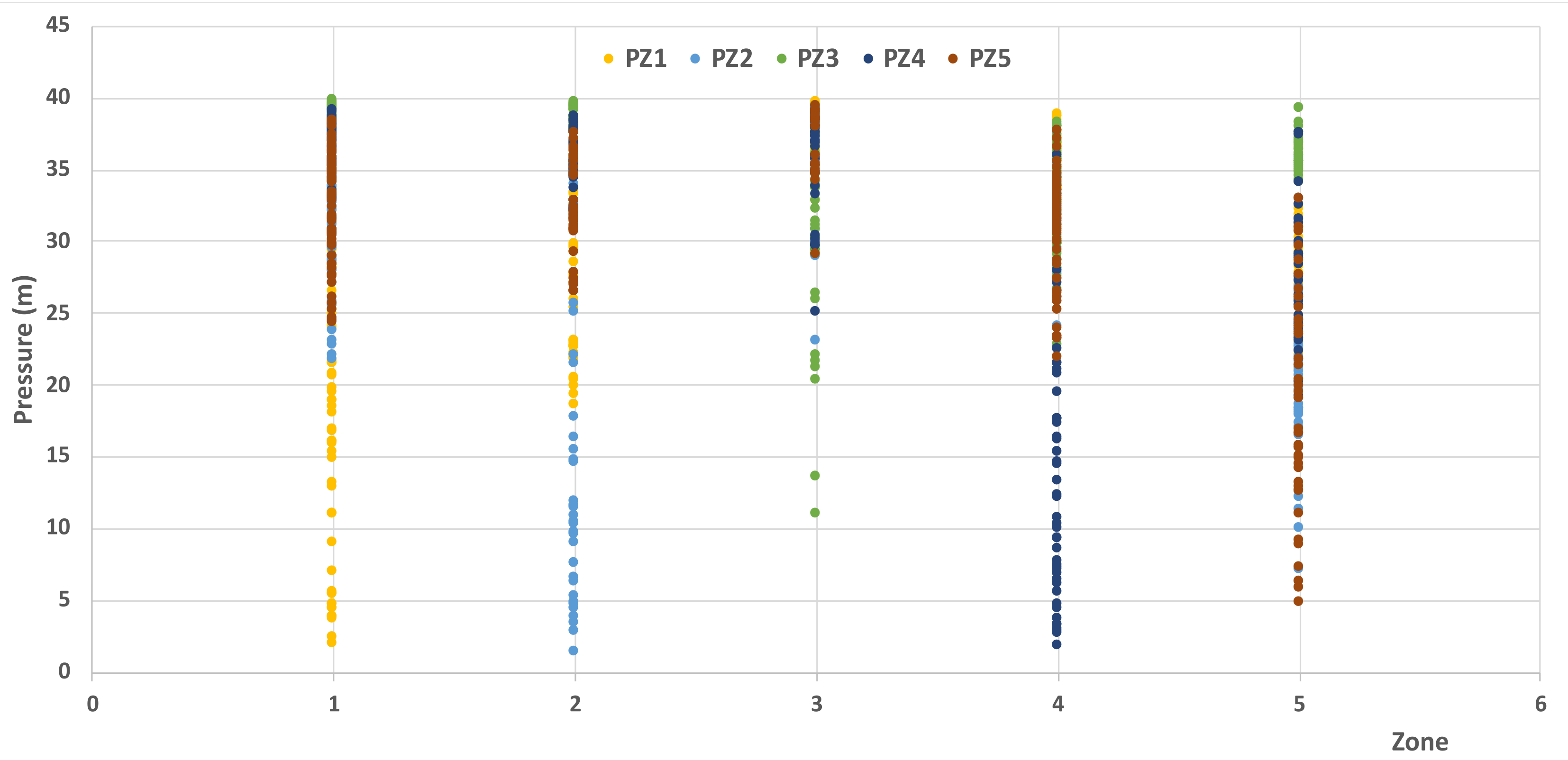
PZ1 (m)2.039.728.49.4
PZ2 (m)1.439.427.49.3
PZ3 (m)11.039.835.64.5
PZ4 (m)1.839.229.210.2
PZ5 (m)4.939.430.07.4
Table
Table 5. Impact of the leak position on the water supply rate.
Table 5. Impact of the leak position on the water supply rate.
Leak ZoneFL1FL2FL3
1StrongMediumLow
2MediumMediumLow to medium
3LowMediumStrong
4LowStrongLow to medium
5MediumMediumLow to medium
Table
Table 6. Classification report for the supervised methods—flow data.
Table 6. Classification report for the supervised methods—flow data.
MethodAccuracyPrecisionRecallF1-Score
Logistic Regression1.01.01.01.0
Decision Tree0.950.960.950.95
Random Forest1.01.01.01.0
Table
Table 7. Classification report for the supervised methods—pressure data.
Table 7. Classification report for the supervised methods—pressure data.
MethodAccuracyPrecisionRecallF1-Score
Logistic Regression1.01.01.01.0
Decision Tree0.880.910.940.91
Random Forest1.01.01.01.0
Table
Table 8. Classification report for the decision tree method—flow and pressure data.
Table 8. Classification report for the decision tree method—flow and pressure data.
MethodAccuracyPrecisionRecallF1-Score
Decision Tree0.980.970.970.96
Table
Table 9. Results obtained with the ANN.
Table 9. Results obtained with the ANN.
DataAccuracyPrecisionRecallF1-Score
Flow data1.01.01.01.0
Pressure data1.01.01.01.0
Flow and pressure data1.01.01.01.0
Table
Table 10. Statistical descriptive analysis of the daily water supply of the campus.
Table 10. Statistical descriptive analysis of the daily water supply of the campus.
F1D
m3/Day		F2D
m3/Day		F3D
m3/Day		Total (Qd)
m3/Day
Minimum10019751414
Maximum7724624541680
Average442251197890
Standard deviation1433359219
Table
Table 11. Leak events in the water distribution of the scientific campus.
Table 11. Leak events in the water distribution of the scientific campus.
DayGroupQd (m3/Day)Qd-Average (m3/Day)
76G1 (76)1354464
86G2 (86)1216326
260G3 (260. 261)1280390
261G3 (260. 261)1357467
264G4 (264–2675)1383493
265G4 (264–2675)1463573
266G4 (264–2675)1477587
267G4 (264–2675)1404514
268G4 (264–2675)1396506
269G4 (264–2675)1217327
270G4 (264–2675)1201311
271G4 (264–2675)1435545
272G4 (264–2675)1459569
273G4 (264–2675)1455565
274G4 (264–2675)1624734
275G4 (264–2675)1680790
327G5 (327)1208318
Table
Table 12. Repartition of the water supply ratios related to leak events.
Table 12. Repartition of the water supply ratios related to leak events.
DayGroupeFL3 (%)FL2 (%)FL1 (%)
76G1 (76)202357
86G2 (86)212257
260G3 (260, 261)262648
261G3 (260, 261)262648
264G4 (264–2675)282646
265G4 (264–2675)272647
266G4 (264–2675)282745
267G4 (264–2675)292744
268G4 (264–2675)282744
269G4 (264–2675)282942
270G4 (264–2675)293041
271G4 (264–2675)282746
272G4 (264–2675)282646
273G4 (264–2675)282646
274G4 (264–2675)272647
275G4 (264–2675)272745
327G5 (327)222355
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Mashhadi, N.; Shahrour, I.; Attoue, N.; El Khattabi, J.; Aljer, A. Use of Machine Learning for Leak Detection and Localization in Water Distribution Systems. Smart Cities 2021, 4, 1293-1315. https://doi.org/10.3390/smartcities4040069

AMA Style

Mashhadi N, Shahrour I, Attoue N, El Khattabi J, Aljer A. Use of Machine Learning for Leak Detection and Localization in Water Distribution Systems. Smart Cities. 2021; 4(4):1293-1315. https://doi.org/10.3390/smartcities4040069

Chicago/Turabian Style

Mashhadi, Neda, Isam Shahrour, Nivine Attoue, Jamal El Khattabi, and Ammar Aljer. 2021. "Use of Machine Learning for Leak Detection and Localization in Water Distribution Systems" Smart Cities 4, no. 4: 1293-1315. https://doi.org/10.3390/smartcities4040069

APA Style

Mashhadi, N., Shahrour, I., Attoue, N., El Khattabi, J., & Aljer, A. (2021). Use of Machine Learning for Leak Detection and Localization in Water Distribution Systems. Smart Cities, 4(4), 1293-1315. https://doi.org/10.3390/smartcities4040069

Article Metrics

Back to TopTop