Radar Foot Gesture Recognition with Hybrid Pruned Lightweight Deep Models

Abstract

Foot gesture recognition using a continuous-wave (CW) radar requires implementation on edge hardware with strict latency and memory budgets. Existing structured and unstructured pruning pipelines rely on iterative training–pruning–retraining cycles, increasing search costs and making them significantly time-consuming. We propose a NAS-guided bisection hybrid pruning framework on foot gesture recognition from a continuous-wave (CW) radar, which employs a weighted shared supernet encompassing both block and channel options. The method consists of three major steps. In the bisection-guided NAS structured pruning stage, the algorithm identifies the minimum number of retained blocks—or equivalently, the maximum achievable sparsity—that satisfies the target accuracy under specified FLOPs and latency constraints. Next, during the hybrid compression phase, a global L1 percentile-based unstructured pruning and channel repacking are applied to further reduce memory usage. Finally, in the low-cost decision protocol stage, each pruning decision is evaluated using short fine-tuning (1–3 epochs) and partial validation (10–30% of dataset) to avoid repeated full retraining. We further provide a unified theory for hybrid pruning—formulating a resource-aware objective, a logit-perturbation invariance bound for unstructured pruning/INT8/repacking, a Hoeffding-based bisection decision margin, and a compression (code-length) generalization bound—explaining when the compressed models match baseline accuracy while meeting edge budgets. Radar return signals are processed with a short-time Fourier transform (STFT) to generate unique time–frequency spectrograms for each gesture (kick, swing, slide, tap). The proposed pruning method achieves 20–57% reductions in floating-point operations (FLOPs) and approximately 86% reductions in parameters, while preserving equivalent recognition accuracy. Experimental results demonstrate that the pruned model maintains high gesture recognition performance with substantially lower computational cost, making it suitable for real-time deployment on edge devices.

1. Introduction

Gesture recognition has emerged as a key enabler for natural human–machine interaction across diverse application domains. Beyond its traditional roles in sports rehabilitation [1] and immersive virtual reality training [2,3,4], gesture sensing plays an increasingly critical role in modern industries such as smart manufacturing and autonomous driving, where the timely and accurate interpretation of human movements directly affects operational safety and efficiency. Despite these advances, most research efforts have concentrated on hand gestures or full-body postures, while foot gestures have received relatively little attention, even though they provide significant practical advantages in scenarios requiring hand-free operation or enhanced accessibility.

Foot gesture recognition is particularly valuable in environments where conventional interaction methods are impractical or inconvenient. In smart buildings, users may trigger access systems, elevators, or lighting through simple foot motions when carrying objects or when their hands are otherwise occupied. Existing smart entry solutions are typically bluetooth-based and rely on proximity detection rather than intentional action, which often leads to unintended elevator calls or miscoordination between automated doors and elevator systems, introducing operational bottlenecks. In hospital environments, foot-based interaction provides a hygienic and contactless alternative for medical staff and patients, reducing infection risks when controlling doors, service robots, or equipment. Similarly, in smart vehicles, foot gestures can be leveraged to manage infotainment systems or auxiliary controls without requiring the driver to release the steering wheel, thereby enhancing both convenience and driving safety.

Although various non-contact sensors have been applied to gesture recognition—including cameras, infrared (IR), Bluetooth, and LiDAR—each sensor has critical limitations for these scenarios. Camera-based systems inherently raise privacy concerns in personal or medical spaces and often depend on favorable lighting conditions, which restricts their robustness. IR sensors are sensitive to ambient thermal variations and provide only limited-range motion detection. Bluetooth-based systems primarily function through device proximity rather than explicit gesture recognition, which undermines intentional control. LiDAR offers precise spatial mapping but remains costly, power-intensive, and less practical for compact embedded systems.

In contrast, radar-based gesture recognition provides a robust and privacy-preserving alternative. Radar does not capture visual information, thereby eliminating privacy issues while maintaining reliable performance across diverse environmental conditions. It is inherently resilient to variations in lighting or temperature, operates with low power consumption, and can be miniaturized for seamless integration into embedded platforms. Importantly, radar captures Doppler frequency shifts associated with fine-grained foot motions, enabling accurate classification of subtle gestures. These attributes make radar particularly well-suited for foot gesture recognition in environments where privacy, hygiene, convenience, and robustness are essential.

Motivated by these needs, this paper proposes a radar-based foot gesture recognition system for embedded applications such as smart buildings, hospitals, and smart vehicles. Continuous-wave (CW) radar signals are processed through short-time Fourier transform (STFT) to generate spectrogram representations, which are then classified using a lightweight convolutional neural network (CNN). To enable deployment on resource-constrained devices, we introduce a hybrid pruning scheme that combines block-wise structured pruning with unstructured weight pruning. This approach significantly compresses the network while preserving recognition accuracy, making it suitable for real-time, privacy-preserving gesture recognition in edge environments.

Radar-based foot gesture recognition enables hands-free interaction and privacy-preserving control in scenarios where cameras are impractical, such as clinical or industrial environments. However, MCU- or CPU-class devices impose strict constraints on limited computing power and small memory size. Conventional STFT-based spectrograms (e.g., 256 × 256 with 1–2 s windows) face these challenges, motivating efficient yet accurate compression strategies.

Existing model compression and neural architecture search (NAS) frameworks primarily focus on accuracy–efficiency tradeoffs but often rely on repetitive train–prune–retrain cycles [5,6,7]. Few methods jointly optimize model search and pruning under explicit hardware constraints such FLOPs or latency, which limits their practical implementation on CPU-class edge devices [8,9,10].

This work addresses these limitations by introducing a NAS-guided bisection pruning framework that integrates structural and unstructured compression with low-cost decision protocols. Our key contributions are fourfold. First, the bisection-guided NAS structured pruning efficiently identifies a semi-optimal number of retained blocks or equivalent sparsity ratio that satisfies a target accuracy within defined FLOP or latency constraints, effectively reducing search complexity. Second, the hybrid compression approach applies to a global L1-norm-based unstructured pruning, followed by channel-wise repacking to translate sparsity into structural reductions. Third, a low-cost decision protocol—consisting of short fine-tuning, partial validation on data subsets, and margin-based thresholding—allows reliable evaluation without repeated full retraining cycles. Finally, extensive deployment validation across popular lightweight backbones such as MobileNetV3/V2, EfficientNet-B0, and SqueezeNet demonstrates a consistent balance between accuracy and efficiency, significantly reducing FLOPs, parameter counts, and latency on CPU-embedded devices. Unlike prior channel-only, unstructured-only, or one-shot NAS approaches that still require dense evaluations, our framework embeds a bisection mechanism within NAS and couples it with hybrid sparsity. This design explicitly minimizes search and training cost while ensuring deployment feasibility on CPU-embedded edge platforms.

2. Related Works

Recent studies on radar-based foot gesture recognition have made notable progress in achieving efficient on-device inference through compact input design, lightweight architecture, and hybrid compression strategies. In our prior works [2,5], high-compression micro-Doppler representations have demonstrated that reducing radar input dimension can enhance synergy with structured pruning and NAS, maintaining accuracy while lowering computational load. Similarly, transitioning from computationally intensive 3D FFT stacks to 2D range-Doppler maps (RDM) or even FFT-free time-domain signals has shown promise in reducing memory and latency for edge deployment [11,12]. Graph-based frameworks have also enabled real-time performance on embedded hardware by mapping sparse MIMO radar data into message-passing neural networks (MPNNs) [13]. Furthermore, integrated compression pipelines combining structured pruning, NAS, quantization, and lightweight backbones have narrowed the resource gap to MCU- or SoC-class devices while preserving gesture dynamics through hybrid CNN–temporal designs [14]. These approaches underscore radar’s suitability for hands-busy and privacy-sensitive applications such as automotive kick sensors, in-cabin interfaces, and smart-home control.

Table 1. Survey of lightweight radar-based foot gesture recognition methods.

Tech. Fields	Key Approaches	Key Contributions	Refs.
Radar sensing & representations	FMCW micro-Doppler for foot gestures	High-compression micro-Doppler signatures enable compact CNN inputs while keeping high recognition for foot kicks, taps, pushes; hands-free operation suggested for vehicle trunk and home control.	[2,10]
	Range-Doppler/ Range-Angle maps	Standard 2-D RDM pipeline with light CNN/Bi-LSTM; extended to MIMO fusion of range, velocity, angle to raise separability and robustness across view angles.	[11,12]
	Sparse point clouds (MIMO)	Graph NN on radar point clouds runs real-time on Raspberry Pi; ~8× faster than prior SOTA while maintaining accuracy → viable edge path.	[13]
	Lightweight time-domain features	FFT-free preprocessing collapses 3-D radar cubes to few 1-D streams (range/azimuth/elevation/magnitude), cutting compute before NN.	[14]
	Robustness in clutter	End-to-end mmWave pipeline with interference-aware modeling for similar/overlapping gestures in crowded scenes.	[15]
Lightweight model design	Structured pruning + NAS	Block/channel structured pruning guided by NAS to auto-select compact backbones for radar gestures with minimal accuracy drop; edge-deployable CNNs.	[16]
	Mobile-class backbones	MobileNet-inspired or multi-branch lightweight CNNs with attention keep accuracy at low FLOPs; practical on ARM/Edge-TPU.	[17]
	Quantization for edge	60 GHz FMCW pipeline with five features and slim classifier fits in <280 kB flash; 8-bit inference with high F1 → MCU/SoC feasibility.	[18]
	Hybrid CNN–Transformer/TCN	CNN with temporal modeling (TCN/Transformer) improves dynamic gesture separability at modest cost; suited after front-end compression.	[19]
Compression–accuracy trade-offs	Edge-optimized classifiers	Comparative study shows Mobile-class nets keep accuracy with large latency/energy savings vs. heavy CNNs; guidance for radar HGR on constrained HW.	[17]
	Feature- vs. model-level reduction	Foot-specific: compressing radar signature images reduces input size drastically yet sustains accuracy; model compression then compounds gains.	[2]
	Person-independent generalization	Lightweight, FFT-free preprocessing improves cross-user stability before compact NN, aiding domain shift.	[20]
Applications	Automotive foot-HCI	Kick-sensor for door/trunk; radar-CNN pipeline detects foot kicks under varying placements; leverages radar’s non-line-of-sight and lighting robustness.	[21]
	Hands-busy HCI	Real-time mmWave gesture on Raspberry Pi demonstrates natural, low-power control channels applicable to foot UIs.	[13]
	Smart-home control	Memory-tight FMCW edge pipeline points to in-appliance deployment for privacy-preserving, touch-free control via lower-limb cues.	[18]
	FMCW radar gesture reviews	Methodologies, datasets, signal paths (RDM/RA/point cloud), and challenges summarized; informs design choices for foot gesture extensions.	[22]
	Foot gesture HMI overview	Cross-sensor FGR landscape, limitations of contact/non-contact sensing, and deployment issues; motivates radar + model compression.	[23]

summarizes their core technologies of radar-based foot gesture lightweight recognition.

Despite these advances, existing methods remain fragmented across different optimization layers. Most focus on either compact input signal representation or network-level compression but seldom address the combined optimization of both under explicit hardware constraints (e.g., FLOPs, latency, or computing power). Moreover, iterative search–prune–retrain pipelines remain computationally expensive, limiting scalability for diverse backbones or deployment environments. Consequently, there is a critical need for a unified framework that jointly integrates search-guided structural pruning, hybrid sparsity conversion, and cost-aware decision mechanisms to achieve accuracy-efficient, hardware-constrained learning for radar-based foot gesture recognition.

3. Methods

3.1. Radar Data Acquisition and STFT Processing

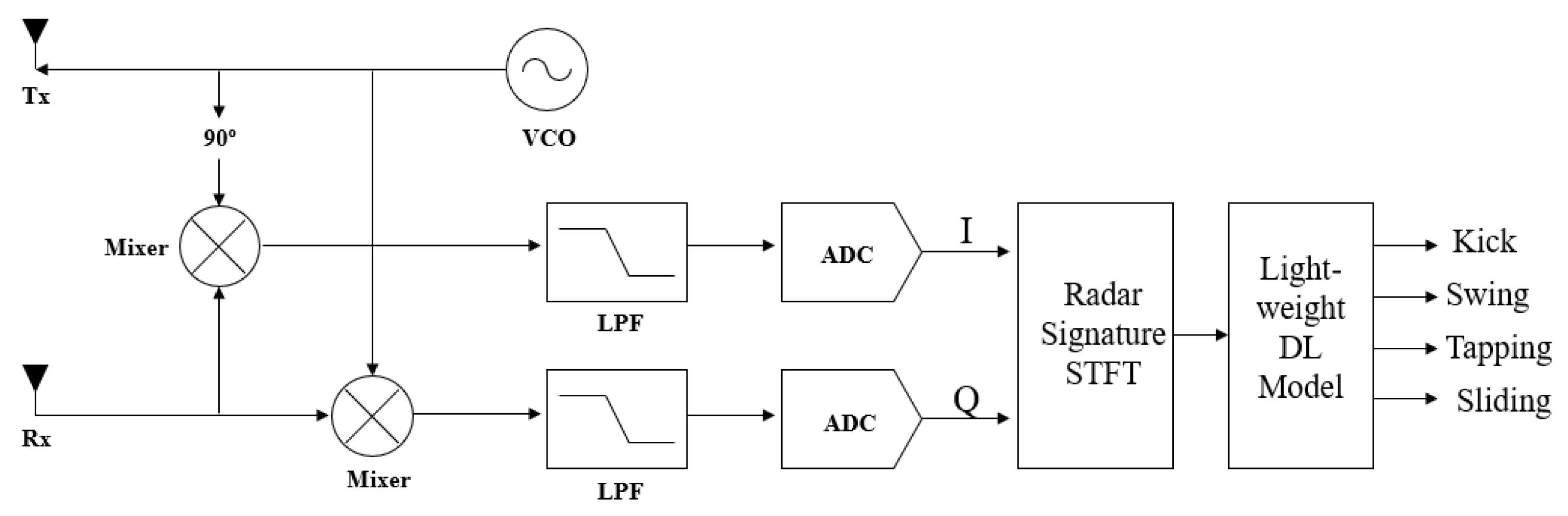
We collected an in-laboratory radar dataset for experimental validation because no public radar micro-Doppler dataset contains foot gesture classes suitable for this study; five participants (one female and four male) were involved in data acquisition to obtain radar spectrograms for each foot gesture. A continuous-wave (CW) Doppler radar operating at 24 GHz was used to record foot gesture data [14]. Four gesture classes were recorded: kick, swing, slide, and tap. For each gesture trial, a radar transmitted a single-tone continuous-wave signal and captured the reflected echoes from a moving foot. The received signal undergoes cell-average CFAR (Constant False Alarm Rate) detection and denoising preprocessing and is then transformed via a short-time Fourier transform (STFT). The STFT produces a time–frequency spectrogram of size 227 × 227 pixels, which is converted to a three-channel (RGB) image as the input to the CNN. The radar parameters (operating frequency, sampling rate, and antenna beam width) were chosen to ensure distinct Doppler signatures for different gestures. A block diagram of the CW radar system is shown on Figure 1. The radar system was installed at a right angle (90 degrees) with respect to the ground to ensure effective detection of foot-level motion. Data was recorded under two radar installation heights (0.6 m and 1.5 m) and two different surface conditions (ground and concrete floor) to ensure sufficient variability in geometry and reflection characteristics. The sensor emitted a continuous wave transmission directed downward towards the target surface. Three installation scenarios were examined to represent typical deployment environments: the bumper of a passage vehicle, the bumper of an SUV, and the entrance door of a smart building. The radar configuration consists of a single transmitter-receiver antenna pair, providing a field of view of 80° in the horizontal direction and 12° in the vertical direction.

Figure 2 illustrates example STFT spectrograms for each gesture class. The kicking and sliding gestures produce roughly symmetric Doppler patterns, whereas the swinging and tapping gestures yield asymmetric frequency distributions. Variations in bandwidth reflect the distinct kinematics of each movement. In particular, the kicking gesture generates a strong frequency sweep from negative to positive Doppler frequencies, while the swinging and sliding gestures share similar Doppler ranges but differ in signal amplitude. The tapping gesture produces narrow-band spectral lines that remain over a longer time, with intermittent bursts of higher-bandwidth energy. These unique spectro-temporal signatures serve as the basis for classification [2]. In total, 3500 spectrogram images were collected. For every gesture class, 600 samples were used for training and cross-validation (at a 90:10 ratio), and an additional 100 samples were reserved for evaluation. To implement foot gesture recognition on MCU-class devices, model training is performed on a PC equipped with an Intel Core i5-13600K processor, while inference is designed to run on an ARM 32-bit Cortex-based MCU platform. A random 20% subset of each training class (120 images) was held out for validation, leaving 480 training samples per class. These images were used to train and evaluate the CNN models. In our prior work [2], this dataset was classified using standard networks (Google Net, ResNet, VGG, AlexNet) and a PCA-SVM, yielding accuracy of 0.96, 0.96, 0.98, 0.97, and 0.97, respectively. The present study builds on that dataset and focuses on compressing the CNN model to suit embedded applications.

3.2. Proposed Hybrid Pruning Framework for Gesture Recognition

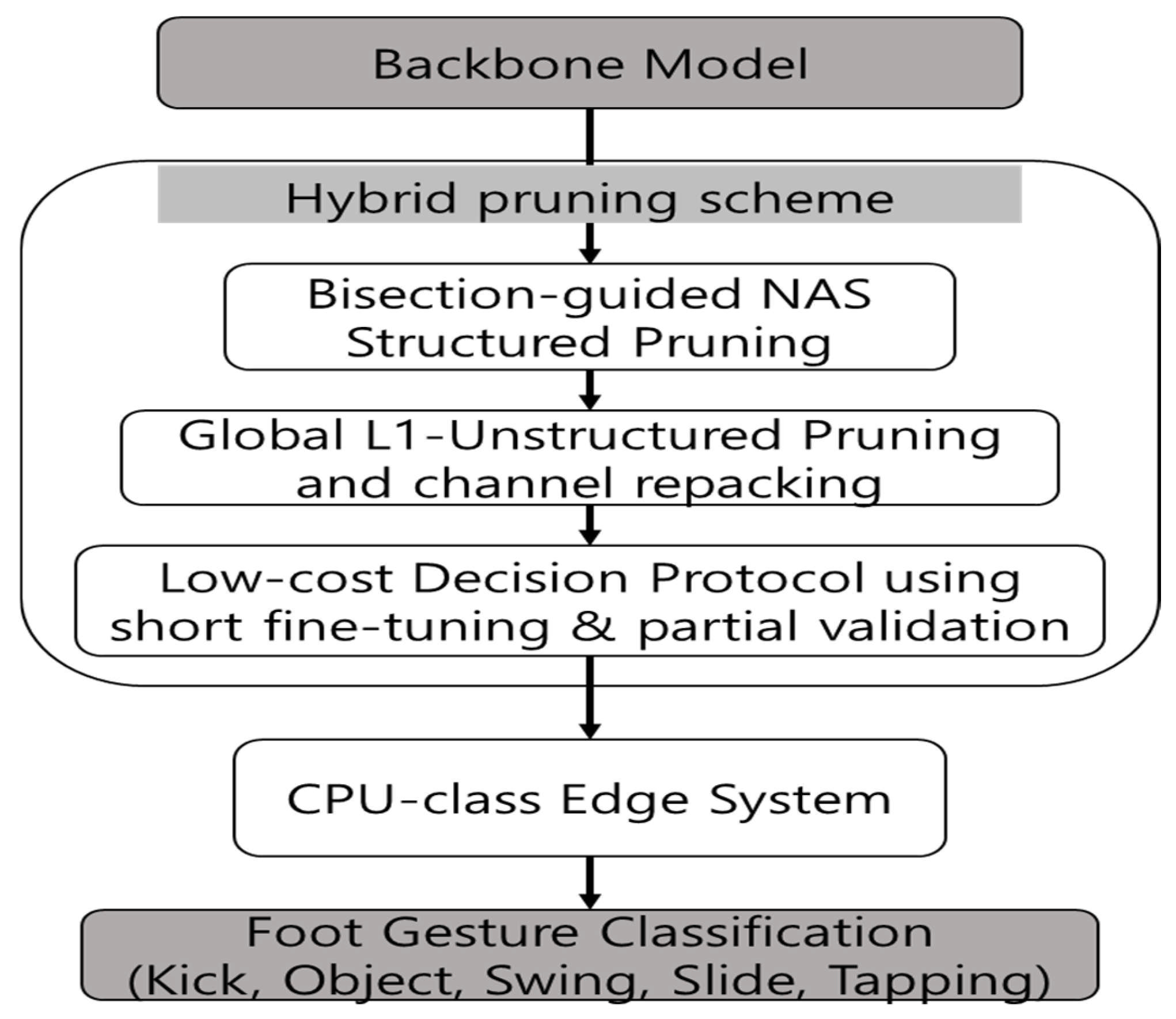
The proposed hybrid pruning scheme is designed to enable real-time inference on CPU-class edge devices by introducing a novel network compression method to the baseline model.

Figure 3 illustrates the proposed hybrid pruning framework for foot gesture recognition, consisting of three sequential steps as follows:

First, NAS-guided bisection pruning employs a weight-sharing supernet that spans block and channel configurations. A bisection rule is used to efficiently determine the minimal number of retained blocks (B*) or the maximal sparsity (r*) required to meet the target accuracy under FLOPs and latency constraints. Second, global L1-percentile unstructured pruning is applied, with optional channel repacking to convert weight sparsity into practical structural speedups in real deployment. Third, each pruning decision is verified using a cost-efficient protocol featuring short fine-tuning (1–3 epochs) and partial validation (10–30% of the dataset), minimizing the need for repeated full retraining.

By sequentially integrating these steps, the framework produces a highly compact model suitable for edge devices, enabling efficient and accurate foot gesture classification from STFT spectrogram inputs.

The baseline models under consideration are lightweight CNN architectures suitable for real-time inference. The STFT spectrogram images are used as input to CNN. Four network backbones were evaluated: MobileNetV3, MobileNetV2 [24,25,26], EfficientNet-B0 [27], and SqueezeNet [28]. These models are selected for their small size and low FLOPs requirements. Each CNN was trained using the categorical cross-entropy loss and Adam optimized with sufficient epochs to ensure convergence. During training, the learning curves were monitored for the accuracy and loss trajectories for each network, demonstrating stable convergence with the chosen training protocol. Baseline training used the same learning rate = 0.01, batch size = 64, L2 weight decay = 1 × 10⁻⁴ for all backbones. Unless specified otherwise, baseline and hybrid models were trained using identical procedures. Only the pruning, quantization, or NAS parameters explicitly stated in the main text were varied.

3.3. Bisection-Guided NAS Structured Pruning

Bisection-guided NAS structured pruning operates at the block level (e.g., residual, inverted-bottleneck, or inception blocks), excluding the classifier head and input stem from pruning. A fixed drop order for blocks is first established, using either depthwise suffix order or an important ranking metric. For any candidate configuration retaining B blocks, the network is instantiated by simultaneously removing the last N − B blocks according to this order. This preserves early, high-resolution processing and leverages the observed empirical redundancy in later blocks, as evidenced by plateaus in block–accuracy curves. Each pruned candidate undergoes brief fine-tuning to recover any loss of accuracy.

The candidate space is defined as a weight-sharing network parameterized by block retention, expansion ratios ($t\in \{\mathrm{1,3},\mathrm{4,6}\}$), depthwise kernel sizes ($k\in \left\{\mathrm{3,5}\right\}$), optional squeeze-and-excitation (SE) modules and output channels quantized on 8/16-aligned grids. The pruning objective is formulated as:

$$\hspace{0.25em}\max \{Ac{c}_{\mathrm{val}}\left(B\right) \ge \tau \}$$

$$\mathrm{subject} \mathrm{to} \mathrm{FLOPs}(B)\le F_{\mathrm{m}\mathrm{a}\mathrm{x}},\hspace{0.25em}\mathrm{Latency}(B)\le L_{\mathrm{m}\mathrm{a}\mathrm{x}},\hspace{0.25em}\mathrm{Params}(B)\le P_{\mathrm{m}\mathrm{a}\mathrm{x}}.$$

(1)

The bisection process sequentially chooses a single decision variable—the number of retained blocks B*. At each iteration, the midpoint candidate is evaluated with short fine-tuning (1–3 epochs) and partial validation (10–30% subset), repeated twice for robustness. A configuration is accepted if $Acc\ge \tau +ϵ$ and all resource constraints are satisfied; the interval is iteratively halved until the stopping criterion is met—either $hi-lo\le 1$ block (for B*) or $\le \delta$ (for r*). The parameters were set as follows: $\tau =0.92$, $ϵ=0.3\% point$, and $\delta =0.1$. Here, $\tau$ represents the accuracy target, $ϵ$ the accuracy margin, and $\delta$ the sparsity goal. This bisection search reduces the required evaluations from $N$ to $\lceil {\mathrm{l}\mathrm{o}\mathrm{g}}_{2}N\rceil$, efficiently identifying a semi-optimal “knee” point where further block removal would precipitate a rapid accuracy decline, thus balancing deployment efficiency and accuracy retention.

3.4. Unstructured Pruning and Quantization

Building on the structured pruned backbone, we apply global magnitude-based unstructured pruning, quantization, and channel repacking in sequence. The target sparsity r* is selected via a bisection search. Specifically, a global $L1$ percentile threshold $\theta \left(r\right)$ is computed over all convolution and linear layer weights $W$ as the ($1-r$) quantile of their absolute values $\mid W\mid$, and weights below this threshold $\theta \left(r\right)$ are zeroed. After pruning, batch normalization (BN) statistics are re-estimated on a held-out calibration buffer, followed by a short fine-tuning phase (1–3 epochs) to recover accuracy.

Each pruning candidate is evaluated on a validation subset $v\in \left[\mathrm{0.1,0.3}\right]$ with $m=5$ repeated trials; the candidate is accepted if it meets the accuracy threshold while satisfying FLOPs, latency, and parameter constraints. The bisection interval shrinks until a convergence criterion is reached.

To further reduce model size and accelerate inference, the remaining weights and optional activations are quantized to 8-bit precision using symmetric per channel scaling for convolution layers and per tensor scaling for linear layers. The quantization scales are calibrated on a small unlabeled dataset to mitigate the influence of outliers. This quantization approximately halves parameter memory relative to 16-bit floating point and improves cache locality on edge CPUs.

Finally, repacking converts fine-grained sparsity into structural efficiency by removing channels with near-zero activation energy, measured over a calibration set (e.g., mean activation magnitude). For depthwise–pointwise convolution pairs, the corresponding depthwise filter and input channel of subsequent pointwise convolution are pruned jointly. Residual and concatenation branches are pruned consistently to maintain network integrity.

Thus, the hybrid pipeline combines block level removal for coarse compute reduction with fine-grained unstructured pruning, quantization, and repacking for additional compactness and real latency improvements, enabling efficient edge deployment.

3.5. Theoretical Analysis of the Hybrid Pruning

A. 

Resource-Constrained Objective Function

We formalize the proposed hybrid pruning framework with the following elements: (i) accuracy preservation under unstructured pruning, INT8 quantization, and channel repacking; (ii) recognition probability and statistical confidence bounds for the bisection-guided decision rule; and (iii) compression-based generalization after pruning and quantization.

Let $\left(x, y\right)$ ~ $\mathcal{D}$. A model $f_{\theta }$ with $\theta \in {\mathbb{R}}^p$ output logits $z= f_{\theta }\left(x\right) \in {\mathbb{R}}^K$ and $p_{\theta }\left(c|x\right)={softmax(z)}_c$. The empirical loss $\widehat{\mathcal{L}}(\theta )$ is cross-entropy:

$$\widehat{\mathcal{L}}\left(\theta \right)={\mathbb{E}}_{\left(x, y\right)~ D}[-{log}_{p_{\theta }}\left(y|x\right)]$$

Resource constraints are enforced by linear hinge penalties:

$$\underset{\mathit{\theta ϵ}\mathcal{S}}{\min }\widehat{\mathcal{L}}\left(\theta \right)+{{\lambda }_{\mathrm{F}}\left[{\displaystyle \frac{\mathrm{F}\mathrm{L}\mathrm{O}\mathrm{P}\mathrm{s}\left(\theta \right)}{{\mathrm{F}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}}-1\right]}_{+}+{{\lambda }_{\mathrm{L}}\left[{\displaystyle \frac{\mathrm{L}\mathrm{a}\mathrm{t}(\theta )}{{\mathrm{L}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}}-1\right]}_{+}+{{\mathsf{\lambda }}_{\mathrm{P}}\left[{\displaystyle \frac{\mathrm{P}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{s}(\theta )}{{\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}}-1\right]}_{+}$$

(2)

where ${\left[ u\right]}_{+}=\mathrm{m}\mathrm{a}\mathrm{x}(0,\mathrm{u})$, $\mathcal{S}$ is the supernet search space (retained blocks B, expansion $t\in \{\mathrm{1,3},\mathrm{4,6}\}$, depthwise kernel $k\in \left\{\mathrm{3,5}\right\}$, SE on/off, 8/16-aligned channels).

B. 

Logit-Perturbation Bounds and Classification Invariance

After pruning, quantization, and channel repacking, ${\theta }^{\prime }= \theta +∆\theta$ and $∆z\left(x\right)= f_{{\theta }^{\prime }}\left(x\right)-f_{ \theta }(x)$ [29]. With 1-Lipschitz activations and layer spectral norms $s_l$ = ${‖W_l‖}_2$, the upper bound holds:

$${‖∆z(x)‖}_2 \le \left({\displaystyle {\prod }_{l=1}^L}{s}_l\right){\displaystyle {\sum }_{l=1}^L}{\displaystyle \frac{{‖{∆W}_l‖}_2}{s_l}}{‖x‖}_2+ {\mathsf{\Xi }}_{repack }$$

(3)

Hence, the total distortion is governed by the global scale ${\prod }_{\mathcal{l}}{s}_l$ and the relative per-layer perturbation magnitudes ${‖{∆W}_l‖}_2/s_l$. We bound each component:

• Unstructured pruning (global L1 percentile):

$${‖{\Delta W}_l ‖}_F \le {\theta }_l(r)\sqrt{k_l }$$

(4)

with threshold ${\theta }_l(r)$ at target sparsity r, and $k_l$ zeroed weights.

• INT8 quantization (symmetric, per-channel):

  $${‖{\Delta W}_l ‖}_F\le {\displaystyle \frac{1}{2}}{\displaystyle {\Delta }_{\mathcal{l}}^{max}}\sqrt{d_{\mathcal{l}}}, {\displaystyle {\Delta }_{\mathcal{l}}^{\mathrm{m}\mathrm{a}\mathrm{x}}}={\mathrm{m}\mathrm{a}\mathrm{x}}_c{\Delta }_{\mathcal{l},c}$$

  (5)

  where $d_{\mathcal{l}}$ is the number of weights in layer $\mathcal{l}$.

• Channel repacking (activation-energy-based):

  $${\mathsf{\Xi }}_{repack}\le {\sum }_{c\in C}\parallel {\mathrm{W}}_{out} [:,c]{\parallel }_2{a}_c\le \eta$$

  (6)

  with RMS activation $a_c$ and budget $\eta$.

Combining (3)–(6) yields the consolidated perturbation inequality:

$${‖∆z(x)‖}_2 \le \left({\prod }_k{s}_k\right)\sum _l({\displaystyle \frac{{\theta }_l\left(r\right)\sqrt{k_l} + \frac{1}{ 2}{\displaystyle {\Delta }_{\mathcal{l}}^{max}}\sqrt{d_{\mathcal{l}}}}{s_l}}{ ) ‖x‖}_2 +\eta ,$$

(7)

Let the logit margin be $\gamma (x)=z_y-\underset{j\ne y}{\mathrm{m}\mathrm{a}\mathrm{x}} z_j.$ Since $\parallel ∆z\left(x\right){\parallel }_{\mathrm{\infty }}\le \parallel ∆z\left(x\right){\parallel }_2$, classification invariance holds whenever

$$\parallel ∆z\left(x\right){\parallel }_2<{\displaystyle \frac{1}{2}}\underset{\_}{\gamma }\hspace{0.25em}\Rightarrow \hspace{0.25em}\arg \underset{c}{\mathrm{m}\mathrm{a}\mathrm{x}} {\displaystyle z_c^{\prime }}=\mathrm{a}\mathrm{r}\mathrm{g} \underset{c}{\mathrm{m}\mathrm{a}\mathrm{x}} z_c$$

(8)

where $\underset{\_}{\gamma }\hspace{0.25em}$ is the minimum validated margin. Equations (7) and (8) constitute the accuracy-preservation (design-invariance) criterion.

C. 

Bisection Decision Rule: Recognition Probability and Statistical Reliability

The bisection acceptance rule is

$$Acc\ge \tau +ϵ,$$

(9)

with target $\tau$ and tolerance $\epsilon$. For $n_{\mathrm{v}\mathrm{a}\mathrm{l}}$ validation samples and observed accuracy $\widehat{p}$ (a Bernoulli mean), Hoeffding’s inequality [30] gives

$$\mathrm{Pr}\left( ∣\widehat{p}-p∣\ge \epsilon \right)\le 2e^{-2n_{\mathrm{e}\mathrm{f}\mathrm{f}}{\epsilon }^2},n_{\mathrm{e}\mathrm{f}\mathrm{f}}=m\cdot v\cdot n_{\mathrm{v}\mathrm{a}\mathrm{l}},$$

(10)

where $m$ is the number of repeats and $v$ the validation fraction. For confidence 1 − $\delta$,

$$\epsilon =\sqrt{{\displaystyle \frac{\mathrm{l}\mathrm{n}(2/\delta )}{2n_{\mathrm{e}\mathrm{f}\mathrm{f}}}}}.$$

(11)

Given a logit perturbation radius $\parallel ∆z\left(x\right){\parallel }_{\mathrm{\infty }}\le {\epsilon }_z$, the softmax recognition probability lower bound is

$$p_{{\theta }^{\prime }}(y\mid x)\ge {\displaystyle \frac{1}{1+\left(K-1\right)\exp \left\{-\gamma \left(x\right)+2{\epsilon }_z\right\} }}$$

(12)

which reduces in the baseline (no hybrid compression) to $p_{\theta }(y\mid x)\ge [1+(K-1)e^{-\gamma (x)}{]}^{-1}$ by setting ${\epsilon }_z=0$.

D. 

Compression-Based Generalization after Pruning/Quantization

Let the compressed model’s code length be $S$ bits (structural header $S_{\mathrm{h}\mathrm{d}}$, sparse indices, quantized values). An Occam–PAC-Bayes style bound [31,32,33] gives

$$\left({\theta }^{\prime }\right)\le \widehat{R}\left({\theta }^{\prime }\right)+\sqrt{{\displaystyle \frac{\mathrm{Sln}2+\ln \left(\frac{1}{\delta }\right)}{2n_{tr}}}},$$

(13)

with

$$S\lesssim S_{\mathrm{h}\mathrm{d}}+ \underset{sparse indices}{\underbrace{s{\mathrm{l}\mathrm{o}\mathrm{g}}_2({\displaystyle \frac{e d_{\mathrm{e}\mathrm{f}\mathrm{f}}}{s}})}} +\underset{\mathrm{I}\mathrm{N}\mathrm{T}b values}{\underbrace{sb}}$$

(14)

where $s$ is the number of nonzero after pruning, $d_{\mathrm{e}\mathrm{f}\mathrm{f}}$ is effective dimension after repacking, and $b=8$ for INT8. Hybrid pruning reduces both $s$ and $d_{\mathrm{e}\mathrm{f}\mathrm{f}}$, it effectively tightens the generalization gap in the PAC-Bayes bound, tightening (13) at matched empirical risk.

E. 

Unified Compression–Optimization

For compact citation, we summarize the hybrid pruning objective:

$$\underset{\mathit{\theta ϵS}}{\min }\widehat{L}\left(\theta \right)+\sum _{q\in \{F,L,P\}}{{\lambda }_{\mathrm{q}}\left[{\displaystyle \frac{{\mathrm{R}}_q\left(\theta \right)}{{\mathrm{R}}_{q,max}}}-1\right]}_{+}$$

$$\mathrm{s}.\mathrm{t}. \left({\prod }_k{s}_k\right){\sum }_l{\displaystyle \frac{{\theta }_l\left(r\right)\sqrt{k_l}+\frac{1}{ 2}{\displaystyle {\Delta }_{\mathcal{l}}^{max}}\sqrt{d_{\mathcal{l}}}}{s_l}}{‖x‖}_2+\underset{Repacking}{\underbrace{\eta }}<{\displaystyle \frac{1}{2}}\underset{\_}{\gamma }\hspace{0.25em},$$

(15)

$$\epsilon =\sqrt{{\displaystyle \frac{\mathrm{l}\mathrm{n}(2/\delta )}{2n_{\mathrm{e}\mathrm{f}\mathrm{f}}}}}, p_{{\theta }^{\prime }}\left(y∣x\right)\ge {\displaystyle \frac{1}{1+\left(K-1\right)\exp \left\{-\gamma \left(x\right)+2{\epsilon }_z\right\}}},$$

$$R\left({\theta }^{\prime }\right)\le \widehat{R}\left({\theta }^{\prime }\right)+\sqrt{{\displaystyle \frac{\mathrm{Sln}2+\ln \left(\frac{1}{\delta }\right)}{2n_{tr}}}}.$$

Equation (15) unifies optimization (budgets), invariance (logit stability), statistical reliability (bisection), and generalization (compression), enabling an easy comparison between the baseline and the hybrid model with a single, testable formation.

4. Results

4.1. Baselines

A radar-based foot gesture recognition system using a hybrid pruned lightweight CNN has been developed. CW radar return signals were converted to STFT spectrograms and classified by a CNN whose structure was optimized via pruning. Block-wise structured pruning via NAS followed by magnitude-based unstructured pruning yields compact networks suitable for edge deployment.

To quantify performance, accuracy, precision, recall, and F1-score metrics were computed on the test set. Let TP, TN, FP, and FN denote the numbers of true positives, true negatives, false positives, and false negatives, respectively. The metrics are defined as follows:

$$Accuracy={\displaystyle \frac{(TP+TN)}{(TP+TN+FP+FN)}}$$

(16)

$$Precision={\displaystyle \frac{TP}{(TP+FP)}}$$

(17)

$$Recall={\displaystyle \frac{TP}{\left(TP+FN\right)}}$$

(18)

$$F1 score=2{\displaystyle \frac{Precision\times Recall}{(Precision+Recall)}}$$

(19)

Table 2. Performance–complexity of baseline models (MobileNetV3, MobileNetV2, EfficientNet-B0, and SqueezeNet).

Baseline Models	Acc.	Precision	Recall	F1	FLOPs (M)	Size (MB)
MobileNetV3	0.94	0.943	0.939	0.939	71	5.94
MobileNetV2	0.928	0.931	0.927	0.927	287	2.78
EfficientNet-B0	0.932	0.935	0.932	0.932	27	15.59
SqueezeNet	0.928	0.931	0.927	0.927	287	2.78

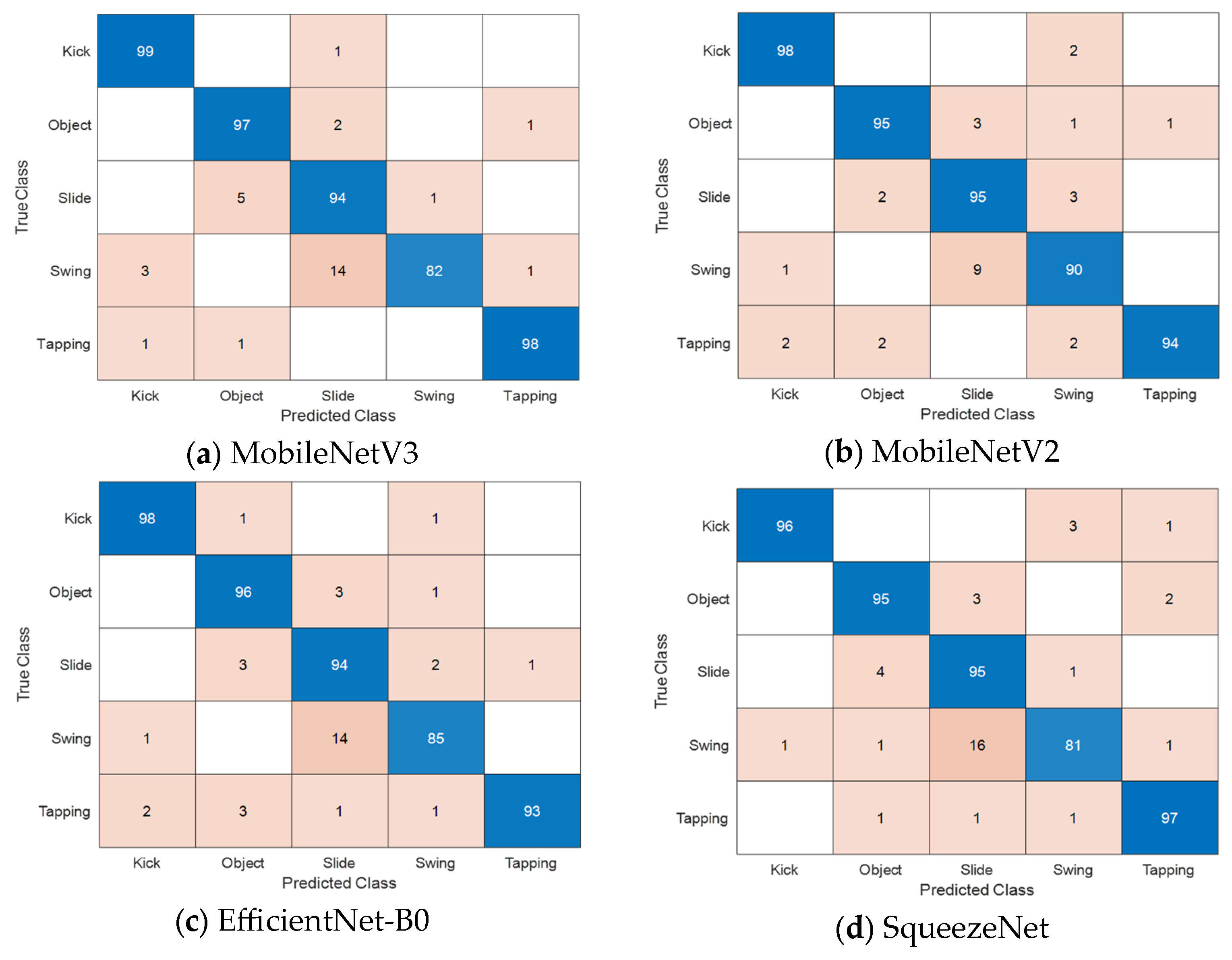
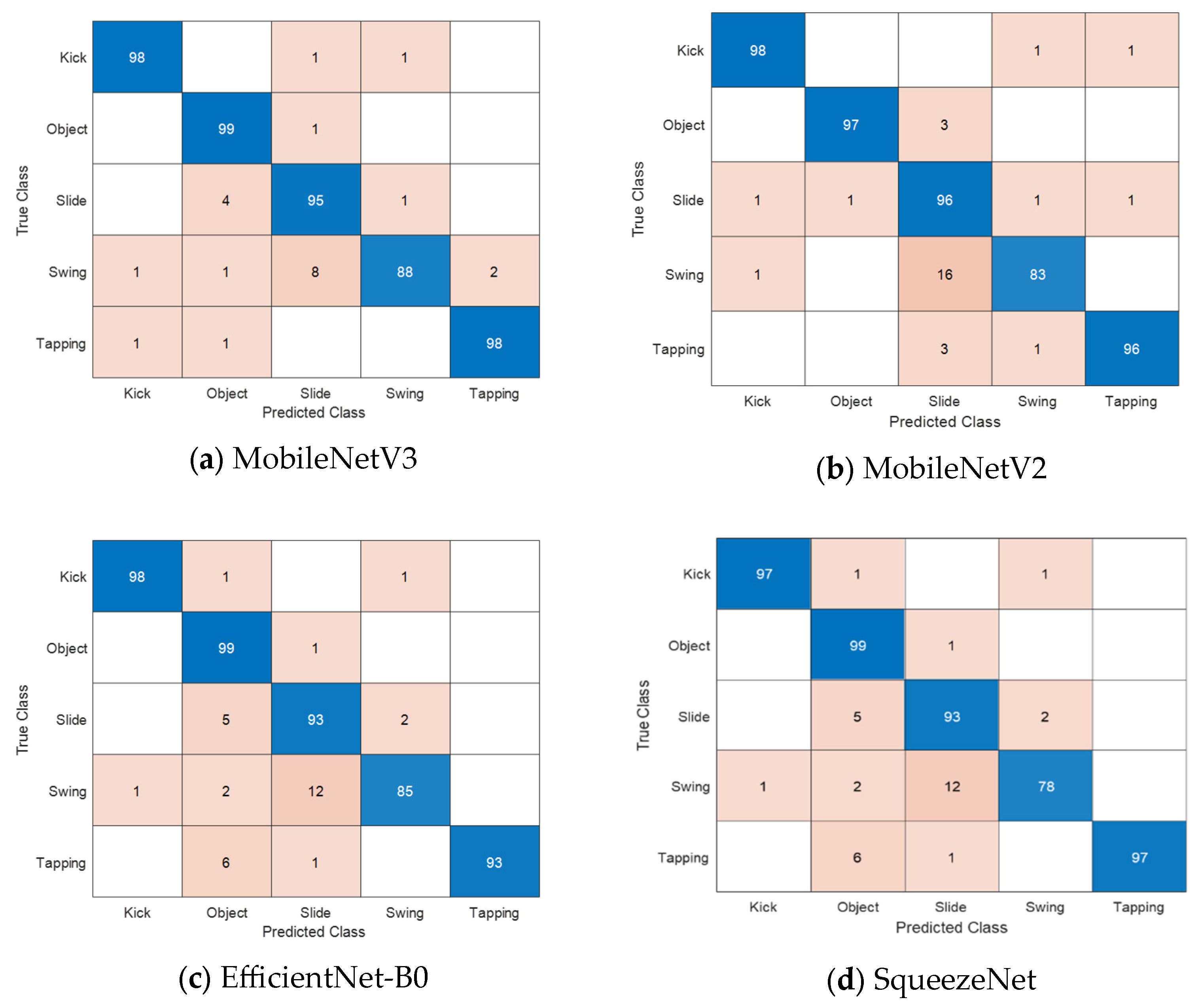
summarizes the baseline recognition accuracy and computational cost (in FLOPs and model parameter count) for four backbone networks-MobileNetV3, MobileNetV2, EfficientNet-B0, and SqueezeNet. These values serve as the reference against which the pruned models will be compared. Figure 4 shows confusion matrices of different foot gestures for mobile baseline networks. Mobile baseline models achieve high recognition accuracy exceeding 93%, but at the cost of substantially larger computational demands, with FLOPs reaching up to 287 million and memory footprints up to 15.59 MB.

4.2. Hybrid Pruning Outcomes

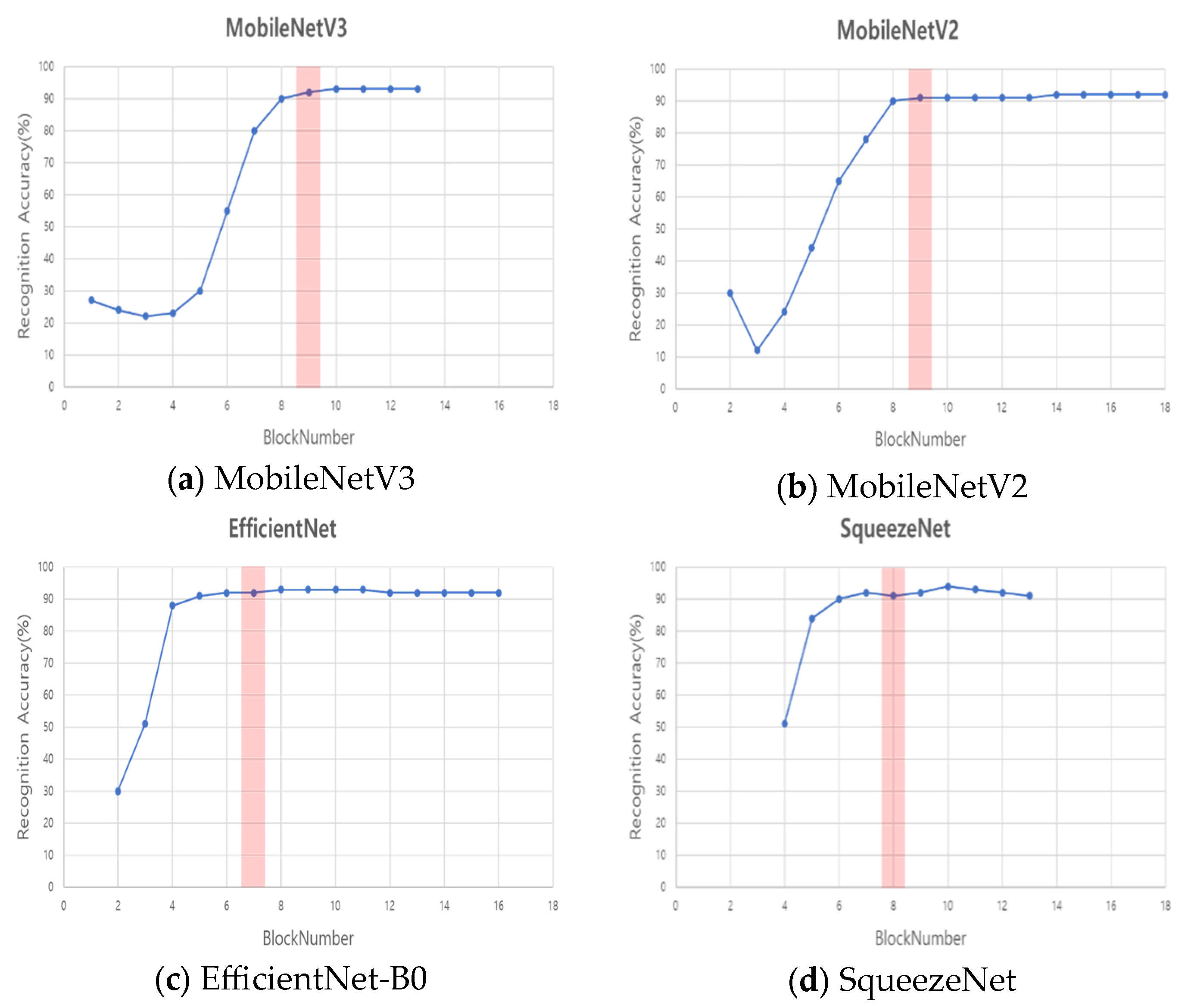
Figure 5 shows recognition performance vs. the kept-block count B for structured pruning (SP) models. The vertical red line marks the block count selected by the bisection-guided NAS defined as $B^{*}=min\left\{B \right| {Acc}_{val}\left(B\right)\ge \tau \}$ and constraints (FLOPs, latency, parameters) are satisfied. Although ${Acc}_{val}\left(B\right)$ is not strictly monotonic due to stochastic variations, the pass/fail criterion $Acc\ge \tau$ behaves as a quasi-monotone predicate after batch normalization re-estimation and short fine-tuning. At each bisection step, midpoint B is evaluated using 1–3 epochs of fine-tuning on 10–30% of the validation data and repeated twice, and accepted if $Acc> \tau +ϵ$. The search interval continues to shrink until the minimum block. This process requires ${log}_{2}N$ evaluations and identifies the “knee” point where further block removal sharply degrades accuracy.

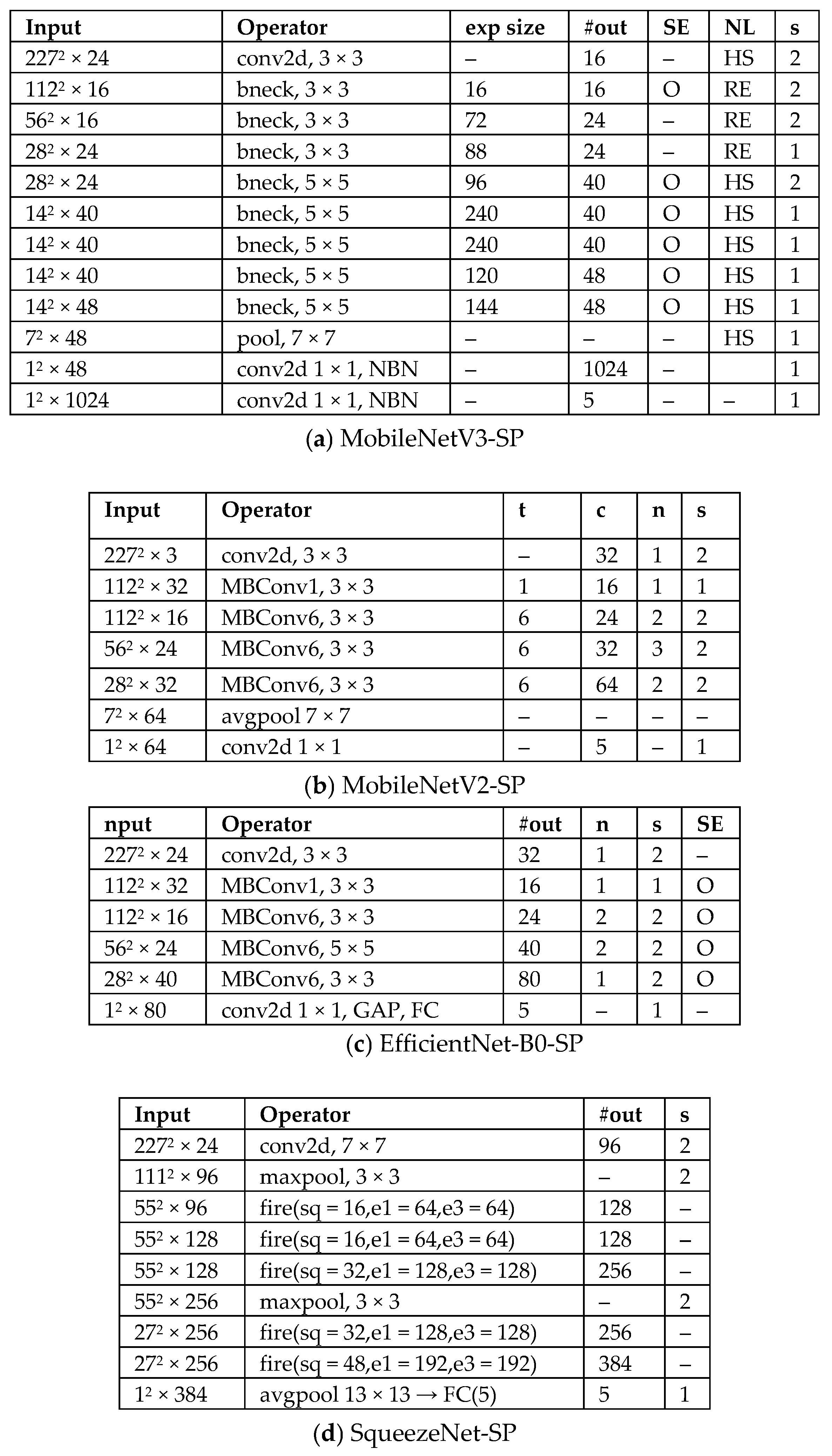
Figure 6 depicts the network reduced architecture selected by the bisection-guided NAS pruning across the baseline backbones. Here, “operator” refers to the layer or block operator type, with kernel size indicated when relevant (e.g., conv2d 3 × 3). The term “conv2d” denotes a standard 2D convolutional layer, while “bneck” stands for an inverted-residual bottleneck block, commonly referred to as MBConv or IRB, characterized by a 1 × 1 expansion, followed by a depthwise convolution with kernel size $k\times k$, and a 1 × 1 projection. “pool” indicates global average pooling (GAP) unless otherwise specified. “NBN” denotes layers where batch normalization is omitted. “exp size” refers to the number of expansion channels within a bottleneck. “#out” indicates the number of output channels for the layer or stage. “SE” designates the use of the Squeeze-and-Excitation module, with “O” indicating presence and “–” indicating absence. “NL” stands for nonlinearity or activation function, where “HS” is hard-swish and “RE” is ReLU. “s” represents stride, with $s=2$ indicating spatial resolution reduction by half. The parameter “t” is the expansion ratio within the bottleneck (distinct from dilation). “c” represents the number of output channels in a stage, and “n” indicates the number of repeated blocks in that stage. This notation concisely specifies variable network configurations produced by NAS-guided pruning while remaining faithful to implementation details.

Table 3. Performance–complexity changes: baseline vs. NAS-pruned models. An upward arrow (↑) denotes an increase, and a downward arrow (↓) denotes a decrease; The rightward arrow (⟶) indicates how the hybrid model changes relative to the baseline model.

Network	Blocks (Baseline)	Acc	$∆$Acc (%p)	$∆$FLOPs (M)	Size (MB)
MobilenetV3-SP	9 (13)	0.942	0.2 ↑	71.1 ⟶ 44.0	1.05
MobilenetV2-SP	9 (18)	0.950	0.6 ↑	373.1 ⟶ 160.1	0.58
EfficientNet B0-SP	7 (15)	0.936	0.4 ↑	27.2 ⟶ 21.5	1.35
SqueezeNet-SP	8 (9)	0.922	0.6 ↓	287.9 ⟶ 170.7	0.47

and Figure 7 show recognition accuracy and structure complexity changes before and after bisection-guided NAS structure pruning models and the confusion matrices of the structure pruned models, respectively. The structured-pruned models achieved recognition performance comparable to the baselines, with substantially reduced size. Table 3 indicates that after structured pruning, the MobileNetV2 model was compressed to 15% of its baseline parameter count and 42.9% of its original FLOPs, while maintaining accuracy above 95%. These results demonstrate that many convolutional blocks in the original networks are redundant for this task.

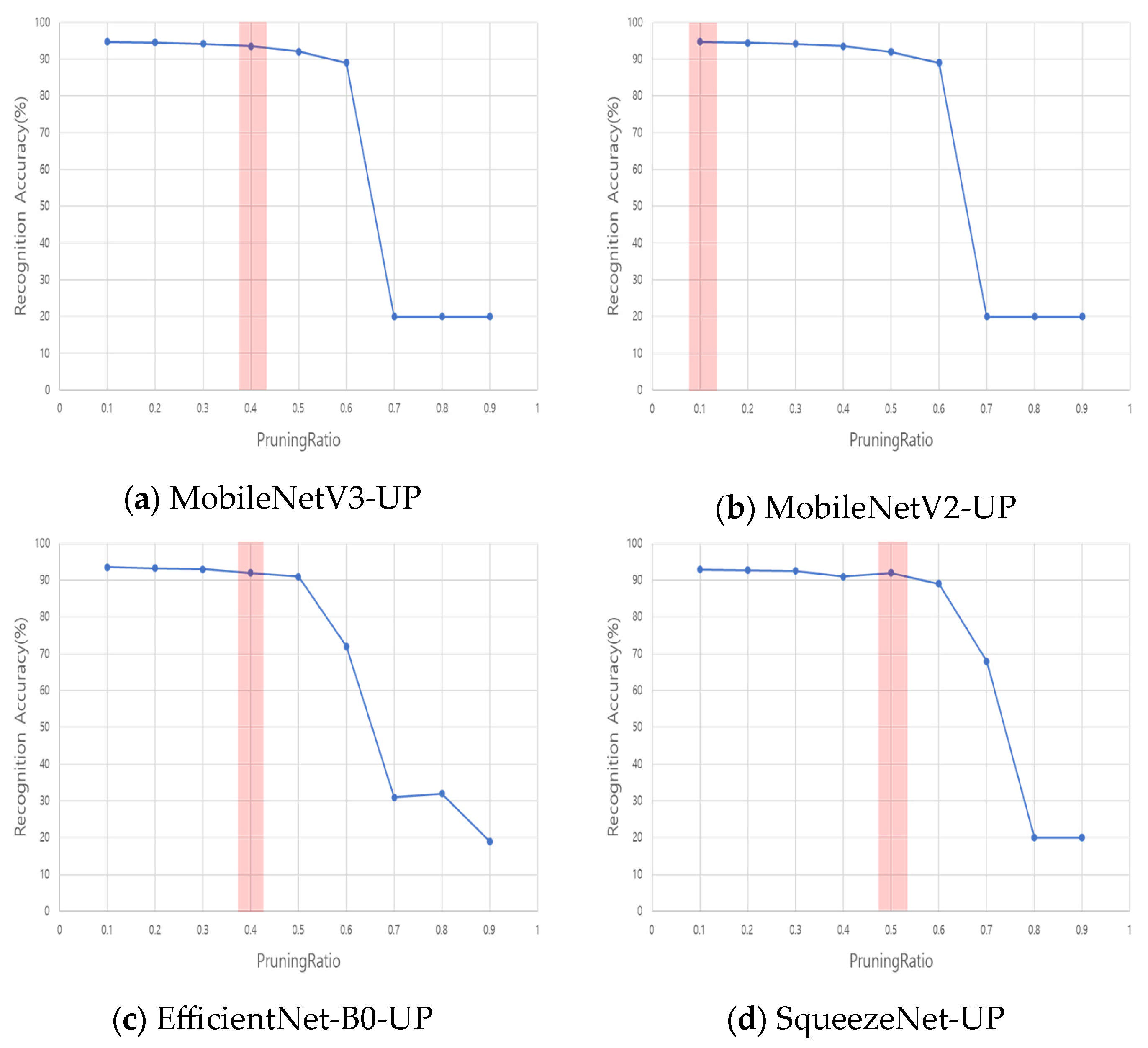
Figure 8 plots validation accuracy against the global unstructured sparsity r for each structured-pruned backbone model. The vertical red line indicates the sparsity r* selected by the bisection rule, $r^{*}=max\left\{ r \in \left[r_{min},r_{max}\right] \right| {Acc}_{val}\left(r\right)\ge \tau \}$, subject to constraints on FLOPs and parameter count. Although ${Acc}_{val}\left(r\right)$ is not strictly monotonic due to stochastic variations, the pass/fail criterion $Acc\left(r\right)> \tau$ behaves as an effective quasi-monotone predicate after batch normalization re-estimation and short fine-tuning. Each midpoint candidate is evaluated with 1–3 epochs on 10–30% of the validation data, repeated twice, and accepted if $Acc\left(r\right)> \tau +ϵ$. The selected sparsity r* typically lies near the knee point, where further sparsity induces a steep drop in accuracy. Following pruning, channel repacking converts the fine-grained sparsity into structural channel removals, improving latency on dense kernels without altering r*. Revalidation is performed after repacking to ensure accuracy remains within the target margin.

4.3. Cross-Backbone Summary

We evaluate four backbones—MobileNetV3, MobileNetV2, EfficientNet-B0, and SqueezeNet—under four regimes: baseline, unstructured pruning + INT8 quantization (UP+Q), structured pruning (SP), and the proposed hybrid approach integrating SP, UP, and quantization (SP+UP+Q). Baselines models deliver high accuracy but come with large FLOPs and parameter footprints.

Table 4. Comparisons of Baselines, Structured Pruning (SP), Unstructured Pruning (UP+Q), and Hybrid Pruning (SP+UP+Q).

Baseline	Acc.	Recall	F1	Sparsity	FLOPs (M)	Size (MB)
MobileNetV3	0.94	0.939	0.939	0	71	5.94
-UP-	0.944	0.944	0.943	0.7	71	4.42
-SP	0.942	0.942	0.941	0	44	1.05
-Hybrid	0.948	0.948	0.956	0.4	44	1.02
MobileNetV2	0.944	0.944	0.944	0	373	8.74
-UP-	0.928	0.927	0.929	0.3	373	6.50
-SP-	0.95	0.95	0.950	0	160	0.58
-Hybrid	0.936	0.936	0.936	0.1	160	0.48
EfficientNet-B0	0.932	0.932	0.932	0	27	15.59
-UP-	0.946	0.946	0.946	0.8	27	15.59
-SP-	0.936	0.935	0.936	0	21	1.35
-Hybrid	0.934	0.934	0.934	0.4	21	1.20
SqueezeNet	0.928	0.927	0.927	0	287	2.78
-UP-	0.93	0.93	0.93	0.8	287	2.48
-SP-	0.922	0.922	0.922	0	170	0.47
-Hybrid	0.922	0.921	0.921	0.5	170	0.47

compares the accuracy and computational complexity of different models, while Figure 9 presents confusion matrices for the hybrid (SP+UP+Q) models. Compared to unpruned baselines, the unstructured pruning with quantization (UP+Q) primarily reduces parameter memory with negligible changes in FLOPs. In contrast, structured pruning (SP) achieves significant reductions in computation with either neutral or slightly improved accuracy. The hybrid pruning approach attains the best accuracy–efficiency trade-off across diverse backbone architectures.

For instance, in the most pronounced case of MobileNetV2, the parameter count decreases from 4.37 million to 0.58 million (approximately 15% of the baseline), and FLOPs reduce from 373.1 million to 160.1 million (42.9% of the baseline), while accuracy increases from 94.4% to 95.0%, reflecting a +0.6-percentage point gain. Similar trends are observed for MobileNetV3 (38% FLOPs reduction, 65% parameter reduction, +0.2 pp accuracy), and EfficientNet-B0 (21% FLOPs reduction, 83% parameter reduction, +0.4 pp accuracy). SqueezeNet exhibits decreases by 41% in FLOPs and 66% in parameters with a slight accuracy loss of 0.6 percentage points.

Applying UP+Q approximately halves parameter memory, while keeping FLOPs largely unchanged, with accuracy deviations within ±0.3 percentage points. The hybrid method yields the best accuracy–efficiency tradeoff across all backbones. Additionally, the bisection-guided NAS controller reduces search evaluations from $N$ to $\lceil {\mathrm{l}\mathrm{o}\mathrm{g}}_{2}N\rceil$ (e.g., 13 → 4, 18 → 5), cutting search time by ~60–70% without compromising final accuracy. Overall, these results substantiate the contribution: hybrid pruning delivers compact, low-latency radar foot gesture models suitable for edge deployment while preserving recognition performance, and bisection-guided NAS efficiently reduces repeated training overhead.

Table 5. CPU hours before/after applying the hybrid pruning (per baseline). The down arrow (↓) indicates a reduction.

Model	Train CPU-h (Base)	Train CPU-h (Hybrid)	Search CPU-h (Bisection)	Total CPU-h (Hybrid)	Training Cost Saving (%)
MobileNetV3	0.00682	0.00422	0.00092	0.00514	24.7 ↓
MobileNetV2	0.03581	0.01537	0.00602	0.02139	40.3 ↓
EfficientNet-B0	0.00261	0.00206	0.00035	0.00241	7.6 ↓
SqueezeNet	0.02764	0.01639	0.00371	0.02010	27.3 ↓

shows the CPU-hours before and after applying the proposed hybrid pruning to each baseline, measured on an Intel Core i5-13600K. With bisection-guided NAS, the search evaluation count drops, yielding up to ~70% lower search cost. When search and training are combined, the total CPU-hours decrease by 7.6–40.3% (largest on MobileNetV2), in line with the 21–57% FLOPs reductions delivered by structured pruning. The time savings are therefore driven primarily by computation cuts rather than accuracy changes.

Table 6. End-to-End inference latency on the target edge platform. The down arrow (↓) indicates a reduction.

Baseline–Hybrid Model Pairs	Latency Baseline (ms)	Latency Hybrid (ms)	Latency Saving (%)
MobileNetV3-V3-hybrid	592.5	366.7	38.1 ↓
MobileNetV2-V2-hybrid	3108.8	1334.2	57.1 ↓
EfficientNet-B0-B0-hybrid	226.5	179.2	20.9 ↓
SqueezeNet-SQ-hybrid	2399.2	1422.5	40.7 ↓

presents the end-to-end inference latency measured on the target edge platform. Under fixed hardware and batch size, latency scales approximately linearly with FLOPs; accordingly, the hybrid models achieve latency reductions proportional to their computational savings, with the largest improvement observed in MobileNetV2 (≈57%). On an ARM Cortex-M4–class MCU executing INT8 kernels at typical clock rates, CNNs with 227 × 227 input dimensions execute within several hundred milliseconds to a few seconds, depending on backbone complexity. The weights-only memory footprints of the hybrid models are approximately 1.05 MB (MobileNetV3), 0.58 MB (MobileNetV2), 1.35 MB (EfficientNet-B0), and 0.47 MB (SqueezeNet). Note that peak SRAM usage also includes activation maps and temporary buffers. These results confirm that hybrid pruning achieves meaningful latency reductions on resource-constrained hardware, satisfying several sub-second inference on MCU-class devices.

5. Discussion

5.1. Limitations

The proposed system employs a single 24 GHz continuous-wave (CW) Doppler radar that produces 227 × 227 short-time Fourier transform (STFT) spectrograms. Because a single CW channel captures only the radial velocity component, lateral or oblique foot motions yield weak Doppler returns, making sensing coverage highly dependent on radar placement and foot trajectory. Extending to multi-input multi-output (MIMO) or multi-view radar configurations could alleviate self-occlusion and enrich angular and range diversity, thereby improving spatial robustness.

From a data perspective, this study uses a single in-house dataset of 3500 spectrograms representing four-foot gestures plus an Object (negative) class, all collected indoors at indoor site. The use of random holdout splits may overestimate generalization compared with more rigorous subject-disjoint or session-disjoint evaluation. Broader validation, encompassing multi-site data acquisition, cross-device replication, and subject-wise partitioning, is needed for a more representative robustness assessment.

In the compression pipeline, unstructured pruning applies a global L1-norm threshold followed by linear 8-bit quantization based on global min–max scaling. This approach can suffer from layer-wise scale mismatch and outlier sensitivity. Adopting per-channel quantization with calibration on representative data would enhance numerical stability and reduce accuracy fluctuations. Structured pruning identifies a semi-optimal knee in the block–accuracy trade-off curve; however, the precise knee position may vary with dataset and backbone architecture. Reporting confidence intervals and performing multiple experimental runs are therefore necessary to confirm statistical reliability.

Our experiments were restricted to backbone networks capable of end-to-end training on CPU-class hardware, which constrained this study to lightweight CNN architectures. Consequently, more computationally demanding models such as Temporal Convolutional Networks (TCNs) and Vision Transformers (ViTs) were not included. This limitation arises from the training environment rather than the proposed pruning method itself. To address this, future work will involve (i) migrating the training process to GPU or cluster environments with mixed precision support, (ii) integrating one-shot or supernet-based search and training-free proxy methods to save NAS search costs, (iii) applying knowledge distillation or low-rank adapters to stabilize compression of TCN and ViT models, and (iv) incorporating advanced pruning techniques such as head/channel pruning and token sparsification combined with channel repacking. These improvements will enable controlled comparisons with contemporary architecture while maintaining the stringent edge-deployment accuracy and latency requirements.

5.2. Robustness

Spectro-temporal radar signatures are influenced by footwear type and material, floor surface, stance, and moving speed. Class-dependent variations in bandwidth and spectral asymmetry reveal sensitivity to these physical factors. To enhance robustness, future models should be incorporated:

• Physics-aware data augmentation—including time-stretching, Doppler scaling, and frequency masking—to simulate diverse kinematic conditions.
• Test-time batch-normalization re-estimation using small unlabeled calibration buffers
• Systematic performance evaluation across deployment distances and horizontal and vertical aspect angles (0.5–2 m).

Architecturally, the block–accuracy curves saturate at moderate network depths (about 7–10 blocks), indicating that high-resolution early stages dominate feature extraction and computation. Hence, pruning strategies should preserve these early layers while compressing later redundant blocks. Reporting confusion matrices and per-class F1-scores would further clarify robustness to viewpoint changes and inter-class similarities, such as swing versus slide.

5.3. Edge Implications

The hybrid compression pipeline (structured pruning followed by unstructured pruning and quantization) yields substantial reductions in computational complexity while preserving accuracy. For instance, MobileNetV2 and MobileNetV3 are compressed to 160.1 M and 44.0 M FLOPs with model sizes of 0.58 MB and 1.05 MB, respectively, achieving accuracies near 95% and 94%. Given latency and energy scale roughly with FLOPs and memory traffic, these compressed models are well-suited for real-time edge devices, significantly reducing DRAM bandwidth pressure—critical for always-on sensing scenarios. The 8-bit parameter quantization halves memory relative to FP16 and facilitates deployment on neural processing units optimized for INT8 operations.

For practical deployment, we recommend (i) hardware-aware latency budgeting by choosing minimal block counts above accuracy thresholds (the accuracy knee point); (ii) implementing calibrated, per-channel INT8 quantization; and (iii) converting fine-grained sparsity into structured representations to exploit dense kernel optimizations. Notably, the framework is backbone-agnostic and applies equally to MobileNetV3/V2, EfficientNet-B0, and SqueezeNet, serving as a general compression wrapper for future radar or multimodal human–computer interaction systems.

5.4. Future Directions

Building on these insights, future research should explore multimodal sensing architectures integrating radar with complementary modalities such as vision or inertial sensors to enhance robustness and contextual awareness. Expanding to richer gesture vocabularies and diverse environmental conditions will further validate generalization. Developing adaptive pruning and quantization schemes that respond dynamically to runtime constraints and device heterogeneity also presents promising avenues. Finally, deploying and benchmarking these models on real-world edge hardware, evaluating latency, energy, and user experience holistically, will concretize their practical utility.

6. Conclusions

We presented a bisection-guided neural architecture search (NAS) hybrid pruning framework for radar-based foot gesture recognition, specifically designed to meet the strict computing power and memory constraints of CPU-class edge deployment. Our approach integrates three complementary techniques—structured pruning, unstructured pruning with quantization, and channel repacking—to minimize model complexity while preserving high recognition accuracy.

In the initial stage, bisection-guided NAS structured pruning determines the minimal number of blocks retained (or equivalently, the maximal safe sparsity) that satisfies a target accuracy under given FLOPs and memory constraints. By leveraging a weight-sharing supernet to define the search space and a binary search strategy to guide exploration, the framework reduces evaluation costs from $N$ to $\lceil {\mathrm{l}\mathrm{o}\mathrm{g}}_{2}N\rceil$, cutting search time by approximately 60–70% compared to traditional iterative pruning, without sacrificing model performance. This results in pruned backbones retaining only the most critical blocks for recognition accuracy.

Subsequently, unstructured pruning applies to a global L1-norm threshold inducing fine-grained sparsity across convolutional and linear layers, followed by INT8 quantization and channel repacking that convert sparsity into structured channel removals. This hybrid compression pipeline effectively eliminates redundant parameters and channels, reducing memory usage and enabling faster inference on dense kernels. Consequently, models exhibit both theoretic reductions in FLOPs and practical decreases in latency on real hardware.

Extensive experiments on four lightweight CNN backbones—MobileNetV3, MobileNetV2, EfficientNet-B0, and SqueezeNet—under various pruning regimes demonstrate that the hybrid method consistently achieves the best accuracy–efficiency trade-off. On average, FLOPs decrease by 21–57% and parameters by 65–87%, with accuracy variation within ±0.6 percentage points (e.g., MobileNetV2 +0.6 pp; SqueezeNet −0.6 pp). MobileNetV2 shows the most notable improvements, compressing to 15% of its original parameters and 42.9% of original FLOPs while improving accuracy from 94.4% to 95.0%. These results confirm the viability of aggressive hybrid pruning for creating compact yet accurate models for continuous-wave radar foot gesture recognition.

The primary contribution of this work is the development of a training-cost-aware compression pipeline. Our low-cost decision protocol uses short fine-tuning (1–3 epochs) with partial validation (10–30% of data, repeated twice) to eliminate the need for costly full retraining cycles typical of NAS methods. Together, these enable compact, highly efficient CNN models for contactless gesture recognition without significant loss of accuracy, enabling real-time operation on resource-constrained hardware. We contribute a unified hybrid-pruning theory that (i) couples training with resource budgets, (ii) guarantees label invariance via a logit-perturbation bound that combines unstructured pruning, INT8 quantization, and channel repacking under a half-margin condition, (iii) provide a decision reliability for bisection with a closed-form tolerance and the corresponding recognition lower bound, and (iv) link compression to generalization through an Occam/PAC-Bayes code-length bound that tightens as nonzero and effective dimension shrink. These results explain why the proposed method preserves accuracy while reducing FLOPs, parameters, and latency, and how to adjust pruning and quantization settings to achieve efficient, deployable edge models.

Beyond empirical validation, this framework offers a generalizable, backbone-agnostic, and hardware-aware methodology for efficient model compression applicable across radar and multimodal sensing systems. Future research will focus on scaling datasets for subject- and session-disjoint evaluation, integrating adaptive quantization for diverse devices, and deploying models on operational edge hardware to assess latency, energy efficiency, and user responsiveness. Further, extending this approach to multimodal sensor fusion promises enhanced robustness and new avenues for human–computer interaction applications.

In summary, the proposed bisection-guided NAS hybrid pruning framework enables real-time, privacy-preserving radar foot gesture recognition with compact models optimized for accuracy and computational efficiency, marking a significant advance toward practical, always-on embedded human–computer interfaces.